Рассчитать балку: Расчёт балки бесплатно онлайн

alexxlab | 31.07.2020 | 0 | Разное

Расчёт балки бесплатно онлайн

Добро пожаловать! Данный онлайн-калькулятор предназначен для расчёта балки и позволит построить эпюры внутренних силовых факторов (изгибающих моментов, поперечных и осевых или продольных сил), рассчитать реакции в опорах. В итоге формируется отчёт с готовым решением. Удачи! 12

Операции Объекты В данном расчёте не задано ни одного закрепления или нагрузки. Для задания нагрузки и закреплений балки перейдите в раздел “Операции”

Расчет балок часть 1 | Онлайн калькулятор

В данном разделе можно выполнить онлайн расчеты статически определимых балок в условиях прямого поперечного изгиба под действием сосредоточенной нагрузки. Расчеты определяют прогиб, угол поворота и изгибающий момент в произвольно заданной точке балки при различных граничных условиях. Определив наибольший изгибающий момент и соответствующее опасное сечение балки легко подобрать его размеры исходя из допускаемых напряжений в сечении.

Исходные данные:

L – длина балки, в миллиметрах;

a – координата точки приложения сосредоточенной нагрузки, в миллиметрах;

X – координата точки нахождения изгибающего момента, угла поворота и прогиба балки, в миллиметрах;

F – нагрузка, в ньютонах;

I_x – момент инерции сечения относительно оси, перпендикулярной действию нагрузки, в метрах ⁴;

Е – модуль упругости материала балки, в паскалях.

Расчет балки # 1.1

Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке консольно закрепленной балки под действием сосредоточенной нагрузки.

Граничные условия:

R_L = 0 – реакция опоры в крайней левой точке;

M_L = 0 – изгибающий момент в крайней левой точке;

θ_R = 0 – угол поворота в крайней правой точке;

Y_R = 0 – прогиб балки в крайней правой точке.

Расчет балки # 2.1

Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c защемленным концом и скользящей опорой под действием сосредоточенной нагрузки.

Граничные условия:

R_L = 0 – реакция опоры в крайней левой точке;

θ_L = 0 – угол поворота в крайней левой точке;

θ_R = 0 – угол поворота в крайней правой точке;

Y_R = 0 – прогиб балки в крайней правой точке.

Расчет балки # 3.1

Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c защемленным концом и шарнирной опорой под действием сосредоточенной нагрузки.

Граничные условия:

М_L = 0 – изгибающий момент в крайней левой точке;

Y_L = 0 – прогиб балки в крайней левой точке;

θ_R = 0 – угол поворота в крайней правой точке;

Y_R = 0 – прогиб балки в крайней правой точке.

Расчет балки # 4.1

Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c защемленными концами под действием сосредоточенной нагрузки.

Граничные условия:

θ_L = 0 – угол поворота в крайней левой точке;

Y_L = 0 – прогиб балки в крайней левой точке;

θ_R = 0 – угол поворота в крайней правой точке;

Y_R = 0 – прогиб балки в крайней правой точке.

Расчет балки # 5.1

Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c шарнирными опорами под действием сосредоточенной нагрузки.

Граничные условия:

М_L = 0 – изгибающий момент в крайней левой точке;

Y_L = 0 – прогиб балки в крайней левой точке;

М_R = 0 – изгибающий момент в крайней правой точке;

Y_R = 0 – прогиб балки в крайней правой точке.

Расчет балки # 6.1

Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c шарнирной и скользящей опорами под действием сосредоточенной нагрузки.

Граничные условия:

R_L = 0 – реакция опоры в крайней левой точке;

θ_L = 0 – угол поворота балки в крайней левой точке;

М_R = 0 – изгибающий момент в крайней правой точке;

Y_R = 0 – прогиб балки в крайней правой точке.

Расчет балки онлайн

Для расчета балок первым делом необходимо определить усилия, возникающие в конструкциях. В данном разделе показано, как находить усилия, опорные реакции, прогибы и углы поворота в различных изгибаемых конструкциях. Для самых распространенных из них вы можете воспользоваться онлайн расчетом. Для редких – приведены все формулы определения необходимых значений.

Онлайн расчет балки на двух опорах (калькулятор).

Приведен расчет на момент, прогиб и опорные реакции от сосредоточенной и распределнной силы.

Синие ячейки – ввод данных. (Белые ячейки – ввод координаты для определения промежуточного итога).

Зеленые ячейки – расчетные, промежуточный итог.

Оранжевые ячейки –  максимальные значения.

>>> Перейти к расчету балки на двух опорах <<<

Онлайн расчет консольной балки (калькулятор).

Приведен расчет на момент, прогиб и опорные реакции от сосредоточенной и распределнной силы.

Синие ячейки – ввод данных. (Белые ячейки – ввод координаты для определения промежуточного итога).

Зеленые ячейки – расчетные, промежуточный итог.

Оранжевые ячейки –  максимальные значения.

>>> Перейти к расчету консольной балки <<<

Расчет однопролетной балки на двух шарнирных опорах.

 

Рис.1 Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке

 

Рис.2 Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках

 

Рис.3 Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке

 

Рис4. Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке

 

 

Рис5. Расчет балки на двух шарнирных опорах при действии изгибающего момента

Расчет балок с жестким защемлением на двух опорах

Рис6. Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке

 

Рис7. Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках

Рис8. Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке

Рис9. Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке

Рис10.Расчет балки с жестким защемлением на опорах при действии изгибающего момента

Расчет консольных балок

Рис11. Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке

Рис12. Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке

Рис13. Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке

Рис14. Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента

Расчет двухпролетных балок

Рис15. Расчет двухпролетной балки с шарнирными опорами при одной сосредоточенной нагрузке

Рис16. Расчет двухпролетной балки с шарнирными опорами при одной равномерно-распределенной нагрузке

Рис17. Расчет двухпролетной  балки с шарнирными опорами при одной неравномерно-распределенной нагрузке

 

 

Расчёт балки, рамы бесплатно онлайн

Лимит расчётов:

Добро пожаловать! Данный онлайн-калькулятор предназначен для расчёта балки или рамы и позволит построить эпюры внутренних силовых факторов (изгибающих моментов, поперечных и осевых или продольных сил), рассчитать реакции в опорах. В итоге формируется отчёт с готовым решением. Удачи!

Онлайн калькулятор для расчета желебобетонных балок перекрытия дома

Далее
Пересчитать

Назначение калькулятора

Калькулятор для расчёта железобетонных балок перекрытий предназначен для определения габаритов, конкретного типа и марки бетона, количества и сечения арматуры, требующихся для достижения балкой максимального показателя выдерживаемой нагрузки.

Соответственно СНиП 2.03.01-84 «Бетонные и железобетонные конструкции» габариты железобетонных балок перекрытия и их устройство подсчитываются по дальнейшим принципам:

• Минимальная высота балки перекрытия должна составлять не меньше 1/20 части длины перекрываемого проёма. К примеру при длине проёма в 5 м минимальная высота балок должна составлять 25 см;
• Ширина железобетонной балки устанавливается по соотношению высоты к ширине в коэффициентах 7:5;
• Армировка балки состоит минимум из 4 арматур – по два прута снизу и сверху. Применяемая арматура должна составлять не меньше 12 мм в диаметре. Нижнюю часть балки можно армировать прутами большего сечения, чем верхнюю;
• Железобетонные балки перекрытия бетонируются без перерывов заливки, одной порцией бетонной смеси, чтобы не было расслоения бетона.

Дистанцию между центрами укладываемых балок определяют длиной блоков и установленной шириной балок. К примеру, длина блока составляет 0,60 м, а ширина балки 0,15. Дистанция между центрами балок будет равна – 0,60+0,15=0,75 м.

Принцип работы

Согласно ГОСТ 26519-85 «Конструкции железобетонные заглублённых помещений с перекрытием балочного типа. Технические условия» формула расчёта полезной нагрузки железобетонных балок перекрытия складывается из следующих характеристик:

• Нормативно-эксплуатационная нагрузка на балки перекрытия с определённым коэффициентным запасом. Для жилых зданий данный показатель нагрузки составляет 151 кг на м2, а коэффициентный запас равен 1,3. Получаемая нагрузка – 151*1,3=196,3 кг/м2;
• Нагрузка от общей массы блоков, которыми закладываются промежутки между балками. Блоки из лёгких материалов, к примеру из пенобетона или газобетона, показатель плотности которых D-500, а толщина 20 см будут нести нагрузку – 500*0,2=100 кг/м2;
• Испытываемая нагрузка от массы армированного каркаса и последующей стяжки. Вес стяжки с толщиной слоя 5 см и показателем плотности 2000 кг на м3 будет образовывать следующую нагрузку – 2000*0,05=100 кг/м2 (масса армировки добавлена в плотность бетонной смеси).

Показатель полезной нагрузки железобетонной балки перекрытия составляется из суммы всех трёх перечисленных показателей – 196,3+100+100=396,3 кг/м2.

Расчёт балки бесплатно онлайн

---

Закрыть

Примечание. Иллюстрации в отчёте сформированы шириной в 420px (диалог “Настройки”).

Исходные данные

L = 10м; q = 12кН/м; M = 15кН·м; F = 19кН.

Рис. 1. Исходная схема

Расчёт

Рис. 2. Схема реакций

Рис. 3. Эпюра Qy, кН (поперечная сила)

Рис. 4. Эпюра Mx, кН·м (изгибающий момент)

1. Определение реакций опор

Составим уравнения статического равновесия.

∑F_y = -q·7м – F + Y_A + Y_B = 0;

∑M_A = -q·7м·3.5м + M – F·10м + Y_B·7м = 0.

Решение уравнений статики даёт следующие значения реакций:

Y_A = 36кН;

Y_B = 67кН.

2. Построение эпюр внутренних силовых факторов

Участок №1 (0 ≤ z₁ ≤ 7м)

Q_y = Y_A – q·z₁;

при z₁ = 0; Q_y = 36кН.

при z₁ = 7м; Q_y = -48кН.

M_x = Y_A·z₁ – q·z₁²/2;

при z₁ = 0; M_x = 0.

при z₁ = 3м; M_x = 54кН·м.

при z₁ = 7м; M_x = -42кН·м.

Участок №2 (0 ≤ z₂ ≤ 3м)

Q_y = F = 19кН.

M_x = M – F·z₂;

при z₂ = 0; M_x = 15кН·м.

при z₂ = 3м; M_x = -42кН·м.

Закрыть

---

Калькулятор отклонения балки

Пример расчета отклонения балки

Для примера расчета прогиба балки рассмотрим простую деревянную скамью с ножками на расстоянии 1,5 метра друг от друга в их центрах. Допустим, у нас есть доска из восточной белой сосны толщиной 4 см и шириной 30 см, которая служит сиденьем для этой скамейки. Мы можем рассматривать это сиденье как балку, которая отклоняется, когда кто-то садится на скамейку. Учитывая размеры этого сиденья, мы можем затем вычислить его момент инерции, как в нашем примере выше.Поскольку нам нужно рассчитать Iₓ, его момент инерции будет:

Iₓ = ширина * высота³ / 12
= 30 * (4³) / 12
= 160,0 см⁴ или 1,6x10⁻⁶ м⁴

Сосна восточная белая имеет модуль упругости 6800 МПа (6,8x10⁹ Па) , что является значением, которое мы получили из Справочника по древесине. Вы также можете легко получить значение модуля упругости для других материалов, таких как сталь и бетон, в Интернете или в местной библиотеке.Теперь, когда мы знаем эти значения, давайте рассмотрим нагрузку, которую будет нести этот стенд. Предположим, что ребенок 400 N сидит в центре скамейки. Теперь мы можем рассчитать прогиб сиденья скамьи из-за точечной нагрузки в его центре:

δₘₐₓ = P * L³ / (48 * E * I)
δₘₐₓ = (400 Н) * (1,5 м) ³ / (48 * 6,8x10⁹ Па * 1,6x10⁻⁶ м⁴)
δₘₐₓ = 0,002585 m = 2,5850 мм

Это означает, что многоместное сиденье прогнется примерно на 2.6 миллиметров от исходного положения, когда ребенок сидит в середине скамейки.

Если вы нашли эту тему интересной и хотели бы узнать больше о прочности материалов, вам также может понравиться наш калькулятор запаса прочности. Вы также можете воспользоваться нашим конвертером силы, если хотите изучить различные единицы измерения точечных нагрузок и расчета сил.

Николас Суонсон и Кеннет Аламбра

.

BEAM (BEAM) Горный калькулятор

Калькулятор горных работ BEAM (BEAM)

BEAM Калькулятор горного дела

Последнее обновление: 54 секунды назад (Нет в списке)

Ср.Последняя цена:	0,00004090 BTC
24ч Ср. Nethash:	421.101 к / с
Текущий Nethash:	418.349 к / с
Рыночная капитализация:	32 893 508 долларов США
Объем:	4 169 823 долл. США
Изменение цены (24 часа):	-0.92%
Самая высокая цена:	0,00004080 BTC
Самая низкая цена запроса:	0.00004100 BTC
ROI:	0

Per	Комиссия пула	Est.Награды	Ред. BTC	Ред. $	Стоимость	Прибыль
Час	0	0,17098018	0.00000698	0,08	0,02 доллара США	0,06 доллара США
День	0	4.10352443	0,00016740	1,95	0,48 доллара США	1,47 $
Неделя	0	28.72467099	0,00117182	13,68	3,36 доллара США	10,32 долл. США
Месяц	0	123.10573281	0,00502208	58,64	14,40 долл. США	44,24 доллара США
Год	0	1497.78641584	0,06110201	713,41	175,20 долл. США	$ 538,21

Обмен	База тикеров	Последняя цена (BTC)	Самая высокая ставка (BTC)	Последняя цена (USD)	Объем USD	Смена 24ч	Последнее обновление
Бит-Z	BEAM-USDT	0.00004097	–	$ 0,4783	$ 1 029 569	-2,92%	85 секунд назад
Бинанс	BEAM-USDT	0.00004097	–	$ 0,4783	$ 996 740	–	88 секунд назад
Бинанс	BEAM-BTC	0.00004090	0,00004080	$ 0,4775	$ 602 438	–	88 секунд назад
Хотбит	BEAM-BTC	0.00004108	0,00004074	$ 0,4796	$ 571 169	–	149 секунд назад
Хотбит	BEAM-USDT	0.00004085	–	0,4770 долл. США	$ 567 284	–	149 секунд назад
Хотбит	BEAM-ETH	0.00004063	–	0,4743 долл. США	402 502 долл. США	–	149 секунд назад
Tradeogre	BEAM-BTC	0.00004047	0,00004047	$ 0,4725	$ 212	–	85 секунд назад
Gate.io	BEAM-ETH	0.00004086	–	0,4770 долл. США	$ 6	-6.96%	67 секунд назад
Gate.io	BEAM-BTC	0.00004050	0,00000000	$ 0,4729	$ 0	-4,16%	67 секунд назад
Graviex	BEAM-BTC	0.00003939	0,00003938	$ 0,4599	$ 0	–	12377 секунд назад
Graviex	BEAM-ETH	0.00037760	–	4,4088	$ 0	–	12377 секунд назад
Gate.io	BEAM-USDT	0.00004037	–	$ 0,4713	$ 0	-4,26%	67 секунд назад
Graviex	BEAM-USDT	0.00013712	–	1,60 долл. США 10	$ 0	–	12377 секунд назад

График сложности за последние 24 часа

График цен за последние 24 часа

.

Beam нагрузки – Поддержка калькулятор Force

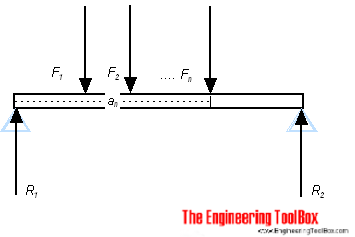
Online Force Support Beam Calculator

Калькулятор ниже может быть использована для расчета сил поддержки – R ₁ и R ₂ – для балок с до 6 несимметричных нагрузок.

Длина балки (м, фут)

Усилие F1 (Н, фунт _f ) расстояние от R ₁ (м, фут)

Усилие F2 (Н, фунт _{) f} ) расстояние от ₁ (м, фут)

Сила F3 (Н, фунт _f ) расстояние от ₁ (м, фут)

Сила F4 ( Н, фунт _f ) расстояние от ₁ (м, фут)

Сила F5 (Н, фунт _f ) расстояние от ₁ (м, фут)

Сила F6 (Н, фунт _f ) расстояние от R ₁ (м, фут)

Для балансирующей балки, нагруженной грузами (или другими нагрузочными силами), силы реакции – R – на опорах равно , сила нагрузки – F . Баланс сил может быть выражен как

F ₁ + F ₂ + …. + F _n = ₁ + R ₂ (1)

где

F = сила от нагрузки (Н, фунт _f )

R = сила от опоры (Н, фунт _f )

Дополнительно для балки в балансе алгебраическая сумма моментов равно нулю .Баланс момента может быть выражен как

F ₁ a _f1 + F ₂ a _f2 + …. + F _n a _fn = R a _r1 + R a _r2 (2)

, где

a = расстояние от силы до общей точки отсчета – обычно расстояние до одной из опор (м, фут)

Пример – A балка с двумя симметричными нагрузками

A 10 м длинная балка с двумя опорами нагружена двумя равными и симметричными нагрузками F ₁ и F ₂ , каждая 500 кг .Опорные силы F ₃ и F ₄ можно вычислить

(500 кг) (9,81 м / с ² ) + (500 кг) (9,81 м / с ² ) = R ₁ + R ₂

=>

R ₁ + R ₂ = 9810 N

= 9,8 кН

Примечание! Нагрузка от веса груза – м. – мг Ньютона – где г = 9.81 м / с ² .

При симметричных и равных нагрузках опорные силы также будут симметричными и равными. Используя

R ₁ = R ₂

, приведенное выше уравнение можно упростить до

R ₁ = _{R0 = (9810 N) / 2}

= 4905 N

= 4,9 кН

Связанные мобильные приложения из Engineering ToolBox

– бесплатные приложения для автономного использования на мобильных устройствах.

Пример – Балка с двумя несимметричными нагрузками

A 10 м длинная балка с двумя опорами нагружена двумя нагрузками, 500 кг расположен 1 м от конца ( R ₁ ) , а другой груз 1000 кг расположен 6 м с того же конца. Баланс сил можно выразить как

(500 кг) (9,81 м / с ² ) + (1000 кг) (9,81 м / с ² ) = ₁ + ₂ рэнд

=>

R ₁ + R ₂ = 14715 N

= 14.7 кН

Алгебраическая сумма моментов (2) может быть выражена как

(500 кг) (9,81 м / с ² ) (1 м) + (1000 кг) (9,81 м / с ² ) (6 м) =? R ₁ (0 м) + R ₂ (10 м)

=>

R ₂ = 6377 (N)

= 6,4 кН

F ₃ можно рассчитать как:

R ₁ = (14715 Н) – (6377 Н)

= 8338 N

= 8.3 кН

Вставьте балки в вашу модель Sketchup с помощью Engineering ToolBox Sketchup Extension

.

Определение уравнений поперечной силы и изгибающего момента балки с опорой

Рассчитайте реакции на опорах балки

 1. Балка находится в равновесии, когда она неподвижна относительно инерциальной системы отсчета. Следующие условия выполняются, когда балка, на которую действует система сил и моментов, находится в равновесии: 
  ΣF  x  = 0:  P  1  * cos (45) + H  A  = 0 
  ΣM  A  = 0:  Сумма моментов относительно точки A равна нулю: 
 - P  1  * sin (45) * 2 + q  1  * 3.5 * (2 - 3,5 / 2) - P  2  * 4,5 + M  1  + R  B  * 7 = 0 
  ΣM  B  = 0:  Сумма моментов относительно точки B равна ноль: 
 - P  1  * sin (45) * 9 + q  1  * 3,5 * (9 - 3,5 / 2) - R  A  * 7 + P  2  * 2,5 + M  1  = 0 
 2. Решите эту систему уравнений: 
 H  A  = - P  1  * cos (45) = - 5 * 0.7071 = -3,54 (кН) 
 Рассчитайте реакцию опоры ролика относительно точки B: 
 R  B  =  ( P  1  * sin (45) * 2 - q  1  * 3.5 * (2 - 3,5 / 2) + P  2  * 4,5 - M  1  ) / 7  =  ( 5 * sin (45) * 2 - 10 * 3,5 * (2 - 3,5 / 2) + 5 * 4,5 - 10 ) / 7  = 1,55 (кН) 
 Рассчитайте реакцию опоры штифта относительно точки A: 
 R  A  =  ( - P  1  * sin (45) * 9 + q  1  * 3,5 * (9 - 3,5 / 2) + P  2  * 2,5 + M  1  ) / 7  =  ( - 5 * sin (45) * 9 + 10 * 3,5 * (9 - 3,5 / 2) + 5 * 2,5 + 10 ) / 7  = 34,92 (кН) 
 3. Сумма сил равна нулю:  ΣF  y  = 0:  P  1  * sin (45) - q  1  * 3.5 + R  A  - P  2  + R  B  = 5 * sin (45) - 10 * 3,5 + 34,92 - 5 + 1,55 = 0 
 

Нарисуйте схемы балки

Первый пролет балка: 0 ≤ x ₁ <1

 Нагрузки на этот пролет не указаны. 

Второй пролет балки: 1 ≤ x ₂ <3

 Определите уравнения для осевой силы (Н): 
 Н (x  2 ) = - P  1  * cos (45) 
 Н  2  (1) = - 5 * 0,7071 = -3.54 (кН) 
 Н  2  (3) = - 5 * 0,7071 = -3,54 (кН) 
 Определите уравнения для поперечной силы (Q): 
 Q (x  2 ) = P  1  * sin (45) - q  1  * (x  2  - 1) 
 Q  2  (1) = 3,54 * sin (45) - 10 * (1 - 1) = 3,54 (кН) 
 Q  2  (3) = 3,54 * sin (45) - 10 * (3 - 1) = -16,46 (кН) 
 Значение Q на этом пролете, который пересекает горизонтальную ось. Точка пересечения: 
 x = 0,35 
 Определите уравнения для изгибающего момента (M): 
 M (x  2 ) = P  1  * (x  2  - 1) * sin (45) - q  1  * (x  2  - 1)  2 /2 
 M  2  (1) = 5 * (1 - 1) * sin (45) - 10 * (1 - 1)  2 /2 = 0 (кН * м) 
 M  2  (3) = 5 * (3 - 1) * sin (45) - 10 * (3 - 1)  2 /2 = -12.93 (кН * м) 
 
 Локальный экстремум в точке x = 0,35: 
 M  2  (1,35) = 5 * (1,35 - 1) * sin (45) - 10 * (1,35 - 1)  2  / 2 = 0,63 (кН * м) 
 
 

Третий пролет балки: 3 ≤ x ₃ <4,5

 Определите уравнения для осевой силы (Н): 
 Н (x  3 ) = - P  1  * cos (45) + H  A  
 N  3  (3) = - 5 * 0,7071 + 3,54 = 0 (кН) 
 N  3  (4,50) = - 5 * 0,7071 + 3,54 = 0 (кН) 
 Определите уравнения для поперечной силы (Q): 
 Q (x  3 ) = P  1  * sin (45) - q  1  * (x  3  - 1) + R  А  
 Q  3  (3) = 3.54 * sin (45) - 10 * (3 - 1) + 34,92 = 18,45 (кН) 
 Q  3  (4,50) = 3,54 * sin (45) - 10 * (4,5 - 1) + 34,92 = 3,45 (кН ) 
 Определите уравнения для изгибающего момента (M): 
 M (x  3 ) = P  1  * (x  3  - 1) * sin (45) - q  1  * (x  3  - 1)  2 /2 + R  A  * (x  3 -3) 
 M  3  (3) = 5 * (3 - 1) * sin (45) - 10 * (3 - 1)  2 /2 + 34,92 * (3 - 3) = -12,93 (кН * м) 
 M  3  (4,50) = 5 * (4.50 - 1) * sin (45) - 10 * (4,50 - 1)  2 /2 + 34,92 * (4,50 - 3) = 3,50 (кН * м) 
 

Четвертый пролет балки: 4,5 ≤ x ₄ <7,5

 Определите уравнения для осевой силы (Н): 
 Н (x  4 ) = - P  1  * cos (45) + H  A  
 N  4  (4,50) = - 5 * 0,7071 + 3,54 = 0 (кН) 
 Н  4  (7,50) = - 5 * 0,7071 + 3,54 = 0 (кН) 
 Определите уравнения для поперечной силы (Q): 
 Q (x  4  ) = P  1  * sin (45) - q  1  * (4.5 - 1) + R  A  
 Q  4  (4,50) = 3,54 * sin (45) - 10 * (4,5 - 1) + 34,92 = 3,45 (кН) 
 Q  4  (7,50) = 3,54 * sin (45) - 10 * (4,5 - 1) + 34,92 = 3,45 (кН) 
 Определите уравнения для изгибающего момента (M): 
 M (x  4 ) = P  1  * (x  4  - 1) * sin (45) - q  1  * (4,5 - 1) *  [ (x  4  - 4,50) + (4,50 - 1) / 2 ]  + R  A  * (x  4  - 3) 
 M  4  (4,50) = 5 * (4,50 - 1) * sin (45) - 10 * 3.5 * (0 + 1,75) + 34,92 * (4,50 - 3) = 3,50 (кН * м) 
 M  4  (7,50) = 5 * (7,50 - 1) * sin (45) - 10 * 3,5 * (3 + 1,75) + 34,92 * (7,50 - 3) = 13,86 (кН * м) 
 

5-й пролет балки: 7,5 ≤ x ₅ <9

 Определите уравнения для осевой силы (Н): 
 Н (x  5 ) = - P  1  * cos (45) + H  A  - P  2  
 N  5  (7,50) = - 5 * 0,7071 + 3,54 - 5 = 0 (кН) 
 N  5  (9) = - 5 * 0,7071 + 3,54 - 5 = 0 (кН) 
 Определите уравнения для поперечной силы (Q): 
 Q (x  5 ) = P  1  * sin (45 ) - q  1  * (4.5 - 1) + R  A  - P  2  
 Q  5  (7,50) = 3,54 * sin (45) - 10 * (4,5 - 1) + 34,92 - 5 = -1,55 (кН) 
 Q  5  (9) = 3,54 * sin (45) - 10 * (4,5 - 1) + 34,92 - 5 = -1,55 (кН) 
 Определите уравнения для изгибающего момента (M): 
 M (x  5 ) = P  1  * (x  5  - 1) * sin (45) - q  1  * (4,5 - 1) *  [ (x  5  - 4,50) + (4,50 - 1) / 2 ]  + R  A  * (x  5  - 3) - P  2  * (x  5  - 7.5) 
 M  5  (7,50) = 5 * (7,50 - 1) * sin (45) - 10 * 3,5 * (3 + 1,75) + 34,92 * (7,50 - 3) - 5 * (7,50 - 7,5) = 13,86 (кН * м) 
 M  5  (9) = 5 * (9-1) * sin (45) - 10 * 3,5 * (4,50 + 1,75) + 34,92 * (9-3) - 5 * (9 - 7,5) = 11,55 (кН * м) 
 

6-й пролет балки: 9 ≤ x ₆ <10

 Определите уравнения для осевой силы (Н): 
 Н (x  6 ) = - P  1  * cos (45) + H  A  - P  2  
 N  6  (9) = - 5 * 0.7071 + 3,54 - 5 = 0 (кН) 
 Н  6  (10) = - 5 * 0,7071 + 3,54 - 5 = 0 (кН) 
 Определите уравнения для поперечной силы (Q): 
 Q (x  6 ) = P  1  * sin (45) - q  1  * (4,5 - 1) + R  A  - P  2  
 Q  6  (9) = 3,54 * sin (45) - 10 * (4,5 - 1) + 34,92 - 5 = -1,55 (кН) 
 Q  6  (10) = 3,54 * sin (45) - 10 * (4,5 - 1) + 34,92 - 5 = -1,55 (кН) 
 Определите уравнения для изгибающего момента (M): 
 M (x  6 ) = P  1  * (x  6  - 1) * sin (45) - q  1  * (4.5 - 1) *  [ (x  6  - 4,50) + (4,50 - 1) / 2 ]  + R  A  * (x  6  - 3) - P  2  * (x  6  - 7,5) - M  1  
 M  6  (9) = 5 * (9 - 1) * sin (45) - 10 * 3,5 * (4,50 + 1,75) + 34,92 * (9 - 3) - 5 * (9 - 7,5) - 10 = 1,55 (кН * м) 
 M  6  (10) = 5 * (10-1) * sin (45) - 10 * 3,5 * (5,50 + 1,75) + 34,92 * (10 - 3) - 5 * (10 - 7,5) - 10 = 0 (кН * м) 
 

Решено BEAMGURU.COM.