Рассчитать массу стального круга: Калькулятор веса стального круга
alexxlab | 05.09.2021 | 0 | Разное
Рассчитать массу круга стального | ТРАСТ МЕТАЛЛ
Рассчитать массу круга стального
Такие изделия используются в качестве заготовки перед производством фасонного или сортового проката. В зависимости от нормируемых показателей фасонный и сортовой прокат подразделяют на пять категорий. Согласно ГОСТ круг стальной, вес погонного метра которого указан в таблице, используется 2-х основных стандартов: калиброванная круглая сталь (холоднотянутая или холоднокатаная) и горячекатаный. Последний класс позволяет отклониться от стандарта на величину в пределах от +0.8мм до -4.0мм. Они находят применение в качестве заготовок для производства втулок, валов, осей, толкателей, анкеров и прочих деталей техники.
Допустимое отклонение от параметра для класса «А» – от +0.3мм до -0.9мм. Расчет веса круга. Круглая сталь поставляется диаметром: свыше 9 мм – в прутках, до 9 мм – в мотках. Этот параметр для класса «Б» варьируется от +0.6мм до -2.0мм. Расчет массы одного метра круга можно осуществить по формуле: m = Pi*d*d*R/4000.
Рассчитать массу круга
Минимальная партия изделий определяется индивидуально, она зависит от множества факторов, как правило, это 60-300 тонн. Точность самого круга, произведенного непосредственно горячекатаным способом, подразделяется на три класса – А, Б и В, высокой, повышенной и обыкновенной точности. Pi = 3,14 (величина постоянная), m – теоретическая масса 1 п/ м круга (кг), R – плотность стали (измеряется в г/куб.см), d – наружный диаметр (мм). Срок изготовления и поставки варьируются от 15 до 45 дней. Вес стального круга.
Рассчитать массу круга стального
Произведем расчет веса круга стального . Более точный параметр отклонения зависит от класса точности, а так же от самой длины металлического изделия. Теперь вы знаете, как определить вес стального круга. Для обозначения категории к марке стали добавляется номер, например, Ст3пс5 или Ст3сп1. OОО «ТРАСТ МЕТАЛЛ» имеет в наличии на складах круглую горячекатаную сталь высокого качества.
Смотрите также
Рассчитать массу круга
Далее, нажимаете «Рассчитать всю заявку онлайн», и система переведет Вас на страницу, где будут показаны результаты обработки цен поставщиков.
 Для этого…
Для этого…Круг стальной вес рассчитать
Таблица Металлопроката. Таблица расчета веса круга стального. Вес метра погонного квадрата стального. Таблица расчета веса листа стального. Вес, в кг…
Рассчитать вес круга стального калькулятор
При вводе размеров и длин, Вы можете рассчитать вес изделий. Калькулятор работает в онлайн-режиме для оперативного расчета веса, для этого необходимо:…
Рассчитать вес круга стального
Точность самого круга, произведенного непосредственно горячекатаным способом, подразделяется на три класса – А, Б и В, высокой, повышенной и обыкновенной…
Рассчитать вес круга
К каждому типу металлопроката прилагается графическое изображение его среза с отображением в виде букв названия каждой грани, полочки и т.п. От того,…
Калькуляторы стального проката
Калькуляторы стального проката
Калькулятор стальных круговАвто: |
|
|---|---|
| Диаметр D, мм | |
| Длина, м | |
| Результаты: | |
| Масса 1 метра, кг | |
Расчет. |
|
Калькулятор стальных квадратовАвто: |
|
|---|---|
| Размер А, мм | |
| Длина, м | |
| Результаты: | |
| Масса 1 метра, кг | |
Расчет.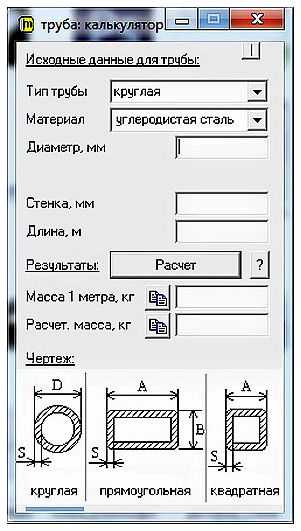 масса, кг масса, кг |
|
Калькуляторстальных шестигранников Авто: |
|
|---|---|
| Размер S, мм | |
| Длина, м | |
| Результаты: | |
| Масса 1 метра, кг | |
Расчет. масса, кг масса, кг |
|
Калькулятор стальныхнеравнополочных уголков Авто: |
|
|---|---|
| Ширина полки А, мм | |
| Ширина полки В, мм | |
| Толщина полки S, мм | |
| Длина, м | |
| Результаты: | |
| Масса 1 метра, кг | |
Расчет. масса, кг масса, кг |
|
Калькулятор стальныхравнополочных уголков Авто: |
|
|---|---|
| Ширина полки А, мм | |
| Толщина полки S, мм | |
| Длина, м | |
| Результаты: | |
| Масса 1 метра, кг | |
Расчет. масса, кг масса, кг |
|
Как рассчитывается масса стальных кругов
Расчет примерной массы стального круга производится согласно формуле: Mкр = L * ρу, где:
- L — длина круга
- ρу — теоретическая масса 1 м круга
Равная произведению плотности материала (справочная согласно ГОСТу) на диаметр круга в миллиметрах.
Как рассчитывается масса стальных квадратов
Расчет примерной массы одного погонного метра квадратного металлопроката определяется по формуле: Mk = L * ρу, где:
- ρу — теоретическая масса 1 м проката квадратного сечения, вычисленная по его номинальным размерам (
- a — сторона квадрата в мм
- L — длина проката квадратного сечения.

Как рассчитывается масса стальных равнополочных уголков
Для расчета массы погонного метра уголков применяется формула: ρу = [(2A-t)·t+(1-π/4)·(r2внутр-2·r2внешн)]·ρ; где:
- t — толщина полок
- А — ширина полки
- ρ — плотность материала
- rвнешн — радиус внешнего закругления полок
- rвнутр — радиус внешнего внутреннего
Так как вес погонного метра уголка является справочной величиной, калькулятор металлопроката в первую очередь сверится с информацией в таблицах ГОСТ, в случае если в справочнике не будет найден уголок нужного вам размера, то вес будет вычислен по приблизительной формуле.
Калькулятор позволяет произвести предварительный расчет массы основных видов металлопродукции, реализуемых компанией «ТД Трубник» со склада в Минске.
С помощью калькулятора стального проката можно рассчитать примерный вес 1 погонного метра продукции и расчетный вес всего объема заказа. Исходя из расчетной массы металлопроката определяется цена, способ погрузки, транспорт, вид резки и монтажа изделия.
Все расчеты в калькуляторе производятся автоматической подстановкой значений диаметра и длины изделия в формулу расчета. Расчет производится на основании справочных величин соответствующих таблиц сортаментов и технических условий ГОСТов на выбранный вид металлопроката.
Перейти к трубному калькулятору
Обращаем ваше внимание на то, что онлайн калькулятор стального проката помогает рассчитать лишь примерную массу продукции. Узнать реальный вес товара, можно при оформлении заказа у менеджера до отгрузки.
X
Оставьте Ваш номер телефона, и мы свяжимся с вами в течение нескольких минут Готово
| jpg” alt=””> | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Copyright Dhiraj Metals |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Видео с вопросами: Определение диаметра сферы по ее массе и плотности
Стенограмма видео
Стальной шарикоподшипник имеет массу 0,034 грамма. Найдите диаметр шарикоподшипника в миллиметрах, округлив до ближайшего миллиметра. Используйте значение 8000 килограммов на кубический метр для плотности стали.
Найдите диаметр шарикоподшипника в миллиметрах, округлив до ближайшего миллиметра. Используйте значение 8000 килограммов на кубический метр для плотности стали.
Итак, этот вопрос касается стального шарикоподшипника. Мы знаем, что он будет иметь сферическую форму, и нас просят найти его диаметр. Обозначим этот неизвестный диаметр как 𝑑. Мы также обозначим массу мяча как 𝑚, и нам сказали, что она равна 0,034 грамма. Еще одна вещь, о которой нам говорят, — это плотность стали, материала, из которого сделан шарикоподшипник. Мы обычно обозначаем плотность символом 𝜌, и нам говорят, что в этом случае плотность имеет значение 8000 килограммов на кубический метр. Мы можем вспомнить, что плотность 𝜌 объекта равна массе объекта 𝑚, деленной на его объем 𝑉. Мы также можем вспомнить, что объем 𝑉 сферы равен четырем третям, умноженным на 𝜋, умноженному на куб радиуса сферы 𝑟.
Теперь, в этом вопросе, мы на самом деле не пытаемся вычислить значение радиуса, а скорее диаметр сферы, которую мы пометили как 𝑑.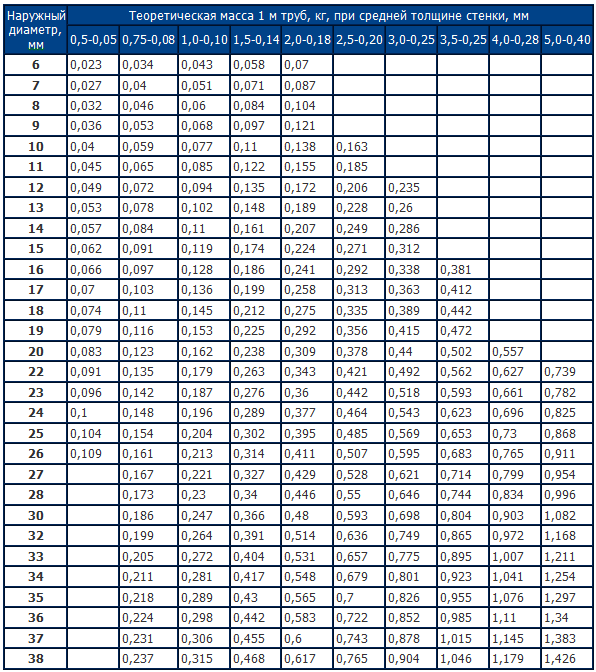 Радиус 𝑟 — это расстояние от центра сферы до края, а диаметр 𝑑 — это расстояние по всей сфере от одной стороны до другой, проходящей через центр сферы. Значит, диаметр 𝑑 равен радиусу 𝑟, умноженному на два. Или, если мы разделим обе части этого уравнения на два, то в правой части двойки сокращаются, и мы получим, что радиус 𝑟 равен диаметру 𝑑, деленному на два.
Радиус 𝑟 — это расстояние от центра сферы до края, а диаметр 𝑑 — это расстояние по всей сфере от одной стороны до другой, проходящей через центр сферы. Значит, диаметр 𝑑 равен радиусу 𝑟, умноженному на два. Или, если мы разделим обе части этого уравнения на два, то в правой части двойки сокращаются, и мы получим, что радиус 𝑟 равен диаметру 𝑑, деленному на два.
Мы можем использовать эту связь между радиусом и диаметром, чтобы заменить радиус 𝑟 в этом уравнении для объема сферы. Заменив 𝑟 на 𝑑 на два, мы получим, что 𝑉 равно четырем третям, умноженным на 𝜋, умноженному на куб 𝑑 на два. Мы также можем записать это как четыре трети, умноженные на 𝜋, умноженные на 𝑑 в кубе на восемь. Или, если мы умножим вместе три и восемь в знаменателе, это даст нам 24. Итак, у нас есть дробь от четырех, деленная на 24, что упрощается до единицы, деленной на шесть. Итак, мы имеем, что объем 𝑉 сферы равен одной шестой, умноженной на 𝜋, умноженной на куб диаметра сферы. Мы можем использовать это уравнение вместе с этим здесь для плотности 𝜌, чтобы решить нашу проблему.
Если мы изменим это уравнение плотности, чтобы сделать 𝑉 предметом, то мы можем использовать наши значения массы 𝑚 и плотности 𝜌 шарикоподшипника, чтобы вычислить его объем. Затем, как только мы рассчитали этот объем, мы можем изменить это другое уравнение для объема сферы, чтобы сделать диаметр 𝑑 предметом. Затем, подставив в наше расчетное значение объем 𝑉, мы сможем определить диаметр 𝑑, что и требуется в вопросе. Одна трудность, с которой мы здесь столкнемся, связана с единицами величин. Нас просят найти диаметр в миллиметрах, нам дают массу в граммах и плотность в килограммах на кубический метр.
Давайте начнем с преобразования массы 𝑚 в единицы килограммов, чтобы она соответствовала единицам плотности 𝜌. Напомним, что один килограмм равен 1000 граммов. Разделив обе части на 1000 и сократив 1000 в правой части, мы получим, что один грамм равен одной тысячной килограмма. Итак, чтобы перевести из граммов в килограммы, нам нужно разделить значение на 1000. Когда мы делим значение массы шарикоподшипника в граммах на 1000, мы получаем результат 0,000034 килограмма.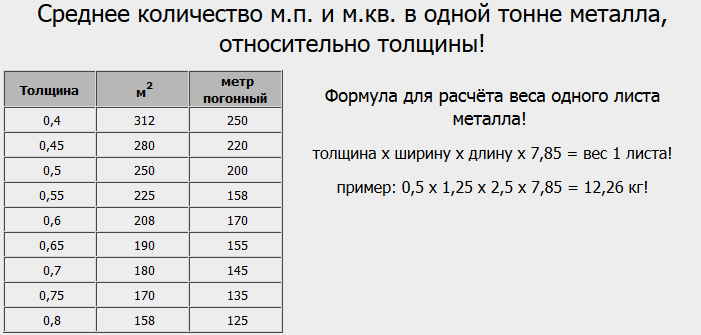 Мы могли бы также записать это значение в экспоненциальной записи как 3,4 умножить на 10 с минус пятью килограммами, где у нас есть степень минус пять, потому что нам пришлось переместить десятичную точку на пять знаков, чтобы превратить это значение в 3,4.
Мы могли бы также записать это значение в экспоненциальной записи как 3,4 умножить на 10 с минус пятью килограммами, где у нас есть степень минус пять, потому что нам пришлось переместить десятичную точку на пять знаков, чтобы превратить это значение в 3,4.
Теперь, когда у нас есть масса 𝑚 в килограммах, соответствующая нашей плотности в килограммах на кубический метр, мы можем использовать эти значения в этом уравнении для расчета объема сферы 𝑉. Однако сначала нам нужно сделать 𝑉 предметом уравнения. Для этого мы сначала умножим обе части уравнения на 𝑉. В правой части 𝑉 в числителе сокращается с 𝑉 в знаменателе. Итак, мы получили объем 𝑉, умноженный на плотность 𝜌, что равно массе 𝑚. Теперь разделим обе части уравнения на плотность 𝜌. Два 𝜌 с левой стороны компенсируют друг друга. И мы приходим к уравнению, которое говорит, что объем 𝑉 равен массе 𝑚, деленной на плотность 𝜌.
Если мы подставим наши значения 𝑚 и 𝜌 для стального шарикоподшипника в правую часть этого уравнения, то получим, что объем сферы 𝑉 равен 3,4 умножить на 10 минус пять килограммов, деленных на 8000 килограммов на кубический метр. Что касается единиц измерения, то килограммы в числителе и знаменателе компенсируют друг друга. И это оставляет единицу, деленную на единицу, на метры в кубе или просто единицы метров в кубе. Когда мы оцениваем выражение, мы вычисляем результат 4,25 умножить на 10 с отрицательными девятью метрами в кубе. И это значение является объемом стального шарикоподшипника.
Что касается единиц измерения, то килограммы в числителе и знаменателе компенсируют друг друга. И это оставляет единицу, деленную на единицу, на метры в кубе или просто единицы метров в кубе. Когда мы оцениваем выражение, мы вычисляем результат 4,25 умножить на 10 с отрицательными девятью метрами в кубе. И это значение является объемом стального шарикоподшипника.
Теперь, когда у нас есть значение объема 𝑉, мы хотим использовать это значение в этом уравнении для расчета диаметра шарикоподшипника. Итак, давайте изменим уравнение, чтобы диаметр 𝑑 стал предметом. Мы начнем с умножения обеих частей уравнения на шесть, разделенных на 𝜋. В правой части шестерки и 𝜋 в числителе и знаменателе компенсируют друг друга. И у нас есть шесть умноженных на 𝑉, деленное на 𝜋, равно 𝑑 в кубе. Если мы затем возьмем кубический корень с обеих сторон, то справа кубический корень из 𝑑 в кубе будет просто равен 𝑑. Наконец, переписав уравнение наоборот, мы получим, что диаметр 𝑑 равен кубическому корню из шестикратного объема 𝑉, деленному на 𝜋.
Теперь мы готовы подставить наше значение объема 𝑉 шарикоподшипника в это уравнение. Когда мы это сделаем, мы получим вот это выражение для его диаметра 𝑑. Вычисление выражения внутри кубического корня дает результат 8,1169 умножить на 10 с отрицательными девятью метрами в кубе, где эллипсы показывают, что есть дополнительные десятичные знаки. Затем, оценивая кубический корень, мы получаем диаметр 𝑑 2,0097 и так далее, умноженный на 10 с точностью до минус трех метров. Обратите внимание, что поскольку объем 𝑉 был выражен в кубических метрах, у нас есть диаметр 𝑑 в метрах.
Однако нас просят дать ответ в миллиметрах. Напомним, что один метр равен 1000 миллиметрам, или, что эквивалентно, один метр равен 10 трем миллиметрам. Итак, чтобы перевести метры в миллиметры, мы просто умножаем на 10 в степени три. Если мы возьмем наше значение диаметра 𝑑 в метрах и умножим его на 10 в степени три, то мы получим 10 в отрицательной тройке, умноженное на 10 в тройке, и это просто равно единице.


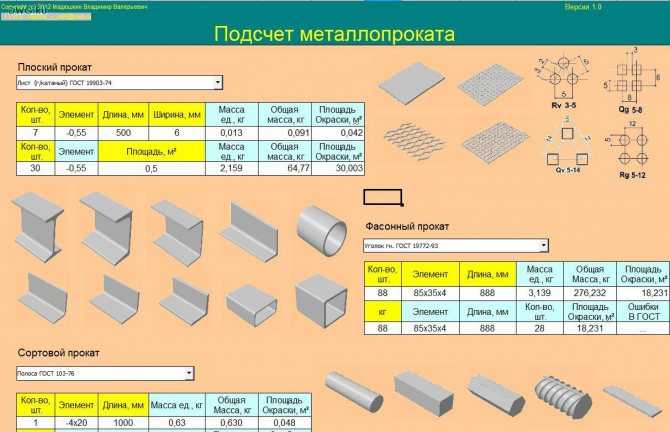 Толщина (мм) X 0,0248 = Вес. За метр.
Толщина (мм) X 0,0248 = Вес. За метр.  За метр.
За метр. 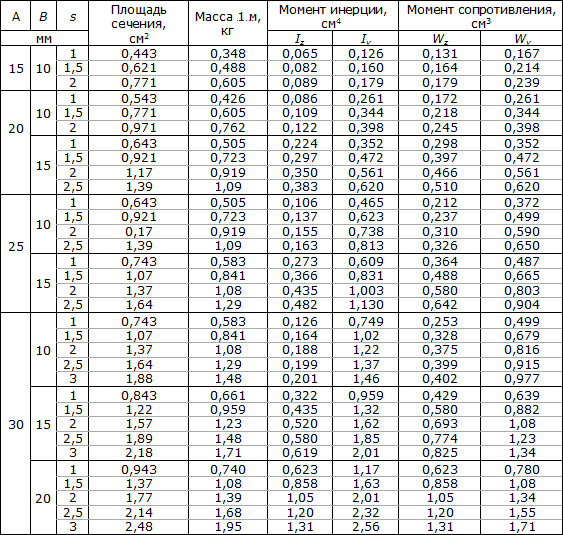 За метр.
За метр.  Пер
ПК
Пер
ПК 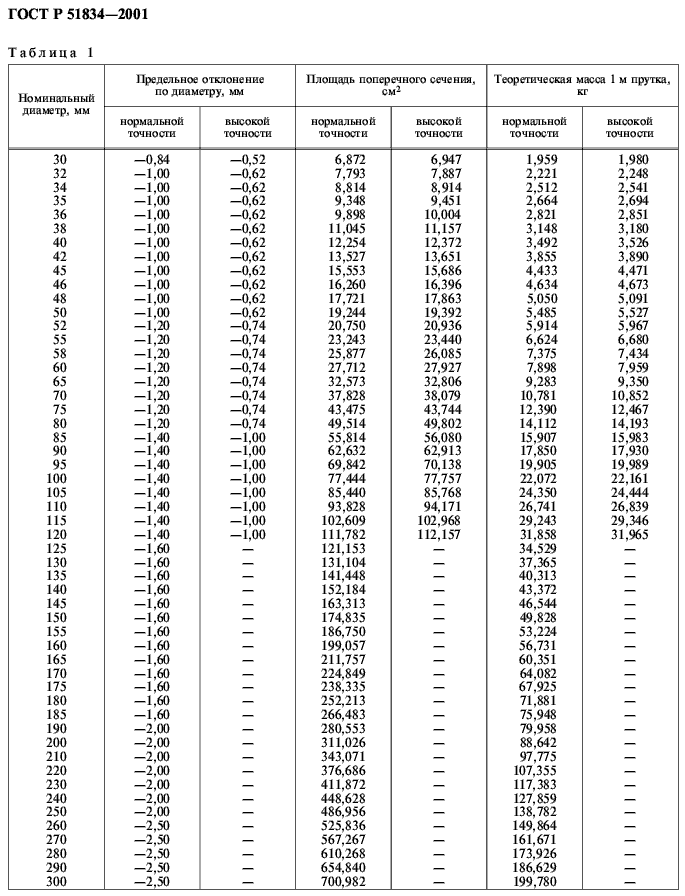 За метр.
За метр. ) X Толщина (мм) 2,69 = Вес. На ПК
) X Толщина (мм) 2,69 = Вес. На ПК дюйм.
дюйм.