Равнобокий уголок: ГОСТ 8509-93 Сортамент уголков стальных равнополочных
alexxlab | 08.06.1985 | 0 | Разное
Уголок равнобокий 2200 х 30 х 30 мм, массив сосны
Скорее всего в вашем браузере отключён JavaScript.
Вы должны включить JavaScript в вашем браузере, чтобы использовать все возможности этого сайта.
МО, г. Одинцово
- Доставка по России
- МО, г. Одинцово г. Одинцово, ул. Восточная, 19 Как добраться
- МО, г.

- Москва, г. Щербинка г. Щербинка, ул. Восточная, д. 8 Как добраться
- Казань Советский район, проспект Альберта Камалеева, д. 44 Как добраться
- Краснодар ул.
 Шоссе Нефтяников, д. 40 Как добраться
Шоссе Нефтяников, д. 40 Как добраться - Ростов-на-Дону ул.Малиновского, д.23 Д Как добраться
- Пермь Индустриальный район, ул. 2-я Казанцевская, д. 11 Как добраться
- Воронеж пр.
 Патриотов, д. 45г Как добраться
Патриотов, д. 45г Как добраться - Нижний Новгород ул. Бетанкура, д. 1 ТРЦ “Седьмое небо” Как добраться
- Челябинск ул. Труда, д. 203, ТРК Родник Как добраться
- Екатеринбург ул.

- Саратов Вольский тракт, д.2, ТЦ “Happy Молл” Как добраться
- Оренбург Шарлыкское ш., д. 1, молл “Армада” Как добраться
Поделиться
Добавить отзыв
Код товара: 209676
Уголок равнобокий 2200 х 30 х 30 мм, массив сосны
Нет в наличии
Отзывов пока нет
Вы можете первым добавить отзыв об этом товаре
* Словосочетание «лучшая цена» используется на сайте www. castorama.ru для обозначения товаров с самой низкой ценой среди товаров этой же категории, представленных на сайте www.castorama.ru в выбранном магазине.
castorama.ru для обозначения товаров с самой низкой ценой среди товаров этой же категории, представленных на сайте www.castorama.ru в выбранном магазине.
Все цены указаны в рублях с учетом НДС. Цена товара не включает в себя стоимость аксессуаров и оснастки, если это специально не оговорено. Товары могут незначительно отличаться от изображения на сайте.
Наличие и цена товара в гипермаркетах Вашего города могут отличаться от указанных на сайте. Подробную информацию о характеристиках товаров, их наличии и стоимости уточняйте по телефонам, указанным на сайте www.castorama.ru.
Гипермаркеты Касторама оставляют за собой право в любое время изменять стоимость товаров, указанных в каталоге на сайте.
Цена товара, указанная за квадратный метр, предоставляется исключительно для ознакомления. Соответствующий товар реализуется только упаковками.
Условия использования сайта
Получать новости и спецпредложения
Cогласен на обработку моих персональных данных
Сортамент равнополочных уголков: виды, характеристики, ГОСТ
Довольно распространенным металлопрокатом можно назвать уголки равнополочные. При их изготовлении применяются стандарты, установленные в ГОСТ. За счет этого продукция представлена унифицированными видами. Рассматривая сортамент равнополочных уголков, следует учитывать тот момент, что вес и размеры имеют значение для проведения точных расчетов при разработке проектной или технической документации. Распространение материала можно связать с его исключительными эксплуатационными качествами, о чем далее поговорим подробнее.
При их изготовлении применяются стандарты, установленные в ГОСТ. За счет этого продукция представлена унифицированными видами. Рассматривая сортамент равнополочных уголков, следует учитывать тот момент, что вес и размеры имеют значение для проведения точных расчетов при разработке проектной или технической документации. Распространение материала можно связать с его исключительными эксплуатационными качествами, о чем далее поговорим подробнее.
Уголки равнополочные
Содержание
Основные характеристики
В технической документации можно встретить самую различную информацию, которая может применяться при расчетах. Применяемая таблица позволяет определить нижеприведенные характеристики:
- Масса одного погонного метра. Вес уголка равнополочного учитывается при расчете того, какая будет оказываться нагрузка на создаваемую конструкцию. Вес стального уголка во многом зависит от размеров и типа применяемого материала при изготовлении. Плотность применяемого металла может варьироваться в достаточно большом диапазоне.

- Основные размеры. Уголок размеры может иметь самые различные. Они учитываются при расчетах. Размеры металлического уголка могут варьироваться в достаточно большом диапазоне, так как применяются при создании различных конструкций.
- Профиль металлического равнополочного материала может иметь самую различную площадь поперечного сечения. Этот параметр также указывает на то, какая будет оказываться нагрузка.
- Чертеж и другая техническая информация также содержит информацию о том, какой радиус закругления у профиля. Этот показатель не является контролируемым параметром, но применяется для калибровки изделия. Сортамент уголков стальных горячекатаных равнополочных может быть представлен материалом, который имеет ровные или разные полки. Неравнополочные варианты исполнения также получили широкое распространение.
- В таблице указывается толщина стенок полок. При увеличении показателя толщины момент сопротивления увеличивается, изделие становится способным выдерживать большую нагрузку.
 Однако, за счет применения большего количества металла вес изделия существенно возрастает.
Однако, за счет применения большего количества металла вес изделия существенно возрастает.
Характеристики уголков по ГОСТ 8509-93
Уголок равнополочный может классифицироваться по показателю точности. Примером назовем следующие группы изделий:
- Обычная точность, маркируемая буквой «В».
- Повышенной точности, маркировка представлена буквой «А».
Показатель толщины полки может иметь отклонение в соответствии с табличными данными.
В нормативной документации также указывает то, какой длины заготовки могут отправляться заказчику. Примером назовем то, что показатель длины должен составлять 3-12 м. При предварительной договоренности может отпускаться материал большей длины.
Виды равнополочных уголков
Равнополочные варианты исполнения на сегодняшний день получили весьма широкое распространение. Выпускаются они в различных вариантах исполнения. Рассматривая виды металлических уголков отметим, что геометрические размеры и классификация изделий регулируется двумя основными нормативными документами:
- Уголок горячекатаный равнополочный получается при применении технологии, которая предусматривает оказание воздействия высокой температуры.
 В качестве нормативной документации применяется ГОСТ 8509-93. За счет применения особой технологии производства получаемое изделие обладает весьма высокими эксплуатационными качествами. Однако, производственный процесс связан с достаточно большим количеством технологических сложностей.
В качестве нормативной документации применяется ГОСТ 8509-93. За счет применения особой технологии производства получаемое изделие обладает весьма высокими эксплуатационными качествами. Однако, производственный процесс связан с достаточно большим количеством технологических сложностей. - Уголок стальной гнутый также получил широкое применение. Для стандартизации основных параметров в этом случае применяется ГОСТ 19771-93. За счет применения технологии холодной гибки существенно ускоряется производственный процесс.
Скачать ГОСТ 19771-93. Уголки стальные гнутые равнополочные. Сортамент.»
Отличительной особенностью равнополочных уголков назовем то, что полки у них имеют одинаковые геометрические размеры. Горячекатаные изделия производятся путем пропуска раскаленной заготовки через валики. При воздействии давления на размягченный сплав формируется геометрическая форма и определенные размеры.
 Стоит учитывать, что в данном случае в качестве заготовки может использоваться исключительно листовой прокат с относительно небольшой толщиной поперечного сечения.
Стоит учитывать, что в данном случае в качестве заготовки может использоваться исключительно листовой прокат с относительно небольшой толщиной поперечного сечения.- Уголок горячекатаный
- Уголок стальной гнутый
Горячекатаные изделия характеризуются следующими достоинствами:
- высокая прочность;
- более сложный профиль.
Гнутые обладают более точными геометрическими размерами, что также определило их распространение. Кроме этого, применение листового металла в качестве сырья позволило существенно снизить вес изделия и расширить сортамент.
- Устойчивость материала к воздействию окружающей среды, к примеру, повышенной влажности.
- Прочность структуры и твердость поверхности.
- Плотность, которая определяет соотношение веса и геометрических размеров.
- Степень обрабатываемости.

При изготовлении равнополочного уголка могут применять следующие металлы:
- Стали повышенной прочности. Они обладают весьма большой прочностью, могут выдерживать существенное механическое воздействие. Стоит учитывать, что для достижения некоторых показателей проводится термическая обработка уже после получения требуемой формы и размеров.
- Легированные металлы с различной концентрацией примесей. За счет включения в состав различных веществ можно существенно изменить эксплуатационные качества изделия. К примеру, повышение концентрации хрома повышает коррозионную стойкость поверхности. При легировании металла учитывается, что получаемые равнополочные материалы должны обладать высокой прочностью.
- Сплавы, которые характеризуются высокой жаропрочностью, жаростойкостью или коррозионной устойчивостью. Некоторые равнополочные варианты исполнения строительных материалов могут применяться в особых эксплуатационных условиях. Для достижения требуемых качеств при их изготовлении могут применять высоколегированные сплавы.

Стальные уголки
Наиболее распространенным металлом, который применяется при производстве равнополочных уголков, является углеродистая сталь. Это связано с ее высокой прочностью и относительно низкой стоимостью, простотой получения.
Размеры уголков
Вопрос размеров был затронут ранее при рассмотрении основных показателей, которые характеризуют уголок стальной. При этом также следует отметить нижеприведенные моменты:
- Указывается вес изделия. Металлический уголки применяются при изготовлении ответственных изделий. Именно поэтому при расчетах учитывается также вес самого материала.
- Основные размеры равнополочного уголка указываются также для разработки проектной документации и подбора наиболее подходящего изделия.
- Уголки стальные равнополочные также характеризуются площадью сечения профиля, шириной полки, радиусом закругления, толщиной стенок. Все эти показатели выдерживаются в качестве стандартов и не указываются производителями, при необходимости их можно найти в справочной документации.

Равнобокий уголок может иметь самые различные размеры. Широкой сортамент позволяет подобрать наиболее подходящий материал для применения в конкретном случае.
Применение стального уголка
Металлы сегодня встречаются практически на каждом шагу. При сочетании легкости и высокой прочности материал стал практически незаменим, применяется при строительстве различных сооружений и механизмов. Стальные уголки могут изготавливаться при применении различных металлов. За счет особой геометрии они могут воспринимать большую нагрузку, чем, к примеру, листовой материал. Прокат угловой или уголок стальной гнутый применяют:
- При строительстве несущих конструкций. Для того чтобы сооружение могло воспринимать большую нагрузку в качестве основного материала может применяться рассматриваемое изделие. Примером можно назвать возведение складских помещений, когда в качестве обшивки применяется легкий листовой металл, который покрывает устойчивый каркас.
 За счет этого существенно снижаются расходы и повышается прочность сооружения.
За счет этого существенно снижаются расходы и повышается прочность сооружения. - В машиностроении и станкостроении. Особая форма определяет высокую жесткость и способность гашения вибрационной нагрузки. Именно поэтому рассматриваемый материал применяется для создания усиливающего каркаса, несущей рамы и других элементов.
Применение равнополочных уголков
Широкая область применения определила то, что в продаже можно встретить уголок с различной формой профиля и размерами.
Государственные стандарты на уголки
Как ранее было отмечено, при производстве применяется система стандартизации основных показателей. К примеру, ГОСТ 8509-93 (уголки стальные горячекатаные равнополочные) определяет геометрические размеры профиля: радиус закругления, толщины полок и другие показатели. Обозначение различных параметров позволяет проводить точные расчеты при проектировании.
Скачать ГОСТ 8509-93 «Уголки стальные горячекатаные равнополочные. Сортамент.»
Госстандарт позволяет:
- Контролировать качество выпускаемой продукции.
 Отклонение от определенных параметров может привести к существенным изменениям эксплуатационных качеств. Именно поэтому все параметры должны контролироваться на момент производства материала.
Отклонение от определенных параметров может привести к существенным изменениям эксплуатационных качеств. Именно поэтому все параметры должны контролироваться на момент производства материала. - Упростить обозначение. Как ранее было отмечено, металлический угол обладает довольно большим количеством геометрических показателей. Для того чтобы не указывать все на проектном чертеже или в маркировке все они должны соответствовать установленным стандартам.
- Быстро найти наиболее подходящий вариант исполнения. Сортамент уголков равнoполочных (ГОСТ 8509-86) включает просто огромное количество различных изделий. Для того чтобы упростить поиск по основным параметрам применяются стандартные методы классификации.
ГОСТ используется для указания более одного десятка параметров. Для определения применяемых обозначений указывается чертеж поперечного сечения.
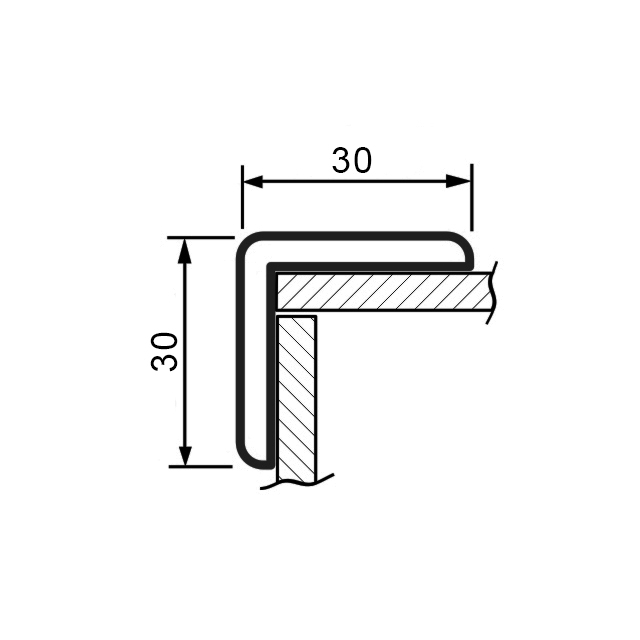
Гнутые равнополочные уголки, как и другие варианты исполнения рассматриваемого материала, имеют собственную таблицу классификации, по которой можно определить основные геометрические размеры и вес.
В заключение отметим, что сегодня приобрести рассматриваемый материал можно практически в любом городе. При этом огромный сортамент позволяет подобрать наиболее подходящее изделие по основным параметрам. На момент приобретения равнополочных уголков следует уделить внимание тому, что на поверхности не должно быть ярко выраженной ржавчины и механических повреждений. Кроме этого, изделие должно выпускать согласно установленным стандартам ГОСТ. Во время погрузки равнополочных уголков должны соблюдаться все установленные нормы, нагрузка равномерно распределяться для исключения вероятности провисания материала и его деформации.
Сортамент. Уголки равнобокие (ГОСТ 8509-86) 004
| ТК СТАЛЬ-ИНТЕКС ТРЕЙД, ООО | ЕВРАЗ МЕТАЛЛ ИНПРОМ, ОАО | ОМЕГА МЕТАЛЛ, ГК | ДИПОС, ГК | МЕТАЛЛО-КОМПЛЕКТ-М, АО | АРИЭЛЬ МЕТАЛЛ, ОАО | А ГРУПП, ООО | МЕТАГОР, ООО | АТОН-СТАЛЬ, ООО | АМГ, ООО | СПЕЦСТАЛЬ-СЕРВИС, ООО |
| 20x20x4,0 мм | ||||||||||
| 25x25x3,0 мм | 43 080 | 46 000 | 47 500 | 48 490 | 44 700 | 46 600 | 47 490 | 42 990 | 44 900 | |
| 25х25х4,0 мм | 43 080 | 45 400 | 45 500 | 45 800 | 45 490 | 45 900 | 46 000 | 47 490 | 43 490 | |
| 32x32x3,0 мм | 43 880 | 46 600 | 45 800 | 48 490 | 46 600 | 46 490 | 44 490 | 44 900 | ||
| 32х32х4,0 мм | 43 380 | 44 800 | 46 000 | 47 500 | 44 990 | 45 700 | 46 000 | 46 490 | 43 490 | |
| 35x35x3,0 мм | 41 580 | 46 000 | 46 000 | 44 490 | 43 990 | |||||
| 35х35х4,0 мм | 45 400 | 46 000 | 43 900 | 44 990 | 46 000 | 44 490 | ||||
| 35×35х5,0 мм | 33 490 | |||||||||
| 40x40x3,0 мм | 45 580 | 46 000 | 46 600 | 47 990 | ||||||
| 40х40х4,0 мм | 43 880 | 44 400 | 44 700 | 44 700 | 43 990 | 44 700 | 44 700 | 45 490 | 44 490 | |
| 40х40х5,0 мм | 46 990 | 43 990 | ||||||||
| 45х45х3,0 мм | 45 000 | 45 000 | ||||||||
| 45х45х4,0 мм | 43 480 | 41 900 | 44 700 | 42 200 | 41 490 | 43 800 | 44 700 | 42 990 | 41 790 | |
| 45х45х5,0 мм | 42 480 | 42 600 | 38 200 | 41 990 | 45 700 | 45 000 | 43 490 | 42 990 | ||
| 50x50x4,0 мм | 41 580 | 41 500 | 42 000 | 44 200 | 42 490 | 42 000 | 42 990 | 41 790 | ||
| 50х50х5,0 мм | 41 580 | 41 900 | 42 500 | 42 000 | 42 700 | 42 490 | 46 000 | 42 000 | 42 990 | 41 490 |
| 63x63x4,0 мм | 43 380 | 42 490 | 45 000 | 43 490 | ||||||
| 63х63х5,0 мм | 43 480 | 41 900 | 42 000 | 42 000 | 42 500 | 42 490 | 44 000 | 42 000 | 43 790 | 42 990 |
| 63х63х6,0 мм | 43 480 | 42 000 | 42 700 | 42 000 | 43 500 | 42 000 | 42 990 | 42 990 | ||
| 70x70x5,0 мм | 42 780 | 42 300 | 45 000 | 45 500 | 44 490 | 45 000 | 46 490 | 44 490 | ||
| 70х70х6,0 мм | 42780 | 44900 | 44490 | 45100 | 45990 | 43490 | ||||
| 70x70x7,0 мм | 45490 | 42490 | ||||||||
| 75х75х5,0 мм | 42680 | 42300 | 42600 | 45200 | 44490 | 44700 | 42600 | 45490 | 42790 | |
| 75х75х6,0 мм | 42680 | 42300 | 42500 | 42300 | 44700 | 44490 | 44300 | 42300 | 44990 | 42790 |
| 75х75х7,0 мм | 42680 | 45000 | 44490 | 45000 | 46990 | 43990 | ||||
| 75х75х8,0 мм | 42680 | 44150 | 44900 | 43990 | 44900 | 44150 | 45990 | 43490 | ||
| 80х80х6,0 мм | 43880 | 42300 | 45600 | 44900 | 45490 | 46000 | 45600 | 45990 | 43490 | |
| 80х80х7,0 мм | 43880 | 45600 | 45600 | 45990 | 42490 | |||||
| 80х80х8,0 мм | 43880 | 45600 | 45200 | 45600 | 44490 | |||||
| 90х90х6,0 мм | 43380 | 42300 | 42300 | 44900 | 44490 | 44200 | 42300 | 42990 | ||
| 90х90х7,0 мм | 42780 | 42300 | 44000 | 42300 | 43500 | 43490 | 45700 | 42300 | 45490 | 42290 |
| 90х90х8,0 мм | 42900 | 45900 | 45490 | 46300 | 45900 | 46490 | 43490 | |||
| 90х90х9,0 мм | 45600 | 42790 | 45600 | |||||||
| 100×100х6,5 мм | 45680 | |||||||||
| 100х100х7,0 мм | 43480 | 42800 | 43500 | 42900 | 47900 | 43990 | 43900 | 42900 | 37990 | |
| 100х100х8,0 мм | 43480 | 42800 | 43500 | 42000 | 44700 | 44990 | 47800 | 42900 | 37990 | |
| 100х100х10,0 мм | 43480 | 42800 | 47700 | 48900 | 48490 | 48900 | 47700 | 44990 | ||
| 100x100x12,0 мм | 38990 | |||||||||
| 110x110x7,0 мм | 43580 | 49500 | 45700 | 49500 | 45990 | |||||
| 110х110х8,0 мм | 43080 | 42900 | 50500 | 49500 | 43990 | |||||
| 125х125х8,0 мм | 43080 | 45300 | 39200 | 49500 | 49500 | 51490 | 45700 | 49500 | 44990 | |
| 125х125х9,0 мм | 43080 | 45300 | 49500 | 48400 | 46000 | 49500 | 44490 | |||
| 125х125х10,0 мм | 43080 | 45300 | 49500 | 48500 | 48990 | 45700 | 49500 | 37990 | ||
| 125х125х12,0 мм | 46990 | 37990 | ||||||||
| 140х140х9,0 мм | 54180 | 53600 | 55000 | 55500 | 54950 | 55000 | 55950 | |||
| 140х140х10,0 мм | 54180 | 53600 | 55000 | 54950 | 55000 | 55950 | ||||
| 140x140x12,0 мм | 55000 | 55000 | ||||||||
| 160х160х10,0 мм | 54180 | 54800 | 55000 | 55500 | 54950 | 55000 | 55950 | 57200 | ||
| 160х160х11,0 мм | ||||||||||
| 160х160х12,0 мм | 52580 | 55000 | 54950 | 55000 | 58200 | 57200 | ||||
| 160х160х14,0 мм | 58200 | |||||||||
| 160x160x16,0 мм | 53580 | 54800 | 54950 | 58200 | 57200 | |||||
| 160x160x20,0 мм | ||||||||||
| 180x180x11,0 мм | 56800 | 57500 | 57200 | 57200 | 57500 | 58200 | ||||
| 180х180х12,0 мм | 57500 | 57500 | 58200 | |||||||
| 180×180х14,0 мм | ||||||||||
| 200х200х12,0 мм | 53580 | 55000 | 54950 | 55000 | 55950 | 54950 | ||||
| 200х200х14,0 мм | 51180 | 54000 | 55000 | 55000 | 55950 | 54950 | ||||
| 200х200х16,0 мм | 51180 | 54000 | 54950 | 55950 | 54950 | |||||
| 200х200х20,0 мм | 55950 | 54950 |
Рейтинг
( 1 оценка, среднее 5 из 5 )
Равнобедренный треугольник – определение, свойства, углы, примеры
Равнобедренные треугольники – это треугольники, у которых по крайней мере две стороны равны. Мы знаем, что треугольники представляют собой трехсторонние замкнутые многоугольники, и они классифицируются как равносторонние, равнобедренные и разносторонние в зависимости от длины их сторон. В этой статье мы узнаем об определении равнобедренного треугольника и его свойствах.
Мы знаем, что треугольники представляют собой трехсторонние замкнутые многоугольники, и они классифицируются как равносторонние, равнобедренные и разносторонние в зависимости от длины их сторон. В этой статье мы узнаем об определении равнобедренного треугольника и его свойствах.
| 1. | Что такое равнобедренный треугольник? |
| 2. | Свойства равнобедренного треугольника |
| 3. | Углы равнобедренного треугольника |
| 4. | Разносторонний равносторонний и равнобедренный треугольник |
| 5. | Часто задаваемые вопросы о равнобедренном треугольнике |
Что такое равнобедренный треугольник?
Равнобедренный треугольник — это треугольник, две стороны которого имеют одинаковую длину. Давайте выполним небольшое задание, чтобы лучше понять это. Возьмите прямоугольный лист бумаги и сложите его пополам. Проведите линию от верхнего загнутого угла к нижнему краю (как показано на рисунке ниже). Когда вы откроете лист, вы увидите треугольник. Отметьте вершины треугольника как O, D и C. Теперь измерьте OD и OC. Повторяйте это упражнение с разными размерами и наблюдайте закономерность. Мы можем заметить, что OD и OC всегда равны. Этот тип треугольника, где две стороны равны, называется равнобедренный треугольник .
Возьмите прямоугольный лист бумаги и сложите его пополам. Проведите линию от верхнего загнутого угла к нижнему краю (как показано на рисунке ниже). Когда вы откроете лист, вы увидите треугольник. Отметьте вершины треугольника как O, D и C. Теперь измерьте OD и OC. Повторяйте это упражнение с разными размерами и наблюдайте закономерность. Мы можем заметить, что OD и OC всегда равны. Этот тип треугольника, где две стороны равны, называется равнобедренный треугольник .
На приведенном выше рисунке △ODC представляет собой равнобедренный треугольник с OD = OC и ∠ODC = ∠OCD. Давайте теперь изучим некоторые свойства равнобедренных треугольников в разделе ниже.
Свойства равнобедренного треугольника
Каждая геометрическая форма имеет некоторые свойства, которые отличают ее от других и делают ее уникальной. Вот список некоторых свойств равнобедренных треугольников:
- Две равные стороны и два равных угла.
- Две равные стороны равнобедренного треугольника называются сторонами , а угол между ними называется углом при вершине или углом при вершине.

- Сторона, противоположная углу при вершине, называется основанием, а углы при основании равны.
- Перпендикуляр из угла при вершине делит пополам основание и угол при вершине.
- Перпендикуляр, проведенный из угла при вершине, делит равнобедренный треугольник на два конгруэнтных треугольника и также известен как его линия симметрии.
Угол равнобедренного треугольника
Как и в любом другом треугольнике, в равнобедренном треугольнике есть три угла, которые в сумме составляют 180 градусов. Из трех внутренних углов углы, кроме угла при вершине, равны по величине. Теорема о равнобедренном треугольнике гласит, что углы, противоположные равным сторонам равнобедренного треугольника, равны по измерению. Итак, в равнобедренном треугольнике △ABC, где AB = AC, имеем ∠B = ∠C.
Если мера равных углов меньше 45 градусов каждый, то угол при вершине будет тупым. Если каждый из равных углов равен ровно 45 градусам, то угол при вершине будет прямым. И, если каждый из равных углов больше 45 градусов и меньше 90 градусов, угол при вершине будет острым углом.
И, если каждый из равных углов больше 45 градусов и меньше 90 градусов, угол при вершине будет острым углом.
Разносторонний равносторонний и равнобедренный треугольник
Три распространенных типа треугольников: разносторонний, равносторонний и равнобедренный. Каждый треугольник отличается от другого своими уникальными свойствами. Разносторонний треугольник — это тот, в котором все три стороны и все три угла имеют разную величину, равносторонний треугольник — это тот, у которого все три стороны и углы равны, а в равнобедренном треугольнике две стороны и два угла равны по величине. Посмотрите на таблицу ниже, чтобы понять различия и сходства разносторонних, равносторонних и равнобедренных треугольников.
| Критерии | Разносторонний треугольник | Равнобедренный треугольник | Равносторонний треугольник |
|---|---|---|---|
| Стороны | Все три стороны разного размера. | По крайней мере две стороны равны по размеру. | Все три стороны имеют одинаковую длину. |
| Уголки | Все три внутренних угла разные. | По крайней мере, два угла равны по величине. | Все три угла равны и равны 60 градусам каждый. |
| Биссектриса | Нет особой связи | Биссектриса, проведенная из вершины угла, делит пополам этот угол и неравную сторону треугольника. | Биссектриса, проведенная из любого угла, делит пополам этот угол и сторону, противоположную ему. |
☛ Статьи по теме
Посмотрите еще несколько интересных статей, связанных с равнобедренным треугольником в математике.
- Калькулятор равнобедренного треугольника
- Формулы для равнобедренных треугольников
- Равнобедренный остроугольный треугольник
- Тупоугольный равнобедренный треугольник
Примеры равнобедренного треугольника
Пример 1: Найдите в данном треугольнике меру BD и площадь треугольника ADB.

Решение:
В равнобедренном треугольнике перпендикуляр из вершины делит основание пополам. Итак, BD = DC = 3 см. В треугольнике ADB основание (b) = 3 см, высота (h) = 4 см. Формула площади треугольника: 1/2 × b × h. Следовательно, площадь треугольника ADB равна 1/2 × 3 × 4 = 3 × 2 = 6 см 2 .
Пример 2: Найдите периметр равнобедренного треугольника, если основание равно 24 дюймам, а равные стороны по 36 дюймов каждая.
Решение:
Мы знаем, что формула периметра равнобедренного треугольника (p) = 2a + b, где a — длина каждой из равных сторон.
Здесь a = 36 дюймов и b = 24 дюйма.
Подставляя значения периметра в формулу равнобедренного треугольника, получаем P = 2(36) + 24 = 96 дюймов.
Следовательно, периметр данного треугольника равен 96 дюймов.Пример 3: Какова площадь равнобедренного треугольника с основанием 8 единиц и боковой стороной 5 единиц?
Решение:
Мы знаем, что формула площади равнобедренного треугольника (A) = b/4[√(4a 2 – b 2 )], где a длина каждого из равные стороны.

Здесь a = 5 единиц и b = 8 единиц.
Подставляя значения в формулу площади равнобедренного треугольника, получаем A = 2√(4 × 25 – 64) = 12 квадратных единиц.
Следовательно, площадь данного треугольника равна 12 квадратных единиц.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Вопросы о равнобедренном треугольнике
перейти на слайдперейти на слайд
Часто задаваемые вопросы о равнобедренном треугольнике
Что такое равнобедренный треугольник?
Треугольник, у которого хотя бы две стороны равны, называется равнобедренным. Следуя этому факту, если две стороны треугольника равны, то и углы, противолежащие этим сторонам, также равны.
Что такое теорема о равнобедренном треугольнике?
Теорема о равнобедренном треугольнике утверждает, что когда две стороны равны, углы при основании также равны. Также верна обратная теорема о равнобедренном треугольнике, которая гласит, что в треугольнике, если два угла равны, то стороны, противоположные этим углам, также равны.
Также верна обратная теорема о равнобедренном треугольнике, которая гласит, что в треугольнике, если два угла равны, то стороны, противоположные этим углам, также равны.
Как узнать, является ли треугольник равнобедренным?
Треугольник может быть разносторонним, равнобедренным или равносторонним, если его классифицировать на основе длины его сторон. В треугольнике, если любые две стороны имеют одинаковую длину, он считается равнобедренным.
Имеют ли равнобедренные треугольники равные углы?
В равнобедренном треугольнике два угла равны. Эти углы лежат против равных сторон. Когда все три угла равны, треугольник называется равносторонним.
Какие углы в равнобедренном треугольнике?
Равнобедренный треугольник имеет угол при вершине и два угла при основании. Углы при основании равнобедренного треугольника равны.
Какой треугольник является прямоугольным равнобедренным треугольником?
В прямоугольном равнобедренном треугольнике равные стороны образуют прямой угол. Другими словами, любой треугольник с углами 90°, 45°, 45° является прямоугольным равнобедренным треугольником. Он содержит свойства как прямоугольных, так и равнобедренных треугольников.
Другими словами, любой треугольник с углами 90°, 45°, 45° является прямоугольным равнобедренным треугольником. Он содержит свойства как прямоугольных, так и равнобедренных треугольников.
Могут ли равнобедренные треугольники быть правильными?
Да, равнобедренные треугольники могут быть прямоугольными, если их три угла равны 90°, 45° и 45° соответственно. В прямоугольном равнобедренном треугольнике равные стороны соединяются, образуя прямой угол, а гипотенуза является неравной стороной.
Как найти площадь равнобедренного треугольника?
Площадь равнобедренного треугольника можно определить по формуле Герона: Площадь (A) = b/4[√(4a 2 – b 2 )], где a — длина равнобедренной стороны, а b является основанием треугольника. Если известны основание и высота/высота треугольника, то площадь равнобедренного треугольника можно найти по формуле A = 1/2 × основание (b) × высота (h) в квадратных единицах.
Каковы свойства равнобедренного треугольника?
Несколько важных свойств равнобедренного треугольника перечислены ниже:
- По крайней мере, две стороны имеют одинаковую длину.

- Углы, противолежащие равным сторонам, равны по размеру.
- Перпендикуляр, проведенный из угла при вершине равнобедренного треугольника, действует как линия симметрии, которая делит треугольник на два конгруэнтных треугольника.
- Перпендикуляр, проведенный из вершины угла, делит пополам этот угол и сторону, противоположную ему.
- Площадь равнобедренного треугольника с использованием длин сторон можно рассчитать по формуле Площадь (A) = b/4[√(4a 2 – b 2 )] квадратных единиц, где a = длина равнобедренного треугольника. сторона, а b = основание треугольника.
- Периметр равнобедренного треугольника равен 2a + b единиц, где a = длина равной стороны, а b = основание треугольника.
Каков периметр равнобедренного треугольника?
Периметр любого треугольника равен сумме всех трех его сторон. Периметр равнобедренного треугольника можно найти по формуле P = 2a + b единиц, где b — основание, а a — длина равной стороны.
Какой угол при вершине равнобедренного треугольника?
Угол при вершине равнобедренного треугольника — это угол, отличный от двух равных сторон. Он соединяет две равные стороны этого треугольника. Угол при вершине также известен как угол при вершине треугольника. Калькулятор равнобедренного треугольника
Калькулятор равнобедренного треугольника – лучший выбор, если вы ищете быстрое решение ваших задач по геометрии. Узнайте площадь равнобедренного треугольника, его периметр, радиус внутренней и описанной окружности, высоты и углы – все в одном месте. Если вы хотите построить конуру, узнать площадь равнобедренного фронтона греческого храма или просто сделать домашнее задание по математике, этот инструмент для вас. Поэкспериментируйте с калькулятором или продолжайте читать, чтобы узнать больше о формулах равнобедренного треугольника.
Поэкспериментируйте с калькулятором или продолжайте читать, чтобы узнать больше о формулах равнобедренного треугольника.
Что такое равнобедренный треугольник?
Равнобедренный треугольник — это треугольник с двумя сторонами одинаковой длины, которые называются катетами. Третья сторона треугольника называется основанием. Угол при вершине — это угол между катетами и углами с основанием, так как одна из их сторон называется углами при основании.
Вот важнейшие свойства равнобедренных треугольников:
- Имеет ось симметрии по высоте вершины;
- Два угла, противоположные катетам, равны по длине; и
- Равнобедренный треугольник может быть остроугольным, прямоугольным или тупоугольным, но зависит только от угла при вершине (углы при основании всегда острые)
Равносторонний треугольник является частным случаем равнобедренного треугольника. Вы можете узнать обо всех возможных типах треугольников в калькуляторе классификации треугольников.
Формулы площади и периметра равнобедренного треугольника
Для расчета площади равнобедренного треугольника можно использовать множество различных формул. Наиболее популярными являются уравнения:
Данная ножка
aи основаниеb:площадь = (1/4) × b × √(4 × a² - b²)Дано
hвысота от вершины и основанияbилиh3высота от двух других вершин и ножкиa:площадь = 0,5 × h × b = 0,5 × h3 × aПри любом угле и катете или основании
площадь = (1/2) × a × b × sin(base_angle) = (1/2) × a² × sin(vertex_angle)
Кроме того, вы можете проверить наш калькулятор площади треугольника, чтобы узнать другие уравнения, которые работают для любого типа треугольника, а не только для равнобедренного.
Чтобы вычислить периметр равнобедренного треугольника, просто сложите все стороны треугольника:
периметр = a + a + b = 2 × a + b
Что такое теорема о равнобедренном треугольнике?
Теорема о равнобедренном треугольнике, также известная как теорема об углах при основании, утверждает, что если две стороны треугольника конгруэнтны, то и углы, противоположные этим сторонам, конгруэнтны .
Также существует обратная теорема, утверждающая, что если два угла треугольника равны, то стороны, противоположные этим углам, равны .
Калькулятор золотого треугольника
Золотой треугольник, который также называют возвышенным треугольником, представляет собой равнобедренный треугольник, в котором катет находится в золотом отношении к основанию:
a/b = φ ~ 1,618
Золотой треугольник обладает некоторыми необычными свойствами:
- Это единственный треугольник с тремя углами в соотношении 2:2:1
- Это форма треугольников, найденных в точках пентаграмм
- Используется для формирования логарифмической спирали
Как найти площадь с помощью этого калькулятора равнобедренного треугольника?
Давайте разберемся, как пользоваться этим инструментом на простом примере. Взгляните на это пошаговое решение:
- Определите первое заданное значение . Предположим, мы хотим проверить свойства золотого треугольника.
 Введите 1,681 дюйма в ногу 9Коробка 0064.
Введите 1,681 дюйма в ногу 9Коробка 0064. - Введите второй известный параметр . Например, возьмем основание, равное 1 дюйму.
- Все остальные параметры рассчитываются в мгновение ока! Например, мы проверили, что периметр равнобедренного треугольника равен 4,236 дюйма, а углы в золотом треугольнике равны 72° и 36° — соотношение действительно равно 2:2:1.
Вы можете использовать этот калькулятор для определения других параметров, чем в примере, но помните, что в общем случае есть два различных равнобедренных треугольника с заданной площадью и другим параметром, например. длина ноги. Наш калькулятор покажет одно из возможных решений.
Часто задаваемые вопросы
Как рассчитать площадь равнобедренного треугольника по катету и основанию?
Чтобы вычислить площадь равнобедренного треугольника с катетом a и основанием b , выполните следующие действия:
Применить теорему Пифагора к найти высоту :
√( a² - b²/4 ).
Примените стандартную формулу площади треугольника , т. е. умножьте основание
bна высоту, найденную в шаге 1, а затем разделите на2.То есть итоговая формула у нас получилась такая:
площадь = ½ × b × √(a² - b²/4)
Как вычислить периметр равнобедренного треугольника по катету и основанию?
Периметр равнобедренного треугольника с катетом a и основанием b вычисляем по формуле периметр = 2 × a + b . В этой формуле используется тот факт, что две стороны равнобедренного треугольника имеют одинаковую длину.
Какова площадь равнобедренного треугольника со стороной 4 и основанием 4?
Ответ: 6,93 . Чтобы получить его, мы можем использовать формулу площадь = ½ × b × √(a² - b²/4) с a = b = 4 .
В качестве альтернативы мы можем заметить, что на самом деле здесь у нас есть равносторонний треугольник : формула are упрощается до площадь = a² × √3 / 4 с a = 4 .
Ханна Памула, докторант
Нога (а)
Основание (b)
Высота от вершины (hb)
Высота от основания (га)
Угол вершины (β)
Угол основания (α)
Площадь и периметр
Периметр аналогично
5 калькуляторы треугольников 🔺
30 60 90 треугольник45 45 90 треугольникПлощадь прямоугольного треугольника… 15 more
Равнобедренные треугольники – GRE Math
Равнобедренные треугольники – GRE Math–>
Все математические ресурсы GRE
13 диагностических тестов 452 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
GRE Math Help » Геометрия » Плоская геометрия » Треугольники » Равнобедренные треугольники
Тупой равнобедренный треугольник, показанный выше, имеет две стороны с длиной и одну сторону с длиной . Длина стороны в дюймах. Длина стороны . Найдите периметр треугольника.
Длина стороны в дюймах. Длина стороны . Найдите периметр треугольника.
Возможные ответы:
дюйма
дюйма
дюйма
дюйма
дюйма
Правильный ответ:
дюйма
7 Объяснение:
Чтобы найти периметр этого треугольника, примените формулу периметра:
Так как, , и , то должно иметь значение:
У этого треугольника две стороны имеют длину в дюймах, а одна сторона в дюймах.
Таким образом, решение:
Сообщить об ошибке
Треугольник имеет две стороны длины и одну сторону длины . Длина бокового двора. Если длина длина стороны , каков периметр треугольника?
Возможные ответы:
Ярд
Ярд
Ярд
Ярд
Ярд
Правильный ответ:
Ярд
Объяснение:
Первый шаг к решению этой задачи состоит в том, что мы должны найти длину длины. Поскольку длина стороны равна 4, выполните следующие действия:
Поскольку длина стороны равна 4, выполните следующие действия:
Теперь применим формулу:
Угол равнобедренного треугольника равен 110°. Какие из следующих углов также могут быть в треугольнике?
Возможные ответы:
90
110
35
20
55
Правильный ответ:
35
Пояснение:
В равнобедренном треугольнике всегда два угла равны. Поскольку других 110 ° быть не может (у треугольника не может быть больше 180 °), два других угла должны быть равны друг другу. 180° – 110° = 70°. 70° представляет собой два других угла, поэтому его нужно разделить на 2, чтобы получить ответ 35°.
Сообщить об ошибке
Равнобедренный треугольник ABC лежит плоско на основании. Учитывая, что угол Возможные ответы: 84 20 12 96 42 507 0
Объяснение: Так как треугольник равнобедренный, а Поскольку Сообщить об ошибке Треугольник ABC IS ISocseles X и Y положительные целые числа A —- x – Y – Y – Y 9000 – Y 9000 – Y 9000 Количество A больше Количество B больше Связь не может быть определена Две величины равны Правильный ответ: Количество B больше Объяснение: Поскольку нам даны выражения для двух конгруэнтных углов равнобедренного треугольника, мы можем приравнять выражения, чтобы увидеть, как x относится к y. Мы получаем, x – 3 = y – 7 –> y = x + 4 Логически, y должно быть большим числом, если для достижения его значения требуется x еще 4 единицы (зная, что они оба положительны). Сообщить об ошибке В равнобедренном треугольнике один тупой угол равен . Чему равен один из других углов? Возможные ответы: Правильный ответ: Пояснение: Мы знаем, что у равнобедренного треугольника две равные стороны и, следовательно, два равных угла напротив этих равных сторон. Поскольку существует один тупой угол в 112 градусов, мы автоматически знаем, что этот угол является вершиной. Если сложить внутренние углы любого треугольника, всегда получится 180 градусов. 180 – 112 = 68 градусов. Таким образом, для двух равных углов остается 68 градусов. Таким образом, каждый угол должен быть равен 34 градусам. Сообщить об ошибке ← Предыдущая 1 2 Следующая → Уведомление об авторских правах 13 Диагностические тесты
452 практических теста
Вопрос дня
Карточки
Учитесь по концепции Треугольник с двумя сторонами равной длины является равнобедренным треугольником. Многие вещи в мире имеют форму равнобедренного треугольника. Некоторые популярные примеры этих треугольников в реальной жизни: Части равнобедренного треугольника 1. Катеты: Две равные стороны равнобедренного треугольника известны как катеты. В треугольнике ABC (данном выше) AB и AC являются двумя катетами равнобедренного треугольника. 2. Основание: Основанием равнобедренного треугольника является третья и неравная сторона. В треугольнике АВС основание равнобедренного треугольника ВС. 3. Угол при вершине: «Угол при вершине» — это угол, образованный двумя равными сторонами равнобедренного треугольника. ∠BAC — угол при вершине равнобедренного треугольника. 4. Углы при основании: «Углы при основании» — это углы, которые опираются на основание равнобедренного треугольника. Вот список некоторых свойств равнобедренных треугольников: В приведенном выше равнобедренном треугольнике два угла ∠B и ∠C, лежащие напротив равных сторон AB и AC, равны друг другу. Как правило, равнобедренные треугольники подразделяются на три различных типа: два его угла равны по измерению. Одним из примеров углов равнобедренного остроугольного треугольника являются 50 °, 50 ° и 80 °. Площадь (A) = ½ × основание (b) × высота (h) Периметр (P) = 2a + основание (b) Здесь «a» относится к длине равных сторон равнобедренного треугольника, а «b» относится к длине третья неравная сторона. Какова высота равнобедренного треугольника с площадью 12 кв.см и основанием 6см? Решение: Площадь Isockeles Triangle = ½ x основание x Высота , т. , т.е. равен периметру равнобедренного треугольника, если равные стороны равны a см каждая, а неравная сторона равна b см? Решение: Периметр равнобедренного треугольника = сумма его сторон Периметр равнобедренного треугольника = (a + a + b) см, т. е. (2a + b) см Решение: Формула периметра равнобедренного треугольника, P = 2a + b Здесь a (стороны) = 24 см и b (основание) = 16 см Следовательно, периметр равнобедренного треугольника , Р = 2(24) + 16 = 64 см. Следовательно, периметр равен 64 см. С SplashLearn есть несколько игр о треугольниках, которые дети могут попробовать. Давайте рассмотрим некоторые из них: Ученикам также может быть сложно запомнить свойства равнобедренных треугольников. Но именно здесь вам потребуется много терпения при обучении вашего ребенка. Позвольте вашему ребенку сиять ярко с SplashLearn . 10 см 5 см 2 см 4 см Правильный ответ: 4 см 21 см 2 45 см 2 90 см 2 180 см 2 Правильный ответ – это: 45 CM 2 Правильный ответ – 45 CM 2 . = ½ x 15 см x 6 см = 45 см 2 Как узнать, является ли треугольник равнобедренным? Треугольник называется равнобедренным, если две его стороны равны. Может ли прямоугольный треугольник быть равнобедренным? Да, прямоугольный или прямоугольный треугольник может быть равнобедренным. В равнобедренном прямоугольном треугольнике 1 прямой угол и 2 других угла равны. Сможете ли вы найти все углы равнобедренного треугольника, если знаете один из равных углов? Да, если мы знаем два равных угла, то мы можем легко вычесть их сумму из 180°, так как сумма всех углов треугольника равна 180°. Какими свойствами обладает равнобедренный треугольник? Площадь равнобедренного треугольника – это пространство, ограниченное сторонами треугольника. Равносторонний треугольник: Треугольник, у которого все три стороны равны. Равнобедренный треугольник: Треугольник, у которого две стороны равны. Разносторонний треугольник: Треугольник, все стороны которого не равны. Равнобедренный треугольник — это треугольник с двумя равными сторонами. Два угла, противолежащие двум равным сторонам, также равны. Предположим, что в треугольнике △ABC, если стороны AB и AC равны, ABC является равнобедренным треугольником с ∠B = ∠C. Полное пространство внутри границы равнобедренного треугольника называется его площадью. В равнобедренном треугольнике площадь легко вычислить, если известны высота и основание треугольника. Произведение половины на основание и высоту равнобедренного треугольника дает площадь равнобедренного треугольника. Площадь Isockeles Triangle дается по формуле, перечисленной ниже: = ½ × основание × высота , , где a, b — стороны равнобедренного треугольника. Для нахождения площади равнобедренного треугольника используются различные формулы. Некоторые из наиболее часто используемых формул для площади равнобедренного треугольника перечислены ниже: треугольника, то высота треугольника также может быть рассчитана по данной формуле: Высота равнобедренного треугольника = √(a 2 − b 2 /4) Площадь равнобедренного треугольника Треугольник (если даны все стороны) = ½[√(a 2 − b 2 /4) × b] где, Чтобы найти площадь равнобедренного треугольника, выполните следующие действия: Шаг 1: Отметьте длину (l) и ширину (b) данного треугольника. Шаг 2: Умножьте значения, полученные на шаге 1, и разделите их на 2. Шаг 3: Полученный результат представляет собой искомую площадь, она измеряется в м 2 Площадь равнобедренного треугольника = ½[√(a 2 − b 2 /4) × b] где, b = основание равнобедренного треугольника равной длины) BD = DC = ½ BC = ½ b (Перпендикуляр от угла при вершине ∠A делит основание BC пополам) Используя теорему Пифагора об ΔABD, a 2 = (b/2) 2 + (AD) 2 AD = Высота равнобедренного треугольника = Известно, что общая формула площади треугольника: Площадь = ½ × b × h Подставив значение высоты, получим Площадь равнобедренного треугольника = ½ [√ (A 2 – B 2 /4) × B] Право для ESOCELES For For For For For For For For For For For For For For For For For For For For For For For For For For For For For For For For For For For For For For For For For Right Triang Прямоугольный треугольник Площадь = ½ × a 2 Вывод: Площадь равнобедренного треугольника 2 Периметр равнобедренного прямоугольного треугольника P = (2+√2)a Вывод: Периметр равнобедренного прямоугольного треугольника равен сумме всех сторон равнобедренного прямоугольного треугольника. Пусть две равные стороны равны и . По теореме Пифагора неравная сторона равна a√2. Периметр Isockeles Правой треугольник = a+a+a√2 Когда даны длина двух сторон и угол между ними, A = ½ × b × c × sin(α) где, Стороны между ними приведены, A = , где Пример 1: Найдите площадь равнобедренного треугольника, сторона которого равна 13 см, а основание равно 24 см. Решение: У нас есть, a = 13 и B = 24. Площадь Isockeles Triangle дается, A = = = 1/2 × 5 × 24 0005 = = 60 см 2 Пример 2: Найдите площадь равнобедренного треугольника с сторона равна 10 см и основание 12 см. Решение: У нас есть, A = 10 и B = 12. Площадь Isockeles Triangle дается, A = = = 1/2 × 8 × 12 . = 48 см 2 Пример 3. Найдите площадь равнобедренного треугольника, сторона которого равна 5 см, а основание равно 6 см. Решение: У нас есть, A = 5 и B = 6. Площадь Isockeles Triangle определяется, A = = = 1/2 × 4 × 70005 = 12 см 2 Пример 4. Решение: Имеем a = 15 и b = 24, Площадь равнобедренного треугольника определяется как Решение: Имеем a = 17 и b = 30.0002 = 1/2 × 8 × 30 = 120 см 2 . Решение: У нас есть, A = 20 и B = 24. Площадь Isockeles Triangle дается, A = = = 1/2 × 16 × 24 0005 = = 1/2 × 16 × 24 0005 . = 192 см 2 Пример 7: Найдите площадь равнобедренного треугольника с равные стороны 25 см и основание 30 см. Решение: У нас есть, A = 25 и B = 30. Площадь Isockeles Triangle дается, A = = = 1/2 × 20 × 300005 . = 300 см 2 Вопрос 1: Какова площадь равнобедренного треугольника? Ответ: Площадь фигуры – это пространство, ограниченное границами фигуры. Итак, площадь равнобедренного треугольника можно определить как пространство, занимаемое равнобедренным треугольником. Вопрос 2: Что вы подразумеваете под равнобедренным треугольником? Ответ: Равнобедренный треугольник можно определить как треугольник, который имеет две равные стороны, также в равнобедренном треугольнике противоположные углы также равны. Некоторые из свойств равнобедренного треугольника: Вопрос 3: Напишите формулу для нахождения площади равнобедренного треугольника. Ответ: Для вычисления площади равнобедренного треугольника используется следующая формула: A = ½ × b × h где b — основание треугольника, Вопрос 4 : Напишите формулу для нахождения периметра равнобедренного треугольника. Ответ: Для вычисления периметра равнобедренного треугольника используется следующая формула: P = 2a + b где, a, b — стороны равнобедренного треугольника. Вопрос 5: Напишите формулу площади равнобедренного прямоугольного треугольника. Ответ: Для расчета площади правого углового треугольника используется следующая формула: a = ½ × A 2 Где A 3 Где A . IS . сторона треугольника, Треугольник состоит из трех сторон, которые образуют три угла друг с другом. Сумма этих углов равна 180°. Существуют различные типы треугольников В этой статье мы сосредоточимся на определении, площади, периметре и некоторых решенных примерах прямоугольного равнобедренного треугольника. Этот треугольник удовлетворяет всем свойствам прямоугольного треугольника и равнобедренного треугольника. Прямоугольный треугольник — это треугольник, в котором один из углов равен ровно 90 градусам, а сумма двух других углов равна еще 90 градусам. Так как сумма всех трех углов равна 180 градусов. Две перпендикулярные стороны прямоугольного треугольника называются катетами, а самая длинная сторона, лежащая напротив прямого угла, называется гипотенузой треугольника. Вам может быть интересно, может ли прямоугольный треугольник быть равнобедренным треугольником? Да, прямоугольный треугольник может быть равнобедренным и разносторонним, но никогда не может быть равносторонним. Равнобедренный треугольник — это треугольник, в котором по крайней мере две стороны равны. Так как две стороны треугольника равны, то и соответствующие углы равны между собой. Равнобедренный прямоугольный треугольник имеет один из углов ровно 90 градусов и две стороны, которые равны друг другу. Поскольку две стороны равны, соответствующий угол равен. Таким образом, в равнобедренном прямоугольном треугольнике две стороны равны, а соответствующие углы равны 45 градусов каждый, что в сумме равно 9.0 градусов. Значит сумма трех углов треугольника будет 180 градусов. Теорема Пифагора — самая важная формула для любого прямоугольного треугольника. Теорема Пифагора утверждает, что квадрат гипотенузы треугольника равен сумме квадратов двух других сторон прямоугольного треугольника. В равнобедренном прямоугольном треугольнике два других катета конгруэнтны, поэтому их длина будет равна «S», а гипотенуза равна «H». Then the formula for isosceles right triangle will be: (Hypotenuse) 2 = (Side) 2 + (Side) 2 H 2 = S 2 + S 2 H 2 = 2S 2 Общая формула для нахождения площади прямоугольного треугольника: (1/2xBxH), где H – высота треугольника, а B является основанием треугольника. В равнобедренном прямоугольном треугольнике длины двух сторон треугольника равны. Предположим, что обе стороны измеряются «S», тогда формулу можно изменить в соответствии с равнобедренным прямоугольным треугольником. 92}{2}\] квадратных единиц. Общая формула для нахождения площади любого данного треугольника представляет собой сумму всех его сторон. Периметр треугольника = X+Y+Z единиц. В равнобедренном прямоугольном треугольнике смежные стороны равны между собой, примем сторону «S» и гипотенузу «H». Таким образом, периметр равнобедренного прямоугольного треугольника будет: ПЕРИМЕТР (P) = H+S+S. Следовательно, периметр равнобедренного прямоугольного треугольника P равен H + 2S единиц. Примеры на равнобедренном прямоугольном треугольнике Вопрос 1. Найдите гипотенузы равнобедренного прямоугольного треугольника со стороной 6 см. Решение: Дано: Длина стороны, S = 6 см Мы знаем, что H 2 = 2S 2 Подставим значение «S» = 28 в H 3 29088 2 H 2 = 2(6) 2 H 2 = 144 H = \[\sqrt{144}\] H = 12 Therefore, H = 12 Следовательно, длина гипотенузы равна 12 см. Вопрос 2. Найдите площадь и периметр равнобедренного прямоугольного треугольника, сторона гипотенузы которого равна 12 см. Решение: Дано: Длина стороны гипотенузы, H = 12 см Мы знаем, что H 2 = 2S 92}{2}\] A = \[\frac{(36\times 2)}{2}\] A = 36 Следовательно, площадь равнобедренного прямоугольного треугольника равна 36 см 2 Периметр равнобедренного прямоугольного треугольника, P = H+ 2S единиц P = 12 + 2\[(6\sqrt{2})\] P = 12 + 12\[\sqrt{2}\] Подставить \[\sqrt{2}\] = 1,414 P = 12 + 12(1,414) P = 12 + 13,14 P=25,14 Следовательно, периметр равнобедренного треугольника равен 25,1 см. Прямоугольный равнобедренный треугольник имеет сходные черты с равнобедренным треугольником. Он имеет один угол, равный 90º, который является прямым углом. Стороны прямоугольного равнобедренного треугольника перпендикулярны друг другу, также известному как основание и высота. Два других угла прямоугольного равнобедренного треугольника соединены и равны 45° каждый. Сумма всех внутренних углов равна 180°. Высота, проведенная под прямым углом, является серединным перпендикуляром к гипотенузе (противоположная сторона). Площадь прямоугольного равнобедренного треугольника определяется как (1/2) × Основание × Высота квадратных единиц. Равнобедренный треугольник — это треугольник, имеющий не менее двух (равных) длин. Если все три стороны равны, треугольник также равен. Равнобедренные треугольники очень полезны для определения неизвестных углов. Очень популярным примером равнобедренного треугольника в реальной жизни является кусок пиццы, пара сережек. Равные стороны равнобедренного треугольника называются катетами. Третий и неравный аспект равнобедренного треугольника известен как основание. Прямоугольный равнобедренный треугольник имеет черты как равнобедренного, так и прямоугольного треугольника. У него две равные стороны, два равных угла и один прямой угол. (Прямой угол может не совпадать с одним из углов или общий угол может превышать 180°.957  целые числа).
целые числа). Все ресурсы GRE Math
Что такое равнобедренный треугольник? – [Определение, факты и примеры]
Что такое равнобедренный треугольник?

Примеры равнобедренного треугольника:
Неравнобедренный треугольник:
Примеры равнобедренного треугольника в реальной жизни:
Части равнобедренного треугольника ∠ABC и ∠ACB — два угла при основании равнобедренного треугольника.
∠ABC и ∠ACB — два угла при основании равнобедренного треугольника. Свойства равнобедренного треугольника
Типы равнобедренных треугольников

Площадь и периметр равнобедренного треугольника
Решенные примеры
Пример 1
 е. 12 = ½ x 6 x Высота
е. 12 = ½ x 6 x Высота Пример 3 треугольник, если основание равно 16 см, а равные стороны по 24 см каждая.
Игры с треугольниками
 Они будут использовать данные атрибуты, чтобы определить правильный треугольник и изучить характеристики треугольника. Учащиеся выбирают правильный ответ из предложенных.
Они будут использовать данные атрибуты, чтобы определить правильный треугольник и изучить характеристики треугольника. Учащиеся выбирают правильный ответ из предложенных. Другие игры
 Эта игра подтолкнет вашего ребенка к мастерству, развивая при этом общие математические способности.
Эта игра подтолкнет вашего ребенка к мастерству, развивая при этом общие математические способности. Практические задачи на Isosceles Triangles
Область Изосколеса Треуууурина = ½ x Базовая высота x. ½ x 5 см x высота… т. е. высота = 4 см. также равны. ∠A = ∠B, BC противоположен ∠A, а AC противоположен углу B. Следовательно, AC = BC в ΔABC. Часто задаваемые вопросы
 Возьмем треугольник, у которого три стороны АВ, ВС и СА. Если хотя бы одно из этих утверждений верно — AB = BC, BC = CA или CA = AB, — то треугольник равнобедренный.
Возьмем треугольник, у которого три стороны АВ, ВС и СА. Если хотя бы одно из этих утверждений верно — AB = BC, BC = CA или CA = AB, — то треугольник равнобедренный. Площадь равнобедренного треугольника – формула, определение, примеры, часто задаваемые вопросы
 Общая формула нахождения площади равнобедренного треугольника определяется как половина произведения основания и высоты треугольника. Помимо этого, для нахождения площади треугольников используются различные формулы. Треугольники классифицируются в зависимости от их сторон, различные типы треугольников в зависимости от сторон приведены ниже:
Общая формула нахождения площади равнобедренного треугольника определяется как половина произведения основания и высоты треугольника. Помимо этого, для нахождения площади треугольников используются различные формулы. Треугольники классифицируются в зависимости от их сторон, различные типы треугольников в зависимости от сторон приведены ниже:
Что такое равнобедренный треугольник?  Равнобедренный треугольник описывается теоремой «Если две стороны треугольника равны, то и угол, противолежащий им, также равен».
Равнобедренный треугольник описывается теоремой «Если две стороны треугольника равны, то и угол, противолежащий им, также равен». PERIMETRESTERSESELES ISOSCELES ISOSCELES. = 2a + b
Высота равнобедренного треугольника (h) = √(a 2 − b 2 /4) 
Формула площади равнобедренного треугольника со сторонами
b = основание равнобедренного треугольника
a = длина двух равных сторон Как найти площадь треугольника Равнобедренный треугольник?

a = длина двух равных сторон
Площадь правой угловой изобленки Triangle
Область Isosceles Triangle Использование Тригонометрия 
= 2a+a√2
= a (2+√2)
= a (2+√2)
b, c — стороны данного треугольника
α — угол между ними
Рельсные примеры на зоне. Равнобедренный треугольник
C – это стороны данного треугольника
α, β – это угол, связанный с ними
 Найдите площадь равнобедренного треугольника, сторона которого равна 15 см, а основание равно 24 см.
Найдите площадь равнобедренного треугольника, сторона которого равна 15 см, а основание равно 24 см.
равные стороны 17 см и основание 30 см. 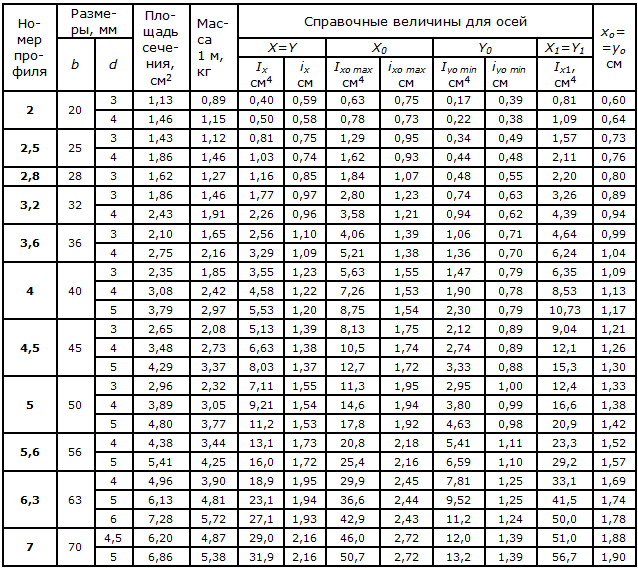
Часто задаваемые вопросы о площади равнобедренного треугольника 
h — высота треугольника.
Связанные статьи
Равнобедренный прямоугольный треугольник – определение и виды
 Прежде чем узнать о равнобедренном прямоугольном треугольнике, давайте рассмотрим свойства прямоугольного и равнобедренного треугольника.
Прежде чем узнать о равнобедренном прямоугольном треугольнике, давайте рассмотрим свойства прямоугольного и равнобедренного треугольника. Прямоугольный треугольник
Равнобедренный треугольник
 Может ли равнобедренный треугольник быть прямоугольным или разносторонним треугольником? Да, равнобедренный может быть прямоугольным и разносторонним треугольником.
Может ли равнобедренный треугольник быть прямоугольным или разносторонним треугольником? Да, равнобедренный может быть прямоугольным и разносторонним треугольником. Определение равнобедренного прямоугольного треугольника
Формула равнобедренного прямоугольного треугольника

Площадь равнобедренного прямоугольного треугольника
Периметр равнобедренного прямоугольного треугольника
 Таким образом, периметр треугольника со стороной X, Y и Z будет равен:
Таким образом, периметр треугольника со стороной X, Y и Z будет равен:
Свойства равнобедренного прямоугольного треугольника
 Давайте посмотрим на список структур, за которыми следует равнобедренный прямоугольный треугольник:
Давайте посмотрим на список структур, за которыми следует равнобедренный прямоугольный треугольник:
Почему важны равнобедренные треугольники?
Как равнобедренный треугольник используется в реальной жизни?
Что особенного в прямоугольном равнобедренном треугольнике?


