Развертка конуса: прямой, наклонный и усеченный конус

alexxlab | 25.04.2023 | 0 | Разное

прямой, наклонный и усеченный конус

Развертка поверхности конуса – это плоская фигура, полученная путем совмещения боковой поверхности и основания конуса с некоторой плоскостью.

Варианты построения развертки:

• Прямой круговой конус
• Наклонный конус
• Усеченный конус

Развертка прямого кругового конуса

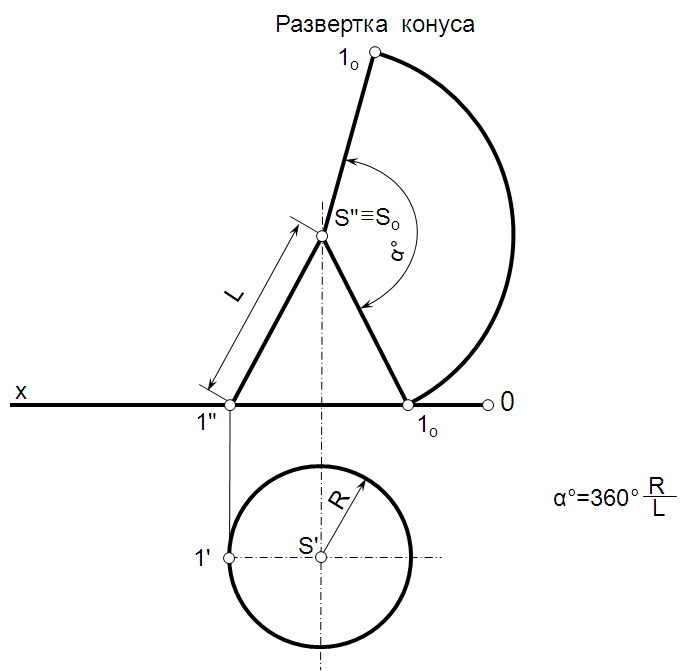
Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ определяется по формуле φ=360*R/l, где R – радиус окружности основания конуса.

В ряде задач начертательной геометрии предпочтительным решением является аппроксимация (замена) конуса вписанной в него пирамидой и построение приближенной развертки, на которую удобно наносить линии, лежащие на конической поверхности.

Алгоритм построения

1. Вписываем в коническую поверхность многоугольную пирамиду. Чем больше боковых граней у вписанной пирамиды, тем точнее соответствие между действительной и приближенной разверткой.
2. Строим развертку боковой поверхности пирамиды способом треугольников. Точки, принадлежащие основанию конуса, соединяем плавной кривой.

Пример

На рисунке ниже в прямой круговой конус вписана правильная шестиугольная пирамида SABCDEF, и приближенная развертка его боковой поверхности состоит из шести равнобедренных треугольников – граней пирамиды.

Рассмотрим треугольник S₀A₀B₀. Длины его сторон S₀A₀ и S₀B₀ равны образующей l конической поверхности. Величина A₀B₀ соответствует длине A’B’. Для построения треугольника S₀A₀B₀ в произвольном месте чертежа откладываем отрезок S₀A₀=l, после чего из точек S₀ и A₀ проводим окружности радиусом S₀B₀=l и A₀B₀= A’B’ соответственно. Соединяем точку пересечения окружностей B

0 с точками A₀ и S₀.

Грани S₀B₀C₀, S₀C₀D₀, S₀D₀E₀, S₀E₀F₀, S₀F₀A₀ пирамиды SABCDEF строим аналогично треугольнику S₀A₀B₀.

Точки A, B, C, D, E и F, лежащие в основании конуса, соединяем плавной кривой – дугой окружности, радиус которой равен l.

Развертка наклонного конуса

Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

Алгоритм

1. Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
2. Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S.
   Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’₁ занимает положение, при котором она параллельна фронтальной плоскости π₂. Соответственно, S’’5’’₁ – натуральная величина S5.
3. Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S₀1₀6₀, S₀6₀5₀, S₀5₀4₀, S₀4₀3₀, S₀3₀2₀
   , S₀2₀1₀. Построение каждого треугольника выполняется по трем сторонам. Например, у △S₀1₀6₀ длина S₀1₀=S’’1’’₀, S₀6₀=S’’6’’₁, 1₀6₀=1’6’.

Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.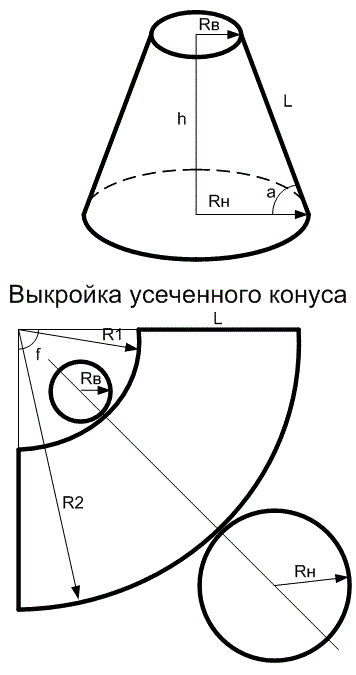

Перенос линии с поверхности конуса на развертку

Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

Алгоритм

1. Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
2. Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’₁, SC=S’’C’’₁.
3. Находим положение точек A₀, B₀, C₀ на соответствующих им ребрах пирамиды, откладывая на развертке отрезки S₀A₀=S’’A’’, S₀B₀=S’’B’’₁, S₀C₀=S’’C’’₁.
4. Соединяем точки A₀, B₀, C₀ плавной линией.

Развертка усеченного конуса

Описываемый ниже способ построения развертки прямого кругового усеченного конуса основан на принципе подобия.

Алгоритм

1. Строим вспомогательный конус ε, подобный конусу ω, как это показано на рисунке выше. Для удобства построения величину диаметра d выбираем таким образом, чтобы соотношение t=D/d выражалось целым числом. В рассматриваемом примере t=2.
2. Строим развертку боковой поверхности конуса ε – S₀A₀1₀2₀3₀4₀5₀A₀ и на биссектрисе угла A₀S₀A₀ отмечаем точку O₀, выбрав ее расположение произвольно.
3. Проводим прямые O₀A₀, O₀1₀, O₀2₀, O₀3₀, O₀4₀, O₀5₀, O₀A₀ и на них откладываем отрезки [O₀A₁₀]=t×|O₀A₀|, [O₀1₁₀]= t×|O₀1₀|, [O₀2₁₀]=t×|O₀2₀|, [O₀3₁₀]=t×|O₀3₀|, [O₀4₁₀]=t×|O₀4₀|, [O₀5₁₀]=t×|O₀5₀|, [O
   0A₁₀]=t×|O₀A₀| соответственно, где t=D/d. Соединяем точки A₁₀, 1₁₀, 2₁₀, 3₁₀, 4₁₀, 5₁₀, A₁₀ плавной линией.
4. Из точек A₁₀, 1₁₀, 2₁₀, 3₁₀, 4₁₀, 5₁₀, A₁₀ проводим лучи, которые параллельны соответственно прямым A₀S₀, 1₀S₀, 2₀S₀, 3₀S₀, 4₀S₀, 5₀S₀, A₀S₀, и на них откладываем отрезки A₁₀B₁₀, 1₁₀1₂₀, 2₁₀2₂₀, 3₁₀3₂₀, 4₁₀4₂₀, 5₁₀5₂₀, A₁₀B₁₀, равные l – образующей усеченного конуса. Проводим линию B
   101₂₀2₂₀3₂₀4₂₀5₂₀B₁₀.

Заказать чертеж

Построение развертки конуса.

| МеханикИнфо

Развертка конуса. Построение развертки конуса.

Оцените запись

 

 

Поверхность конуса состоит из боковой поверхности и поверхности основания.

 

Расчет развертки конуса.

 

Возьмем вертикальную и горизонтальную проекции конуса (рис. 1, а). Вертикальная проекция конуса будет иметь вид треугольника, основание которого равно диаметру окружности, а стороны равны образующей конуса. Горизонтальная проекция конуса будет изображаться окружностью. Если задана высота конуса Н, то длина образующей определяется по формуле:

 

 

т. е. как гипотенуза прямоугольного треугольника.

 

Обвернем картоном поверхность конуса. Развернув картон снова в одну плоскость (рис. 1, б), получим сектор, радиус которого равен длине образующей конуса, а длина дуги равна длине окружности основания конуса. Полную развертку боковой поверхности конуса выполняют следующим образом.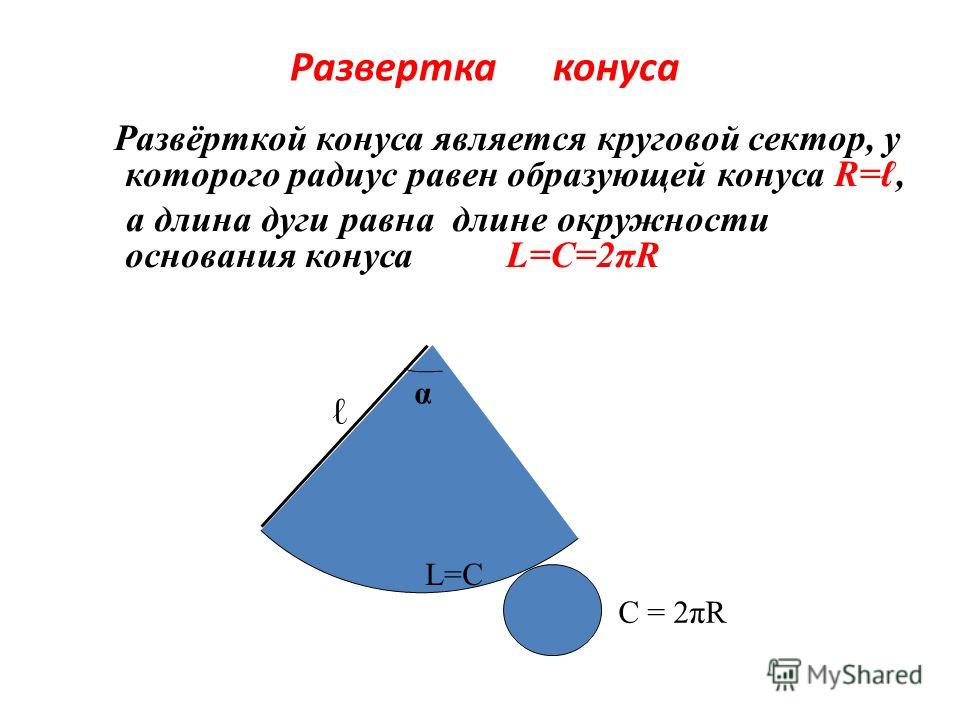

Рис. 1. Развертка конуса:

а — проекция; б — развертка.

 

Угол развертки конуса.

 

Принимая за радиус образующую конуса (рис. 1, б), на металле вычерчивают дугу, на которой затем откладывают отрезок дуги КМ, равный длине окружности основания конуса 2 π r. Длине дуги в 2 π r соответствует угол α, величина которого определяется по формуле:

 

 

где

г — радиус окружности основания конуса;

l — длина образующей конуса.

 

Построение развертки сводится к следующему. На длине ранее вычерченной дуги откладывается не часть дуги КМ, что практически является невозможным, а хорда, соединяющая концы этой дуги и соответствующая углу α. Величина хорды для заданного угла находится в справочнике или проставляется на чертеже.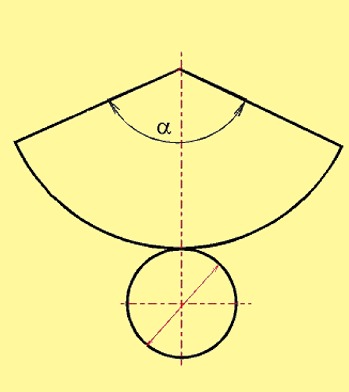

 

Найденные точки КМ соединяются с центром окружности. Круговой сектор, полученный в результате построения, будет развернутой боковой поверхностью конуса.

 

 

Построение развертки наклонного эллиптического цилиндра с круговыми основаниями.

Наклонная пирамида развертка. Усеченная четырехгранная пирамида.

Развертка наклонного усеченного цилиндра. Наклонный цилиндр развертка.

Как сделать развертку многогранника?! Развертка неправильного многогранника с параллельными основаниями.

Правильная пятиугольная пирамида. Развертка усеченной пирамиды.

Развертка уголка гнутого. Посчитать развертку уголка.

Расчет развертки трубы при гибке. Длина развертки. Формула расчета развертки трубы.

Правильная пирамида развертка.

Развертка цилиндра эллиптического, усеченного наклонной плоскостью.

Развертка усеченного цилиндра. Построение развертки цилиндра.

Разработка компоновки конуса с помощью метода маркировки и расчета

Полный конус — очень распространенная форма в производственной промышленности, поскольку она наиболее часто используется в производстве, поэтому очень важно, чтобы каждый инженер-технолог или профессионал в области производства должен был знать компоновку конуса. Развитие Если у вас есть подробные знания по изготовлению конусов, это очень полезно для вас при работе в повседневной деятельности по изготовлению. Итак, в этом посте мы рассмотрим все моменты, связанные с разработкой компоновки полного конуса, чтобы вы могли подробно изучить и использовать этот метод в повседневной деятельности по изготовлению.

Мы собираемся объяснить эту компоновку конуса как с помощью геометрических, так и численных методов, и в конце изучения этого метода мы взяли один практический пример разработки компоновки полного изготовления конуса, чтобы понять использование этого метода для разработки компоновки. Мы также предоставили вам пример метода проверки решения с помощью нашего инструмента «Калькулятор изготовления», чтобы вы могли проверить свои расчеты с помощью некоторых проверенных инструментов и убедиться в правильности схемы изготовления. Вы можете попрактиковаться в этом методе, взяв больше примеров самостоятельно, проверить свой ответ с помощью наших инструментов и стать экспертом в разработке компоновки изготовления полного конуса.

Геометрический метод или метод маркировки для компоновки полного конуса

Геометрический метод разработки макета изготовления полного конуса также называется графическим методом разработки компоновки полного конуса, в этом макете маркировка макета метода разрабатывается с использованием прямого измерения геометрической формы полного конуса. Конус. Этот метод является основным методом для изготовления макета, но он требует много времени для рисования геометрии реального размера, а также имеет ограничение для больших размеров, чтобы избежать этого ограничения, вы должны использовать компьютеризированный инструмент, такой как программное обеспечение AutoCad, и для разработанного макета с использованием этого Программное обеспечение также требовало квалифицированной рабочей силы для создания макета, оно стоило нам больше с точки зрения дополнительных квалифицированных рабочих и дополнительного времени для рисования макета. Если форма макета изготовления сложная, то это неэкономично. Теперь мы перейдем к изучению разработки полного макета изготовления конуса с использованием геометрического метода в пошаговом процессе.

Мы рекомендуем вам всегда использовать средние размеры для разработки макета изготовления, это дает большую точность маркировки макета изготовления по сравнению с внешними или внутренними размерами.

Шаг 1: Начертите вид фасада и вид сверху для полного конуса.

Шаг 1: Конус, вид сверху и вид сверху.

Шаг 2: . частей.

Шаг 2

Шаг 3: Измерьте высоту наклона конуса на виде сбоку.

Шаг : 3

Шаг 4: Нарисуйте окружность проявления с радиусом в качестве высоты наклона.

Шаг: 4

Шаг 5: Измерьте разделяющее расстояние (L) от вида сверху разделенного круга.

Шаг : 5

Шаг 6: Отметьте окружность проявления с разделительным расстоянием (L), равным количеству частей на виде сверху.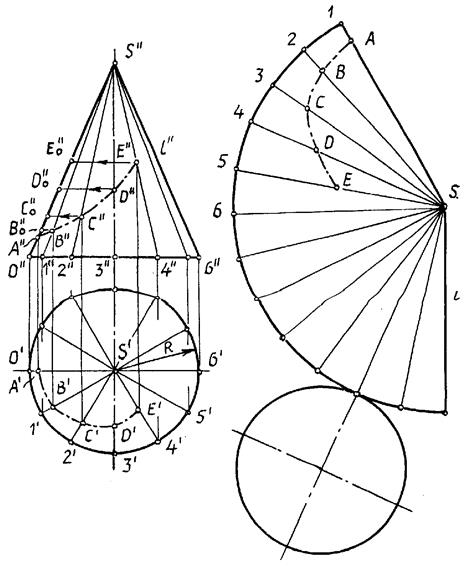

Шаг: 6

Шаг 7: Обрежьте оставшуюся часть, чтобы получить макет полного конуса.

Шаг : 7

Таким образом, мы можем создать производственную схему полного конуса, используя геометрический метод или графический метод разработки производственной схемы.

Численный метод или метод расчета для полного конуса

Численный метод для полного конуса Разработка — это очень быстрый и экономящий время метод для макета, вы можете рассчитать значения размера макета, решив вручную на инженерном калькуляторе, или вы можете используйте любой компьютеризированный инструмент для решения, такой как MS Excel или любой другой инструмент для более быстрого расчета значений.

Теперь мы перейдем к изучению численного метода разработки макета изготовления полного конуса. В этом методе мы обсуждаем два случая разработки макета.

Случай 1: Угол конуса и диаметр конуса заданы

Шаг 1: Определите обобщенную схему полного развертывания конуса.

Обобщенная диаграмма конуса

Шаг 2: Определите переменные для компоновки полного конуса.

Let,

D = средний диаметр основания конуса.

α = угол конуса

β = угол конуса.

R = Радиус развития.

Θ = угол раскрытия.

X = Длина шнура конуса.

Шаг 3: Рассчитать радиус раскрытия R полного конуса.

Если задано α , то

R = (D/2) / Cos (α)

Если задано β, то

/ Sin/

R = (D/2) β/2)

Шаг 4: Рассчитать угол развертывания Θ.

Θ = ((D/2) / R ) x 360

Шаг 4: Рассчитать длину шнура конуса X

X = 2 x R x Sin (Θ/2)

Шаг 5: Схема конуса.

Окончательный макет конуса

Таким образом, мы можем разработать макет изготовления, когда у нас была проблема, подобная случаю 1, где заданы угол конуса и диаметр конуса. Теперь мы увидим задачу типа Case-2 разработки макета изготовления.

Случай 2: диаметр конуса и высота конуса заданы

Шаг 1: Определите обобщенную схему для разработки компоновки полного конуса.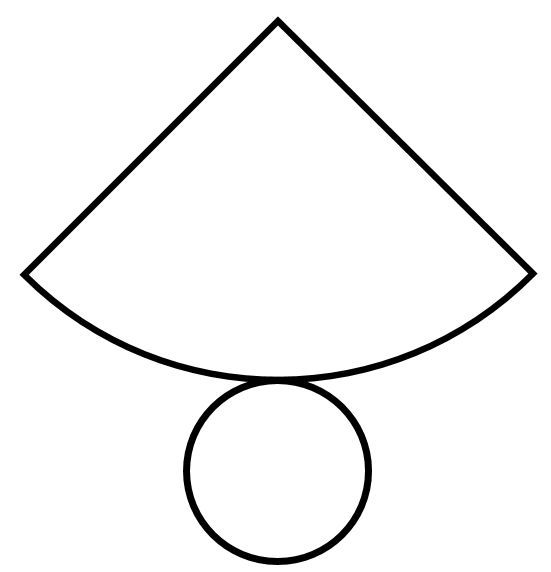

Обобщенная диаграмма конуса

Шаг 2: Определение переменных для компоновки полного конуса

Пусть,

D = Базовый средний диаметр конуса.

H = Высота конуса.

R = Радиус развития.

Θ = угол раскрытия.

X = Длина шнура конуса.

Шаг 3: Рассчитать радиус развертки R.

R = √ ( H ² + (D/2) ² )

или

2) )

R = (D/2) / Cos (α)

Шаг 4: Рассчитать угол развертывания Θ .

Θ = ((D/2) / R) х 360

Шаг 5: Рассчитать длину шнура конуса X.

X = 2 x R x Sin (Θ/2)

Шаг 6: Разработка схемы конуса.

Окончательный макет конуса

Таким образом, используя числовые формулы, вы можете очень быстро и эффективно создать макет изготовления полного конуса.

 В приведенных выше двух методах мы узнаем, как разметить полный конус с помощью геометрических и численных методов, теперь мы увидим один практический пример решения с использованием численного метода, чтобы мы могли лучше понять компоновку, практикуя его на практике.

Практический пример Решение с помощью численного метода или метода расчета

Пример: Создание маркировки разработки схемы изготовления полного конуса для следующих размеров:

Решение:

Шаг 1: Запишите данные примера .

Данные:

D = 500

H = 750.

Шаг 2: Расчет радиуса развертки R0137 2 )

R = √ ( 750 ² + (500/2) ² )

R = √ ( 562500 + (62500) )

907902 .

Шаг 3: Рассчитать угол раскрытия Θ.

Θ = ((D/2) / R ) x 360

Θ = ((500/2) / 790,56 ) x 360

Θ = 113,84 градуса.

Шаг 4: Рассчитайте длину конусного шнура X.

X = 2 x R x Sin (Θ/2)

X = 2 x 790,56 x Sin (113,84 / 2)

X = 1324,84 мм.

Шаг 4: Отметьте макет проявки, используя вышеуказанные размеры.

Это окончательная схема изготовления. Маркировка полного конуса для данного примера решена с помощью численного метода. Вы попрактикуетесь в этом методе, чтобы стать мастером в этом типе макета, и после практики вы будете уверены в своих макетах, а в последней части, став экспертом, вы сократите свою работу, используя метод с помощью компьютеризированных числовых инструментов, чтобы увеличить свои точность и сэкономить время расчетов.

Теперь мы рассмотрим этот пример процесса проверки решения, чтобы вы могли быть уверены в своих вычислениях и проверить свой результат с помощью какого-либо стандартного проверенного эталона.

Пример решения Проверка компоновки полного конуса с помощью калькулятора изготовления

Мы предоставляем вам этот пример метода проверки решения, чтобы вы могли легко проверить свои расчетные значения с помощью какого-либо стандартного проверенного инструмента, чтобы стать более уверенным при компоновке и легко попрактиковаться в использовании этого метод, пока вы не станете экспертом в верстке с помощью численного метода. Мы уже протестировали этот инструмент с расширенным компьютерным инструментом, чтобы вы могли доверять этому инструменту и стали более точными в расчетах значений.

Теперь мы увидим пример метода проверки решения. Сначала вам нужно загрузить наше мобильное приложение с нашего веб-сайта или из магазина Google Play или Apple App Store.

Ссылки для скачивания нашего приложения Fabrication Calculator :

Приложение Fabrication Calculator с нашего веб-сайта.

Приложение Fabrication Calculator из магазина Google Play.

Приложение Fabrication Calculator из Apple App Store.

Процесс проверки решения: Загрузите вышеприведенное мобильное приложение на свой мобильный пример проверки Result Values ​​with App results in Value. Следуйте приведенным ниже шагам проверки решения для макетов полного конуса, мы также добавили снимки экрана для лучшего понимания этих методов проверки.

Шаг 1: Выберите вариант полного конуса на главном экране приложения, как показано на рисунке ниже для шага 1.

Шаг 2: Введите входные данные диаметра конуса как 500 мм и высоты конуса как 750 мм во входных данных Поля и нажмите кнопку «Рассчитать», как показано на изображении шага 2 ниже.

Шаг 3: Проверьте значения результатов с вашими расчетными значениями, если ваши расчетные значения совпадают с этим значением страницы результатов, тогда вы правы, если ваши значения не совпадают с значения страницы результатов, затем перепроверьте свой расчет и найдите правильные значения для точного результата. См. шаг 4.

Снимки экрана для примера компоновки конуса Процесс проверки

Таким образом, вы можете проверить свой результат с помощью этого приложения калькулятора изготовления, вы также можете проверить его любыми известными вам методами. Мы используем этот метод, мы уже протестировали результат этого приложения, поэтому мы тестируем наш результат с помощью этого приложения.

Теперь мы изучаем весь процесс разработки макета конуса, используя все методы. Точно так же, если вы хотите подробно изучить разработку макета изготовления всех форм изготовления, вы можете присоединиться к нашему 70-дневному видеокурсу по разработке макета изготовления. Нажмите здесь, чтобы узнать подробности курса.

70-дневный видеокурс по разработке макетов для изготовления

Если вы работаете в сфере производства, то мы упростили вашу повседневную деятельность по изготовлению, разработав различные калькуляторы, чтобы вы могли минимизировать время и затраты на изготовление, а также повысить точность ваших производственных работ и улучшить свое мастерство, поэтому давайте попробуем наши бесплатные приложения,  Нажмите здесь для получения более подробной информации…

Если вы хотите самостоятельно изучить схему изготовления или разработать макет развертки различных форм изготовления, вы можете купить наше книга «Магистр разработки макетов для изготовления» или Нажмите здесь, чтобы узнать о наших книгах.

Мы надеемся, что вы изучите все методы разработки компоновки конусов во всех аспектах.

Cone Development – Небольшая инновационная студия разработки

Мы создаем веб-сайты и веб-приложения от небольших до крупных на WordPress и Laravel.

Наши сервисы Познакомьтесь с нами

Мы проектируем, разрабатываем и поддерживаем

Мы можем вам помочь

Разработка приложений

В зависимости от требований мы используем WordPress или Laravel для разработки. Если идея сложная, то мы можем решить ее с помощью уникальной системы.

• Разработка веб-приложений — Используя Laravel, мы создаем быстрое и надежное приложение, отвечающее вашим потребностям.
• Разработка сайтов — Делаем сайты на заказ на базе WordPress CMS.

Дизайн

Мы не только пишем код, но и разрабатываем интерфейсы. Наша цель — сделать функциональный и простой пользовательский интерфейс. Кроме того, мы можем помочь вам со многими другими вещами, связанными с Интернетом.

• Дизайн – Мы заботимся о хорошем фундаменте и дизайне.

Все делают по-своему

Как мы разрабатываем и думаем

Почему мы используем WordPress

WordPress — это доступная и довольно эффективная система управления контентом, которая способна управлять большинством вещей, которые необходимы сайту, и даже больше.

Если приложение, то Laravel

Мы используем Laravel, самый динамично развивающийся и совершенствующийся PHP-фреймворк. Конечно, ваше приложение будет надежным, но гибким.

Мы заботимся о том, что делаем

Код в основном невидим для конечного пользователя и клиента, но это не повод делать его максимально чистым.

Мы стараемся упростить

Сложная система также должна быть прозрачной и простой. Если мы достигаем этого, мы знаем, что результат достаточно хорош.

Мы заботимся о производительности

Производительность является сложной областью при разработке. Мы пытаемся контролировать каждый аспект этого на каком-то уровне.

Ищем партнеров

Мы хотим работать не на вас, а с вами. Мы заботимся о подходящих партнерских отношениях, при которых каждая сторона получает то, что хочет.

Мы знаем свое дело, и у нас есть официальная сертификация Laravel, которую получил Герго. Мы можем помочь вам с кодом высокого качества.

Детали

Как мы работаем

Мы движемся вперед, выполняя следующие шаги

Мы измеряем, говорим

Мы изучаем требования и измеряем конкретные потребности.

Дизайн и каркас

На основе полученной информации мы создаем HTML-дизайн, который вы можете протестировать на любом устройстве.

Разрабатываем

На этом этапе мы начинаем писать код как на фронтенде, так и на бэкенде.

Проверка и исправление

Мы (включая вас) постоянно тестируем сайт. После того, как он работает как надо, мы запускаем его в производство.

Мы строим с помощью этих инструментов

Стек технологий

Серверная часть

• Ларавель
• PHP
• MySQL
• Редис

Внешний интерфейс

• Vue.js
• Ваниль JS
• Начальная загрузка
• Ларавель Микс
• н/мин
• Пряжа
• Веб-пакет

Интеграция

• PayPal
• Брейнтри
• SimplePay
• MailChimp
• Карты Google
• Диспетчер тегов Google
• Google Аналитика

Серверы

• Netlify
• Хостинг A2
• Кузница Ларавела
• АВС

Познакомьтесь с нами

Мы увлеченные разработчики, которым нравится выкладываться на полную, развиваться и учиться.

Подробнее о нас

Наши последние статьи

Из нашего блога

29 марта 2022 г., CSS

Ель CSS Введение

31 января 2022 г.