Руд это физика: Равноускоренное движение — формулы, законы и примеры
alexxlab | 01.12.2022 | 0 | Разное
Равноускоренное движение — формулы, законы и примеры
Основные определения
Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. Иногда его определяют как скорость изменения скорости. Проще говоря, ускорение показывает, на какую величину изменяется скорость за 1 секунду.
Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется на одну и ту же величину за равные промежутки времени. Под «изменяется» мы подразумеваем не только ускорение (т. е. увеличение скорости), но и замедление. Торможение также относится к движению с постоянным ускорением.
Несколько примеров равноускоренного движения:
разгон самолета перед взлетом;
торможение лыжника на горном склоне;
свободное падение в результате прыжка с парашютом;
велосипедист, спускающийся с горки;
мальчишки, играющие в догонялки.
Кстати, уже известное нам равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.
Формула ускорения при равноускоренном движении
,
где a — ускорение тела [м/с2],
V — мгновенная скорость [м/с],
V0 — начальная скорость [м/с],
t — время [с].
Во время движения тела ускорение остается постоянным. График зависимости ускорения от времени имеет следующий вид:
При прямолинейном равноускоренном движении скорость тела в момент времени t численно равна площади фигуры под графиком зависимости ускорения от времени.
Если из формулы ускорения выразить мгновенную скорость, т.
е. скорость в момент времени t, то мы получим уравнение скорости при равноускоренном движении:
V(t) = V0 + at,
где V(t) — скорость в момент времени t [м/с],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с2],
t — время [с].
Задача 1
Арсений, двигавшийся на электросамокате со скоростью 6 м/с, начал разгоняться на горке. Чeму будeт paвнa его cкopocть чepeз 10 с, ecли уcкopeниe пpи разгоне paвнo 0,5 м/с
Решение.
По условию задачи Арсений ускоряется, следовательно, его скорость увеличивается. Подставим числа в закон изменения скорости при равноускоренном движении:
V(10) = 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10 с Арсений разгонится до скорости 11 м/с.
Важно запомнить, что ускорение — это векторная величина. А взаимное расположение векторов ускорения и начальной скорости определяет характер движения. Рассмотрим анимацию.
Как мы видим, оранжевый автомобиль увеличивает свою скорость, т. е. совершает разгон. В то же время синий автомобиль уменьшает скорость и тормозит. В случае а движение называется равноускоренным. Вектор ускорения сонаправлен с вектором начальной скорости. Следовательно, мгновенная скорость растет с течением времени. В случае б движение называется равнозамедленным. Ускорение и начальная скорость имеют противоположные направления. Следовательно, мгновенная скорость со временем уменьшается.
Зачастую в задачах мы будем работать с проекцией ускорения на координатные оси. Если проекция ускорения на ось положительна, тело увеличивает свою скорость, а если отрицательна — уменьшает.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
График зависимости скорости от времени при равноускоренном движении
Из уравнения скорости следует, что зависимость скорости автомобиля от времени описывается линейной функцией, график которой — прямая.
На анимации мы видим разгон автомобиля с некоторой начальной скоростью. Проекция ускорения на ось Ox положительна. На графике этому соответствует монотонно возрастающая прямая, выходящая из точки (0; V0).
При равнозамедленном движении прямая на графике будет убывать.
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени:
.
Из графика скорости получим формулу пути при равноускоренном движении тела.
Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника V0t и треугольника .
Формула пути при равноускоренном движении
,
где S — путь, пройденный за время t [м],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с2],
t — время [с].
В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:
,
где S — путь, пройденный за время t [м],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с2].
Задача 2
Таксист Роман получил заказ и начал движение с ускорением 0,1 м/с2 после долгой остановки. Ha кaкoм paccтoянии oт нaчaлa движeния его cкopocть cтaнeт paвнoй 15 м/с?
Решение.
По условию задачи таксист начал движение из состояния покоя, следовательно, начальная скорость равна нулю.
Поскольку время движения неизвестно, то определим путь по второй формуле:
Подставим числа и выполним расчет:
м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.
Перемещение при равноускоренном движении
Важно напомнить разницу между путем и перемещением тела.
Путь — длина траектории.
Если тело движется в любом направлении, то его путь увеличивается. Шагомер в вашем телефоне или смарт-часах измеряет именно путь. Для расчета пути по графику скорости необходимо найти площади отдельных фигур и сложить их, как было показано выше.
Перемещение — вектор, соединяющий начальное и конечное положение тела. Чтобы по графику скорости найти перемещение, необходимо взять площади над осью времени со знаком «+», под осью — со знаком «−», а затем найти их сумму.
Например, на этом графике путь тела равен S1 + S2, а перемещение — S1 − S2.
Уравнение перемещения при равноускоренном движении
,
где S — перемещение за время t [м],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с2],
t — время [с].
Вы, скорее всего, заметили удивительное сходство формул расстояния при равноускоренном движении. Так и есть, только помните, что проекция перемещения может принимать отрицательное значение, а путь — нет. В некоторых задачах путь и перемещение могут совпадать, но далеко не всегда.
Важнейшая задача кинематики — определение положения тела относительно других тел с течением времени. Для ее решения вам понадобится знать зависимость координаты от времени (уравнение движения).
Уравнение равноускоренного движения
,
где x(t) — координата в момент времени t [м],
x0 — начальная координата [м],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с2],
t — время [с].
Задача 3
Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2 с после начала движения из начала координат.
Решение.
Поскольку скорость лыжника увеличивается, он движется с положительным ускорением. Начальная скорость V0 = 3 м/с. Начальная координата равна нулю.
Найдем ускорение из формулы пути при равноускоренном движении:
м/с2.
Составим уравнение движения лыжника:
.
По уравнению определим координату лыжника в момент времени t = 2 с:
м.
Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Графики равноускоренного движения
Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.
Обратите внимание, что, когда проекция скорости меняет знак, автомобиль совершает разворот и движется в противоположном направлении.
Вся наша жизнь — в движении, а онлайн-уроки физики в Skysmart помогут вам ускориться на пути к освоению теории и покорению самых разнообразных задач!
Скорость РУД. График скорости
Урок 6. Физика 9 класс (ФГОС)
В этом видеоуроке мы вспомним, какое движение называется прямолинейным равноускоренным движением. Выясним, как зависит скорость от времени при движении с постоянным ускорением.
Узнаем, как строится график зависимости проекции скорости от времени при равноускоренном движении. А также научимся извлекать информацию из такого графика.
Конспект урока “Скорость РУД. График скорости”
На прошлом уроке мы с вами рассматривали неравномерное движение и самый простой его вид — прямолинейное равноускоренное движение. Давайте вспомним, что это такое движение, при котором тело движется вдоль прямой, а проекция его вектора скорости за любые равные промежутки времени изменяется одинаково.
Для характеристики такого движения вводится понятие мгновенной скорости, то есть скорости в данный момент времени или в данной точке траектории.
А также величина, называемая ускорением. Ускорение — это физическая векторная величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Из формулы для ускорения, выполнив небольшие преобразования, легко получить формулу для определения скорости тела в любой момент времени:
Полученное уравнение называется уравнением скорости.
При вычислении скорости, как и в случае с ускорением, мы будем пользоваться формулой, в которую входят не векторы, а их проекции на координатную ось:
Вы уже знаете, что описать механическое движение тела можно не только с помощью формул, но и с помощью графиков. Давайте рассмотрим, как строятся такие графики на примере равноускоренного движения шарика по наклонному жёлобу. Пусть в начальный момент времени скорость шарика была равна v0, а в конце жёлоба — v. Ускорение шарика мы обозначим через a.
Направим координатную ось Ox вдоль жёлоба по направлению движения шарика. Тогда проекция векторов начальной скорости и ускорения на выбранную координатную ось будут положительными.
Построим график зависимости проекции ускорения от времени.
Так как модуль ускорения с течением времени не меняется, а проекция ускорения
положительна, то графиком будет являться прямая линия, параллельная оси
времени, расположенная выше этой оси.
Теперь исследуем график зависимости проекции скорости от времени. Из курса математики вам известна функция, вида
Графиком этой функции является прямая линия. Функция зависимости проекции скорости от времени тоже линейная с аргументом t, постоянным коэффициентом axи свободным членом v0x. Значит, графиком этой функции тоже является прямая линия, расположение которой по отношению к осям координат определяется значениями проекций начальной скорости и ускорения.
Рассмотрим другой пример — движение шарика вверх по наклонному жёлобу.
Теперь начальная скорость шарика направлена вдоль жёлоба вверх. Двигаясь вверх, шарик будет постепенно терять скорость. В некоторой точке он на мгновение остановится и начнёт скатываться вниз. Точку, в которой шарик на мгновение остановился, называют точкой поворота.
Как и в прошлом примере, направим координатную ось вдоль
жёлоба по направлению движения шарика.
Тогда, проекция вектора начальной
скорости на ось будет положительной, а проекция вектора ускорения — отрицательной.
Следовательно, графиком зависимости проекции ускорения от времени будет являться прямая линия, параллельная оси времени, расположенная ниже этой оси.
А графиком зависимости проекции скорости от времени является прямая линия, расположение которой по отношению к осям координат определяется значениями проекций начальной скорости и ускорения.
График скорости показывает, что вначале, пока шарик двигался вверх, проекция скорости была положительна. Она уменьшалась и в некоторый момент времени стала равной нулю. В этот момент шарик достиг точки поворота. В данной точке направление скорости шарика изменилось на противоположное — проекция скорости стала отрицательной.
По графику зависимости проекции скорости на ось Ох от
времени можно определить проекции ускорения тела на эту ось. Для этого на
графике достаточно выбрать два произвольных момента времени и найти изменение
скорости за этот промежуток времени.
А дальше воспользоваться формулой для
определения проекции ускорения при равноускоренном движении.
Закрепления материала.
На рисунке приведены графики зависимости от времени проекций скоростей двух тел. Постройте графики зависимости проекций ускорений от времени для каждого тела.
Предыдущий урок 5 Прямолинейное равноускоренное движение. Ускорение
Следующий урок 7 Перемещение тела при РУД
Получите полный комплект видеоуроков, тестов и презентаций Физика 9 класс (ФГОС)
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Скотт Баалруд получает финансирование для исследования плазмы с высокой плотностью энергии
Баалруд будет исследовать динамическую структуру намагниченной плазмы с высокой плотностью энергии.
Автор: Сара Норман
Скотт Баалруд, профессор Департамента ядерной инженерии и радиологии Университета штата Массачусетс, получил финансирование для исследования плазмы с высокой плотностью энергии.
Проект Баалруда «Динамическая структура намагниченной плазмы высокой плотности» является одним из 21 проекта лабораторной плазмы высокой плотности энергии (HEDLP), выбранных для получения финансирования от Управления науки (SC) Министерства энергетики (DOE). в сотрудничестве с Национальным управлением по ядерной безопасности (NNSA).
Лабораторная плазма высокой плотности энергии (HEDLP) исследует поведение ионизированного вещества в экстремальных условиях, таких как высокая температура, плотность или давление. Согласно DOE, исследователи применяют эти исследования в таких областях, как астрофизика, ядерная физика и физика элементарных частиц, медицина, национальная безопасность и наука о плазме.
«Намагниченные HEDLP — передовая область физических исследований», — сказал Баалруд. «Недавние достижения в области высокоинтенсивных лазеров и импульсных генераторов энергии позволили одновременно сжимать материю до самых высоких давлений, существующих на Земле (миллионы атмосфер), и магнитные поля до самых высоких значений силы поля, обнаруженных на Земле (десятки тысяч тесла). )».
«При этом HEDLP создают экзотическое состояние намагниченной материи, которое в противном случае встречается только в плотных астрофизических объектах, таких как атмосфера магнитара», — продолжил Баалруд. «Мало что известно об этом состоянии материи. Исследования, вероятно, откроют новую физику, которая в конечном итоге может привести к непредвиденным технологическим применениям, возможно, в исследованиях термоядерной энергии или источников излучения. Возможность создать это экзотическое состояние материи на Земле также позволяет выполнять новую категорию лабораторной астрофизики».
Предлагаемое исследование Баалруда будет использовать теорию и вычисления для изучения особенно нового состояния намагниченной плазмы с высокой плотностью энергии, в котором плазма настолько плотна, что сильно связана, и находится в присутствии такого сильного магнитного поля, что она сильно намагниченный.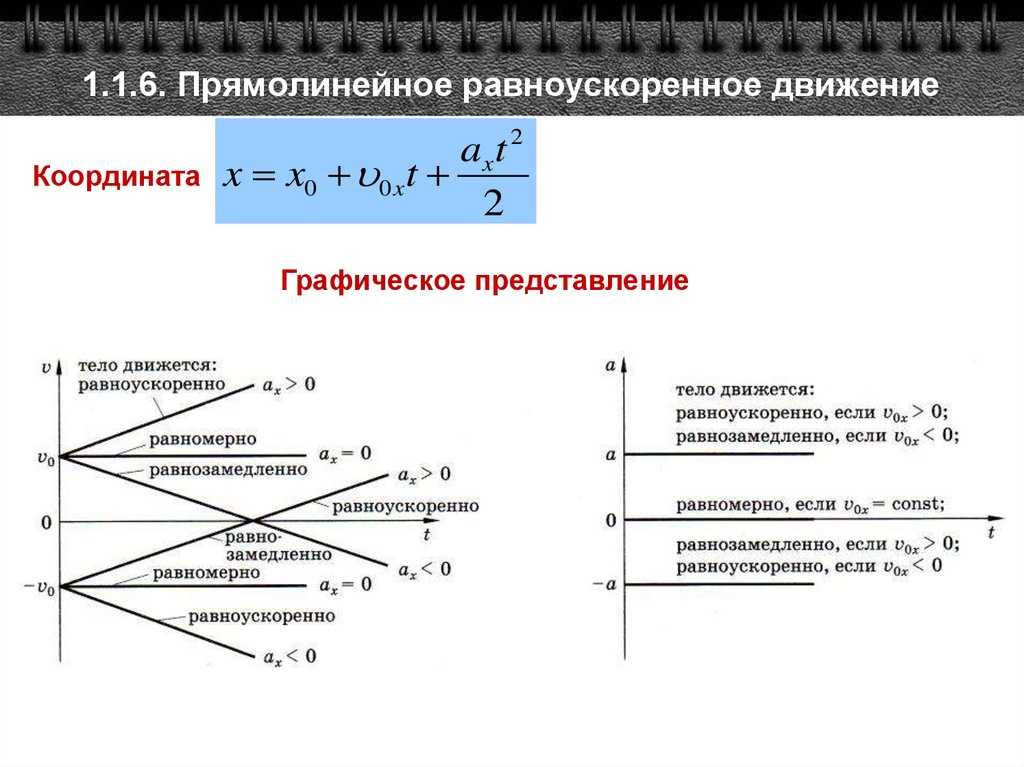
— Большинство плазм слабо связаны в том смысле, что ведут себя как разбавленные ионизированные газы, — сказал Баалруд. «Сильно связанная плазма принципиально отличается тем, что она достаточно плотная, чтобы вести себя скорее как ионизированные сверхкритические флюиды или жидкости, чем как газы. Точно так же большинство плазмы слабо намагничены в том смысле, что гиромоция частиц происходит в масштабе, который намного больше, чем масштаб, в котором частицы взаимодействуют друг с другом (длина Дебая). Сильно намагниченная плазма — это плазма, в которой магнитное поле настолько велико, что происходит гиромоция в масштабе взаимодействий. В совокупности эти эффекты приводят к новому состоянию материи, которое мы только начинаем исследовать».
Предлагаемое Баалрудом исследование разработает теорию, объясняющую основные свойства этого состояния материи, и будет использовать молекулярную динамику, метод моделирования из первых принципов, для проверки предсказаний теории. Они будут сосредоточены на прогнозировании динамической структуры-функции.
Динамическая структурная функция выбрана в качестве фокуса данного исследования, поскольку она содержит большое количество информации о транспортных свойствах плазмы и является наиболее вероятной величиной, которая будет измеряться в будущих экспериментах (с помощью рентгеновского рассеяния Томпсона). ).
Интерпретация этих экспериментов потребует теоретического описания динамической структурной функции, которая связана с измеренным спектром рассеяния. Такого описания еще не существует. Предлагаемое исследование призвано восполнить этот пробел в нашем понимании.
КОНТАКТ ДЛЯ СМИ
Сара Норман
Специалист по маркетингу и коммуникациям
(734) 763-7760
Награды и награды факультета ядерной инженерии и радиологии Плазменные науки0003
| |||||||||||||||||||||||
Ключевое слово SearchAdvanced Search Поисковые книги для: Советы по поиску
| 77777777 годы 9012 7. | ||||||||||||||||||||||
