С 1 м: В 1м сколько см? в 1 км сколько м? в 1дм сколько см? в 1см...

С 1 м: В 1м сколько см? в 1 км сколько м? в 1дм сколько см? в 1см…

alexxlab | 21.04.2023 | 0 | Разное

Содержание

1M Smartphone

Достаточно одного устройства и смартфон

1M Smartphone – ВАШ УМНЫЙ ДОМ

Это децентрализованная система, которой не требуются сервер или центральный контроллер управления, каждое устройство может работать как самостоятельно, так и в связи с другими устройствами. Управляя в своем смартфоне.

Вы в любое время cможете добавлять новые устройства, постепенно упрощая ежедневные действия.

Система наделяет каждое устройство индивидуальными функциями и свойствами, с возможностью обмена информацией друг с другом, что позволяет строить различные сценарии взаимодействия.

ЭТО ПРОСТО

Автоматизируйте электрические устройства с помощью системы

1M Smartphone в Вашем мобильном устройстве!

Управление всегда рядом: воротами, роллетами, освещением, газом и водой, шлагбаумом, климатом и отоплением, поливом, бытовой техникой.

Мы работаем над расширением возможностей системы для Вас, чтобы Вы получили все доступные технологические возможности в одной системе.

Скачайте и установите приложение с Google Play.

Доступна бета-версия приложения с последними дополнениями и функциями – выбрать Подключиться к бета-тестированию.

Подключите питание к устройству 1М и выполните необходимые подключения к Вашему домашнему прибору – согласно инструкции.

Настройте устройство в приложении.

Создайте сценарии, таймеры для автоматизации Ваших повседневных действий.

Работает без интернета

Для работы устройства – интернет не требуется!

Конечно сегодня для Нас важен доступ из любой точки к контролю и управлению, но также Мы хотим быть уверены, что система будет работать при отключении от серверов обеспечивающих удаленный доступ.

Система 1M Smartphone использует внешние сервера только для обеспечения возможности удаленного контроля, управления, облачной статистики, оповещений – настройка и работа устройств не зависит от состояния облака 1М.

ЛОКАЛЬНО, независимо – даже одно устройство является системой с доступом к ней.

ЧЕРЕЗ РОУТЕР (при наличии роутера), все связывается в одну «домашнюю сеть»

УДАЛЕННО, в любой точке мира, при подключении Вашего роутера к «сети интернет»

Использование роутера с домашней WiFi сетью (даже без подключения к интернету) позволяет полностью использовать возможности системы в управлении и взаимодействии устройств между собой через сценарии.

Контроль и управление вашего устройства

Простым включением и выключением каналов устройства сегодня не удивишь никого.

Важным является возможность самостоятельного выполнения команд устройством по каким-либо условиям.

В системе 1M Smartphone реализованы Сценарии и Таймеры, которые позволяют Вам автоматизировать выполнение Ваших задач.

В приложении 1M Smartphone реализована функция голосового управления на любом языке (доступном в Вашем смартфоне), управление голосом возможно и без интернета.

Ваши данные защищены

В прессе, мы постоянно слышим о повсеместном взломе IoT устройств. Часто производители недооценивают эту проблему.

Мы уделили внимание защите данных передаваемых в системе.
Все каналы шифруются уникальным для каждой системы ключом.

Все данные передаваемые для управления, настройки устройств системы – закрыты для облака 1М.

Устройства созданные для работы в системе 1М

Прошивки под сторонние устройства
и платы разработчика
для работы в системе 1М

ГПИБ | Военно-статистическое обозрение Российской империи : издаваемое по высочайшему повелению при 1-м отделении Департамента Генерального штаба [трудами офицеров Генерального штаба].

ГПИБ | Военно-статистическое обозрение Российской империи : издаваемое по высочайшему повелению при 1-м отделении Департамента Генерального штаба [трудами офицеров Генерального штаба]. – СПб., 1848-1858.

2321 / 12407

Электронная библиотека ГПИБ Книжные издания Военно-статистическое обозрение Российской империи : издаваемое по …

Описание

Библиографическое описание	Военно-статистическое обозрение Российской империи : издаваемое по высочайшему повелению при 1-м отделении Департамента Генерального штаба [трудами офицеров Генерального штаба]. – СПб. : Тип. Деп. Ген.штаба, 1848-1858. – Загл. Т. 16, ч. 5 : Статистические описания губерний и областей Российской империи, по высочайшему повелению издаваемые Департаментом Генерального штаба Военного министерства.
Тип издания	книжное издание (23838)
Заглавие	Военно-статистическое обозрение Российской империи (1)
Сведения, относящиеся к заглавию	издаваемое по высочайшему повелению при 1-м отделении Департамента Генерального штаба [трудами офицеров Генерального штаба]
Место издания	СПб. (3105)
Издательство	Тип. Деп. Ген. Штаба (3)
Год издания	1848-1858 (1)
Коллекции	Военная история (1197)
Примечание	Загл. Т. 16, ч. 5: Статистические описания губерний и областей Российской империи, по высочайшему повелению издаваемые Департаментом Генерального штаба Военного министерства

Т. 1 : Великое Княжество Финляндия : Ч. 1-8. – 1850-1851.
Т. 2 : Северо-Восточные губернии : Ч. 1-4. – 1850-1853.
Т. 3 : Северо-Западные губернии : Ч. 1-3. – 1849-1852.
Т. 4 : Верховые Приволжские губернии : Ч. 1-4. – 1848-1852.
Т. 5 : Низовые Приволжские губернии : Ч. 1-5. – 1850-1853.
Т. 6 : Великороссийские губернии : Ч. 1-6. – 1848-1853.
Т. 7 : Остзейские губернии : Ч. 1-3. – 1848-1853.
Т. 8 : Белорусские губернии : Ч. 1-3. – 1848-1852.
Т. 9 : Западные губернии : Ч. 1-4. – 1848-1849.
Т. 10 : Юго-Западные губернии : Ч. 1-3. – 1849-1850.
Т. 11 : Новороссийские губернии, Бессарабская область и Земля Войска Донского : Ч. 1-5. – 1849-1850.
Т. 12 : Малороссийские губернии : Ч. 1-3.
– 1848-1851.
Т. 13 : Средние (черноземные) губернии : Ч. 1-4. – 1849-1851.
Т. 14 : Оренбургский край : Ч. 1-3. – 1848.
Т. 15 : Царство Польское : Ч. 1-5. – 1849-1851.
Т. 16 : Кавказский край : Ч. 1-10. – 1851-1858.
Т. 17 : Западная Сибирь : Ч. 1 – 4. – 1849.

2.2 Скорость и скорость — физика

Раздел Цели обучения

К концу этого раздела вы сможете делать следующее:

Вычислять среднюю скорость объекта
Соотнесите перемещение и среднюю скорость

Поддержка учителей

Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:

(4) Научные концепции. Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
- (B) описывать и анализировать движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.

Кроме того, в Руководстве по физике для средней школы рассматривается содержание этого раздела лабораторной работы под названием «Положение и скорость объекта», а также следующие стандарты:

(4) Научные концепции. Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
- (Б) описывать и анализировать движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.

Основные термины раздела

средняя скорость	средняя скорость	мгновенная скорость
мгновенная скорость	скорость	скорость

Поддержка учителей

В этом разделе учащиеся будут применять полученные знания о расстоянии и перемещении к понятиям скорости и скорости.

[BL][OL] Прежде чем учащиеся прочитают этот раздел, попросите их привести примеры того, как они слышали употребление слова «скорость». Затем спросите их, слышали ли они слово «скорость». Объясните, что эти слова часто взаимозаменяемы в повседневной жизни, но их научные определения различны. Скажите студентам, что они узнают об этих различиях, когда будут читать этот раздел.

[AL] Объясните учащимся, что скорость, как и перемещение, является векторной величиной. Попросите их предположить, чем скорость отличается от скорости. После того, как они поделятся своими идеями, задайте вопросы, которые углубят их мыслительный процесс, например: Почему вы так думаете? Что такое пример? Как можно применить эти термины к движению, которое вы видите каждый день?

Скорость

Движение — это нечто большее, чем расстояние и смещение. Такие вопросы, как «Сколько времени занимает пеший забег?» и «Какова была скорость бегуна?» нельзя ответить без понимания других понятий. В этом разделе мы рассмотрим время, скорость и скорость, чтобы расширить наше понимание движения.

Описание того, насколько быстро или медленно движется объект, называется его скоростью. Скорость — это скорость, с которой объект меняет свое местоположение. Как и расстояние, скорость является скаляром, поскольку имеет величину, но не направление. Поскольку скорость — это скорость, она зависит от временного интервала движения. Вы можете рассчитать прошедшее время или изменение во времени ΔtΔt движения как разницу между временем окончания и временем начала

Δt=tf−t0.Δt=tf−t0.

Единицей времени в СИ является секунда (с), а единицей скорости в СИ является метр в секунду (м/с), но иногда километры в час (км/ч), мили в час (миль в час) или другие единицы измерения скорости.

Когда вы описываете скорость объекта, вы часто описываете среднее значение за определенный период времени. Средняя скорость v _avg — это пройденное расстояние, деленное на время, в течение которого происходит движение.

vavg=distancetimevavg=distancetime

Вы можете, конечно, изменить уравнение, чтобы решить либо расстояние, либо время

время = distancevavg.time = distancevavg.

расстояние = срч × времярасстояние = срч × время

Предположим, например, что автомобиль проезжает 150 километров за 3,2 часа. Его средняя скорость за поездку

ср=расстояние/время=150 км3,2 ч=47 км/ч. ср=расстояние/время=150 км3,2 ч=47 км/ч.

Скорость автомобиля может увеличиваться и уменьшаться во много раз за 3,2-часовую поездку. Однако его скорость в конкретный момент времени является его мгновенной скоростью. Спидометр автомобиля описывает его мгновенную скорость.

Поддержка учителей

[OL][AL] Предупредите учащихся, что средняя скорость не всегда является средним значением начальной и конечной скоростей объекта. Например, предположим, что автомобиль проехал расстояние 100 км. Первые 50 км он едет со скоростью 30 км/ч, а вторые 50 км – со скоростью 60 км/ч.

Его средняя скорость будет равна расстоянию /(интервал времени) = (100 км)/[(50 км)/(30 км/ч) + (50 км)/(60 км/ч)] = 40 км/ч. Если бы автомобиль проехал одинаковое время 30 км и 60 км, а не равное расстояние на этих скоростях, его средняя скорость была бы 45 км/ч.

[BL][OL] Предупредите учащихся, что термины «скорость», «средняя скорость» и «мгновенная скорость» в повседневном языке часто называются просто скоростью. Подчеркните важность использования правильной терминологии в науке, чтобы избежать путаницы и правильно передать идеи.

Рисунок 2,8 За 30-минутную поездку туда и обратно до магазина общее пройденное расстояние составляет 6 км. Средняя скорость 12 км/ч. Перемещение для кругового рейса равно нулю, потому что нет чистого изменения положения.

Рабочий пример

Вычисление средней скорости

Мрамор катится на 5,2 м за 1,8 с. Какова была средняя скорость шарика?

Стратегия

Мы знаем расстояние, которое проходит шарик, 5,2 м, и интервал времени, 1,8 с. Мы можем использовать эти значения в уравнении средней скорости.

Решение

vavg=distancetime=5,2 м1,8 с=2,9 м/svavg=distancetime=5,2 м1,8 с=2,9 м/с отвечать. Мы можем проверить разумность ответа, оценив: 5 метров разделить на 2 секунды равно 2,5 м/с. Поскольку 2,5 м/с близко к 2,9м/с, ответ разумный. Речь идет о скорости быстрой ходьбы, так что это тоже имеет смысл.

Практические задачи

Питчер бросает бейсбольный мяч с насыпи питчера на домашнюю тарелку за 0,46 с. Расстояние 18,4 м. Какова была средняя скорость бейсбольного мяча?

40 м/с
– 40 м/с
0,03 м/с
8,5 м/с

10.

Кэсси шла к дому своей подруги со средней скоростью 1,40 м/с. Расстояние между домами 205 м. Сколько времени заняла у нее поездка?

146 с
0,01 с
2,50 мин
287 с

Скорость

Векторная версия скорости – это скорость.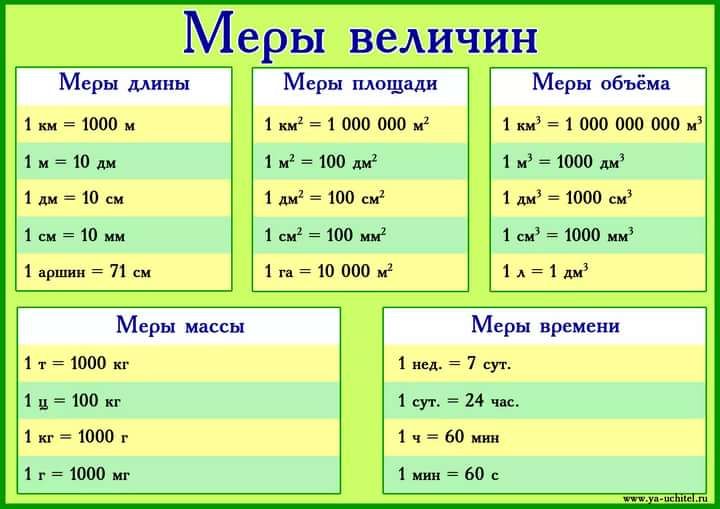 Скорость описывает скорость и направление объекта. Как и в случае со скоростью, полезно описывать либо среднюю скорость за период времени, либо скорость в конкретный момент. Средняя скорость равна смещению, деленному на время, в течение которого происходит смещение.

vavg=displacementtime=ΔdΔt=df−d0tf−t0vavg=displacementtime=ΔdΔt=df−d0tf−t0

Скорость, как и скорость, измеряется в единицах СИ в метрах в секунду (м/с), но поскольку это вектор, вы также должен включать направление. Кроме того, переменная v для скорости выделена жирным шрифтом, потому что это вектор, в отличие от переменной v для скорости, которая выделена курсивом, потому что это скалярная величина.

Советы для успеха

Важно помнить, что средняя скорость — это не то же самое, что средняя скорость без направления. Как мы видели со смещением и расстоянием в предыдущем разделе, изменения направления во временном интервале оказывают большее влияние на скорость и скорость.

Предположим, что пассажир двигается к задней части самолета со средней скоростью –4 м/с. Мы не можем сказать по средней скорости, остановился ли пассажир на мгновение или дал задний ход, прежде чем он добрался до задней части самолета. Чтобы получить больше деталей, мы должны рассмотреть меньшие сегменты пути за более короткие интервалы времени, такие как те, что показаны на рис. 2.9. Если вы рассматриваете бесконечно малые интервалы, вы можете определить мгновенную скорость, то есть скорость в определенный момент времени. Мгновенная скорость и средняя скорость одинаковы, если скорость постоянна.

Рисунок 2,9 На диаграмме показана более подробная запись пассажира самолета, направляющегося к задней части самолета, с указанием меньших сегментов его поездки.

Ранее вы читали, что пройденное расстояние может отличаться от величины перемещения. Точно так же скорость может отличаться от величины скорости. Например, вы едете в магазин и через полчаса возвращаетесь домой. Если одометр вашего автомобиля показывает, что общее пройденное расстояние составило 6 км, значит, ваша средняя скорость составила 12 км/ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение за кругосветное путешествие равно нулю.

Смотреть физику

Вычисление средней скорости или скорости

В этом видео рассматриваются векторы и скаляры, а также описывается, как вычислить среднюю скорость и среднюю скорость, когда известны перемещение и изменение во времени. В видео также рассматривается, как преобразовать км/ч в м/с.

Что из следующего полностью описывает вектор и скалярную величину и правильно дает пример каждого из них?

Скалярная величина полностью описывается своей величиной, тогда как для полного описания вектору необходимы и величина, и направление. Перемещение является примером скалярной величины, а время — примером векторной величины.
Скалярная величина полностью описывается своей величиной, тогда как для полного описания вектору необходимы и величина, и направление. Время — пример скалярной величины, а перемещение — пример векторной величины.
Скалярная величина полностью описывается своей величиной и направлением, в то время как вектору для полного описания требуется только величина. Перемещение является примером скалярной величины, а время — примером векторной величины.
Скалярная величина полностью описывается своей величиной и направлением, в то время как вектору для полного описания требуется только величина. Время — пример скалярной величины, а перемещение — пример векторной величины.

Поддержка учителей

В этом видео хорошо видна разница между векторами и скалярами. Студент знакомится с идеей использования «s» для обозначения перемещения, которое вы можете поощрять или не поощрять. Прежде чем учащиеся посмотрят видео, обратите внимание на то, что преподаватель использует s→s→ для смещения вместо d, как в этом тексте. Объясните, что использование маленьких стрелок над переменными является распространенным способом обозначения векторов в курсах физики более высокого уровня. Предупредите учащихся, что в этом видео не используются общепринятые сокращения для часов и секунд. Напомните учащимся, что в своей работе они должны использовать сокращения h для обозначения часов и s для обозначения секунд.

Рабочий пример

Вычисление средней скорости

Студент переместился на 304 м на север за 180 с. Какова была средняя скорость студента?

Стратегия

Мы знаем, что смещение 304 м на север и время 180 с. Для решения задачи можно использовать формулу средней скорости.

Решение

ср=ΔdΔt=304 м180 с=1,7 м/с север срвг=ΔdΔt=304 м180 с=1,7 м/с север

2,1

Обсуждение

Поскольку средняя скорость является векторной величиной, вы должны указать в ответе не только величину, но и направление. Обратите внимание, однако, что направление можно опустить до конца, чтобы не загромождать задачу. Обратите внимание на значащие цифры в задаче. Расстояние 304 м имеет три значащих цифры, а временной интервал 180 с — только две, поэтому частное должно иметь только две значащие цифры.

Советы для успеха

Обратите внимание на способ представления скаляров и векторов. В этой книге d представляет собой расстояние и перемещение. Точно так же v представляет скорость, а v представляет скорость. Переменная, не выделенная жирным шрифтом, указывает на скалярную величину, а переменная, выделенная жирным шрифтом, указывает на векторную величину. Векторы иногда представляются маленькими стрелками над переменной.

Поддержка учителей

Используйте это задание, чтобы подчеркнуть важность использования правильного количества значащих цифр в вычислениях. Некоторые учащиеся склонны включать много цифр в свои окончательные расчеты. Они ошибочно полагают, что повышают точность своего ответа, записывая многие из цифр, показанных на калькуляторе. Обратите внимание, что это приводит к ошибкам в расчетах. В более сложных расчетах эти ошибки могут распространяться и приводить к неправильному окончательному ответу. Вместо этого напомните учащимся всегда использовать одну или две дополнительные цифры в промежуточных вычислениях и округлять окончательный ответ до правильного количества значащих цифр.

Рабочий пример

Решение для смещения, когда известны средняя скорость и время

Лейла бежит трусцой со средней скоростью 2,4 м/с на восток. Каково ее водоизмещение через 46 секунд?

Стратегия

Мы знаем, что средняя скорость Лейлы составляет 2,4 м/с на восток, а временной интервал равен 46 секундам. Мы можем изменить формулу средней скорости, чтобы найти смещение.

Решение

vср=ΔdΔtΔd=vaсрΔt=(2,4 м/с)(46 с)=1,1×102 м истср=ΔdΔtΔd=vaсрΔt=(2,4 м/с)(46 с)=1,1×102 м восток

2.2

Обсуждение

Ответ примерно 110 м на восток, что является разумным смещением для чуть менее минуты бега трусцой. Калькулятор показывает ответ как 110,4 м. Мы решили написать ответ, используя экспоненциальную запись, потому что хотели, чтобы было ясно, что мы использовали только две значащие цифры.

Советы для успеха

Анализ размерностей — хороший способ определить, правильно ли вы решили задачу. Запишите расчет, используя только единицы измерения, чтобы убедиться, что они совпадают по разные стороны от знака равенства. В рабочем примере у вас есть
м = (м/с)(с). Поскольку секунды находятся в знаменателе средней скорости и в числителе времени, единица измерения сокращается, оставляя только m и, конечно же, m = m.

Рабочий пример

Решение для времени, когда известны перемещение и средняя скорость

Филипп идет по прямой дорожке от своего дома до школы. Сколько времени потребуется ему, чтобы добраться до школы, если он пройдет 428 м на запад со средней скоростью 1,7 м/с на запад?

Стратегия

Мы знаем, что перемещение Филиппа составляет 428 м к западу, а его средняя скорость — 1,7 м/с к западу. Мы можем рассчитать время, необходимое для поездки, изменив уравнение средней скорости.

Solution

vavg=ΔdΔtΔt=Δdvavg=428 m1.7 m/s=2.5×102 svavg=ΔdΔtΔt=Δdvavg=428 m1.7 m/s=2.5×102 s

2.3

Discussion

Here again we пришлось использовать научную запись, потому что ответ мог иметь только две значащие цифры. Поскольку время является скаляром, ответ включает только величину, а не направление.

Практические задачи

11.

Дальнобойщик едет по прямому шоссе 0,25 ч со смещением 16 км на юг. Какова средняя скорость дальнобойщика?

4 км/ч на север
4 км/ч на юг
64 км/ч север
64 км/ч на юг

12.

Птица перелетает со средней скоростью 7,5 м/с на восток с одной ветки на другую за 2,4 с. Затем он делает паузу перед полетом со средней скоростью 6,8 м/с на восток в течение 3,5 с к другой ветке. Каково полное перемещение птицы от исходной точки?

42 м на запад
6 м на запад
6 м на восток
42 м на восток

Виртуальная физика

Ходячий человек

В этой симуляции вы будете наводить курсор на человека и перемещать его сначала в одном направлении, а затем в противоположном. Держите вкладку Introduction активной. Вы можете использовать вкладку Диаграммы после того, как узнаете о построении графиков движения позже в этой главе. Внимательно следите за знаком чисел в полях положения и скорости. На данный момент игнорируйте поле ускорения. Посмотрите, сможете ли вы сделать положение человека положительным, а скорость отрицательной. Затем посмотрите, сможете ли вы сделать наоборот.

Проверка захвата

Какая ситуация правильно описывает ситуацию, когда положение движущегося человека было отрицательным, но его скорость была положительной?

Человек движется к 0 слева от 0
Человек движется к 0 справа от 0
Человек уходит от 0 слева от 0
Человек уходит от 0 справа от 0

Поддержка учителей

Это мощная интерактивная анимация, которую можно использовать во многих уроках. На этом этапе его можно использовать, чтобы показать, что смещение может быть как положительным, так и отрицательным. Это также может показать, что когда смещение отрицательно, скорость может быть как положительной, так и отрицательной. Позже его можно использовать, чтобы показать, что скорость и ускорение могут иметь разные знаки. Настоятельно рекомендуется, чтобы вы удерживали учащихся на уровне 9. 0081 Введение табл. Вкладку Charts можно использовать после того, как учащиеся узнают о построении графиков движения позже в этой главе.

Проверьте свое понимание

13.

Два бегуна, движущиеся по одной и той же прямой дорожке, начинают и заканчивают свой бег в одно и то же время. На полпути они имеют разные мгновенные скорости. Могут ли их средние скорости за весь путь быть одинаковыми?

Да, потому что средняя скорость зависит от чистого или полного водоизмещения.
Да, потому что средняя скорость зависит от общего пройденного пути.
Нет, потому что скорости обоих бегунов должны оставаться одинаковыми на протяжении всего пути.
Нет, потому что мгновенные скорости бегунов должны оставаться одинаковыми в средней точке, но могут различаться в других точках.

14.

Если вы делите общее расстояние, пройденное за автомобильную поездку (определяемое одометром), на время в пути, вычисляете ли вы среднюю скорость или величину средней скорости и при каких обстоятельствах эти две величины такой же?

Средняя скорость. Оба одинаковы, когда автомобиль движется с постоянной скоростью и меняет направление.
Средняя скорость. Оба одинаковы, когда скорость постоянна и автомобиль не меняет своего направления.
Величина средней скорости. Оба одинаковы, когда автомобиль движется с постоянной скоростью.
Величина средней скорости. Оба одинаковы, когда автомобиль не меняет своего направления.

15.

Может ли средняя скорость быть отрицательной?

Да, если чистый водоизмещение отрицательное.
Да, если направление объекта меняется во время движения.
Нет, потому что средняя скорость описывает только величину, а не направление движения.
Нет, потому что средняя скорость описывает величину только в положительном направлении движения.

Поддержка учителей

Используйте Проверьте свое понимание вопроса для оценки достижений учащихся по разделам целей обучения. Если учащиеся испытывают трудности с выполнением определенной задачи, тест «Проверка вашего понимания» поможет определить, что именно, и направит учащихся к соответствующему содержанию. Элементы оценки в TUTOR позволят вам переоценить.

Растворы, молярность и разведение

Растворы

Раствор в химии определяется как:

Гомогенная смесь , состоящая из двух или более веществ.
Процесс, при котором газ, жидкость или твердое вещество диспергируются однородно в газе, жидкости или твердом теле без химических изменений.

Вещество (чаще всего жидкость), в котором растворяется другое вещество, называется растворителем , а растворенное вещество называется растворенным веществом .

Раствор приобретает характеристики растворителя ( т. е. , его фаза), когда растворителем является более крупная фракция смеси, как это обычно бывает. Отсюда растворенное вещество обычно является компонентом раствора, присутствующего в меньшая сумма .

Растворимость — это способность растворенного вещества растворяться в растворителе. Растворимость одного вещества в другом не безгранична, и количество растворенного вещества, которое можно растворить в растворителе, сильно различается. Табличные значения растворимости относятся к макс. граммам растворенного вещества в данном количестве растворителя.

растворимость зависит от температуры. В целом, но не без ожидания, растворимость увеличивается с температурой
более мелкие частицы растворяются быстрее, чем более крупные
твердое вещество растворяется быстрее, если смесь перемешивается или встряхивается

насыщенный раствор содержит максимальное количество растворенного вещества в растворителе, определяемое растворимостью.

Примеры распространенных растворов:

чай с сахаром – раствор сахара в горячей воде (чай)
морская вода – раствор соли в воде

Концентрация растворенного вещества в растворе может быть представлена как

масса растворенного вещества, выраженная в процентах от массы всего раствора , которая представляет собой массовый % или массовый %
объем растворенного вещества, выраженная в процентах от объема всего раствора, которая представляет собой объемный %
количество молей растворенного вещества в заданном объеме всего раствора , что является молярностью.
количество молей растворенного вещества в данной массе растворителя , что является моляльностью.
отношение числа молей растворенного вещества и общее количество молей раствора, , что является молярной долей.

См. также Смеси, растворы и суспензии, Константы произведения растворимости и Рекомендации по растворимости ионных соединений в воде в заданном объеме раствора:

M = n / V [1]

n: число молей растворенного вещества [моль]

M: Молярность раствора [моль/л] или [М]

V: Объем раствора [л]

Единицей молярности является молярная, с символом M: 1 M = 1 моль/л, где L относится к объему всего раствора. Раствор с концентрацией 1 моль/л эквивалентен 1 моль (1 М).

Из определения можно рассчитать количество молей растворенного вещества, n,:

n = M _* V [2]

Разведение

Разбавление – это процесс, при котором в раствор добавляют большее количество растворителя, чтобы уменьшить концентрацию растворенного вещества.

При разбавлении количество растворенного вещества не меняется, числа молей одинаковы до и после разбавления.

Если нижний индекс “i” представляет начальные значения, а “f” представляет конечные значения задействованных величин, мы имеем:

n _i = M _i * V _i и n _f = M _F * V _F

N _I = N _F и, таким образом,

M _I * V _I = M _F * V _F [3] = M _F * V _F [3] .

Из этого мы можем рассчитать окончательную молярность после разбавления :

M _F = M _I * V _I / V _F [4]

или мы можем рассчитать необходимый финальный объем 66666666. для достижения желаемой конечной молярности:

V _F = M _I * V _I / M _F [5]

Пример 1

Что является упор (в WT%) раствора, где соль 56 грамм расплавлен в 0,8 кг воды?

Во-первых, нам нужно иметь одну и ту же единицу измерения для соли и воды и перевести кг в г: 0,8 кг воды = 800 г воды

Затем мы можем рассчитать процентное содержание соли в водном растворе: г соли / г общего раствора *100%

56 [г]/(800+56) [г]* 100% = 6,54 мас. % соли в водном растворе.

Пример 2

Хлорид натрия, NaCl — это соль, используемая для приготовления пищи. Эта соль имеет растворимость 36 г в 100 г воды при 25°С.

Какова концентрация (в %) насыщенного водного раствора NaCl при 25°C?
Какой будет концентрация (в %) при добавлении 34 г NaCl к 100 г воды?
Какой будет концентрация (в %) раствора соли, если к 100 г воды добавить 38 г NaCl?

1. Насыщенный раствор содержит максимальное количество растворенного вещества в растворителе, которое для NaCl составляет 36 граммов в воде при 25°C. Тогда концентрация насыщенного раствора равна:

концентрация NaCl = 36 [г]/(100 + 36)[г] * 100% = 26,5 мас.%

2. 34 г NaCl меньше, чем растворимость, что означает, что вся соль растворится в воде при 25°C.

Концентрация NaCl = 34 [г]/(100+34) [г] * 100% = 25,4 мас.%

3. 38 г NaCl больше, чем растворимость NaCl в воде. Это означает, что раствор будет насыщенным, а часть соли останется нерастворенной. Концентрация насыщенного раствора такая же, как и в случае 1:

Концентрация NaCl = 36 [г]/(100 + 36)[г] * 100% = 26,5 мас.%

Избыток 2 г соль будет присутствовать в виде твердой фазы.

Пример 3

Вы добавляете 200 г соли (NaCl) в достаточное количество воды, чтобы получилось ровно 5 л раствора соленой воды. Какова молярность раствора?

Молекулярная масса Na составляет 22,99 г/моль, а молярная масса Cl составляет 35,45 г/моль.

Молярная масса NaCl: 22,99 [г/моль] + 35,45 [г/моль] = 58,44 [г/моль]

Количество молей NaCl: 200 [г] /58,44 [г/моль] = 3,42 [моль NaCl]

Молярность раствора: 3,42 моль NaCl / 5 л раствора = 0,684 моль/л = 0,684 М

Пример 4

Требуется 1 л раствора уксусной кислоты (СН ₃ СООН) в воде. Сколько нужно добавить 100% уксусной кислоты (в молях, в граммах и в литрах)?

1М раствор означает 1 моль уксусной кислоты на литр раствора.

Моль , необходимое для 2-литрового раствора: 2 [л] * 1 [моль/л] = 2 моль уксусной кислоты О: 16,00 г/моль.

Молекулярная масса уксусной кислоты: 2*12,01 [г/моль]+ 4*1,01 [г/моль] + 2*16,00 [г/моль] = 60,06 [г/моль]

Грамм необходимо для 2 литр раствора: 2 [моль] * 60,06 [г/моль] = 120,12 г уксусной кислоты

Плотность 100%-ной уксусной кислоты при 20°C составляет 1,048 г/см ³

Объем , необходимый для 2 литров раствора: 120,12 [г] / 1,048 [г/см 2 ^{4] 9072 3} = 114,62 мл = 0,115 л уксусной кислоты

Внимание! Никогда не добавляйте воду в неразбавленную кислоту!

Практический совет : Используйте емкость с точным определением объема 2 л. Добавьте 1 л воды, а затем 0,115 л уксусной кислоты (измеряется при 20°C) и вращайте емкость, чтобы смешать жидкости. Аккуратно добавляйте воду, пока общий объем не достигнет 2 литров.

Пример 5

У вас осталось 500 мл раствора с 1М уксусной кислотой. Теперь вам нужно 100 мл 0,3 М раствора. Как вы можете сделать этот без , используя больше 100% уксусной кислоты?

Самый простой способ — разбавить 1М раствор, что мы и делаем, добавляя в него больше воды.

Из уравнения [3] выше:

V _f = 100 мл = 0,100 л и M _f = 0,3M = 0,3 моль/л

M _i = 1M, а V = 1 моль/л _я = неизвестно (мы не знаем, сколько нам нужно исходного раствора)

V _i = V _f * M _f /M _i = 0,100 [л] * 0,3 [моль/л] / 1 [моль/л] = 0,03 [л] = 30 мл 1М раствора .

Итак, начните с 30 мл 1 М раствора и добавляйте воду, пока не получите ровно 100 мл разбавленного раствора.