Сч20 плотность: Чугун СЧ20 / Auremo
alexxlab | 26.03.2023 | 0 | Разное
Марочник стали и сплавов – Чугун СЧ20 : химический состав и свойства
Марочник стали и сплавов – Чугун СЧ20 : химический состав и свойстваМатериалы -> Чугун серый ИЛИ Материалы -> Чугун-все марки
| Марка | СЧ20 |
| Классификация | Чугун серый |
| Применение | для изготовления отливок |
Химический состав в % материала СЧ20
| C | Si | Mn | S | P |
| 3.3 – 3.5 | 1.4 – 2.4 | 0.7 – 1 | до 0. 15 15 | до 0.2 |
Механические свойства при Т=20oС материала СЧ20 .
| Сортамент | Размер | Напр. | sв | sT | d5 | y | KCU | Термообр. |
| – | мм | – | МПа | МПа | % | % | кДж / м2 | – |
| 200 |
| Твердость материала СЧ20 , | HB 10 -1 = 143 – 255 МПа |
Физические свойства материала СЧ20 .
| T | E 10– 5 | a 10 6 | l | r | C | R 10 9 |
| Град | МПа | 1/Град | Вт/(м·град) | кг/м3 | Дж/(кг·град) | Ом·м |
| 20 | 1 | 54 | 7100 | |||
| 100 | 9.5 | 480 |
Обозначения:
| Механические свойства : | |
| sв | – Предел кратковременной прочности , [МПа] |
| sT | – Предел пропорциональности (предел текучести для остаточной деформации), [МПа] |
| d5 | – Относительное удлинение при разрыве , [ % ] |
| y | – Относительное сужение , [ % ] |
| KCU | – Ударная вязкость , [ кДж / м2] |
| HB | – Твердость по Бринеллю , [МПа] |
Физические свойства : | |
| T | – Температура, при которой получены данные свойства , [Град] |
| E | – Модуль упругости первого рода , [МПа] |
| a | – Коэффициент температурного (линейного) расширения (диапазон 20o – T ) , [1/Град] |
| l | – Коэффициент теплопроводности (теплоемкость материала) , [Вт/(м·град)] |
| r | – Плотность материала , [кг/м3] |
| C | – Удельная теплоемкость материала (диапазон 20o – T ), [Дж/(кг·град)] |
| R | – Удельное электросопротивление, [Ом·м] |
Источник: http://www. splav-kharkov.com/
splav-kharkov.com/
СЧ 20 :: Металлические материалы: классификация и свойства
Чугун СЧ 20 ГОСТ 1412-85
Массовая доля элементов, % | ||||
Углерод | Кремний | Марганец | Фосфор | Сера |
Не более | ||||
3,3-3,5 | 1,4-2,4 | 0,7-1,0 | 0,2 | 0,15 |
Марка чугуна по СТ СЭВ 4560-84 | 31120 |
Временное сопротивление при растяжении , МПА, (кгс/мм2), не менее | 200(20) |
Плотность,кг/м3 | 7,1. |
Линейная усадка, , % | 1,2 |
Модуль упругости при растяжении, Е.10-2 МПА | 850-1100 |
Удельная теплоемкость при температуре 20-200, С, Дж (кг.К) | 480 |
Коэффициент линейного расширения при температуре 20-200, | 9,5.10-6 |
Теплопроводность при 20,, Вт(м.К) | 54 |
Требования к деталям | Применение |
Условные напряжения изгиба примерно до | Станины долбежных станков, вертикальные стойки фрезерных,
строгальных и расточных станков. |
Условные удельные давления между трущимися поверхностями свыше 5 кгс/см2. | Станины с направляющими большинства металлорежущих станков, зубчатые колеса, маховики, тормозные барабаны, диски сцепления. |
Высокая герметичность | Гидроцилиндры, гильзы, корпусы гидронасосов, золотников и клапанов среднего давления (до 80 кгс/см2). |
Средняя прочность и хорошая обрабатываемость | Корпусные детали |
Оценка плотности | © www.achalneupane.com
Данные о
галактикахизMASSсодержат скорости 82 галактик из шести хорошо разделенных конических секций пространства (Postman et al., 1986, Roeder, 1990). Данные предназначены для того, чтобы пролить свет на то, содержит ли наблюдаемая Вселенная сверхскопления галактик, окруженных большими пустотами. Доказательством существования сверхскоплений была бы мультимодальность распределения скоростей.
Доказательством существования сверхскоплений была бы мультимодальность распределения скоростей.а.) Построить гистограммы, используя следующие функции:
-hist() и ggplot()+geom_histogram() -truehist() и ggplot+geom_histogram() (обратите внимание на ось Y!) -qplot()
b.) Создайте новую переменную = \(\log\)(galaxies). Постройте гистограммы, используя функции в части а.), и прокомментируйте форму и различия.
c.) Постройте оценки плотности ядра, используя два разных варианта функций ядра и три варианта ширины полосы пропускания (один слишком большой и «сглаженный», другой слишком маленький и «недостаточно сглаженный» и один, который кажется подходящим). Следовательно, у нас должно быть шесть различных графиков оценок ядерной плотности. Мы можем использовать логарифмическую шкалу или исходную шкалу для переменной.
г.) Каков наш вывод о возможном существовании сверхскопления галактик? Сколько сверхскоплений (1,2, 3,…)?
д.) Сколько кластеров он нашел? Совпало ли это с нашим ответом из (d) выше? Мы сообщим оценки параметров и BIC лучшей модели.

библиотека(МАСС)
библиотека (ggplot2)
## Предупреждение: пакет 'ggplot2' был собран под R версии 4.0.5.
## Зарегистрированные методы S3 перезаписываются 'tibble':
## метод из
## столбец format.tbl
## столп print.tbl
## Предупреждение: замена предыдущего импорта 'vctrs::data_frame' на 'tibble::data_frame'
## при загрузке 'dplyr'
# Загружаем данные
данные (галактики)
сообщение("# 1а.", " ")
## # 1а.
# гистограмма
message("Используя hist и geom_histogram:", " ")
## Используя hist и geom_histogram:
история(галактики,
xlab = 'скорость',
main = 'база R: гистограмма, показывающая галактики',
ylab = 'Частота', freq = ИСТИНА) ggplot() + aes (галактики) + geom_histogram (ширина интервала = 5000, разрывы = c (последовательность (5000, 35000, 5000)), граница = NULL, заливка = «белый», цвет = «черный») + labs(title = 'ggplot: гистограмма, показывающая галактики', x= "скорость", y = "частота")
# истинный
message("Использование truehist и geom_histogram():", " ")
## Использование truehist и geom_histogram():
#нарисовать гистограмму
truehist(галактики,
xlab = 'скорость',
main = 'база R: истинная гистограмма, показывающая галактики',
ylab = 'плотность') ЯЩИКИ <- 6 РАЗРЫВЫ <- seq(5000, 35000, length.out = BINS + 1) ШИРИНА ДИАПАЗОНА <- РАЗРЫВЫ[2] - РАЗРЫВЫ[1] ggplot() + aes(галактики) + geom_histogram(aes(y = ..density..), binwidth = BINWIDTH, breaks = c(seq(5000, 35000, 5000)), border = NULL, fill = 'небесно-голубой', цвет = "черный", закрытый = "левый") + labs(title = "ggplot: Истинная гистограмма, показывающая галактики")
######
# qplot
сообщение("Используя qplot:", " ")
## Использование qplot:
qplot(галактики) +
labs(title='base R: гистограмма, показывающая галактики (qplot)',
х='Скорость',
у='Частота')
## `stat_bin()`, используя `bins = 30`. Выберите лучшее значение с помощью `binwidth`. БИНС <- 30 РАЗРЫВЫ <- seq(5000, 35000, length.out = BINS + 1) ШИРИНА ДИАПАЗОНА <- РАЗРЫВЫ[2] - РАЗРЫВЫ[1] ggplot() + aes (галактики) + geom_histogram(bins = BINS, breaks = BREAKS, binwidth = BINWIDTH, border = NULL, fill = 'grey', color = "black") + labs(x = «скорость», y = «частота», title = 'ggplot: гистограмма, показывающая галактики (qplot)')
сообщение("# 1b. ", " ")
## # 1б.
loggalaxies <- log(галактики)
# гистограмма
message("Используя hist и geom_histogram:", " ")
## Используя hist и geom_histogram:
#установить положение фигуры
# пар(рис=с(0,1,0,1),новый=Т)
#нарисовать гистограмму
история(логалактики,
xlab = 'логарифм скорости',
main = 'база R: гистограмма, показывающая логарифмическую скорость галактик',
ylab = 'Частота', freq = ИСТИНА)
", " ")
## # 1б.
loggalaxies <- log(галактики)
# гистограмма
message("Используя hist и geom_histogram:", " ")
## Используя hist и geom_histogram:
#установить положение фигуры
# пар(рис=с(0,1,0,1),новый=Т)
#нарисовать гистограмму
история(логалактики,
xlab = 'логарифм скорости',
main = 'база R: гистограмма, показывающая логарифмическую скорость галактик',
ylab = 'Частота', freq = ИСТИНА) ЯЩИКИ <- 7 РАЗРЫВЫ <- seq(9, 10.5, length.out = BINS + 1) ШИРИНА ДИАПАЗОНА <- РАЗРЫВЫ[2] - РАЗРЫВЫ[1] ggplot() + aes (логарифм галактик) + geom_histogram (ширина ячейки = 0,15, ячейки = 8, граница = NULL, заливка = «белый», цвет = «черный») + labs(x = "логарифмическая скорость", y = "частота", title = 'ggplot: гистограмма, показывающая логарифмическую скорость галактик')
# истинный
message("Использование truehist и geom_histogram():", " ")
## Использование truehist и geom_histogram():
#нарисовать гистограмму
truehist(логалактики,
xlab = 'логарифм скорости галактик',
main = 'база R: истинная гистограмма логарифмической скорости галактик',
ylab = 'плотность') ######### ***** ЯЩИКИ <- 7 РАЗРЫВЫ <- seq(9, 10.5, length.out = BINS + 1) ШИРИНА ДИАПАЗОНА <- РАЗРЫВЫ[2] - РАЗРЫВЫ[1] # ggplot() + aes(loggalaxies) + geom_histogram(binwidth = BINWIDTH, border = NULL, fill = 'skyblue', color = "black", close = "left") # Частота ggplot() + aes(loggalaxies) + geom_histogram(aes(y = ..density..), binwidth = BINWIDTH, bins = BINS, breaks = BREAKS, border = NULL, fill = 'небесно-голубой', color = "черный", закрытый = "левый") + labs(title = "ggplot: Истинная гистограмма логарифмической скорости галактик")
######
# qplot
сообщение("Используя qplot:", " ")
## Использование qplot:
qplot(loggalaxies) +
labs(title='base R: Гистограмма логарифмической скорости галактик (qplot)',
x='логарифм скорости галактик',
у='Частота')
## `stat_bin()`, используя `bins = 30`. Выберите лучшее значение с помощью `binwidth`. ggplot() + aes (логарифм галактик) + geom_histogram (ячейки = 30, граница = NULL, заливка = «серый», цвет = «черный») + labs(x = "логарифмическая скорость", title = 'ggplot: гистограмма, показывающая логарифмическую скорость галактик (qplot)')
сообщение ("#1c. ", "")
## # 1с.
truehist (галактики, ymax = 0,0002, col = "синий", main = "база R: гауссово сверхгладкое")
линии (плотность (галактики, ядро = "гаусс", bw = 5000), col = "красный")
", "")
## # 1с.
truehist (галактики, ymax = 0,0002, col = "синий", main = "база R: гауссово сверхгладкое")
линии (плотность (галактики, ядро = "гаусс", bw = 5000), col = "красный") ЯЩИКИ <- 6 РАЗРЫВЫ <- seq(5000, 35000, length.out = BINS + 1) ШИРИНА ДИАПАЗОНА <- РАЗРЫВЫ[2] - РАЗРЫВЫ[1] ggplot() + aes (галактики) + geom_histogram(aes(y=..density..), bins = BINS, binwidth = BINWIDTH, breaks = BREAKS, border = NULL, fill = 'синий', color = "black", close = "left") + stat_density (ядро = "гауссово", bw = 5000, fill = NA, col = "red") + labs(title = "ggplot: Gaussian Over Smooth")
truehist (галактики, ymax = 0,0002, col = "синий", main = "база R: гауссова сглаженная") линии (плотность (галактики, ядро = "гаусс", bw = 500), цвет = "красный")
ЯЩИКИ <- 6 ggplot() + aes (галактики) + geom_histogram(aes(y=..density..), bins = BINS, binwidth = BINWIDTH, breaks = BREAKS, border = NULL, fill = 'синий', color = "black", close = "left") + stat_density (ядро = "гауссово", bw = 500, fill = NA, col = "red") + labs(title = "ggplot: Gaussian Under Smooth")
truehist (галактики, ymax = 0,0002, col = "синий", main = "база R: Гауссово лучшее приложение") линии (плотность (галактики, ядро =" гауссово", bw = 1100), col = "красный")
ЯЩИКИ <- 6 РАЗРЫВЫ <- seq(5000, 35000, length.out = BINS + 1) ШИРИНА ДИАПАЗОНА <- РАЗРЫВЫ[2] - РАЗРЫВЫ[1] ggplot() + aes (галактики) + geom_histogram(aes(y=..density..), bins = BINS, binwidth = BINWIDTH, breaks = BREAKS, border = NULL, fill = 'синий', color = "black", close = "left") + stat_density (ядро = "гауссово", чб = 1100, заливка = нет данных, столбец = "красный") + labs(title = "ggplot: Gaussian Best Appx")
truehist (галактики, ymax = 0,0002, col = "зеленый", ylab = "плотность", main = "база R: треугольная над гладкой") линии (плотность (галактики, ядро =" треугольная", ширина = 5000), цвет = "красный")
ЯЩИКИ <- 6 РАЗРЫВЫ <- seq(5000, 35000, length.out = BINS + 1) ШИРИНА ДИАПАЗОНА <- РАЗРЫВЫ[2] - РАЗРЫВЫ[1] ggplot() + aes (галактики) + geom_histogram(aes(y=..density..), bins = BINS, binwidth = BINWIDTH, breaks = BREAKS, border = NULL, fill = 'green', color = "black", close = "left") + stat_density(kernel = "треугольный", bw = 5000, fill = NA, col = "red") + labs(title = "ggplot: Triangular Over Smooth")
truehist (галактики, ymax = 0,0002, col = "зеленый", ylab = "плотность", main = "база R: треугольная под гладкой") линии (плотность (галактики, ядро =" треугольная", bw = 500), col = "красный", main = "Triangular_Under")
ЯЩИКИ <- 6 РАЗРЫВЫ <- seq(5000, 35000, length.out = BINS + 1) ШИРИНА ДИАПАЗОНА <- РАЗРЫВЫ[2] - РАЗРЫВЫ[1] ggplot() + aes (галактики) + geom_histogram(aes(y=..density..), bins = BINS, binwidth = BINWIDTH, breaks = BREAKS, border = NULL, fill = 'green', color = "black", close = "left") + stat_density(kernel = "треугольный", bw = 500, fill = NA, col = "red") + labs(title = "ggplot: Triangular Under Smooth")
truehist (галактики, ymax = 0,0002, col = "зеленый", ylab = "плотность", main = "база R: треугольное лучшее приложение") линии (плотность (галактики, ядро =" треугольная", bw = 1100), col = "красный", main = "Triangular_Appx")
ЯЩИКИ <- 6 РАЗРЫВЫ <- seq(5000, 35000, length.out = BINS + 1) ШИРИНА ДИАПАЗОНА <- РАЗРЫВЫ[2] - РАЗРЫВЫ[1] ggplot() + aes (галактики) + geom_histogram(aes(y=..density..), bins = BINS, binwidth = BINWIDTH, breaks = BREAKS, border = NULL, fill = 'green', color = "black", close = "left") + stat_density(kernel = "треугольный", bw = 1100, fill = NA, col = "red") + labs(title = "ggplot: Triangular Best Appx")
сообщение("# 1e. "," ")
## # 1д.
# мы можем использовать:
библиотека (макласт)
## Предупреждение: пакет mclust был собран под R версии 4.0.5.
## Пакет mclust версии 5.4.9
## Введите 'citation("mclust")' для цитирования этого пакета R в публикациях.
mod=Mclust(галактики)
печать (мод)
## Объект модели 'Mclust': (V,4)
##
## Доступные компоненты:
## [1] "вызов" "данные" "имя модели" "n"
## [5] "d" "G" "BIC" "loglik"
## [9] "df" "bic" "icl" "hypvol"
## [13] "параметры" "z" "классификация" "неопределенность"
печать (резюме (мод, параметры = ИСТИНА))
## ------------------------------------------------ ----
## Гауссова модель конечной смеси, аппроксимированная EM-алгоритмом
## ------------------------------------------------ ----
##
## Модель Mclust V (одномерная, неравная дисперсия) с 4 компонентами:
##
## логарифмическое правдоподобие n df BIC ICL
## -765.694 82 11 -15790,862 -1598,907
##
## Таблица кластеризации:
## 1 2 3 4
## 7 35 32 8
##
## Вероятность смешивания:
## 1 2 3 4
## 0,08440635 0,38660329 0,37116156 0,15782880
##
## Означает:
## 1 2 3 4
## 9707.
"," ")
## # 1д.
# мы можем использовать:
библиотека (макласт)
## Предупреждение: пакет mclust был собран под R версии 4.0.5.
## Пакет mclust версии 5.4.9
## Введите 'citation("mclust")' для цитирования этого пакета R в публикациях.
mod=Mclust(галактики)
печать (мод)
## Объект модели 'Mclust': (V,4)
##
## Доступные компоненты:
## [1] "вызов" "данные" "имя модели" "n"
## [5] "d" "G" "BIC" "loglik"
## [9] "df" "bic" "icl" "hypvol"
## [13] "параметры" "z" "классификация" "неопределенность"
печать (резюме (мод, параметры = ИСТИНА))
## ------------------------------------------------ ----
## Гауссова модель конечной смеси, аппроксимированная EM-алгоритмом
## ------------------------------------------------ ----
##
## Модель Mclust V (одномерная, неравная дисперсия) с 4 компонентами:
##
## логарифмическое правдоподобие n df BIC ICL
## -765.694 82 11 -15790,862 -1598,907
##
## Таблица кластеризации:
## 1 2 3 4
## 7 35 32 8
##
## Вероятность смешивания:
## 1 2 3 4
## 0,08440635 0,38660329 0,37116156 0,15782880
##
## Означает:
## 1 2 3 4
## 9707. 492 19804.259 22879.486 24459.536
##
## Отклонения:
## 1 2 3 4
## 177296,7 436160,9 1261611,3 34437115,3
#pot график плотности модели
# пар(рис=с(0,1,0,1),новый=Т)
сюжет (мод, что = "плотность")
title ("График плотности конечной модели смеси")
492 19804.259 22879.486 24459.536
##
## Отклонения:
## 1 2 3 4
## 177296,7 436160,9 1261611,3 34437115,3
#pot график плотности модели
# пар(рис=с(0,1,0,1),новый=Т)
сюжет (мод, что = "плотность")
title ("График плотности конечной модели смеси") # БИК mclustBIC (галактики) ## Байесовский информационный критерий (БИК): ## Э В ## 1 -1622.361 -1622.361 ## 2 -1631.243 -1595.403 ## 3 -1584.016 -1592.299 ## 4 -1592.828 -1579.862 ## 5 -1592.299 -1593.277 № 6 -1601.228 -1604.069 ## 7 -1588.610 -1611.538 №№ 8 -1597.427 -1625.804 №№ 9 -1600.709 -1633.494 ## ## Топ-3 модели по критерию BIC: ## В,4 Е,3 Е,7 ## -1579.862 -1584.016 -1588.610
1.а. Здесь все графики имеют одинаковые формы для hist() и truehist(), за исключением коэффициента масштабирования. Это ожидаемо, так как hist() показывает частоту по оси y, тогда как truehist() дает вероятность, которая представляет собой масштабированную версию частоты. Мы можем сделать некоторую оценку распределения данных, но не можем дать параметрический комментарий. Только на основе графиков мы можем сказать, что данные сильно перегружены в середине диапазона данных. Мы можем лучше всего подумать, что есть три кластера данных, но qplot() показывает дополнительный кластер в среднем перегруженном кластере данных. Наблюдая за qplot(), мы можем предположить, что в наборе данных есть четыре кластера.
Только на основе графиков мы можем сказать, что данные сильно перегружены в середине диапазона данных. Мы можем лучше всего подумать, что есть три кластера данных, но qplot() показывает дополнительный кластер в среднем перегруженном кластере данных. Наблюдая за qplot(), мы можем предположить, что в наборе данных есть четыре кластера.
1.б. Масштабированная версия данных в части (а) используется для построения тех же графиков. Подобные комментарии, как в части (a), действительны и здесь, чтобы описать сходство hist() и truehist(). Из этих масштабированных данных hist() и truehist() все же разумно предположить, что есть три кластера.
1.с. Здесь выбор ширины корзины для сглаживания и сглаживания был простым и понятным. Начиная с крайних значений bw, 5000, 500 и 1100 использовались для создания трех ядер для Гаусса и Треугольника. Поиск наилучшего соответствия только визуализацией был непростым делом. Изменяя ширину бина, мы фактически можем настроить ядро так, чтобы оно лучше подходило для наилучшего приближения кластеров.
1.д. Из цифр, найденных в части (c), мы можем предположить, что в наборе данных есть четыре кластера с неравными дисперсиями. Вручную определить было сложно, но я предположил, что кластеров примерно три-четыре с почти равной вероятностью.
1.е. mclust() нашел четыре кластера с неравной дисперсией для наилучшего соответствия. Однако график плотности модели указывает на наличие трех кластеров. Основываясь на этой информации, мы можем сказать, что в результате этого анализа можно определить как минимум 3 или 4 кластера.
Данные о
рождаемости и смертностиизHSAUR3дают показатели рождаемости и смертности для 69 стран (из Hartigan, 1975). Теперь мы будем работать над следующим:a.) Создайте диаграмму рассеяния данных и наложите контурный график расчетной двумерной плотности.
b.) Дает ли график нам какое-нибудь интересное представление о возможной структуре данных?
c.) Построить перспективный график (persp() в R, GGplot для этого вопроса не требуется).

d.) Кластеризация на основе моделей (Mclust). Предоставьте график сводки нашей подгонки (BIC, классификация, неопределенность и плотность).
д.) Обсудите результаты (структура данных, выбросы и т. д.). Напишите обсуждение в контексте проблемы.
библиотека (HSAUR3)
## Предупреждение: пакет «HSAUR3» был собран под R версии 4.0.5.
## Загрузка требуемого пакета: инструменты
библиотека (KernSmooth)
## KernSmooth 2.23 загружен
## Copyright M. P. Wand 1997-2009
библиотека (изменить форму2)
## Предупреждение: пакет reshape2 был собран под R версии 4.0.2.
библиотека (dplyr)
## Предупреждение: пакет dplyr был собран под R версии 4.0.2.
##
## Прикрепление пакета: 'dplyr'
## Следующий объект замаскирован от 'package:MASS':
##
## выбирать
## Следующие объекты маскируются из 'package:stats':
##
## фильтр, отставание
## Следующие объекты маскируются из 'package:base':
##
## пересечение, setdiff, setequal, объединение
данные(рождаемостьсмерть)
голова (рождениясмерти)
## рождение смерть
## алг 36,4 14,6
## кон 37,3 8,0
## египет 42,1 15,3
## га 55,8 25,6
## икт 56,1 33,1
## магазин 41,8 15,8
длина (смертность при рождении)
## [1] 2
сейчас (рождениясмерти)
## [1] 69сообщение ("#2а", "")
## # 2а
BDRd <- bkde2D (число смертей, пропускная способность = sapply (число смертей, dpik))
контур(x=BDRd$x1, y=BDRd$x2, z=BDRd$fhat,
main = "база R: диаграмма рассеяния Countour of Birth_Death_Rates",
xlab="Рождаемость",
ylab="Уровень смертности",
xlim = c (0,60), ylim = c (0,35))
очки(количество смертей при рождении, pch=16, col="red") ggplot(data=birthdeathrates,aes(рождение,смерть)) + geom_density2d (aes (цвет = .. уровень ..)) + scale_color_gradient (низкий = "зеленый", высокий = "красный") + тема_bw() + геометрическая_точка() + labs(title='ggplot: График рассеяния рождаемости_смерти_коэффициентов', х='Рождаемость', y='Смертность') + scale_x_continuous (пределы = c (0,60)) + scale_y_continuous (пределы = c (0,35))
сообщение("# 2c.", " ")
## # 2с.
persp (x=BDRd$x1, y=BDRd$x2, z=BDRd$fhat,
xlab="Рождаемость",
ylab="Уровень смертности",
zlab="Расчетная плотность",
theta=-35, axes=TRUE, box=TRUE, main = "Перспективный график для данных о рождаемости и смертности")
сообщение("# 2d.", " ")
## # 2г.
библиотека (макласт)
mod <- Mclust(birthdeathrates)
мод
## Объект модели 'Mclust': (EII,4)
##
## Доступные компоненты:
## [1] "вызов" "данные" "имя модели" "n"
## [5] "d" "G" "BIC" "loglik"
## [9] "df" "bic" "icl" "hypvol"
## [13] "параметры" "z" "классификация" "неопределенность"
сводка (мод, параметры = ИСТИНА)
## ------------------------------------------------ ----
## Гауссова модель конечной смеси, аппроксимированная EM-алгоритмом
## ------------------------------------------------ ----
##
## Модель Mclust EII (сферическая, равнообъемная) с 4 компонентами:
##
## логарифмическое правдоподобие n df BIC ICL
## -424,4194 69 12 -899,6481 -906. 4841
##
## Таблица кластеризации:
## 1 2 3 4
## 2 17 38 12
##
## Вероятность смешивания:
## 1 2 3 4
## 0,02898652 0,24555002 0,55023375 0,17522972
##
## Означает:
## [1] [2] [3] [4]
## рождения 55,94967 43,80396 19,922913 33,730672
## смерть 29.34960 12.09411 9.081348 8.535812
##
## Отклонения:
## [1]
## рождение смерть
## рождения 10.2108 0.0000
## смерть 0.0000 10.2108
## [2]
## рождение смерть
## рождения 10.2108 0.0000
## смерть 0.0000 10.2108
## [3]
## рождение смерть
## рождения 10.2108 0.0000
## смерть 0.0000 10.2108
## [4]
## рождение смерть
## рождения 10.2108 0.0000
## смерть 0.0000 10.2108
message("Значение для mod$parameters$mean", " ")
## Значение для mod$parameters$mean
sqrt(mod$parameters$дисперсия$sigmasq)
## [1] 3.195434
BIC.data<- as.data.frame(mod$BIC[])
BIC.data$NumComp<-названия строк(BIC.data)
Melted.BIC<- reshape2::melt(BIC.data, var.ids= "NumComp")
## Использование NumComp в качестве переменных идентификатора
пар(mfrow=с(1,1), спросить=ЛОЖЬ)
# БИК
plot(mod, what="BIC", main = "база R: График BIC")
4841
##
## Таблица кластеризации:
## 1 2 3 4
## 2 17 38 12
##
## Вероятность смешивания:
## 1 2 3 4
## 0,02898652 0,24555002 0,55023375 0,17522972
##
## Означает:
## [1] [2] [3] [4]
## рождения 55,94967 43,80396 19,922913 33,730672
## смерть 29.34960 12.09411 9.081348 8.535812
##
## Отклонения:
## [1]
## рождение смерть
## рождения 10.2108 0.0000
## смерть 0.0000 10.2108
## [2]
## рождение смерть
## рождения 10.2108 0.0000
## смерть 0.0000 10.2108
## [3]
## рождение смерть
## рождения 10.2108 0.0000
## смерть 0.0000 10.2108
## [4]
## рождение смерть
## рождения 10.2108 0.0000
## смерть 0.0000 10.2108
message("Значение для mod$parameters$mean", " ")
## Значение для mod$parameters$mean
sqrt(mod$parameters$дисперсия$sigmasq)
## [1] 3.195434
BIC.data<- as.data.frame(mod$BIC[])
BIC.data$NumComp<-названия строк(BIC.data)
Melted.BIC<- reshape2::melt(BIC.data, var.ids= "NumComp")
## Использование NumComp в качестве переменных идентификатора
пар(mfrow=с(1,1), спросить=ЛОЖЬ)
# БИК
plot(mod, what="BIC", main = "база R: График BIC") ggplot(melted.BIC, aes(x=as.numeric(NumComp), y=значение, цвет=переменная, группа=переменная))+ scale_x_continuous ("Количество компонентов")+ scale_y_continuous ("БИК")+ scale_color_hue("")+ геом_точка()+ геометрическая_линия()+ тема_bw() + лаборатории (название = "ggplot: BIC") ## Предупреждение: удалено 19строки, содержащие пропущенные значения (geom_point). ## Предупреждение: удалено 19 строк, содержащих отсутствующие значения (geom_path).
# неопределенность пар(mfrow=с(1,1), спросить=ЛОЖЬ) сюжет (мод, что = "неопределенность") title(main = "base R: График неопределенности")
рождаемостьсмертность%>% мутировать(неопределенность = мод$неопределенность,
классификация = фактор (мод $ классификация)) %>%
ggplot(aes(рождение, смерть, размер = неопределенность, цвет = классификация)) +
геометрическая_точка() +
направляющие (размер = guide_legend(), цвет = "легенда") + theme_classic() +
stat_ellipse (уровень = 0,5, тип = "t") +
labs(x = "рождение", y = "смерть", title = "ggplot: неопределенность")
## Слишком мало точек для вычисления эллипса
## Предупреждение: удалены 1 строка(и), содержащие отсутствующие значения (geom_path).
# классификация пар(mfrow=с(1,1), спросить=ЛОЖЬ) сюжет (мод, что = "классификация") title(main = "base R: График классификации")
рождаемостьсмертность%>% мутировать(неопределенность = мод$неопределенность,
классификация = фактор (мод $ классификация)) %>%
ggplot(aes(рождение, смерть, форма = классификация, цвет = классификация)) +
геометрическая_точка() +
направляющие (размер = направляющая_легенда(), форма = направляющая_легенда()) + тема_классическая() +
stat_ellipse (уровень = 0,5, тип = "t") +
labs(x = "рождение", y = "смерть", title = "ggplot: график классификации")
## Слишком мало точек для вычисления эллипса
## Предупреждение: удалены 1 строка(и), содержащие отсутствующие значения (geom_path). # плотность пар(mfrow=с(1,1), спросить=ЛОЖЬ) сюжет (мод, что = "плотность") title(main = "base R: График плотности")
ggplot (уровень рождаемости, aes (x = рождение, y = смерть)) + геометрическая_точка() + geom_density_2d() + labs ( title = "ggplot: График плотности")
2. b. Сравнивая данные о рождаемости от 10 до примерно 50 со смертностью, мы можем сказать, что смертность относительно низкая. Я бы сказал, что людей рождается в два раза больше, чем умирает (то есть соотношение рождений и смертей 2:1). Счетчик показывает, что в большинстве стран рождаемость составляет 20, а смертность — 10.
b. Сравнивая данные о рождаемости от 10 до примерно 50 со смертностью, мы можем сказать, что смертность относительно низкая. Я бы сказал, что людей рождается в два раза больше, чем умирает (то есть соотношение рождений и смертей 2:1). Счетчик показывает, что в большинстве стран рождаемость составляет 20, а смертность — 10.
2.д. График BIC показывает, что имеется 4 кластера. График классификации, по-видимому, указывает на группировку данных. Таблица средних значений показывает, что рождаемость группируется примерно в 20, 34, 44 и 56 лет. Смертность группируется примерно в 9, 8, 12 и 30 лет.
- Крепелин (1919). Последующие эпидемиологические исследования расстройства последовательно показали более раннее начало у мужчин, чем у женщин. Одна модель, которая была предложена для объяснения этого наблюдаемого различия, известна как модель подтипа, которая постулирует два типа шизофрении, один из которых характеризуется ранним началом, типичными симптомами и плохой преморбидной компетентностью; а другой - поздним началом, атипичными симптомами и хорошей преморбидной компетентностью.
 Предполагается, что тип с ранним началом чаще встречается у мужчин, а тип с поздним началом — у женщин. Подгонка конечных смесей нормальной плотности отдельно к данным начала для мужчин и женщин, приведенным в
Предполагается, что тип с ранним началом чаще встречается у мужчин, а тип с поздним началом — у женщин. Подгонка конечных смесей нормальной плотности отдельно к данным начала для мужчин и женщин, приведенным в шизофренияданные изHSAUR3. Посмотрим, сможем ли мы привести доказательства за или против модели подтипа.
Ответ:
Основываясь на этом графике плотности с разбивкой по полу, мы можем сказать, что распределение при диагностике заболеваний центрировано в сторону 20 лет (возраст) у мужчин, тогда как у женщин оно более равномерно на протяжении всей жизни.
данные(шизофрения)
# отобразите данные о шизофрении, используя stat_density в ggplot2, с разбивкой по полу
# пар(рис=с(0,1,0,1),новый=Т)
ggplot(данные=шизофрения)+
stat_density (ядро = 'гауссовский', настроить = 1, aes (возраст, заполнение = пол)) +
facet_grid(пол~.) +
labs(title = 'График плотности (по Гауссу) данных диагностики шизофрении',
x = «Возраст диагноза»,
y='Оценка плотности') +
scale_fill_manual(значения = c("красный","синий")) +
тема(
strip. background = element_blank(),
strip.text.y = element_blank(),
панель.фон = element_blank()
)
background = element_blank(),
strip.text.y = element_blank(),
панель.фон = element_blank()
) Мы также можем проверить распределение данных, используя гистограммы. Эти графики также показывают, что число возрастных диагнозов у мужчин больше сосредоточено вокруг середины 20-летнего возраста, тогда как пациенты женского пола также могут быть диагностированы в возрасте 40 лет и меньше (по сравнению с мужчинами) в середине 20-летнего возраста.
# пар(рис=с(0,1,0,1),нов=Т)
ggplot(данные=шизофрения)+
geom_histogram (aes (возраст, заполнение = пол)) +
facet_grid(пол~.) +
labs(title = 'Гистограмма диагностики шизофрении по полу',
x = «Возраст диагноза»,
у='Частота') +
scale_fill_manual(значения = c("красный","синий")) +
# scale_color_brewer (палитра = "Set2") +
тема(
strip.background = element_blank(),
strip.text.y = element_blank(),
панель.фон = element_blank()
)
## `stat_bin()`, используя `bins = 30`. Выберите лучшее значение с помощью `binwidth`.
Выберите лучшее значение с помощью `binwidth`. Или мы можем визуализировать оба вместе и увидеть те же самые результаты, которые обсуждались выше, построив этот график ниже: setWmn <- subset(шизофрения, пол!="мужской")$возраст номинал (mfrow = c (1,1)) hist (schizophrenia$age, xlab="Age", ylab="Density", main="Распределение начала шизофрении по возрасту", freq=FALSE, ylim=c(0,075), border=4) линии (плотность (setMen), столбец = 1,) линии (плотность (setWmn), столбец = 2) легенда (40, 0,05, легенда = с («Женщина», «Мужчина»), col=c(1,2), lty=c(1,1), cex=0,8)
Мы можем разделить данные о шизофрении по мужчинам и женщинам для соответствия модельного анализа по полу:
голова (шизофрения)
## возраст пол
## 1 20 жен.
## 2 30 жен.
## 3 21 женщина
## 4 23 жен.
## 5 30 жен.
## 6 25 жен.
начало = шизофрения
мужчина = подмножество (начало, пол = = "мужской")
женский = подмножество (начало, пол = = "женский")
сообщение("
Данные Mclust
","")
##
## Данные Mclust
##
mod_male = Макласт (мужской $ возраст)
mod_female = Макласт (женский возраст $)
# пар(mfrow=c(2,2))
сюжет (mod_male, что = "БИК")
title(main='БИК шизофрении у мужчин') сюжет(mod_female, что = "БИК") title(main='БИК шизофрении у женщин')
сообщение("Мужчина
","")
## Мужской
##
печать (mod_мужчина)
## Объект модели 'Mclust': (V,2)
##
## Доступные компоненты:
## [1] "вызов" "данные" "имя модели" "n"
## [5] "d" "G" "BIC" "loglik"
## [9] "df" "bic" "icl" "hypvol"
## [13] "параметры" "z" "классификация" "неопределенность"
печать (сводка (mod_male, параметры = ИСТИНА))
## ------------------------------------------------ ----
## Гауссова модель конечной смеси, аппроксимированная EM-алгоритмом
## ------------------------------------------------ ----
##
## Модель Mclust V (одномерная, неравная дисперсия) с двумя компонентами:
##
## логарифмическое правдоподобие n df BIC ICL
## -520,9747 152 5 -1067,069 -1134,392
##
## Таблица кластеризации:
## 1 2
## 99 53
##
## Вероятность смешивания:
## 1 2
## 0,5104189 0,4895811
##
## Означает:
## 1 2
## 20. 23922 27.74615
##
## Отклонения:
## 1 2
## 9.395305 111.997525
# print(mod_male$параметры)
сообщение("Женщина
","")
## Женский
##
печать (mod_female)
## Объект модели 'Mclust': (E,2)
##
## Доступные компоненты:
## [1] "вызов" "данные" "имя модели" "n"
## [5] "d" "G" "BIC" "loglik"
## [9] "df" "bic" "icl" "hypvol"
## [13] "параметры" "z" "классификация" "неопределенность"
печать (сводка (mod_female, параметры = ИСТИНА))
## ------------------------------------------------ ----
## Гауссова модель конечной смеси, аппроксимированная EM-алгоритмом
## ------------------------------------------------ ----
##
## Модель Mclust E (одномерная, равнодисперсионная) с двумя компонентами:
##
## логарифмическое правдоподобие n df BIC ICL
## -373.6992 994 -765,7788 -774,8935
##
## Таблица кластеризации:
## 1 2
## 74 25
##
## Вероятность смешивания:
## 1 2
## 0,7472883 0,2527117
##
## Означает:
## 1 2
## 24.93517 46.85570
##
## Отклонения:
## 1 2
## 44.55641 44.55641
# print(mod_female$параметры)
# мужская группа среднее
message(paste0("Среднее значение мужской группы 0,51*20,23+(1-0,51)*27,75 = ", 0,51*20,23+(1-0,51)*27,75))
## Среднее значение мужской группы составляет 0,51 * 20,23 + (1-0,51) * 27,75 = 23,9148.
23922 27.74615
##
## Отклонения:
## 1 2
## 9.395305 111.997525
# print(mod_male$параметры)
сообщение("Женщина
","")
## Женский
##
печать (mod_female)
## Объект модели 'Mclust': (E,2)
##
## Доступные компоненты:
## [1] "вызов" "данные" "имя модели" "n"
## [5] "d" "G" "BIC" "loglik"
## [9] "df" "bic" "icl" "hypvol"
## [13] "параметры" "z" "классификация" "неопределенность"
печать (сводка (mod_female, параметры = ИСТИНА))
## ------------------------------------------------ ----
## Гауссова модель конечной смеси, аппроксимированная EM-алгоритмом
## ------------------------------------------------ ----
##
## Модель Mclust E (одномерная, равнодисперсионная) с двумя компонентами:
##
## логарифмическое правдоподобие n df BIC ICL
## -373.6992 994 -765,7788 -774,8935
##
## Таблица кластеризации:
## 1 2
## 74 25
##
## Вероятность смешивания:
## 1 2
## 0,7472883 0,2527117
##
## Означает:
## 1 2
## 24.93517 46.85570
##
## Отклонения:
## 1 2
## 44.55641 44.55641
# print(mod_female$параметры)
# мужская группа среднее
message(paste0("Среднее значение мужской группы 0,51*20,23+(1-0,51)*27,75 = ", 0,51*20,23+(1-0,51)*27,75))
## Среднее значение мужской группы составляет 0,51 * 20,23 + (1-0,51) * 27,75 = 23,9148. # Среднее значение женской группы
message(paste0("Среднее значение женской группы 0,746*24,93+(1-0,747)*46,85 = ", 0,746*24,93+(1-0,747)*46,85))
## Среднее значение женской группы составляет 0,746 * 24,93 + (1-0,747) * 46,85 = 30,45083
# Среднее значение женской группы
message(paste0("Среднее значение женской группы 0,746*24,93+(1-0,747)*46,85 = ", 0,746*24,93+(1-0,747)*46,85))
## Среднее значение женской группы составляет 0,746 * 24,93 + (1-0,747) * 46,85 = 30,45083 . Из сводки модели выше мы можем видеть, что женская модель, показывающая точки данных, сосредоточена на возрастных отметках примерно 25 и 47 лет, тогда как для у мужчин это было в возрасте около 20 и 27 лет (т. Е. В пределах 20 лет). Для мужчин среднее значение составило 23,91. Точно так же среднее значение для всей женской группы составило 30,45. Таким образом, женская группа имеет большее среднее значение возраста, что говорит нам о том, что у мужчин расстройство начинается раньше, чем у женщин. Кроме того, график BIC показывает, что оптимальное количество кластеров как для мужчин, так и для женщин равно 2.
Сладкий запах плотности? Влияние подсознания на восприятие городской формы
Одна из сложнейших задач, стоящих перед планировщиками, заключается в том, как увеличить плотность городов перед лицом часто широко распространенной оппозиции со стороны широкого круга участников, от местных жителей до политиков. В то время как уплотнение все чаще рассматривается как важный компонент усилий по борьбе с изменением климата и считается, что оно имеет другие социальные и экономические преимущества, на самом деле увеличение плотности во многих случаях оказалось сложной задачей. Институт городских земель утверждает, что во всем мире существует долгая история неудачных усилий по уплотнению (Скотт, 2015). Подчеркивая сложность уплотнения, The New York Times описала конфликты, связанные с предлагаемым уплотнением вокруг одного участка в одном из образцов прогрессивной политики, Беркли, Калифорния (Dougherty, 2017). Но что объясняет эти противоречия и широко расходящиеся мнения относительно плотности? Я исследовал это в статье, недавно опубликованной в Journal of Planning Education and Research (JPER) под названием «Напыщенность, грязь и городская форма: влияют ли праймы на гигиену на восприятие городской плотности?»
В то время как уплотнение все чаще рассматривается как важный компонент усилий по борьбе с изменением климата и считается, что оно имеет другие социальные и экономические преимущества, на самом деле увеличение плотности во многих случаях оказалось сложной задачей. Институт городских земель утверждает, что во всем мире существует долгая история неудачных усилий по уплотнению (Скотт, 2015). Подчеркивая сложность уплотнения, The New York Times описала конфликты, связанные с предлагаемым уплотнением вокруг одного участка в одном из образцов прогрессивной политики, Беркли, Калифорния (Dougherty, 2017). Но что объясняет эти противоречия и широко расходящиеся мнения относительно плотности? Я исследовал это в статье, недавно опубликованной в Journal of Planning Education and Research (JPER) под названием «Напыщенность, грязь и городская форма: влияют ли праймы на гигиену на восприятие городской плотности?»
Одно из объяснений глубоко расходящихся точек зрения на уплотнение заключается в том, что эти чувства могут быть основаны не на «объективных» характеристиках плотности, а на подсознательных факторах. Исследования в области психологии и смежных наук о поведении утверждают, что «большая часть повседневной жизни человека определяется не его сознательными намерениями, а психическими процессами… которые действуют за пределами сознательного понимания» (Bargh and Chartrand, 1999: 462). Один из аспектов обширной работы над этими подсознательными влияниями на восприятие был сосредоточен на «прайминге», эффекте, при котором воздействие одного стимула влияет на реакцию на другой. Прайминг-исследования показали, что, например, размышления о профессорах улучшают результаты в Trivial Pursuit (Dijksterhuis and Van Knippenberg, 19).98), а чтение слов, связанных с пожилыми людьми, таких как «Флорида», ассоциируется с тем, что люди ходят медленнее (Bargh, Chen and Burrows, 1996). Прайминг-исследования стали почти повсеместными в социальной психологии и смежных поведенческих областях, но, что примечательно, очень редко изучали городской контекст и не обращались к проблеме плотности. В документе JPER была предпринята попытка исправить этот пробел путем изучения того, было ли восприятие плотности, как и многие другие социальные, политические и моральные установки, податливым и открытым для влияния через прайминг.
Исследования в области психологии и смежных наук о поведении утверждают, что «большая часть повседневной жизни человека определяется не его сознательными намерениями, а психическими процессами… которые действуют за пределами сознательного понимания» (Bargh and Chartrand, 1999: 462). Один из аспектов обширной работы над этими подсознательными влияниями на восприятие был сосредоточен на «прайминге», эффекте, при котором воздействие одного стимула влияет на реакцию на другой. Прайминг-исследования показали, что, например, размышления о профессорах улучшают результаты в Trivial Pursuit (Dijksterhuis and Van Knippenberg, 19).98), а чтение слов, связанных с пожилыми людьми, таких как «Флорида», ассоциируется с тем, что люди ходят медленнее (Bargh, Chen and Burrows, 1996). Прайминг-исследования стали почти повсеместными в социальной психологии и смежных поведенческих областях, но, что примечательно, очень редко изучали городской контекст и не обращались к проблеме плотности. В документе JPER была предпринята попытка исправить этот пробел путем изучения того, было ли восприятие плотности, как и многие другие социальные, политические и моральные установки, податливым и открытым для влияния через прайминг.
Чтобы изучить взаимосвязь между праймингом и плотностью городского населения, я использовал оборудование Гарварда для проведения поведенческих экспериментов. В Гарвардской научной лаборатории принятия решений есть несколько комнат, в каждой из которых есть отдельные компьютерные терминалы, за которыми отдельные участники исследования могут участвовать в тестах и отвечать на вопросы. В своем исследовании я сосредоточился на праймах или сигналах гигиены из-за сильной концептуальной связи с городской плотностью. Связь между представлениями о гигиене и плотности населения существует давно: богатые жители густонаселенных средневековых городов уезжали в сельские районы во время чумы, а в последнее время мотивы гигиены занимают видное место в обосновании многих плановых вмешательств, начиная от создания Стандартный закон о разрешении зонирования в 1926 к росту пригородов в середине 20 века.
В исследовании приняли участие 437 участников, которые участвовали в двух опросах о визуальных предпочтениях и двух повествовательных сценариях. Отвечая на вопросы об опросах и сценариях визуальных предпочтений, участники были случайным образом распределены по четырем группам. В первой группе участники просто просматривали и оценивали изображения с различными настройками плотности, которые были взяты из базы данных визуализации плотности Института Линкольна, и отвечали на вопросы о предполагаемом увеличении плотности в их районе. Участники, случайно распределенные по трем другим группам, выполняли те же самые задачи, но подсознательно подвергались воздействию правил гигиены. Эти простые числа были выбраны на основе обширных прошлых исследований, которые утверждают, что такие простые числа могут влиять на моральные, политические и социальные взгляды. Тремя главными были: продезинфицировать руки до и после ответов на вопросы; на клавиатуре осталась банановая кожура, которую нужно выбросить в мусорное ведро, прежде чем отвечать на вопросы; и подвергся воздействию пердёжного спрея, который был введен в комнату в начале сеанса (да, последнее вы правильно прочитали!).
Отвечая на вопросы об опросах и сценариях визуальных предпочтений, участники были случайным образом распределены по четырем группам. В первой группе участники просто просматривали и оценивали изображения с различными настройками плотности, которые были взяты из базы данных визуализации плотности Института Линкольна, и отвечали на вопросы о предполагаемом увеличении плотности в их районе. Участники, случайно распределенные по трем другим группам, выполняли те же самые задачи, но подсознательно подвергались воздействию правил гигиены. Эти простые числа были выбраны на основе обширных прошлых исследований, которые утверждают, что такие простые числа могут влиять на моральные, политические и социальные взгляды. Тремя главными были: продезинфицировать руки до и после ответов на вопросы; на клавиатуре осталась банановая кожура, которую нужно выбросить в мусорное ведро, прежде чем отвечать на вопросы; и подвергся воздействию пердёжного спрея, который был введен в комнату в начале сеанса (да, последнее вы правильно прочитали!). Было показано, что праймы каждого из этих типов влияют на политические и социальные установки и моральные суждения, и цель состояла в том, чтобы увидеть, могут ли восприятия плотности быть аналогичным образом подвержены влиянию.
Было показано, что праймы каждого из этих типов влияют на политические и социальные установки и моральные суждения, и цель состояла в том, чтобы увидеть, могут ли восприятия плотности быть аналогичным образом подвержены влиянию.
Результаты исследования не показали последовательного влияния гигиенического прайминга на восприятие плотности. Это несколько удивительно, учитывая очень обширный объем исследований прайминга, которые до сих пор показывают, что практически все восприятия и установки могут быть праймированы. Если бы прайминг повлиял на восприятие плотности, это могло бы открыть множество подсознательных вмешательств для изменения этих восприятий. Хотя это, возможно, звучит неправдоподобно, правительства и частный сектор уже начали предпринимать такие усилия, хотя и не в сфере городского планирования. В сфере государственной политики в более широком смысле, например, правительство Великобритании создало Группу изучения поведения, или «Подразделение подталкивания», которая стремится использовать поведенческие знания, чтобы «дать людям возможность сделать «лучший выбор для себя»» (Кабинет министров Великобритании). Офис, 2018). В частном секторе предварительные исследования, такие как исследования, показывающие, что запах шоколада связан с тем, что люди покупают больше книг, побудили компании разработать технологию ароматизации, которая может распространять более 300 различных запахов в магазинах, чтобы влиять на предпочтения покупателей.
Офис, 2018). В частном секторе предварительные исследования, такие как исследования, показывающие, что запах шоколада связан с тем, что люди покупают больше книг, побудили компании разработать технологию ароматизации, которая может распространять более 300 различных запахов в магазинах, чтобы влиять на предпочтения покупателей.
Это исследование предполагает, что восприятие плотности относительно стабильно по отношению к праймингу, что может иметь потенциальные последствия для планирования. Несмотря на относительно небольшое количество отрицательных результатов прайминга, результаты этого исследования показывают, что, по крайней мере, в отношении гигиенических праймингов, восприятие плотности относительно стабильно. Это, в свою очередь, может означать, что усилия по изменению плотности могут столкнуться с сопротивлением и что стратегии уплотнения должны будут сопровождаться обширными усилиями по завоеванию скептически настроенных и потенциально трудно убедительных сторонников. Помимо рассмотрения вопроса о гигиеническом прайминге и плотности, в документе также предлагается уделять больше внимания поведенческим аспектам городского планирования и расширять разнообразие методов, включая большее внимание экспериментальным методам, в наборе инструментов ученых и практиков в области планирования.
Ссылки:
Bargh, J., and T. Chartrand. 1999. «Невыносимая автоматизация бытия». Американский психолог, 54 (7): 462–79.
Барг, Дж., М. Чен и Л. Берроуз. 1996. «Автоматизм социального поведения: прямое влияние конструкции черт и активации стереотипов на действия». Журнал личности и социальной психологии, 71 (2): 230–44.
Дейкстерхуис, Ап и Эд Ван Книппенберг. 1998. «Связь между восприятием и поведением, или как выиграть игру тривиального преследования». Журнал личности и социальной психологии, 74 (4): 865–77.
Догерти, К. 2017. «Великая американская проблема домов на одну семью». The New York Times, 1 декабря 2017 г.
Грот, П. Жизнь в центре города: история жилых отелей в Соединенных Штатах. Беркли: Калифорнийский университет Press; 1994.
Скотт, Л. 2015. «Преодоление сопротивления большей плотности». Журнал Urban Land, 6 июля 2015 г.
Кабинет министров Соединенного Королевства. 2018. «Группа изучения поведения». По состоянию на 15 июня 2018 г.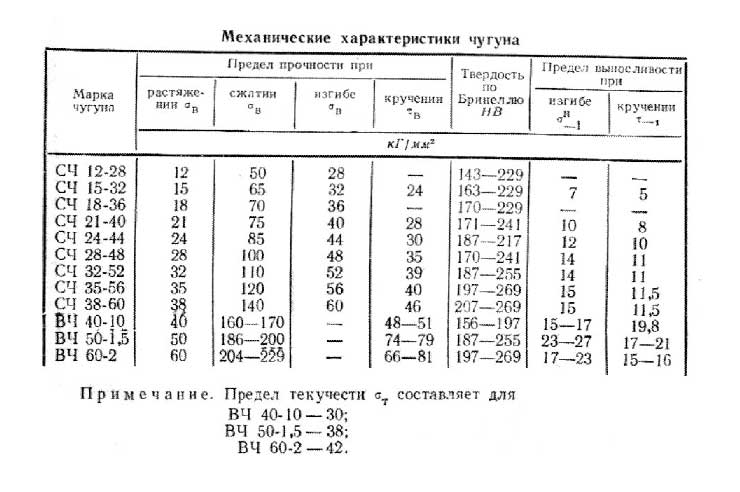


 103
103
 Доказательством существования сверхскоплений была бы мультимодальность распределения скоростей.
Доказательством существования сверхскоплений была бы мультимодальность распределения скоростей.
 out = BINS + 1)
ШИРИНА ДИАПАЗОНА <- РАЗРЫВЫ[2] - РАЗРЫВЫ[1]
ggplot() + aes(галактики) + geom_histogram(aes(y = ..density..), binwidth = BINWIDTH, breaks = c(seq(5000, 35000, 5000)), border = NULL, fill = 'небесно-голубой', цвет = "черный", закрытый = "левый") +
labs(title = "ggplot: Истинная гистограмма, показывающая галактики")
out = BINS + 1)
ШИРИНА ДИАПАЗОНА <- РАЗРЫВЫ[2] - РАЗРЫВЫ[1]
ggplot() + aes(галактики) + geom_histogram(aes(y = ..density..), binwidth = BINWIDTH, breaks = c(seq(5000, 35000, 5000)), border = NULL, fill = 'небесно-голубой', цвет = "черный", закрытый = "левый") +
labs(title = "ggplot: Истинная гистограмма, показывающая галактики")  ", " ")
## # 1б.
loggalaxies <- log(галактики)
# гистограмма
message("Используя hist и geom_histogram:", " ")
## Используя hist и geom_histogram:
#установить положение фигуры
# пар(рис=с(0,1,0,1),новый=Т)
#нарисовать гистограмму
история(логалактики,
xlab = 'логарифм скорости',
main = 'база R: гистограмма, показывающая логарифмическую скорость галактик',
ylab = 'Частота', freq = ИСТИНА)
", " ")
## # 1б.
loggalaxies <- log(галактики)
# гистограмма
message("Используя hist и geom_histogram:", " ")
## Используя hist и geom_histogram:
#установить положение фигуры
# пар(рис=с(0,1,0,1),новый=Т)
#нарисовать гистограмму
история(логалактики,
xlab = 'логарифм скорости',
main = 'база R: гистограмма, показывающая логарифмическую скорость галактик',
ylab = 'Частота', freq = ИСТИНА)  5, length.out = BINS + 1)
ШИРИНА ДИАПАЗОНА <- РАЗРЫВЫ[2] - РАЗРЫВЫ[1]
# ggplot() + aes(loggalaxies) + geom_histogram(binwidth = BINWIDTH, border = NULL, fill = 'skyblue', color = "black", close = "left") # Частота
ggplot() + aes(loggalaxies) + geom_histogram(aes(y = ..density..), binwidth = BINWIDTH, bins = BINS, breaks = BREAKS, border = NULL, fill = 'небесно-голубой', color = "черный", закрытый = "левый") +
labs(title = "ggplot: Истинная гистограмма логарифмической скорости галактик")
5, length.out = BINS + 1)
ШИРИНА ДИАПАЗОНА <- РАЗРЫВЫ[2] - РАЗРЫВЫ[1]
# ggplot() + aes(loggalaxies) + geom_histogram(binwidth = BINWIDTH, border = NULL, fill = 'skyblue', color = "black", close = "left") # Частота
ggplot() + aes(loggalaxies) + geom_histogram(aes(y = ..density..), binwidth = BINWIDTH, bins = BINS, breaks = BREAKS, border = NULL, fill = 'небесно-голубой', color = "черный", закрытый = "левый") +
labs(title = "ggplot: Истинная гистограмма логарифмической скорости галактик")  ", "")
## # 1с.
truehist (галактики, ymax = 0,0002, col = "синий", main = "база R: гауссово сверхгладкое")
линии (плотность (галактики, ядро = "гаусс", bw = 5000), col = "красный")
", "")
## # 1с.
truehist (галактики, ymax = 0,0002, col = "синий", main = "база R: гауссово сверхгладкое")
линии (плотность (галактики, ядро = "гаусс", bw = 5000), col = "красный")  out = BINS + 1)
ШИРИНА ДИАПАЗОНА <- РАЗРЫВЫ[2] - РАЗРЫВЫ[1]
ggplot() +
aes (галактики) +
geom_histogram(aes(y=..density..), bins = BINS, binwidth = BINWIDTH, breaks = BREAKS, border = NULL, fill = 'синий', color = "black", close = "left") +
stat_density (ядро = "гауссово", чб = 1100, заливка = нет данных, столбец = "красный") +
labs(title = "ggplot: Gaussian Best Appx")
out = BINS + 1)
ШИРИНА ДИАПАЗОНА <- РАЗРЫВЫ[2] - РАЗРЫВЫ[1]
ggplot() +
aes (галактики) +
geom_histogram(aes(y=..density..), bins = BINS, binwidth = BINWIDTH, breaks = BREAKS, border = NULL, fill = 'синий', color = "black", close = "left") +
stat_density (ядро = "гауссово", чб = 1100, заливка = нет данных, столбец = "красный") +
labs(title = "ggplot: Gaussian Best Appx")  out = BINS + 1)
ШИРИНА ДИАПАЗОНА <- РАЗРЫВЫ[2] - РАЗРЫВЫ[1]
ggplot() +
aes (галактики) +
geom_histogram(aes(y=..density..), bins = BINS, binwidth = BINWIDTH, breaks = BREAKS, border = NULL, fill = 'green', color = "black", close = "left") +
stat_density(kernel = "треугольный", bw = 500, fill = NA, col = "red") +
labs(title = "ggplot: Triangular Under Smooth")
out = BINS + 1)
ШИРИНА ДИАПАЗОНА <- РАЗРЫВЫ[2] - РАЗРЫВЫ[1]
ggplot() +
aes (галактики) +
geom_histogram(aes(y=..density..), bins = BINS, binwidth = BINWIDTH, breaks = BREAKS, border = NULL, fill = 'green', color = "black", close = "left") +
stat_density(kernel = "треугольный", bw = 500, fill = NA, col = "red") +
labs(title = "ggplot: Triangular Under Smooth")  "," ")
## # 1д.
# мы можем использовать:
библиотека (макласт)
## Предупреждение: пакет mclust был собран под R версии 4.0.5.
## Пакет mclust версии 5.4.9
## Введите 'citation("mclust")' для цитирования этого пакета R в публикациях.
mod=Mclust(галактики)
печать (мод)
## Объект модели 'Mclust': (V,4)
##
## Доступные компоненты:
## [1] "вызов" "данные" "имя модели" "n"
## [5] "d" "G" "BIC" "loglik"
## [9] "df" "bic" "icl" "hypvol"
## [13] "параметры" "z" "классификация" "неопределенность"
печать (резюме (мод, параметры = ИСТИНА))
## ------------------------------------------------ ----
## Гауссова модель конечной смеси, аппроксимированная EM-алгоритмом
## ------------------------------------------------ ----
##
## Модель Mclust V (одномерная, неравная дисперсия) с 4 компонентами:
##
## логарифмическое правдоподобие n df BIC ICL
## -765.694 82 11 -15790,862 -1598,907
##
## Таблица кластеризации:
## 1 2 3 4
## 7 35 32 8
##
## Вероятность смешивания:
## 1 2 3 4
## 0,08440635 0,38660329 0,37116156 0,15782880
##
## Означает:
## 1 2 3 4
## 9707.
"," ")
## # 1д.
# мы можем использовать:
библиотека (макласт)
## Предупреждение: пакет mclust был собран под R версии 4.0.5.
## Пакет mclust версии 5.4.9
## Введите 'citation("mclust")' для цитирования этого пакета R в публикациях.
mod=Mclust(галактики)
печать (мод)
## Объект модели 'Mclust': (V,4)
##
## Доступные компоненты:
## [1] "вызов" "данные" "имя модели" "n"
## [5] "d" "G" "BIC" "loglik"
## [9] "df" "bic" "icl" "hypvol"
## [13] "параметры" "z" "классификация" "неопределенность"
печать (резюме (мод, параметры = ИСТИНА))
## ------------------------------------------------ ----
## Гауссова модель конечной смеси, аппроксимированная EM-алгоритмом
## ------------------------------------------------ ----
##
## Модель Mclust V (одномерная, неравная дисперсия) с 4 компонентами:
##
## логарифмическое правдоподобие n df BIC ICL
## -765.694 82 11 -15790,862 -1598,907
##
## Таблица кластеризации:
## 1 2 3 4
## 7 35 32 8
##
## Вероятность смешивания:
## 1 2 3 4
## 0,08440635 0,38660329 0,37116156 0,15782880
##
## Означает:
## 1 2 3 4
## 9707. 492 19804.259 22879.486 24459.536
##
## Отклонения:
## 1 2 3 4
## 177296,7 436160,9 1261611,3 34437115,3
#pot график плотности модели
# пар(рис=с(0,1,0,1),новый=Т)
сюжет (мод, что = "плотность")
title ("График плотности конечной модели смеси")
492 19804.259 22879.486 24459.536
##
## Отклонения:
## 1 2 3 4
## 177296,7 436160,9 1261611,3 34437115,3
#pot график плотности модели
# пар(рис=с(0,1,0,1),новый=Т)
сюжет (мод, что = "плотность")
title ("График плотности конечной модели смеси") 
 . уровень ..)) +
scale_color_gradient (низкий = "зеленый", высокий = "красный") +
тема_bw() +
геометрическая_точка() +
labs(title='ggplot: График рассеяния рождаемости_смерти_коэффициентов',
х='Рождаемость',
y='Смертность') +
scale_x_continuous (пределы = c (0,60)) +
scale_y_continuous (пределы = c (0,35))
. уровень ..)) +
scale_color_gradient (низкий = "зеленый", высокий = "красный") +
тема_bw() +
геометрическая_точка() +
labs(title='ggplot: График рассеяния рождаемости_смерти_коэффициентов',
х='Рождаемость',
y='Смертность') +
scale_x_continuous (пределы = c (0,60)) +
scale_y_continuous (пределы = c (0,35))  4841
##
## Таблица кластеризации:
## 1 2 3 4
## 2 17 38 12
##
## Вероятность смешивания:
## 1 2 3 4
## 0,02898652 0,24555002 0,55023375 0,17522972
##
## Означает:
## [1] [2] [3] [4]
## рождения 55,94967 43,80396 19,922913 33,730672
## смерть 29.34960 12.09411 9.081348 8.535812
##
## Отклонения:
## [1]
## рождение смерть
## рождения 10.2108 0.0000
## смерть 0.0000 10.2108
## [2]
## рождение смерть
## рождения 10.2108 0.0000
## смерть 0.0000 10.2108
## [3]
## рождение смерть
## рождения 10.2108 0.0000
## смерть 0.0000 10.2108
## [4]
## рождение смерть
## рождения 10.2108 0.0000
## смерть 0.0000 10.2108
message("Значение для mod$parameters$mean", " ")
## Значение для mod$parameters$mean
sqrt(mod$parameters$дисперсия$sigmasq)
## [1] 3.195434
BIC.data<- as.data.frame(mod$BIC[])
BIC.data$NumComp<-названия строк(BIC.data)
Melted.BIC<- reshape2::melt(BIC.data, var.ids= "NumComp")
## Использование NumComp в качестве переменных идентификатора
пар(mfrow=с(1,1), спросить=ЛОЖЬ)
# БИК
plot(mod, what="BIC", main = "база R: График BIC")
4841
##
## Таблица кластеризации:
## 1 2 3 4
## 2 17 38 12
##
## Вероятность смешивания:
## 1 2 3 4
## 0,02898652 0,24555002 0,55023375 0,17522972
##
## Означает:
## [1] [2] [3] [4]
## рождения 55,94967 43,80396 19,922913 33,730672
## смерть 29.34960 12.09411 9.081348 8.535812
##
## Отклонения:
## [1]
## рождение смерть
## рождения 10.2108 0.0000
## смерть 0.0000 10.2108
## [2]
## рождение смерть
## рождения 10.2108 0.0000
## смерть 0.0000 10.2108
## [3]
## рождение смерть
## рождения 10.2108 0.0000
## смерть 0.0000 10.2108
## [4]
## рождение смерть
## рождения 10.2108 0.0000
## смерть 0.0000 10.2108
message("Значение для mod$parameters$mean", " ")
## Значение для mod$parameters$mean
sqrt(mod$parameters$дисперсия$sigmasq)
## [1] 3.195434
BIC.data<- as.data.frame(mod$BIC[])
BIC.data$NumComp<-названия строк(BIC.data)
Melted.BIC<- reshape2::melt(BIC.data, var.ids= "NumComp")
## Использование NumComp в качестве переменных идентификатора
пар(mfrow=с(1,1), спросить=ЛОЖЬ)
# БИК
plot(mod, what="BIC", main = "база R: График BIC") 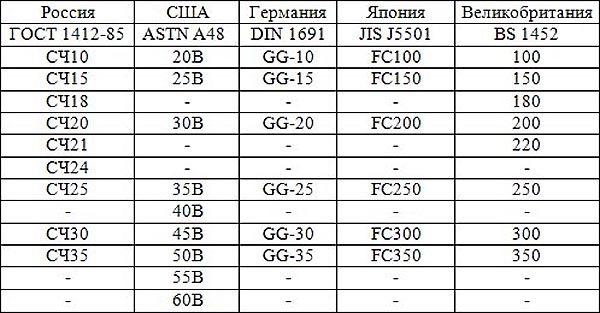 BIC, aes(x=as.numeric(NumComp), y=значение, цвет=переменная, группа=переменная))+
scale_x_continuous ("Количество компонентов")+
scale_y_continuous ("БИК")+
scale_color_hue("")+
геом_точка()+
геометрическая_линия()+
тема_bw() +
лаборатории (название = "ggplot: BIC")
## Предупреждение: удалено 19строки, содержащие пропущенные значения (geom_point).
## Предупреждение: удалено 19 строк, содержащих отсутствующие значения (geom_path).
BIC, aes(x=as.numeric(NumComp), y=значение, цвет=переменная, группа=переменная))+
scale_x_continuous ("Количество компонентов")+
scale_y_continuous ("БИК")+
scale_color_hue("")+
геом_точка()+
геометрическая_линия()+
тема_bw() +
лаборатории (название = "ggplot: BIC")
## Предупреждение: удалено 19строки, содержащие пропущенные значения (geom_point).
## Предупреждение: удалено 19 строк, содержащих отсутствующие значения (geom_path). 
 Предполагается, что тип с ранним началом чаще встречается у мужчин, а тип с поздним началом — у женщин. Подгонка конечных смесей нормальной плотности отдельно к данным начала для мужчин и женщин, приведенным в
Предполагается, что тип с ранним началом чаще встречается у мужчин, а тип с поздним началом — у женщин. Подгонка конечных смесей нормальной плотности отдельно к данным начала для мужчин и женщин, приведенным в  background = element_blank(),
strip.text.y = element_blank(),
панель.фон = element_blank()
)
background = element_blank(),
strip.text.y = element_blank(),
панель.фон = element_blank()
)  Выберите лучшее значение с помощью `binwidth`.
Выберите лучшее значение с помощью `binwidth`.  23922 27.74615
##
## Отклонения:
## 1 2
## 9.395305 111.997525
# print(mod_male$параметры)
сообщение("Женщина
","")
## Женский
##
печать (mod_female)
## Объект модели 'Mclust': (E,2)
##
## Доступные компоненты:
## [1] "вызов" "данные" "имя модели" "n"
## [5] "d" "G" "BIC" "loglik"
## [9] "df" "bic" "icl" "hypvol"
## [13] "параметры" "z" "классификация" "неопределенность"
печать (сводка (mod_female, параметры = ИСТИНА))
## ------------------------------------------------ ----
## Гауссова модель конечной смеси, аппроксимированная EM-алгоритмом
## ------------------------------------------------ ----
##
## Модель Mclust E (одномерная, равнодисперсионная) с двумя компонентами:
##
## логарифмическое правдоподобие n df BIC ICL
## -373.6992 994 -765,7788 -774,8935
##
## Таблица кластеризации:
## 1 2
## 74 25
##
## Вероятность смешивания:
## 1 2
## 0,7472883 0,2527117
##
## Означает:
## 1 2
## 24.93517 46.85570
##
## Отклонения:
## 1 2
## 44.55641 44.55641
# print(mod_female$параметры)
# мужская группа среднее
message(paste0("Среднее значение мужской группы 0,51*20,23+(1-0,51)*27,75 = ", 0,51*20,23+(1-0,51)*27,75))
## Среднее значение мужской группы составляет 0,51 * 20,23 + (1-0,51) * 27,75 = 23,9148.
23922 27.74615
##
## Отклонения:
## 1 2
## 9.395305 111.997525
# print(mod_male$параметры)
сообщение("Женщина
","")
## Женский
##
печать (mod_female)
## Объект модели 'Mclust': (E,2)
##
## Доступные компоненты:
## [1] "вызов" "данные" "имя модели" "n"
## [5] "d" "G" "BIC" "loglik"
## [9] "df" "bic" "icl" "hypvol"
## [13] "параметры" "z" "классификация" "неопределенность"
печать (сводка (mod_female, параметры = ИСТИНА))
## ------------------------------------------------ ----
## Гауссова модель конечной смеси, аппроксимированная EM-алгоритмом
## ------------------------------------------------ ----
##
## Модель Mclust E (одномерная, равнодисперсионная) с двумя компонентами:
##
## логарифмическое правдоподобие n df BIC ICL
## -373.6992 994 -765,7788 -774,8935
##
## Таблица кластеризации:
## 1 2
## 74 25
##
## Вероятность смешивания:
## 1 2
## 0,7472883 0,2527117
##
## Означает:
## 1 2
## 24.93517 46.85570
##
## Отклонения:
## 1 2
## 44.55641 44.55641
# print(mod_female$параметры)
# мужская группа среднее
message(paste0("Среднее значение мужской группы 0,51*20,23+(1-0,51)*27,75 = ", 0,51*20,23+(1-0,51)*27,75))
## Среднее значение мужской группы составляет 0,51 * 20,23 + (1-0,51) * 27,75 = 23,9148. # Среднее значение женской группы
message(paste0("Среднее значение женской группы 0,746*24,93+(1-0,747)*46,85 = ", 0,746*24,93+(1-0,747)*46,85))
## Среднее значение женской группы составляет 0,746 * 24,93 + (1-0,747) * 46,85 = 30,45083
# Среднее значение женской группы
message(paste0("Среднее значение женской группы 0,746*24,93+(1-0,747)*46,85 = ", 0,746*24,93+(1-0,747)*46,85))
## Среднее значение женской группы составляет 0,746 * 24,93 + (1-0,747) * 46,85 = 30,45083