Шкалы измерений: Измерение. Шкалы измерений
alexxlab | 25.02.2023 | 0 | Разное
Шкалы измерений | Портал основных средств
В качестве начальных понятий в курсе статистики, которая является базовой дисциплиной для всех, получающих профессиональное экономическое (финансовое, бухгалтерское) образование как средне-специальное, так и высшее, рассматриваются шкалы измерений, их свойства и последствия отсутствия шкалы.
Отсутствие шкалы
В отсутствие шкалы значения даже нельзя сравнивать. Одинаковые по смыслу значения могут быть текстуально различными, и потому фиксация текстуального неравенства не означает неравенства смыслового. Пример: наименования объектов основных средств не образуют шкалы, потому что одинаковые объекты могут называться по-разному.
В отсутствие шкалы никакие статистические операции невозможны.
Номинальная шкала
Номинальная (категориальная) шкала – значения (категории) можно сравнить и выяснить, равны они или различаются. Если значения текстуально равны, то они одинаковы по смыслу, если значения текстуально различны, то смысл их разный.
Пример: коды общероссийских классификаторов образуют номинальную шкалу. Объекты с одинаковым кодом схожи, с разными – различны.
На номинальной шкале возможны только группировка объектов по категориям и упорядочение категорий по числу объектов.
Ординальная шкала
Ординальная (порядковая) шкала – значения (категории) можно сравнить и выяснить, равны ли они, и если нет, то какое больше (лучше). Т. е. значения на шкале выстроены в определенном порядке. Пример: номера амортизационных групп образуют ординальную шкалу. Объект из более высокой группы имеет больший срок полезного использования.
На ординальной шкале, помимо группировки по категориям, возможно вычисление медианной категории (в которую попадает объект, разделяющий множество исследуемых объектов на две равные части).
Интервальная шкала
Интервальная (разностная) шкала – шкала, в которой уровни упорядочены, а интервалы между ними равны. Её можно рассматривать как расширение порядковой шкалы.
Основным отличием является свойство равных интервалов. Интервальная шкала не только позволяет однозначно определить, какое значение больше (меньше), но и на сколько.
Примером интервальных шкал могут служить температурные шкалы Цельсия и Фаренгейта.
На интервальной шкале можно рассчитывать средние значения, медиану, моду и т. п. статистики.
Абсолютная шкала
Абсолютная шкала (релятивная шкала, шкала отношений) – интервальная шкала, на которой установлено абсолютное нулевое значение. На такой шкале возможна не только фиксация равноудаленности/неравноудаленности позиций, но и количественное сравнение длин любых интервалов (отношение интервалов). Примером абсолютной шкалы является шкала измерения любого количества (в штуках) или физической величины (длины, массы, объема, времени и т. п.). Например, срок полезного использования объекта является значением абсолютной шкалы, и, скажем, объект со сроком использования 120 мес. служит вдвое дольше объекта со СПИ 60 мес.
На абсолютной шкале возможны расчеты не только центрированных статистик (среднего значения, моды, медианы и т. п.), но и отклонений (дисперсии, размаха, стандартного отклонения и т. п.).
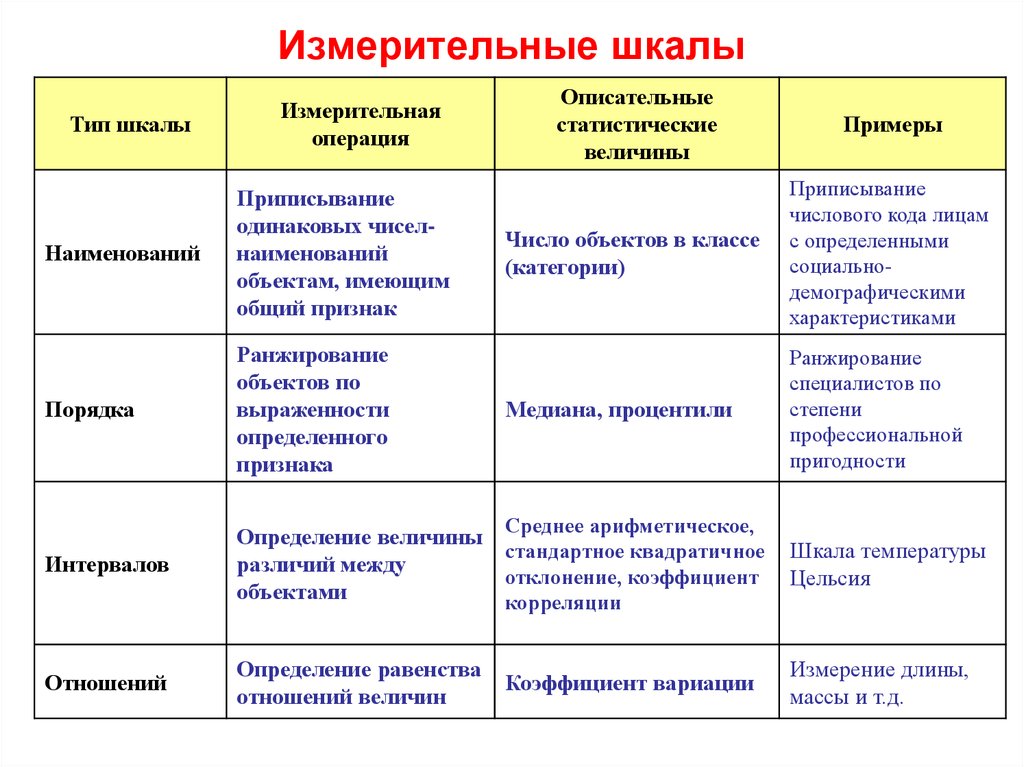
1. Понятие шкалы измерений. Типы шкал измерений, их основные характеристики. Примеры различных типов шкал измерений.
Понятия
физическая величина и измерение тесным
образом связаны с понятием шкалы
физической величины – упорядоченной
совокупностью значений физической
величины, служащей исходной основой
для измерений данной величины. Шкалой
измерений называют порядок определения
и обозначения возможных значений
конкретной величины или проявлений
какого-либо свойства. Понятия шкалы
возникли в связи с необходимостью
изучать не только количественные, но и
качественные свойства природных и
рукотворных объектов и явлений. Различают
несколько типов шкал: 1. Шкала наименований
(классификации) – это самая простая
шкала, которая основана на приписывании
объекту знаков или цифр для их идентификации
или нумерации.
Например, атлас цветов
(шкала цветов) или шкала (классификация)
растений Карла Линнея. Данные шкалы
характеризуются только отношением
эквивалентности (равенства) и в них
отсутствуют понятия больше, меньше,
отсутствуют единицы измерения и нулевое
значение. Этот вид шкал приписывает
свойствам объектов определенные числа,
которые выполняют функцию имен. Процесс
оценивания в таких шкалах состоит в
достижении эквивалентности путем
сравнения испытуемого образца с одним
из эталонных образцов. Таким образом,
шкала наименований отражает качественные
свойства. 2. Шкала порядка (ранжирования)
– упорядочивает объекты относительно
какого-либо их свойства в порядке
убывания или возрастания, например,
шкала землетрясений, силы ветра. Эти
шкалы описывают уже количественные
свойства. В данной шкале невозможно
ввести единицу измерения, так как эти
шкалы в принципе нелинейны. В ней можно
говорить лишь о том, что больше или
меньше, хуже или лучше, но невозможно
дать количественную оценку во сколько
раз больше или меньше.
Примером
шкалы отношений является шкала масс –
массы тел можно суммировать, даже если
они не находятся в одном месте. 5.
Абсолютные шкалы – это шкалы отношений,
в которых однозначно (а не по соглашению)
присутствует определение единицы
измерения. Абсолютные шкалы присущи
относительным единицам (коэффициенты
усиления, полезного действия и др.),
единицы таких шкал являются безразмерными.
Условные шкалы – шкалы, исходные значения
которых выражены в условных единицах.
К таким шкалам относятся шкалы наименований
и порядка. Шкалы разностей, отношений
и абсолютные называются метрическими
(физическими) шкалами.Характеристики шкал измерений:
Шкала | Характеристики | |||
Нуль ФВ | Возрастание / убывание ФВ | Единица измерения | Применяемые математические операции | |
Наименований | Отсутствует | Отсутствует | Отсутствует | Невозможно |
Порядка | Отсутствует или задан условно | Применимо | Отсутствует | Невозможно |
Интервалов | Произвольно выбранный | Применимо | Имеется | «+», «–», «», «» над интервалами |
Отношений | Естественный | Применимо | Имеется | «+», «–», «», «» над величинами |
Абсолютные | Естественный | Применимо | Естественная | |
Типы данных и шкалы измерения
Данные являются ценным активом настолько, что это самый ценный ресурс в мире.
Это делает понимание различных типов данных и роль специалиста по обработке и анализу данных более важными, чем когда-либо. В деловом мире все больше компаний пытаются понять большие числа и то, что они могут с ними сделать. Экспертиза данных пользуется большим спросом. Определение правильных данных и шкал измерения позволяет компаниям организовывать, идентифицировать, анализировать и, в конечном счете, использовать данные для обоснования стратегий, которые позволят им оказывать реальное влияние.
Данные высшего уровня: качественные и количественные
Что такое данные? Короче говоря, это совокупность измерений или наблюдений, разделенных на два разных типа: качественные и количественные.
Качественные данные относятся к информации о качествах или к информации, которую невозможно измерить. Как правило, описательный и текстовый. Примеры включают цвет глаз человека или тип автомобиля, на котором он ездит. В опросах он часто используется для классификации ответов «да» или «нет»..gif)
Количественные данные являются числовыми. Он используется для определения информации, которую можно подсчитать. Некоторые примеры количественных данных включают расстояние, скорость, рост, длину и вес. Легко запомнить разницу между качественными и количественными данными, поскольку одни относятся к качествам, а другие — к количествам.
Книжная полка, например, может иметь 100 книг на полках и иметь высоту 100 сантиметров. Это количественные точки данных. Цвет книжной полки — красный — является качественной точкой данных.
Что такое количественные (числовые) данные?
Количественные или числовые данные можно разделить на два типа: дискретные и непрерывные.
Дискретные данные
Дискретные данные — это целое число, которое нельзя разделить или разбить на отдельные части, дроби или десятичные дроби. Примеры дискретных данных включают количество домашних животных у кого-то — можно иметь двух собак, но не двух с половиной собак. Количество побед чьей-либо любимой команды также является формой дискретных данных, потому что у команды не может быть полувыигрыша — это либо победа, либо поражение, либо ничья.
Непрерывные данные
Непрерывные данные описывают значения, которые можно разбить на различные части, единицы, дроби и десятичные дроби. Можно измерять непрерывные точки данных, такие как рост и вес. Время также можно разбить – на полсекунды или на полчаса. Температура — еще один пример непрерывных данных.
Дискретные и непрерывные
Существует простой способ запомнить разницу между двумя типами количественных данных: данные считаются дискретными, если их можно подсчитать, и непрерывными, если их можно измерить. Кто-то может считать студентов, купленные билеты и книги, а кто-то измеряет рост, расстояние и температуру.
Что такое качественные (категориальные) данные?
Качественные данные описывают качество точек данных и не являются числовыми. Он используется для определения информации, а также может быть дополнительно разбит на подкатегории по четырем шкалам измерения.
Свойства и масштабы измерения
Шкалы измерения определяют и классифицируют переменные.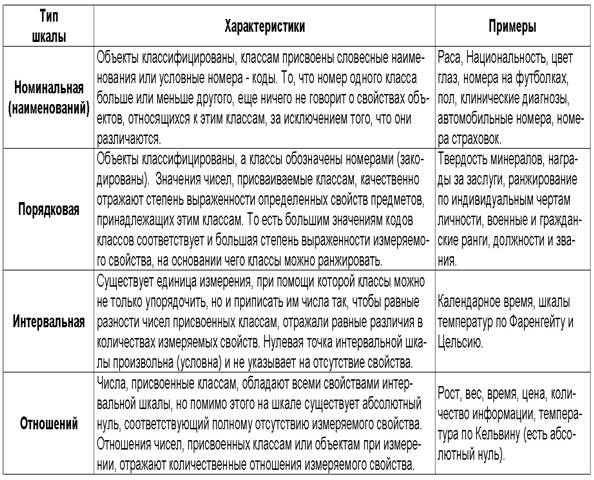
Психолог Стэнли Стивенс разработал четыре общепринятые шкалы измерения: .номинал , порядковый номер , интервал и коэффициент . Каждая шкала измерения имеет свойства, которые определяют, как правильно анализировать данные. Оцениваются следующие свойства: идентичность , величина , равные интервалы и минимальное значение, равное нулю .
Свойства измерения
Идентичность: Идентичность относится к каждому значению, имеющему уникальное значение.
Величина: Величина означает, что значения имеют упорядоченное отношение друг к другу, поэтому переменные имеют определенный порядок.
Равные интервалы: Равные интервалы означают, что точки данных вдоль шкалы равны, поэтому разница между точками данных 1 и 2 будет такой же, как разница между точками данных 5 и 6.
Минимальное значение нуля: Минимальное значение нуля означает, что весы имеют истинную нулевую точку.
Градусы, например, могут упасть ниже нуля и все еще иметь значение. Но если вы ничего не весите, вы не существуете.
Градусы, например, могут упасть ниже нуля и все еще иметь значение. Но если вы ничего не весите, вы не существуете.Четыре шкалы измерения
Понимая масштаб измерения своих данных, специалисты по данным могут определить тип статистического теста для выполнения.
1. Номинальная шкала измерения
Номинальная шкала измерения определяет свойство идентичности данных. Эта шкала имеет определенные характеристики, но не имеет числового значения. Данные могут быть помещены в категории, но не могут быть умножены, разделены, добавлены или вычтены друг из друга. Также невозможно измерить разницу между точками данных.
Примеры номинальных данных включают цвет глаз и страну рождения. Номинальные данные можно снова разбить на три категории:
Номинал с заказом: Некоторые номинальные данные могут быть разбиты на подкатегории по порядку, например, «холодный, теплый, горячий и очень горячий».
Номинальные без порядка: Номинальные данные также могут быть подразделены на номинальные без порядка, например, мужские и женские.
Дихотомические: Дихотомические данные определяются наличием только двух категорий или уровней, таких как «да» и «нет».
2. Порядковая шкала измерения
Порядковая шкала определяет данные, которые располагаются в определенном порядке. Хотя каждое значение ранжировано, нет информации, которая бы указывала, что отличает категории друг от друга. К этим значениям нельзя ни добавить, ни вычесть.
Примером такого рода данных могут быть точки данных об удовлетворенности в опросе, где «один = счастливый, два = нейтральный и три = несчастный». Когда кто-то финишировал в гонке, также описываются порядковые данные. Хотя первое, второе или третье место показывает, в каком порядке финишировали бегуны, оно не указывает, насколько далеко финишер, занявший первое место, был впереди бегуна, занявшего второе место.
3. Интервальная шкала измерения
Интервальная шкала содержит свойства номинальных и упорядоченных данных, но разницу между точками данных можно определить количественно.
Эта шкала также характеризуется тем, что число ноль является существующей переменной. В порядковой шкале ноль означает, что данные не существуют. В интервальной шкале ноль имеет значение — например, если вы измеряете градусы, ноль имеет значение температуры.
Точки данных на шкале интервалов имеют одинаковую разницу между собой. Разница на шкале между 10 и 20 градусами такая же, как и между 20 и 30 градусами. Эта шкала используется для количественной оценки различий между переменными, тогда как две другие шкалы используются только для описания качественных значений. Другие примеры интервальных шкал включают год выпуска автомобиля или месяцы года.
4. Шкала отношений
Шкалы отношений включают свойства всех четырех шкал измерения.
Данные являются номинальными и определяются тождеством, могут быть классифицированы по порядку, содержат интервалы и могут быть разбиты на точные значения. Вес, рост и расстояние — все это примеры переменных отношений. Данные в шкале отношений можно складывать, вычитать, делить и умножать.
Шкалы отношений также отличаются от шкал интервалов тем, что шкала имеет «истинный ноль». Число ноль означает, что данные не имеют точки значения. Примером этого является рост или вес, поскольку кто-то не может быть ростом ноль сантиметров или весить ноль килограммов, или иметь отрицательные сантиметры или отрицательные килограммы. Примерами использования этой шкалы являются расчет акций или продаж. Из всех типов данных на шкалах измерения специалисты по данным могут больше всего сделать с точками данных отношения.
Подводя итог, номинальные весы используются для маркировки или описания значений. Порядковые шкалы используются для предоставления информации о конкретном порядке точек данных, что в основном наблюдается при использовании опросов удовлетворенности.
Шкала интервалов используется для понимания порядка и различий между ними. Шкалы отношений дают больше информации об идентичности, порядке и различиях, а также разбивку числовых деталей в каждой точке данных.
Использование количественных и качественных данных в статистике
После того, как специалисты по обработке данных получат исчерпывающий набор данных из своей выборки, они могут начать использовать эту информацию для составления описаний и выводов. Для этого они могут использовать как описательную, так и логическую статистику.
Описательная статистика
Описательная статистика помогает продемонстрировать, представить, проанализировать и обобщить результаты, содержащиеся в выборке. Они представляют данные в простой для понимания и презентабельной форме, например, в виде таблицы или графика. Без описания данные были бы в необработанном виде без пояснений.
Подсчет частоты
Один из способов, которым специалисты по данным могут описать статистику, — это использование подсчета частоты или статистики частоты, которая описывает количество раз, когда переменная присутствует в наборе данных.
Например, количество людей с голубыми глазами или количество людей с водительскими правами в выборке можно подсчитать по частоте. Другие примеры включают квалификацию образования, такую как аттестат о среднем образовании, университетский диплом или докторскую степень, а также категории семейного положения, такие как холост, женат или разведен.
Частотные данные представляют собой форму дискретных данных, так как части значений не могут быть разбиты на части. Вместо этого для расчета непрерывных точек данных, таких как возраст, специалисты по данным могут использовать центральную статистику тенденций. Для этого они находят среднее или среднее значение точки данных. Используя пример возраста, это может сказать им средний возраст участников в выборке.
Хотя специалисты по обработке и анализу данных могут делать выводы на основе описательной статистики и представлять их в понятной форме, они не обязательно могут делать выводы. Вот тут-то и приходит на помощь статистика выводов.
Логическая статистика
Логическая статистика используется для выдвижения гипотезы из набора данных. Было бы невозможно получить данные от всего населения, поэтому специалисты по данным могут использовать логическую статистику для экстраполяции своих результатов. Используя эту статистику, они могут делать обобщения и прогнозы в отношении более широкой выборки, даже если они не опросили их всех.
Примером использования логической статистики являются выборы. Еще до того, как вся страна проголосовала, специалисты по данным могут использовать подобную статистику, чтобы делать предположения относительно того, кто может победить на основе меньшего размера выборки.
Использование визуализации данных для обмена идеями
Визуализация данных описывает методы, используемые для создания графического представления образца данных путем кодирования его с помощью визуальных фрагментов информации. Это помогает передавать данные зрителям четким и эффективным способом.
Характеристики эффективных графических дисплеев
Эффективная визуализация может помочь людям анализировать сложные значения данных и делать выводы. Целью этого процесса является максимально четкое изложение результатов. Графический дисплей с эффективным обменом сообщениями будет четко отображать данные и позволит зрителю получить представление и тенденции из набора данных и выявить различные результаты между данными.
Примеры визуализации данных
Наилучшее визуальное представление набора данных определяется отношениями, которые специалисты по данным хотят передать между точками данных. Они хотят представить распределение с выбросами? Они хотят сравнить несколько переменных или проанализировать одну переменную во времени? Представляют ли они тенденции в вашем наборе данных? Вот некоторые из ключевых примеров визуализации данных.
Гистограмма используется для сравнения двух или более значений в категории и того, как несколько фрагментов данных соотносятся друг с другом.
Линейная диаграмма используется для визуального представления тенденций, шаблонов и колебаний в наборе данных. Линейные графики обычно используются для прогнозирования информации.
Точечная диаграмма используется для отображения взаимосвязи между точками данных в компактной визуальной форме.
Круговая диаграмма используется для сравнения частей целого.
Воронкообразная диаграмма используется для представления того, как данные перемещаются по различным шагам или стадиям процесса.
Гистограмма используется для представления данных за определенный период времени или интервал.
Количественные сообщения
Количественные сообщения описывают отношения данных. В зависимости от выборки существуют разные способы передачи количественных данных.
Номинальное сравнение: Подкатегории сравниваются по отдельности в произвольном порядке.
Временной ряд: Индивидуальная переменная отслеживается в течение периода времени, обычно представленного в виде линейной диаграммы.
Ранжирование: Подкатегории ранжируются по порядку, обычно представленному в виде гистограммы.
Часть к целому: Подкатегории представлены в виде соотношения по сравнению с целым, обычно представленным в виде гистограммы или круговой диаграммы.
Отклонение: Подкатегории сравниваются с контрольной точкой, обычно представленной в виде гистограммы.
Частотное распределение: Подкатегории подсчитываются в интервалах, обычно представленных в виде гистограммы.
Корреляция: Два набора мер сравниваются, чтобы определить, движутся ли они в одном и том же или противоположном направлении, обычно представленном на диаграмме рассеивания.
Расширьте свои знания в области обработки данных
Поскольку наука о данных становится все более востребованным навыком, самое время расширить свои знания о самом ценном ресурсе в мире: данных.
Степень в области науки о данных позволит вам выявлять, анализировать и представлять сложные и переплетенные сети данных. Затем вы можете использовать эти идеи для прогнозирования и создания стратегий, особенно в бизнес-среде. Магистр наук о данных UNSW может дать вам навыки, необходимые для того, чтобы раскрыть всю мощь данных и помочь компаниям принимать более эффективные решения, позволяя им добиваться значительных изменений и результатов.
Шкалы измерения / Уровень измерения
Четыре шкалы измерения
Посмотрите видео, чтобы ознакомиться с четырьмя шкалами измерения.
Четыре шкалы измерения
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Данные можно классифицировать по одной из четырех шкал: номинальной, порядковой, интервальной или относительной. Каждый уровень измерения имеет некоторые важные свойства, которые полезно знать. Например, только шкала отношений имеет значащие нули.
Круговая диаграмма отображает группы номинальных переменных (т.е. категории). 1. Номинальная шкала. Номинальные переменные (также называемые категориальными переменными) могут быть помещены в категории. Они не имеют числового значения , поэтому их нельзя складывать, вычитать, делить или умножать. У них тоже нет порядка; если кажется, что они имеют порядок, то у вас, вероятно, вместо этого есть порядковые переменные.
Порядковая шкала классифицирует по рангу.2. Порядковая шкала. Порядковая шкала содержит вещи, которые можно расположить по порядку. Например, от самого горячего к самому холодному, от легкого к самому тяжелому, от самого богатого к самому бедному. По сути, если вы можете ранжировать данные по 1-му, 2-му, 3-му месту (и так далее), то у вас есть данные в порядковой шкале.
3. Интервальная шкала. Интервальная шкала имеет упорядоченные числа со значимыми делениями. Температура находится на интервальной шкале: разница в 10 градусов между 90 и 100 означает то же самое, что и 10 градусов между 150 и 160.
Сравните это с рейтингом средней школы (который является порядковым), где разница между 1-м и 2-м может быть 0,01. и между 10 и 11 .5. Если у вас есть значимые деления, у вас есть что-то на шкале интервалов.
Вес измеряется на весах пропорций.4. Шкала соотношения. Шкала отношений точно такая же, как и шкала интервалов, с одним важным отличием: ноль имеет смысл. Например, высота, равная нулю, имеет смысл (это означает, что вы не существуете). Сравните это с нулевой температурой, которая, пока существует, ничего особенного не значит (хотя, надо признать, по шкале Цельсия это точка замерзания воды).
Ссылки
Агрести А. (1990) Категориальный анализ данных. Джон Уайли и сыновья, Нью-Йорк.
Додж, Ю. (2008). Краткая энциклопедия статистики. Спрингер.
Эверитт, Б. С.; Скрондал, А. (2010), Кембриджский статистический словарь, издательство Кембриджского университета.
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен .