Сколько весит 1м профильной трубы: Трубный калькулятор для расчета веса трубы

alexxlab | 19.09.2020 | 0 | Разное

Удельный вес профильной трубы, вес погонного метра профильной трубы

Стальной трубный прокат с квадратным или прямоугольным сечением называется профильной трубой, или просто – «коробочкой». К профильным можно отнести виды трубного проката, сечение которых отличается от квадратного – это трех-, шести-, восьмигранные, ребристые, овальные, каплевидные и прочие формы. Создается такое изделие на прокатном стане путем деформации стальной листовой заготовки. Впоследствии шов заваривается.

Особенности производства профилированных труб

«Труба-коробочка» может быть изготовлена из различных металлов, но наиболее широко используемый – сталь, как углеродистая, легированная или нержавеющая, так и оцинкованная. Также встречаются и алюминиевые профильные трубы.

Диапазон размерности трубного проката самый большой, среди них можно встретить образцы с размером наружного диаметра 0,3 мм и до 2520 мм, толщина стенки варьируется от 0,05 мм до 75 мм. Наиболее популярными размерами все же являются профильные трубы прямоугольной формы в диапазоне 15х15 мм и до 450х350 мм. Максимальная толщина стенок таких труб достигает 12 мм.

В зависимости от способа производства различают:

• холоднокатаные,
• горячекатаные,
• сварные углеродистые профильные трубы.

Стоит отметить, что цена на деформированный трубный прокат выше, как и его качество. Основные параметры трубы профильной:

• геометрия: вес погонного метра трубы, качество поверхности, соответствие нормам толщина стенок и длина, отсутствие максимально допустимых отклонений ровности, толщины и прочих параметров;
• технические: способ производства, качество материала, качество шва (регламентируется ГОСТом).

Как узнать вес трубы?

Чтобы узнать, сколько весит труба, необходимо выяснить, сколько и какого материала пошло на ее производство. Для расчетов достаточно узнать вес 1м погонного профильной трубы. Это касается как изделий большого размера, например, 180х180х60, так и маленького (50х50х5). Значение массы зависит от таких параметров:

• форма – наиболее популярны изделия прямоугольного сечения, сфера их применения очень велика (от строительства до станко- и автомобилестроения). Узнать вес погонного метра такой трубы довольно просто, не прибегая к сложным проектным программам;
• размер – данные, прописанные в маркировании изделия, используются для подсчета теоретической массы профиля;
• Плотность (или удельный вес металла) – в зависимости от сплава, характеристики которого прописаны в ГОСТе, данный показатель будет отличаться. Стали распространенных марок имеют среднюю плотность в пределах 7,5 – 7,8 г/см3.

Точный вес профильной трубы необходимо знать для проведения правильных расчетов массы конструкции, веса, который будет давить на опору, определения тоннажа при транспортировке, массу авто, себестоимость материалов и т.д.

На металлобазах в основном указывают цену за тонну изделия, и отдельно каждую трубу никто не взвешивает. Но для расчетов необходим параметр – вес погонного метра профильной трубы. Можно использовать сложные методики расчета или воспользоваться таблицей веса стальной трубы квадратной самых востребованных параметров:

Удельный вес профильной трубы в погонном метре

Размер профильной трубы (мм)	Толщина стенки (мм)	Удельный вес профильной трубы (кг/мп)
15х15	1,0	0,48
15х15	1,5	0,71
15х15	2,0	0,93
20х20	1,0	0,62
20х20	1,5	0,93
20х20	2,0	1,23
25х25	1,0	0,79
25х25	1,5	1,18
25х25	2,0	1,55
30х30	1,0	0,94
30х30	1,5	1,40
30х30	2,0	2,30
40х40	1,0	1,24
40х40	1,5	1,85
40х40	2,0	2,45
50х50	1,5	2,34
50х50	2,0	3,10
50х50	2,5	3,86
60х60	1,5	2,80
60х60	2,0	3,72
60х60	2,5	4,63

Как рассчитать вес профильной трубы

Профильная труба – востребованный вид металлопроката, используемый для сооружения металлоконструкций, в производстве мебели, для прокладки электрокабеля, изготовления производственного оборудования и техники. При проектировании любой конструкции или механизма необходимо знать все параметры используемых элементов, в том числе их массу.

 

Какие характеристики профильных труб влияют на массу?

Наиболее востребованными разновидностями этой металлопродукции являются изделия с прямоугольным и квадратным профилем.

Размеры

Это определяющие факторы, и к ним относятся: ширина и высота поперечного сечения, толщина стенки. Углы профильных изделий могут быть четкими прямыми или скругленными. Скругленность незначительно влияет на вес погонного метра, особенно в случае маломерных изделий. Сортамент квадратных и прямоугольных стальных труб, предназначенных для создания металлоконструкций, определяется ГОСТом Р 54157-2010.

Плотность стали

Усредненно для расчетов плотность стали принимают равной 7850 кг/м³. Но, в зависимости от содержания углерода, эта величина изменяется: чем выше процентное соотношение углерода в сплаве, тем меньше масса металла.

Таблица плотности различных марок стали

Наименование	Марки	Плотность, кг/м3
Коррозионностойкие стали	12Х18Н10Т, 08Х18Н10Т	7900
Конструкционные углеродистые стали обыкновенного качества	Ст3 пс/сп	7870
Конструкционные углеродистые качественные стали	10, 20, 30, 40	7850
Инструментальные стали	Х12МФ	7700
Низколегированные стали	09Г2С, 30ХГСА	7850
Стали рессорно-пружинные	65Г	7850
Инструментальные штамповые стали	5ХНМ	7800

Расчет веса профильной стальной трубы по формулам

Для определения массы погонного метра воспользуемся формулой M=V*p, где:

M – масса 1 м, кг;

V – объем материала, м³;

p – плотность стали, кг/м³.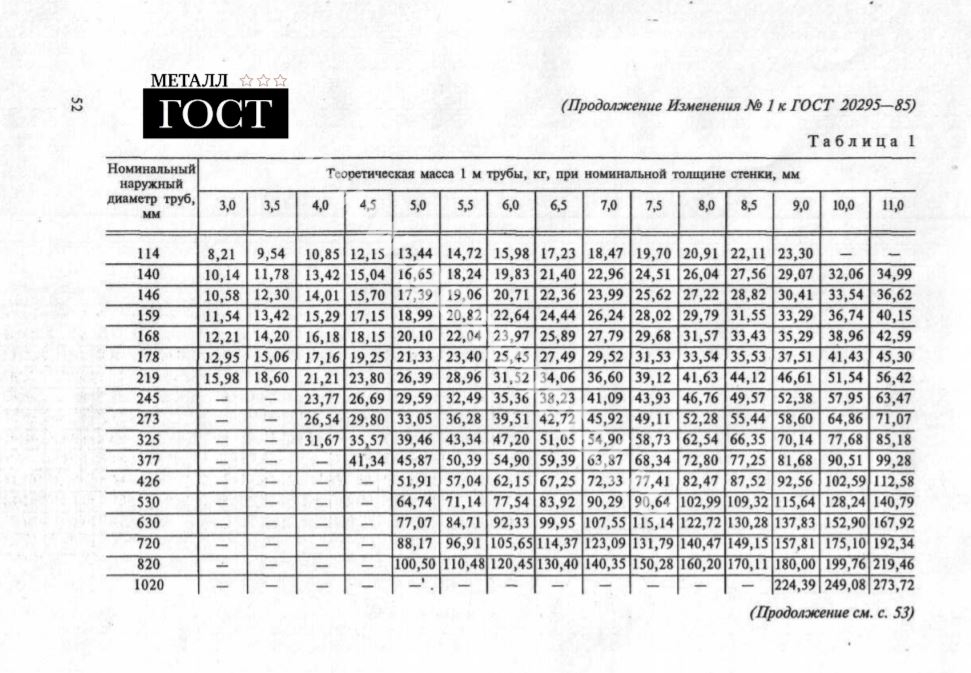

V = (A+B)*s, где:

A– ширина сечения, м;

B – высота сечения, м;

s – толщина стенки, м.

При использовании формул для определения, сколько весит метр профильной трубы, скругленность углов не учитывается. Если толщина стенки неоднородна, производят по 2-3 измерения для каждой стенки и находят среднюю величину.

Расчет массы погонного метра профильной трубы с использованием таблиц

Внимание! В таблицах представлены массы металлопродукции, характерные для усредненного показателя плотности 7850 кг/м³. Если необходимо получить результат для другого значения плотности, табличную величину делят на 7850 и умножают на реальную плотность марки стали.

Таблица массы 1 м (кг) для прямоугольного профиля

Типоразмер	Толщина стенки, мм
	0,7	0,8	1,0	1,2	1,5	1,6	1,8	2,0	2,2	2,35	2,5	2,8	3,0
20х10	0,308	0,348	0,426	0,501	0,605
20х15	0,363	0,411	0,505	0,595	0,723
28х25	0,560	0,637	0,787	0,934	1,150	1,220	1,350	1,490	1,620	1,710	1,800
30х15	0,473	0,536	0,661	0,783	0,959	1,02	1,130	1,230	1,340	1,410	1,490
30х20	0,527	0,599	0,740	0,877	1,080	1,140	1,270	1,390	1,510	1,600	1,680
35х15	0,527	0,599	0,740	0,877	1,080	1,140	1,270	1,390	1,510	1,600	1,680
40х20	0,637	0,725	0,897	1,070	1,310	1,390	1,550	1,700	1,860	1,970	2,070
40х25			0,976	1,160	1,430	1,520	1,690	1,860	2,030	2,150	2,270
40х28					1,500	1,590	1,780	1,950	2,130	2,260	2,390
50х25			1,130	1,350	1,670	1,770	1,970	2,170	2,370	2,520	2,660	2,940	3,130

Таблица массы 1 м (кг) для квадратного профиля

Типоразмер	Толщина стенки, мм
	0,7	0,8	1,0	1,2	1,6	1,8	2,0	2,2	2,35	2,5	2,8	3,0	3,2	3,5	4,0
10х10	0,198	0,222	0,269	0,312
15х15	0,308	0,348	0,426	0,501	0,639	0,702	0,762	0,819
20х20	0,418	0,474	0,583	0,589	0,890	0,985	1,075	1,160
25х25		0,599	0,74	0,88	1,14	1,27	1,39	1,51	1,60	1,68
30х30			0,897	1,07	1,39	1,55	1,7	1,86	1,97	2,07
40х40			1,21	1,44	1,89	2,12	2,333	2,54	2,7	2,85	3,16	3,36
50х50				1,82	2,4	2,68	2,96	3,24	3,44	3,64	4,04	4,31	4,56	4,95	5,56
60х60					2,9	3,25	3,59	3,93	4,18	4,43	4,92	5,25	5,57	6,04	6,82
80х80					3,9	4,38	4,84	5,31	5,66	6,0	6,68	7,13	7,58	8,24	9,33
100х100							6,1	6,69	7,13	7,57	8,44	9,13	9,59	10,44	12,05

Вес 1-го метра квадратной 20х40х2 трубы!

С учетом существования огромного сортамента профильных ТР, возникают определенные сложности, если необходимо рассчитать вес 1 м 20х40х2 профильной трубы, узнать стоимость за метр зная цену за кг, посчитать сколько весит металл в заявке зная суммарную длину профиля.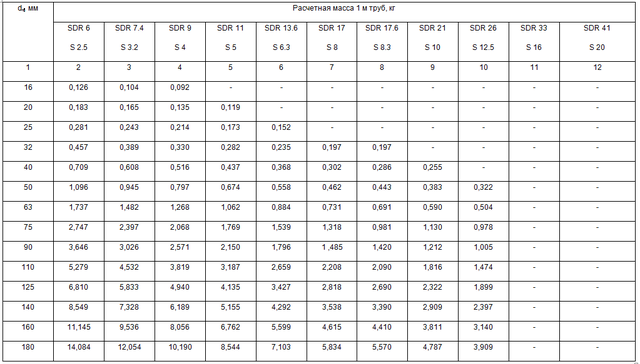

Масса погонного метра проф. трубы зависит от размера сечения и толщины стенок, т. е. от площади поперечного сечения. В таблице металлопроката указывается теоретический вес 1 метра погонного, однако при расчете количества ТР с использованием таблиц массы профтрубы квадратного и прямоугольного сечения необходимо учитывать, что ГОСТом предусматривается допустимое отклонение фактического веса от теоретического до 12%.

Вес трубы 20х40х2 за метр

Стальная прямоугольная труба 20х40×2 вес 1 метра погонного – это удельный, табличный, теоретический, справочный, условный или погонный вес металлопроката, в данном случае замкнутого профиля. Названия масс используются как синонимы и означают на практике не точный реальный вес, полученный в результате непосредственного взвешивания на весах, а теоретически рассчитанный, соответствующий параметрам металлопроката по ГОСТу.

То есть условный, хотя его часто, не совсем точно, называют удельным. Данные о теор массе 1 метра трубы 20х40×2 мм стальной мы можем найти в таблице из справочника по удельному массу металлического проката или рассчитать самостоятельно. Однако, такие расчеты веса 1 метра трубы требуют некоторого опыта и знания формулы пересчета массы.

Например, расчет массы 1 м.п. квадратной трубы из металла, сводится к вычислению массы железной полосы. Поэтому, гораздо удобнее пользоваться таблицей. В принципе, нам нужна таблица удельного, условного, справочного, расчетного, теоретического или погонного веса профильной стальной трубы, та часть ее, которая относится к прямоугольным трубкам.

Профильная металлическая труба 20 40 2 мм хорошо сваривается, легко режется, удобно гнется при необходимости. Поэтому из металлической трубы 20х40×2 мм изготавливаются гнутые и арочные стальные конструкции. Прокат имеет легкий вес, при сравнительно высокой жесткости, поэтому металлические конструкции из трубы 20 40 2 мм называют облегченными или легкими.

Для тех задач, где важным условием изготовления металлической сварной конструкции является высокая прочность или высокая устойчивость к коррозии, лучше использовать трубки такого же сечения, но с большей толщиной стенки.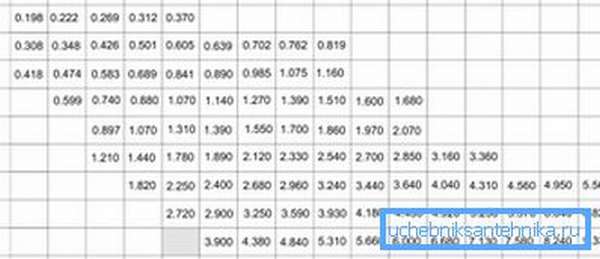 Для водо и газопроводов рекомендуется использовать стальные металлические ТР не электро сварные, а цельнотянутые. А теперь труба 20х40х2 вес 1 метра, смотрите в таблице ниже.

Тип трубы	Размер	Вес 1 метра
Квадратная	20х40х2	Вес 1 метра равен 1.70 кг.

Теоретический вес профильной трубы квадратной

Сортамент квадратных трубок определяется стандартом ГОСТ 8645-68, который устанавливает требования к электросварным трубам.

Квадратная ТР представляет собой полый металлический профить замкнутого сечения. Размеры квадрата соответствует стандарту ГОСТ 8639-82, технические требования должны соответствовать ГОСТ 13663-86, который регламентирует сортамент на трубы профильные электросварные общего назначения из углеродистой стали.

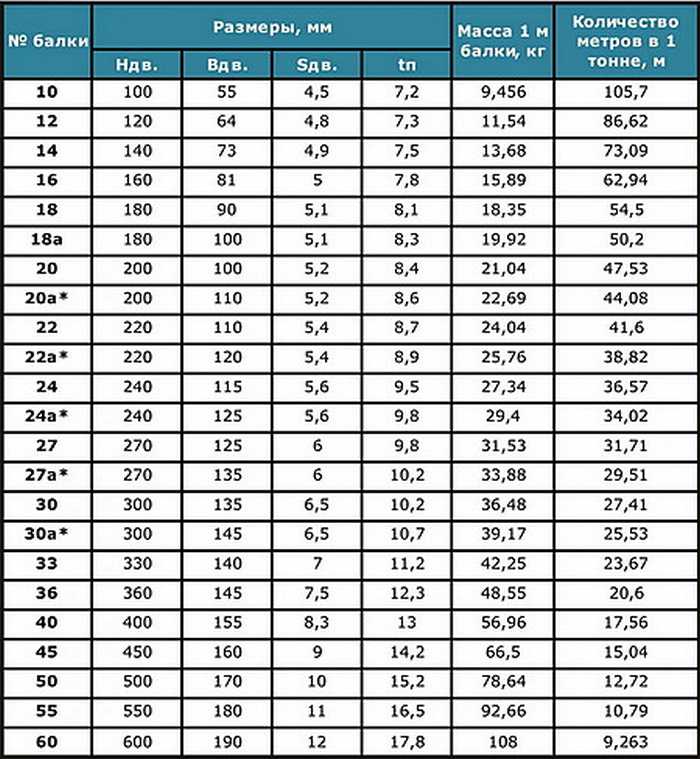
Таблица веса 1 метра круга стального и количество метров в тонне кругляка

При закупке металлопроката заказчику следует точно определить необходимое его количество в весовом эквиваленте. Чтобы рассчитать вес стального круга нужно учитывать такие параметры, как его диаметр, марку стали, из которой он изготовлен, а также ее удельный вес. Для облегчения этой задачи ниже мы представили таблицу, по которой можно быстро определить вес круга, количество метров в одной тонне и другие важные параметры.

Она показывает массу 1 м круга разных диаметров, площадь его поперечного сечения, допуски по качеству поверхности, а также общий метраж кругляка на 1 тонну. Данная информация поможет вам в составлении технической и проектной документации, подсчете транспортных и складских расходов, ведении бухгалтерского учета. Также в отдельных таблицах, представленных ниже, вы можете найти удельный вес й м3 сталей разных марок. Это поможет вам самостоятельно рассчитать вес стального круга.

Таблица 1. Вес круга и количество метров в тонне

Диаметр круга	Площадь поперечного сечения круга	Масса 1 метра круга	Количество метров в тонне
Мотки
5 мм	19,63 мм2	0,154 кг	6487,8 м
5,5 мм	23,76 мм2	0,187 кг	5361,9 м
6 мм	28,27 мм2	0,222 кг	4505,4 м
6,3 мм	31,17 мм2	0,245 кг	4086,6 м
6,5 мм	33,18 мм2	0,260 кг	3839,0 м
7 мм	38,48 мм2	0,302 кг	3310,1 м
8 мм	50,27 мм2	0,395 кг	2534,3 м
9 мм	63,62 мм2	0,499 кг	2002,4 м
Прутки
10 мм	78,54 мм2	0,617 кг	1622,0 м
11 мм	95,03 мм2	0,746 кг	1340,5 м
12 мм	113,10 мм2	0,888 кг	1126,4 м
13 мм	132,73 мм2	1,042 кг	959,7 м
14 мм	153,94 мм2	1,208 кг	827,5 м
15 мм	176,71 мм2	1,387 кг	720,9 м
16 мм	201,06 мм2	1,578 кг	633,6 м
17 мм	226,98 мм2	1,782 кг	561,2 м
18 мм	254,47 мм2	1,998 кг	500,6 м
19 мм	283,53 мм2	2,226 кг	449,3 м
20 мм	314,16 мм2	2,466 кг	405,5 м
21 мм	346,36 мм2	2,719 кг	367,8 м
22 мм	380,13 мм2	2,984 кг	335,1 м
23 мм	415,48 мм2	3,261 кг	306,6 м
24 мм	452,39 мм2	3,551 кг	281,6 м
25 мм	490,87 мм2	3,853 кг	259,5 м
26 мм	530,93 мм2	4,168 кг	239,9 м
27 мм	572,56 мм2	4,495 кг	222,5 м
28 мм	615,75 мм2	4,834 кг	206,9 м
29 мм	660,52 мм2	5,185 кг	192,9 м
30 мм	706,89 мм2	5,549 кг	180,2 м
31 мм	754,77 мм2	5,925 кг	168,8 м
32 мм	804,25 мм2	158,4 кг	158,4 м
33 мм	855,30 мм2	6,714 кг	148,9 м
34 мм	907,92 мм2	7,127 кг	140,3 м
35 мм	962,11 мм2	7,553 кг	132,4 м
36 мм	1017,88 мм2	7,990 кг	125,2 м
37 мм	1075,21 мм2	8,440 кг	118,5 м
38 мм	1134,11 мм2	8,903 кг	112,3 м
39 мм	1194,96 мм2	9,378 кг	106,6 м
40 мм	1256,64 мм2	9,865 кг	101,4 м
41 мм	1320,25 мм2	10,364 кг	96,5 м
42 мм	1385,44 мм2	10,876 кг	91,9 м
43 мм	1452,20 мм2	11,400 кг	87,7 м
44 мм	1520,53 мм2	11,936 кг	83,8 м
45 мм	1590,43 мм2	12,485 кг	80,1 м
46 мм	1661,90 мм2	13,046 кг	76,7 м
47 мм	1734,90 мм2	13,619 кг	73,4 м
48 мм	1809,56 мм2	14,205 кг	70,4 м
50 мм	1963,5 мм2	15,413 кг	64,9 м
52 мм	2123,72 мм2	16,671 кг	60,0 м
53 мм	2206,18 мм2	17,319 кг	57,7 м
54 мм	2290,22 мм2	17,978 кг	55,6 м
55 мм	2375,83 мм2	18,650 кг	53,6 м
56 мм	2463,01 мм2	19,335 кг	51,7 м
58 мм	2642,08 мм2	20,740 кг	48,2 м
60 мм	2827,43 мм2	22,195 кг	45,1 м
62 мм	3019,07 мм2	23,700 кг	42,2 м
63 мм	3117,25 мм2	24,470 кг	40,9 м
65 мм	3318,31 мм2	26,049 кг	38,4 м
67 мм	3525,65 мм2	27,676 кг	36,1 м
68 мм	3631,68 мм2	28,509 кг	35,1 м
70 мм	3848,45 мм2	30,210 кг	33,1 м
72 мм	4071,50 мм2	31,961 кг	31,3 м
75 мм	4417,86 мм2	34,680 кг	28,8 м
78 мм	4778,36 мм2	37,510 кг	26,7 м
80 мм	5026,55 мм2	39,458 кг	25,3 м
82 мм	5281,02 мм2	41,456 кг	24,1 м
85 мм	5674,50 мм2	44,545 кг	22,4 м
87 мм	5944,68 мм2	46,666 кг	21,4 м
90 мм	6361,73 мм2	49,940 кг	20,0 м
92 мм	6647,61 мм2	52,184 кг	19,2 м
95 мм	7088,22 мм2	55,643 кг	18,0 м
97 мм	7389,81 мм2	58,010 кг	17,2 м
100 мм	7853,98 мм2	61,654 кг	16,2 м
105 мм	8659,01 мм2	67,973 кг	14,7 м
110 мм	9503,32 мм2	74,601 кг	13,4 м
115 мм	10386,89 мм2	81,537 кг	12,3 м
120 мм	11309,73 мм2	88,781 кг	11,3 м
125 мм	12271,85 мм2	96,334 кг	10,4 м
130 мм	13273,23 мм2	104,195 кг	9,6 м
135 мм	14313,88 мм2	112,364 кг	8,9 м
140 мм	15393,80 мм2	120,841 кг	8,3 м
145 мм	16513 мм2	129,627 кг	7,7 м
150 мм	17671,46 мм2	138,721 кг	7,2 м
155 мм	18869,19 мм2	148,123 кг	6,8 м
160 мм	20106,19 мм2	157,834 кг	6,3 м
165 мм	21382,46 мм2	167,852 кг	6,0 м
170 мм	22698,01 мм2	178,179 кг	5,6 м
175 мм	24052,82 мм2	188,815 кг	5,3 м
180 мм	25446,90 мм2	199,758 кг	5,0 м
185 мм	26880,25 мм2	211,010 кг	4,7 м
190 мм	28352,87 мм2	222,570 кг	4,5 м
195 мм	29864,77 мм2	234,438 кг	4,3 м
200 мм	31415,93 мм2	246,615 кг	4,1 м
210 мм	34636,06 мм2	271,893 кг	3,7 м
220 мм	38013,27 мм2	298,404 кг	3,4 м
230 мм	41547,56 мм2	326,148 кг	3,1 м
240 мм	45238,93 мм2	355,126 кг	2,8 м
250 мм	49087,39 мм2	385,336 кг	2,6 м
260 мм	53092,92 мм2	416,779 кг	2,4 м
270 мм	57255,53 мм2	449,456 кг	2,2 м

Таблица 2. Удельный вес марок стали

Тип стали	Марка стали	Удельный вес
Сталь нержавеющая конструкционная криогенная	12Х18Н10Т	7900 кг/м3
Сталь нержавеющая коррозионно-стойкая жаропрочная	08Х18Н10Т	7900 кг/м3
Сталь конструкционная низколегированная	09Г2С	7850 кг/м3
Сталь конструкционная углеродистая качественная	10,20,30,40	7850 кг/м3
Сталь конструкционная углеродистая	Ст3сп, Ст3пс	7870 кг/м3
Сталь инструментальная штамповая	Х12МФ	7700 кг/м3
Сталь конструкционная рессорно-пружинная	65Г	7850 кг/м3
Сталь инструментальная штамповая	5ХНМ	7800 кг/м3
Сталь конструкционная легированная	30ХГСА	7850 кг/м3
Никельхромовая сталь	ЭИ 418	8510 кг/м3
Хромомарганцовоникелевая сталь	Х13Н4Г9 (ЭИ100)	8500 кг/м3
Хромистая сталь	1Х13 (ЭЖ1)	7750 кг/м3
	2Х13 (ЭЖ2)	7700 кг/м3
	3Х13 (ЭЖ3)	7700 кг/м3
	4Х14 (ЭЖ4)	7700 кг/м3
	Х17 (ЭЖ17)	7700 кг/м3
	Х18 (ЭИ229)	7750 кг/м3
	Х25 (ЭИ181)	7550 кг/м3
	Х27 (Ж27)	7550 кг/м3
	Х28 (ЭЖ27)	7850 кг/м3
Хромоникелевая сталь	0Х18Н9 (ЭЯ0)	7850 кг/м3
	1Х18Н9 (ЭЯ1)	7850 кг/м3
	2Х18Н9 (ЭЯ2)	7850 кг/м3
	Х17Н2 (ЭИ268)	7750 кг/м3
	ЭИ307	7700 кг/м3
	ЭИ334	8400 кг/м3
	Х23Н18 (ЭИ417)	7900 кг/м3
Хромокремнемолибденовая сталь	ЭИ107	7620 кг/м3
Хромоникельвольфрамовая сталь	ЭИ69	8000 кг/м3
Хромоникельвольфрамовая с кремнием сталь	Х25Н20С2 (ЭИ283)	8000 кг/м3
Хромоникелькремнистая сталь	ЭИ72	7700 кг/м3
Прочая особая сталь	ЭИ401	7900 кг/м3
	ЭИ418	8510 кг/м3
	ЭИ434	8130 кг/м3
	ЭИ435	8510 кг/м3
	ЭИ437	8200 кг/м3
	ЭИ415	7850 кг/м3
Высокоуглеродистая сталь	70 (ВС и ОВС)	7850 кг/м3
Среднеуглеродистая сталь	45	7850 кг/м3
Малоуглеродистая сталь	10 и 10А; 20 и 20А	7850 кг/м3
Малоуглеродистая электротехническая сталь	А и Э; ЭА; ЭАА	7800 кг/м3
Хромистая сталь	15ХА	7740 кг/м3
Хромоалюминиевомолибденовая азотируемая сталь	38ХМЮА	7650 кг/м3
Хромомарганцовокремнистая сталь	25ХГСА	7850 кг/м3
хромованадиевая сталь	30ХГСА	7850 кг/м3
	20ХН3А	7850 кг/м3
	40ХФА	7800 кг/м3
	50ХФА	7740 кг/м3

Если у вас возникнут вопросы по расчету веса и стоимости стального круга, наши консультанты с радостью на них ответят. Также вам может быть полезной следующая информация:

• «Круг стальной» – здесь вы можете узнать о том, что такое круглый металлопрокат, каким он бывает, его характеристики, стандарты, применение и т. д.
• «Как рассчитать вес круга стального» – общая информация о том, как самостоятельно подсчитать вес кругляка необходимого диаметра и марки стали.

Труба профильная 50х50 вес 1 метр

Труба стальная 40х40х2 погонной массой 1 метр – это удельная, табличная, теоретическая, справочная, условная или погонная масса металлопроката. Названия используются как синонимы и означают не реальный вес, полученный в результате прямого взвешивания на весах, а теоретически рассчитанный по ГОСТу. Данные о весе 1 метра стальной трубы 40х40х2 мм мы можем найти в таблице из справочника по удельному весу металлических изделий или рассчитать его самостоятельно.Однако такие расчеты веса 1 метра трубы требуют определенного опыта и знания формулы пересчета массы. Например, расчет массы 1 мп квадратной металлической трубы сводится к расчету веса железной полосы.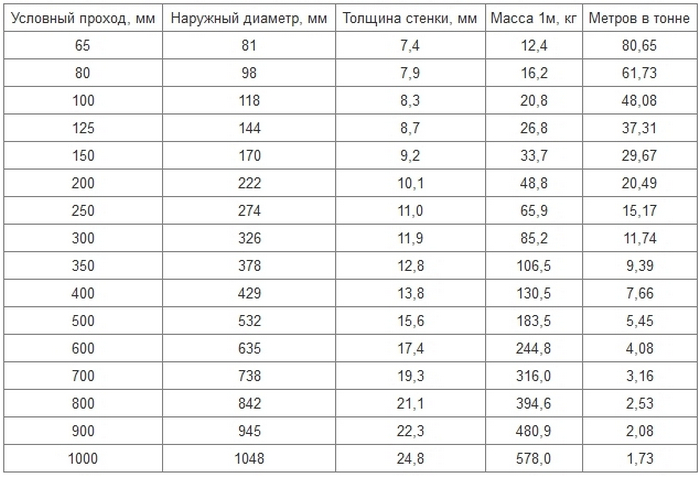 Поэтому пользоваться таблицей намного удобнее. В принципе, нам нужна таблица удельного, условного, справочного, расчетного, теоретического или линейного веса стальной профильной трубы, той ее части, которая относится к квадратным трубам. Стальные трубы квадратного сечения 40х40х2 мм также являются профильными, но с одинаковой шириной обеих полок.Если ширина полки у металлической профильной трубы разная, то такие трубы называют стальными прямоугольными. Более правильное название для указанной в справке стальной трубы квадратного сечения – стальной квадратный замкнутый профиль. Металлическая квадратная труба 40х40х2 мм может быть сварной или цельной, но на практике стальные трубы с такой толщиной стенки обычно делают сварными. И по праву считаются тонкостенными световодами. Стальная труба 40х40х2 мм чаще всего используется для производства металлоконструкций бытового, декоративного, строительного и промышленного назначения.Профильная металлическая труба 40х40х2 мм хорошо сваривается, легко режется, а при необходимости удобно гнется. Поэтому гнутые и арочные стальные конструкции изготавливают из металлической трубы 40х40х2 мм. Прокат имеет малый вес, при относительно высокой жесткости, поэтому металлоконструкции из трубы 40х40х2 мм называют легкими или легкими. Для тех задач, где важным условием изготовления сварной металлоконструкции является высокая прочность или высокая устойчивость к коррозии, лучше использовать трубы такого же сечения, но с большей толщиной стенки.Для водопроводов и газопроводов рекомендуется использовать стальные металлические трубы не сварные, а бесшовные. В редких случаях для отопления и водоснабжения можно использовать стальную профильную трубу 40х40х2 мм. Толщина стенки квадратной стальной трубы 40х40х2 мм в принципе позволяет использовать не только сварные соединения, но и винты или заклепки. Но в целом профильная труба 40х40х2 мм для этого не предназначена. Хотя изредка находит такое применение, например: при изготовлении заборов из профнастила и различных каркасов, беседок, беседок, навесов, козырьков и входных групп. Профильная труба стальная 40х40х2 мм оказалась очень удобным материалом для изготовления арочных металлических изделий, пергол, декоративных заборов, заборов, заборов, палисадников для растительных и цветочных насаждений, садовых конструкций, ворот, решеток, металлических дверей, качелей. и автоматические ворота, садовые мостики, перила и перила для лестниц. Применяется как на улице, так и внутри дома, на даче. Условный, теоретический, табличный, расчетный удельный вес 1 м p трубы 40x40x2 никогда не соответствует массе, полученной путем взвешивания на весах, и не может служить «заменой» весов.Однако знание линейного веса 1 метра трубы 40х40х2 мм позволяет быстро сделать теоретические, приблизительные оценки массы имеющегося количества профильных труб. А также служит дополнительным способом проверки правильности работы весов. Для того, чтобы рассчитать вес имеющегося количества стальной трубы 40х40х2 мм, нужно измерить ее длину, обычно для этого используют рулетку. После чего количество метров – метр трубы 40х40х2 мм умножается на теоретический вес 1 метра погонного. За результат принимается ориентировочный или расчетный вес трубы 40х40х2 мм. Очень простая формула расчета веса любых труб, как профильных, так и круглых.

1. Масса теоретическая по ГОСТ 30245-2003 одна 1 м / п – 7,07 кг

2. Отклонения стенки профильной трубы могут быть идентичны отклонению по ширине заготовки по ГОСТ 19903. Отклонения по толщине не распространяются на места загиба профиля (углы)

3.Отклонения по высоте и ширине профильной трубы по ГОСТ 30245-2003 должны быть в процентах: при высоте трубы до 100 мм +/- 1,0, не менее +/- 0,5 мм; более 100 мм +/- 0,8

4. В поперечном сечении профиля отклонения от угла 90 градусов не должны превышать +/- 1,30.

5. Профиль изготавливается длиной от 6,0 до 12,0 м ; По согласованию с покупателем труба профильная 80х80х3 может изготавливаться длиной от 4мм.От 0 до 13,0 об / м

6. Извилистость пр. Трубу следует укладывать в пределах 2,0 мм плюс 0,5 мм через каждые 1 п / м профиля по ГОСТ 30245

7. Временное сопротивление продольному разрыву сварного шва должно быть не менее 0,95 Временное сопротивление растяжению основного металла

8. Прием и условия контроля за приемом продукции и др. Трубы 80х80х3 см, ГОСТ 30245-2003 поз. № 5

9. Гарантийный срок хранения профильной трубы составляет 24 месяца со дня отгрузки изготовителем заказчику.

10.Профиль маркируется по ГОСТ 7566, в маркировке должно быть указано
– товарный знак компании, наименование.
– размеры другой трубы.
– количество плавок;
– длина профиля;
– номер профиля;
– вес и количество пачек;
– марка OTC.

Труба профильная 80х80х3 изготавливается, как правило, по ГОСТ 30245-2003 (профиль стальной гнутый закрытый сварной квадратный для строительных конструкций) и ТУ-14-105-568-93 из углеродистой стали обыкновенного качества Ст3, либо из сталь углеродистая качественная с легирующими добавками 09Г2С.Труба 80х80х3 – одна из самых популярных в ассортименте квадратных труб большого сечения. Эти изделия широко используются при строительстве жилых домов, модульных зданий, промышленных предприятий, ангаров, спортивных комплексов, гаражей и других построек.

Мощная стенка и четыре ребра жесткости этой профильной трубы квадратного сечения выдерживают довольно большие механические нагрузки. Кроме того, труба 80х80 имеет небольшой вес, что позволяет экономить металл и позволяет использовать менее мощную строительную технику при монтаже профильной трубы 80х80х3.Еще одно преимущество квадратной трубы – простота укладки на ровные поверхности. В этом плане стальная профильная труба на 20–25% экономичнее круглой.

По способу изготовления труба профильная 80х80х3 бывает горячедеформирована, холоднодеформирована и электросварна. Если в дальнейшем предполагается эксплуатировать трубу под высоким давлением, труба проходит гидравлические испытания с заданным давлением.

Основными производителями профильных труб 80х80х3 в РФ являются такие заводы и металлургические предприятия, как ОАО «ЕВРАЗ», ОАО «Северсталь», ООО «Северсталь Трубный профиль Шексна», ОАО «ММЗ» и др.

1. Масса теоретическая по ГОСТ 30245-2003 одна 1 м / п – 3,56 кг

2. Отклонения стенки профильной трубы могут быть идентичны отклонению по ширине заготовки по ГОСТ 19903. Отклонения по толщине не распространяются на места загиба профиля (углы)

3. Отклонения в высота и ширина профильной трубы по ГОСТ 30245-2003 должны быть в процентах: при высоте трубы до 100 мм +/- 1.0, не менее +/- 0,5 мм; более 100 мм +/- 0,8

4. В поперечном сечении профиля отклонения от угла 90 градусов не должны превышать +/- 1,30.

5. Профиль изготавливается длиной от 6,0 до 12,0 м ; по согласованию с покупателем труба профильная 80х40х2 может изготавливаться длиной от 4,0 до 13,0 п / м .

6. Скрутка пр. Трубы не должны входить в 2,0 мм плюс 0,5 мм каждые 1 п / м профиля по ГОСТ 30245

7.Прочность на разрыв продольного шва должна быть не менее 0,95 временная прочность на разрыв основного металла

8. Приемка и условия контроля приемки изделий и др. Труб 80х40х2 см. ГОСТ 30245-2003 абзац № 5

9. Гарантийный срок хранения профильной трубы составляет 24 месяца со дня отгрузки изготовителем заказчику

10. Профиль маркируется по ГОСТ 7566, маркировка Должен содержать
– товарный знак компании, наименование.
– размеры другой трубы.
– количество плавок;
– длина профиля;
– номер профиля;
– вес и количество пачек;
– марка OTC.

Труба прямоугольная 80х40х2 6м Ст1пс

Для придания прямоугольным трубам определенных физико-механических характеристик используются различные методы их изготовления и последующей термообработки. Профильные трубы могут изготавливаться методом холодной прокатки, горячей прокатки или вытягивания. В результате термической обработки металл может увеличиваться в твердости (закаливаться) или, наоборот, становиться более мягким и вязким (отпуск).Дополнительные условия изготовления должны быть оговорены потребителем и зафиксированы в специальном договоре. Стандарты качества контролируются ГОСТ 8645-68 с новыми дополнениями и изменениями.

Заготовки для профильных труб представляют собой бесшовные или сварные круглые трубы; визуальный контроль качества проводится перед приемкой продукции на склад. Лабораторные испытания могут быть выполнены по желанию оптового покупателя, каждая партия проходит испытания, вес партии не более 60 тонн. Для обеспечения одинаковых механических характеристик партию труб следует изготавливать из одного плавильного ковша, обеспечивая тем самым однородность металла по химическому составу.Физические свойства трубы соответствуют международному стандарту EN 10219: 2006, момент сопротивления поперечного сечения W для прямоугольных труб размером 80 × 60 × 2 составляет 6,38 см3 в ширину (ось X) и 9,38 см3 в высоту (ось Y) в высоту. .

Труба стальная 80х80х3 погонной массой 1 метр – это удельный, табличный, теоретический, справочный, условный или погонный вес металлопроката. Названия используются как синонимы и означают не реальный вес, полученный в результате прямого взвешивания на весах, а теоретически рассчитанный по ГОСТу. Данные о весе 1 метра трубы из стали 80х80х3 мм можно найти в таблице из справочника по удельному весу металлопроката или рассчитать самостоятельно. Однако такие расчеты веса 1 метра трубы требуют определенного опыта и знания формулы пересчета массы. Например, расчет массы 1 мп квадратной металлической трубы сводится к расчету веса железной полосы. Поэтому пользоваться таблицей намного удобнее. В принципе, нам нужна таблица удельных, условных, справочных, расчетных, теоретических или линейных масс стальной профильной трубы, той ее части, которая относится к квадратным трубам.Трубы стальные квадратного сечения 80х80х3 мм также являются профильными, но с одинаковой шириной обеих полок. Если ширина полки у металлической профильной трубы разная, то такие трубы называют стальными прямоугольными. Более правильное название для указанной в справке стальной трубы квадратного сечения – стальной квадратный замкнутый профиль. Металлическая квадратная труба 80х80х3 мм может быть сварной или цельной, но на практике стальные трубы с такой толщиной стенки обычно делают сварными.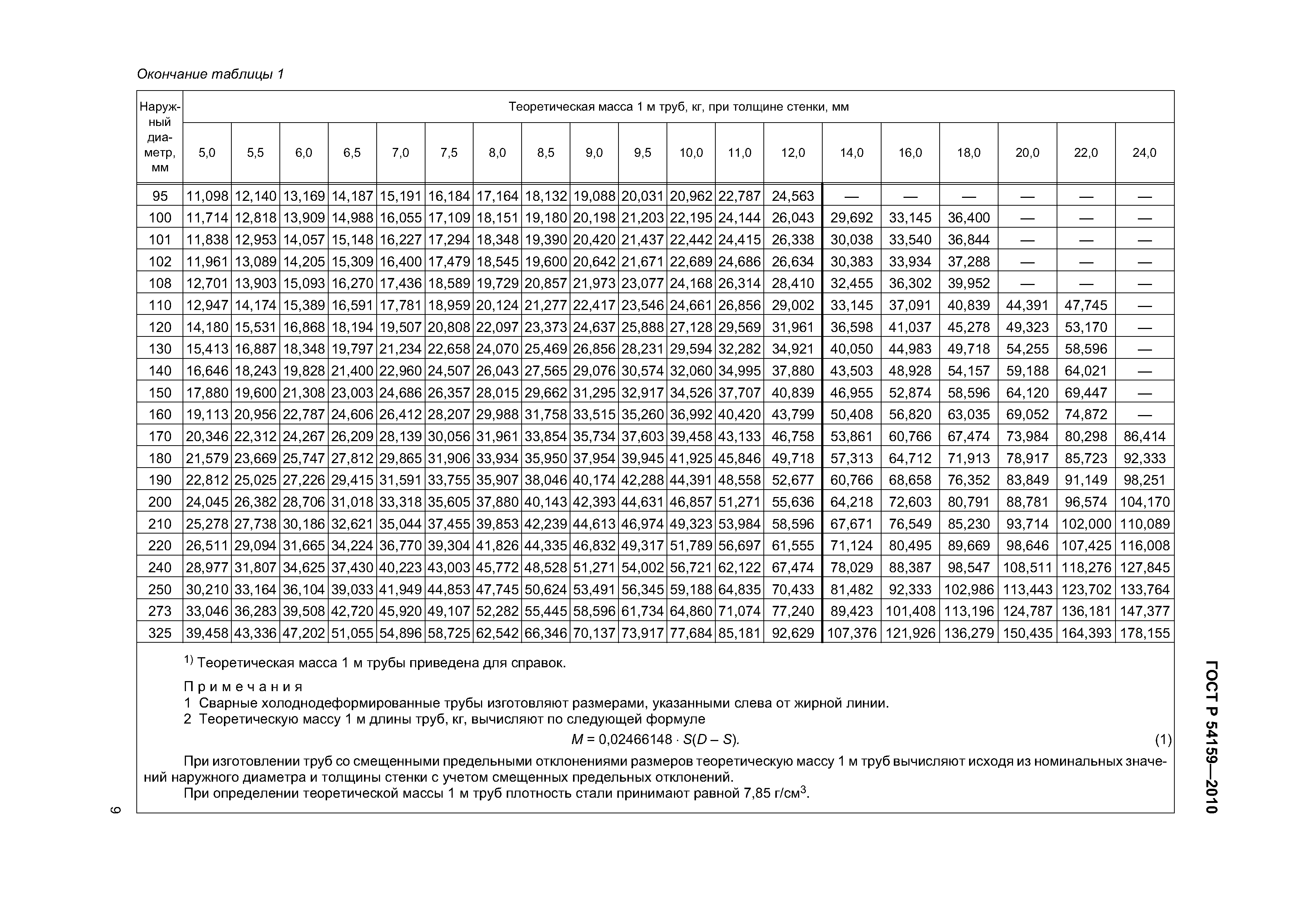 И по праву считаются тонкостенными световодами.Стальная труба 80х80х3 мм чаще всего используется для производства металлоконструкций бытового, декоративного, строительного и промышленного назначения. Профильная металлическая труба 80х80х3 мм хорошо сваривается, легко режется, а при необходимости удобно гнется. Поэтому гнутые и арочные металлоконструкции изготавливают из металлической трубы 80х80х3 мм. Прокат имеет небольшой вес, при относительно высокой жесткости, поэтому металлоконструкции из трубы 80х80х3 мм называют легкими или легкими. Для тех задач, где важным условием изготовления сварной металлоконструкции является высокая прочность или высокая устойчивость к коррозии, лучше использовать трубы такого же сечения, но с большей толщиной стенки.Для водопроводов и газопроводов рекомендуется использовать стальные металлические трубы не сварные, а бесшовные. В редких случаях для отопления и водоснабжения можно использовать стальную профильную трубу 80х80х3 мм. Толщина стенки стальной трубы квадратного сечения 80х80х3 мм в принципе позволяет использовать не только сварные соединения, но и винты или заклепки при изготовлении из нее конструкций. Но в целом профильная труба 80х80х3 мм для этого не предназначена. Хотя изредка находит такое применение, например: при изготовлении заборов из профнастила и различных каркасов, беседок, беседок, навесов, козырьков и входных групп.Труба стальная профильная 80х80х3 мм оказалась очень удобным материалом для изготовления арочных металлических изделий, пергол, декоративных заборов, заборов, заборов, палисадников, растительных и цветочных насаждений, садовых конструкций, ворот, решеток, металлических дверей, качелей. и автоматические ворота, садовые мостики, перила и перила для лестниц. Применяется как на улице, так и внутри дома, на даче. Условный, теоретический, табличный, расчетный, удельный вес 1 м трубы 80х80х3 никогда в точности не совпадает с массой, полученной взвешиванием на весах и не может служить «заменой» весов.Однако знание линейного веса 1 метра трубы 80 × 80 × 3 мм позволяет быстро сделать теоретические, приблизительные оценки массы количества профильных труб, имеющихся у вас на складе. А также служит дополнительным способом проверки правильности работы весов. Чтобы рассчитать вес имеющегося количества стальной трубы 80х80х3 мм, нужно измерить ее длину, обычно для этого используют рулетку. После этого количество метров – квадратный метр трубы 80х80х3 мм умножается на теоретический вес 1 погонный метр.В результате принимается ориентировочный или расчетный вес трубы 80х80х3 мм. Очень простая формула расчета веса любых труб, как профильных, так и круглых.

Масса 1 метра стальной трубы. Калькулятор профильной трубы

Трубы бывают электросварные и бесшовные, круглые, водогазопроводные или профильные. Определите Тип , трубы . Проверьте его внешний диаметр и толщину стенки в мм. Измерьте длину одной труб в метрах и количество труб в заказе.

Найдите тип и конструкцию в справочнике теоретических масс стальных труб соответствующего ГОСТ масса один погонный метр труб нужного диаметра и толщины стенки.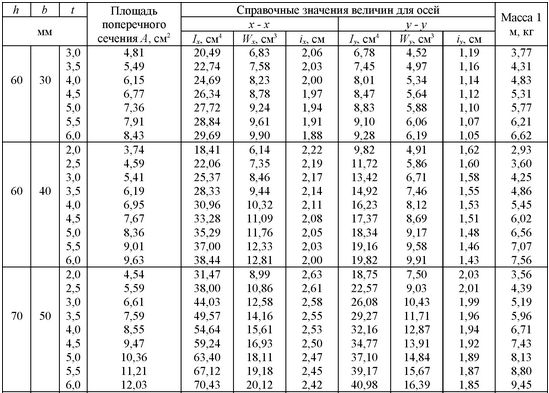 Умножив массу погонного метра на длину труб , получим один вес труб в килограммах. Рассчитайте общий вес заказа, умножив вес 1 труб на их количество в заказе.

Рассчитайте вес полиэтилена аналогично. трубы зная тип, диаметр, толщину стенки и длину. Для расчетов используйте справочные данные ГОСТ для полиэтиленовых труб. Для определения веса одного погонного метра полиэтиленовых труб согласно инструкции необходимо рассчитать SDR или коэффициент типоразмера.

Разделите диаметр полиэтиленовой трубы на толщину ее стенки. Таким образом, вы найдете SDR в мм. Зная стандартное размерное соотношение, найдите расчетной массы погонных метров труб желаемого диаметра .Далее рассчитываем массу искомого участка труб или всего пролета, умножив массы погонных метров труб на ее длину.

Обычно труба имеет форму полого цилиндра, поэтому ее масса зависит от толщины стенки, материала изготовления и длины. Если эти параметры заданы в условиях задачи, ее решение сведется к нахождению формулы в общем виде, подстановке значений переменных и вычислению результата.Для практических расчетов массы трубы как промышленного изделия значения переменных можно найти в нормативных документах – ГОСТах.

Инструкция по эксплуатации

Чтобы составить формулу расчета массы трубы, нужно узнать площадь сечения полого цилиндра. Для этого необходимо знать толщину стенки (а). Если условий задачи не существует, но заданы внутренний (d) и внешний (D) диаметры, выразите толщину стенки через половину разницы этих значений: a = (D-d) / 2.Площадь поперечного сечения определяется как разница между произведением внешнего диаметра и толщины стенки и квадратом толщины стенки, умноженным на число Пи: π * (D * a-a²).

Используя формулу площади сечения, определите объем, заключенный между внешней и внутренней стенками – умножьте формулу, полученную на предыдущем шаге, на длину трубы (L): π * (D * a-a²) * L.

Подставьте значения, указанные в условиях задачи, в формулу и вычислите результат.При этом учитывайте размерность исходных значений. Предположим, что внешний диаметр стальной трубы составляет 30 см, толщина стенки 5 мм, длина 4 м, а плотность стали 7,95 г / см³. В этом случае можно подставить в формулу все значения в сантиметрах, получить результат в граммах и перевести в килограммы: 3,14 * (30 * 0,5-0,5²) * 400 * 7,95 = 3,14 * 14, 75 * 400 * 7,95 = 147281,7 г ≈ 147,3 кг.

В практических расчетах для определения значений переменных, которые необходимо подставить в формулу, используйте нанесенную на трубы маркировку или указанную в сопроводительных документах.Зная его, можно определить требуемые значения согласно нормативным документам – ГОСТам. Например, плотность стальных труб можно найти в ГОСТ 9941-8, а плотность пластиковых труб – в ГОСТ 18599-2001.

Источники:

• Онлайн-калькулятор
• как рассчитать вес трубы

Необходимость обозначения диаметром труб часто возникает при замене канализационных труб, выборе полотенцесушителя и других домашних делах. Вы можете определить это самостоятельно, для этого вам понадобится только рулетка или штангенциркуль.

Вам понадобится

• – труба;
• – рулетка;
• – штангенциркуль;
• – линейка.

Инструкция по эксплуатации

Измерить рулетку с помощью рулетки или рулетки , для этого оберните ее вокруг и посмотрите на значение на шкале. Затем разделите полученное значение на число Пи, равное 3.1415. В итоге получается наружный диаметр труб .

Если у вас есть штангенциркуль, вы можете измерить внешний диаметр напрямую (для труб до 15 см). Для этого возьмитесь за трубу губками инструмента и посмотрите на двойную шкалу, сколько сантиметров , диаметр .

Для того, чтобы узнать внутренний диаметр , измерьте толщину стенки на отрезке трубы . Измерения производите линейкой или штангенциркулем (второй способ, конечно, более точный).Вычтем из внешнего диаметра и толщину стенки, умноженную на два – полученное число будет внутренним диаметром .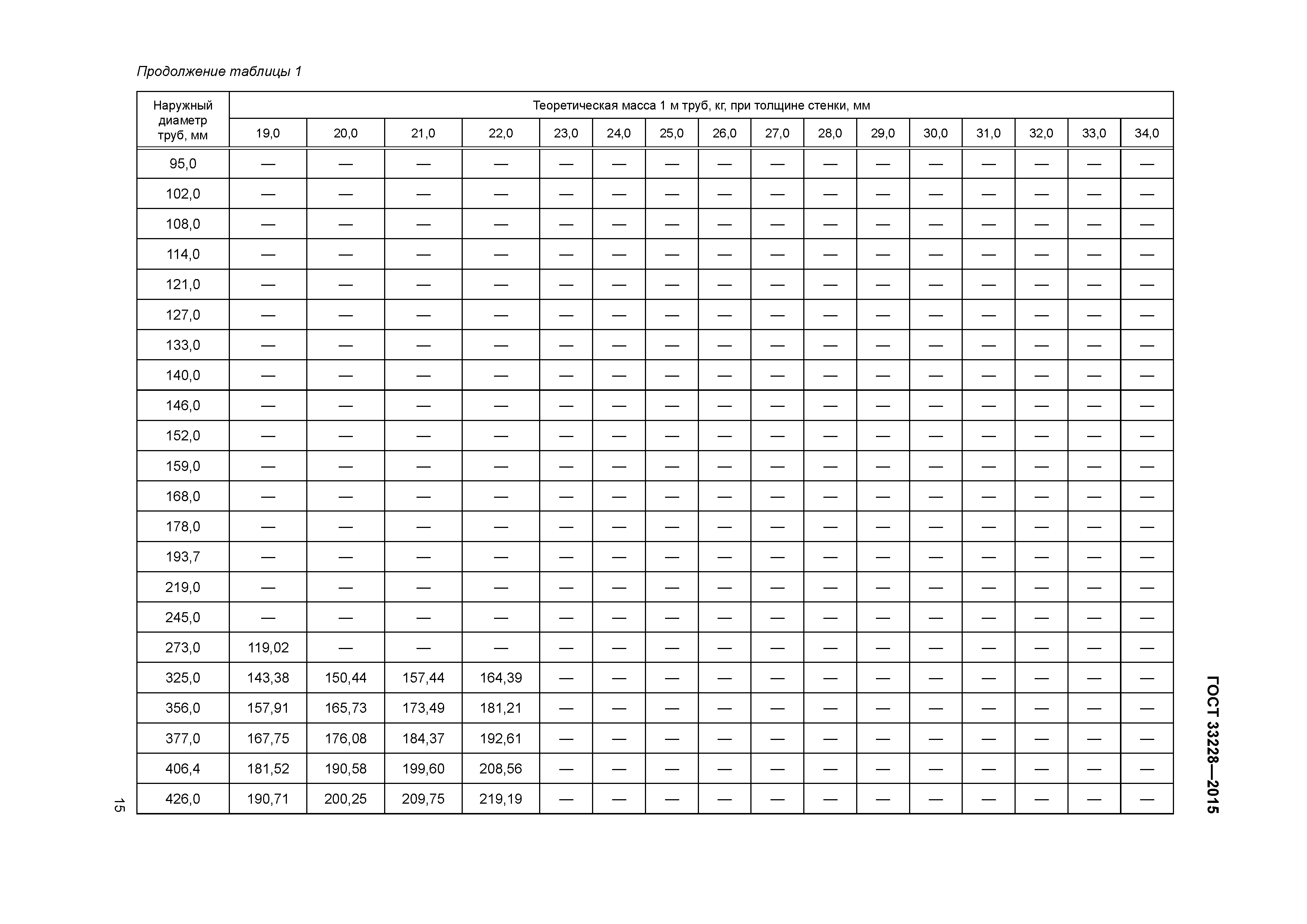

Выбирая полотенцесушитель или другую работу, в которой вам нужно узнать диаметра стандартного крана труб проходящих у вас дома, воспользуйтесь следующим несложным методом. Прикрепите к трубе линейку и оцените ее приблизительный диаметр . Если вы видите на глаз, что труба имеет ширину около 32 см – смело делайте вывод, что посадка диаметром у нее 1 дюйм.Стандартная труба в дюйм соответствует размеру 25-28 см, а 1,2 дюйма соответствует значению 16 мм.

примечание

При обозначении металлических труб, например, труб для металлических конструкций или нержавеющих труб, используются внешний диаметр и толщина стенки. Например, запись выглядит так: 530×12. Для водогазопроводных труб большое значение имеет внутренний диаметр, поэтому указываются они, например, 15х2 (на первый взгляд точно такие же). Чтобы определить, какая труба перед вами, посмотрите ГОСТ.Водогазопроводные трубы (ВГП) изготавливаются по ГОСТ 3262.

.

Точный расчет количества бетона , который будет уложен в опалубку – одно из условий грамотного выполнения строительных работ. Лишний бетон, как правило, использовать некуда. Миксер либо заберет заказанный и заранее оплаченный бетон, либо сбросит его в указанном месте, создав «памятник» вашей головной боли. Нарушение технологии строительства из-за отсутствия бетона приведет к еще более серьезным последствиям.Рассмотрим на примере ленточного фундамента, как избежать подобных ошибок.

Вам понадобится

• – линейка
• – рулетка
• – калькулятор.

Инструкция по эксплуатации

Товарный бетон различных марок, представляющий собой полужидкую массу, в зависимости от своего состава имеет неравномерную усадку – чем меньше в нем цемента и воды, тем менее значительно изменение объема бетон при затвердевании. Кроме того, на величину усадки бетона влияют и другие факторы, например, на способ уплотнения: при копании лопатой усадка меньше, чем при уплотнении бетона глубоким вибратором.При расчете необходимого количества бетона обычно используют единый средний коэффициент усадки, равный 1,015–1,02.

Рассчитать объем бетонной конструкции заранее, согласно проекту (эскизу). Для этого умножьте ширину, высоту и длину фундамента.

После устройства опалубки проверьте соответствие высоты, ширины и длины фундамента расчетным значениям. Небольшие отклонения размеров вверх приводят к значительному увеличению необходимого количества бетона .Применение инвентарной опалубки из стального каркаса и влагостойкой фанеры позволяет свести к минимуму эти ошибки.

Умножьте полученный объем на коэффициент усадки.

Из полученного значения вычтите объем всех проемов и ниш инженерных сетей (трубы, воздуховоды). Для этого нужно рассчитать соответствующие объемы по формулам для определения объема цилиндра (площадь круга, умноженная на высоту) или параллелепипеда (длина, умноженная на ширину и высоту).В результате будет получено количество бетона , которое необходимо для заливки данной конструкции.

примечание

Во избежание ошибок в расчетах все измерения (длина, ширина и высота фундамента и проемов в нем) следует проводить в одних и тех же единицах измерения – метрах.

Очень важно, чтобы в случае использования щитовой опалубки она была максимально выровнена и жестко закреплена, иначе опалубка может оторваться от массы залитого бетона.Немаловажное значение имеет отсутствие зазоров между досками, через которые будет просачиваться вода при уплотнении залитого бетона, что также приводит к изменению большей стороны коэффициента усадки.

Если приходится проводить в дом холодную воду, очень важно своевременно рассчитать вес труб, который станет дополнительной нагрузкой для фундамента.

1 Почему рассчитывается вес трубы?

Вы решили начать укладку труб и точно знаете, сколько метров вам понадобится.Казалось бы, все может пойти по магазинам, отрегулировав багажник на крыше своей машины, или наняв грузовик с открытым кузовом. И тут возникает необходимость точного расчета веса стальной профильной трубы, онлайн-калькулятор по месту покупки без знания формул вам вряд ли поможет. Ведь вам нужно знать, сколько погонных метров трубы определенного диаметра можно загрузить в вашу легковую машину, имеющую предел грузоподъемности.

Расчет веса прямоугольного профиля

2

Редко какой материал можно сравнить по прочности со сталью, поэтому трубы из этого металлического сплава являются наиболее предпочтительными.Они производятся и продаются в погонных метрах, а на складе можно найти круглые и прямоугольные профили как поштучно, так и в пачках. Казалось бы, что еще нужно для приобретения необходимого количества труб? Однако зачастую очень важно знать вес приобретенного материала.

Основные причины этого перечислены выше, теперь нам нужно выяснить, как именно рассчитать массу различных профилей. ГОСТ 8732-78 предлагает общий способ для всех типов стальных труб, различающихся только диаметром, для которого принята средняя плотность металла 7850 кг / м 3 .Для получения желаемого результата следует по таблицам, предложенным в ГОСТ 8732-78, определить значения диаметра и толщины стенки, а затем воспользоваться формулой М = 0,02466. С (Д н – С) .

Здесь D n – наружный диаметр, а S – толщина стенки круглого профиля. Однако, как уже упоминалось, этот метод даст только приблизительный расчет массы одного погонного метра трубы. Его стоит использовать, если вы заранее не определились с весом необходимых профилей и сейчас быстро его рассчитываете.Для более точного расчета существует еще одна формула, для работы которой нам понадобятся такие значения, как внешний и внутренний диаметр, объем, площадь сечения, плотность металла.

Этот метод удобен тем, что он подходит как для стальных труб, так и для чугуна с медью. Сама формула выглядит так: м = pV , где p – плотность, а V – объем. Однако это только начало расчетов, нам нужно получить объем.Его у нас такие: V = SL , здесь S – площадь поперечного сечения трубы, а L – ее длина. Причем первое значение зависит от внутреннего и внешнего диаметров. Отсюда S = π (D 2 – d 2) / 4 , где D – наружный диаметр, а d – внутренний, что нам далеко не всегда известно и определяется следующим образом: d = D – 2b , где b – толщина стенки трубы.

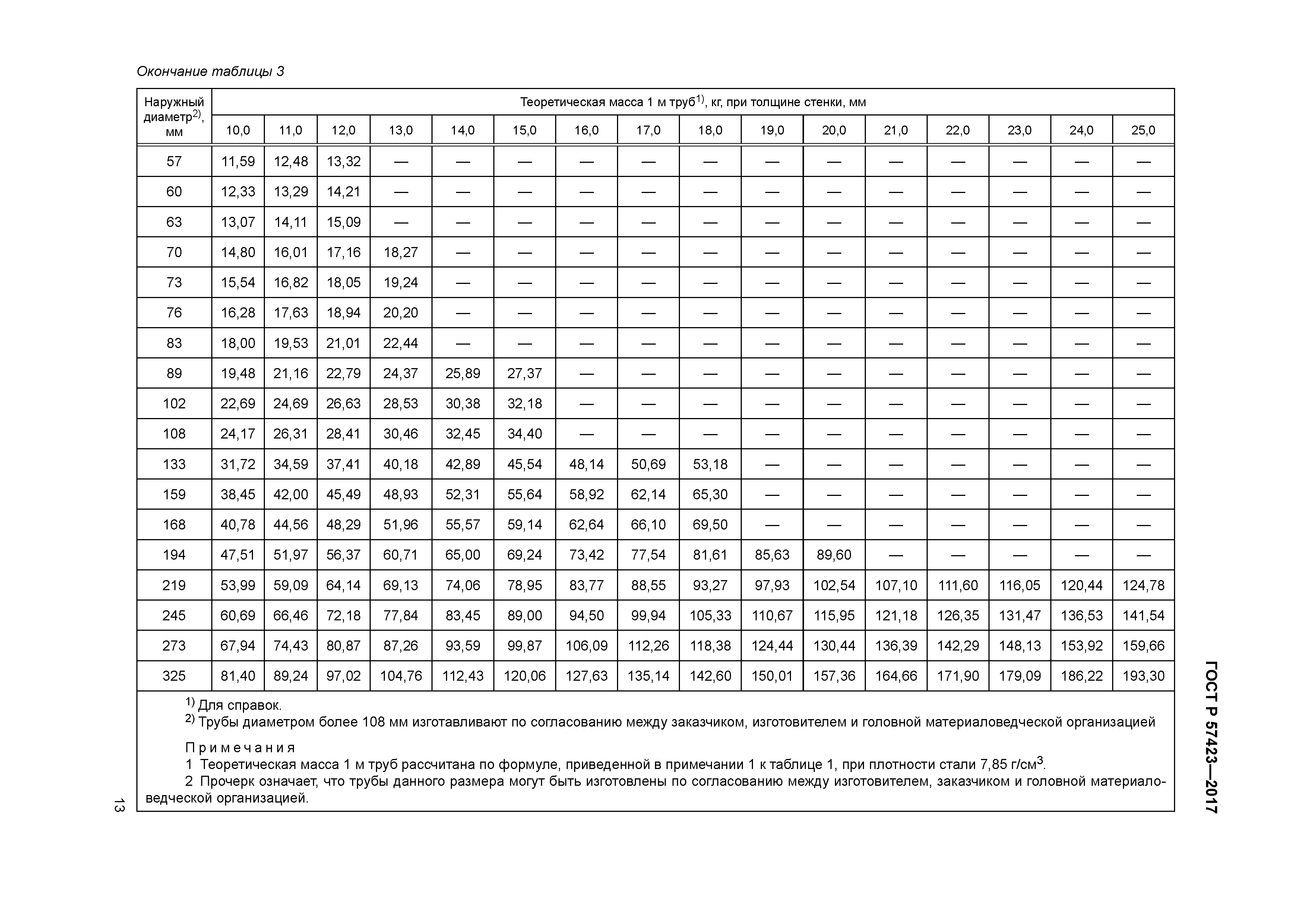
Однако из всех значений данной универсальной формулы для круглых профилей одно нам остается неизвестным, а именно плотность металла.Можно, конечно, использовать среднее значение, как это предложено в ГОСТ 8732-78, но тогда формула теряет всю универсальность. Поэтому пойдем дальше и воспользуемся ГОСТ 1050-88 для получения плотности стали, ГОСТ 1412-85 для серого чугуна и так далее. Мы выяснили, что стали 10, 20, 40 и 60 имеют плотность 7856, 7859, 7850 и 7800 кг / м 3 соответственно.

Для высокопрочного чугуна плотность 7000, для высокопрочного – 7200. Для серого чугуна марок СЧ10, СЧ20 и СЧ30 плотность 6800, 7100 и 7300 соответственно, а для меди марок М0, М1, М2 и М3, суммарное значение 8940 кг / м 3.Чтобы получить правильный результат в килограммах, все расчеты с длинами и другими размерами обычно проводят в метрах, так как значения плотности берутся в кг / м 3.

3

Вышеупомянутый метод подходит только для круглых профилей, но что, если вам нужно? Для этого есть отдельный метод, однако он тоже дает только средний результат, конечно, при условии, что вы используете среднее значение плотности металла, а именно 7850 кг / м3.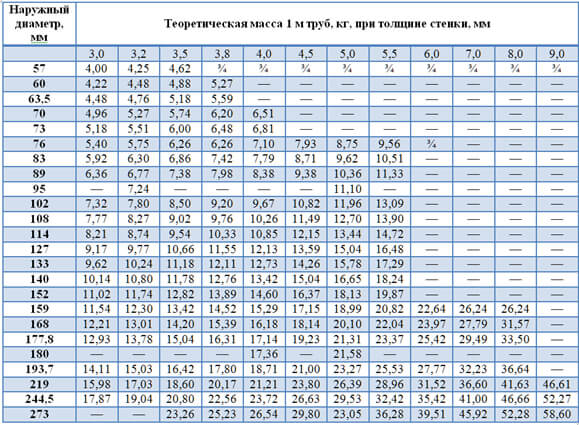 Однако ничто не мешает применить значения плотности различных сплавов и цветных металлов, уже найденные нами по предыдущей формуле.

Сама формула следующая: M P = b. 2 (А + В). ρ , где b – толщина стенки профиля, A и B – длины сторон, а p – плотность. Как найти толщину стенки трубы, вы уже знаете из ряда приведенных выше формул.
Есть еще один способ, для которого нам понадобится формула для расчета массы профиля круглого сечения. Кто-то спросит: «При чем тут диаметр, если для расчетов нужен диаметр?» Однако напомним, что основное определение массы выглядит как м = pV , то есть нам нужна плотность и объем трубы из того или иного металла.Первое значение у нас в изобилии, можно подставлять разные значения, благодаря всевозможным ГОСТам, а второе ничего не стоит, и даже не одним, а тремя способами. Правда, каждый из способов немного изменит калькулятор трубы, во всех трех случаях вес трубы будет не одинаковым.

Итак, рассмотрим первый способ получить объем.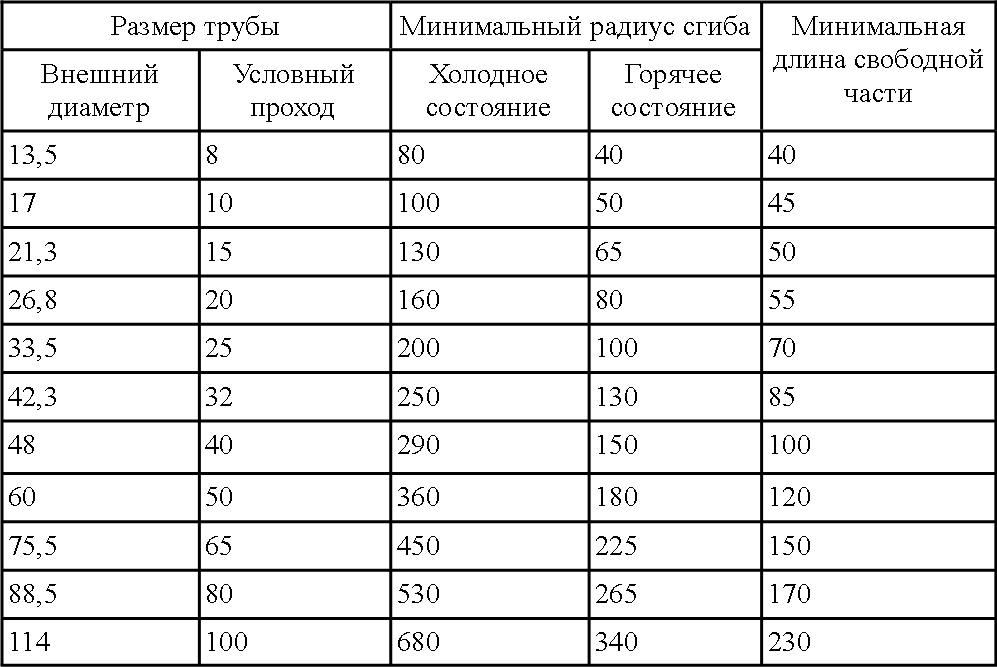 Сначала представьте трубу в виде стержня. Другими словами, нам нужны внешние длины сторон и длина прямоугольного профиля.Умножьте эти значения и получите общий объем трубы, вместе с пустотой. Теперь нам нужно рассчитать объем, так сказать, «бублика», то есть внутренней полости профиля. Умножьте длину внутренних сторон на длину. Вычтите второй результат из первого и получите объем металла, содержащегося в стенках трубы. Теперь, чтобы рассчитать вес трубы, остается подставить в калькулятор любое подходящее значение плотности.

Второй способ несколько сложнее, при условии, что стенка профиля имеет неодинаковую толщину по всему периметру (в горячекатаном профиле), которую нам необходимо измерить.Для этого измерьте одну сторону и умножьте полученное значение на среднюю толщину этой стены. Аналогичная процедура повторяется еще 3 раза для остальных участников. Таким образом, мы получаем объемы четырех граней прямоугольного профиля, складывая их, получаем итоговое значение. Результат расчетов следует умножить на плотность металла, из которого изготовлена ​​труба. Третий способ – использовать данные в таблице ниже, согласно которой вы можете найти массу в килограммах:

Сторона A	Сторона B	Стенка 3	Стенка 4	Стенка 5	Стенка 6	Стенка 7	Стенка 8	Стенка 9	Стенка 10

Вес металла – важная характеристика, играющая большую роль при приобретении, транспортировке и расчете конструкций. Калькулятор позволяет быстро определить теоретическую массу труб.

1 Зачем нужно определять вес профильных труб

Профильными трубами называют трубы, которые в отличие от обычных водопроводных труб имеют некруглое сечение. Наиболее распространены и востребованы профильные трубные изделия прямоугольного и квадратного сечения. Обычно его используют для изготовления различных видов металлических конструкций и их элементов в строительной индустрии и различных сферах производства.

В первую очередь данные о массе профильного изделия необходимы для расчетов, которые выполняются при проектировании и разработке металлоконструкций, а также для заполнения различных технико-бухгалтерских документов. Необходимо знать вес проката при его покупке и продаже, так как все платежи обычно производятся за килограммы (тонны) и только за редким исключением за погонные метры, штуки. Необходимо определить, сколько весит перевозимая партия, а также выбрать способ транспортировки и способы доставки продукции.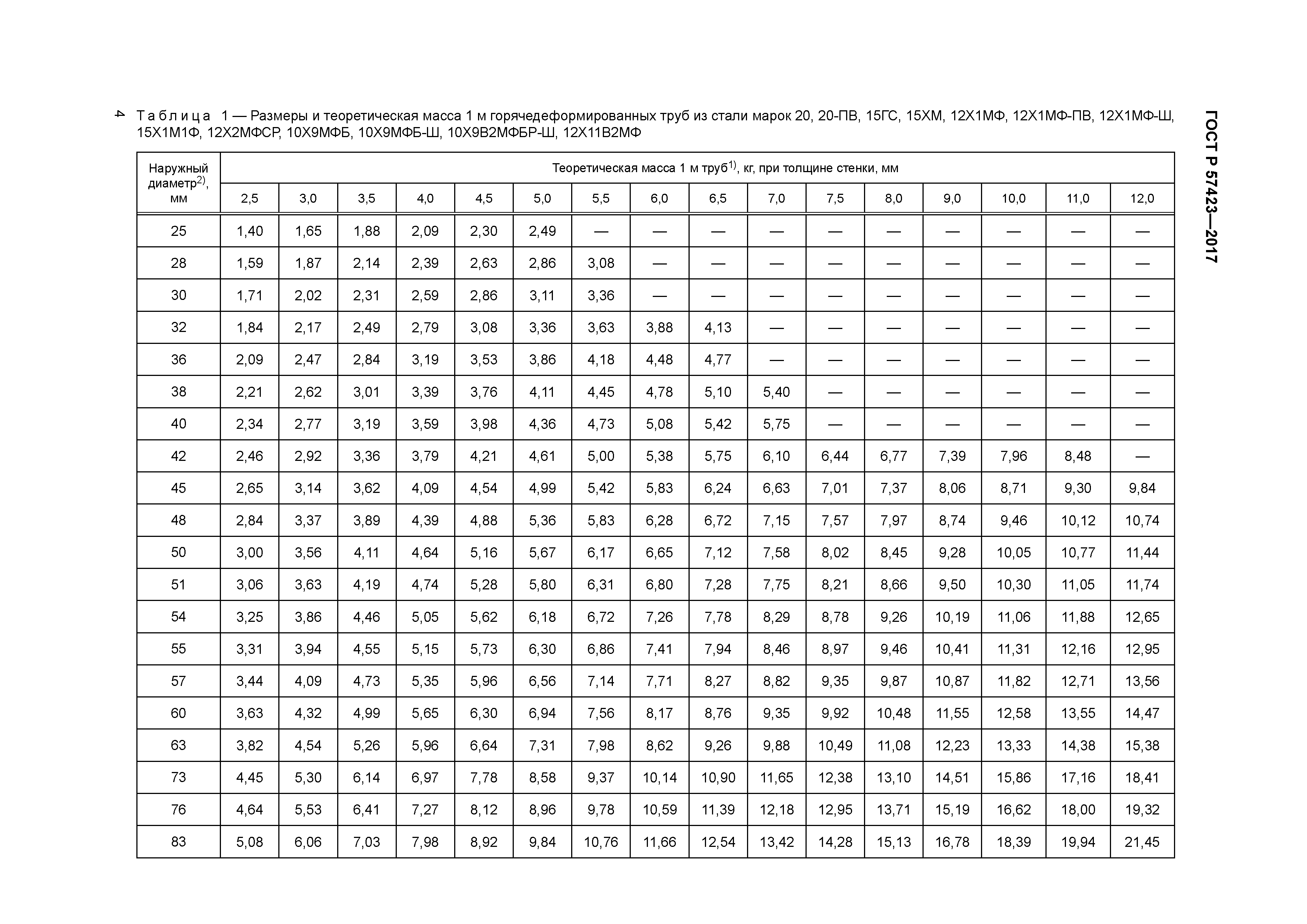

Кроме того, на рынке металла и строительных материалов встречаются недобросовестные продавцы (или поставщики и производители), которые пытаются обмануть себя в потребителях. Они могут предложить некондиционную, бракованную, профильную трубную продукцию, не соответствующую стандартам и ГОСТам, внешне неотличимую от качественной. Так, например, нередки попытки сбыта продукции китайского производства, у которой заявленные (технологически регламентированные) размеры (толщина) стенок присутствуют только по краям, где, по сути, проверяют соответствие типоразмерам. .А на самом деле труба 100х100х5 мм посередине может иметь другие параметры – 100х100х4 мм. Таким образом, металл экономится в процессе производства, и в результате продажи может возникнуть «обвес» – если продажа осуществляется штучными или погонными метрами. Покупатель получит некачественные изделия из металла, которые не стоят потраченных денег и могут привести к серьезным негативным последствиям. Этот «дефицит» легко определить, если знать, какой вес должна иметь труба заданных размеров.

2 Методы определения веса профильной трубы

Все существующие методы определения веса металла без его взвешивания позволяют получить теоретическое значение по имеющимся размерным характеристикам (диаметр, ширина, высота, толщина, длина).Только взвешивание покажет точную массу. Существуют следующие методы определения теоретической массы:

• с использованием таблиц для этого типа металла;
• с помощью калькулятора профильных труб;
• путем расчета по математической формуле.

Во всех случаях для определения веса используется теоретическая плотность используемого металла (для стали 7850 кг / м 3), а также стандартные размеры изделия, предусмотренные техническими условиями ГОСТ.

Но существует много разных сплавов, и их фактическая плотность всегда, хоть и немного, отличается от теоретической. Фактические размеры и форма металлического изделия также могут не совпадать с табличными в пределах допусков, установленных ГОСТ. Следовательно, масса, определенная этими методами, является теоретической.

В таблицах указан вес 1 погонного метра профильной трубной продукции (в килограммах) для каждого размера и количество метров в 1 тонне продукции.Для определения общей массы партии проката необходимо вес 1 м.л. умножить на общую длину всего объема трубы (в метрах).

Самый быстрый способ узнать массу профильной продукции – с помощью онлайн-калькулятора. Вручную по формулам – самый медленный и менее надежный, так как этот метод имеет больше, чем первые две возможности ошибиться (можно неправильно использовать формулу или ошибиться при выборе и вводе данных).

3 Расчет профильной трубы с помощью онлайн-калькулятора

Специальные калькуляторы, расположенные в Интернете, позволяют быстро рассчитать массу профильной трубы. Все, что требуется, это ввести параметры проката в соответствующие поля калькулятора:

• боковые длины (высота и ширина) профиля;
Толщина стенки
• ;
• длина трубы.

Далее необходимо указать марку стали (сплава), из которой изготовлено профильное изделие, и нажать кнопку ввода. В результате будет получено значение теоретического веса трубы. Причем калькуляторы не рассчитывают массу 1 метра профильных изделий, а сразу подставляют нормированные табличные значения в соответствии с номером изделия.В этом принципиальное отличие от расчетов по формуле, где этот параметр определяется независимо. Благодаря этому расчет на калькуляторе более точный.

На калькуляторе можно произвести расчет для труб из следующих металлов:

• чугун;
• стать;
• медь;
• бронзы;
• алюминий;
• латунь;
• титан;
• магний
• сплавы прочие.

Также определите метраж трубы по ее весу (количество метров на 1 кг или тонну продукта).

4 Расчет веса профильной трубы по формуле

Расчет профильной трубы по формуле основан на расчете объема металла стенок сегмента изделия длиной 1 м. Когда это значение умножается на плотность сплава, используемого для производства металлопроката, получается теоретический вес 1 м трубы.Умножив этот вес на общую длину изделия, определяется его масса. Формула расчета 1 м изделий из профильной трубы следующая: 26,376 * 200 = 5275,2 кг

Полученный по формуле теоретический вес 1 м отличается от табличного значения, взятого из ГОСТа – 24,18 кг. Это расхождение связано с тем, что предложенная формула расчета не учитывает внешние и внутренние кривые на углах профиля реальной трубы. Расчеты производились для изделия правильной геометрической формы (с прямыми углами), но фактически такие изделия не производятся.А теоретические значения по таблицам ГОСТ рассчитывались с учетом реальной геометрии профиля трубного производства, поэтому они более точные. Поскольку формулы, используемые в этих расчетах, намного сложнее приведенной выше и требуют гораздо больше времени для расчетов, мы их не приводим. В условиях, когда под рукой нет интернета и справочников, для определения примерного веса трубы будет достаточно упрощенного быстрого расчета. А точную массу лучше узнать, взвесив продукты.

Если вы не специалист по трубам, но вам нужно узнать, сколько будет весить стальная труба, не отчаивайтесь. Вы можете рассчитать вес стальной прямоугольной трубы или какой-либо другой, используя современные технологии в виде всемирной сети, где вы можете использовать онлайн-программы, в которых есть таблицы для расчета веса различных стальных труб.

Вес трубы узнаем по формуле

Если у вас нет доступа в интернет, то есть формулы для расчета удельного веса труб.Нужно знать, что вес одного метра стальной трубы принято считать в килограммах. Существуют две формулы расчета, и практика показывает, что обе они эффективны и дают результаты, которые мало чем отличаются друг от друга. По формулам рассчитывается большее количество размеров трубы, например, вес стальной электросварной круглой трубы от цельнотянутой ничем не отличается и зависит только от толщины стенки.

1. Вариант первой формулы : Mn = ((Du – Tc) / 40. 5) * Тс. Du – диаметр трубы, указанный в миллиметрах, Tc – толщина ее стенки в миллиметрах, результат – Mn. Результат покажет вам, сколько весит один килограмм трубы в килограммах.

2. Вариант второй формулы : Mn = (Du – Tc) * Tc * 0,0246615. В этом случае Du также будет диаметром самой трубы в миллиметрах, Tc – толщиной стенки трубы в миллиметрах. Суммарный Mn показывает вес в килограммах одного метра линейной трубы.

Узнать вес трубы калькулятором в интернете

В настоящее время существует достаточно большой ассортимент стали металлической. Иногда возникают определенные трудности, если нужно знать, например, вес профиля из стальной трубы. Приведенные выше формулы здесь не подойдут, потому что для того, чтобы узнать вес квадратной стальной трубы или такого же профиля, нужно будет учитывать сечение трубы: прямоугольное или квадратное. Для этого существуют программы, позволяющие легко рассчитать желаемый вес трубы.Калькулятор можно легко скачать из Интернета и у вас всегда будут цифры по характеристикам труб разного размера. Для использования калькулятора необходимо знать толщину стенки трубы и ее сечение. Найти такой калькулятор совсем несложно, достаточно воспользоваться для этого любой поисковой системой.

Когда нужен расчет веса трубы?

ПРО основные причины следующие:

– для расчета прочности построенной конструкции .Если каркас модульного дома монтируется, например, из профильной или круглой трубы, то вес полезной нагрузки – оконных проемов, людей в доме, мебели и т.п. – будет давить на основание. Сюда также входит вес верхних уровней рамы. Довольно часто несущий каркас здания весит намного больше, чем все, что находится в здании;

– по весу, закупка труб и других металлических изделий осуществляется . Если вы не знаете веса, кладовщик никогда не согласится отмерить вам полтора километра магистральных труб рулеткой;

– При погрузке труб на автомобили могут возникнуть трудности, если неизвестен их вес. ИЗ пластиковых труб намного проще, достаточно знать кубатуру и соизмерить ее вместимостью транспортных средств, на которых будет осуществляться транспортировка. Но при транспортировке стальных труб все иначе. Здесь нужно все точно рассчитать, так как такие трубы весят в десять раз больше, а техника от перезагрузки просто не сдвинется с места.

Как рассчитать вес алюминия

Обновлено 28 декабря 2019 г.

Автор: S. Hussain Ather

Используйте атомный вес элемента, чтобы определить, сколько веса составляет каждый атом элемента.Алюминий имеет атомный вес 26,9815 в Дальтонах или граммах на моль (г / моль). Это означает, что если у вас есть определенное количество молей алюминия, вы можете умножить его на атомный вес, чтобы определить, сколько у вас граммов на моль алюминия.

Это составляет вес алюминия в чистом виде. Этот тип алюминиевой гири не содержит каких-либо других элементов, которые могут смешиваться с ней или загрязнять ее. На практике во многих случаях алюминий используется в качестве сплава. Это означает, что они используют металлические предметы, содержащие алюминий наряду с другими элементами, такими как медь или железо.

Вес и масса

Вы можете легко измерить вес, поместив вещество на весы или весы. В зависимости от типа весов или весов, которые вы используете, вы получите результат либо по массе, либо по весу. Вы также должны принять во внимание вес или массу контейнера, который вы используете для взвешивания алюминиевого образца.

Если у вас есть определенная масса, которую вы хотите преобразовать в вес, вы можете использовать уравнение веса W = mg для веса W , массы m и гравитационной постоянной g из 9.8 м / с ² . Имейте в виду, что это дает вес в ньютонах для массы в килограммах. Чтобы перевести ньютоны в фунты, нужно умножить вес в ньютонах на 0,2248.

Вы выводите это уравнение из второго закона Ньютона, F = ma для силы F и ускорения a . В случае собственного веса объекта сила – это сила тяжести между объектом и Землей.

Онлайн-калькулятор веса

Существует несколько онлайн-калькуляторов для расчета веса металлов, например алюминия.Калькулятор веса от OnlineMetals.com позволяет рассчитать вес в зависимости от способа изготовления металла и формы самого металлического предмета.

Вы можете использовать подобные калькуляторы для практических целей оценки того, насколько тяжелыми могут быть определенные металлические элементы. Убедитесь, что вы учли подходящую форму и компоненты металла, который хотите взвесить.

Механические преимущества алюминия

Вы также можете протестировать простые машины, такие как клинья или шкивы из алюминия, на их эффективность при использовании прилагаемых к ним сил.Чем эффективнее эти машины используют приложенную к ним силу, тем выше их механическое преимущество. Эти машины, такие как шкивы или рычаги, имеют идеальное механическое преимущество (IMA), или отношение силы, которую они выводят, к силе, приложенной к ним.

Идеальная формула механического преимущества: F ₀ / F _i для выходной силы F _o для входной силы F _i . Различные сплавы алюминия имеют разные механические свойства, что приводит к различиям в механических преимуществах.

Вы также можете измерить идеальное механическое преимущество как d _o / d _i _ для выходного расстояния _d _o , на которое действует сила, и входного расстояния d _i . Это будет равно расстоянию, на которое вы тянете одну веревку шкива, или расстоянию, которое проходит рычаг при использовании в качестве простой машины.

Это работает, потому что, согласно закону сохранения энергии, работа, вложенная в систему, равна работе, которую выполняет система.Работа – это продукт силы и расстояния. Если W _i = W _o для входной работы W _i и выходной работы W _o и IMA = F ₀ / F _i , то F _o xd _o = F _i xd _{i и IMA = d o / d i .}

Справка по тесту: поток жидкости | EZ-pdh.com

Используйте поиск, чтобы быстро найти ответы на вопросы – откройте окно поиска (ctrl + f), затем введите ключевое слово из вопроса, чтобы перейти к этим терминам в материале курса

Введение

Поток жидкости – важная часть большинства промышленных процессов; особенно те, которые связаны с передачей тепла.Часто, когда требуется отвести тепло из точки, в которой оно генерируется, в процессе теплопередачи участвует какой-либо тип жидкости. Примерами этого являются охлаждающая вода, циркулирующая через бензиновый или дизельный двигатель, поток воздуха, проходящий через обмотки двигателя, и поток воды через активную зону ядерного реактора. Системы подачи жидкости также обычно используются для смазки.

Течение жидкости в ядерной области может быть сложным и не всегда подлежит строгому математическому анализу.В отличие от твердых тел, частицы жидкости движутся по трубопроводу и компонентам с разной скоростью и часто подвергаются разным ускорениям.

Несмотря на то, что подробный анализ потока жидкости может быть чрезвычайно трудным, основные концепции, связанные с проблемами потока жидкости, довольно просты. Эти базовые концепции могут быть применены при решении проблем потока жидкости путем использования упрощающих допущений и средних значений, где это необходимо. Несмотря на то, что такого типа анализа было бы недостаточно при инженерном проектировании систем, он очень полезен для понимания работы систем и прогнозирования приблизительной реакции жидкостных систем на изменения рабочих параметров.

Основные принципы потока жидкости включают три концепции или принципа; первые два из которых студент изучал в предыдущих руководствах. Первый – это принцип количества движения (приводящий к уравнениям сил жидкости), который был рассмотрен в руководстве по классической физике. Второй – это сохранение энергии (ведущее к первому закону термодинамики), которое изучалось в термодинамике. Третий – это сохранение массы (приводящее к уравнению неразрывности), которое будет объяснено в этом модуле.

Свойства жидкостей

Жидкость – это любое вещество, которое течет, потому что его частицы не прикреплены жестко друг к другу. Сюда входят жидкости, газы и даже некоторые материалы, которые обычно считаются твердыми телами, например стекло. По сути, жидкости – это материалы, которые не имеют повторяющейся кристаллической структуры.

Некоторые свойства жидкостей обсуждались в разделе «Термодинамика» этого текста. К ним относятся температура, давление, масса, удельный объем и плотность. Температура была определена как относительная мера того, насколько горячий или холодный материал. Его можно использовать для прогнозирования направления передачи тепла. Давление определялось как сила на единицу площади. Обычными единицами измерения давления являются фунты силы на квадратный дюйм (psi). Масса определялась как количество вещества, содержащегося в теле, и ее следует отличать от веса, который измеряется силой тяжести на теле. Удельный объем вещества – это объем на единицу массы вещества.Типичные единицы – футы ³ / фунт. Плотность – это масса вещества на единицу объема. Типичные единицы – фунт / фут ³ . Плотность и удельный объем противоположны друг другу. И плотность, и удельный объем зависят от температуры и в некоторой степени от давления жидкости. По мере увеличения температуры жидкости плотность уменьшается, а удельный объем увеличивается. Поскольку жидкости считаются несжимаемыми, увеличение давления не приведет к изменению плотности или удельного объема жидкости.На самом деле жидкости можно слегка сжимать при высоких давлениях, что приводит к небольшому увеличению плотности и небольшому уменьшению удельного объема жидкости.

Плавучесть

Плавучесть определяется как тенденция тела плавать или подниматься при погружении в жидкость. У всех нас было множество возможностей наблюдать плавучие эффекты жидкости. Когда мы идем плавать, наши тела почти полностью поддерживаются водой. Дерево, лед и пробка плавают на воде.Когда мы поднимаем камень с русла ручья, он внезапно кажется тяжелее, выходя из воды. Лодки полагаются на эту плавучую силу, чтобы оставаться на плаву. Величина этого плавучего эффекта была впервые вычислена и указана греческим философом Архимедом. Когда тело помещается в жидкость, оно поддерживается силой, равной весу вытесняемой им воды.

Если тело весит больше, чем жидкость, которую оно вытесняет, оно тонет, но будет казаться, что теряет количество, равное весу вытесненной жидкости, как наша скала.Если тело весит меньше, чем вес вытесненной жидкости, тело поднимется на поверхность, в конце концов, плавая на такой глубине, которая вытеснит объем жидкости, вес которой будет равен ее собственному весу. Плавающее тело вытесняет текучую среду, в которой оно плавает, под собственным весом.

Сжимаемость

Сжимаемость – это мера изменения объема, которому подвергается вещество, когда на вещество оказывается давление. Жидкости обычно считаются несжимаемыми.Например, давление 16 400 фунтов на квадратный дюйм приведет к уменьшению данного объема воды всего на 5% от его объема при атмосферном давлении. С другой стороны, газы очень сжимаются. Объем газа можно легко изменить, оказав на газ внешнее давление.

Взаимосвязь между глубиной и давлением

Любой, кто ныряет под поверхность воды, замечает, что давление на его барабанные перепонки даже на глубине несколько футов заметно больше атмосферного давления.Тщательные измерения показывают, что давление жидкости прямо пропорционально глубине, и для данной глубины жидкость оказывает одинаковое давление во всех направлениях.

Рисунок 1: Давление в зависимости от глубины

Как показано на Рисунке 1, давление на разных уровнях в резервуаре меняется, и это заставляет жидкость покидать резервуар с разными скоростями. Давление определялось как сила на единицу площади. В случае этого резервуара сила обусловлена ​​весом воды выше точки, в которой определяется давление.

Давление = Сила / Площадь

= Вес / Площадь

P = (мг) / (A g _c )

= (ρ V g) / (A g _c )

Где:

m = масса в фунтах / м

g = ускорение свободного падения 32,17 фут / сек ²

g _c = 32 фунт-фут / фунт-сила-сек ²

A = площадь в футах ²

V = объем в футах ³

ρ = плотность жидкости в фунтах / фут ³

Объем равен площади поперечного сечения, умноженной на высоту (h) жидкости.Подставляя это в приведенное выше уравнение, получаем:

P = (ρ A hg) / (A g _c )

P = (ρ hg) / (g _c )

Это уравнение говорит нам, что давление оказываемое водяным столбом прямо пропорционально высоте столба и плотности воды и не зависит от площади поперечного сечения столба. Давление на тридцать футов ниже поверхности стояка диаметром один дюйм такое же, как давление на тридцать футов ниже поверхности большого озера.

Пример 1:

Если резервуар на Рисунке 1 заполнен водой с плотностью 62,4 фунта / фут3, рассчитайте давление на глубинах 10, 20 и 30 футов.

Решение:

P = (ρhg) / g _c

P _{10 футов} = (62,4 фунт / фут ³ ) (1o ft) (32,17 фут / сек ² / (32,17 фунт-метр- фут / фунт-сила / дюйм ² )

= 624 фунт-сила / фут ² (1 фут ² /144 дюйм ² )

= 4,33 фунт-силы / дюйм ²

P ₂₀ = ( 624 фунт / фут ³ ) (20 футов) (32.17 футов / с ² / (32,17 фунт-фут / фунт-сила-с ² )

= 1248 фунт-сила / фут ² (1 фут ² /144 дюйма ² )

= 8,67 фунт-фут / дюйм

P _{30 футов} = (62,4 фунт / фут3) (30 футов) (32,17 фут / сек ² / 32,17 фунт-фут / фунт-сила-сек ² )

= 1872 фунт-сила / фут ² (1 футов ^{2 /144} дюймов ² )

= 13,00 фунт-сил / дюйм ²

Пример 2:

Цилиндрический резервуар для воды высотой 40 футов и диаметром 20 футов заполнен водой с плотностью из 61.9 фунт / фут ³ .

(а) Какое давление воды на дне резервуара?

(b) Какая средняя сила действует на дно?

Решение:

(a) P = (phg) / g _c

P = (61,9 фунт / фут ³ ) (40 футов) (32,17 фут / сек ² / 32,17 фунт-фут / фунт-сила-сек ² )

= 2476 фунт-сила / фут ² (1 фут ² /144 дюйм ² )

= 17,2 фунт-сила / дюйм ²

(b) Давление = сила / площадь

Сила = (Давление) (Площадь)

Площадь = πr ²

F = (17.2 фунта-силы / дюйм ² ) π (10 футов) ² (144 дюйма ² /1 фут ² )

= 7,78 x 10 ⁵ фунт-сила

Закон Паскаля

Давление жидкостей в каждом из ранее упомянутых случаев было связано с весом жидкости. Давление жидкости также может быть результатом приложения внешних сил к жидкости. Рассмотрим следующие примеры. На рисунке 2 изображен контейнер, полностью заполненный жидкостью. A, B, C, D и E представляют собой поршни одинаковой площади поперечного сечения, вставленные в стенки резервуара.На поршни C, D и E будут действовать силы из-за давления, вызванного разной глубиной жидкости. Предположим, что силы, действующие на поршни из-за давления, вызванного весом жидкости, следующие: A = 0 фунтов-силы, B = 0 фунтов-силы, C = 10 фунтов-силы, D = 30 фунтов-силы и E = 25 фунтов-силы. Теперь позвольте приложить к поршню A внешнюю силу в 50 фунтов-силы. Эта внешняя сила вызовет повышение давления во всех точках контейнера на такую ​​же величину. Поскольку все поршни имеют одинаковую площадь поперечного сечения, увеличение давления приведет к тому, что силы, действующие на поршни, увеличатся на 50 фунтов силы.Таким образом, если к поршню A приложена внешняя сила в 50 фунтов-силы, сила, оказываемая жидкостью на другие поршни, теперь будет следующей: B = 50 фунтов-силы, C = 60 фунтов-силы, D = 80 фунтов-силы и E = 75 фунтов-силы. . »

Этот эффект внешней силы на замкнутый флюид был впервые заявлен Паскалем в 1653 году.

Давление, приложенное к замкнутому флюиду, передается в неизменном виде через ограничивающий сосуд системы.

Рисунок 2: Закон Паскаля

Контрольный объем

В термодинамике контрольный объем был определен как фиксированная область в пространстве, где изучаются массы и энергии, пересекающие границы области.Эта концепция контрольного объема также очень полезна при анализе проблем с потоком жидкости. Граница контрольного объема для потока жидкости обычно принимается за физическую границу части, через которую протекает поток. Концепция контрольного объема используется в приложениях гидродинамики с использованием принципов непрерывности, импульса и энергии, упомянутых в начале этой главы. После того, как контрольный объем и его граница установлены, различные формы энергии, пересекающие границу с жидкостью, могут быть рассмотрены в форме уравнения для решения проблемы жидкости.Поскольку в задачах потока жидкости обычно рассматривается жидкость, пересекающая границы контрольного объема, подход контрольного объема упоминается как «открытый» системный анализ, аналогичный концепциям, изучаемым в термодинамике. В ядерной области есть особые случаи, когда жидкость не пересекает контрольную границу. Подобные случаи изучаются с использованием «закрытого» системного подхода.

Независимо от природы потока, все ситуации, связанные с потоком, подчиняются установленным основным законам природы, которые инженеры выразили в форме уравнений.Сохранение массы и сохранение энергии всегда выполняются в задачах с жидкостью, наряду с законами движения Ньютона. Кроме того, каждая задача будет иметь физические ограничения, называемые математически граничными условиями, которые должны быть выполнены, прежде чем решение проблемы будет согласовано с физическими результатами.

Объемный расход

Объемный расход расход расход (V˙) системы является мерой объема жидкости, проходящей через точку в системе в единицу времени.Объемный расход можно рассчитать как произведение площади поперечного сечения (A) потока и средней скорости потока (v).

V˙ = A v (3-1)

Если площадь измеряется в квадратных футах, а скорость – в футах в секунду, уравнение 3-1 приводит к объемному расходу, измеренному в кубических футах в секунду. Другие распространенные единицы объемного расхода включают галлоны в минуту, кубические сантиметры в секунду, литры в минуту и ​​галлоны в час.

Пример:

Труба с внутренним диаметром 4 дюйма содержит воду, которая течет со средней скоростью 14 футов в секунду.Рассчитайте объемный расход воды в трубе.

Решение:

Используйте уравнение 3-1 и замените площадь.

V˙ = (π r 2) v

V˙ = (3,14) (2/12 фута) ² (14 футов / сек)

V˙ = 1,22 фута ³ / сек

Масса Расход

Массовый расход (м²) системы – это мера массы жидкости, проходящей через точку в системе за единицу времени. Массовый расход связан с объемным расходом, как показано в уравнении 3-2, где ρ – плотность жидкости.

м˙ = ρV˙ (3-2)

Если объемный расход выражен в кубических футах в секунду, а плотность выражена в фунтах массы на кубический фут, уравнение 3-2 приводит к массовому расходу, измеренному в фунтах: масса в секунду. Другие распространенные единицы измерения массового расхода включают килограммы в секунду и фунты массы в час.

Замена V˙ в уравнении 3-2 соответствующими членами из уравнения 3-1 позволяет напрямую рассчитать массовый расход.

m˙ = ρ A v (3-3)

Пример:

Вода в трубе из предыдущего примера имела плотность 62.44 фунт / фут3. Рассчитайте массовый расход.

Решение:

м˙ = ρ V˙

м˙ = (62,44 фунта / фут ³ ) (1,22 фута ³ / сек)

м˙ = 76,2 фунта / сек

Сохранение массы

Из термодинамики вы узнали, что энергия не может быть ни создана, ни уничтожена, а только изменена по форме. То же самое и с массой. Сохранение массы – это инженерный принцип, который гласит, что все массовые расходы в контрольном объеме равны всем массовым расходам из контрольного объема плюс скорость изменения массы в контрольном объеме.Математически этот принцип выражается уравнением 3-4.

м˙

_дюйм = м˙ _выход + ∆m / ∆t (3-4)

где:

∆m / ∆t = увеличение или уменьшение массы в пределах контрольного объема за ( заданный период времени)

Устойчивый поток

Устойчивый поток относится к состоянию, при котором свойства жидкости в любой отдельной точке системы не меняются с течением времени. Эти свойства жидкости включают температуру, давление и скорость.Одним из наиболее важных свойств, которое является постоянным в системе с установившимся потоком, является массовый расход системы. Это означает, что в каком-либо компоненте системы не происходит накопления массы.

Уравнение неразрывности

Уравнение неразрывности – это просто математическое выражение принципа сохранения массы. Для контрольного объема с одним входом и одним выходом принцип сохранения массы гласит, что для установившегося потока массовый расход в объеме должен равняться массовому расходу на выходе.Уравнение неразрывности для этой ситуации выражается уравнением 3-5.

м˙

_вход = м˙ _выход (3-5)

(ρAv) _вход = (ρAv) _выход

Для контрольного объема с несколькими входами и выходами принцип сохранения масса требует, чтобы сумма массовых расходов в контрольном объеме была равна сумме массовых расходов из контрольного объема. Уравнение неразрывности для этой более общей ситуации выражается уравнением 3-6.

∑ м˙

_входов = м˙ _{выходов} (3-6)

Одним из простейших приложений уравнения неразрывности является определение изменения скорости жидкости
из-за расширения или сжатия диаметра трубка.

Пример: уравнение непрерывности – расширение трубопровода

Установившийся поток существует в трубе, которая постепенно расширяется с диаметра 6 дюймов до диаметра 8 дюймов. Плотность жидкости в трубе постоянна и равна 60 .8 фунт / фут3. Если скорость потока составляет 22,4 фута / сек в секции 6 дюймов, какова скорость потока в секции 8 дюймов?

Решение:

Из уравнения неразрывности мы знаем, что массовый расход в секции 6 дюймов должен равняться массовому расходу в секции 8 дюймов. Пусть нижний индекс 1 представляет 6-дюймовую секцию, а 2 – 8-дюймовую секцию, мы получим следующее.

m˙ ₁ = m˙ ₂

ρ ₁ A ₁ v _{1 =} ρ ₂ A ₂ v ₂

v _{2 =} v (ρ _1/ ρ ₂ ) (A ₁ / A ₂ )

v _{2 =} v ₁ (π _/ r ₁ ² ) (π / r ₂ ² )

v _{2 =} (22.4 фута / сек) [(3 дюйма) ² / (4 дюйма) ² ]

v _{2 =} 12,6 фута / сек

Таким образом, используя уравнение неразрывности, мы увеличиваем диаметр трубы от От 6 до 8 дюймов скорость потока снизилась с 22,4 до 12,6 футов / сек.

Уравнение неразрывности также может использоваться, чтобы показать, что уменьшение диаметра трубы приведет к увеличению скорости потока.

Пример: уравнение непрерывности – центробежный насос Рисунок 3: Уравнение непрерывности

Входной диаметр насоса охлаждающей жидкости реактора, показанный на рисунке 3, составляет 28 дюймов.в то время как поток на выходе через насос составляет 9200 фунтов / м3. Плотность воды составляет 49 фунтов на кубический метр. Какая скорость на входе в насос?

Решение:

Вход = πr ² = (3,13) (14 дюймов ((1 фут / 12 дюймов)) ²

= 4,28 фута ²

м˙ _вход = м ˙ _выход = 9200 фунтов / с

(ρAv) _вход = 9200 фунтов / с

v _вход = 9200 фунтов / с / Aρ

= (9200 фунтов / с) / [(4.28 футов 2) (49 фунтов / фут ³ )]

v _вход = 43,9 футов / сек

Приведенный выше пример показывает, что скорость потока в систему такая же, как и вне системы. Та же самая концепция верна, даже если более одного пути потока могут входить или выходить из системы одновременно. Баланс массы просто регулируется, чтобы указать, что сумма всех потоков, входящих в систему, равна сумме всех потоков, покидающих систему, если существуют установившиеся условия. Пример этого физического случая включен в следующий пример.

Пример: уравнение непрерывности – несколько выходов Рисунок 4: Y-образная конфигурация для примера задачи

Трубопроводная система имеет Y-образную конфигурацию для разделения потока, как показано на рисунке 4. Диаметр входной ветви составляет 12 дюймов, а диаметры выпускных колен составляют 8 и 10 дюймов. Скорость в 10-дюймовых опорах составляет 10 футов / сек. Поток через основную часть составляет 500 фунтов / м3. Плотность воды 62,4 фунта / фут3. Какова скорость на участке трубы диаметром 8 дюймов?

Решение:

A ₈ = π [4 дюйм.(1 фут / 12 дюймов)] ²

= 0,349 фута ²

A ₁₀ = π [5 дюймов (1 фут / 12 дюймов)] ²

= 0,545 фута ²

Σm˙ _входы = Σm˙ _выходы

м˙ ₁₂ = m˙ ₁₀ + m˙ ₈

м˙ ₈ = m˙ ₁₂ 10 – m˙

(ρAv) ₈ = m˙ ₁₂ – (ρAv) ₁₀

v ₈ = (m˙ ₁₂ – (ρAv) ₁₀ ) / (ρA) ₈

= [(500 фунт / сек) – (62.4 фунта / фут3) (0,545 фута 2) (10 футов / сек)] / (62,4 фунта / фут3) (0,349 фута ² )

v ₈ = 7,3 фута / сек

Основные положения данной главы кратко изложены на следующей странице.

• Изменения плотности жидкости обратно пропорциональны изменениям температуры.

• Плавучесть – это тенденция тела плавать или подниматься при погружении в жидкость.

• Давление , оказываемое водяным столбом, прямо пропорционально высоте столба и плотности воды.

P = ρ h г / г _c

• Закон Паскаля гласит, что давление, приложенное к замкнутой жидкости, передается в неизменном виде по замкнутому сосуду системы.

• Объемный расход – это объем жидкости в единицу времени, проходящий через точку в жидкостной системе.

• Массовый расход – это масса жидкости в единицу времени, проходящая через точку в жидкостной системе.

• Объемный расход рассчитывается как произведение средней скорости жидкости и площади поперечного сечения потока.

V˙ = A v

• Массовый расход рассчитывается как произведение объемного расхода и плотности жидкости.

m˙ = ρ A v

• Принцип сохранения массы гласит, что все массовые расходы в контрольном объеме равны всем массовым расходам из контрольного объема плюс скорость изменения масса в контрольном объеме.

• Для контрольного объема с одним входом и выходом уравнение неразрывности может быть выражено следующим образом:

м˙ на входе = м˙ на выходе

• Для контрольного объема с несколькими входами и выходов уравнение непрерывности:

m входов = m выходов

Режимы потока

Весь поток жидкости классифицируется по одной из двух широких категорий или режимов.Эти два режима потока – ламинарный поток и турбулентный поток. Режим потока, будь то ламинарный или турбулентный, важен при проектировании и работе любой жидкостной системы. Величина гидравлического трения, которая определяет количество энергии, необходимое для поддержания желаемого потока, зависит от режима потока. Это также является важным соображением в некоторых приложениях, связанных с теплопередачей жидкости.

Ламинарный поток

Ламинарный поток также называют обтекаемым или вязким потоком.Эти термины описывают поток, потому что в ламинарном потоке (1) слои воды текут друг над другом с разными скоростями практически без перемешивания между слоями, (2) частицы жидкости движутся по определенным и наблюдаемым траекториям или линиям тока и (3) ) течение характерно для вязкой (густой) жидкости или является потоком, в котором вязкость жидкости играет значительную роль.

Турбулентный поток

Турбулентный поток характеризуется неравномерным движением частиц жидкости. Нет определенной частоты, как в волновом движении.Частицы движутся по неправильным путям, без видимого рисунка и определенных слоев.

Профили скорости потока

Не все частицы жидкости движутся по трубе с одинаковой скоростью. Форма кривой скорости (профиль скорости на любом заданном участке трубы) зависит от того, является ли поток ламинарным или турбулентным. Если поток в трубе ламинарный, распределение скорости в поперечном сечении будет параболическим по форме с максимальной скоростью в центре, примерно вдвое превышающей среднюю скорость в трубе.В турбулентном потоке существует довольно равномерное распределение скорости по сечению трубы, в результате чего вся жидкость течет с заданным единственным значением. Рисунок 5 помогает проиллюстрировать изложенные выше идеи. Скорость жидкости, контактирующей со стенкой трубы, по существу равна нулю и увеличивается по мере удаления от стенки.

Рисунок 5: Профили скорости ламинарного и турбулентного потока

Обратите внимание на рисунок 5, что профиль скорости зависит от состояния поверхности стенки трубы. Более гладкая стенка дает более равномерный профиль скорости, чем грубая стенка трубы.

Средняя (объемная) скорость

Во многих задачах потока жидкости вместо определения точных скоростей в разных местах в одном и том же поперечном сечении потока достаточно позволить одной средней скорости представлять скорость всей жидкости в этой точке в трубе. Это довольно просто для турбулентного потока, поскольку профиль скорости плоский по большей части поперечного сечения трубы. Разумно предположить, что средняя скорость равна скорости в центре трубы.

Если режим потока ламинарный (профиль скорости параболический), все еще существует проблема попытки представить «среднюю» скорость в любом заданном поперечном сечении, поскольку среднее значение используется в уравнениях потока жидкости. Технически это делается с помощью интегрального исчисления. На практике ученик должен использовать среднее значение, равное половине значения средней линии.

Вязкость

Вязкость – это свойство жидкости, которое измеряет сопротивление жидкости деформации из-за силы сдвига.Вязкость – это внутреннее трение жидкости, которое заставляет ее сопротивляться протеканию мимо твердой поверхности или других слоев жидкости. Вязкость также можно рассматривать как меру сопротивления жидкости течению. Густое масло имеет высокую вязкость; вода имеет низкую вязкость. Единица измерения абсолютной вязкости:

µ = абсолютная вязкость жидкости (фунт-сила-сек / фут2).

Вязкость жидкости обычно существенно зависит от температуры жидкости и относительно не зависит от давления.Для большинства жидкостей, когда температура жидкости увеличивается, вязкость жидкости уменьшается. Пример этого можно увидеть в смазочном масле двигателей. Когда двигатель и его смазочное масло холодные, масло очень вязкое или густое. После запуска двигателя и повышения температуры смазочного масла вязкость масла значительно снижается, и масло кажется намного более жидким.

Идеальная жидкость

Идеальная жидкость – это несжимаемая жидкость без вязкости.Идеальных жидкостей на самом деле не существует, но иногда полезно рассмотреть, что случилось бы с идеальной жидкостью в конкретной задаче потока жидкости, чтобы упростить задачу.

Число Рейнольдса

Режим потока (ламинарный или турбулентный) определяется путем оценки числа Рейнольдса потока (см. Рисунок 5). Число Рейнольдса, основанное на исследованиях Осборна Рейнольдса, представляет собой безразмерное число, состоящее из физических характеристик потока. Уравнение 3-7 используется для расчета числа Рейнольдса (N _R ) для потока жидкости.

N

_R = PvD / мкг _c (3-7)

где:

N _R = число Рейнольдса (без единицы измерения)

v = средняя скорость (фут / сек)

D = диаметр трубы (футы)

µ = абсолютная вязкость жидкости (фунт-сила-сек / фут2)

ρ = массовая плотность жидкости (фунт / фут3)

г _c = гравитационная постоянная (32,2 фут-фунт-сила / фунт-сила-сек2) )

Для практических целей, если число Рейнольдса меньше 2000, поток является ламинарным.Если оно больше 3500, поток турбулентный. Потоки с числами Рейнольдса от 2000 до 3500 иногда называют переходными. Большинство жидкостных систем на ядерных установках работают с турбулентным потоком. Числа Рейнольдса можно удобно определить с помощью диаграммы Moody Chart; пример которого приведен в Приложении B. Дополнительные сведения об использовании диаграммы Moody Chart представлены в последующем тексте.

Основные положения этой главы кратко изложены ниже.

• Ламинарный поток Слои воды текут друг над другом с разной скоростью, практически без перемешивания между слоями.Профиль скорости потока для ламинарного потока в круглых трубах имеет параболическую форму с максимальным потоком в центре трубы и минимальным потоком на стенках трубы. Средняя скорость потока составляет примерно половину максимальной скорости.

• Турбулентный поток Поток характеризуется неравномерным движением частиц жидкости. Профиль скорости потока для турбулентного потока довольно плоский в центральной части трубы и быстро падает очень близко к стенкам.Средняя скорость потока примерно равна скорости в центре трубы.

• Вязкость – это свойство жидкости, которое измеряет сопротивление жидкости деформации из-за силы сдвига. Для большинства жидкостей температура и вязкость обратно пропорциональны.

• Идеальная жидкость – это несжимаемая жидкость без вязкости.

• Увеличение числа Рейнольдса указывает на усиление турбулентности потока.

Общее уравнение энергии

Принцип сохранения энергии гласит, что энергия не может быть ни создана, ни уничтожена.Это эквивалентно Первому закону термодинамики, который использовался для разработки общего уравнения энергии в модуле по термодинамике. Уравнение 3-8 представляет собой формулировку общего уравнения энергии для открытой системы.

Q + (U + PE + KE + PV) _в =

W + (U + PE + KE + PV)

_из + (U + PE + KE + PV) _{в памяти} (3-8 )

где:

Q = тепло (британские тепловые единицы)

U = внутренняя энергия (британские тепловые единицы)

PE = потенциальная энергия (фут-фунт-сила)

KE = кинетическая энергия (фут-фунт-сила)

P = давление ( фунт-сила / фут ² )

V = объем (фут ³ )

W = работа (фут-фунт-сила)

Упрощенное уравнение Бернулли

Уравнение Бернулли является результатом применения общего уравнения энергии и первого закона термодинамики к системе с установившимся потоком, в которой никакая работа не выполняется с жидкостью или ею, не передается тепло к или от жидкости и не происходит изменений внутренней энергии (т.е.е., без изменения температуры) жидкости. В этих условиях общее уравнение энергии упрощается до уравнения 3-9.

(PE + KE + PV)

₁ = (PE + KE + PV) ₂ (3-9)

Подставив соответствующие выражения для потенциальной энергии и кинетической энергии, уравнение 3-9 можно переписать как Equation 3-10.

мгz

_1/ г _c + mv ₁ ^2/ 2g _c + P ₁ V ₁ = мгz _{2/ 2/} mv ₂ ^2/ 2g _c + P ₂ V ₂ (3-10)

где:

m = масса (фунт-метр)

z = высота над ссылка (фут)

v = средняя скорость (фут / сек)

g = ускорение свободного падения (32.17 фут / сек ² )

gc = гравитационная постоянная, (32,17 фут-фунт / фунт-сила-сек ² )

Примечание: коэффициент g _c требуется только при использовании английской системы измерения и Масса измеряется в фунтах массы. По сути, это коэффициент преобразования, необходимый для непосредственного вывода единиц измерения. Нет необходимости в множителе, если масса измеряется в пробках или если используется метрическая система измерения.

Каждый член в уравнении 3-10 представляет форму энергии, которой обладает движущаяся жидкость (потенциальная, кинетическая энергия и энергия, связанная с давлением).По сути, уравнение физически представляет собой баланс энергий KE, PE, PV, так что если одна форма энергии увеличивается, одна или несколько других уменьшаются, чтобы компенсировать, и наоборот.

Умножение всех членов в уравнении 3-10 на коэффициент gc / mg дает форму уравнения Бернулли, показанного уравнением 3-11.

z

₁ + v ₁ ² / 2g + P ₁ ν ₁ g _c / g = z ₂ + v ₂ ² / 2g + P ₂ ν ₂ г _{c /} г (3-11)

Напор

Поскольку единицы для всех различных форм энергии в уравнении 3-11 измеряются в единицах расстояния, эти термины иногда называют «Напоры» (напор, напор скорости и напор).Термин «напор» используется инженерами применительно к давлению. Это ссылка на высоту, обычно в футах, водяного столба, который будет выдерживать данное давление. Каждую из энергий, которыми обладает жидкость, можно выразить через голову. Высота напора представляет потенциальную энергию жидкости из-за ее возвышения над контрольным уровнем. Скоростной напор представляет собой кинетическую энергию жидкости. Это высота в футах, на которую текущая жидкость поднялась бы в столбе, если бы вся ее кинетическая энергия была преобразована в потенциальную.Напор представляет собой энергию потока столба жидкости, вес которой эквивалентен давлению жидкости.

Сумма подъемного напора, скоростного напора и напора жидкости называется общим напором. Таким образом, уравнение Бернулли утверждает, что общий напор жидкости постоянен.

Преобразование энергии в жидкостных системах

Уравнение Бернулли позволяет легко исследовать, как происходит передача энергии между вертикальным, скоростным и напорным напором.Можно исследовать отдельные компоненты трубопроводных систем и определить, какие свойства жидкости изменяются и как это влияет на энергетический баланс.

Если труба, содержащая идеальную жидкость, подвергается постепенному расширению в диаметре, уравнение неразрывности говорит нам, что по мере увеличения диаметра и площади проходного сечения скорость потока должна уменьшаться, чтобы поддерживать тот же массовый расход. Поскольку скорость на выходе меньше скорости на входе, скоростной напор потока должен уменьшаться от входа к выходу.Если труба лежит горизонтально, напор не меняется; следовательно, уменьшение скоростного напора должно быть компенсировано увеличением напора. Поскольку мы рассматриваем идеальную несжимаемую жидкость, удельный объем жидкости не изменится. Единственный способ увеличения напора несжимаемой жидкости – это увеличение давления. Таким образом, уравнение Бернулли показывает, что уменьшение скорости потока в горизонтальной трубе приведет к увеличению давления.

Если труба постоянного диаметра, содержащая идеальную жидкость, подвергается уменьшению отметки, результат будет таким же, но по другим причинам. В этом случае скорость потока и скоростной напор должны быть постоянными, чтобы удовлетворять уравнению неразрывности массы.

Таким образом, уменьшение напора можно компенсировать только увеличением напора. Опять же, жидкость несжимаема, поэтому увеличение напора должно приводить к увеличению давления.

Несмотря на то, что уравнение Бернулли имеет несколько ограничений, существует множество задач с физической жидкостью, к которым оно применяется.Как и в случае сохранения массы, уравнение Бернулли может применяться к задачам, в которых более одного потока могут одновременно входить в систему или выходить из нее. Особо следует отметить тот факт, что задачи последовательной и параллельной системы трубопроводов решаются с помощью уравнения Бернулли.

Пример: уравнение Бернулли

Предположим, что поток без трения в длинной горизонтальной конической трубе. Диаметр составляет 2,0 фута на одном конце и 4,0 фута на другом. Напор на меньшем конце составляет 16 футов водяного столба.Если вода течет через этот конус со скоростью 125,6 фут3 / сек, найдите скорости на двух концах и напор на большем конце.

Решение:

V˙ ₁ = A ₁ v ₁

v ₁ = V˙ ₁ / A ₁ v ₂ = 9080 ₂ / A ₂

v ₁ = 125.6 футов ³ / сек / π (1 фут) ² v ₂ = 125,6 футов ³ / сек / π (2 фута) ²

v ₁ = 40 футов / с v ₂ = 10 футов / с

z ₁ + v ₁ ² / 2g + P ₁ ν ₁ g _c / g = z ₂ + v ₂ ² / 2g + P ₂ ν ₂ g _{c /} g

P ₂ ν ₂ g _{c /} g = P ₁ ν ₁ g _c / g + (z ₁ – z ₂ ) + (v ₁ ² – v ₂ ² ) / 2g

= 16 футов + 0 футов + [(40 футов / сек) ² – (10 футов / сек) ² /2 (32.17 фут-фунт-сила / фунт-сила – сек ² )]

= 39,3 фута

Ограничения упрощенного уравнения Бернулли

Практическое применение упрощенного уравнения Бернулли к реальным трубопроводным системам невозможно из-за двух ограничений. Одно серьезное ограничение уравнения Бернулли в его нынешней форме состоит в том, что при решении проблем трубопроводов недопустимо жидкое трение. Следовательно, уравнение 3-10 применимо только к идеальным жидкостям. Однако в действительности общий напор жидкости не может быть полностью перенесен из одной точки в другую из-за трения.Учет этих потерь напора даст гораздо более точное описание того, что происходит физически. Это особенно верно, потому что одна из задач насоса в гидравлической системе – преодоление потерь давления из-за трения трубы.

Второе ограничение в уравнении Бернулли состоит в том, что нельзя выполнять какую-либо работу с жидкостью или с ней. Это ограничение предотвращает анализ двух точек в потоке жидкости, если между двумя точками существует насос. Поскольку большинство проточных систем включает насосы, это существенное ограничение.К счастью, упрощенное уравнение Бернулли можно модифицировать таким образом, чтобы удовлетворительно учитывать потери напора и работу насоса.

Расширенное Бернулли

Уравнение Бернулли можно модифицировать, чтобы учесть приросты и потери напора. Полученное уравнение, называемое расширенным уравнением Бернулли, очень полезно при решении большинства задач потока жидкости. Фактически, расширенное уравнение Бернулли, вероятно, используется больше, чем любое другое уравнение потока жидкости. Уравнение 3-12 – это одна из форм расширенного уравнения Бернулли.

z

_{1 +} v ₁ ² / 2g + P ₁ ν ₁ g _c / g + H _p = z _{2 +} v ₂ ² / 2g + P ₂ ν ₂ g _c / g + H _f (3-12)

где:

z = высота над исходным уровнем (футы)

v = средняя скорость жидкости ( фут / сек)

P = давление жидкости (фунт-сила / фут ² )

ν = удельный объем жидкости (фут ³ / фунт-метр)

л.с. = напор, добавляемый насосом (футы)

Hf = потеря напора из-за гидравлического трения (футы)

g = ускорение свободного падения (фут / сек ² )

Потеря напора из-за гидравлического трения (Hf) представляет собой энергию, используемую для преодоления трения, вызванного стенками трубка.Хотя это представляет собой потерю энергии с точки зрения потока текучей среды, обычно это не означает значительную потерю общей энергии текучей среды. Это также не нарушает закон сохранения энергии, поскольку потеря напора из-за трения приводит к эквивалентному увеличению внутренней энергии (u) жидкости. Эти потери являются наибольшими, когда жидкость протекает через входы, выходы, насосы, клапаны, фитинги и любые другие трубопроводы с шероховатой внутренней поверхностью.

Большинство методов оценки потери напора из-за трения являются эмпирическими (основанными почти исключительно на экспериментальных данных) и основаны на константе пропорциональности, называемой коэффициентом трения (f), который будет обсуждаться в следующем разделе.

Пример: Extended Bernoulli

Вода перекачивается из большого резервуара в точку на 65 футов выше резервуара. Сколько футов напора должно быть добавлено насосом, если через 6-дюймовую трубу течет 8000 фунтов / час, а потеря напора на трение составляет 2 фута? Плотность жидкости составляет 62,4 фунта / фут3, а площадь поперечного сечения 6-дюймовой трубы составляет 0,2006 фута ² .

Решение:

Чтобы использовать модифицированную форму уравнения Бернулли, ориентиры выбираются на поверхности резервуара (точка 1) и на выходе из трубы (точка 2).Давление на поверхности резервуара такое же, как давление на выходе из трубы, то есть атмосферное давление. Скорость в точке 1 будет практически равна нулю.

Использование уравнения массового расхода для определения скорости в точке 2:

м˙ ₂ = ρ A ₂ v ₂

v ₂ = m˙ ₂ / ρ A ₂

v ₂ = 8000 фунтов / час / (62,4 фунта / фут ³ ) 0,2006 футов ²

v ₂ = 639 футов / час (1 час / 3600 с)

v ₂ = 0.178 фут / с

z _{1 +} v ₁ ² / 2g + P ₁ ν ₁ g _c / g + H _p = z _{2 +} v ₂ ² / 2g + P ₂ ν ₂ g _c / g + H _f

H _{p =} (z _{2 –} z ₁ ) + (v ₂ ² – v ₁ ² ) / 2g + (P ₂ – P ₁ ) ν (g _c / g) + H _f

H _p = 65 футов + [(0.178 фут / сек) ² – (o фут / сек) ² ] / [2 (32,17 фут-фунт / фунт-сила-сек ² )] + 0 футов + 2 фута

H _p = 67 футов [/ box]

Следует отметить, что решение этой примерной задачи имеет числовое значение, которое «имеет смысл» из данных, приведенных в задаче. Общее увеличение напора на 67 футов в основном связано с увеличением оценки на 65 футов и увеличением напора трения на 2 фута.

Применение уравнения Бернулли к трубке Вентури

Многие компоненты установки, такие как трубка Вентури, могут быть проанализированы с использованием уравнения Бернулли и уравнения неразрывности.Вентури – это устройство для измерения расхода, которое состоит из постепенного сжатия с последующим постепенным расширением. Пример трубки Вентури показан на рисунке 6. Измеряя перепад давления между входом трубки Вентури (точка 1) и горловиной трубки Вентури (точка 2), можно определить скорость потока и массовый расход на основе формулы Бернулли. уравнение.

Рис. 6. Измеритель Вентури

Уравнение Бернулли утверждает, что общий напор потока должен быть постоянным. Так как высота не изменяется значительно, если вообще не изменяется между точками 1 и 2, высота напора в этих двух точках будет по существу одинакова и будет исключена из уравнения.Таким образом, уравнение Бернулли упрощается до уравнения 3-13 для трубки Вентури.

v

₁ ² / 2g + P ₁ ν ₁ g _c / g = v ₂ ² / 2g + P ₂ ν ₂ g c / 9080 g (3-13)

Применение уравнения неразрывности к точкам 1 и 2 позволяет нам выразить скорость потока в точке 1 как функцию скорости потока в точке 2 и отношения двух областей потока.

ρ ₁ A ₁ v ₁ = ρ ₂ A ₂ v ₂

v ₁ = ρ ₂ A ₂ v ₂ / A ₁

v _{1 =} v ₂ A ₂ / A ₁

Использование алгебры для преобразования уравнения 3-13 и замена приведенного выше результата на v ₁ позволяет нам решить для v ₂ .

v ₂ ² – v ₁ ² / 2g = (P ₁ –P ₂ ) ν g _{c /} g

v ₂ ² – (v ₂ A ₂ / A ₁ ) ² = (P ₁ – P ₂ ) 2 ν g _c

v ₂ ² (1 – (A ₂ / A ₁ ) ² ) = (P ₁ – P ₂ ) 2 ν g _c

v ₂ ² = (P ₁ – P ₂ ) 2 ν g _c / (1 – (A2 / A1) ² )

v _{2 =} √ [(P ₁ – P ₂ ) 2 ν g _c / (1 – (A2 / A1) ² )]

v _{2 =} √ (P ₁ – P ₂ ) √ [2 ν g _c / (1 – (A2 / A1) ² )]

Следовательно, скорость потока в горловине трубки Вентури и объемный расход являются прямыми y пропорционально квадратному корню из перепада давления.

Давления на участке выше по потоку и в горловине являются фактическими давлениями, а скорости из уравнения Бернулли без потерь являются теоретическими скоростями. Когда потери учитываются в уравнении энергии, скорости являются фактическими скоростями. Во-первых, с помощью уравнения Бернулли (то есть без члена потери напора) получается теоретическая скорость в горловине. Затем умножив это на коэффициент Вентури (C _v ), который учитывает потери на трение и равен 0.98 для большинства Вентури получается фактическая скорость. Фактическая скорость, умноженная на фактическую площадь горловины, определяет фактический объемный расход нагнетания.

Падение давления P ₁ – P ₂ на трубке Вентури можно использовать для измерения расхода с помощью U-образного манометра, как показано на рисунке 6. Показание R ‘манометра пропорционально падению давления и, следовательно, скорости жидкости.

Основные положения этой главы кратко изложены ниже.

• Краткое изложение уравнения Бернулли

• Уравнение Бернулли представляет собой приложение Первого закона термодинамики.

• Уравнение Бернулли представляет собой приложение общего уравнения энергии к системе с установившимся потоком, в которой никакая работа не совершается с жидкостью или жидкостью, тепло не передается к жидкости или от нее, и не происходит никаких изменений во внутренней энергии жидкости.

• Напор – это термин, используемый для описания давления, оказываемого на жидкость или со стороны жидкости.

• Поскольку жидкость течет в системе трубопроводов, изменения высоты, скорости и напора должны быть согласованными, чтобы удовлетворялось уравнение Бернулли.

• Уравнение Бернулли можно модифицировать, чтобы учесть потери на трение и работу насоса.

• Вентури можно использовать для определения массового расхода из-за изменений давления и скорости жидкости.

• Объемный расход через трубку Вентури прямо пропорционален квадратному корню из перепада давления между входом трубки Вентури и ее горловиной.

Потеря напора

Потеря напора – это мера уменьшения общего напора (сумма подъемного напора, скоростного напора и напора) жидкости при ее движении через жидкостную систему. В реальных жидкостях потеря напора неизбежна. Это происходит из-за: трения между жидкостью и стенками трубы; трение между соседними частицами жидкости при их движении относительно друг друга; и турбулентность, вызываемая всякий раз, когда поток перенаправляется или каким-либо образом влияет на такие компоненты, как входы и выходы трубопроводов, насосы, клапаны, редукторы потока и фитинги.

Потери на трение – это часть общей потери напора, которая возникает, когда жидкость течет по прямым трубам. Потеря напора для потока жидкости прямо пропорциональна длине трубы, квадрату скорости жидкости и члену, учитывающему трение жидкости, называемому коэффициентом трения. Потеря напора обратно пропорциональна диаметру трубы.

Потеря напора ∝ f Lv ² / D

Коэффициент трения

Коэффициент трения был определен как зависящий от числа Рейнольдса для потока и степени шероховатости внутренней поверхности трубы.

Величина, используемая для измерения шероховатости трубы, называется относительной шероховатостью, которая равна средней высоте неровностей поверхности (ε), деленной на диаметр трубы (D).

Относительная шероховатость = ε / D

Значение коэффициента трения обычно получают из диаграммы Moody Chart (Рисунок A). Диаграмму Moody Chart можно использовать для определения коэффициента трения на основе числа Рейнольдса и относительной шероховатости.

Рисунок A: Moody Chart Пример:

Определите коэффициент трения (f) для потока жидкости в трубе, имеющей число Рейнольдса 40 000 и относительную шероховатость 0.01.

Решение:

Используя диаграмму Moody Chart, число Рейнольдса 40 000 пересекает кривую, соответствующую относительной шероховатости 0,01 при коэффициенте трения 0,04.

Уравнение Дарси

Потери напора на трение могут быть рассчитаны с использованием математической зависимости, известной как уравнение Дарси для потери напора. Уравнение принимает две различные формы. Первая форма уравнения Дарси определяет потери в системе, связанные с длиной трубы.

H

_r = f L v ² / D 2 g (3-14)

где:

f = коэффициент трения (без агрегата)

L = длина трубы (футы)

D = диаметр длины трубы (футы)

v = скорость жидкости (фут / сек)

g = ускорение свободного падения (фут / сек ² )

Пример:

Уравнение потери напора Дарси Труба длиной 100 футов и диаметром 20 дюймов содержит воду при температуре 200 ° F, текущую с массовым расходом 700 фунтов / м3.Вода имеет плотность 60 фунтов / фут ³ и вязкость 1,978 x 10 ^-7 фунт-сила-сек / фут ² . Относительная шероховатость трубы 0,00008. Рассчитайте потерю напора для трубы.

Решение:

Последовательность шагов, необходимых для решения этой проблемы, заключается в том, чтобы сначала определить скорость потока. Во-вторых, используя скорость потока и заданные свойства жидкости, вычислите число Рейнольдса. В-третьих, определите коэффициент трения по числу Рейнольдса и относительной шероховатости.Наконец, используйте уравнение Дарси, чтобы определить потерю напора.

m˙ = ρ A v

v = m˙ / ρ A

= (700 фунт / сек) / (60 фунт / фут ³ ) π (10 дюймов) ² (1 фут ² / 144 дюйма ²⁾

v = 5,35 фут / сек

N _R = ρ v D / мкг _c

N _R = (60 фунтов / фут ³ ) (5,35 футов / сек) (20 дюймов) (1 фут / 12 дюймов) / (1,978 x 10 ^-7 фунт-сила-сек / фут ² ) (32,17 фут-фунт-сила / фунт-сила-фут-сек ²⁾ =

N _R = 8.4 x 10 ⁷

Используйте диаграмму Moody для числа Рейнольдса 8,4 x 10 ⁷ и относительной шероховатости 0,00008.

f = 0,012

H _f = f (L / D) (v ² / 2g)

H _f = (o.o12) [100 футов / (20 дюймов) (1 фут / 12 дюймов) )] * (5,35 фут / сек) ² /(2)(32,17 фут / сек ² )

H _f = 0,32 фута

Незначительные потери

Потери, возникающие в трубопроводах из-за изгибов, локти, суставы, клапаны и т. д.иногда называют незначительными потерями. Это неправильное название, потому что во многих случаях эти потери более важны, чем потери из-за трения трубы, рассмотренные в предыдущем разделе. Для всех незначительных потерь в турбулентном потоке потеря напора изменяется пропорционально квадрату скорости. Таким образом, удобный метод выражения незначительных потерь потока – это коэффициент потерь (k). Значения коэффициента потерь (k) для типичных ситуаций и арматуры можно найти в стандартных справочниках. Форма уравнения Дарси, используемого для расчета незначительных потерь отдельных компонентов жидкостной системы, выражается уравнением 3-15.

H

_f = kv ² / 2g (3-15)

Эквивалентная длина трубопровода

Незначительные потери могут быть выражены через эквивалентную длину (Leq) трубы, которая будет иметь такую ​​же потерю напора для такая же скорость нагнетаемого потока. Эту взаимосвязь можно найти, установив две формы уравнения Дарси равными друг другу.

f L v ² / D 2g = kv ² / 2g

Это дает два полезных соотношения

L

_eq = k D / f (3-16)

k = f L

_eq / D (3-17)

Типичные значения L _eq / D для общих компонентов трубопроводной системы перечислены в таблице 1.Эквивалентная длина трубопровода, которая вызовет такую ​​же потерю напора, как и конкретный компонент, может быть определена путем умножения значения L _экв. / D для этого компонента на диаметр трубы. Чем выше значение L _eq / D, тем длиннее эквивалентная длина трубы.

Таблица 1: Типичные значения Leq / D Пример:

Полностью открытая задвижка находится в трубе диаметром 10 дюймов. Какая эквивалентная длина трубы вызовет такую ​​же потерю напора, как и задвижка?

Решение:

Из таблицы 1 мы находим, что значение L _экв. / D для полностью открытой задвижки равно 10.

L _eq = (L / D) D

= 10 (10 дюймов)

= 100 дюймов

Добавляя эквивалентные длины всех компонентов к фактической длине трубы в системе, мы можем получить L _экв. значение для всей системы трубопроводов.

Основные положения этой главы кратко изложены ниже.

• Потеря напора – это уменьшение общего напора (сумма потенциального напора, скоростного напора и напора) жидкости, вызванное трением, присутствующим при движении жидкости.

• Потери на трение – это часть общей потери напора, которая возникает, когда жидкость течет по прямым трубам.

• Незначительные потери – это потери напора, возникающие из-за изгибов, колен, соединений, клапанов и других компонентов. Каждый раз, когда поток изменяет направление или изменяется площадь поперечного сечения, он испытывает потерю напора.

• Коэффициент трения для потока жидкости можно определить с помощью диаграммы Moody Chart, если можно определить относительную шероховатость трубы и число Рейнольдса потока.

• Уравнение Дарси можно использовать для расчета потерь на трение.

• Для расчета мелких потерь можно использовать специальную форму уравнения Дарси.

• Длину трубы, которая может вызвать такую ​​же потерю напора, как у клапана или фитинга, можно определить, умножив значение L / D для компонента, указанного в справочниках или руководствах поставщиков, на диаметр трубы.

Принудительная и естественная циркуляция

В предыдущих главах, посвященных потоку жидкости, было объяснено, что каждый раз, когда жидкость течет, возникает некоторое трение, связанное с движением, которое вызывает потерю напора.Было отмечено, что эта потеря напора обычно компенсируется в системах трубопроводов насосами, которые действительно работают с жидкостью, компенсируя потерю напора из-за трения. Циркуляция жидкости в системах с помощью насосов обозначается как принудительная циркуляция .

Некоторые жидкостные системы можно спроектировать таким образом, чтобы не было необходимости в насосах для обеспечения циркуляции. Напор, необходимый для компенсации потерь напора, создается градиентами плотности и перепадами высоты.Поток, возникающий в этих условиях, называется естественной циркуляцией .

Тепловая приводная головка

Тепловая приводная головка – это сила, которая вызывает естественную циркуляцию. Это вызвано разницей в плотности между двумя телами или областями жидкости.

Рассмотрим два равных объема жидкости одного и того же типа. Если два объема имеют разную температуру, тогда объем с более высокой температурой также будет иметь меньшую плотность и, следовательно, меньшую массу.Поскольку объем при более высокой температуре будет иметь меньшую массу, на него также будет оказываться меньшая сила тяжести. Эта разница в силе тяжести, действующей на жидкость, будет приводить к тому, что более горячая жидкость поднимается, а более холодная жидкость опускается.

Этот эффект наблюдается во многих местах. Один из примеров – воздушный шар. Сила, заставляющая воздушный шар подниматься вверх, является результатом разницы в плотности между горячим воздухом внутри воздушного шара и более холодным воздухом, окружающим его.

Тепло, добавляемое воздуху в воздушном шаре, добавляет энергию молекулам воздуха. Движение молекул воздуха увеличивается, и молекулы воздуха занимают больше места. Молекулы воздуха внутри воздушного шара занимают больше места, чем такое же количество молекул воздуха вне воздушного шара. Это означает, что горячий воздух менее плотный и легкий, чем окружающий воздух. Поскольку воздух в воздушном шаре менее плотный, сила тяжести оказывает на него меньшее влияние. В результате воздушный шар весит меньше окружающего воздуха.Гравитация втягивает более холодный воздух в пространство, занимаемое воздушным шаром. Движение более холодного воздуха вниз выталкивает воздушный шар из ранее занятого пространства, и он поднимается.

Условия, необходимые для естественной циркуляции

Естественная циркуляция будет иметь место только при наличии правильных условий. Даже после того, как естественное кровообращение началось, устранение любого из этих условий приведет к остановке естественного кровообращения. Условия естественной циркуляции следующие.

1. Существует разница температур (имеется источник тепла и радиатор).

2. Источник тепла находится ниже радиатора.

3. Жидкости должны контактировать друг с другом.

Должны быть два тела жидкости с разными температурами. Это также может быть одно жидкое тело с участками с разной температурой. Разница в температуре необходима для разницы в плотности жидкости. Разница в плотности является движущей силой естественного циркуляционного потока.

Для продолжения естественной циркуляции необходимо поддерживать разницу температур. Добавление тепла от источника тепла должно происходить в зоне с высокой температурой. В области низких температур должен существовать непрерывный отвод тепла радиатором. В противном случае температуры в конечном итоге выровнялись бы, и дальнейшая циркуляция прекратилась.

Источник тепла должен располагаться ниже радиатора. Как показано на примере воздушного шара, более теплая жидкость менее плотна и имеет тенденцию подниматься, а более холодная жидкость более плотная и имеет тенденцию опускаться.Чтобы воспользоваться преимуществом естественного движения теплых и холодных жидкостей, источник тепла и радиатор должны располагаться на соответствующей высоте.

Две области должны соприкасаться, чтобы был возможен поток между ними. Если путь потока заблокирован или заблокирован, естественная циркуляция невозможна.

Пример охлаждения с естественной циркуляцией

Естественная циркуляция часто является основным средством охлаждения реакторов бассейнового типа и облученных тепловыделяющих сборок, хранящихся в бассейнах с водой после извлечения из реактора.Источником тепла является тепловыделяющая сборка. Радиатор – это основная часть воды в бассейне.

Вода в нижней части тепловыделяющей сборки поглощает энергию, генерируемую сборкой. Температура воды повышается, а плотность уменьшается. Сила тяжести втягивает более холодную (более плотную) воду в нижнюю часть узла, вытесняя более теплую воду. Более теплая (более легкая) вода вынуждена уступить свое место более холодной (более тяжелой) воде. Более теплая (более легкая) вода поднимается выше в сборке. По мере продвижения воды по длине сборки она поглощает больше энергии.Вода становится все светлее и легче, когда она непрерывно поднимается вверх более плотной водой, движущейся под ней. В свою очередь, более холодная вода поглощает энергию из узла и также вынуждена подниматься по мере продолжения естественного циркуляционного потока. Вода, выходящая из верхней части топливной сборки, отдает свою энергию, смешиваясь с большей частью воды в бассейне. Основная часть воды в бассейне обычно охлаждается путем циркуляции через теплообменники в отдельном процессе.

Расход и разница температур

Тепловая приводная головка, которая вызывает естественную циркуляцию, возникает из-за изменения плотности, вызванного разницей температур.Как правило, чем больше разница температур между горячей и холодной областями жидкости, тем больше тепловая приводная головка и результирующая скорость потока. Однако рекомендуется держать горячую жидкость переохлажденной, чтобы предотвратить изменение фазы. Можно иметь естественную циркуляцию в двухфазном потоке, но, как правило, поддерживать поток труднее.

Для индикации или проверки естественной циркуляции могут использоваться различные параметры. Это зависит от типа растения.Например, для реактора с водой под давлением (PWR) выбранные параметры системы охлаждения реактора (RCS), которые будут использоваться, следующие.

1. RCS ∆T (T _Hot – T _Cold ) должен составлять 25-80% от значения полной мощности и должен быть постоянным или медленно уменьшаться. Это указывает на то, что остаточное тепло удаляется из системы с достаточной скоростью для поддержания или снижения внутренней температуры.

2. RCS Температура горячих и холодных ног должна быть постоянной или медленно снижаться. Опять же, это указывает на то, что тепло удаляется, а тепловая нагрузка распада, как и ожидалось, уменьшается.

3. Давление пара парогенератора (давление вторичного контура) должно соответствовать температуре RCS. Это подтверждает, что парогенератор отводит тепло от охлаждающей жидкости RCS.

Если естественная циркуляция для PWR происходит или неизбежна, можно выполнить несколько действий, чтобы обеспечить или улучшить возможности охлаждения активной зоны. Во-первых, уровень в компенсаторе давления может поддерживаться выше 50%. Во-вторых, поддерживайте переохлаждение RCS на уровне 15 ^o F или выше.

Оба эти действия помогут предотвратить образование паровых карманов в RCS, где они ограничат поток RCS.В-третьих, поддерживайте уровень воды в парогенераторе ≥ нормального диапазона. Это обеспечивает соответствующий теплоотвод, чтобы гарантировать, что отвод тепла будет достаточным для предотвращения закипания RCS.

Основные положения этой главы перечислены ниже.

• Естественный циркуляционный поток – это циркуляция жидкости без использования механических устройств.

• Принудительный циркуляционный поток – это циркуляция жидкости в системе с помощью насосов.

• Тепловая приводная головка является движущей силой для естественной циркуляции, вызванной разницей в плотности между двумя областями жидкости.

• Для поддержания естественной циркуляции необходимы три элемента:

• Должны быть теплоотвод и источник тепла.
• Источник тепла должен располагаться под радиатором.
• Между теплой и холодной жидкостью должны существовать пути потока.

• Как правило, чем больше разница температур, тем выше расход естественной циркуляции.

• Естественную циркуляцию в PWR можно проверить с помощью мониторинга:

• RCS ∆T – 25% -80% значение полной мощности
• T _{Горячий} / T _{Холодный} – постоянно или медленно снижение
• Давление пара S / G – отслеживание температуры RCS

• Естественная циркуляция в PWR может быть увеличена за счет:

• поддерживать уровень компенсатора давления> 50%
• поддерживать RCS ≥ 15o F переохлаждение. .В некоторых важных местах в системах потока жидкости происходит одновременный поток жидкой воды и пара, известный как двухфазный поток. Этих простых соотношений, используемых для анализа однофазного потока, недостаточно для анализа двухфазного потока.

  Существует несколько методов, используемых для прогнозирования потери напора из-за трения жидкости для двухфазного потока. Трение двухфазного потока больше, чем трение однофазного потока, при тех же размерах трубопровода и массовом расходе. Разница, по-видимому, зависит от типа потока и является результатом увеличения скорости потока.Потери на двухфазное трение экспериментально определяются путем измерения перепада давления на различных элементах трубопровода.

  Двухфазные потери обычно связаны с однофазными потерями через те же элементы. Один принятый метод определения потерь на двухфазное трение на основе однофазных потерь включает множитель двухфазного трения (R), который определяется как отношение двухфазных потерь напора к потерям напора, оцененным с использованием насыщенного жидкие свойства.

  R = H

  _f, двухфазный / H _f, насыщенная жидкость (3-18)

  где:

  R = двухфазный множитель трения (без единиц)

  H _f, два -фаза = двухфазная потеря напора из-за трения (футы)

  H _f, насыщенная жидкость = однофазная потеря напора из-за трения (футы)

  Множитель трения (R) оказался намного выше при более низких давлениях, чем при более высоких давлениях.Двухфазная потеря напора может быть во много раз больше, чем однофазная потеря напора.

  Хотя для моделей двухфазного потока использовалось множество названий, мы определим только три типа потока. Используемые схемы течения определены следующим образом:

  1. Пузырьковый поток: происходит рассеяние пузырьков пара в континууме жидкости.

  2. Пробковый поток: в пузырьковом потоке пузырьки растут за счет слияния и в конечном итоге становятся того же диаметра, что и труба. При этом образуются типичные пузыри пулевидной формы, характерные для снарядного режима.

  3. Кольцевой поток: теперь жидкость распределяется между жидкой пленкой, текущей вверх по стенке, и дисперсией капель, текущих в паровом ядре потока.

  Нестабильность потока

  Нестабильный поток может возникать в виде колебаний потока или его реверсирования. Колебания потока – это изменения потока из-за образования пустот или механических препятствий при проектировании и производстве. Колебания потока в одном канале теплоносителя реактора иногда вызывают колебания потока в окружающих каналах теплоносителя из-за перераспределения потока.Колебания потока нежелательны по нескольким причинам. Во-первых, устойчивые колебания потока могут вызывать нежелательную вынужденную механическую вибрацию компонентов. Это может привести к выходу этих компонентов из строя из-за усталости. Во-вторых, колебания потока могут вызвать проблемы управления системой, имеющие особое значение в ядерных реакторах с жидкостным охлаждением, поскольку теплоноситель также используется в качестве замедлителя. В-третьих, колебания потока влияют на местные характеристики теплообмена и кипение. В ходе испытаний было обнаружено, что критический тепловой поток (CHF), необходимый для отклонения от пузырькового кипения (DNB), может быть снижен на целых 40%, когда поток колеблется.Это сильно снижает тепловой предел и плотность мощности по длине активной зоны реактора. Опять же, посредством испытаний было обнаружено, что колебания потока не являются серьезной проблемой для некоторых реакторов с водой под давлением, если мощность не превышает 150% для нормальных условий потока. Колебания потока могут быть проблемой при работе с естественной циркуляцией из-за присутствующих низких скоростей потока.

  Во время естественной циркуляции пузырьки пара, образующиеся при колебаниях потока, могут иметь достаточно влияния, чтобы фактически вызвать полное реверсирование потока в затронутом канале.

  И колебания потока, и реверсирование потока приводят к очень нестабильному состоянию, поскольку паровые подушки, образующиеся на нагретых поверхностях, напрямую влияют на способность отводить тепло от этих поверхностей.

  Штыревой патрубок

  В случае разрыва трубы сила реакции, создаваемая высокоскоростной струей жидкости, может вызвать смещение трубопровода и серьезное повреждение компонентов, приборов и оборудования в зоне разрыва. Эта характеристика аналогична необслуживаемому садовому шлангу или пожарному шлангу, который непредсказуемо «хлестает».Этот тип отказа анализируется, чтобы свести к минимуму повреждение, если бы труба изгибалась в непосредственной близости от оборудования, связанного с безопасностью.

  Гидравлический молот

  Гидравлический удар – это ударная волна жидкости, возникающая в результате внезапного начала или остановки потока. На него влияют начальное давление в системе, плотность жидкости, скорость звука в жидкости, эластичность жидкости и трубы, изменение скорости жидкости, диаметр и толщина трубы, а также клапан. рабочее время.

  Во время закрытия клапана кинетическая энергия движущейся жидкости преобразуется в потенциальную энергию. Эластичность жидкости и стенки трубы создает волну положительного давления, направленную к источнику жидкости. Когда эта волна достигнет источника, масса жидкости будет в покое, но под огромным давлением. Сжатая жидкость и растянутые стенки трубы теперь начнут выпускать жидкость из трубы обратно к источнику и вернуться к статическому давлению источника. Это высвобождение энергии сформирует еще одну волну давления, возвращающуюся к клапану.Когда эта ударная волна достигает клапана, из-за импульса жидкости стенка трубы начинает сокращаться. Это сжатие передается обратно источнику, что снижает давление в трубопроводе ниже статического давления источника. Эти волны давления будут перемещаться вперед и назад несколько раз, пока трение жидкости не демпфирует переменные волны давления до статического давления источника. Обычно весь процесс молота занимает менее одной секунды.

  Первоначальный толчок внезапной остановки потока может вызвать переходные изменения давления, превышающие статическое давление.Если клапан закрывается медленно, потеря кинетической энергии будет постепенной. Если его закрыть быстро, потеря кинетической энергии будет очень быстрой. Из-за быстрой потери кинетической энергии возникает ударная волна. Ударная волна, вызванная гидравлическим ударом, может иметь достаточную силу, чтобы вызвать физическое повреждение трубопроводов, оборудования и персонала. Гидравлический удар в трубах, как известно, срывает опоры труб с их креплений, разрывает трубопроводы и вызывает биение труб.

  Пик давления

  Пик давления – это результирующий быстрый рост давления выше статического, вызванный гидроударами.Максимальный всплеск давления будет в момент изменения расхода и регулируется следующим уравнением.

  ∆P = ρ _c ∆v / g _c

  где:

  ∆P = скачок давления (фунт-сила / фут ² )

  ρ = плотность жидкости (фунт / фут ³ )

  c = Скорость волны давления (фут / сек) (Скорость звука в жидкости)

  ∆v = Изменение скорости жидкости (фут / сек)

  gc = Гравитационная постоянная 32.17 (фунт-фут / фунт-сила-сек ² )

  Пример:

  Пик давления Вода с плотностью 62,4 фунт / фут ³ и давлением 120 фунтов на квадратный дюйм течет по трубе со скоростью 10 футов / сек. Скорость звука в воде 4780 футов / сек. Внезапно закрылся обратный клапан. Какое максимальное давление жидкости в фунтах на квадратный дюйм?

  Раствор

  P _Макс. = P _{статический} + ΔP _Пик

  P _{Макс. = 120 фунт-сила / дюйм ² + (62.4 фунта / фут ³ ) (4780 фут / сек) (10 фут / сек) / (32,17 фунт-фут / фунт-сила-сек) / (32,17 фунт-фут / фунт-сила-сек) / (32,17 фунт-фут / фунт-сила-сек) / (32,17 фунт-фут / фунт-сила-сек)}

  P _{Макс. в ²}

  P _Макс = 76,3 фунтов на кв. дюйм

  Паровой молот

  Паровой молот похож на гидравлический молот, за исключением того, что он предназначен для паровой системы. Паровой молот – это газовая ударная волна, возникающая в результате внезапного запуска или остановки потока. Паровой молот не так силен, как гидравлический, по трем причинам:

  1.Сжимаемость пара гасит ударную волну

  2. Скорость звука в паре составляет примерно одну треть скорости звука в воде.

  3. Плотность пара примерно в 1600 раз меньше плотности воды.

  Проблемы, связанные с паропроводом, включают термический удар и водяные пробки (то есть конденсацию в паровой системе) в результате неправильного нагрева.

  Рекомендации по эксплуатации

  Гидравлический и паровой молот – не редкость на промышленных предприятиях.Изменения расхода в трубопроводных системах должны производиться медленно, что является частью надлежащей практики оператора. Чтобы предотвратить гидравлический и паровой удар, операторы должны обеспечить надлежащую вентиляцию жидкостных систем и обеспечить надлежащий слив газовых или паровых систем во время запуска. Если возможно, инициируйте запуск насоса при закрытом нагнетательном клапане и медленно откройте нагнетательный клапан, чтобы запустить поток в системе. Если возможно, запускайте насосы меньшей производительности перед насосами большей производительности. По возможности используйте клапаны разогрева вокруг запорных клапанов основного потока.Если возможно, закройте нагнетательные клапаны насоса перед остановкой насосов. Периодически проверяйте правильность работы влагоуловителей и воздухоотводчиков во время работы.

  Основные положения этой главы кратко изложены ниже.

  Комбинация жидкости и пара, протекающей по трубе, называется двухфазным потоком.

  Типы двухфазного потока включают:

  • Пузырьковый поток: происходит диспергирование пузырьков пара в непрерывном потоке жидкости.

  • Пробковый поток: пузырьки растут за счет слияния и в конечном итоге становятся того же диаметра, что и труба, образуя пузырьки в форме пули.

  • Кольцевой поток: жидкость распределяется между жидкой пленкой, текущей вверх по стенке, и дисперсией капель, текущей в паровой сердцевине потока.

  Колебания и нестабильность основного потока могут вызвать:

  • нежелательную механическую вибрацию компонентов.

  • уменьшение теплового потока, необходимого для возникновения DNB.

  • прерывание фактического циркуляционного потока.

  Колебания и нестабильности потока могут возникать при следующих условиях:

  • сердечник находится вне расчетных условий, мощность> 150%

  • механический отказ, вызывающий закупорку потока

  • недостаточное охлаждение активной зоны во время естественная циркуляция, при которой происходит кипение

  Изгиб трубопровода – это смещение трубопровода, создаваемое реакционными силами высокоскоростной струи жидкости после разрыва трубы.

  Гидравлический удар – это ударная волна жидкости, возникающая в результате внезапного начала или остановки потока.

  Преобразование энергии в центробежном насосе

  Жидкость, поступающая в центробежный насос, сразу же направляется в зону низкого давления в центре или в проушине рабочего колеса. При вращении крыльчатки и лопастей они передают импульс поступающей жидкости. Передача количества движения движущейся жидкости увеличивает скорость жидкости. По мере увеличения скорости жидкости увеличивается ее кинетическая энергия.Жидкость с высокой кинетической энергией вытесняется из области рабочего колеса и попадает в улитку.

  Улитка – это область с постоянно увеличивающейся площадью поперечного сечения, предназначенная для преобразования кинетической энергии жидкости в давление жидкости. Механизм этого преобразования энергии такой же, как и для дозвукового потока через расширяющуюся часть сопла. Математический анализ потока через улитку основан на общем уравнении энергии, уравнении неразрывности и уравнении, связывающем внутренние свойства системы.Ключевыми параметрами, влияющими на преобразование энергии, являются увеличивающаяся площадь поперечного сечения улитки, более высокое противодавление системы на выходе улитки и несжимаемый дозвуковой поток жидкости. В результате взаимозависимости этих параметров поток жидкости в улитке, аналогичный дозвуковому потоку в расширяющемся сопле, испытывает уменьшение скорости и увеличение давления.

  Рабочие характеристики центробежного насоса

  Рис. 7: Типичные характеристики центробежного насоса Кривая

  Обычно центробежный насос создает относительно небольшое повышение давления в жидкости.Это повышение давления может составлять от нескольких десятков до нескольких сотен фунтов на квадратный дюйм в центробежном насосе с одноступенчатым рабочим колесом. Термин PSID (фунт-сила на квадратный дюйм дифференциала) эквивалентен ∆P. В данном контексте это разница давлений на всасывании и нагнетании насоса. PSID также можно использовать для описания перепада давления в компоненте системы (сетчатые фильтры, фильтры, теплообменники, клапаны, деминерализаторы и т. Д.). Когда центробежный насос работает с постоянной скоростью, увеличение противодавления системы на текущий поток приводит к уменьшению величины объемной скорости потока, которую центробежный насос может поддерживать.

  Анализ взаимосвязи между объемным расходом (), который центробежный насос V˙ может поддерживать, и перепадом давления в насосе (∆Ppump) основан на различных физических характеристиках насоса и жидкости в системе. Переменные, оцениваемые инженерами-конструкторами для определения этой взаимосвязи, включают эффективность насоса, мощность, подаваемую на насос, скорость вращения, диаметр рабочего колеса и лопастей, плотность жидкости и вязкость жидкости. Результат этого сложного анализа для типичного центробежного насоса, работающего на одной конкретной скорости, показан на графике на рисунке 7.

  Напор насоса по вертикальной оси – это разница между противодавлением в системе и давлением на входе насоса (∆Ppump). Объемный расход (V) по горизонтальной оси – это скорость, с которой жидкость протекает через насос. График предполагает одну конкретную скорость (N) для рабочего колеса насоса.

  Кавитация

  Когда перекачиваемая жидкость попадает в проушину центробежного насоса, давление значительно снижается. Чем больше скорость потока через насос, тем больше перепад давления.Если перепад давления достаточно велик или если температура жидкости достаточно высока, перепад давления может быть достаточным, чтобы заставить жидкость мгновенно превращаться в пар, когда местное давление падает ниже давления насыщения для перекачиваемой жидкости. Эти пузырьки пара перемещаются вдоль рабочего колеса насоса вместе с жидкостью. По мере уменьшения скорости потока давление жидкости увеличивается. Это вызывает внезапное схлопывание пузырьков пара на внешних частях крыльчатки. Образование этих пузырьков пара и их последующее схлопывание – кавитация.

  Кавитация может быть очень серьезной проблемой для центробежных насосов. Некоторые насосы могут быть рассчитаны на работу с ограниченным количеством кавитации. Большинство центробежных насосов не могут выдерживать кавитацию в течение значительных периодов времени; они повреждаются из-за эрозии рабочего колеса, вибрации или других проблем, вызванных кавитацией.

  Чистый положительный напор на всасывании

  Чтобы избежать кавитации во время работы насоса, можно контролировать чистый положительный напор на всасывании насоса.Чистый положительный напор на всасывании (NPSH) для насоса – это разница между давлением всасывания и давлением насыщения перекачиваемой жидкости. NPSH используется для измерения того, насколько жидкость близка к насыщенным условиям. Уравнение 3-19 можно использовать для расчета чистой положительной высоты всасывания, доступной для насоса. Единицы NPSH – футы воды.

  NPSH = P

  _{всасывание} – P _{насыщение} (3-19)

  где:

  P _{всасывание} = давление всасывания насоса

  P _{насыщение} = давление насыщения для жидкости

  Путем поддержания доступный NPSH на уровне больше, чем NPSH, требуемый производителем насоса, кавитации можно избежать.

  Законы о насосах

  Центробежные насосы обычно подчиняются так называемым законам о насосах. Эти законы гласят, что скорость потока или производительность прямо пропорциональны скорости насоса; напор прямо пропорционален квадрату скорости насоса; и мощность, требуемая двигателем насоса, прямо пропорциональна кубу скорости насоса. Эти законы суммированы в следующих уравнениях.

  V˙ ∝ n (3-20)

  H

  _P ∝ n ² (3-21)

  P ∝ n

  ³ (3-22)

  где:

  n = скорость рабочее колесо насоса (об / мин)

  V = объемный расход насоса (галлонов в минуту или фут3 / час)

  H _p = напор, развиваемый насосом (фунты на квадратный дюйм или футы)

  p = мощность насоса (кВт)

  Использование этих пропорциональности, можно разработать уравнения, связывающие условия на одной скорости с условиями на другой скорости.

  V˙

  ₁ (n ₂ / n ₁ ) = V ₂ (3-23)

  H

  _p1 (n ₂ / n ₁ ) ² = H _p2 (3-24)

  P

  ₁ (n ₂ / n ₁ ) ³ = P ₂ (3-25) Пример: законы о насосах

  Насос охлаждающей воды работает со скоростью 1800 об / мин. Его расход составляет 400 галлонов в минуту при напоре 48 футов. Мощность насоса составляет 45 кВт.Определите расход, напор и потребляемую мощность насоса, если скорость насоса увеличится до 3600 об / мин.

  Решение:

  Расход

  V˙ ₂ = V˙ ₁ (n ₂ / n ₁ )

  = (400 галлонов в минуту) (3600 об / мин / 1800 об / мин)

  = 800 галлонов в минуту

  Напор

  H _p2 = H _p1 (n ₂ / n ₁ ) ²

  = 48 футов (3600 об / мин / 1800 об / мин) ²

  = 192 футов

  Мощность

  P ₂ = P ₁ (n ₂ / n ₁ ) ³

  = 45 кВт (3600 об / 1800 об / мин) ³

  = 360 кВт

  Рисунок 8 : Изменение скоростей центробежного насоса

  Можно построить характеристическую кривую для новой скорости насоса на основе кривой для его исходной скорости.Метод состоит в том, чтобы взять несколько точек на исходной кривой и применить законы насоса для определения нового напора и расхода при новой скорости. Кривая зависимости напора насоса от расхода, которая возникает в результате изменения скорости насоса, графически проиллюстрирована на Рисунке 8.

  Характеристическая кривая системы

  Рисунок 9: Типичная кривая потери напора в системе

  В главе, посвященной потере напора, было определено, что оба фрикционные потери и незначительные потери в трубопроводных системах были пропорциональны квадрату скорости потока.Поскольку скорость потока прямо пропорциональна объемному расходу, потеря давления в системе должна быть прямо пропорциональна квадрату объемного расхода. Исходя из этого соотношения, можно построить кривую потери напора в системе в зависимости от объемного расхода. Кривая потери напора для типичной системы трубопроводов имеет форму параболы, как показано на Рисунке 9.

  Рабочая точка системы

  Рисунок 10: Рабочая точка центробежного насоса

  Точка, в которой насос работает в данной системе трубопроводов, зависит от от расхода и потери напора этой системы.Для данной системы объемный расход сравнивается с потерями напора в системе на характеристической кривой. Построив график характеристической кривой системы и характеристической кривой насоса в одной и той же системе координат, можно определить точку, в которой насос должен работать. Например, на рисунке 10 рабочая точка центробежного насоса в исходной системе обозначена пересечением кривой насоса и кривой системы (h _Lo ).

  Система имеет расход, равный V˙ ₀ , и полную потерю напора в системе, равную ∆P ₀ .Для поддержания расхода V˙ ₀ напор насоса должен быть равен ∆P _o . В системе, описанной системной кривой (h _L1 ), в системе был открыт клапан, чтобы уменьшить сопротивление системы потоку. В этой системе насос поддерживает большой расход (V˙ ₁ ) при меньшем напоре насоса (∆P ₁ ).

  Использование в системе нескольких центробежных насосов

  Типичный центробежный насос имеет относительно небольшое количество движущихся частей и может быть легко адаптирован к различным первичным двигателям.Эти первичные двигатели включают электродвигатели переменного и постоянного тока, дизельные двигатели, паровые турбины и пневмодвигатели. Центробежные насосы, как правило, имеют небольшие размеры и могут быть изготовлены с относительно низкими затратами. Кроме того, центробежные насосы обеспечивают высокий объемный расход при относительно низком давлении.

  Для увеличения объемного расхода в системе или для компенсации большого сопротивления потоку центробежные насосы часто используются параллельно или последовательно. На рисунке 11 изображены два идентичных центробежных насоса, работающих параллельно с одинаковой скоростью.

  Рисунок 11: Кривая характеристик насоса для двух идентичных центробежных насосов, используемых параллельно Центробежные насосы

  , подключенные параллельно

  Поскольку вход и выход каждого насоса, показанные на рисунке 11, находятся в идентичных точках в системе, каждый насос должен производить один и тот же насос глава. Однако общий расход в системе является суммой индивидуальных расходов для каждого насоса.

  Когда характеристическая кривая системы рассматривается с кривой для параллельных насосов, рабочая точка на пересечении двух кривых представляет более высокий объемный расход, чем для одиночного насоса, и большую потерю напора в системе.Как показано на Рисунке 12, большая потеря напора в системе происходит с увеличением скорости жидкости в результате увеличения объемного расхода. Из-за большего напора системы объемный расход фактически в два раза меньше расхода, достигаемого при использовании одного насоса.

  Рисунок 12: Рабочая точка для двух параллельных центробежных насосов

  Центробежные насосы серии

  Центробежные насосы используются последовательно для преодоления больших потерь напора в системе, чем один насос может компенсировать по отдельности.Как показано на Рисунке 13, два идентичных центробежных насоса, работающих с одинаковой скоростью и одинаковым объемным расходом, создают одинаковый напор. Поскольку вход второго насоса является выходом первого насоса, напор, создаваемый обоими насосами, является суммой отдельных напоров. Объемный расход от входа первого насоса до выхода второго остается прежним.

  Рисунок 13: Кривая характеристик насоса для двух идентичных центробежных насосов, используемых в серии

  Как показано на Рисунке 14, использование двух насосов последовательно не увеличивает сопротивление потоку в системе вдвое.Два насоса обеспечивают достаточный напор для новой системы, а также поддерживают немного более высокий объемный расход.

  Рисунок 14: Рабочая точка для двух центробежных насосов серии

  Основные моменты этой главы кратко изложены ниже.

  • Чистый положительный напор на всасывании – это разница между давлением всасывания насоса и давлением насыщения жидкости.

  • Кавитация – это образование и последующее схлопывание пузырьков пара на рабочем колесе насоса, когда местное давление падает ниже, а затем поднимается выше давления насыщения перекачиваемой жидкости.

  • Законы насоса можно использовать для определения влияния изменения скорости центробежного насоса на расход, напор и мощность.

  V˙ ₁ (n ₂ / n ₁ ) = V˙ ₂
  H _p1 (n ₂ / n ₁ ) ² = H _p2
  P ₁ (n ₂ / n ₁ ) ³ = P ₂

  • Кривая комбинированного насоса для двух центробежных насосов, подключенных параллельно, может быть определена путем сложения индивидуальные потоки для любой данной головы.

  • Комбинированная характеристика насосов для двух последовательно включенных центробежных насосов может быть определена путем добавления отдельных напоров для любого заданного расхода.

  • Рабочая точка (напор и расход) системы может быть определена путем построения кривой насоса и кривой потери напора системы на одних и тех же осях. Система будет работать на пересечении двух кривых.

  Трубы HDPE

  Трубы HDPE

  Физико-механические свойства
  Свойства предмета	Блок	Метод испытаний	Характеристическое значение
  Плотность	г / см3	ASTM D4883	0.95
  Индекс текучести расплава	г / 10 мин	ASTM D1238	0,7-0,8
  Содержание технического углерода	%	BS2782 МЕТОД 452 B
  Предел прочности при растяжении Доходность	кгс / см 2	ASTM D638	> 200
  Удлинение при разрыве	%	ASTM D638	> 600
  Твердость	ПОЛОЖЕННЫЙ	ISO 868	60-65
  Коэффициент линейного Расширение	К -1	DIN 53752
  Теплопроводность	WK-1m-1	DIN 52612 ЧАСТЬ 1
  Модуль упругости	Н / мм 2	DIN 53475
  Электрическая поверхность Сопротивление		DIN 53482	> 10 12

  В соответствии с DIN 8074, 8075, SFS 2336, 2337, ISO 161

  Размер Обозначение d (мм)	Класс давления
  	PN 2.5		номер 4		PN 6		PN 10		PN 16
  	S (мм)	Масса (Кг / м)	S (мм)	Масса (Кг / м)	S (мм)	Масса (Кг / м)	S (мм)	Масса (Кг / м)	S (мм)	Масса (Кг / м)
  16	–	–	–	–	–	–	1.8	0,084	2,3	0,103
  20	–	–	–	–	1,8	0,108	1,9	0,113	2,8	0.154
  25	–	–	–	–	1,8	0,138	2,3	0,171	3,5	0,241
  32	–	–	1.8	0,179	1,9	0,187	3,0	0,279	4,5	0,397
  40	–	–	1,8	0,228	2,3	0.286	3,7	0,431	5,6	0,610
  50	–	–	2,0	0,321	2,9	0,441	4,6	0,667	6.9	0,938
  63	1,8	0,365	2,5	0,496	3,6	0,689	5,8	1.058	8,7	1.491
  75	1.9	0,457	2,9	0,677	4,3	0,978	6,9	1.491	10,4	2,116
  90	2,2	0,642	3,5	0.979	5,1	1,390	8,2	2,126	12,5	3,042
  110	2,7	0,945	4,3	1.461	6,3	2,085	10.0	3,153	15,2	4.523
  125	3,1	1,239	4,9	1.884	7,1	2,670	11,4	4.090	17,3	5.843
  140	3,5	1,551	5,4	2.327	8,0	3.345	12,8	5.128	19,4	7,324
  160	3.9	1.954	6,2	3,052	9,1	4,362	14,6	6,679	22,1	9,540
  180	4,4	2.488	7,0	3.848	10,2	5,470	16,4	8,442	24,9	12.089
  200	4,9	3,063	7,7	4,705	11,4	6.800	18.2	10,376	27,6	14.910
  225	5,5	3,868	8,7	5.974	12,8	8,573	20,5	13,197	31,1	18.839
  250	6,1	4,765	9,7	7,384	14,2	10,578	22,8	16,219	34,5	23,271
  280	6.9	5.994	10,8	9.198	15,9	13,197	25,5	20,350	38,7	29,114
  315	7,7	7,525	12,2	11.686	17,9	16,723	28,7	25,790	43,5	36.871
  355	8,7	9,570	13,7	14,809	20,1	21.256	32,3	32.640	49,0	46,774
  400	9,8	12.089	15,4	18,738	22,7	26,898	36,4	41.505	55,2	59,437

  Соответствие промышленным стандартам Таиланда 982-1990

  Размер Обозначение d (мм)	Класс давления
  	PN 6.3		PN 8		PN 10		PN 12.5		PN 16
  	S (мм)	Масса (Кг / м)	S (мм)	Масса (Кг / м)	S (мм)	Масса (Кг / м)	S (мм)	Масса (Кг / м)	S (мм)	Масса (Кг / м)
  16	–	–	–	–	1.6	0,077	1,8	0,085	2,3	0,104
  20	–	–	1,6	0,099	1,9	0,113	2,3	0.134	2,8	0,156
  25	1,6	0,126	1,9	0,0145	2,3	0,172	2,8	0.202	3,5	0,243
  32	1.9	0,189	2,4	0,234	3,0	0,281	3,6	0,330	4,5	0,396
  40	2,4	0,298	3,0	0.359	3,7	0,433	4,5	0,513	5,6	0,614
  50	3,0	0,457	3,8	0,566	4,6	0,671	5.6	0,794	6,9	0,943
  63	3,8	0,726	4,7	0,880	5,8	1.059	7,0	1,245	8,7	1.496
  75	4,5	1.023	5,6	1,245	6,9	1.495	8,4	1.778	10,4	2,126
  90	5.4	1.469	6,7	1,782	8,2	2,139	10,0	2,532	12,5	3,061
  110	6,6	2,182	8,2	2.664	10,0	3,168	12,3	3.805	15,2	4,547
  125	7,5	2,815	9,3	3,427	11,4	4.109	13.9	4,878	17,3	5,875
  140	8,3	3,490	10,4	4,285	12,8	5,153	15,6	6,129	19,4	7.370
  160	7,7	3,743	9,6	4.595	11,8	5.545	14,5	6,619	18,1	8.113
  180	8.6	4,701	10,8	5.803	13,3	7.035	16,3	8,444	20,3	10.230
  200	9,6	5,820	12,0	7.151	14,8	8,674	18,1	10,414	22,6	12,634
  225	10,8	7,352	13,5	9.060	16,6	10.948	20,4	13,186	25,4	15.977
  250	12,0	9.061	15,0	11,159	18,4	13,484	22,6	16.220	28,2	19.707
  280	13,4	11,348	16,8	13.997	20,6	16,890	25,3	20,399	31,6	24.709
  315	15,0	14,255	18,9	17.698	23,2	21.401	28,5	25.750	35,5	21,226
  355	17.0	18.188	21,2	22.398	26,2	27,214	32,1	32,688	40,0	39.615
  400	19,1	23,549	23.9	29.025	29,5	35,254	36,2	42,382	45,1	51.359
  450	21,5	30.100	26,9	36.750	33.1	44.800	40,7	53,570	50,8	65,000
  500	23,9	37.100	29,9	45.330	36,8	55.400	45.2	66.100	56,4	80.100
  560	26,7	46.400	33,5	56.910	41,2	69.400	50,6	82,790	–	–
  630	30.0	58.600	37,7	71.830	46,4	87.700	56,9	104.700	–	–

  Примечание:

  1. d = внешний диаметр трубы

  s = толщина стенки трубы

  PN = номинальное номинальное давление, дюйм бар при 20C

  2.Вес трубы на 1 метр оценивается по трубе. плотность при 0,952 г / см 3 .

  3. Стандартная длина 6 метров, но для малых размером от 16 мм до 110 мм может быть намотана длиной 50 и 100 м на бухту.

  • Легкий вес, всего 0,95 г / см ² . Только вес 1/5 стальных труб такого же размера.
  • Высокая гибкость.Можно согнуть в 25-40 раз диаметры труб, что сокращает количество ненужных стыков труб.
  • Защита от ржавчины и высокая стойкость к поврежденным химическим веществам, что делает срок службы изделия до 50 лет.
  • Гладкая внутренняя поверхность, снижающая вероятность образования трубы засорение.
  • Безопасен для питьевой воды без токсичных или химических веществ загрязнение.

  За дополнительной информацией обращайтесь: [email protected].

  Тел .: (662) 424-9440, 433-0021, 433-0034, 883-3175
  Факс: (662) 433-5264, 433-8358, 433-5266, 424-7856, 883-3109
  Адрес: 441 Somdet Phrapinklao Road, Bangplad, Бангкок 10700, Таиланд

  [На главную] [ Компания Профиль ] [ Продукты и услуги ] [ Polywin Doors & WIndows ] [Свяжитесь с нами]

  Высота трубы Изменения и влияние на потерю давления

  Поскольку жидкость течет через систему трубопроводов, где трубы поднимаются и опускаются, изменяя высоту, давление в определенной точке трубы также зависит от произошедших изменений высоты подъема жидкости.

  Например, рассмотрим одиночную вертикальную трубу, по которой жидкость течет вверх, набирая высоту над уровнем моря. Вес текучей среды, действующей «поверх» текучей среды в какой-либо точке трубы, уменьшается, поскольку мы рассматриваем точки выше по трубе, поскольку над ней находится меньше текучей среды. Следовательно, по мере подъема жидкости в трубе происходит потеря давления.

  И наоборот, внизу вертикальной трубы полный вес жидкости в трубе «толкает вниз» в этой точке, и из-за этого давление в этой точке увеличивается (по сравнению с давлением на жидкость в точке верх трубы).Следовательно, по мере падения жидкости в трубе увеличивается давление.

  Поток при многократном изменении отметки

  Как описано выше, давление текучей среды в точке участка трубопровода изменяется с увеличением высоты текучей среды. По мере подъема жидкости происходит потеря давления, а при ее падении происходит эквивалентное увеличение давления (при таком же изменении высоты). Поэтому нам нужно учитывать только чистое изменение высоты флюида между начальной и конечной точкой потока, чтобы рассчитать потерю / усиление давления из-за изменения высоты.

  Если жидкость входит в участок трубы, который имеет начальную высоту, скажем, 2 м (относительно некоторой нулевой точки), а затем течет через систему труб, многократно поднимаясь и опускаясь, прежде чем, наконец, выходит на высоте, скажем, 5 м, тогда чистая изменение высоты составляет 3 м (5 м – 2 м), и результатом будет потеря давления из-за изменения высоты напора жидкости на 3 м (который может быть преобразован в единицы бар или фунт / кв. дюйм, если требуется).

  Конечно, также будут потери давления из-за трения трубы, и на приведенной выше диаграмме насосу потребуется создать достаточный дополнительный напор (давление) для жидкости, чтобы преодолеть как потерю давления из-за изменения высоты, так и потерю давления из-за трение в трубе.

  Линия оценки энергии

  Линия уровня энергии, также называемая линией энергии (EL), представляет собой график уравнения Бернулли или сумму трех членов в уравнении работы-энергии. EL равен сумме скоростного напора жидкости, давления и подъемного напора.

  EL = (V² / 2g) + (p / γ) + h

  где
  V = скорость
  г = ускорение свободного падения
  p = статическое давление (относительно движущейся жидкости)
  γ = удельный вес
  h = высота над уровнем моря

  Трубка Пито может быть вставлена ​​в трубу так, что жидкость первоначально течет в конец трубки, пока высота жидкости в трубке не уравновесит поступающую энергию, после чего поток в трубку прекратится и скорость жидкости на самом конце трубки Пито становится равным нулю.Давление и скоростной напор текучей среды фактически преобразуются в эквивалентный напор текучей среды по высоте (т.е. текучая среда поднимется до отметки EL для этой конкретной точки потока).

  Гидравлический маркер

  Гидравлический уклон (HGL) представляет собой сумму напора и напора. Эта сумма известна как пьезометрическая головка, и ее можно измерить, вставив трубку пьезометра в трубу так, чтобы она была заподлицо с краем трубы.

  HGL = (p / γ) + h

  где
  p = статическое давление (относительно движущейся жидкости)
  γ = удельный вес
  h = высота над уровнем моря

  Схема гидравлической линии сортировки и линии оценки энергии

  HGL и EL потока в трубе можно проиллюстрировать на диаграмме, при этом труба нарисована под углом, а соответствующие высоты, напоры и напоры скорости нанесены на вертикальной оси на каждом конце трубы.Полученные в результате линии HGL и EL можно затем провести между определенными точками на каждой вертикальной оси, чтобы обеспечить хорошую визуализацию того, как они меняются для потока жидкости в разных точках вдоль трубы.
  

  Размеры стальных труб

  
  Таблицы размеров продуктов Železiarne Podbrezová.

  Размеры и вес бесшовных стальных труб

  
  50 50 вес прецизионных труб

  Размеры и вес холоднотянутых труб

  Допуски на размер прецизионных труб

  Размеры и вес фитинга для стыковой сварки

  
  Размеры трубок относятся к важнейшим характеристикам трубок.В связи с этим размеры трубы должны быть указаны таким образом, чтобы можно было полностью определить трубу. Для труб с круглым поперечным сечением тремя основными размерами, за исключением длины, являются: внешний диаметр (OD), внутренний диаметр (ID) и толщина стенки (WT). Для круглых труб даны два из этих значений. В зависимости от типа трубы также относятся соответствующие размеры и допуски на размеры.

  Размерный ряд стальных труб

  Размеры отдельных труб не производятся случайным образом, а располагаются в соответствии с размерными рядами на основе определенных систем.Размеры трубок указаны в мм. В США и некоторых других странах размеры указаны в дюймах (нем. Zoll). В этом случае трубки делятся на две группы, так называемые ТРУБКИ. Эти трубы используются для механических и энергетических установок, и в дюймах даны размеры внешнего диаметра. PIPE – это трубы для трубопроводов для различных типов сред. Размеры ТРУБЫ даны как номинальные размеры трубы. Для размеров до 12 дюймов указан приблизительный размер (зазор) внутреннего диаметра трубы.Из размеров ТРУБЫ после их преобразования в миллиметры создается первая предпочтительная линия внешнего диаметра стальной трубы (1-я строка в EN 10220, DIN 2448 и т. Д.). Это не означает, что размеры трубок 2-й и 3-й серий не используются. Размеры в серии 2 и 3 (для использования в Европе изменены на округленные размеры в мм) являются стандартами для ТРУБ, используемых в строительстве энергетических объектов, и для труб для механического применения.

  Ряд толщин стенок стальных труб Ряд толщин стенок берет свое начало в системе британских единиц (дюймы), в которой для выражения размеров используются дроби.Толщина стенок в ТРУБЕ создается «Графиком» (40, 60, 80, 120 ….), привязанным по некоторым размерам к весовой категории (STD, XS, XXS). Эти значения, пересчитанные в миллиметры, составляют часть ряда толщин стенок. (Примечание: размер – значение Schedule, например, 40 не является постоянным, а зависит от внешнего диаметра трубы).

  
  Для трубы значения толщины стенки берутся из «шкал» BWG, SWG и других. После пересчета в миллиметры эти значения представляют собой другую часть ряда толщин стенок стальных труб.Для прецизионных стальных труб, используемых в Европе и странах, использующих систему SI, размерная линия создается с округленными размерами наружных диаметров и толщин стенок. Допуски по внешнему диаметру, внутреннему диаметру и толщине стенки действительны только для двух заказанных значений. Допуск третьего измерения можно согласовать только на прецизионных трубках.
  
  

  Овальность стальных труб

  (из-за округлости), разница между макс. и мин. значения диаметров, снятые в том же сечении.Овальность должна быть в пределах допуска OD.

  (абсолютное значение в мм) (в%)

  
  

  Эксцентриситет стальных труб

  (среднее отклонение), является мерой расстояния между центрами внешнего и внутреннего диаметров. Эксцентриситет должен быть в пределах допусков WT и рассчитывается по WT в одном поперечном сечении по формуле:

  (абсолютное значение в мм) (в%)

  Отклонение от прямолинейности трубы (e)

  указывает максимальное отклонение трубки от линии, соединяющей два ее конца, где L – длина трубки.Он дан в процентах на единицу длины. Обычно необходимая прямолинейность составляет 3 мм на 1 метр.
  

  (в%)

  FB

  .