Коэффициент жесткости пружины: определение, формулы, измерение

Пружины можно назвать одной из наиболее распространенных деталей, которые являются частью простых и сложных механизмов. При ее изготовлении применяется специальная проволока, накручиваемая по определенной траектории. Выделяют довольно большое количество различных параметров, характеризующих это изделие. Наиболее важным можно назвать коэффициент жесткости. Он определяет основные свойства детали, может рассчитываться и применяться в других расчетах. Рассмотрим особенности подобного параметра подробнее.

Определение и формула жесткости пружины

При рассмотрении того, что такое коэффициент жесткости пружины следует уделить внимание понятию упругости. Для ее обозначения применяется символ F. При этом сила упругости пружины характеризуется следующими особенностями:

1. Проявляется исключительно при деформации тела и исчезает в случае, если деформация пропадает.
2. При рассмотрении, что такое жесткость пружины следует учитывать, после снятия внешней нагрузки тело может восстанавливать свои размеры и форму, частично или полностью. В подобном случае деформация считается упругой.

Не стоит забывать о том, что жесткость – характеристика, свойственная упругим телам, способным деформироваться. Довольно распространенным вопросом можно назвать то, как обозначается жесткость пружины на чертежах или в технической документации. Чаще всего для этого применяется буква k.

Слишком сильная деформация тела становится причиной появления различных дефектов. Ключевыми особенностями можно назвать следующее:

1. Деталь может сохранять свои геометрические параметры при длительной эксплуатации.
2.  
3. При увеличении показателя существенно снижается сжатие пружины под воздействие одинаковой силы.
4. Наиболее важным параметром можно назвать коэффициент жесткости. Он зависит от геометрических показателей изделия, типа применяемого материала при изготовлении.

Довольно большое распространение получили красные пружины и другого типа. Цветовое обозначение применяется в случае производства автомобильных изделий. Для расчета применяется следующая формула: k=Gd⁴/8D³n. В этой формуле указываются нижеприведенные обозначения:

1. G – применяется для определения модуля сдвига. Стоит учитывать, что это свойство во многом зависит от применяемого материала при изготовлении витков.
2. d – диаметральный показатель проволоки. Она производится путем проката. Этот параметр указывается также в технической документации.
3. D – диаметр создаваемых витков при накручивании проволоки вокруг оси. Он подбирается в зависимости от поставленных задач. Во многом диаметр определяет то, какая нагрузка оказывается для сжатия устройства.
4. n – число витков. Этот показатель может варьировать в достаточно большом диапазоне, также влияет на основные эксплуатационные характеристики изделия.

Рассматриваемая формула применяется в случае расчета коэффициента жесткости для цилиндрических пружин, которые устанавливаются в самых различных механизмах. Подобная единица измеряется в Ньютонах. Коэффициент жесткости для стандартизированных изделий можно встретить в технической литературе.

Формула жесткости соединений пружин

Не стоит забывать о том, что в некоторых случаях проводится соединение тела нескольким пружинами. Подобные системы получили весьма широкое распространение. Определить жесткость в этом случае намного сложнее. Среди особенностей соединения можно отметить нижеприведенные моменты:

1. Параллельное соединение характеризуется тем, что детали размещаются последовательно. Подобный метод позволяет существенно повысить упругость создаваемой системы.
2. Последовательный метод характеризуется тем, что деталь подключаются друг к другу. Подобный способ подсоединения существенно снижает степень упругости, однако позволяет существенно увеличить максимальное удлинение. В некоторых случаях требуется именно максимальное удлинение.

В обеих случаях применяется определенная формула, которая определяет особенности подключения. Модуль силы упругости может существенно отличаться в зависимости от особенностей конкретного изделия.

При последовательном соединении изделий показатель рассчитывается следующим образом: 1/k=1/k₁+1/k₂+…+1/k_n. Рассматриваемый показатель считается довольно важным свойством, в данном случае он снижается. Параллельный метод подключения рассчитывается следующим образом: k=k₁+k₂+…k_n.

Подобные формулы могут использоваться при самых различных расчетах, чаще всего на момент решения математических задач.

Коэффициент жесткости соединений пружин

Приведенный выше показатель коэффициента жесткости детали при параллельном или последовательном соединении определяет многие характеристики соединения. Довольно часто проводится определение тому, чему равно удлинение пружины. Среди особенностей параллельного или последовательного соединения можно отметить нижеприведенные моменты:

1. При параллельном подключении удлинение обоих изделий будет равным. Не стоит забывать о том, что оба варианта должны характеризоваться одинаковой длиной в свободном положении. При последовательном показатель увеличивается в два раза.
2. Свободное положение – ситуация, в которой деталь находится без прикладывания нагрузки. Именно оно в большинстве случаев учитывается при проведении расчетов.
3. Коэффициент жесткости изменяется в зависимости от применяемого способа подсоединения. В случае параллельного соединения показатель увеличивается в два раза, при последовательном уменьшается.

Для проведения расчетов нужно построить схему подключения всех элементов. Основание представлено линией со штриховкой, изделие обозначается схематически, а тело в упрощенном виде. Кроме этого, от упругой деформации во многом зависит кинетическая и другая энергия.

Коэффициент жесткости цилиндрической пружины

На практике и в физике довольно большое распространение получили именно цилиндрические пружины. Их ключевыми особенностями можно назвать следующие моменты:

1. При создании указывается центральная ось, вдоль которой и действует большинство различных сил.
2. При производстве рассматриваемого изделия применяется проволока определенного диаметра. Она изготавливается из специального сплава или обычных металлов. Не стоит забывать о том, что материал должен обладать повышенной упругостью.
3. Проволока накручивается витками вдоль оси. При этом стоит учитывать, что они могут быть одного или разного диаметра. Довольно большое распространение получил вариант исполнения цилиндрического типа, но большей устойчивостью характеризуется цилиндрический вариант исполнения, в сжатом состоянии деталь обладает небольшой толщиной.
4. Основными параметрами можно назвать больший, средний и малый диаметр витков, диаметр проволоки, шаг расположения отдельных колец.

Не стоит забывать о том, что выделяют два типа деталей: сжатия и растяжения. Их коэффициент жесткости определяется по одной и той же формуле. Разница заключается в следующем:

1. Вариант исполнения, рассчитанный на сжатие, характеризуется дальним расположением витков. За счет расстояние между ними есть возможность сжатия.
2. Модель, рассчитанная на растяжение, имеет кольца, расположенные практически вплотную. Подобная форма определяет то, что при максимальная сила упругости достигается при минимальном растяжении.
3. Также есть вариант исполнения, который рассчитан на кручение и изгиб. Подобная деталь рассчитывается по определенным формулам.

Расчет коэффициента цилиндрической пружины может проводится при использовании ранее указанной формулы. Она определяет то, что показатель зависит от следующих параметров:

1. Наружного радиуса колец. Как ранее было отмечено, при изготовлении детали применяется ось, вокруг которой проводится накручивание колец. При этом не стоит забывать о том, что выделяют также средний и внутренний диаметр. Подобный показатель указывается в технической документации и на чертежах.
2. Количества создаваемых витков. Этот параметр во многом определяет длину изделия в свободном состоянии. Кроме этого, количество колец определяет коэффициент жесткость и многие другие параметры.
3. Радиуса применяемой проволоки. В качестве исходного материала применяется именно проволока, которая изготавливается из различных сплавов. Во многом ее свойства оказывают влияние на качества рассматриваемого изделия.
4. Модуля сдвига, который зависит от типа применяемого материала.

Коэффициент жесткости считается одним из наиболее важных параметров, который учитывается при проведении самых различных расчетов.

Единицы измерения

При проводимых расчетах также должно учитываться то, в каких единицах измерениях проводятся вычисления. При рассмотрении того, чему равно удлинение пружины уделяется внимание единице измерения в Ньютонах.

Для того чтобы упростить выбор детали многие производители указывают его цветовым обозначением.

Разделение пружины по цветам проводится в сфере автомобилестроения.

Среди особенностей подобной маркировки отметим следующее:

1. Класс А обозначается белым, желтым, оранжевым и коричневым оттенками.
2. Класса В представлен синим, голубым, черным и желтым цветом.

Как правило, подобное свойство отмечается на внешней стороне витка. Производители наносят небольшую полоску, которая и существенно упрощает процесс выбора.

Особенности расчета жесткости соединений пружин

Приведенная выше информация указывает на то, что коэффициент жесткости является довольно важным параметром, который должен рассчитываться при выборе наиболее подходящего изделия и во многих других случаях. Именно поэтому довольно распространенным вопросом можно назвать то, как найти жесткость пружины. Среди особенностей соединения отметим следующее:

1. Провести определение растяжения пружины можно при вычислении, а также на момент теста. Этот показатель может зависеть в зависимости от проволоки и других параметров.
2. Для расчетов могут применяться самые различные формулы, при этом получаемый результат будет практически без погрешностей.
3. Есть возможность провести тесты, в ходе которых и выявляются основные параметры. Определить это можно исключительно при применении специального оборудования.

Как ранее было отмечено, выделяют последовательный и параллельный метод соединения. Оба характеризуются своими определенными особенностями, которые должны учитываться.

В заключение отметим, что рассматриваемая деталь является важной частью конструкции различных механизмов. Неправильный вариант исполнения не сможет прослужить в течение длительного периода. При этом не стоит забывать о том, что слишком сильная деформация становится причиной ухудшения эксплуатационных характеристик.

Какова жесткость системы из двух пружин

При параллельном соединении двух пружин, имеющих коэффициенты жесткости с₁, с₂ (рис. 2.5), смещение тела равно деформации каждой из пружин:

. (2.9)

Рис. 2.5 Параллельное соединение пружин

Сила упругости эквивалентной пружины с коэффициентом жесткости с* будет равна сумме сил упругости двух установленных пружин, откуда с учетом (2.9) получаем

,

. (2.10)

Последовательное соединение пружин

При последовательном соединении двух пружин, имеющих коэффициенты жесткости с₁, с₂ (рис. 2.6), смещение тела равно сумме деформаций пружин:

. (2.11)

Рис. 3.6 Последовательное соединение пружин

Сила упругости эквивалентной пружины с коэффициентом жесткости с* будет равна каждой из сил упругости установленных пружин, откуда

,

,

Окончательно с учетом (2.11) получаем

. (2.12)

Влияние сопротивления на свободные колебания

Пусть на точку массы m, совершающую прямолинейное движение, действуют две силы (рис. 2.7):

Восстанавливающая сила (сила упругости пружины): .

Сила сопротивления, пропорциональная скорости движения точки (сила сопротивления демпфера): .

Рис. 2.7 Движение массы с демпфированием

Дифференциальное уравнение движения точки запишется как

;

,

, , (2.13)

получаем линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами:

. (2.14)

Характеристическое уравнение имеет вид

, (2.15)

его корни равны

, (2.16)

где – дискриминант.

Как известно из курса высшей математики, общее решение дифференциального уравнения (2.14) существенно зависит от знака дискриминанта , т.е. от соотношения между b и k.

1-й случай (малое сопротивление): b  k , D  0.

Обозначим , причем k*  k. Тогда корни (2.16) характеристического уравнения будут комплексно сопряженными:

,

Общее решение дифференциального уравнения (2.14) в данном случае имеет вид

, (2.17)

это затухающие колебания с частотой k * и периодом (рис.3.8).

Амплитуда колебаний убывает со временем. Отношение последующей амплитуды к предыдущей называется декрементом затухания:

*  k) и к увеличению их периода (Т * > Т).

Корни (2.16) характеристического уравнения получаются кратные, , и решение дифференциального уравнения (2.14) приобретает вид

. (2.19)

Поскольку экспонента убывает быстрее, чем растёт линейная функция времени, в зависимости от начальных условий движения получим ту или иную картину затухающего апериодического (т.е. не колебательного) движения (рис.2.9).

3-й случай (большое сопротивление): b > k, D > 0.

В этом случае обозначим >0, и оба корня (2.16) характеристического уравнения будут действительными и отрицательными:

• 10 – 11 классы
• Физика
• 50 баллов

Жесткость одной пружины к. Какова жесткость системы таких пружин, соединенных последовательно? (С полным объяснением, пожалуйста)

• Попроси больше объяснений
• Следить
• Отметить нарушение

InnaCh 20.10.2012

Ответ

Последовательное соединение пружин:

1/kобщ = 1/k1 + 1/k2 + . + 1/kn

Либо, если это две последовательно соединенные пружины, то можно использовать следующую формулу:

Однако, нам следует еще вспомнить закон Гука:
F = kl
В последовательном соединении имеется n пружин с жесткостями k1, k2, и так далее. Из закона Гука следует, что F = kl. Сумма удлинений каждой пружины равна общему удлинению всего соединения l(или х, по разному в учебниках пишется)1 + l2+ . + ln = lc. (кстати, это одно из свойств последовательно соединения) По закону Гука получим мы можем вывести следующее уравнение: l = F/k, l1 = F/k1 и т.д. Собственно, далее из этого выражения следует: 1/kобщ = 1/k + 1/k + . + 1/kn.
Собственно, отсюда получаем:
kобщ = 1/1/k + 1/k + . + 1/kn.
Ну и как вы уже поняли, k пойдет наверх, и оно будет обратно пропорционально числителю, который в свою очередь зависит от коэффициента жесткости.

Пружины являются важным элементом самых различных механизмов. Для изменения основных эксплуатационных свойств проводится использование нескольких подобных изделий, которые соединяются различным образом. Тип применяемого метода соединения учитывается при проведении самых различных расчетов.

Основные методы крепления пружин

При проведении расчетов уделяется внимание тому, каким образом проводится соединение пружин. Этот момент оказывает влияние на следующее:

1. Жесткость системы. Этот показатель встречается практически во всех проводимых расчетах при последовательном подключении деталей. Зависит он от самых различных моментов, к примеру, коэффициента жесткости каждого.
2. Требуемое усилие для сжатия или растяжения. Рассматриваемая деталь применяется часто по причине того, что может обеспечивает накопление кинетической энергии.
3. Размер кинетической и потенциальной энергии. После того как изделие было выведено из положения равновесия начинает накапливаться кинетическая энергия. При этом она сохраняется на протяжении всего периода, пока к телу приложено усилие.
4. Вероятность возникновения свободного колебательного движения, а также степень сопротивления подобному явлению. Для расчетов колебательного движения также применяются специальные формулы.

Бывают самые различные способы соединения пружин, но наибольшее распространение получил метод последовательного и параллельного подключения.

Они характеризуются довольно большим количеством особенностей. Прежде чем рассматривать применение подобных способов соединения следует уделить внимание особенностям самого изделия:

1. Деталь изготавливается из проволоки, которая получается методом проката. Она обладает высоким показателем упругости, а также устойчивостью к воздействию окружающей среды.
2. Прокат изготавливают из специального сплава, способного выдерживать периодическую деформацию. Под заказ может производится деталь из обычных углеродистых сплавов или легированных металлов, все зависит от конкретного случая.
3. Проволока накручивается в виде колец по спирали. При этом должна выдерживаться едина ось, которая определяет распространение силы в одном направлении.
4. Выделяют два основных типа детали: растяжения и сжатия. Первый вариант исполнения характеризуется тем, что витки находятся практически вплотную. В случае изготовления изделия для сжатия выдерживается определенный зазор, который позволяет кольцам сближаться, а самому изделию сжиматься.
5. Характеризуется изделие самыми различными показателями. Примером можно назвать диаметр проволоки, созданных колец из нее, шаг расположения витков. Все эти параметры указываются в технической документации.

Сегодня они встречаются практически повсеместно. Это связано с тем, что подобное изделие практически незаменимо в случае, когда требуется возвратно-поступательное движение.

Последовательное соединение

При создании многих ме

Лекции по динамике – Сила упругости

 

Сила упругости

 

Механическое напряжение

 

Пусть образец растягивают, прикладывая силу \vec{F}. При этом длина образца увеличивается на \Delta l=l-l_{0}, где l_{0} – начальная длина, l – конечная длина.

 

\Delta l – абсолютное удлинение.

Определение 1: Отношение абсолютного удлинения к начальной длине образца называется относительным удлинением:

\varepsilon=\frac{\Delta l}{l_{0}}

Определение 2: Отношение силы упругости к площади поперечного сечения образца называется механическим напряжением:

\sigma=\frac{F}{S}

 

Закон Гука

 

При малых удлинениях механическое напряжение пропорционально относительному удлинению:

\sigma=E\mid\varepsilon\mid

Подставим \sigma=\frac{F}{S} и \varepsilon=\frac{\Delta l}{l_{0}}:

\frac{F}{S}=\mid\frac{\Delta l}{l_{0}}\mid

l_{0} – всегда положительна, поэтому получаем:

F=\frac{ES}{l_{0}}\mid\Delta L\mid

где коэффициент:

k=\frac{ES}{l_{0}}

называется жесткостью./p>

Итак:

F=k\mid\Delta L\mid

Сила упругости всегда направлена противоположно растяжению:

 

Проекция силы упругости отрицательна:

 

Или положительна:

 

Но всегда противоположна по знаку x:

{F_{упр.}}_{x}=-kx

 

Параллельное и последовательное соединение пружин

 

Последовательное соединение

 

 

 

 

 

 

k_{1}=\frac{ES}{l_{1}} и k_{2}=\frac{ES}{l_{2}}\Rightarrow k=\frac{ES}{l_{1}+l_{2}}

\frac{1}{k}=\frac{l_{1}+l_{2}}{ES} Тогда: \frac{1}{k_{1}}=\frac{l_{1}}{ES} и \frac{1}{k_{2}}=\frac{l_{2}}{ES}

\frac{1}{k}=\frac{l_{1}+l_{2}}{ES} Тогда: \frac{1}{k_{1}}+\frac{1}{k_{2}}=\frac{l_{1}}{ES}+\frac{l_{2}}{ES}=\frac{l_{1}+l_{2}}{ES}=\frac{1}{k}

\frac{1}{k}=\frac{1}{k_{1}}+\frac{1}{k_{2}}

Параллельное соединение

 

\cases{k_{1}=\frac{ES_{1}}{l}\\k_{2}=\frac{ES_{2}}{l}\\k=\frac{E(S_{1}+S_{2}}{l}}\Rightarrow k=\frac{E(S_{1}+S_{2})}{l}=\frac{ES_{1}}{l}+\frac{ES_{2}}{l}=k_{1}+k_{2}

k=k_{1}+k_{2}

 

Пружина (устройство) – Spring (device)

Винтовые или винтовые пружины, рассчитанные на растяжение Сверхмощная спиральная пружина, разработанная для сжатия и растяжения Сила (F) против удлинения. Характеристики пружины: (1) прогрессивная, (2) линейная, (3) пониженная, (4) почти постоянная, (5) прогрессивная с коленом Механически обработанная пружина объединяет несколько функций в один кусок стержня

Пружина является эластичным объект , который хранит механическую энергию . Пружины обычно изготавливаются из пружинной стали . Есть много весенних дизайнов. В повседневном использовании термин часто относится к спиральным пружинам .

Когда обычная пружина без признаков изменчивости жесткости сжимается или растягивается из своего положения покоя, она оказывает противодействующее усилие, приблизительно пропорциональное ее изменению длины (это приближение нарушается при больших отклонениях). Скорости или пружины пружины является изменение в силе оно оказывает, деленное на изменение прогиба пружины. То есть это градиент зависимости силы от кривой отклонения . An внутреннего абонента или компрессии жесткость пружины выражаются в единицах силы , поделенных на расстоянии, например , или Н / м или фунт – сила / дюйм. Торсионная пружина является пружиной , которая работает на скручивание; когда он поворачивается вокруг своей оси на угол, он создает крутящий момент, пропорциональный углу. Скорость пружины кручения выражается в единицах крутящего момента, деленных на угол, например, Н · м / рад или фут · фунт-сила / градус. Обратной величиной скорости пружины является соответствие, то есть: если скорость пружины составляет 10 Н / мм, она соответствует 0,1 мм / Н. Жесткость (или скорость) параллельных пружин является аддитивной , как и жесткость пружин в серии.

Пружины изготовлены из различных упругих материалов, наиболее распространенной из которых является пружинная сталь. Маленькие пружины могут быть намотаны из предварительно закаленной заготовки, в то время как более крупные изготовлены из отожженной стали и закалены после изготовления. Некоторые цветные металлы также используются, в том числе фосфористая бронза и титан для деталей, требующих коррозионной стойкости, и бериллиевая медь для пружин, несущих электрический ток (из-за его низкого электрического сопротивления).

история

На протяжении всей истории человечества использовались простые не спиральные пружины, например лук (и стрела). В бронзовом веке использовались более сложные пружинные устройства, о чем свидетельствует распространение пинцетом во многих культурах. Ктесибий Александрийский разработал метод изготовления бронзы с пружиноподобными характеристиками, изготовив сплав из бронзы с повышенным содержанием олова, а затем упрочнив его молотком после его отливки.

Спиральные пружины появились в начале 15 века в дверных замках. Первые весенние часы с электроприводом появились в этом веке и превратились в первые большие часы к 16 веку.

В 1676 году британский физик Роберт Гук постулировал закон Гука , который гласит, что сила, действующая на пружину, пропорциональна его расширению.

Типы

Спиральная весна . При сжатии катушки скользят друг над другом, обеспечивая более длительное перемещение. Пружины растяжения в сложенном ряду реверберационного устройства. Торсион, скрученный под нагрузкой

Пружины могут быть классифицированы в зависимости от того, как к ним приложено усилие нагрузки:

• Пружина растяжения / растяжения – пружина предназначена для работы с растягивающей нагрузкой, поэтому пружина растягивается при приложении к ней нагрузки.
• Пружина сжатия – предназначена для работы с нагрузкой сжатия, поэтому пружина становится короче при приложении нагрузки к ней.
• Торсионная пружина – в отличие от вышеупомянутых типов, в которых нагрузка представляет собой осевую силу, нагрузка, приложенная к торсионной пружине, представляет собой крутящий момент или крутящую силу, и конец пружины вращается на угол при приложении нагрузки.
• Постоянная пружина – поддерживаемая нагрузка остается неизменной на протяжении всего цикла прогиба
• Переменная пружина – сопротивление катушки нагрузке изменяется при сжатии
• Пружина переменной жесткости – сопротивление катушки нагрузке может динамически изменяться, например, с помощью системы управления, некоторые типы этих пружин также меняют свою длину, тем самым обеспечивая возможность срабатывания

Они также могут быть классифицированы на основе их формы:

• Плоская пружина – этот тип изготовлен из плоской пружинной стали .
• Механически обработанная пружина – этот тип пружины изготавливается путем обработки заготовки с помощью токарного станка и / или фрезерования, а не намотки. Так как она обработана, пружина может включать в себя элементы в дополнение к упругому элементу. Обработанные пружины могут быть изготовлены в типичных случаях нагрузки сжатия / растяжения, кручения и т. Д.
• Змеиная пружина – зигзаг из толстой проволоки – часто используется в современной обивке / мебели.
• Подпружинная пружина – спиральная стальная пружина, которая соединена на каждом конце, чтобы создать круглую форму.

Наиболее распространенные виды весны:

• Консольная пружина – пружина, закрепленная только на одном конце.
• Винтовая пружина или спиральная пружина – пружина (изготовленная намоткой проволоки вокруг цилиндра) бывает двух типов:
  • Натяжные или пружины растяжения предназначены для удлиняются под нагрузкой. Их повороты (петли) обычно соприкасаются в незагруженном положении, и на каждом конце у них есть крюк, ушко или какое-либо другое средство крепления.
  • Пружины сжатия рассчитаны на укорочение при нагрузке. Их повороты (петли) не соприкасаются в незагруженном положении, и им не нужны точки крепления.
  • Полые трубки могут быть либо пружинами растяжения, либо пружинами сжатия. Полая трубка заполнена маслом и средством изменения гидростатического давления внутри трубки, таким как мембрана или миниатюрный поршень и т. Д., Чтобы укрепить или расслабить пружину, так же, как это происходит с давлением воды внутри садового шланга. В качестве альтернативы поперечное сечение трубки выбирается в форме, в которой она меняет свою площадь, когда трубка подвергается деформации кручения – изменение площади поперечного сечения приводит к изменению внутреннего объема трубки и потока масла в / из пружины, который может контролируется клапаном, тем самым контролируя жесткость. Существует много других конструкций пружин из полых труб, которые могут изменять жесткость с любой желаемой частотой, изменять жесткость на множество или перемещаться как линейный привод в дополнение к своим пружинным качествам.
• Пружинная пружина – спиральная пружина сжатия в форме конуса, так что при сжатии витки не прижимаются друг к другу, что обеспечивает более длительное перемещение.
• Дисковая пружина или балансирная пружина – тонкая спиральная пружина, используемая в часах , гальванометрах и местах, где электричество должно передаваться частично вращающимся устройствам, таким как рулевые колеса, не мешая вращению.
• Листовая рессора – плоская пружина, используемая в подвесках транспортных средств, электрических выключателях и дугах .
• V- образная пружина – используется в старинных механизмах огнестрельного оружия , таких как замки на колесах , кремневые и перкуссионные замки. Также пружина дверного замка, используемая в старинных механизмах дверных защелок.

Другие типы включают в себя:

• Шайба Belleville или пружина Belleville – дискообразная пружина, обычно используемая для приложения натяжения к болту (а также в механизме инициирования наземных мин, активируемых давлением)
• Пружина постоянной силы – плотно свернутая лента, которая при развертывании оказывает почти постоянное усилие
• Газовая пружина – объем сжатого газа
• Идеальная пружина – условная пружина, используемая в физике – она ​​не имеет веса, массы или потерь на демпфирование. Сила, действующая на пружину, пропорциональна расстоянию, которое пружина растягивает или сжимает из своего расслабленного положения.
• Главная пружина – пружинная спиралевидная лента, используемая в качестве источника энергии для часовых механизмов: часов , часов , музыкальных шкатулок , игрушек для заводных игрушек и фонариков с механическим приводом

• Пружина отрицателя – тонкая металлическая полоса, слегка вогнутая в поперечном сечении. При намотке он принимает плоское поперечное сечение, но при развертывании возвращается к своей прежней кривой, создавая постоянную силу на протяжении всего перемещения и сводя на нет любую тенденцию к перемотке. Наиболее распространенным применением является правило со стальными лентами.
• Винтовые пружины с прогрессивной скоростью. Винтовая пружина с переменной скоростью, обычно достигаемая за счет неравного шага, так что при сжатии пружины одна или несколько витков упираются в своего соседа.
• Резинка – это пружина растяжения, где энергия накапливается при растяжении материала.
• Пружинная шайба – используется для приложения постоянного растягивающего усилия вдоль оси крепежа .
• Пружина кручения – любая пружина, предназначенная для скручивания, а не сжатия или удлинения. Используется в торсионных системах подвески автомобилей.
• Волновая пружина – любая из множества волнообразных пружин, шайб и расширителей, в том числе линейных пружин, которые, как правило, изготавливаются из плоской проволоки или дисков, которые отделаны в соответствии с промышленными условиями, обычно методом штамповки, в виде волнистой регулярной структуры, в результате в криволинейных долях. Существуют также круглые проволочные волновые пружины. Типы включают волновую шайбу, однооборотную волновую пружину, многооборотную волновую пружину, линейную волновую пружину, расширитель марселя, чересстрочную волновую пружину и вложенную волновую пружину.

физика

Закон Гука

До тех пор, пока они не растянуты и не сжаты за пределы своего предела упругости , большинство пружин подчиняется закону Гука, согласно которому сила, с которой пружина отталкивается назад, линейно пропорциональна расстоянию от ее равновесной длины:

Fзнак равно-КИкс, {\ displaystyle F = -kx, \}

где

х – вектор смещения – расстояние и направление, в котором пружина деформирована от ее равновесной длины.

F – результирующий вектор силы – величина и направление восстанавливающей силы, которую оказывает пружина

k – это скорость , постоянная пружины или постоянная силы пружины, постоянная, которая зависит от материала и конструкции пружины. Отрицательный знак указывает на то, что сила, действующая на пружину, находится в направлении, противоположном ее смещению.

Спиральные пружины и другие распространенные источники обычно подчиняются закону Гука. Существуют полезные пружины, которые этого не делают: пружины, основанные на изгибе балки, могут, например, создавать силы, которые нелинейно изменяются в зависимости от смещения.

Если сделаны с постоянным шагом (толщина проволоки), конические пружины имеют переменную скорость. Однако коническая пружина может иметь постоянную скорость, создавая пружину с переменным шагом. Больший шаг в витках большего диаметра и меньший шаг в витках меньшего диаметра заставляют пружину сжиматься или растягивать все витки с одинаковой скоростью при деформации.

Простые гармонические колебания

Поскольку сила равна массе, m , умноженной на ускорение, a , уравнение силы для пружины, подчиняющейся закону Гука, выглядит следующим образом:

Fзнак равномa⇒-КИксзнак равномa,{\ displaystyle F = ma \ quad \ Rightarrow \ quad -kx = ma. \,}

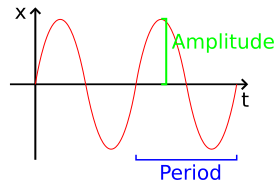Смещение, х , как функция времени. Количество времени, которое проходит между пиками, называется периодом .

Масса пружины мала по сравнению с массой прикрепленной массы и игнорируется. Поскольку ускорение является просто второй производной от x по времени,

-КИксзнак равномd2ИксdT2,{\ displaystyle -kx = m {\ frac {d ^ {2} x} {dt ^ {2}}}. \,}

Это линейное дифференциальное уравнение второго порядка для смещения как функции времени. Перегруппировка: Икс{\ displaystyle x}

d2ИксdT2+КмИксзнак равно0,{\ displaystyle {\ frac {d ^ {2} x} {dt ^ {2}}} + {\ frac {k} {m}} x = 0, \,}

решение которых является суммой синуса и косинуса :

Икс(T)знак равноAгрех⁡(TКм)+Всоз⁡(TКм),{\ displaystyle x (t) = A \ sin \ left (t {\ sqrt {\ frac {k} {m}}} \ right) + B \ cos \ left (t {\ sqrt {\ frac {k} { м}}} \ справа). \,}

A{\ displaystyle A}и являются произвольными постоянными, которые могут быть найдены с учетом начального смещения и скорости движения массы. График этой функции с (нулевая начальная позиция с некоторой положительной начальной скоростью) отображается на рисунке справа. В{\ displaystyle B}Взнак равно0{\ displaystyle B = 0}

теория

В классической физике , пружину можно рассматривать как устройство , которое хранит потенциальная энергию , в частности , упругая потенциальная энергия , напрягают связи между атомами в качестве упругого материала.

Закон упругости Гука гласит, что удлинение упругого стержня (его вытянутая длина минус его расслабленная длина) линейно пропорционально его натяжению , силе, используемой для его растяжения. Точно так же сжатие (отрицательное растяжение) пропорционально сжатию (отрицательное растяжение).

Этот закон фактически выполняется только приблизительно, и только когда деформация (растяжение или сжатие) мала по сравнению с общей длиной стержня. При деформациях, превышающих предел упругости , атомные связи разрушаются или переставляются, и пружина может защелкиваться, сгибаться или постоянно деформироваться. Многие материалы не имеют четко определенного предела упругости, и закон Гука не может быть осмысленно применен к этим материалам. Более того, для суперупругих материалов линейная зависимость между силой и смещением подходит только в области низких напряжений.

Закон Гука является математическим следствием того факта, что потенциальная энергия стержня минимальна, когда он имеет свою расслабленную длину. Любая гладкая функция одной переменной аппроксимирует квадратичную функцию при рассмотрении достаточно близко к ее минимальной точке, что можно увидеть, исследуя ряд Тейлора . Следовательно, сила, которая является производной энергии по смещению, приближается к линейной функции .

Сила полностью сжатой пружины

FмaИксзнак равноЕd4(L-Nd)16(1+ν)(D-d)3N {\ displaystyle F_ {max} = {\ frac {Ed ^ {4} (L-й)} {16 (1+ \ nu) (Dd) ^ {3} n}} \}

где

E – модуль Юнга

d – диаметр пружинной проволоки

L – свободная длина весны

n – количество активных обмоток

ν{\ displaystyle \ nu}- коэффициент Пуассона

D – наружный диаметр пружины

Пружины нулевой длины

«Пружина нулевой длины» – это термин для специально разработанной спиральной пружины, которая будет оказывать нулевое усилие, если она имеет нулевую длину; если бы не было ограничений из-за конечного диаметра проволоки такой спиральной пружины, она имела бы нулевую длину в нерастянутом состоянии. То есть на линейном графике силы пружины в зависимости от ее длины линия проходит через начало координат. Очевидно, что спиральная пружина не может сжиматься до нулевой длины, потому что в какой-то момент витки соприкасаются друг с другом, и пружина больше не может укорачиваться. Пружины нулевой длины изготавливаются путем изготовления спиральной пружины со встроенным натяжением (в проволоку, когда она наматывается во время изготовления, вводится скручивание. Это работает, потому что спиральная пружина «разматывается» при растяжении), поэтому, если она может сжиматься кроме того, точка равновесия пружины, точка, в которой ее восстанавливающая сила равна нулю, возникает на длине ноль. На практике пружины нулевой длины изготавливаются путем объединения пружины «отрицательной длины», выполненной с еще большим натяжением, чтобы ее точка равновесия была на «отрицательной» длине, с куском неэластичного материала надлежащей длины, так что точка нулевой силы будет происходить на нулевой длине.

Пружина нулевой длины может быть прикреплена к массе на шарнирной стреле таким образом, что сила на массу почти точно уравновешивается вертикальной составляющей силы от пружины, независимо от положения стрелы. Это создает горизонтальный «маятник» с очень длительным периодом колебаний . Длиннопериодные маятники позволяют сейсмометрам воспринимать самые медленные волны от землетрясений. ЛаКоста подвеска с нулевой длиной пружинами также используются в гравиметрах , потому что он очень чувствителен к изменениям гравитации. Пружины для закрытия дверей часто имеют примерно нулевую длину, чтобы они прилагали усилие даже при почти закрытой двери, чтобы они могли надежно удерживать ее закрытой.

Пользы

Ссылки

дальнейшее чтение

• Склейтер, Нил. (2011). «Пружинно-винтовые устройства и механизмы». Механизмы и механические устройства. 5-е изд. Нью-Йорк: Макгроу Хилл. С. 279–299. ISBN  9780071704427 . Чертежи и конструкции различных пружинных и винтовых механизмов.
• Пармли, Роберт. (2000). «Раздел 16: Пружины». Иллюстрированный справочник по механическим компонентам. Нью-Йорк: Макгроу Хилл. ISBN  0070486174 Чертежи, конструкции и обсуждение различных пружин и пружинных механизмов.

внешние ссылки

Java – Как настроить пул соединений Spring JDBC с Spring Boot?

Переполнение стека

1. Товары
2. Клиенты
3. Случаи использования

1. Переполнение стека Публичные вопросы и ответы
2. Команды Частные вопросы и ответы для вашей команды
3. предприятие Частные вопросы и ответы для вашего предприятия
4. работы Программирование и связанные с ним технические возможности карьерного роста
5. Талант Нанимать технический талант
6. реклама Связаться с разработчиками по всему миру

,

Java – конфигурации пула соединений Spring

Переполнение стека

1. Товары
2. Клиенты
3. Случаи использования

1. Переполнение стека Публичные вопросы и ответы
2. Команды Частные вопросы и ответы для вашей команды
3. предприятие Частные вопросы и ответы для вашего предприятия
4. работы Программирование и связанные с ним технические возможности карьерного роста
5. Талант Нанимать технический талант
6. реклама Связаться с разработчиками по всему миру

,

Пружинное соединение – переполнение стека

Переполнение стека

1. Товары
2. Клиенты
3. Случаи использования

1. Переполнение стека Публичные вопросы и ответы
2. Команды Частные вопросы и ответы для вашей команды
3. предприятие Частные вопросы и ответы для вашего предприятия
4. работы Программирование и связанные с ним технические возможности карьерного роста
5. Талант Нанимать технический талант
6. реклама

.

Java – понимание пула подключений Spring при загрузке

Переполнение стека

1. Товары
2. Клиенты
3. Случаи использования

1. Переполнение стека Публичные вопросы и ответы
2. Команды Частные вопросы и ответы для вашей команды
3. предприятие Частные вопросы и ответы для вашего предприятия
4. работы Программирование и связанные с ним технические возможности карьерного роста
5. Талант Нанимать технический талант
6. реклама Связаться с разработчиками по всему миру

,