Средняя кинетическая формула: формула, характеристики движения частиц газа, единицы измерения
alexxlab | 17.06.2023 | 0 | Разное
формула, характеристики движения частиц газа, единицы измерения
Физика
12.11.21
13 мин.
Физическую величину, являющуюся мерой взаимодействия материи, то есть перехода из одного состояния в другое, называют энергией. Кинетическая средняя величина определяет перемещение материальной точки. Это понятие было введено Готфридом Вильгельмом Лейбницем, который и сформулировал закон сохранения силы. Фактически это работа движения, зависящая от направления и скорости. Важное значение здесь имеет выбранная система отсчёта.
Оглавление:
- Общие сведения
- Движение частиц
- Температура и энергия
- Решение задач
Общие сведения
В природе есть два закона сохранения: импульса и момента. Они являются следствием свойств пространства. Другими словами, описываются однородностью какого-либо выделенного места и изотропностью. Все направления в пространстве считаются равноправными.
Все направления в пространстве считаются равноправными.
В седьмом классе изучают силу, характеризующуюся работой. Если на тело оказывается воздействие, приводящее к движению, то возникает действие. Например, пусть имеется спица, на которую нанизана бусинка. Она может свободно перемещаться по ней, если к телу приложена сила. Её направление по касательной к спице можно обозначить как F1. Угол, образованный между направлением силы и движения, пусть будет J1.
Чтобы бусинка двигалась по прямой, на неё должны действовать другие силы. Это воздействие определяется реакцией спицы. Представить её можно в виде упругости F2 и трения F3. Углы, которые образуются после перемещения S, можно обозначить так: между F2 и вектором — J2, S и F3 — J3.
Второй закон Ньютона в векторной форме записывается как F1 + F2 + F3 = m * a. Это уравнение можно рассмотреть в проекции вдоль спицы на ось икс. Она имеет следующий вид: F1 * cos (J1) + F2 * cos (J2) + F3 * cos (J3) = m * ax. Пусть силы будут постоянные по направлению и модулю.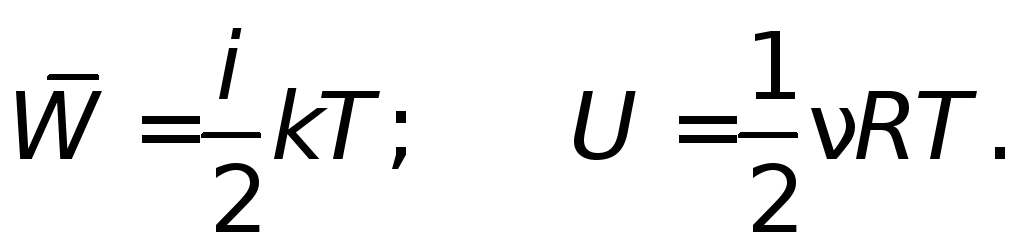
Проекцию вектора перемещения можно записать так: Sa = (Vx2- Vox2) / 2ax. Отсюда: ax = (Vx2- Vox2) / 2 Sx, где Vx — конечная скорость, V0 — начальная. Полученную формулу можно подставить во второй закон Ньютона. В результате получится: F1 * cos (J1) + F2 * cos (J2) + F3 * cos (J3) = m * (Vx2 — V02) / 2 Sx.
Проекция перемещения равна модулю. Левую и правую часть можно умножить на него. В дроби равенства стоят квадраты проекции, поэтому: Sx = S; Vx2 = V2; Vox2 = V02. Учитывая соотношения и разбив дробь на слагаемые, умноженные на массу, можно получить выражение: F1 * cos (J1) + F2 * cos (J2) + F3 * cos (J3) = (m * Vx 2) / 2 — (mV0 2) / 2.
В левой части есть три однотипных слагаемых F * S * cos (J). Эту физическую величину называют работой и обозначают буквой A. Но справедливо равенство только для постоянной силы.
Движение частиц
Молекулы — это частицы, которые подчиняются законам классической механики. В системе они совершают беспорядочное движение. Отсюда следует, что число микросостояний будет определяться интенсивностью перемещений. Для определения этого значения было введено понятие термодинамическая вероятность — мера хаотичности движения молекул (энтропия). Если рассматривать твёрдые тела, то величина параметра будет небольшой. Это связано с тем, что скорости атомов невелики, а сами частицы имеют устойчивые связи.
В газе же взаимодействие проявляется в короткие моменты при столкновении молекул. Этот процесс сопровождается резким изменением скорости. Все законы рассматривают для так называемой идеальной среды. Для неё предполагается, что расстояние между молекулами намного больше, чем радиус воздействия межмолекулярных сил.
Все законы рассматривают для так называемой идеальной среды. Для неё предполагается, что расстояние между молекулами намного больше, чем радиус воздействия межмолекулярных сил.
Так, если размер частицы имеет примерное значение, равное d = 3·10-8 см, то для идеального газа физики считают, что число молекул в единице объёма не должно превышать 3·1022 см-3.
Для рассматриваемого состояния установлено три закона:
- произведение объёма на постоянную температуру определяется таким изменением давления, что выражение p * V будет постоянным значением;
- при определённом давлении величина объёма газа к его температуре является постоянной V / T = const;
- давление связано с температурой формулой pV = n RT, где R — газовая постоянная, n — число молей.
Последнее уравнение с учётом постоянной Больцмана (k = p / nT) является основой кинетической теории газов. Средняя величина давления находится как усреднённое значение квадрата скорости всех групп молекул: p = n * m (V2) / 3. Эта формула получена с учётом того, что каждая молекула имеет приблизительно одинаковую скорость. Её можно переписать так: p = (2 / 3) * n * Ek. Отсюда получается усреднённая кинетическая энергия молекул: Ek = 1 / 2 *(m * V2).
Эта формула получена с учётом того, что каждая молекула имеет приблизительно одинаковую скорость. Её можно переписать так: p = (2 / 3) * n * Ek. Отсюда получается усреднённая кинетическая энергия молекул: Ek = 1 / 2 *(m * V2).
Поступательное движение атомов и молекул, взятое по большему числу хаотично перемещающихся частиц, является мерилом температуры. Если она измеряется в градусах Кельвина, то её связь c энергией описывается отношением Ek = (3 * k T) / 2.
Следует отметить, что выражение справедливо только при расчёте для одной частицы. Такой энергией обладает каждая молекула, так как она находится в тепловом хаотическом движении.
Температура и энергия
Если взять два тела с разной температурой и обеспечить между их поверхностями контакт, то через время произойдёт выравнивание температуры. Ранее считалось, что существует некая субстанция, которая, хаотично смешиваясь, уравновешивает показатели. Но на самом деле происходит просто изменение кинетической энергии. Именно она и определяет состояние равновесия.
Но на самом деле происходит просто изменение кинетической энергии. Именно она и определяет состояние равновесия.
Это свойство позволило связать энергию с температурой через коэффициент пропорциональности Больцмана: T = (2 * m 0 * V
Идеальный газ описывается уравнением Клайперона — Менделеева: p * V = (m * R * T) / µ. В то же время газовую постоянную можно определить как произведение постоянной Больцмана на число Авогадро (Na). Это значение равняется 6,02 * 1023. Измеряется в молях и показывает количество структурных частиц на один моль вещества. Формулу для хаотического движения молекул можно вывести следующим образом:
- Поскольку концентрация этих веществ определяется как (m * Na) / µ * V, выражение для давления легко представить в виде p = n * k * T.

- Подставив в формулу давления для одноатомного газа полученное равенство, можно получить p = (1 / 3) ∗ (n ∗ m ∗ v2c) = (n ∗ k ∗ T).
- После сокращения обеих частей на три вторых и концентрацию молекул получится равенство: m * V2 / 2 = (3 * k * T) / 2.
- В правой части стоит значение полной кинетической работы, поэтому формулу можно записать как Ek = (3 * k * T) / 2.
Таким образом, газовая температура зависит от среднекинетической энергии. Эти две величины связаны прямо пропорционально. Температура имеет абсолютное значение, поэтому её физический смысл заключается в определении средней кинетической энергии, приходящейся на молекулу. Но температура характеризует систему в целом. Значит, с помощью формулы можно установить связь параметров макромира и микромира.
Следует отметить, что средняя суммарная тепловая энергия перемещения молекул определяется только температурой газа. То есть кинетическая энергия поступательного хаотичного движения частиц не зависит от химического состава, массы, давления или занимаемого объёма.
Решение задач
Самостоятельное решение примеров позволяет закрепить теоретические знания. Существуют определённые типы заданий, с помощью которых можно проработать весь изученный материал и наглядно увидеть практическое применение знаний. Вот некоторые из них:
- Выяснить, какова средняя кинетическая энергия поступательного движения молекулы газа неона, если созданное давление при концентрации 2, 65 * 1025 м-3 составляет 98,8 кПа. Решение примера следует начать с записи уравнения для идеального газа: p = (m 0 * n * V2) / 3. Так как энергию молекулы можно вычислить из выражения E = (m 0 V2 ) / 2, то нужная формула примет вид p = (2 * n * E) / 3. Отсюда искомая величина равняется E = 3 p / 2 n. Теперь нужно подставить исходные данные и выполнить количественный расчёт: Ek = (3 * 98,8 * 103) / (2 * 2,65 * 1025) = 5,6 * 10-21 джоулей.
- Средняя энергия поступательного движения частицы гелия равняется 60 Дж, а давление составляет 2 * 105 Па.
 Необходимо найти концентрацию частиц газа. В основе решения лежит уравнение идеальной системы: p = n * k * T. Добавив к нему формулу связи движения и температуры E = (3 / 2) * kT, можно выразить искомую концентрацию: kT = (2 * E) / 3. Отсюда: n = 3p / 2E = 3 * 2 * 105 / 2 * 60 = 6 * 105 / 60 = 105 / 10 = 104 м-3.
Необходимо найти концентрацию частиц газа. В основе решения лежит уравнение идеальной системы: p = n * k * T. Добавив к нему формулу связи движения и температуры E = (3 / 2) * kT, можно выразить искомую концентрацию: kT = (2 * E) / 3. Отсюда: n = 3p / 2E = 3 * 2 * 105 / 2 * 60 = 6 * 105 / 60 = 105 / 10 = 104 м-3. - Найти работу, которая выполняется телом в течение трёх секунд после воздействия, если изменение энергии происходит по графику в виде параболы. Трем секундам соответствует энергия, равная 2 Дж, шести — 4 Дж. Для выяснения работы нужно воспользоваться определением кинетической энергии. Так как существует силовое взаимодействие, то А = ΔEk. В соответствии с графиком энергия изменяется от четырёх джоулей до двух. Значит, работа равна A = 2 — 4 = -2 Дж.
Решать задачи по исследованию кинетической работы несложно. Нужно лишь знать несколько формул и внимательно следить за размерностью величин при выполнении вычислений.
Средняя кинетическая энергия хаотического движения молекул – формула, определение
4.5
Средняя оценка: 4.5
Всего получено оценок: 82.
4.5
Средняя оценка: 4.5
Всего получено оценок: 82.
Согласно молекулярно-кинетической теории в неподвижном теле, находящемся в состоянии механического покоя, молекулы и атомы находятся в постоянном хаотическом (несогласованном) движении. Кинетическая энергия молекул, движущихся внутри вещества, определяет то, что все называют температурой вещества. Можно ли, зная температуру, найти кинетическую энергию хаотического теплового движения молекул?
Кинетическая энергия движущейся частицы
Формула для кинетической энергии Ек движущегося со скоростью v тела массой m была получена в разделе механики. Это соотношение справедливо не только для поведения тел видимых размеров, но и для микрочастиц (молекул, атомов, электронов и т. п_к = Е_1+ Е_2 + Е_3 +…. Е_N$ (2),
п_к = Е_1+ Е_2 + Е_3 +…. Е_N$ (2),
где N — полное число частиц в веществе.
Рис. 1. Хаотически движущиеся с разными скоростями молекулы в веществе.Найти суммарную кинетическую энергию всего вещества с помощью формул (1) и (2), конечно, невозможно: ведь для этого необходимо знать массы и скорости всех частиц, а также их общее количество. Если учесть, что только в одном моле вещества находится огромное число молекул (6,023*1023!), то становится понятно, что для решения этой задачи требуется другой подход.
Наблюдениями и исследованиями процессов передачи тепла ученые занимались задолго до нахождения формул молекулярно-кинетической теории. Для того чтобы придать понятиям “теплый”, “холодный” и т.п. более четкий, числовой вид, были изобретены термометры. Один из первых термометров придумал знаменитый Галилео Галилей, живший в Италии с 1564 г. по 1642 г.
Эксперименты показывали, что чем горячее вещество, тем быстрее (“энергичнее”) двигаются частицы. После изобретения микроскопа появилась возможность визуально наблюдать броуновское движение частиц, которые начинали перемещаться быстрее при нагревании.
После изобретения микроскопа появилась возможность визуально наблюдать броуновское движение частиц, которые начинали перемещаться быстрее при нагревании.
Оказывается в 1 см3 при 00С и 760 мм.рт.ст. находится 2,7*1019 молекул. Чтобы ощутить насколько велико это число приведем такой пример. Предположим, что газ удаляется из крохотного сосуда объемом 1 см3 с такой скоростью, что в каждую секунду “убегает” миллион молекул. Нетрудно подсчитать, что сосуд опустеет через миллион лет!
Молекулярно-кинетический подход
Уже к середине ХIX века стало понятно, что пытаться описывать движение каждого атома — дело безнадежное, т.к. ни один прибор не сможет отследить все молекулы и атомы. Вместо такого, “лобового”, подхода системы, состоящие из большого числа частиц стали рассматривать, не пытаясь учесть свойства отдельных атомов, а усредняя эти свойства по большой их совокупности.
В 1859 г. английский физик Максвелл с помощью такого подхода получил для давления p одноатомного газа формулу:
$p = {1\over 3} * n * m * v^2_c$ (3),
где: n — концентрация молекул, m — масса молекул, v2c = <v2>ср — среднее арифметическое квадратов скоростей молекул.
Температура вещества — мера кинетической энергии
Ранее для идеального газа был открыт закон Клапейрона-Менделеева, связавший в единое уравнение такие физические параметры, как давление p, объем V и температуру T (по шкале Кельвина):
$p * V = {m\over μ} * R * T$ (4),
где:
μ — молярная масса газа, R = 8,3157 джоуль/моль/градус — универсальная газовая постоянная.
Рис. 2. Температуры по шкалам Кельвина и Цельсия.В то же время газовая постоянная R равна:
$R = k * N_a$ (5),
где: k =1,38*10-23 Дж/К — постоянная Больцмана, Na — число Авогадро.
Рис. 3. Число Авогадро.Тогда, подставив в уравнение (4) R из уравнения (5), разделив обе части уравнения (4) на объем V и воспользовавшись тем, что:
${m\over μ} * {Na\over V } = n$ — концентрация молекул, получим из формулы (4) выражение для давления в виде:
$p = n * k * T$ (6). 2\over 2} = { 3 \over 2} * k * T$ (8).
2\over 2} = { 3 \over 2} * k * T$ (8).
В левой части уравнения, пользуясь формулой (1), получаем выражение для средней кинетической энергии хаотического движения молекул:
$Е_к = { 3 \over 2} * k * T$ (9).
Последняя формула (9) демонстрирует, что температура является мерой кинетической энергии молекул. Если газ одноатомный, то вся его энергия — это энергия поступательного движения.
Из формулы (9) следует еще один важный вывод: средняя кинетическая энергия поступательного движения для разных газов будет одинаковой не зависимо от массы молекул, и будет зависеть только от величины температуры.
Что мы узнали?
Итак, мы узнали что суммарная кинетическая энергия вещества складывается из кинетических энергий отдельных частиц. Кинетическая энергия движения частиц, усредненная по их числу, определяет температуру вещества. С помощью уравнения Менделеева-Клапейрона (4) и формулы для давления (3) получили соотношение, связывающее среднюю кинетическую энергию хаотического движения молекул с температурой вещества T.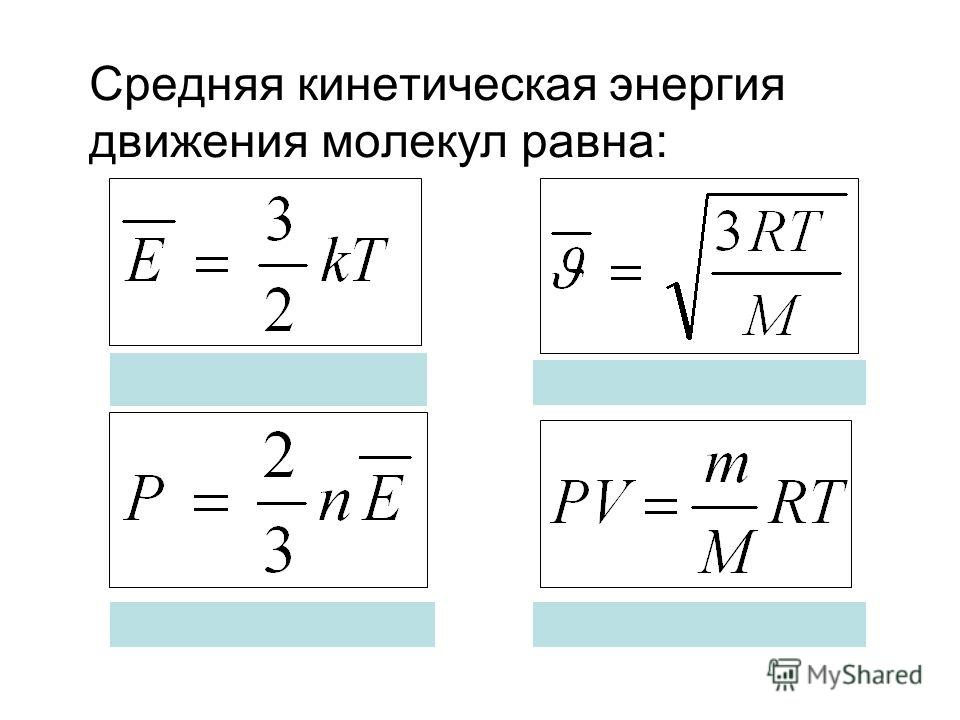
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Кристина Тараканова
11/11
Оценка доклада
4.5
Средняя оценка: 4.5
Всего получено оценок: 82.
А какая ваша оценка?
Какое уравнение связывает среднюю кинетическую энергию с температурой в высокотемпературном пределе?
Короче говоря, наблюдаемая кинетическая энергия (такая, которую мы знаем из повседневной химии и физики) — которая совпадает со средним совокупностью кинетической энергии — для одноатомного идеальный газ , это:
#\mathbf(<< barE >> = U = K = 3/2 RT)#
но средняя кинетическая энергия для одиночная система одноатомных идеальных газов это:
#цвет(синий)(<< E >> = 3/2 нРТ)#
Итак, мы видим, что кинетическая энергия здесь зависит от числа #\mathbf(“mol”)# с газа .
Но, как мы должны знать, #”1 моль”# одноатомного газа равен #”1 моль”# любого другого одноатомного газа при определении в терминах #”моль”#с. Массы в #”g”# различаются на , хотя это не имеет значения, потому что это уравнение требует #”mol”#s газа, а не #”g”# газа.
Кроме того, #R#, универсальная газовая константа , никогда не меняется.
Таким образом, идентичность одноатомного идеального газа не имеет значения при определении его средней кинетической энергии. Только его температура.
Вы можете прочитать ниже интересный вывод.
ЕДИНАЯ СИСТЕМА ОДНОАТОМНЫХ ИДЕАЛЬНЫХ ГАЗОВ
У нас есть то, что называется одиночной системой газов, а затем у нас есть то, что называется ансамблем 9(-34) “J”*”s”# #del# означает «частная производная», что является просто причудливым способом сказать: «давайте сосредоточимся только на этой функции при нахождении ее наклона во всех точках функции». Если мы немного поработаем с первым уравнением, мы сможем понять, почему идентичность одноатомного идеального газа не имеет значения. УПРОЩЕНИЕ ФУНКЦИИ, КОТОРАЯ БУДЕТ ДИФФЕРЕНЦИИРОВАНА 9(“не” бета)]# #= -(-(3N)/(2бета))# #= цвет (зеленый)(3/2 Nk_BT)# Что-то интересное в том, что #Nk_B = nR#, где #n# – количество #”моль”#с, а #R# – универсальная газовая постоянная. Итак, мы действительно только что вывели: #цвет(синий)(<< E >> = 3/2 нРТ)# , который показывает, что средняя кинетическая энергия одиночной системы одноатомных идеальных газов зависит только от числа #”моль”#с (которое одинаково для всех одноатомных идеальных газов) и температуру (которая, как мы предполагали, была одинаковой для всех рассматриваемых систем). ЭНЕРГИЯ, КОТОРУЮ МЫ ЗНАЕМ И ЛЮБИМ?? Хорошо, теперь мы можем перейти к ансамблю систем одноатомных идеальных газов. #<< barE >> = << E >> / n# Это эквивалент нас, наблюдающих кинетическую энергию в реальной жизни. Другими словами, это кинетическая и потенциальная энергия, которую мы наблюдаем на уроках физики и химии: #\mathbf(<< barE >> = U = K = 3/2 RT)# Законы, описывающие поведение газов, были хорошо установлены задолго до того, как кто-либо разработал последовательную модель свойств газов. Одним из ключевых свойств отдельных частиц является их скорость. Однако в образце, состоящем из многих частиц газа, частицы, вероятно, будут иметь разные скорости. Вместо того, чтобы перечислять скорость каждой отдельной молекулы газа, мы можем комбинировать эти отдельные скорости несколькими способами, чтобы получить «коллективные» скорости, которые описывают образец в целом. В следующем примере эти три коллективные скорости определены и рассчитаны для образца газа, состоящего всего из восьми молекул.
 Идея в том, что мы можем сказать, что определенное количество #”mol”#s систем газов составляет ансамбль:
Идея в том, что мы можем сказать, что определенное количество #”mol”#s систем газов составляет ансамбль: 27.1: Средняя поступательная кинетическая энергия газа
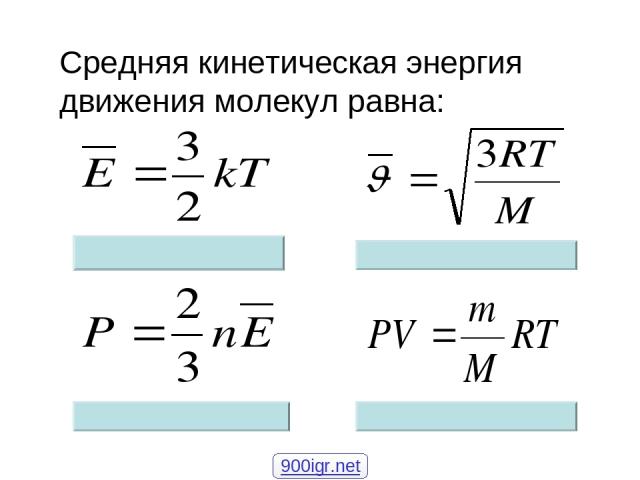 В этом разделе мы вводим теорию, которая описывает, почему газы ведут себя именно так. Теория, которую мы представляем, также может быть использована для вывода таких законов, как закон идеального газа, из фундаментальных принципов и свойств отдельных частиц.
В этом разделе мы вводим теорию, которая описывает, почему газы ведут себя именно так. Теория, которую мы представляем, также может быть использована для вывода таких законов, как закон идеального газа, из фундаментальных принципов и свойств отдельных частиц. Собственность Скорость Кинетическая энергия Наиболее вероятно \( \sqrt{\dfrac{2k_bT}{m}}\) \(к_БТ\) В среднем \( \sqrt{\dfrac{8k_bT}{\pi m}}\) \(\dfrac{4k_BT}{\pi}\) Среднеквадратичное \( \sqrt{\dfrac{3k_bT}{m}}\) \( \dfrac{3}{2} k_BT\) 
Пример 27.1.1
: Образец газа с небольшим количеством молекул
Были найдены скорости восьми молекул, равные 1,0, 4,0, 4,0, 6,0, 6,0, 6,0, 8,0 и 10,0 м/с. Вычислите их среднюю скорость (\(v_{\rm avg}\)) среднеквадратичную скорость (\(v_{\rm rms}\)) и наиболее вероятную скорость (\(v_{\rm mp}\)).
Раствор
Начать с определений:
- средняя скорость (\(v_{\rm avg}\)) = сумма всех скоростей, деленная на число молекул
- среднеквадратическая скорость (\(v_{\rm rms}\)) = квадратный корень из суммы квадратов скоростей, деленный на число молекул
- наиболее вероятная скорость (\(v_{\rm mp}\)) = скорость, с которой движется наибольшее количество молекул 92 \номер\]
- Газ состоит из большого числа частиц, называемых молекулами (одноатомными или многоатомными), которые находятся в постоянном хаотическом движении.
- Поскольку расстояние между молекулами газа намного больше, чем размер молекул, объем молекул пренебрежимо мал.
- Межмолекулярные взаимодействия, как отталкивающие, так и притягивающие, настолько слабы, что ими также можно пренебречь.
- Молекулы газа сталкиваются друг с другом и со стенками сосуда, но эти столкновения абсолютно упругие; то есть они не изменяют среднюю кинетическую энергию молекул.
- Средняя кинетическая энергия молекул любого газа зависит только от температуры, и при данной температуре все молекулы газа имеют точно одинаковую среднюю кинетическую энергию.

Важно помнить, что в термализованной пробе газа будет полное распределение молекулярных скоростей. Одни молекулы будут двигаться быстрее, другие медленнее. Также важно признать, что наиболее вероятная, средняя и среднеквадратичная составляющие кинетической энергии, которые могут быть получены из кинетической молекулярной теории, не зависят от массы молекул (таблица 27. 1.1). Таким образом, можно сделать вывод, что средняя кинетическая энергия молекул в термализованной пробе газа зависит только от температуры. Однако средняя скорость зависит от молекулярной массы. Таким образом, при данной температуре легкие молекулы в среднем будут двигаться быстрее, чем более тяжелые.
1.1). Таким образом, можно сделать вывод, что средняя кинетическая энергия молекул в термализованной пробе газа зависит только от температуры. Однако средняя скорость зависит от молекулярной массы. Таким образом, при данной температуре легкие молекулы в среднем будут двигаться быстрее, чем более тяжелые.
Расчеты, выполненные в примере 27.1.1 становятся громоздкими по мере увеличения числа молекул в пробе газа. Таким образом, требуется более эффективный способ определения различных коллективных скоростей для пробы газа, содержащей большое количество молекул.
Молекулярное описание давления и молекулярной скорости
Кинетическая молекулярная теория газов объясняет законы, описывающие поведение газов. Разработан в середине 19 века несколькими физиками, в том числе австрийцем Людвигом Больцманом (1844–1819 гг.).06), немца Рудольфа Клаузиуса (1822–1888) и шотландца Джеймса Клерка Максвелла (1831–1879), эта теория основана на свойствах отдельных частиц, определенных для идеального газа, и фундаментальных понятиях физики. Таким образом, кинетическая молекулярная теория газов дает молекулярное объяснение наблюдениям, которые привели к развитию закона идеального газа. Кинетическая молекулярная теория газов основана на следующих пяти постулатах:
Таким образом, кинетическая молекулярная теория газов дает молекулярное объяснение наблюдениям, которые привели к развитию закона идеального газа. Кинетическая молекулярная теория газов основана на следующих пяти постулатах:
Рисунок 27.1.1 : Визуализация молекулярного движения. Молекулы газа находятся в постоянном движении и сталкиваются друг с другом и со стенкой сосуда.
Хотя молекулы реальных газов имеют ненулевые объемы и действуют как притягивающие, так и отталкивающие силы друг на друга, сейчас мы сосредоточимся на том, как кинетическая молекулярная теория газов связана с обсуждаемыми нами свойствами газов. В Теме 1C мы объясняем, как эту теорию следует модифицировать, чтобы учесть поведение реальных газов.
Постулаты 1 и 4 утверждают, что молекулы газа находятся в постоянном движении и часто сталкиваются со стенками своих сосудов. Столкновение молекул со стенками контейнера приводит к передаче импульса (импульса) от молекул к стенкам (рис. 27.1.2). ).
Рисунок 27.1.2
: Примечание. На этом рисунке символ \(u\) используется для обозначения скорости. В остальной части этого текста скорость будет представлена символом \(v\). Передача импульса (импульса) от молекулы к стенке контейнера, когда она отскакивает от стенки. Передача импульса (\(\Delta \rho_x\)) при упругом соударении равна m\(\Delta v_x\), где m – масса молекулы, а \(\Delta v_x\) – изменение \ (x\) составляющая молекулярной скорости (\(v_{x_{final}}-v_{x_{initial}})\). Стенка перпендикулярна оси \(x\). Поскольку столкновения упругие, молекула отскакивает с той же скоростью в противоположном направлении, и \(\Delta v_x\) равно \(2v_x\).
Передача импульса (импульса) от молекулы к стенке контейнера, когда она отскакивает от стенки. Передача импульса (\(\Delta \rho_x\)) при упругом соударении равна m\(\Delta v_x\), где m – масса молекулы, а \(\Delta v_x\) – изменение \ (x\) составляющая молекулярной скорости (\(v_{x_{final}}-v_{x_{initial}})\). Стенка перпендикулярна оси \(x\). Поскольку столкновения упругие, молекула отскакивает с той же скоростью в противоположном направлении, и \(\Delta v_x\) равно \(2v_x\).
Передача импульса стенке, перпендикулярной оси \(x\) при ударе молекулы с начальной скоростью \(v_x\) в направлении \(x\), выражается как:
\[\rm импульс \; transfer_x\;= \Delta \rho_x = m\Delta v_x = 2mv_x \label{1.2.1} \]
Частота столкновений , количество столкновений молекул со стенкой на единицу площади в секунду, увеличивается с молекулярной скоростью и числом молекул в единице объема.
92} \label{1.2.5} \] Поскольку объемами и межмолекулярными взаимодействиями можно пренебречь, постулаты 2 и 3 утверждают, что все газообразные частицы ведут себя одинаково, независимо от химической природы составляющих их молекул. В этом суть закона идеального газа, который рассматривает все газы как совокупность частиц, идентичных во всех отношениях, кроме массы. Постулат 2 также объясняет, почему сжать газ относительно легко; вы просто уменьшаете расстояние между молекулами газа. 92} = \dfrac{2}{3} N \epsilon \label{1.2.7} \]
В этом суть закона идеального газа, который рассматривает все газы как совокупность частиц, идентичных во всех отношениях, кроме массы. Постулат 2 также объясняет, почему сжать газ относительно легко; вы просто уменьшаете расстояние между молекулами газа. 92} = \dfrac{2}{3} N \epsilon \label{1.2.7} \]
Коэффициент 2/3 в пропорциональности отражает тот факт, что компоненты скорости в каждом из трех направлений вносят вклад ½ kT к кинетической энергии частицы. Средняя поступательная кинетическая энергия прямо пропорциональна температуре:
\[\epsilon = \dfrac{3}{2} kT \label{1.2.8} \]
, в которых известна константа пропорциональности \(k\) как постоянная Больцмана . Подстановка уравнения \(\ref{1.2.8}\) в уравнение \(\ref{1.2.7}\) дает
\[ PV = \left( \dfrac{2}{3}N \right) \left( \dfrac{3}{2}kT \right) =NkT \label{1.2.9} \]
Постоянная Больцмана \(k\) – это просто газовая постоянная на молекулу, поэтому, если N выбрано в качестве числа Авогадро, \(N_A\), то \(N_Ak\) – это R, газовая постоянная на моль. Таким образом, для n молей частиц уравнение \(\ref{1.2.9}\) принимает вид
Таким образом, для n молей частиц уравнение \(\ref{1.2.9}\) принимает вид
\[ PV = nRT \label{1.2.10} \]
, что является законом идеального газа.
Как указано в примере 27.1.1 , среднеквадратическая скорость (\(v_{\rm rms}\)) представляет собой квадратный корень из суммы квадратов скоростей, деленной на количество частиц: 92}}=\sqrt{\dfrac{3RT}{M}} \label{1.2.16} \]
В уравнении \(\ref{1.2.16}\), \(v_{\rm rms}\ ) имеет единицы измерения метры в секунду; следовательно, единицами молярной массы \(M\) являются килограммы на моль, температура \(T\) выражается в кельвинах, а постоянная идеального газа \(R\) имеет значение 8,3145 Дж/(К•моль). Уравнение \(\ref{1.2.16}\) показывает, что \(v_{\rm rms}\) газа пропорциональна квадратному корню из его температуры Кельвина и обратно пропорциональна квадратному корню из его молярной массы. Среднеквадратичная скорость газа увеличивается с повышением температуры. При данной температуре более тяжелые молекулы газа имеют меньшую скорость, чем более легкие.
Пример 27.1.2 :
Какова среднеквадратичная скорость для молекул \(\rm O_2\) при 25ºC?
Дано: Температура в ºC, тип молекул, газовая постоянная идеального газа
Запрашиваемое значение: \(v_{\rm rms}\), среднеквадратическая скорость
Стратегия:
Преобразование температуры в кельвины:
\(\rm T\; (в\; Кельвин) = (25ºC + 273ºC)\dfrac{1\; K}{1\; ºC} = 298\; K\)
Перевести молярную массу молекул \(\rm O_2\) в кг на моль:
\(\rm M\; (в\; \dfrac{кг}{моль}) = 32,00\dfrac{г}{моль}\rm x\dfrac{1\; кг}{1000\; g}=0,03200 \dfrac{кг}{моль}\)
Используйте уравнение \(\ref{1.2.16}\) для расчета среднеквадратичной скорости.
Решение
\(v_{\rm rms _{\rm O_2}}= \sqrt{\dfrac{3\rm (8,3145\dfrac{J}{K·моль})(298,15\; K)}{\rm 0,03200\dfrac{кг}{моль}}}=482\dfrac{м}{с}\)
Упражнение 27.1.2
Какова среднеквадратичная скорость для молекул \(\rm Cl_2\) при 25ºC?
\(v_{\rm rms _{\rm Cl_2}}= 324\dfrac{m}{s}\)
Много молекул, много скоростей
При температурах выше абсолютного нуля все молекулы находятся в движении. В случае газа это движение состоит из прямолинейных скачков, длина которых весьма велика по сравнению с размерами молекулы. Хотя мы никогда не можем предсказать скорость конкретной отдельной молекулы, тот факт, что мы обычно имеем дело с огромным их числом, позволяет нам знать, какая часть молекул имеет кинетическую энергию (и, следовательно, скорости), которые лежат в пределах любого заданного значения. диапазон.
В случае газа это движение состоит из прямолинейных скачков, длина которых весьма велика по сравнению с размерами молекулы. Хотя мы никогда не можем предсказать скорость конкретной отдельной молекулы, тот факт, что мы обычно имеем дело с огромным их числом, позволяет нам знать, какая часть молекул имеет кинетическую энергию (и, следовательно, скорости), которые лежат в пределах любого заданного значения. диапазон.
Траектория отдельной молекулы газа состоит из серии прямолинейных траекторий, прерываемых столкновениями. Что происходит при столкновении двух молекул, зависит от их относительной кинетической энергии; в общем, более быстрая или тяжелая молекула передает часть своей кинетической энергии более медленной или легкой молекуле. Две молекулы, имеющие одинаковые массы и движущиеся в противоположных направлениях с одинаковой скоростью, после столкновения на мгновение останутся неподвижными.
Если бы мы могли измерить мгновенные скорости всех молекул в образце газа при некоторой фиксированной температуре, мы получили бы широкий диапазон значений. Некоторые из них будут нулевыми, а некоторые будут очень высокими скоростями, но большинство попадет в более или менее четко определенный диапазон. У нас может возникнуть соблазн определить среднюю скорость для набора молекул, но здесь нужно быть осторожным: молекулы, движущиеся в противоположных направлениях, имеют скорости противоположных знаков. Поскольку молекулы в газе находятся в случайном тепловом движении, будет примерно столько же молекул, движущихся в одном направлении, сколько и в противоположном направлении, поэтому все векторы скоростей противоположных знаков будут сокращаться, и средняя скорость будет равна нулю. . Поскольку этот ответ не очень полезен, нам нужно провести усреднение немного по-другому.
Некоторые из них будут нулевыми, а некоторые будут очень высокими скоростями, но большинство попадет в более или менее четко определенный диапазон. У нас может возникнуть соблазн определить среднюю скорость для набора молекул, но здесь нужно быть осторожным: молекулы, движущиеся в противоположных направлениях, имеют скорости противоположных знаков. Поскольку молекулы в газе находятся в случайном тепловом движении, будет примерно столько же молекул, движущихся в одном направлении, сколько и в противоположном направлении, поэтому все векторы скоростей противоположных знаков будут сокращаться, и средняя скорость будет равна нулю. . Поскольку этот ответ не очень полезен, нам нужно провести усреднение немного по-другому.
Правильный подход состоит в том, чтобы усреднить квадратов скоростей, а затем извлечь из этого значения квадратный корень, чтобы получить среднеквадратичную скорость (\(v_{\rm rms}\)), что и мы разработали выше. Эта скорость описывает образец газа в целом, но не говорит нам ни о диапазоне возможных скоростей, ни о распределении скоростей.




 Необходимо найти концентрацию частиц газа. В основе решения лежит уравнение идеальной системы: p = n * k * T. Добавив к нему формулу связи движения и температуры E = (3 / 2) * kT, можно выразить искомую концентрацию: kT = (2 * E) / 3. Отсюда: n = 3p / 2E = 3 * 2 * 105 / 2 * 60 = 6 * 105 / 60 = 105 / 10 = 104 м-3.
Необходимо найти концентрацию частиц газа. В основе решения лежит уравнение идеальной системы: p = n * k * T. Добавив к нему формулу связи движения и температуры E = (3 / 2) * kT, можно выразить искомую концентрацию: kT = (2 * E) / 3. Отсюда: n = 3p / 2E = 3 * 2 * 105 / 2 * 60 = 6 * 105 / 60 = 105 / 10 = 104 м-3.