Таблица массы трубы одного погонного метра: Вес прямоугольной профильной трубы – Трубный калькулятор
alexxlab | 13.04.2023 | 0 | Разное
Вес погонного метра квадратной профильной трубы: таблица
Опубликовано 2023-01-05
- Размеры и вес трубы стальной квадратной (DIN 2395, ТУ 14-105-566-93)
- Расчет веса квадратных профильных труб (ГОСТ 8639-82)
- Формула для расчета массы метра квадратной трубы
Квадратные профильные трубы – это вид металлопроката, который используется при укладке водопроводных и газовых систем. Сечение трубопроката бывает не только квадратное, но и прямоугольное, овальное или шестигранное.
Сортамент зависит от:
- марки стали;
- технологического процесса создания;
- толщины стенок;
- наличия/отсутствия дополнительной обработки.
Стальной металлопрокат создается тремя способами: горячий и холодный прокат, сварка.
Важно!
Сортамент регламентирует ГОСТ 8645-68.
В маркировке стальных профильных труб используются наружный размер изделий.
Например, 80х80х4 ГОСТ 30245-2003 С245. Такая маркировка говорит о том, что размеры сторон 80 мм, толщина стенки 4 мм, используется марка стали С245.
Рассчитать вес можно по формуле m= Pi*ro*S*(D-S)*L, где:
- Pi – это константа, равная 3.14.
- ro – плотность стали (справочное значение).
- S – толщина стенки.
- D – наружный диаметр в мм.
- L – длина в метрах.
Размеры и вес трубы стальной квадратной (DIN 2395, ТУ 14-105-566-93)
| Длина стороны а, мм | Толщина стенки S, мм | Вес, кг/м |
|---|---|---|
| 15 | 1,0 | 0,479 |
| 15 | 1,5 | 0,707 |
| 15 | 2,0 | 0,926 |
| 20 | 1,0 | 0,620 |
| 20 | 1,5 | 0,930 |
| 20 | 2,0 | 1,225 |
| 25 | 1,0 | 0,793 |
| 25 | 1,5 | 1,178 |
| 25 | 2,0 | 1,554 |
| 30 | 1,0 | 0,942 |
| 30 | 1,5 | 1,401 |
| 30 | 2,5 | 2,296 |
| 40 | 1,0 | 1,24 |
| 40 | 1,5 | 1,849 |
| 40 | 2,0 | 2,447 |
| 50 | 1,5 | 2,34 |
| 50 | 2,0 | 3,10 |
| 50 | 2,5 | 3,86 |
| 60 | 1,5 | 2,8 |
| 60 | 2 | 3,72 |
| 60 | 2,5 | 4,63 |
Расчет веса квадратных профильных труб (ГОСТ 8639-82)
| Размеры, мм | Толщина стенки, мм | Вес 1 метра погонного, кг | Метров в тонне, м |
|---|---|---|---|
| 10×10 | 1 | 0,269 | 3717,5 |
| 15×15 | 1 | 0,426 | 2347,4 |
| 15×15 | 1,5 | 0,605 | 1652,9 |
| 20×20 | 1 | 0,583 | 1715,3 |
| 20×20 | 1,5 | 0,841 | 1189,1 |
| 20×20 | 2 | 1,075 | 930,2 |
| 25×25 | 1 | 0,74 | 1351,4 |
| 25×25 | 1,5 | 1,07 | 934,6 |
| 25×25 | 2 | 1,39 | 719,4 |
| 25×25 | 2,5 | 1,68 | 595,2 |
| 25×25 | 3 | 1,95 | 512,8 |
| 30×30 | 2 | 1,7 | 588,2 |
| 30×30 | 2,5 | 2,07 | 483,1 |
| 30×30 | 3 | 2,42 | 413,2 |
| 30×30 | 3,5 | 2,75 | 363,6 |
| 30×30 | 4 | 3,04 | 328,9 |
| 32×32 | 4 | 3,3 | 303 |
| 35×35 | 2 | 2,02 | 495 |
| 35×35 | 2,5 | 2,46 | 406,5 |
| 35×35 | 3 | 2,89 | 346 |
| 35×35 | 3,5 | 3,3 | 303 |
| 35×35 | 4 | 3,67 | 272,5 |
| 35×35 | 5 | 4,37 | 228,8 |
| 36×36 | 4 | 3,8 | 262,2 |
| 40×40 | 2 | 2,33 | 429,2 |
| 40×40 | 2,5 | 2,85 | 350,9 |
| 40×40 | 3,36 | 297,6 | |
| 40×40 | 3,5 | 3,85 | 259,7 |
| 40×40 | 4 | 4,3 | 232,6 |
| 40×40 | 5 | 5,16 | 193,8 |
| 40×40 | 6 | 5,92 | 168,9 |
| 42×42 | 3 | 3,55 | 281,7 |
| 42×42 | 3,5 | 4,07 | 245,7 |
| 42×42 | 4 | 4,56 | 219,3 |
| 42×42 | 5 | 5,47 | 182,8 |
| 42×42 | 6 | 6,3 | 158,7 |
| 45×45 | 3 | 3,83 | 261,1 |
| 45×45 | 3,5 | 4,4 | 227,3 |
| 45×45 | 4 | 4,93 | 202,8 |
| 45×45 | 5 | 5,94 | 168,4 |
| 45×45 | 6 | 6,86 | 145,8 |
| 45×45 | 7 | 7,69 | 130 |
| 45×45 | 8 | 8,43 | 118,6 |
| 50×50 | 3 | 4,31 | 232 |
| 50×50 | 3,5 | 4,94 | 202,4 |
| 50×50 | 4 | 5,56 | 179,9 |
| 50×50 | 5 | 6,73 | 148,6 |
| 50×50 | 6 | 7,8 | 128,2 |
| 50×50 | 7 | 8,79 | 113,8 |
| 50×50 | 8 | 9,69 | 103,2 |
| 60×60 | 3,5 | 6,04 | 165,6 |
| 60×60 | 4 | 6,82 | 146,6 |
| 60×60 | 5 | 8,3 | 120,5 |
| 60×60 | 6 | 9,69 | 103,2 |
| 60×60 | 7 | 11 | 90,9 |
| 60×60 | 8 | 12,2 | 82 |
| 65×65 | 6 | 10,63 | 94,1 |
| 70×70 | 4 | 8,07 | 123,9 |
| 70×70 | 5 | 9,87 | 101,3 |
| 70×70 | 6 | 11,57 | 86,4 |
| 70×70 | 7 | 13,19 | 75,8 |
| 70×70 | 8 | 14,71 | 68 |
| 80×80 | 4 | 9,33 | 107,2 |
| 80×80 | 5 | 11,44 | 87,4 |
| 80×80 | 6 | 13,46 | 74,3 |
| 80×80 | 7 | 15,38 | 65 |
| 80×80 | 8 | 17,22 | 58,1 |
| 90×90 | 5 | 13 | 76,9 |
| 90×90 | 6 | 15,34 | 65,2 |
| 90×90 | 7 | 17,58 | 56,9 |
| 90×90 | 8 | 19,73 | 50,7 |
| 100×100 | 6 | 17,22 | 58,1 |
| 100×100 | 7 | 19,78 | 50,6 |
| 100×100 | 8 | 22,25 | 44,9 |
| 100×100 | 9 | 24,62 | 40,6 |
| 110×110 | 6 | 19,11 | 52,3 |
| 110×110 | 7 | 21,98 | 45,5 |
| 110×110 | 8 | 24,76 | 40,4 |
| 110×110 | 9 | 27,45 | 36,4 |
| 120×120 | 6 | 20,99 | 47,6 |
| 120×120 | 7 | 24,18 | 41,4 |
| 120×120 | 8 | 27,27 | 36,7 |
| 120×120 | 9 | 30,28 | 33 |
| 140×140 | 6 | 24,76 | 40,4 |
| 140×140 | 7 | 28,57 | 35 |
| 140×140 | 8 | 32,29 | 31 |
| 140×140 | 9 | 35,93 | 27,8 |
| 150×150 | 7 | 30,77 | 32,5 |
| 150×150 | 8 | 34,81 | 28,7 |
| 150×150 | 9 | 38,75 | 25,8 |
| 150×150 | 10 | 42,61 | 23,5 |
| 180×180 | 8 | 42,34 | 23,6 |
| 180×180 | 9 | 47,23 | 21,2 |
| 180×180 | 10 | 52,03 | 19,2 |
| 180×180 | 12 | 61,36 | 16,3 |
| 180×180 | 14 | 70,33 | 14,2 |
Формула для расчета массы метра квадратной трубы
m = ρ/7850 × 0.
0157 × t × (2 × a – 2.86 × t), где
0157 × t × (2 × a – 2.86 × t), гдеρ – плотность металла, кг/м3
a – сторона трубы (мм)
t – толщина стенки (мм)
Оцените нашу статью
[Всего голосов: 1 Рейтинг статьи: 5]
Линейные измерения – Математика для торговли: Том 2
Понимание и работа с единицами измерения
Нажмите кнопку воспроизведения в следующем аудиоплеере, чтобы слушать, пока вы читаете этот раздел.
Линейное измерение может быть определено как мера длины. Длина
стола, длина куска трубы и длина футбольного поля — все это примеры линейных измерений. Мы могли бы также назвать это расстоянием.
Линейные измерения представляют одно измерение. Это означает, что измеряется только одна линия или одна плоскость. По сути, это означает, что это линия определенного типа, прямая, изогнутая или куда бы вы ни хотели, чтобы линия шла. Это может быть дорога в Саскачеване, длинная и прямая, или дорога внутри Британской Колумбии, которая может быть узкой и ветреной.
Не имеет значения, находится ли предмет или объект, который вы измеряете, прямо или нет. То, что вы измеряете, будет иметь только длину.
Измерение длины может быть выполнено с использованием различных типов единиц измерения. Вы слышали о миле, футе, ярде и дюйме, но слышали ли вы когда-нибудь о фарлонге, линке, полюсе или лиге? Это все примеры имперских линейных измерений.
Как насчет метрической системы. У нас есть метр, сантиметр и миллиметр. Все это было бы нам знакомо. А как насчет микрометра, нанометра, пентаметра, тетраметра и гекзаметра?
Как мы будем работать в этом разделе, так это сначала определить метрические длины измерения и работать с ними, а затем мы перейдем к имперским единицам измерения и работе с ними. После того, как все это будет сделано и решено, мы перейдем к работе между метрической и имперской системами.
Если бы я спросил вас, что является примером метрической единицы измерения, что бы вы ответили? Я думаю, что большинство из нас могли бы сказать метр, сантиметр или даже километр.
Одна из интересных особенностей метрической системы линейных измерений заключается в том, что все они основаны на измерениях 10 и довольно часто упоминаются как десятичная система.
Например, в сантиметре 10 миллиметров, в дециметре 10 сантиметров, а в метре 10 дециметров. См. образец. Как только вы получите этот шаблон, работа с метрикой станет довольно простой.
Еще одним интересным аспектом метрической системы является то, что все происходит от базовой единицы. Все остальные единицы идут оттуда, используя числа, кратные 10. Взгляните на таблицу ниже, чтобы увидеть, как это работает.
| Блок | Множитель |
|---|---|
| км | 1000 |
| гектометр | 100 |
| декаметр | 10 |
| счетчик (базовый блок) | 1 |
| дециметр | 0,1 |
| сантиметр | 0,01 |
| мм | 0,001 |
Идея приведенной выше таблицы заключается в том, что метр — это место, где все остальные числа работают обратно.
Так, например, чтобы перейти от километров обратно к метрам, мы должны умножить на 1000. Если бы у нас была длина в один километр, это означало бы, что у нас была бы длина в 1000 метров.
Если бы мы перешли от сантиметров к метрам, таблица показала бы нам, что сантиметр равен 1/100 метра. Поэтому, если бы у нас был один сантиметр, мы бы умножили его на 0,01, чтобы получить метры.
В этот момент вам может быть интересно, неужели это все, что есть в метрической системе линейных измерений. На самом деле существует ряд других измерений, основанных на метре. Взгляните на сумасшедшую таблицу ниже, чтобы увидеть, как далеко расходится измерение от метра.
| Общий метрический префикс | Множитель |
|---|---|
| йотта | 1 000 000 000 000 000 000 000 000 |
| зетта | 1 000 000 000 000 000 000 000 |
| экса | 1 000 000 000 000 000 000 |
| пета | 1 000 000 000 000 000 |
| тера | 1 000 000 000 000 |
| гига | 1 000 000 000 |
| мега | 1 000 000 |
| кг | 1000 |
| гекто | 100 |
| дека | 10 |
| счетчик (базовый блок) | 1 |
| деци | 0,1 |
| центи | 0,01 |
| милли | 0,001 |
| микро | 0,000001 |
| нано | 0,000000001 |
| пико | 0,000000000001 |
| фемто | 0,000000000000001 |
| атто | 0,000000000000000001 |
| зепто | 0,0000000000000000000001 |
| Окто | 0,000000000000000000000001 |
Знакомы ли вы с какими-либо из этих префиксов? Вы можете увидеть некоторые из более крупных, таких как мега, гига и терра, используемые в компьютерах при работе с памятью и скоростью.
Не волнуйтесь, поскольку мы, как правило, никогда не будем работать со многими из них в торговле, и мы будем придерживаться тех немногих, которые окружают счетчик.
Сейчас мы хотим работать в метрической линейной системе. Мы хотим иметь возможность переходить от одной единицы измерения к другой, и для этого мы будем использовать две приведенные выше таблицы.
Сколько сантиметров в 2,3 метра?
[латекс]\Large2.3 \text{метры}= \text{X сантиметров}[/латекс]
Подобно тому, как мы делали это в первых четырех главах, мы будем делать это поэтапно.
Шаг 1: Найдите множитель
Мы видим, что при переходе от сантиметров к метрам множитель равен 0,01. Это говорит о том, что сантиметр равен 1/100 метра или что в метре 100 сантиметров.
Здесь важно отметить, что сантиметр меньше метра, и в этом случае мы ожидаем, что наш ответ уменьшится.
Шаг 2: Постройте отношение
[латекс]\Большой \dfrac{1\text{ м}}{2,3\text{ м}} = \dfrac{100\text{ см}}{\text{ X см}}[/latex]
Это соотношение утверждает, что если 1 метр равен 100 сантиметрам, то 2,3 метра равны X сантиметрам.
Шаг 3: Перекрестное умножение.
[латекс]\Large \begin{array}{c} \dfrac{1\text{м}}{2,3\текст{м}} = \dfrac{100\text{см}}{\text{X см }} \\ 1 \times \text{X} = 2,3 \times 100 \\ \text{X}=230 \\ \text{Ответ}= 230\text{ сантиметров}\end{массив}[/latex]
Попробуем другой пример.
Сколько километров в 1057 метрах?
Шаг 1: Найдите множитель.
[латекс]\большой\текст{множитель} = 1000[/латекс]
[латекс]\большой1 \текст{километр} = 1000 \текст{метры}[/латекс]
Шаг 2: Построить отношение
[латекс]\Большой\dfrac{1 \text{км}}{\text{X км}} = \dfrac{1000 \text{м}}{1057 \text{м}}[/латекс]
Шаг 3: Перекрестное умножение.
[латекс]\Large\begin{array}{c} \dfrac{1 \text{км}}{\text{X км}}= \dfrac{1000 \text{м}}{1057 \text{м} } \\ 1\times 1057 = \text{X} \times 1000 \\ \text{X} = \dfrac{1057}{1000}=1,057 \\ \text{Ответ} = 1,057 \text{метры}\end {массив}[/латекс]
Попробуйте сами ответить на пару практических вопросов и посмотрите видеоответы, чтобы узнать, как вы справились.
Обязательно выполните шаги, описанные выше, и подумайте, должен ли ваш ответ быть больше или меньше.
Барри владеет компанией по производству листового металла (Metal Sheet Incorporated), и он делает воздуховоды для системы отопления в строящейся новой студии видеопроизводства. Воздуховоды 0,79м в ширину и 0,45 м в глубину. Какая глубина воздуховодов в сантиметрах?
Имперская система не так проста, как метрическая. Если бы мы попытались следовать тому же принципу, что и в метрической системе, мы бы подумали, что 1 фут равен 10 дюймам, но, к сожалению, это не так. Один фут равен 12 дюймам, а одна миля равна 5280 футам.
Есть предположения, почему в миле 5280 футов? Оказывается, это происходит от древнего линейного измерения, использовавшегося римлянами. Тогда одна миля равнялась 5000 римским футам. Затем британцы начали использовать его и решили связать его с тем, что работало на них, а именно с сельским хозяйством. В сельском хозяйстве они любили использовать фарлонги в качестве меры длины.
Фарлонг составлял 660 футов, а в одной миле было решено иметь 8 фарлонгов. 8 умножить на 660 равно 5280 футов.
Стопа также имеет историческое значение, и если вы догадались, что она была основана на средней человеческой стопе, вы были бы правы. Некоторые считают, что это на самом деле основано на средней длине обуви человека. В любом случае, называть это ногой имеет смысл.
Взгляните на таблицу ниже, чтобы получить представление о том, как работает имперская система линейных измерений.
| Наименование блока | Эквивалентные значения |
|---|---|
| Дюйм | 0,083 фута. 0,028 ярда |
| фут | 12 дюймов, 0,333 ярда |
| двор | 3 фута, 36 дюймов |
| морская сажень | 6 футов, 72 дюйма |
| стержень | 5,50 ярдов, 16,5 футов |
| фарлонг | 660 футов, 220 ярдов, 1/8 мили |
| миля | 5280 футов, 1760 ярдов, 320 удилищ |
| Морская миля | 6 076 футов, 1,151 мили |
На первый взгляд это может показаться немного более запутанным, чем метрическая система, и на самом деле, если бы мы имели дело со всеми этими различными измерениями длины, это могло бы быть так.
К счастью для нас, по большей части мы будем иметь дело только с тремя измерениями. Эти три включают дюймы, футы и мили. Время от времени мы могли видеть, как дворы приходят играть. Например, поле для американского футбола имеет длину 100 ярдов и 120 ярдов, если включить две конечные зоны.
Еще раз наша задача – работать в рамках имперской системы и уметь работать между значениями. Прежде чем мы начнем, я хочу напомнить вам подумать об ответе, который вы пытаетесь найти. Я хочу, чтобы вы подумали о том, будет ли ответ больше или меньше.
Примером может быть преобразование футов в дюймы. Как вы думаете, если бы нам пришлось отрезать кусок трубы длиной 2 фута, длина его оказалась бы больше 2 дюймов или меньше 2 дюймов? Я думаю, мы все согласны с тем, что это было бы больше 2 дюймов, и на самом деле это так. Получается 24 дюйма. Возможно, вы не сможете получить 24 дюйма сразу, но вы, вероятно, сможете понять, что 2 фута, указанные в дюймах, должны работать как большее число.
Давайте использовать это как наш первый пример:
Сколько дюймов в 2 футах?
Шаг 1: Найдите число, обозначающее соотношение между дюймами и футами.
В этом случае:
[латекс]\Large1\text{ фут}= 12 \text{ дюймов}[/latex]
Шаг 2: Постройте соотношение
[латекс]\Large\dfrac{1 \text{ футов}}{2 \text{ футов}}=\dfrac{12 \text{ дюймов}}{\text{X дюймов}}[/latex]
Шаг 3: Перекрестное умножение
[латекс ]\Large\begin{array}{c}\dfrac{1 \text{ футов}}{2 \text{ футов}}=\dfrac{12 \text{ дюймов}}{\text{X дюймов}} \\ 1\times \text{X} = 2 \times 12 \\ \text{X} = 24 \\ \text{Ответ} = 24 \text{ дюймов}\end{массив}[/latex]
Хотя вы могли бы сделать это в уме, важно выполнить необходимые шаги и подумать о ответе, который вы ожидаете получить. Это поможет, когда числа более сложные и их не так просто вычислить.
Сколько ярдов в 247 дюймах?
Шаг 1: Найдите число между ярдами и дюймами.
Обратите внимание, что на самом деле здесь есть 2 числа на выбор. Мы могли бы использовать:
[латекс]\большой 1 \текст{ярд} = 36 \текст{дюймы}[/латекс]
[латекс]\Большой \текст{ИЛИ}[/латекс]
[латекс]\Большой 1 \текст{дюйм}= 0,028 \текст{ярд}[/латекс]
В этом вопросе мы исходим из дюймов в ярды, поэтому работать с числом 0,028 нам будет проще.
Шаг 2: Постройте отношение
[латекс]\Large\dfrac{ 1 \text{ дюйм}}{247 \text{ дюйм}}= \dfrac{0,028 \text{ ярдов}}{\text{ X ярдов}}[/latex]
Шаг 3: Перекрестное умножение
[латекс]\Large\begin{array}{c}\dfrac{ 1 \text{ дюйм}}{247 \text{ дюйм}} = \dfrac{0,028 \text{ ярдов}}{\text{X ярдов}} \\ 1 \times \text{X} = 247 \times 0,028 \\ \text{X}= 6,916 \\ \text{Ответ} = 6,916 \text{ ярдов}\end{массив}[/latex]
Попробуйте сами задать пробный вопрос и посмотрите видеоответы, чтобы узнать, как вы справились. Обязательно выполните шаги, описанные выше, и подумайте, должен ли ваш ответ быть больше или меньше.
Длина воздуховода, который Барри, наш продавец листового металла, должен изготовить для студии видеопроизводства, составляет 193 ярда. Сколько футов воздуховода нужно заказать Барри, чтобы завершить работу?
Что происходит, когда нам приходится работать между метрической и имперской системами? Это действительно работает точно так же, но нам нужно выучить несколько новых чисел.
В таблице ниже приведен список чисел, которые можно использовать для облегчения перевода линейных измерений между метрическими и британскими единицами измерения. Здесь вы заметите, что эквивалентные числа представляют единицы, которые имеют одинаковую длину (или используются сходным образом) в разных ситуациях.
Примером могут быть километры и мили. Оба используются для обозначения таких вещей, как расстояние, пройденное в машине, поезде, автобусе или самолете. Мы не идем и не измеряем эти большие расстояния, используя сантиметры или их имперский эквивалент, который составляет дюймы.
Это просто было бы не удобно.
Точно так же, если бы нам нужно было измерить длину дома, мы, скорее всего, использовали бы метры или их имперский эквивалент, который является футами.
Также обратите внимание, что мы не переводим каждое метрическое и имперское число в их эквиваленты. Поскольку мы не будем работать с большинством единиц измерения, нет необходимости находить все эти числа. Сказав это, если вы хотите просмотреть и найти числа самостоятельно в Интернете или, возможно, даже попытаться вычислить их, используя числа в таблицах выше и ниже, то это, скорее всего, поможет вам понять, как работают линейные единицы измерения. друг с другом.
| Метрическая система | Имперский Эквивалент |
|---|---|
| 1 метр | 3,28 фута |
| 1 км | 0,62 мили |
| 1 сантиметр | 0,393 дюйма |
| 1 миллиметр | 0,0394 дюйма |
Было бы также полезно посмотреть на эти числа в обратном порядке.
| Имперский | Метрический эквивалент |
|---|---|
| 1 фут | 0,305 метра |
| 1 миля | 1,61 км |
| 1 дюйм | 2,54 см |
| 1 дюйм | 25,4 мм |
Несмотря на то, что у нас есть число для перевода миль в километры, а затем число для перехода из километров в мили, на самом деле нам не нужно запоминать оба значения.
Какое из двух чисел вам легче всего запомнить, так это все, что вам нужно запомнить. Как только вы узнаете одно, вы можете получить другое.
Вот как это работает.
В этом упражнении мы будем использовать мили и километры. Мы знаем, что 1 миля равна 1,61 километра.
[латекс]\Большой 1 \текст{миля} = 1,61 \текст{километры}[/латекс]
Теперь нам нужно выяснить обратное. В этом случае сколько миль в одном километре. Еще раз спросите себя, считаете ли вы, что ответ должен быть больше или меньше 1,
.
Итак, чтобы выяснить наш ответ, нам нужно сделать следующее.
[латекс]\Large\begin{array}{c} \# \text{километры} = \# \text{мили} \times 1,61 \\ \downarrow \\ \# \text{мили} = \dfrac{\ # \text{километры}}{1,61} \\ \downarrow \\ 1 \text{миля} = 0,62 \text{километры}\end{массив}[/latex]
Таким образом, мы получаем, что 1 километр равен 0,62 мили.
Мы только что взяли одну константу, чтобы получить другую константу. Вы можете сделать это с любым из чисел, используемых для перевода туда и обратно между метрическими и имперскими.
Идем дальше. Теперь мы начнем работать между имперской и метрической системами, и самый простой способ сделать это — ответить на несколько примеров вопросов.
Сколько метров в 42 футах?
Шаг 1: Найдите номер, с которым вы можете работать.
Мы знаем, что:
[латекс]\Large\begin{array}{c} 1\text{ метр} = 3,28 \text{ фут} \\ 1 \text{ фут} = 0,305 \text{ метр}\ end{array}[/latex]
Поскольку мы переходим от футов к метрам, мы будем использовать 1 фут = 0,305 метра.
Шаг 2: Постройте соотношение
[латекс]\Большой \dfrac{1 \text{ фут}}{42 \text{ футов}}= \dfrac{0,305 \text{ метров}}{\text{ Х метров}}[/латекс]
Шаг 3: Перекрестное умножение
[латекс]\Large\begin{array}{c} \dfrac{1 \text{ фут}}{42 \text{ фут}}= \dfrac{0,305 \text{ метров}}{\text{X метров}} \\ 1\times \text{X} = 42 \times 0,305 \\ \text{X} = 12,81 \\ \text{Ответ} = 12,81 \text{метров}\ конец{массив}[/латекс]
Сколько дюймов в 100 сантиметрах?
Шаг 1: Найдите номер, с которым вы можете работать.
Мы знаем, что:
[латекс]\Large\begin{array}{c} 1 \text{сантиметр}= 0,393 \text{ дюйма} \\ 1 \text{ дюйм} = 2,54 \text{ сантиметра}\end{массив}[/latex]
Поскольку мы переходим от сантиметров к дюймам, мы будем использовать 1 сантиметр = 0,393 дюйма.
Шаг 2: Постройте отношение
[латекс]\Большой \dfrac{1 \text{ см}}{100 \text{ см}}=\dfrac{0,393 \text{ in}}{\text{ X in}}[/latex]
Шаг 3: Перекрестное умножение
[латекс]\Large\begin{array}{c} \dfrac{1 \text{см}}{100 \text{см}} =\dfrac{0,393 \text{ дюйм}}{\text{X дюйм}} \\ 1 \times \text{X} = 100 \times 0,393 \\ \text{X} = 39,3 \\ \text{Ответ} = 39,3 \text{см}\end{массив}[/latex]
Попробуйте сами ответить на пару практических вопросов.
Обязательно выполните шаги, аналогичные приведенным выше примерам вопросов, а также обязательно проверьте видеоответы, чтобы убедиться, что вы правы.
Якоб — плотник, изготавливающий формы для бетонных колонн. Размеры колонны указаны в миллиметрах, но Якоб предпочитает работать в дюймах, поэтому он решает перевести миллиметры в дюймы. Колонны имеют прямоугольную форму и имеют размеры 400 мм на 250 мм. Каковы размеры колонны в дюймах?
Элиас — краснодеревщик из Швеции, который сейчас учится в Канаде. Его попросили заказать материал для работы, и он составляет 427 футов дерева размером 1 x 4 дюйма. Поскольку он привык работать в метрической системе, он хочет изменить ее на метры. Сколько метров 1″ x 4″ ему понадобится?
3.2 Объем воды в шланге
Объем шланга позволяет оценить, сколько воды может быть доставлено к огню, и имеет важное значение при тушении пожара. Диаметр шланга обычно указывается в дюймах, а длина в футах. Объем шланга можно рассчитать, используя уравнение для объема цилиндра в разделе 3.
1.
Пример 1 — Шланг длиной 100 футов и диаметром 1 дюйм наполнен водой. Сколько галлонов воды в шланге такой длины?
Шаг 1. Используйте уравнение для определения объема цилиндра. V = π × r 2 × h
Шаг 2. Определите радиус и высоту.
π = 3,14, r = 1/2 × d = 1/2 × 1 дюйм = 0,5 дюйма, h = 100 футов
Шаг 3. Преобразуйте все измерения в одни и те же единицы. Преобразуйте 100-футовую длину шланга в дюймы.
Шаг 4. Сформулируйте проблему и решите ее. V = 3,14 × 0,5 дюйма × 0,5 дюйма × 1200 дюймов = 942 дюйма 3
Шаг 5. Настройте таблицу отмены, чтобы все единицы измерения исключались, кроме нужной единицы, в данном случае галлонов.
Вместимость 100-футового шланга диаметром 1 дюйм составляет 4 галлона.
ОЦЕНКА В ПОЛЕ
Округление упрощает использование чисел. Иногда оценки или приближения полезны, например, для решения задач в полевых условиях, особенно без калькулятора.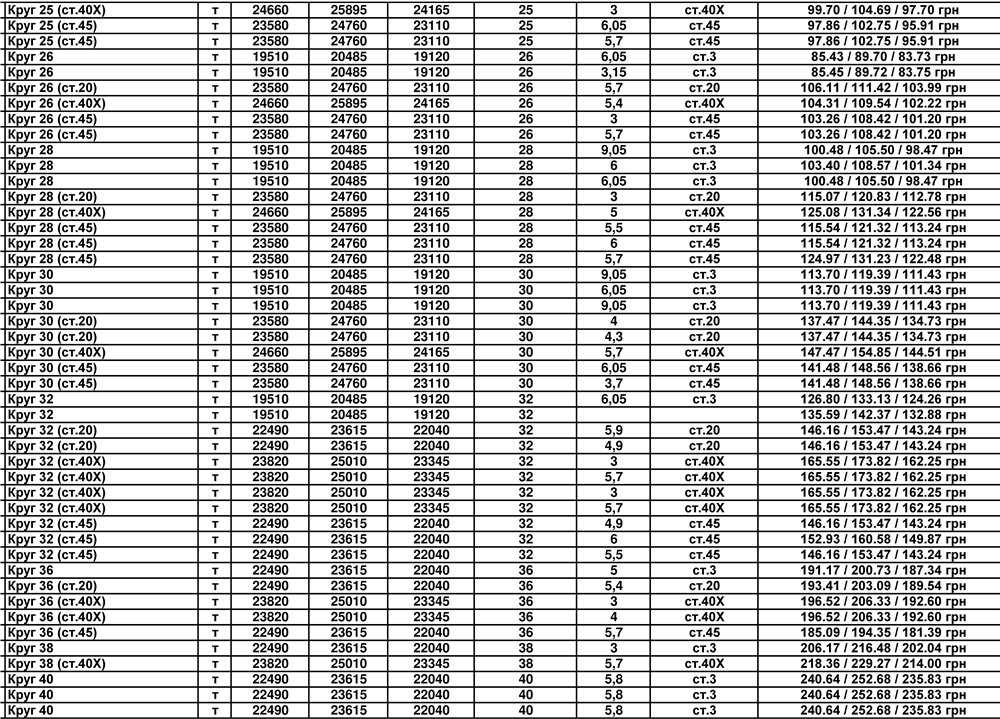
Например, из Таблицы 3.1 мы видим, что 100 футов шланга диаметром 1-1/2 дюйма вмещают 9.2 галлона жидкости. В полевых условиях значение преобразования можно округлить до 9 галлонов при выполнении приблизительных оценок/расчетов. Эти округленные значения легче запомнить.
Пример 2 – Шерман горит. У его команды есть магистральная линия из 6 шлангов длиной 100 футов и 1 и 1/2 дюйма. Ему нужно оценить объем воды в этой магистрали. Что такое хорошая оценка?
Шаг 1. Найдите подходящее преобразование/оценку в Таблице 3.1. Зафиксируйте эти округленные значения в памяти.
Точные таблицы показывают, что один 100-футовый шланг диаметром 1-1/2 дюйма вмещает 9,2 галлона воды (таблица 3.1). Используйте округленное значение 9 галлонов на 100 футов длины 1-1/2-дюймового шланга.
Шаг 2. Настройте стол. Это может или не должно быть сделано на бумаге. Типичные грубые оценки включают только один шаг умножения или деления, и обычно эту математику можно проделать в уме.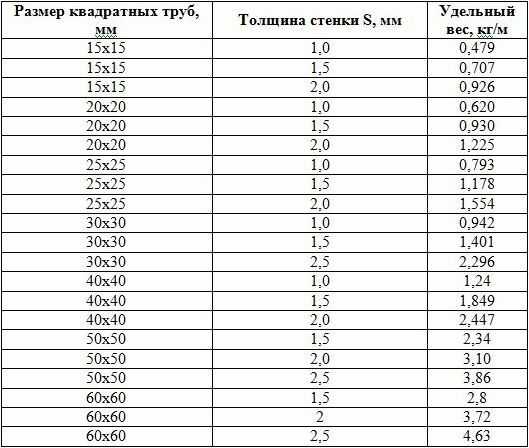
Компания Sherman использовала 54 галлона воды для наполнения шланга.
Шерман теперь знает, что у него около 54 галлонов воды в шланге. Точное значение было бы 6 × 9,2 = 55,2 галлона.
Округленные числа использовать проще, потому что умножать целые числа проще, чем умножать десятичные. В примере 6 число было округлено в меньшую сторону от 9,2 до 9,0. Если бы его округляли от 9,2 до 10,0, решение было бы 6 × 10 = 60 галлонов. Выполняя расчеты с использованием целых чисел, как больших, так и меньших, чем фактическое значение, создается запас. Эта маржа допускает верхний и нижний предел. Поэтому можно с уверенностью сказать, что фактическое значение составляет от 54 галлонов (6 × 9) и 60 галлонов (6 × 10).
ОПРЕДЕЛЕНИЕ ВЕСА И ОБЪЕМА ВОДЫ
В таблице 3.1 показаны объемы воды в шлангах определенной длины, а также вес 1 галлона воды. Вес 1 галлона воды составляет 8,3 фунта (1 галлон = 8,3 фунта). С помощью этого преобразования можно рассчитать вес воды в шланге определенной длины или объеме воды, умножив его на 8 фунтов на галлон (значение округлено).
Пример 3 – Бак двигателя модели 62 заполнен 500 галлонами воды. Какой вес добавляет вода к весу двигателя?
Шаг 1. Найдите соответствующую оценку в таблице 3.1. 1 галлон = 8 фунтов (фунтов)
Шаг 2. Настройте таблицу аннулирования, чтобы все единицы, кроме нужной единицы, аннулировались.
Вода в баке увеличивает вес двигателя на 4000 фунтов.
Пример 4. Два 100-футовых хлопчатобумажно-синтетических шланга диаметром 1 и 1/2 дюйма весят в сухом состоянии около 54 фунтов.
Сколько будет весить тот же шланг при полной зарядке?
Шаг 1. Найдите соответствующую оценку в таблице 3.1. Объем одного шланга с внутренним диаметром 1 и 1/2 дюйма и длиной 100 футов = 9 галлонов. На две длины шланга приходится два раза по 9 галлонов.
Шаг 2. Настройте таблицу аннулирования, чтобы аннулировались все единицы, кроме нужной единицы – фунтов.
Шаг 3. Добавьте сухой вес шланга к весу воды.
54 фунта + 144 фунта = 198 фунтов
Два полностью заряженных шланга с внутренним диаметром 1 и 1/2 дюйма и длиной 100 футов весят 198 фунтов.
Пример 5. Компания-производитель двигателей перекачивает прогрессивную укладку шланга с боковыми отводами 1 дюйм через каждые 100 футов. На высоте 800 футов от двигателя магистральный трубопровод обрывается. Пожарные меняют его, но забывают перекрыть запорный тройник над сломанным шлангом. В результате они случайно осушили десять 100-футовых 1-1/2-дюймовых шлангов и десять 100-футовых 1-дюймовых шлангов. Сколько воды выше разрыва было потеряно из-за этой ошибки?
Шаг 1. Найдите в Таблице 3.1 соответствующую оценку объема воды в шланге длиной 1 дюйм и 1-1/2 дюйма.
Каждый шланг с внутренним диаметром 1-1/2 дюйма и длиной 100 футов вмещает 9 галлонов.
Каждый шланг с внутренним диаметром 1 дюйм и длиной 100 футов вмещает 4 галлона.
Шаг 2. Настройте таблицу аннулирования, чтобы все единицы измерения аннулировались, кроме требуемой единицы измерения, галлонов, для каждой длины шланга
.