Таблица модуль упругости материалов таблица: Модуль упругости стали: таблица, характеристики
alexxlab | 19.06.1987 | 0 | Разное
Модуль нормальной упругости (Модуль Юнга) для различных марок сталей и сплавов
Модуль нормальной упругости (Модуль Юнга) — физическая величина (E) характеризующая сопротивление материала растяжению или сжатию при упругой деформации, а также при воздействии силы вдоль оси, свойство объекта деформироваться вдоль этой оси. Модуль упругости определяется как отношение напряжения к деформации сжатия (удлинения). Параметр характеризует степень жесткости конкретного материала.
Обычно модуль Юнга называют просто модулем упругости. Назван в честь английского физика XIX века Томаса Юнга.
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.
Коэффициент E в этой формуле называется модулем Юнга.
Поиск и выбор модуля нормальной упругости для различных марок сталей и сплавов по таблице, при указанных температурах °C. В таблице использованы справочники [1, 2].
Для выбора марок стали следует пользоваться системой поиска по таблице.
| Марка стали, сплава | 20°C | 100°C | 200°C | 300°C | 400°C | 500°C | 600°C | 700°C | 800°C | 900°C |
|---|---|---|---|---|---|---|---|---|---|---|
| Ст2пс | 198 | 183 | 175 | 167 | 158 | — | — | — | — | — |
| Ст2сп | 198 | 183 | 175 | 167 | 158 | — | — | — | — | — |
| Ст3кп | 213 | 208 | 202 | 195 | 187 | 176 | 167 | 153 | — | — |
| Ст3пс | 213 | 208 | 202 | 195 | 187 | 176 | 167 | 153 | — | — |
| Ст3сп | 194 | 192 | 187 | 183 | 178 | 167 | 159 | 146 | 120 | 99 |
| Ст4пс | 196 | 183 | 174 | 167 | 158 | — | — | — | — | — |
| Ст5пс | 198 | 196 | 186 | 175 | 167 | — | — | — | — | — |
| Ст5сп | 198 | 196 | 191 | 185 | 164 | — | — | — | — | — |
| Ст6пс | 197 | 197 | 186 | 175 | 168 | — | — | — | — | — |
| Ст6сп | 197 | 197 | 186 | 175 | 168 | — | — | — | — | — |
| 08 | 203 | 207 | 182 | 153 | 141 | — | — | — | — | — |
| 08кп | 203 | 207 | 182 | 153 | 141 | — | — | — | — | — |
| 10 | 206 | 190 | 195 | 186 | 178 | 169 | 157 | — | — | — |
| 10кп | 186 | — | — | — | — | — | — | — | — | — |
| 15 | 198 | 183 | — | 166 | 154 | — | — | — | — | — |
| 15кп | 201 | 192 | 185 | 172 | 156 | — | — | — | — | — |
| 20 [3] | 210 | 203 | 199 | 190 | 182 | 172 | 160 | — | — | — |
| 20кп | 212 | 208 | 203 | 197 | 189 | 177 | 163 | 140 | — | — |
| 25 | 198 | 196 | 191 | 185 | 164 | — | — | — | — | — |
| 30 | 200 | 196 | 191 | 185 | — | — | 163 | — | — | — |
| 35 | 206 | 197 | 183 | 176 | 167 | — | — | — | — | — |
| 40 | 209 | 206 | — | 196 | — | — | — | — | — | — |
| 45 | 200 | — | 191 | 190 | 172 | — | — | — | — | |
| 50 | 216 | 211 | — | 216 | — | 177 | — | — | — | — |
| 55 | 210 | — | — | — | — | — | — | — | — | — |
| 60 | 204 | — | 208 | 189 | 175 | — | — | — | — | — |
| 75 | 191 | — | — | — | — | — | — | — | — | — |
| 85 | 191 | — | — | — | — | — | — | — | — | — |
| 20К | 200 | 196 | 191 | 184 | 177 | — | — | — | — | — |
| 22К | 207 | 205 | 201 | 194 | 188 | — | — | — | — | — |
| А12 | 198 | 183 | — | 167 | 154 | — | — | — | — | — |
| 15Г | — | 186 | 183 | — | — | — | — | — | — | — |
| 20Г | 204 | — | — | — | — | — | — | — | — | — |
| 30Г | 204 | — | — | — | — | — | — | — | — | — |
| 40Г | 200 | — | — | — | — | — | — | — | — | — |
| 50Г | 216 | 213 | 208 | 199 | 185 | 174 | 160 | 142 | 130 | — |
| 35Г2 | 204 | — | — | — | — | — | — | — | — | — |
| 40Г2 | 212 | — | — | — | — | — | — | — | — | — |
| 45Г2 | 204 | — | — | — | — | — | — | — | — | — |
| 09Г2С | — | — | — | — | 179 | 169 | 145 | 91 | 80 | 59 |
| 20Х | 216 | 213 | 198 | 193 | 181 | 171 | 165 | 143 | 133 | — |
| 30Х | 208 | 211 | — | 197 | — | 175 | — | — | — | — |
| 35Х | 214 | — | — | — | — | — | — | — | — | — |
| 38ХА | 196 | — | — | — | — | — | — | — | — | — |
| 40Х | 214 | 211 | — | 197 | — | — | — | — | — | — |
| 45Х | 206 | — | — | — | — | — | — | — | — | — |
| 50Х | — | — | — | 206 | — | 207 | — | — | — | — |
| 10ГН2МФА, 10ГН2МФА-ВД, 10ГН2МФА-Ш | 210 | 205 | 198 | 191 | 182 | — | — | — | — | — |
| 12МХ | 212 | 106 | 201 | 195 | 189 | 179 | 170 | 160 | — | — |
| 15ХМ | 204 | — | — | — | 169 | — | — | — | — | — |
| 30ХМ, 30ХМА | 209 | — | 204 | 197 | 188 | — | — | — | — | — |
| 35ХМ | 209 | — | 204 | 197 | 188 | — | — | — | — | — |
| 33ХС | 214 | 206 | 196 | 186 | 176 | 168 | 157 | 137 | 127 | — |
| 38ХС | 219 | — | — | — | — | — | — | — | — | |
| 40ХС | 219 | — | — | — | — | — | — | — | — | — |
| 15ХФ | 206 | — | — | — | — | — | — | — | — | — |
| 14ХГС | 200 | — | — | — | — | — | — | — | — | — |
| 25ХГСА | 213 | 206 | 194 | 187 | 175 | 168 | 163 | 143 | 130 | — |
| 30ХГСА | 194 | — | 174 | 169 | 156 | — | — | — | — | — |
| 18ХГТ | 211 | 205 | 197 | 191 | 176 | 168 | 155 | 136 | 129 | — |
| 30ХГТ | 212 | 202 | 195 | 189 | 174 | 169 | 157 | 138 | 132 | — |
| 12Х1МФ (ЭИ 575) | 209 | 206 | 202 | 197 | 189 | 179 | 166 | — | — | — |
| 13Х1МФ (14Х1ГМФ, ЦТ 1) | 214 | 211 | 205 | 198 | 185 | 179 | 170 | 155 | — | — |
| 15Х1М1Ф | 210 | 204 | 197 | 190 | 182 | 174 | 166 | 157 | — | — |
| 25Х1МФ (ЭИ 10) | 213 | 207 | 202 | 194 | 187 | 177 | 163 | — | — | — |
| 25Х1М1Ф (Р2, Р2МА) | 216 | 214 | 210 | 205 | 197 | 186 | 171 | — | — | — |
| 20Х1М1Ф1ТР (ЭП 182) | 211 | 208 | 204 | 198 | 190 | 179 | 167 | 150 | — | — |
| 20Х1М1Ф1БР (ЭП 44) | 213 | 207 | 201 | 192 | 177 | 164 | 149 | — | — | |
| 40ХН | 200 | — | — | — | — | — | — | — | — | — |
| 30ХН2МА | 204 | 201 | 194 | 186 | 182 | 171 | 159 | — | — | — |
| 12ХН3А | 200 | — | — | — | — | — | — | — | — | — |
| 20ХН3А | 212 | 204 | 194 | 188 | 169 | 169 | 153 | 138 | 132 | — |
| 30ХН3А | 215 | 207 | 195 | 187 | 175 | 171 | — | — | — | — |
| 25Х2М1Ф (ЭИ 723) | 219 | 214 | 209 | 203 | 196 | 188 | 179 | 172 | — | — |
| 10Х2МФБ (ЭИ 531), 12Х2МФБ (ЭИ 531) | 220 | — | — | — | — | 181 | 173 | — | — | — |
| 38Х2МЮА (38ХМЮА) | 209 | 202 | 194 | 190 | 181 | 174 | 162 | 147 | 137 | — |
| 15Х2НМФА, 15Х2НМФА-А, 15Х2НМФА класс 1 | 214 | 210 | 205 | 198 | 190 | — | — | — | — | — |
| 20Х3МВФ (ЭИ 415, ЭИ 579) | 201 | — | 200 | 179 | 171 | 153 | 119 | 118 | — | — |
| 15Х5М (12Х5МА, Х5М) | 211 | — | — | — | 178 | 145 | 102 | — | — | — |
| 65Г | 207 | — | — | — | — | — | — | — | — | — |
| 40ХФА | 203 | — | — | — | — | — | — | — | — | — |
| 50ХФА | 196 | — | — | — | — | — | — | — | — | — |
| 55С2 | 196 | — | — | — | — | — | — | — | — | — |
| 60С2, 60С2А | 245 | — | — | — | — | — | — | — | — | — |
| ШХ15 | 201 | — | — | — | — | — | — | — | — | — |
| 95Х18 (9Х18, ЭИ 229) | 205 | — | — | — | — | — | — | — | — | — |
| 12Х8ВФ (1Х8ВФ) | 218 | — | — | 164 | 153 | — | — | — | — | — |
| 10Х9МФБ (ДИ 82) | 220 | 215 | 210 | 200 | 190 | 180 | 170 | — | — | — |
| 10Х9В2МФБР-Ш | 191 | 184 | 184 | 173 | — | 152 | 98 | — | — | — |
| 40Х10С2М (4Х10С2М, ЭИ 107) | 214 | 211 | 205 | 202 | 196 | 187 | 172 | 151 | 129 | — |
| 15Х11МФ (1Х11МФ) | 224 | 218 | 209 | 201 | 189 | 177 | — | — | — | — |
| 12Х11В2МФ (типа ЭИ 756) | 208 | 204 | 199 | 191 | 182 | 170 | 161 | 148 | — | — |
| 18Х11МНФБ (2Х11МФБН, ЭП 291) | 224 | 177 | 209 | 201 | 189 | 177 | — | — | — | — |
| 03Х11Н10М2Т | 196 | — | — | — | — | — | — | — | — | — |
| 10Х11Н20Т3Р (ЭИ 696) | 160 | — | — | — | 140 | 135 | 132 | 115 | 113 | 90 |
| 10Х11Н23Т3МР (10Х12Н22Т3МР, ЭП 33, ЭИ 696М) | 160 | — | — | — | 142 | 138 | 132 | 115 | — | — |
| 18Х12ВМБФР-Ш (ЭИ 993-Ш) | 224 | — | 211 | 205 | 191 | 184 | 170 | 152 | — | — |
| 20Х12ВНМФ (ЭП 428) | 212 | — | — | 196 | 190 | 180 | 163 | — | — | — |
| 06Х12Н3Д | 212 | 211 | 205 | 198 | 187 | — | — | — | — | — |
| 10Х12Н3М2ФА (Ш), 10Х12Н3М2ФА-А (Ш) | 217 | 212 | 207 | 199 | 189 | 176 | 167 | — | — | — |
| 37Х12Н8Г8МФБ (ЭИ 481) | 171 | — | 157 | 147 | 140 | 133 | 126 | 115 | — | — |
| 08Х13 (0Х13, ЭИ 496) | 217 | 212 | 206 | 198 | 189 | 180 | — | — | — | — |
| 12Х13 (1Х13) | 217 | 212 | 206 | 198 | 189 | 180 | — | — | — | — |
| 20Х13 (2Х13) | 218 | 214 | 208 | 200 | 189 | 181 | 169 | — | — | — |
| 30Х13 (3Х13) | 216 | 212 | 206 | 196 | 187 | 177 | 166 | — | — | — |
| 40Х13 (4Х13) | 214 | 208 | 202 | 194 | 185 | 173 | 160 | — | — | — |
| 12Х13Г12АС2Н2 (ДИ 50) | 188 | — | 185 | — | 159 | — | 142 | — | — | — |
| 10Х13Г12БС2Н2Д2Б (ДИ 59) | 195 | 192 | 185 | 77 | 166 | 160 | 150 | 141 | 137 | — |
| 03Х13Н8Д2ТМ (ЭП 699) | 195 | 191 | 187 | 182 | 171 | — | — | — | — | — |
| 08Х14МФ | 222 | 219 | 213 | 203 | 195 | 183 | 175 | — | — | — |
| 10Х14Г14Н4Т (Х14Г14Н3Т, ЭИ 711) | 194 | 189 | 181 | 170 | 164 | 159 | 161 | — | — | — |
| 1Х14Н14В2М (ЭИ 257) | 198 | — | — | — | — | 168 | 160 | — | — | — |
| 45Х14Н14В2М (ЭИ 69) [3] | 212 | 200 | 194 | 185 | 176 | 169 | 160 | 152 | 144 | — |
| 09Х14Н19В2БР (ЭИ 695Р) [5] | 207 | — | — | — | — | — | 158 | 151 | 147 | — |
| 09Х14Н19В2БР1 (ЭИ 726) | 198 | 195 | 189 | 182 | 175 | 166 | 157 | 149 | — | — |
| 08Х15Н2В4ТР (ЭП 164) [5] | 223 | 215 | 209 | 200 | 191 | 182 | 173 | 165 | 156 | — |
| 07Х16Н6 (Х16Н6, ЭП 288) | 199 | — | — | — | — | — | — | — | — | — |
| 08Х16Н9М2 (Х16Н9М2) | 210 | 198 | 188 | 80 | 172 | 157 | 153 | 143 | 138 | — |
| 08Х16Н13М2Б (ЭИ 405, ЭИ 680) | 202 | 196 | 188 | 180 | 171 | 164 | 155 | 147 | — | — |
| 10Х16Н14В2БР (1Х16Н14В2БР, ЭП 17) | 188 | 181 | 174 | 166 | 158 | 151 | 145 | 136 | — | — |
| 08Х17Т (0Х17Т, ЭИ 645) | 206 | — | — | — | — | — | — | — | — | — |
| 12Х17 (Х17, ЭЖ 17) | 232 | 227 | 219 | 211 | 201 | 192 | 182 | 165 | 148 | — |
| 14Х17Н2 (1Х17Н2, ЭИ 268) | 193 | — | — | 164 | — | 148 | 133 | — | — | — |
| 02Х17Н11М2 | 200 | — | — | — | 170 | — | 150 | — | 135 | — |
| 08Х17Н13М2Т (0Х17Н13М2Т) | 206 | — | 186 | 177 | 177 | 167 | 157 | 147 | — | — |
| 10Х17Н13М2Т (Х17Н13М2Т, ЭИ 448) | 206 | — | 186 | 177 | 177 | 167 | 157 | 147 | — | — |
| 10Х17Н13М3Т (Х17Н13М3Т, ЭИ 432) | 206 | — | 186 | 177 | 177 | 167 | 157 | 147 | — | — |
| 03Х17Н14М3 (000Х17Н13М2) | 195 | — | — | 190 | — | — | — | — | — | — |
| 08Х17Н15М3Т (ЭИ 580) | 203 | — | — | — | — | — | — | — | — | — |
| 015Х18М2Б-ВИ (ЭП 882-ВИ) | 216 | 12 | 206 | 198 | 185 | 179 | 163 | 144 | — | — |
| 12Х18Н9 (Х18Н9) | 199 | — | — | — | — | — | — | — | — | — |
| 12Х18Н9Т (Х18Н9Т) | 195 | 189 | 182 | 175 | 167 | 160 | 153 | 143 | 135 | — |
| 17Х18Н9 (2Х18Н9) | 199 | — | — | — | — | — | — | — | — | — |
| 08Х18Н10 (0Х18Н10) | 196 | — | — | — | — | — | — | — | — | — |
| 08Х18Н10Т (0Х18Н10Т, ЭИ 914) [4] | 196 | — | — | — | 158 | 128 | 127 | 117 | 108 | 102 |
| 12Х18Н10Т [4] | 198 | 194 | 189 | 181 | 174 | 166 | 157 | 147 | — | — |
| 12Х18Н12Т (Х18Н12Т) | 210 | 198 | 193 | 186 | 177 | 170 | 157 | 147 | — | — |
| 10Х18Н18Ю4Д (ЭП 841) | 186 | 182 | 178 | 171 | 165 | 161 | 156 | 146 | 38 | 127 |
| 36Х18Н25С2 (4Х18Н25С2, ЭЯ 3С) | 200 | — | — | 191 | 186 | 178 | 171 | 162 | 154 | 147 |
| 01Х19Ю3БЧ-ВИ (02Х18Ю3Б-ВИ, ЭП 904-ВИ) | 220 | 216 | 210 | 200 | 192 | 183 | 167 | 152 | — | — |
| 31Х19Н9МВБТ (ЭИ 572) | 201 | — | — | 186 | 181 | 176 | 167 | 157 | — | — |
| 08Х21Н6М2Т (0Х21Н6М2Т, ЭП 54) | 196 | 196 | 185 | 178 | 169 | 164 | — | — | — | — |
| 02Х22Н5АМ3 | 200 | 194 | 186 | 180 | — | — | — | — | — | — |
| 08Х22Н6Т (0Х22Н5Т, ЭП 53) | 203 | 201 | 193 | 181 | 165 | 162 | 154 | 141 | 139 | — |
| 20Х23Н13 (Х23Н13, ЭИ 319) | 207 | — | — | — | — | — | — | — | — | — |
| 20Х23Н18 (Х23Н18, ЭИ 417) | 200 | — | — | 182 | 176 | 170 | 160 | 150 | 141 | — |
| 03Х24Н6АМ3 (ЗИ 130) | 200 | 196 | 185 | 180 | 171 | — | — | — | — | — |
| 15Х25Т (Х25Т, ЭИ 439) | 204 | 200 | 197 | 189 | 176 | 164 | 140 | 124 | 119 | 109 |
| 12Х25Н16Г7АР (ЭИ 835) | 193 | 186 | 178 | 171 | 163 | 156 | 147 | 138 | 131 | 127 |
| 20Х25Н20С2 (Х25Н20С2, ЭИ 283) | 195 | 192 | 186 | 185 | 180 | 175 | 150 | 140 | 130 | 120 |
| 03Н18К9М5Т | 185 | — | — | — | — | — | — | — | — | — |
| У8, У8А | 209 | 205 | 199 | 192 | 185 | 175 | 166 | — | — | — |
| У9, У9А | 209 | — | — | — | — | — | — | — | — | — |
| У12, У12А | 209 | 205 | 200 | 193 | 185 | 178 | 166 | — | — | — |
| 9ХС | 190 | — | — | — | — | — | — | — | — | — |
| Р9 | 220 | — | — | — | — | — | — | — | — | — |
| Р12 | 223 | — | — | — | — | — | — | — | — | — |
| 20Л | 201 | 196 | 188 | 183 | 173 | 165 | 152 | 132 | 120 | — |
| 35Л | 212 | 206 | 201 | 192 | 176 | 163 | 151 | 131 | 118 | — |
| 50Л | 219 | 214 | 208 | 196 | 178 | 170 | 155 | 136 | 122 | — |
| 20ГЛ | 204 | — | — | — | — | — | — | — | — | — |
| 110Г13Л | 204 | — | — | — | — | — | — | — | — | — |
| 08ГДНФЛ | 212 | 206 | 201 | 189 | 177 | 167 | 155 | 137 | 127 | — |
| 32Х06Л | 216 | 211 | 207 | 195 | 178 | 174 | 166 | 141 | 131 | — |
| 40ХЛ | 219 | 216 | 210 | 204 | 185 | 176 | 164 | 143 | 132 | — |
| 20ХМФЛ | 197 | 192 | 187 | 182 | 178 | 171 | 163 | 155 | — | — |
| 35ХМЛ | 215 | 212 | 207 | 203 | 192 | 179 | 166 | 141 | 130 | — |
| 35ХГСЛ | 215 | 211 | 203 | 196 | 184 | 174 | 164 | 143 | 125 | — |
| 20Х5МЛ | 211 | — | — | — | 178 | 145 | 102 | — | — | — |
| 15Х11МФБЛ (1Х11МФБЛ, Х11ЛА) | 210 | — | 202 | 195 | 187 | 178 | 162 | — | — | — |
| 10Х12НДЛ | 217 | 216 | 212 | 204 | 198 | 188 | 179 | 164 | — | — |
| 20Х12ВНМФЛ (15Х12ВНМФЛ, Х11ЛБ, ЭИ 802Л) | 210 | — | 202 | 195 | 187 | 178 | 162 | — | — | — |
| 20Х13Л [4] | 222 | 216 | 211 | 203 | 196 | 184 | 167 | 149 | 140 | — |
| 10Х13Н3М1Л | 215 | — | — | — | — | — | — | — | — | — |
| 10Х18Н9Л | 170 | 143 | 135 | 127 | 120 | — | — | — | — | — |
| 12Х18Н9ТЛ [4] | 194 | 189 | 176 | 165 | 149 | 138 | 133 | 125 | 112 | — |
| 06ХН28МДТ (0Х23Н28М3Д3Т, ЭИ 943) | — | 191 | 186 | 179 | 171 | 161 | 156 | 151 | 145 | — |
| ХН32Т (ЭП 670) | 205 | — | — | — | — | — | — | — | — | — |
| ХН35ВТ (ЭИ 612), ХН35ВТ-ВД | 198 | 195 | 190 | 186 | 179 | 177 | 166 | 158 | — | — |
| ХН35ВТК (ЭИ 612К) | 198 | 184 | 175 | — | 171 | 164 | 159 | 141 | — | — |
| ХН35ВТЮ (ЭИ 787) | 214 | 207 | 199 | 195 | 189 | 181 | 170 | 163 | 149 | — |
| ХН35ВТР (ЭИ 725) | 206 | — | 186 | — | 177 | 167 | 167 | 157 | 157 | — |
| 36НХТЮ8М | 210 | — | — | — | — | — | — | — | — | — |
| ХН45Ю (ЭП 747) | 207 | 201 | 192 | 187 | 178 | 171 | 156 | 148 | 124 | 120 |
| 06ХН46Б (Х20Н46Б, ЭП 350) | — | 175 | 173 | 168 | 164 | 157 | 151 | 147 | — | — |
| 05ХН46МВБЧ (ДИ 65) | 207 | 203 | 196 | 190 | 183 | 177 | 170 | 163 | 154 | 144 |
| ХН55ВМТКЮ (ЭИ 929), ХН55ВМТКЮ-ВД (ЭИ 929-ВД) | 218 | — | — | — | — | — | — | 181 | 172 | 163 |
| ХН59ВГ-ИД (ЭК 82-ИД) | 217 | 214 | 208 | 203 | 196 | 191 | 189 | 180 | 172 | 166 |
| ХН60Ю (ЭИ 559А) | 210 | — | — | — | — | — | — | — | 169 | — |
| ХН60ВТ (ЭИ 868) | 218 | — | — | — | 204 | 198 | 192 | 184 | 176 | 160 |
| ХН62МБВЮ (ЭП 709) | 226 | — | — | — | — | 197 | 189 | — | — | — |
| ХН62МВКЮ (ЭИ 867) | 228 | — | — | — | — | — | — | 191 | 179 | 140 |
| ХН65ВМТЮ (ЭИ 893) | 219 | — | 206 | 201 | 196 | 193 | 183 | 176 | 162 | — |
| ХН65КМВЮБ-ВД (ЭП 800-ВД) | 230 | 227 | 222 | 217 | 211 | 204 | 200 | 188 | 181 | 171 |
| ХН65МВУ (ЭП 760) | 200 | — | — | — | — | — | — | — | — | — |
| ХН67МВТЮ (ЭП 202, ЭИ 445Р) | 212 | 208 | 203 | 197 | 192 | 185 | 178 | 170 | 161 | 139 |
| ХН70БДТ (ЭК 59) | 219 | 214 | 208 | 201 | 198 | — | — | — | — | — |
| ХН70ВМЮТ (ЭИ 765) | 222 | 217 | 211 | 205 | 199 | 193 | 186 | 179 | — | — |
| ХН70ВМТЮ (ЭИ 617) | 196 | — | — | — | — | — | 162 | 147 | 142 | 127 |
| ХН70ВМТЮФ (ЭИ 826), ХН70ВМТЮФ-ВД, (ЭИ 826-ВД) | 196 | — | — | — | — | 167 | 162 | 152 | 142 | 127 |
| ХН73МБТЮ (ЭИ 698) | 203 | — | — | — | — | 177 | 177 | 160 | 150 | — |
| ХН75ВМЮ (ЭИ 827) | 240 | 236 | 231 | 225 | 218 | 215 | 204 | 195 | 187 | 178 |
| ХН77ТЮР (ЭИ 437Б) | 210 | — | — | — | — | — | 163 | 153 | 130 | 115 (850°C) |
| ХН78Т (ЭИ 435) | 210 | — | — | — | — | — | — | 169 | — | — |
| ХН80ТБЮ (ЭИ 607) | 216 | 216 | 211 | 206 | 200 | 196 | 186 | 177 | — | — |
| ХН80ТБЮА (ЭИ 607А) | 218 | — | — | — | — | 191 | 184 | 176 | — | — |
| Н70МФВ-ВИ (ЭП 814А-ВИ) | 155 | — | — | — | — | — | — | — | — | — |
| ХН58ВКМТЮБЛ (ЦНК 8МП) | 211 | — | — | — | — | — | — | — | — | — |
| ХН60КВМЮТЛ (ЦНК 7П) | 210 | 207 | 203 | 198 | 192 | 185 | 178 | 171 | 164 | — |
| ХН64ВМКЮТЛ (ЗМИ 3) | 225 | 222 | 219 | 214 | 209 | 201 | 193 | 186 | 177 | 168 |
| ХН65ВМТЮЛ (ЭИ 893Л) | 222 | 214 | 210 | 202 | 195 | 190 | 184 | 174 | 165 | 160 |
| ХН65КМВЮТЛ (ЖС 6К) | 210 | 207 | 203 | 198 | 192 | 185 | 178 | 171 | 164 | — |
| ХН65ВКМБЮТЛ (ЭИ 539ЛМУ) | 213 | 211 | 207 | 203 | 197 | 190 | 183 | 175 | 167 | 158 |
| АД, АД00, АД0, АД1 [6] | 71 | — | — | — | — | — | — | — | — | — |
| АМг2 [6] | — | 59 | — | — | — | — | — | — | — | — |
| АМг2 | 69 | — | — | — | — | — | — | — | — | — |
| АМг3 | 68 | — | — | — | — | — | — | — | — | — |
| АМг5 | 69 | — | — | — | — | — | — | — | — | — |
| АМг6 | 69 | — | — | — | — | — | — | — | — | — |
| ЛС59-1 | 105 | — | — | — | — | — | — | — | — | — |
| ЛЖМц59-1-1 | 106 | — | — | — | — | — | — | — | — | — |
| ЛАМш77-2-0,05 | 102 | — | — | — | — | — | — | — | — | — |
| БрА10Ж3Мц2 (БрАЖМц10-3-1,5) | 102 | — | — | — | — | — | — | — | — | — |
| БрБ2 | 123 | — | — | — | — | — | — | — | — | — |
| БрО5Ц5С5 (БрОЦС5-5-5) | 90 | — | — | — | — | — | — | — | — | — |
| БрО10Ф1 (БрОФ10-1) | 103 | — | — | — | — | — | — | — | — | — |
| Б83 | 48 | — | — | — | — | — | — | — | — | — |
| ВТ1-0 | 103 | — | — | — | — | — | — | — | — | — |
| ВТ1-00 | 103 | — | — | — | — | — | — | — | — | — |
| ВТ5-1 | 115,7 | — | — | — | — | — | — | — | — | — |
| ОТ4 | 107,9 | — | — | — | — | — | — | — | — | — |
| ОТ4-0 | 112,8 | — | — | — | — | — | — | — | — | — |
| ОТ4-1 | 107,9 | — | — | — | — | — | — | — | — | — |
Список литературы:
- Марочник сталей и сплавов.
 2-е изд., исправл. и доп. / Зубченко А.С., Колосков М.М., Каширский Ю.В. и др. Под ред. А.С. Зубченко. М.: Машиностроение, 2003. 784 с.
2-е изд., исправл. и доп. / Зубченко А.С., Колосков М.М., Каширский Ю.В. и др. Под ред. А.С. Зубченко. М.: Машиностроение, 2003. 784 с. - Машиностроение. Энциклопедия. Т. II–3. Цветные металлы и сплавы. Композиционные металлические материалы. /Под общей редакцией И.Н. Фридляндера. М.: Машиностроение, 2001. 880 с.
- Журавлев В.Н., Николаева О.И. Машиностроительные стали. Справочник. 4-е изд., перераб. и доп. М.: Машиностроение, 1992. 480 с.
- Стали и сплавы. Марочник. Справ. изд. /Сорокин В.Г. и др. Науч. ред. В.Г. Сорокин, М.А. Гервасьев. М.: Интермет Инжиниринг, 2001. 608 с.
- Масленков С.Б., Масленкова Е.А. Стали и сплавы для высоких температур. Справочное издание. В 2-х книгах. Кн. 1. М.: Металлургия, 1991. 383 с.
- Михайлов-Михеев П.Б. Справочник по металлическим материалам турбино- и моторостроения. М.: Машгиз, 1961. 838 с.
Просмотров: 4 749
Модуль упругости Юнга и сдвига, коэффициент Пуассона значения (Таблица)
Модуль упругости Юнга и сдвига, коэффициент Пуассона значения (Таблица)
Упругие свойства тел
Ниже приводятся справочные таблицы общеупотребительных констант; если известны две их них, то этого вполне достаточно для определения упругих свойств однородного изотропного твердого тела.
Модуль Юнга или модуль продольной упругости в дин/см2.
Модуль сдвига или модуль кручения G в дин/см2.
Модуль всестороннего сжатия или модуль объемной упругости К в дин/см2.
Объем сжимаемости k=1/K/.
Коэффициент Пуассона µ равен отношению поперечного относительного сжатия к продольному относительному растяжению.
Для однородного изотропного твердого материала имеют место следующие соотношения между этими константами:
G = E / 2(1 + μ) — (α)
μ = (E / 2G) — 1 — (b)
K = E / 3(1 — 2μ) — (c)
Коэффициент Пуассона имеет положительный знак, и его значение обычно заключено в пределах от 0,25 до 0,5, но в некоторых случаях он может выходить за указанные пределы. Степень совпадения наблюдаемых значений µ и вычисленных по формуле (b) является показателем изотропности материала.
Таблицы значений Модуля упругости Юнга, Модуля сдвига и коэффициента Пуассона
Курсивом даны значения, вычисленные из соотношений (a), (b), (c).
| Материал при 18°С | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
| Алюминий | 7,05 | 2,62 | 0,345 | 7,58 |
| Висмут | 3,19 | 1,20 | 0,330 | 3,13 |
| Железо | 21,2 | 8,2 | 0,29 | 16,9 |
| Золото | 7,8 | 2,7 | 0,44 | 21,7 |
| Кадмий | 4,99 | 1,92 | 0,300 | 4,16 |
| Медь | 12,98 | 4,833 | 0,343 | 13,76 |
| Никель | 20,4 | 7,9 | 0,280 | 16,1 |
| Платина | 16,8 | 6,1 | 0,377 | 22,8 |
| Свинец | 1,62 | 0,562 | 0,441 | 4,6 |
| Серебро | 8,27 | 3,03 | 0,367 | 10,4 |
| Титан | 11,6 | 4,38 | 0,32 | 10,7 |
| Цинк | 9,0 | 3,6 | 0,25 | 6,0 |
| Сталь (1% С) 1) | 21,0 | 8,10 | 0,293 | 16,88 |
| (мягкая) | 21,0 | 8,12 | 0,291 | 16,78 |
| Константан 2) | 16,3 | 6,11 | 0,327 | 15,7 |
| Манганин | 12,4 | 4,65 | 0,334 | 12,4 |
1) Для стали, содержащий около 1% С, упругие константы, как известно , меняются при термообработке. 2) 60% Cu, 40% Ni. | ||||
Экспериментальные результаты, приводимые ниже, относятся к обычным лабораторным материалам, главным образом проволокам.
| Вещество | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
| Бронза (66% Cu) | -9,7-10,2 | 3,3-3,7 | 0,34-0,40 | 11,2 |
| Медь | 10,5-13,0 | 3,5-4,9 | 0,34 | 13,8 |
| Нейзильбер1) | 11,6 | 4,3-4,7 | 0,37 | — |
| Стекло | 5,1-7,1 | 3,1 | 0,17-0,32 | 3,75 |
| Стекло иенское крон | 6,5-7,8 | 2,6-3,2 | 0,20-0,27 | 4,0-5,9 |
| Стекло иенское флинт | 5,0-6,0 | 2,0-2,5 | 0,22-0,26 | 3,6-3,8 |
| Железо сварочное | 19-20 | 7,7-8,3 | 0,29 | 16,9 |
| Чугун | 10-13 | 3,5-5,3 | 0,23-0,31 | 9,6 |
| Магний | 4,25 | 1,63 | 0,30 | — |
| Бронза фосфористая2) | 12,0 | 4,36 | 0,38 | — |
| Платиноид3) | 13,6 | 3,6 | 0,37 | — |
Кварцевые нити (плав. ) ) | 7,3 | 3,1 | 0,17 | 3,7 |
| Резина мягкая вулканизированная | 0,00015-0,0005 | 0,00005-0,00015 | 0,46-0,49 | — |
| Сталь | 20-21 | 7,9-8,9 | 0,25-0,33 | 16,8 |
| Цинк | 8,7 | 3,8 | 0,21 | — |
| 1) 60% Cu, 15% Ni, 25% Zn 2) 92,5% Cu, 7% Sn, 0,5% P 3) Нейзильбер с небольшим количеством вольфрама. | ||||
| Вещество | Модуль Юнга E, 1011 дин/см2. | Вещество | Модуль Юнга E, 1011 дин/см2. |
| Цинк (чистый) | 9,0 | Дуб | 1,3 |
| Иридий | 52,0 | Сосна | 0,9 |
| Родий | 29,0 | Красное дерево | 0,88 |
| Тантал | 18,6 | Цирконий | 7,4 |
| Инвар | 17,6 | Титан | 10,5-11,0 |
| Сплав 90% Pt, 10% Ir | 21,0 | Кальций | 2,0-2,5 |
| Дюралюминий | 7,1 | Свинец | 0,7-1,6 |
| Шелковые нити1 | 0,65 | Тиковое дерево | 1,66 |
| Паутина2 | 0,3 | Серебро | 7,1-8,3 |
| Кетгут | 0,32 | Пластмассы: | |
| Лед (-20С) | 0,28 | Термопластичные | 0,14-0,28 |
| Кварц | 7,3 | Термореактивные | 0,35-1,1 |
| Мрамор | 3,0-4,0 | Вольфрам | 41,1 |
| 1) Быстро уменьшается с увеличением нагрузки 2) Обнаруживает заметную упругую усталость | |||
| Температурный коэффициент (при 150С) Et=E11 (1-ɑ (t-15)), Gt=G11 (1-ɑ (t-15)) | Сжимаемость k, бар-1 (при 7-110С) | |||
| ɑ, для Е | ɑ, для G | |||
| Алюминий | 4,8*10-4 | 5,2*10-4 | Алюминий | 1,36*10-6 |
| Латунь | 3,7*10-4 | 4,6*10-4 | Медь | 0,73*10-6 |
| Золото | 4,8*10-4 | 3,3*10-4 | Золото | 0,61*10-6 |
| Железо | 2,3*10-4 | 2,8*10-4 | Свинец | 2,1*10-6 |
| Сталь | 2,4*10-4 | 2,6*10-4 | Магний | 2,8*10-6 |
| Платина | 0,98*10-4 | 1,0*10-4 | Платина | 0,36*10-6 |
| Серебро | 7,5*10-4 | 4,5*10-4 | Стекло флинт | 3,0*10-6 |
| Олово | — | 5,9*10-4 | Стекло немецкое | 2,57*10-6 |
| Медь | 3,0*10-4 | 3,1*10-4 | Сталь | 0,59*10-6 |
| Нейзильбер | — | 6,5*10-4 | ||
| Фосфористая бронза | — | 3,0*10-4 | ||
| Кварцевые нити | -1,5*10-4 | -1,1*10-4 | ||
Модуль сдвига меди
Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы.
Другими словами, они подвергаются деформации.
Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой.
Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга.
В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.
Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.
Модуль Юнга
Основные сведения
Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м2 или в Па.
Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям.
Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E.
И поэтому на практике значения Е для них приводят в гигаПаскалях (1012Па)
Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.
Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.
График теста на растяжение
E- это частное от деления нормальных напряжений σ на относительное удлинение ε.
E=α/ε
Закон Гука также можно сформулировать и с использованием модуля Юнга.
Физический смысл модуля Юнга
Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.
Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.
Виды деформации
Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь.
Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.
В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:
Δl = α * (lF) / S
Величину, обратную α, и называют модулем Юнга:
1/α = E
Относительная деформация:
ε = (Δl) / l = α * (F/S)
Отношение растягивающей силы F к S называют упругим напряжением σ:
ε=α σ
Закон Гука, записанный с использованием модуля Юнга, выглядит так:
σ = ε/α = E ε
Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.
В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.
Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l
Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.
Значения модуля юнга для некоторых материалов
В таблице показаны значения E ряда распространенных веществ.
| Материал | модуль Юнга E, ГПа |
| Алюминий | 70 |
| Бронза | 75-125 |
| Вольфрам | 350 |
| Графен | 1000 |
| Латунь | 95 |
| Лёд | 3 |
| Медь | 110 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 200/210 |
| Стекло | 70 |
Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.
Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.
Предел прочности материала
Это предел возникающего напряжения, после которого образец начинает разрушаться.
Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.
Инструмент для определения предела прочности
Кроме того, существуют пределы прочности на сжатие материала и на растяжение.
Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления.
В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.
Допускаемое механическое напряжение в некоторых материалах при растяжении
Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия.
По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.
Испытание на растяжение
Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала.
В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно.
Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.
Значения σраст в МПа:
| Материалы | σраст | |
| Бор | 5700 | 0,083 |
| Графит | 2390 | 0,023 |
| Сапфир | 1495 | 0,030 |
| Стальная проволока | 415 | 0,01 |
| Стекловолокно | 350 | 0,034 |
| Конструкционная сталь | 60 | 0,003 |
| Нейлон | 48 | 0,0025 |
Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты.
Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности.
Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.
Запасы прочности, закладываемые в ответственные конструкции, также многократны.
Коэффициент запаса прочности
Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности.
Он характеризует способность изделия к перегрузкам выше номинальных.
Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.
Запас прочности
Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.
Связь с другими модулями упругости
Модуль Юнга связан с модулем сдвига, определяющим способность образца к сопротивлению против деформации сдвига, следующим соотношением:
E связан также и с модулем объёмной упругости, определяющим способность образца к сопротивлению против одновременного сжатия со всех сторон.
, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Модуль упругости — что это такое? Определение модуля упругости для материалов
Модуль упругости — это физическая величина, которая характеризует упругое поведение материала при приложении к нему внешней силы в конкретном направлении. Под упругим поведением материала подразумевается его деформация в упругой области.
История исследования упругости материалов
Физическая теория упругих тел и их поведения при действии внешних сил была подробно рассмотрена и изучена английским ученым XIX века Томасом Юнгом.
Физический смысл модуля Юнга
Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.
Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.
Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.
В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:
Величину, обратную α, и называют модулем Юнга:
ε = (Δl) / l = α * (F/S)
Отношение растягивающей силы F к S называют упругим напряжением σ:
Закон Гука, записанный с использованием модуля Юнга, выглядит так:
Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.
В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.
Значение E вычисляют с помощью косвенного метода на малых деформациях.
Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l
Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.
Модуль сдвига стали таблица
Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.
Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними. Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда. С повышением прочностных характеристик совершенствовались инструменты и способы производства.
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
- Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.
- Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.
- Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида.
 В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
- Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.
- Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.
Понятие о модуле упругости
В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:
Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:
- Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
- Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).
Формула по закону Гука записывается в виде ε = σz/E, где:
- ε – относительное удлинение;
- σz – нормальное напряжение.
Демонстрация закона Гука для упругих тел:
Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.
В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.
Значения модуля упругости для некоторых материалов приведены в таблице 1.
Таблица 1: Модуль упругости для металлов и сплавов
| Наименование материала | Значение модуля упругости, 10¹²·Па |
| Алюминий | 65…72 |
| Дюралюминий | 69…76 |
| Железо, содержание углерода менее 0,08 % | 165…186 |
| Латунь | 88…99 |
| Медь (Cu, 99 %) | 107…110 |
| Никель | 200…210 |
| Олово | 32…38 |
| Свинец | 14…19 |
| Серебро | 78…84 |
| Серый чугун | 110…130 |
| Сталь | 190…210 |
| Стекло | 65…72 |
| Титан | 112…120 |
| Хром | 300…310 |
Модуль упругости для разных марок стали
Металлурги разработали несколько сотен марок сталей. Им свойственны разные значения прочности. В таблице 2 показаны характеристики для наиболее распространенных сталей.
Им свойственны разные значения прочности. В таблице 2 показаны характеристики для наиболее распространенных сталей.
Таблица 2: Упругость сталей
| Наименование стали | Значение модуля упругости, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 |
| Сталь 3 | 179…189 |
| Сталь 30 | 194…205 |
| Сталь 45 | 211…223 |
| Сталь 40Х | 240…260 |
| 65Г | 235…275 |
| Х12МФ | 310…320 |
| 9ХС, ХВГ | 275…302 |
| 4Х5МФС | 305…315 |
| 3Х3М3Ф | 285…310 |
| Р6М5 | 305…320 |
| Р9 | 320…330 |
| Р18 | 325…340 |
| Р12МФ5 | 297…310 |
| У7, У8 | 302…315 |
| У9, У10 | 320…330 |
| У11 | 325…340 |
| У12, У13 | 310…315 |
Видео: закон Гука, модуль упругости.
Модули прочности
Кроме нормального нагружения, существуют и иные силовые воздействия на материалы.
Модуль сдвига G определяет жесткость. Эта характеристика показывает предельное значение нагрузки изменению формы предмета.
Модуль объемной упругости К определяет упругие свойства материала изменить объем. При любой деформации происходит изменение формы предмета.
Для разных сталей значения указанных модулей приведены в таблице 3.
Таблица 3: Модули прочности для сталей
| Наименование стали | Модуль упругости Юнга, 10¹²·Па | Модуль сдвига G, 10¹²·Па | Модуль объемной упругости, 10¹²·Па | Коэффициент Пуассона, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 | 87…91 | 45…49 | 154…168 |
| Сталь 3 | 179…189 | 93…102 | 49…52 | 164…172 |
| Сталь 30 | 194…205 | 105…108 | 72…77 | 182…184 |
| Сталь 45 | 211…223 | 115…130 | 76…81 | 192…197 |
| Сталь 40Х | 240…260 | 118…125 | 84…87 | 210…218 |
| 65Г | 235…275 | 112…124 | 81…85 | 208…214 |
| Х12МФ | 310…320 | 143…150 | 94…98 | 285…290 |
| 9ХС, ХВГ | 275…302 | 135…145 | 87…92 | 264…270 |
| 4Х5МФС | 305…315 | 147…160 | 96…100 | 291…295 |
| 3Х3М3Ф | 285…310 | 135…150 | 92…97 | 268…273 |
| Р6М5 | 305…320 | 147…151 | 98…102 | 294…300 |
| Р9 | 320…330 | 155…162 | 104…110 | 301…312 |
| Р18 | 325…340 | 140…149 | 105…108 | 308…318 |
| Р12МФ5 | 297…310 | 147…152 | 98…102 | 276…280 |
| У7, У8 | 302…315 | 154…160 | 100…106 | 286…294 |
| У9, У10 | 320…330 | 160…165 | 104…112 | 305…311 |
| У11 | 325…340 | 162…170 | 98…104 | 306…314 |
| У12, У13 | 310…315 | 155…160 | 99…106 | 298…304 |
Для других материалов значения прочностных характеристик указывают в специальной литературе. Однако, в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводят испытания по определению предельных значений.
Однако, в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводят испытания по определению предельных значений.
Таблица 1. Модуль сдвига G для материалов, используемых при изготовлении пружин
Модуль сдвига, G·10 3 кгс/мм 2
Стали 70С2ХА, 50ХФА, 4Х13, 60С2, 60С2Н2А, 65Г, У8А
Бронза БрКМц3-1, БрОФ6.5-0.15, БрОЦ4-3
Таблица 2. Модуль сдвига G для различных материалов
Модуль сдвига, G · 10 3 кгс/мм 2
Алюминиевый сплав литейный
Бакелит (без наполнителей)
Бронза фосфористая катанная
Дюралюмин после отжига при 370 0 С
Медь холоднотянутая прокатная
Чугун серый, белый
И.Я. Левин “Справочник конструктора точных приборов”,Государственное научно-техническое издательство, М.,1962г.
Д.Н. Решетилов “Детали машин”,М.:Машиностроение, 1974г
Web-сайт “ГРАФОАНАЛИТИЧЕСКИЕ СИСТЕМЫ”. Контактная информация. E-mail: [email protected]
Контактная информация. E-mail: [email protected]
Copyright © 2005-2017 г. Все права защищены.
Модулем сдвига (модуль упругости II рода, модуль упругости при сдвиге) – называется физическая величина, характеризующая упругие свойства материалов и их способность сопротивляться сдвигающим деформациям.
Обозначается латинской буквой G ,
единица измерения – Паскаль [Па] (гигапаскаль [ГПа])
В сопромате данный модуль используется в расчетах на сдвиг, срез и кручение.
Рис. 1 Деформация сдвига
Теоретически определяется отношением касательных напряжений τ к углу сдвига γ (рис. 1)
где
τ =F/A — касательные напряжения;
γ — угол сдвига;
F — сдвигающая сила;
A — площадь приложения силы F ;
ΔS — величина сдвига;
a — размер элемента.
Таблица 1. Сравнительные значения модуля для некоторых материалов
Модуль упругости для стали, а также для других материалов
Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.
Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.
Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.
Модуль упругости — что это?
Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.
Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:
- Модуль Юнга (Е) описывает сопротивление материала любому растяжению или сжатию при упругой деформации.
 Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости.
Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости. - Модуль сдвига (G), называемый также модулем жёсткости. Этот способ выявляет способность материала оказывать сопротивление любому изменению формы, но в условиях сохранения им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, которая определяется в виде изменения прямого угла между имеющимися плоскостями, подвергающимися воздействию касательных напряжений. Модуль сдвига, кстати, является одной из составляющих такого явления, как вязкость.
- Модуль объёмной упругости (К), которые также именуется модулем объёмного сжатия. Данный вариант обозначает способность объекта из какого-либо материала изменять свой объём в случае воздействия на него всестороннего нормального напряжения, являющимся одинаковым по всем своим направлениям. Выражается этот вариант отношением величины объёмного напряжения к величине относительного объёмного сжатия.

- Существуют также и другие показатели упругости, которые измеряются в других величинах и выражаются другими отношениями. Другими ещё очень известными и популярными вариантами показателей упругости являются параметры Ламе или же коэффициент Пуассона.
Общие понятия
Модуль упругости (модуль Юнга) — это показатель механического свойства материала, характеризующий его сопротивляемость деформации растяжения. Иными словами, это значение пластичности материала. Чем выше значения модуля упругости, тем меньше будет какой-либо стержень растягиваться при иных равных нагрузках (площадь сечения, величина нагрузки и другие).
Иными словами, это значение пластичности материала. Чем выше значения модуля упругости, тем меньше будет какой-либо стержень растягиваться при иных равных нагрузках (площадь сечения, величина нагрузки и другие).
Модуль Юнга в теории упругости обозначается буквой Е. Он является составляющей закона Гука (о деформации упругих тел). Эта величина связывает возникающее в образце напряжение и его деформацию.
Измеряется эта величина согласно стандартной международной системе единиц в МПа (Мегапаскалях). Но инженеры на практике больше склоняются к применению размерности кгс/см2.
Опытным путём осуществляется определение этого показателя в научных лабораториях. Сутью этого метода является разрыв гантелеобразных образцов материала на специальном оборудовании. Узнав удлинение и натяжение, при которых образец разрушился, делят переменные данные друг на друга. Полученная величина и является модулем (Юнга) упругости.
Таким образом определяется только модуль Юнга материалов упругих: медь, сталь и прочее. А материалы хрупкие сжимают до того момента, пока не появятся трещины: бетон, чугун и им подобные.
А материалы хрупкие сжимают до того момента, пока не появятся трещины: бетон, чугун и им подобные.
Таблица показателей упругости материалов
Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.
Модуль упругости различных материалов
Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.
После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.2012/037/37_2.jpg) 2 .
2 .
Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.
Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).
Модуль упругости бетона: что это такое, способы его определения
Одной из главных задач инженерного проектирования является выбор материала конструкции и оптимального сечения профиля. Необходимо найти тот размер, который при минимально возможной массе будет обеспечивать сохранение формы системы под воздействием нагрузки.
Например, какой номер стального двутавра использовать в качестве пролетной балки сооружения? Если взять профиль размерами ниже требуемого, то гарантировано получим разрушение строения. Если больше, то это ведет к нерациональному использованию металла, а, следовательно, утяжелению конструкции, усложнению монтажа, увеличению финансовых затрат. Знание такого понятия как модуль упругости стали даст ответ на вышепоставленный вопрос, и позволит избежать появления данных проблем на самом раннем этапе производства.
Если больше, то это ведет к нерациональному использованию металла, а, следовательно, утяжелению конструкции, усложнению монтажа, увеличению финансовых затрат. Знание такого понятия как модуль упругости стали даст ответ на вышепоставленный вопрос, и позволит избежать появления данных проблем на самом раннем этапе производства.
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
- Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.
- Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.

- Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
- Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.
- Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.

алюминий, медь, стекло, железо и многое другое
| Материал | Коэффициент линейного теплового расширения | |
| (10-6 м/(мK)) / ( 10-6 м/(мoС)) | (10-6 дюйм/(дюйм oF)) | |
| ABS (акрилонитрил-бутадиен-стирол) термопласт | 73.8 | 41 |
| ABS — стекло, армированное волокнами | 30.4 | 17 |
| Акриловый материал, прессованный | 234 | 130 |
| Алмаз | 1.1 | 0.6 |
| Алмаз технический | 1.2 | 0.67 |
| Алюминий | 22.2 | 12. 3 |
| Ацеталь | 106.5 | 59.2 |
| Ацеталь , армированный стекловолокном | 39.4 | 22 |
| Ацетат целлюлозы (CA) | 130 | 72.2 |
| Ацетат бутират целлюлозы (CAB) | 25.2 | 14 |
| Барий | 20.6 | 11. 4 4 |
| Бериллий | 11.5 | 6.4 |
| Бериллиево-медный сплав (Cu 75, Be 25) | 16.7 | 9.3 |
| Бетон | 14.5 | 8.0 |
| Бетонные структуры | 9.8 | 5.5 |
| Бронза | 18.0 | 10.0 |
| Ванадий | 8 | 4. 5 |
| Висмут | 13 | 7.3 |
| Вольфрам | 4.3 | 2.4 |
| Гадолиний | 9 | 5 |
| Гафний | 5.9 | 3.3 |
| Германий | 6.1 | 3.4 |
| Гольмий | 11.2 | 6.2 |
| Гранит | 7.9 | 4.4 |
| Графит, чистый | 7.9 | 4.4 |
| Диспрозий | 9.9 | 5.5 |
| Древесина, пихта, ель | 3.7 | 2.1 |
| Древесина дуба, параллельно волокнам | 4.9 | 2. 7 |
| Древесина дуба , перпендикулярно волокнам | 5. 4 4 | 3.0 |
| Древесина, сосна | 5 | 2.8 |
| Европий | 35 | 19.4 |
| Железо, чистое | 12.0 | 6.7 |
| Железо, литое | 10.4 | 5.9 |
| Железо, кованое | 11.3 | 6.3 |
| Золото | 14.2 | 8.2 |
| Известняк | 8 | 4.4 |
| Инвар (сплав железа с никелем) | 1.5 | 0.8 |
| Инконель (сплав) | 12.6 | 7.0 |
| Иридий | 6.4 | 3. 6 |
| Иттербий | 26.3 | 14.6 |
| Иттрий | 10.6 | 5.9 |
| Кадмий | 30 | 16.8 |
| Калий | 83 | 46.1 — 46.4 |
| Кальций | 22.3 | 12.4 |
| Каменная кладка | 4.7 — 9.0 | 2.6 — 5.0 |
| Каучук, твердый | 77 | 42.8 |
| Кварц | 0.77 — 1.4 | 0. 43 — 0.79 43 — 0.79 |
| Керамическая плитка (черепица) | 5.9 | 3.3 |
| Кирпич | 5.5 | 3.1 |
| Кобальт | 12 | 6.7 |
| Констанан (сплав) | 18. 8 | 10.4 |
| Корунд, спеченный | 6.5 | 3.6 |
| Кремний | 5.1 | 2.8 |
| Лантан | 12.1 | 6.7 |
| Латунь | 18.7 | 10.4 |
| Лед | 51 | 28.3 |
| Литий | 46 | 25.6 |
| Литая стальная решетка | 10.8 | 6.0 |
| Лютеций | 9.9 | 5.5 |
| Литой лист из акрилового пластика | 81 | 45 |
| Магний | 25 | 14 |
| Марганец | 22 | 12.3 |
| Медноникелевый сплав 30% | 16. 2 | 9 |
| Медь | 16.6 | 9.3 |
| Молибден | 5 | 2.8 |
| Монель-металл (никелево-медный сплав) | 13. 5 5 | 7.5 |
| Мрамор | 5.5 — 14.1 | 3.1 — 7.9 |
| Мыльный камень (стеатит) | 8.5 | 4.7 |
| Мышьяк | 4.7 | 2.6 |
| Натрий | 70 | 39.1 |
| Нейлон, универсальный | 72 | 40 |
| Нейлон, Тип 11 (Type 11) | 100 | 55.6 |
| Нейлон, Тип 12 (Type 12) | 80.5 | 44. 7 |
| Нейлон литой , Тип 6 (Type 6) | 85 | 47.2 |
| Нейлон, Тип 6/6 (Type 6/6), формовочный состав | 80 | 44.4 |
| Неодим | 9.6 | 5.3 |
| Никель | 13.0 | 7.2 |
| Ниобий (Columbium) | 7 | 3.9 |
| Нитрат целлюлозы (CN) | 100 | 55.6 |
| Окись алюминия | 5.4 | 3.0 |
| Олово | 23.4 | 13.0 |
| Осмий | 5 | 2.8 |
| Палладий | 11. 8 8 | 6.6 |
| Песчаник | 11.6 | 6.
|
| Платина | 9.0 | 5.0 |
| Плутоний | 54 | 30.2 |
| Полиалломер | 91.5 | 50.8 |
| Полиамид (PA) | 110 | 61.1 |
| Поливинилхлорид (PVC) | 50.4 | 28 |
| Поливинилденфторид (PVDF) | 127.8 | 71 |
| Поликарбонат (PC) | 70.2 | 39 |
| Поликарбонат — армированный стекловолокном | 21.5 | 12 |
| Полипропилен — армированный стекловолокном | 32 | 18 |
| Полистирол (PS) | 70 | 38. 9 |
| Полисульфон (PSO) | 55.8 | 31 |
| Полиуретан (PUR), жесткий | 57.6 | 32 |
| Полифенилен — армированный стекловолокном | 35.8 | 20 |
| Полифенилен (PP), ненасыщенный | 90.5 | 50. 3 3 |
| Полиэстер | 123.5 | 69 |
| Полиэстер, армированный стекловолокном | 25 | 14 |
| Полиэтилен (PE) | 200 | 111 |
| Полиэтилен — терефталий (PET) | 59.4 | 33 |
| Празеодимий | 6.7 | 3.7 |
| Припой 50 — 50 | 24.0 | 13. 4 |
| Прометий | 11 | 6.1 |
| Рений | 6.7 | 3.7 |
| Родий | 8 | 4.5 |
| Рутений | 9.1 | 5.1 |
| Самарий | 12.7 | 7.1 |
| Свинец | 28.0 | 15.1 |
| Свинцово-оловянный сплав | 11.6 | 6.5 |
| Селен | 3.8 | 2.1 |
| Серебро | 19.5 | 10.7 |
| Скандий | 10.2 | 5.7 |
| Слюда | 3 | 1.7 |
| Сплав твердый (Hard alloy) K20 | 6 | 3. 3 |
| Сплав хастелой (Hastelloy) C | 11. 3 3 | 6.3 |
| Сталь | 13.0 | 7.3 |
| Сталь нержавеющая аустенитная (304) | 17.3 | 9.6 |
| Сталь нержавеющая аустенитная (310) | 14.4 | 8.0 |
| Сталь нержавеющая аустенитная (316) | 16.0 | 8.9 |
| Сталь нержавеющая ферритная (410) | 9.9 | 5.5 |
| Стекло витринное (зеркальное, листовое) | 9.0 | 5.0 |
| Стекло пирекс, пирекс | 4.0 | 2.2 |
| Стекло тугоплавкое | 5.9 | 3. 3 |
| Строительный (известковый) раствор | 7.3 — 13.5 | 4.1-7.5 |
| Стронций | 22.5 | 12.5 |
| Сурьма | 10.4 | 5.8 |
| Таллий | 29.9 | 16.6 |
| Тантал | 6.5 | 3.6 |
| Теллур | 36.9 | 20.5 |
| Тербий | 10.3 | 5.7 |
| Титан | 8.6 | 4. 8 8 |
| Торий | 12 | 6.7 |
| Тулий | 13.3 | 7.4 |
| Уран | 13.9 | 7.7 |
| Фарфор | 3.6-4.5 | 2.0-2. 5 |
| Фенольно-альдегидный полимер без добавок | 80 | 44.4 |
| Фторэтилен пропилен (FEP) | 135 | 75 |
| Хлорированный поливинилхлорид (CPVC) | 66.6 | 37 |
| Хром | 6.2 | 3.4 |
| Цемент | 10.0 | 6.0 |
| Церий | 5.2 | 2.9 |
| Цинк | 29.7 | 16.5 |
| Цирконий | 5.7 | 3.2 |
| Шифер | 10.4 | 5.8 |
| Штукатурка | 16.4 | 9.2 |
| Эбонит | 76.6 | 42. 8 |
| Эпоксидная смола , литая резина и незаполненные продукты из них | 55 | 31 |
| Эрбий | 12.2 | 6.8 |
| Этилен винилацетат (EVA) | 180 | 100 |
| Этилен и этилакрилат (EEA) | 205 | 113. 9 9 |
| Эфир виниловый | 16 — 22 | 8.7 — 12 |
www.dpva.ru
Понятие о модуле упругости
В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:
- Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
- Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).
Формула по закону Гука записывается в виде ε = σz/E, где:
- ε – относительное удлинение;
- σz – нормальное напряжение.
Демонстрация закона Гука для упругих тел:
Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.
Модуль упругости – это постоянная величина, характеризующая сопротивление тела и его конструкционного материала при нормальной растягивающей или сжимающей нагрузке.
В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.
Значения модуля упругости для некоторых материалов приведены в таблице 1.
Таблица 1: Модуль упругости для металлов и сплавов
| Наименование материала | Значение модуля упругости, 10¹²·Па |
| Алюминий | 65…72 |
| Дюралюминий | 69…76 |
| Железо, содержание углерода менее 0,08 % | 165…186 |
| Латунь | 88…99 |
| Медь (Cu, 99 %) | 107…110 |
| Никель | 200…210 |
| Олово | 32…38 |
| Свинец | 14…19 |
| Серебро | 78…84 |
| Серый чугун | 110…130 |
| Сталь | 190…210 |
| Стекло | 65…72 |
| Титан | 112…120 |
| Хром | 300…310 |
Источник: https://molotok34. ru/spravochnik/modul-sdviga-stali.html
ru/spravochnik/modul-sdviga-stali.html
Механические свойства
Только при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала . А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры:
Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства . Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.
У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.
Понятие о модуле упругости
В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:
Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:
- Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
- Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).
Формула по закону Гука записывается в виде ε = σz/E, где:
- ε – относительное удлинение;
- σz – нормальное напряжение.
Демонстрация закона Гука для упругих тел:
Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.
Модуль упругости – это постоянная величина, характеризующая сопротивление тела и его конструкционного материала при нормальной растягивающей или сжимающей нагрузке.
В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.
Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.
Значения модуля упругости для некоторых материалов приведены в таблице 1.
Таблица 1: Модуль упругости для металлов и сплавов
7.5. Сопротивление материалов
Модуль Юнга (модуль упругости первого рода) Е, МПа, Н/мм2 — постоянная упругости в законе Гука в пределах, когда деформация пропорциональна напряжению.
Модуль Юнга численно равен напряжению, увеличивающему длину образца в два раза: для стали, Ест = (2,0-2,2)×105 МПа; для чугуна, Еч = 1,2×105 МПа; для меди, Ем = 1,0×105 МПа; для алюминия, Еал = 0,6×105 МПа; для каната, Ек = (1,1-1,7)×105 МПа: канат с органическим сердечником, Ео = (1,1-1,3)×105 МПа; канат с металлическим сердечником, Емет = 1,4×105 МПа; канат закрытый, Ез = 1,7×105 МПа.
Закон Гука: возникающее удлинение образца Δl под действием внешней силы Р пропорционально величине действующей силы, первоначальной длине l и обратно пропорционально площади поперечного сечения S:
Δl = (l × Р) / (Е × S) или р = Е × ε,
где р = Р / S — напряжение; ε = Δl / l — относительная продольная деформация.
Материалы разделяются на хрупкие и пластичные. Хрупкие вещества разрушаются при очень малых относительных удлинениях. Хрупкие материалы обычно выдерживают, не разрушаясь, большее сжатие, чем растяжение.
Совместно с деформацией растяжения наблюдается уменьшение диаметра образца. Если Δd — изменение диаметра образца, то ε1 = Δd / d принято называть относительной поперечной деформацией. Абсолютная величина μ = ε1 / ε носит название коэффициента поперечной деформации — коэффициента Пуассона. Коэффициент Пуассона для стали: μст = 0,3.
Сдвиг — деформация, при которой все слои тела, параллельные некоторой плоскости, смещаются друг относительно друга.
Закон Гука для деформации сдвига: р = G × α, где G — модуль сдвига; α — угол сдвига (относительный сдвиг). Модуль упругости стали при сдвиге: Gст = 0,8×105 МПа.
Соотношение между упругими постоянными: G = Е / 2 × (1 + μ).
Температурный коэффициент линейного расширения — величина, равная среднему (в интервале температур [0; t] °С) относительному удлинению тела (град-1): α = (l1 – l) / (t × l0). Температурный коэффициент линейного расширения: для стали, αст = (11-12)×10-6 град-1; для меди, αм = 16,5×10-6 град-1; для алюминия, αал = 23,0×10-6 град-1.
Температурный коэффициент линейного расширения: для стали, αст = (11-12)×10-6 град-1; для меди, αм = 16,5×10-6 град-1; для алюминия, αал = 23,0×10-6 град-1.
Отсутствие тепловых зазоров приводит к возникновению значительных сил, определяемых площадью сечения вала:
Fa = E × S × α × Δt,
где E — модуль Юнга, МПа; S — площадь сечения вала, м2; α — коэффициент линейного расширения, град-1; Δt — повышение температуры, °С.
Предел текучести — напряжение, при котором появляется текучесть (увеличение деформации без увеличения деформирующей силы). Предел текучести: рядовая сталь, σт = 200 МПа; сталь средней прочности, σт = 400 МПа; легированная сталь, σт = 800 МПа.
Предел упругости — напряжение, при котором остаточные деформации впервые достигают некоторой величины, характеризуемой определенным допуском, устанавливаемым техническими условиями.
Предел прочности — напряжение, отвечающее наибольшей нагрузке, предшествовавшей разрушению образца.
Усталость — процесс постепенного возникновения и развития трещины в материале под воздействием многократно повторяющихся силовых воздействий.
Предел выносливости — наибольшее напряжение, которое может выдержать материал при заданном числе циклов нагружения.
Ползучесть — нарастание во времени пластической деформации материала при силовых воздействиях, меньших чем те, которые вызывают остаточную деформацию.
| < 7.4. Мерительный инструмент | Содержание | 7.6. Основы термообработки > |
0 0 голоса
Рейтинг статьи
Модули прочности
Кроме нормального нагружения, существуют и иные силовые воздействия на материалы.
Модуль сдвига G определяет жесткость. Эта характеристика показывает предельное значение нагрузки изменению формы предмета.
Модуль объемной упругости К определяет упругие свойства материала изменить объем. При любой деформации происходит изменение формы предмета.
Коэффициент Пуассона μ определяет изменения отношение величины относительного сжатия к растяжению. Эта величина зависит только от свойств материала.
Для разных сталей значения указанных модулей приведены в таблице 3.
Таблица 3: Модули прочности для сталей
| Наименование стали | Модуль упругости Юнга, 10¹²·Па | Модуль сдвигаG, 10¹²·Па | Модуль объемной упругости, 10¹²·Па | Коэффициент Пуассона, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 | 87…91 | 45…49 | 154…168 |
| Сталь 3 | 179…189 | 93…102 | 49…52 | 164…172 |
| Сталь 30 | 194…205 | 105…108 | 72…77 | 182…184 |
| Сталь 45 | 211…223 | 115…130 | 76…81 | 192…197 |
| Сталь 40Х | 240…260 | 118…125 | 84…87 | 210…218 |
| 65Г | 235…275 | 112…124 | 81…85 | 208…214 |
| Х12МФ | 310…320 | 143…150 | 94…98 | 285…290 |
| 9ХС, ХВГ | 275…302 | 135…145 | 87…92 | 264…270 |
| 4Х5МФС | 305…315 | 147…160 | 96…100 | 291…295 |
| 3Х3М3Ф | 285…310 | 135…150 | 92…97 | 268…273 |
| Р6М5 | 305…320 | 147…151 | 98…102 | 294…300 |
| Р9 | 320…330 | 155…162 | 104…110 | 301…312 |
| Р18 | 325…340 | 140…149 | 105…108 | 308…318 |
| Р12МФ5 | 297…310 | 147…152 | 98…102 | 276…280 |
| У7, У8 | 302…315 | 154…160 | 100…106 | 286…294 |
| У9, У10 | 320…330 | 160…165 | 104…112 | 305…311 |
| У11 | 325…340 | 162…170 | 98…104 | 306…314 |
| У12, У13 | 310…315 | 155…160 | 99…106 | 298…304 |
Для других материалов значения прочностных характеристик указывают в специальной литературе. Однако, в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводят испытания по определению предельных значений.
Однако, в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводят испытания по определению предельных значений.
Одной из главных задач инженерного проектирования является выбор материала конструкции и оптимального сечения профиля. Необходимо найти тот размер, который при минимально возможной массе будет обеспечивать сохранение формы системы под воздействием нагрузки.
Например, какой номер стального двутавра использовать в качестве пролетной балки сооружения? Если взять профиль размерами ниже требуемого, то гарантировано получим разрушение строения. Если больше, то это ведет к нерациональному использованию металла, а, следовательно, утяжелению конструкции, усложнению монтажа, увеличению финансовых затрат. Знание такого понятия как модуль упругости стали даст ответ на вышепоставленный вопрос, и позволит избежать появления данных проблем на самом раннем этапе производства.
Способы расчета модуля упругости
Известны также и другие характеристики упругости, которые описывают сопротивление материалов к воздействиям как к линейным, так и отличным от них.
Обозначается как Е и выражается в Па или ГПа.
Показывает зависимость относительного удлинения от нормальной составляющей cилы (F) к ее площади распространения (S) и упругости (Е):
σz = F/ES (3)
Параметр также называют модулем Юнга или модулем упругости первого рода, в таблице показаны величины для материалов различной природы.
| Название материала | Значение параметра, ГПа |
| Алюминий | 70 |
| Дюралюминий | 74 |
| Железо | 180 |
| Латунь | 95 |
| Медь | 110 |
| Никель | 210 |
| Олово | 35 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 190/210 |
| Стекло | 70 |
| Титан | 112 |
| Хром | 300 |
Модулем упругости второго рода называют модуль сдвига (G), который показывает сопротивление материала к сдвигающей силе (FG). Может быть выражена двумя способами.
Может быть выражена двумя способами.
Через касательные напряжения (τz) и угол сдвига (γ):
G = τz/γ (4)
Через соотношение модуля упругости первого рода и коэффициента Пуасонна (ν):
G = E/2(1+υ) (5)
Определенное в результате экспериментов значение сопротивления материала изгибу, называется модулем упругости при изгибе, и вычисляется следующим образом:
EИ = ((0,05-0,1)Fр— 0,2Fр)L2 / 4bh4(ƒ2-ƒ1) (6)
где Fр – разрушающая сила, Н;
L – расстояние между опорами, мм;
b, h – ширина и толщина образца, мм;
ƒ1, ƒ2– прогибы, образованные в результате нагрузки F1 и F2.
При равномерном давлении по всему объему на объект, возникает его сопротивление, называемое объемным модулем упругости или модулем сжатия (К). Выразить этот параметр можно, практически через все известные модули и коэффициент Пуассона.
Определение модуля упругости щебеночного основания
Параметры Ламе также используют для описания оценки прочности материала. Их два μ – модуль сдвига и λ. Они помогают учитывать все изменения внутри материала в трехмерном пространстве, тогда соотношения между нормальным напряжением и деформацией будет выглядеть следующим образом:
Их два μ – модуль сдвига и λ. Они помогают учитывать все изменения внутри материала в трехмерном пространстве, тогда соотношения между нормальным напряжением и деформацией будет выглядеть следующим образом:
σ = 2με + λtrace(ε)I (7)
Оба параметра могут быть выражены из следующих соотношений:
λ = νE / (1+ν)(1-2ν) (8)
μ = E / 2(1+ν) (9)
Модуль упругости для разных марок стали
Металлурги разработали несколько сотен марок сталей. Им свойственны разные значения прочности. В таблице 2 показаны характеристики для наиболее распространенных сталей.
Таблица 2: Упругость сталей
| Наименование стали | Значение модуля упругости, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 |
| Сталь 3 | 179…189 |
| Сталь 30 | 194…205 |
| Сталь 45 | 211…223 |
| Сталь 40Х | 240…260 |
| 65Г | 235…275 |
| Х12МФ | 310…320 |
| 9ХС, ХВГ | 275…302 |
| 4Х5МФС | 305…315 |
| 3Х3М3Ф | 285…310 |
| Р6М5 | 305…320 |
| Р9 | 320…330 |
| Р18 | 325…340 |
| Р12МФ5 | 297…310 |
| У7, У8 | 302…315 |
| У9, У10 | 320…330 |
| У11 | 325…340 |
| У12, У13 | 310…315 |
Видео: закон Гука, модуль упругости.
Модуль упругости для стали, а также для других материалов
Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.
Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.
Модуль упругости бетона: таблица, как определить
Выбор стройматериала является важнейшей задачей строителя перед началом выполнения работ. Модуль упругости бетона — один из главных критериев, влияющих на эксплуатационные характеристики. Параметр определяет возможность стеснения и расширения материала, зависит от многих факторов, которые важно учитывать.
Содержание
- Что за величина?
- Разновидности бетона и их показатель упругости
- Таблица, содержащая классы и соответствующие модули упругости
- От чего зависит величина?
- Как определить?
Что за величина?
Модуль упругости бетона — это возможность конструкции противостоять изменениям под воздействиями внешних факторов. Это важный критерий выбора марки материала для определенной работы, так как затвердевший материал в процессе эксплуатации сжимается и растягивается. Поэтому на этапе проектирования нужно правильно рассчитать допустимые значения для той или иной конструкции. Для расчетов пользуются таблицами определения модуля упругости, что представлены в нормативах для строительных работ.
Разновидности бетона и их показатель упругости
Бетонный камень в окончательном виде — твердый материал, что под влиянием внешней среды способен деформироваться. При постоянных механических нагрузках, даже модуль упругости железобетона может быть недостаточно высоким.
Для определения вида прочности учитывается 2 критерия — растяжение и сжатие, что влияют на сопротивление нагрузкам.
Различают следующие виды материала:
Материал может производиться в нескольких разновидностях.- тяжелые;
- легкие;
- мелкозернистые;
- поризованные;
- автоклавного твердения.
Таблица, содержащая классы и соответствующие модули упругости
Классификация в таблице производится согласно СП 52—101—2003:
| Класс бетона | Модуль упругости |
| 19,0 | В10 |
| 24,0 | В15 |
| 27,5 | В20 |
| 30,0 | В25 |
| 32,5 | В30 |
| 34,5 | В35 |
| 36,0 | В40 |
| 37,0 | В45 |
| 38,0 | В50 |
| 39,0 | В55 |
| 39,5 | В60 |
От чего зависит величина?
На величину данного показателя значительно влияет наполнитель в материала.
Упругость раствора зависит от множества факторов. Первое, на что обращают внимание — наполнитель. Коэффициент напрямую связан с упругостью раствора. Так, высокими показателями являются тяжелые бетоны, наполнителями в которых являются гравий и щебень. Допустимые нагрузки на постройки из такого материала самые высокие, поэтому важно выбирать правильные заполнители. Учитывают не только интенсивность нагрузок, но и частоту.
Возраст и время укладки материала играют немаловажную роль в показателях модуля упругости. Крепость материала возрастает на протяжении 50 лет с момента заливки, вне зависимости от внешних температур (до 230 ⁰C). Кроме того, характеристики завися от процесса затвердевания (автоклавный, естественный). Чтобы узнать продолжительность предполагаемых нагрузок, нужно начальный показатель перемножать с показателем: 0,7 для поризованных бетонов, 0,85 — для тяжелых легких и мелкозернистых.
Возраст залитого материала находится в прямопропорциональной зависимости с данным показателем.
Классы бетонного раствора в частной стройке варьируют в пределах В7,5—30 (марки М100—400), но таких прочностных и других характеристик хватает вне зависимости от требований и сложностей конструкций. Показатели модуля увеличивает арматура, так как характеристики арматуры повышают показатели общей конструкции. Методика укладки арматуры в бетон определяется ГОСТом 24452—80.
Посмотреть «ГОСТ 24452-80» или cкачать в PDF (350 KB)
Как определить?
СП 52 101 2003 — стандарт определения параметров применения бетона. Здесь указаны значения всех необходимых коэффициентов для расчета параметров, а подтверждение проводится путем эксперимента на изготовленных образцах. Суть испытания заключается в постепенной нагрузке на образцы (цилиндры или призмы из бетонной смеси) путем осевого сжимающего нагружения до разрушения. Параллельно измеряется степень деформации.
Посмотреть «СП 52-101-2003» или cкачать в PDF (1007.4 KB)
Результаты можно обозначить следующим образом:
- Показатель соответствует расчетам, образец поддался пластической деформации без растрескивания.

- Предварительные подсчеты неверные: при предполагаемом нагружении образец подвергается сильным разрушениям.
Расчетным способом определяют запас прочности не только обычных зданий, но и арочных сооружений, перекрытий, мостов и дорог. Модуль упругости асфальтобетона при использовании — проблемная задача проектирования, так как подход, разрешающий провести точные расчеты еще не выведен. Не удается определить взаимосвязь между статическим и динамическим модулями в процессе использования дорог.
Что такое модуль упругости бетона
Бетонные строительные конструкции постоянно испытывают большие нагрузки. Это необходимо учитывать еще на этапе их планирования. Поэтому технологами была разработана система придания бетону способности упруго деформироваться под воздействием таких факторов, как давление и сила. Величина, характеризующая данный показатель, получила название модуль упругости бетона.
Величина, характеризующая данный показатель, получила название модуль упругости бетона.
Рассчитывая строительную конструкцию, специалисты с помощью формулы вычисляют соотношение напряжения и модуль деформации бетона B25 или материала другого класса. Для удобства данные, полученные лабораторным путем, занесены в таблицы, которые соответствуют СНиП. Ими всегда можно воспользоваться при проектировании любой конструкции.
Модуль упругости бетона – таблица
Модуль упругости бетона – таблица
Разработанная согласно Своду правил 52 101 2003 таблица поможет определить величину начального модуля упругости для различных классов бетона:
Зная класс материала, а также имея информацию о плотности стройматериала и технологии изготовления, несложно определить величину параметра по специальной таблице.
Определение упругости и единицы измерения
Значение модуля любого вида бетона определяется согласно действующему СП 52-101-2003. Это нормативный документ, таблицы которого содержат все необходимые коэффициенты для определения упругости материала на м2.
Это нормативный документ, таблицы которого содержат все необходимые коэффициенты для определения упругости материала на м2.
Выполняя специальные расчеты с учетом того, какова деформация используемого материала, специалисты могут точно определить величину запаса прочности сооружения арочного типа, любого перекрытия здания, автомобильного или железнодорожного моста.
В литературе для профессионалов параметр упругости принято обозначать буквой Е. На его величину влияет действующая нагрузка и структура бетона. За единицу измерения взят паскаль, поскольку напряжение, вызванное в опытном образце действующей на него силой, измеряется в паскалях.
На модуль упругости В20 и других видов влияет технология производства, в частности способ твердения: естественный, автоклавный или тепловой обработки. Важную роль играют эксплуатационные характеристики материала.
Поэтому такой показатель, как упругость не одинаковый у одного класса. Например, если рассматривать ячеистые или тяжелые материалы, имеющие одно и то же значение прочности на м2, то величины их модулей будут разные.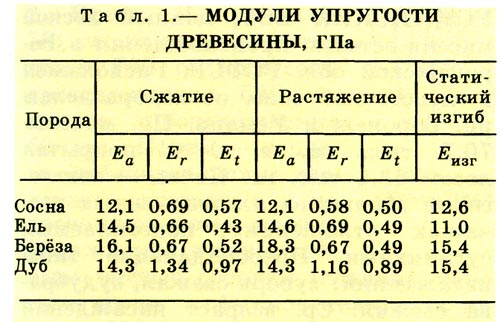
Табличные данные помогают определить значение сопротивления и в соответствии с ним выбрать нужный тип бетона для проведения тех или иных видов строительных работ.
Для того чтобы повысить модуль упругости бетона В15, специалисты рекомендуют использовать различные методы его изготовления. Так, при автоклавной обработке появляются более высокие упругие свойства, достигающие цифры 17. Применяя тепловую обработку с использованием атмосферного давления, можно увеличить значение до 20,5. Наибольшая величина модуля достигается при естественном твердении.
Подобным образом можно поднять модуль упругости В25 — самого популярного у строителей. При этом важно помнить, что при увеличении показателя класса материала растет и показатель его сопротивляемости упругим деформациям.
Рекомендации
Профессиональные строители рекомендуют для повышения величины модуля упругости применять различные технологии изготовления. Рассмотрим, как изменяет свойства бетон б15, изготовленный различными методами:
Аналогичная тенденция прослеживается для других классов бетона, включая популярный b25 бетон.
С рассматриваемой точки зрения прослеживаются следующие тенденции:
Используя табличные значения, несложно определить модуль сопротивления, и выбрать класс бетона для выполнения конкретных задач.
Что влияет на модуль упругости?
- Прямое воздействие оказывают свойства компонентов в бетоне. Мало того, данная подвластность полностью прямолинейная. У бетонов с небольшим весом этот показатель меньше, а вот у более тяжелых крупнозернистых видов он больше.
- Классификация бетона. Для выяснения зависимости искомого коэффициента составлена специальная таблица. Обычный потребитель в работе применяет небольшой перечень данных изделий, в связи с этой причиной нет необходимости приводить ее целиком. По известным показателям прочности и модуля понятно, что они пропорционально зависят друг от друга. Причем, данная зависимость не меняется при температурном воздействии ниже 230С. То есть в основном показатели не меняются вообще. Данный нюанс дает возможность контролировать такую характеристику продукта, как упругость, к тому же это выполнимо в одних и тех же классах материала.
 Это свойство учитывают для того, чтобы знать какой из продуктов может быть установлен. При возведении загородных частных домов применяют довольно маленький перечень бетонных растворов, согласно их классности. Чаще всего этот выбор происходит в диапазоне от В7 до В30, а также М100, М150, М200, М250, М300, М350, М400. Однако данного ассортимента полностью хватает для возведения малоэтажных зданий. Это возможно, даже если в строительстве применяются плитные цоколи, а также формируются арки для декорирования.
Это свойство учитывают для того, чтобы знать какой из продуктов может быть установлен. При возведении загородных частных домов применяют довольно маленький перечень бетонных растворов, согласно их классности. Чаще всего этот выбор происходит в диапазоне от В7 до В30, а также М100, М150, М200, М250, М300, М350, М400. Однако данного ассортимента полностью хватает для возведения малоэтажных зданий. Это возможно, даже если в строительстве применяются плитные цоколи, а также формируются арки для декорирования. - Возраст бетона. Известна зависимость между повышением искомого коэффициента и периода эксплуатации. По этой причине во время определения показателя в нужный отрезок времени, применяют специальные таблицы. В ней указаны первичные данные, которые необходимо умножить на поправочные модули.
- Метод переработки компонентов. Большую роль играет то, в каких условиях происходило застывание бетона. Ведь он мог отвердеть естественным образом, во время термического воздействия либо с применением автоклава.

- Длительность влияния давления. Чтобы выяснить этот показатель, начальный показатель множат на требуемый модуль. Для каждого из типов бетона данный модуль имеет свое значение. Для легких, тяжелых и мелкозернистых – 0,85, для поризованных – 0,7.
Прежде чем изучить другие нюансы, оказывающие воздействие на анализируемую характеристику, необходимо подробнее рассмотреть такое определение, как ползучесть бетона. Данный показатель оказывает большое влияние на стадию разрушения изделия. Ведь при недолгой малой нагрузке материал деформируется, но после прекращения воздействия он возвращается в изначальное состояние.
Данный момент можно детально не разбирать, так как весьма сложно определить вид деформации. Внешне пластичная и упругая деформация никак не отличается. Однако стоит указать, что пластичное разрушение объясняется свойством ползучести бетона. В частности, именно этот параметр берется в расчет при долгом воздействии на материал. Модуль ползучести также имеет свое буквенное обозначение:
- Влагосодержание в окружающем воздухе.
 Данное обстоятельство связано с модулем ползучести. Если необходимо точное значение, то она также узнается из соответствующих таблиц. В таком случае во внимание также берутся температура и уровень радиационного фона.
Данное обстоятельство связано с модулем ползучести. Если необходимо точное значение, то она также узнается из соответствующих таблиц. В таком случае во внимание также берутся температура и уровень радиационного фона. - Наличие металлического каркаса для армирования. Благодаря своему составу, металл не так сильно подвержен разрушениям вследствие воздействия, в отличие от простого бетона.
ПРОВЕДЕНИЕ ИСПЫТАНИЙ
4.1. При определении модуля упругости и коэффициента Пуассона шкалу силоизмерителя испытательного пресса (машин) выбирают из условия, что ожидаемое значение разрушающей нагрузки должно быть от 70% до 80% от максимальной, допускаемой выбранной шкалой. При определении призменной прочности шкалу силоизмерителя выбирают в соответствии с требованиями ГОСТ 10180-78.
4.2. Перед испытанием образец с приборами устанавливают центрально по разметке плиты пресса и проверяют совмещение начального отсчета с делением шкалы прибора.
4.5. При центрировании образцов деформации фиктивных волокон, совпадающих с центрами отверстий, в которых крепят индикаторы (см. чертеж), относят к граням образца и определяют по формулам:
чертеж), относят к граням образца и определяют по формулам:
где и — деформации фиктивных волокон на противоположных гранях образца;
и — деформации, отнесенные к граням образца;
— размер стороны образца;
— расстояние от грани образца до центра отверстий, в которых крепят индикаторы.
Определения
Расчетное сопротивление – это показатель стойкости материала нагружающим воздействиям. Используется он при проектировочных расчетах, и неотъемлемо связан с нормативными показателями сопротивления сжатию.
До 2000−х годов ориентировались только на марки материала, которые и принимали как расчетный показатель, но по новым техническим документам, каждой марке присвоен новый критерий соответствия образца сжимающим нагрузкам.
Согласно СП 52−101−2003, нормативные значения сопротивления представлены на фото ниже.
Есть еще такое определение, как предел прочности на растяжение. По своей природе, данный материал в разы хуже выдерживает растягивающие нагрузки./95.jpg) Поэтому его и армируют в ЖБИ, стяжках пола большой толщины, фундаментах и прочее.
Поэтому его и армируют в ЖБИ, стяжках пола большой толщины, фундаментах и прочее.
Таблица 6.7 из СП 63.13330.2012″СНиП 52-01-2003, в которой указаны марки сопротивление к сжатию, растяжению.
| Вид | Бетон | Нормативные сопротивления МПа, и расчетные сопротивления для предельных состояний второй группы и МПа, при классе материалапо прочности на сжатие | |||||||||||||||||||||
| В1,5 | В2 | В2,5 | В3,5 | В5 | В7,5 | В10 | В12,5 | В15 | В20 | В25 | В30 | В35 | В40 | В45 | В50 | В55 | В60 | В70 | В80 | В90 | В100 | ||
| Сжатие осевое растяжение | Тяжелый, мелкозернистый и напрягающий | — | — | — | 2,7 | 3,5 | 5,5 | 7,5 | 9,5 | 11 | 15 | 18,5 | 22 | 25,5 | 29 | 32 | 36 | 39,5 | 43 | 50 | 57 | 64 | 71 |
| Легкий | — | — | 1,9 | 2,7 | 3,5 | 5,5 | 7,5 | 9,5 | 11 | 15 | 18,5 | 22 | 25,5 | 29 | — | — | — | — | — | — | — | — | |
| Ячеистый | 1,4 | 1,9 | 2,4 | 3,3 | 4,6 | 6,9 | 9,0 | 10,5 | 11,5 | — | — | — | — | — | — | — | — | — | — | — | — | — | |
| Растяжение осевое | Тяжелый, мелкозернистый и напрягающий | — | — | — | 0,39 | 0,55 | 0,70 | 0,85 | 1,00 | 1,10 | 1,35 | 1,55 | 1,75 | 1,95 | 2,10 | 2,25 | 2,45 | 2,60 | 2,75 | 3,00 | 3,30 | 3,60 | 3,80 |
| Легкий | — | — | 0,29 | 0,39 | 0,55 | 0,70 | 0,85 | 1,00 | 1,10 | 1,35 | 1,55 | 1,75 | 1,95 | 2,10 | — | — | — | — | — | — | — | — | |
| Ячеистый | 0,22 | 0,26 | 0,31 | 0,41 | 0,55 | 0,63 | 0,89 | 1,00 | 1,05 | — | — | — | — | — | — | — | — | — | — | — | — | ||
Кавабанга! Марки и разновидности цементов и их особенности
От прочности в срезе при скалывании, зависит устойчивость к сжатию от корреляционных показателей.
Примечание. Сопротивление сжатию В25 наиболее часто встречающийся показатель при проектировании материала.
ПРИЛОЖЕНИЕ 1 (обязательное). МЕТОДЫ НАСЫЩЕНИЯ ОБРАЗЦОВ ВОДОЙ И ЖИДКИМИ НЕФТЕПРОДУКТАМИ
3. Перед насыщением образцы взвешивают, определяют их массу с точностью не менее 0,5 г.
5. При насыщении легкими нефтепродуктами и водой образцы помещают в ванны и заливают жидкость так, чтобы ее уровень был не менее чем на 10 мм выше верхней грани образцов. Ванны должны быть герметично закрыты крышками.
6. Образцы взвешивают при насыщении их водой или легкими нефтепродуктами один раз в сутки, а при насыщении тяжелыми нефтепродуктами — один раз в 7 сут.
От чего зависит упругость бетона
Главной характеристикой, определяющей прочность бетона, является коэффициент его упругости. Он важен для профессиональных проектировщиков, которые проводят расчеты нагрузочных способностей бетонных конструкций.
Существует специальная таблица, разработанная согласно СП. По ней определяется начальный модуль упругости бетона.
По ней определяется начальный модуль упругости бетона.
Модуль упругости бетонных конструкций – важный параметр
Модуль упругости бетона, характеризующий способность массива сохранять целостность под воздействием деформации, используют проектировщики при выполнении прочностных расчетов строительных конструкций. Главная отличительная черта бетонных изделий и конструкций – твердость. Вместе с тем, воздействие нагрузки, величина которой превышает допустимые значения, вызывает сжатие и растяжение композита. Затвердевший монолит в процессе деформации изменяется. Причина – ползучесть материала.
В зависимости от значения коэффициента ползучести и величины приложенной нагрузки, структура монолита изменяется постепенно:
- на первом этапе приложения нагрузки происходит кратковременное изменение структуры бетона. Он сохраняет целостность и восстанавливает первоначальное состояние. Растягивающие и сжимающие усилия, а также изгибающие моменты вызывают упругую деформацию без необратимых разрушений;
- на следующей стадии при резком возрастании нагрузки возникают разрушения необратимого характера.
 В результате пластичной деформации возникают глубокие трещины, являющиеся, в дальнейшем, причиной постепенного разрушения зданий и различных бетонных конструкций.
В результате пластичной деформации возникают глубокие трещины, являющиеся, в дальнейшем, причиной постепенного разрушения зданий и различных бетонных конструкций.
Коэффициент упругости – главная характеристика, определяющая прочностные свойства бетона. Показатель представляет интерес для профессиональных проектантов, занимающихся расчетом нагрузочной способности бетонных конструкций. Индивидуальным застройщикам следует ориентироваться на класс материала, с возрастанием которого увеличивается значение модуля упругости бетона.
Коэффициент упругости – главная характеристика, определяющая прочностные свойства бетона
Новые редакции указателей нормативных документов по энергетике
Для работы с текстом документа (печать документа, поиск по тексту) необходимо авторизоваться.
Сервис содержит 19095 бесплатных документов
, которые доступны зарегистрированным пользователям. Регистрируйся бесплатно >>>
- Информация о документе
- Ссылки на документы
- Ссылки из других документов
| Наименование документа | ГОСТ 24452-80. Бетоны. Методы определения призменной прочности, модуля упругости и коэффициента Пуассона Бетоны. Методы определения призменной прочности, модуля упругости и коэффициента Пуассона |
| Дата начала действия | 01.01.1982 |
| Дата принятия | 18.11.1980 |
| Дата отмены действия | 01.09.2010 |
| Статус | Недействующий |
| Новый документ | ДСТУ Б В.2.7-217:2009 |
| Вид документа | ГОСТ (Межгосударственный стандарт) |
| Шифр документа | 24452-80 |
| Разработчик | Госстрой СССР |
| Принявший орган | Госстрой СССР |
В данном документе нет ссылок на другие нормативные документы.
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
Методы определения призменной прочности,
модуля упругости и коэффициента Пуассона
Concretes. Methods of prismatic, compressive strength,
modulus of elasticity and Poisson’s ratio determination
Дата введения 1982-01-01
УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по делам строительства от 18 ноября 1980 г. № 177.
№ 177.
ПЕРЕИЗДАНИЕ. Июль 1989 г.
Стандарт устанавливает методы определения призменной прочности, модуля упругости и коэффициента Пуассона бетона.
Стандарт соответствует рекомендации СЭВ РС 279-65 и РИЛЕМ Р8 в части требований к образцам.
Размеры образцов в зависимости от наибольшей крупности заполнителя должны удовлетворять требованиям ГОСТ 10180-78
Нормативные данные для расчетов железобетонных конструкций:
Таблица 2. Начальные модули упругости бетона (согласно СП 52-101-2003)
Таблица 2.1. Начальные модули упругости бетона согласно СНиП 2.03.01-84*(1996)
Примечания: 1. Над чертой указаны значения в МПа, под чертой — в кгс/см 2 .
2. Для легкого, ячеистого и поризованного бетонов при промежуточных значениях плотности бетона начальные модули упругости принимают по линейной интерполяции.
3. Для ячеистого бетона неавтоклавного твердения значения Еb принимают как для бетона автоклавного твердения с умножением на коэффициент 0,8.
4. Для напрягающего бетона значения Еb принимают как для тяжелого бетона с умножением на коэффициент a = 0,56 + 0,006В.
5. Приведенные в скобках марки бетона не точно соответствуют указанным классам бетона.
Таблица 3. Нормативные значения сопротивления бетона (согласно СП 52-101-2003)
Таблица 4. Расчетные значения сопротивления бетона (согласно СП 52-101-2003)
Таблица 4.1. Расчетные значения сопротивления бетона сжатию согласно СНиП 2.03.01-84*(1996)
Таблица 5. Расчетные значения сопротивления бетона растяжению (согласно СП 52-101-2003)
Таблица 6. Нормативные сопротивления для арматуры (согласно СП 52-101-2003)
Таблица 6.1 Нормативные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)
Таблица 6.2. Нормативные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996)
Таблица 7. Расчетные сопротивления для арматуры(согласно СП 52-101-2003)
Таблица 7.
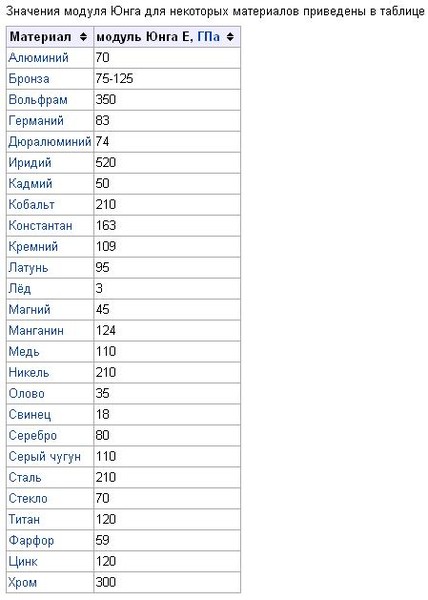 1. Расчетные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)
1. Расчетные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)Расчетное и нормативное сопротивление бетона
Что такое расчетное сопротивление?
Вернуться к оглавлению
Кавабанга! Расслоение бетонной смеси
Как производить расчеты?
Вернуться к оглавлению
Нормативные показатели
Вернуться к оглавлению
Характеристики расчетного значения
Вернуться к оглавлению
Другие характеристики
Помимо вышеуказанных параметров для выполнения определенных расчетов, понадобится ряд дополнительных характеристик:
Заключение
Этот параметр является важным для проектирования несущих стен и других конструкций. Расчеты значений просты: они сводятся к делению нормативных значений на определенные коэффициенты.
Таблицы свойств материалов | МеханиКальк
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения.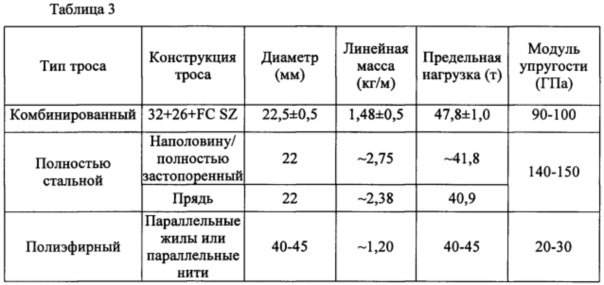 Пожалуйста, включите JavaScript.
Пожалуйста, включите JavaScript.
В приведенных ниже таблицах представлены свойства обычных конструкционных материалов. Предоставленные данные о свойствах материала должны быть репрезентативными для описываемого материала. Предоставленные значения имеют тенденцию к консервативному концу спектра и могут использоваться в качестве базовых расчетных значений для предварительного проектирования. Однако эти значения не соответствуют какой-либо конкретной спецификации, поэтому их не следует использовать в окончательном проекте без предварительной консультации с соответствующими спецификациями материалов. Данные предоставляются «как есть» без каких-либо явных или подразумеваемых гарантий. MechaniCalc, Inc. не несет ответственности за любые убытки, возникшие в результате использования этих данных.
Черные сплавы
Углеродистая сталь
| Материал | Состояние | Предел текучести Прочность [ksi] | Максимальная Прочность [тыс.  фунтов/кв.дюйм] фунтов/кв.дюйм] | Удлинение % | Эластичность Модуль упругости [psi] | Плотность [фунт/дюйм 3 ] | Коэффициент Пуассона |
|---|---|---|---|---|---|---|---|
| AISI 1020 | Горячекатаный | 32 | 50 | 25 | 29e6 | 0,283 | 0,32 |
| Холодная обработка | 60 | 70 | 5 | ||||
| Снятие стресса | 50 | 65 | 10 | ||||
| Отожженный | 28 | 48 | 30 | ||||
| Нормализованный | 34 | 55 | 22 | ||||
| АИСИ 1045 | Горячекатаный | 45 | 75 | 15 | 29e6 | 0,283 | 0,32 |
| Холодная обработка | 80 | 90 | 5 | ||||
| Снятие стресса | 70 | 80 | 8 | ||||
| Отожженный | 35 | 65 | 20 | ||||
| Нормализованный | 48 | 75 | 15 | ||||
| АСТМ А36 | 36 | 58 | 21 | 29e6 | 0,283 | 0,3 | |
| АСТМ А516 | Класс 70 | 38 | 70 | 17 | 29e6 | 0,283 | 0,3 |
ПРИМЕЧАНИЕ : См. нашу базу данных материалов для получения данных, соответствующих спецификациям конкретных материалов. нашу базу данных материалов для получения данных, соответствующих спецификациям конкретных материалов. | |||||||
Легированная сталь
| Материал | Состояние | Предел текучести Прочность [ksi] | Максимальная Прочность [тыс.фунтов/кв.дюйм] | Удлинение % | Эластичность Модуль упругости [psi] | Плотность [фунт/дюйм 3 ] | Коэффициент Пуассона |
|---|---|---|---|---|---|---|---|
| AISI 4130 | Горячекатаный | 70 | 90 | 20 | 29e6 | 0,283 | 0,32 |
| Снятие стресса | 85 | 105 | 10 | ||||
| Отожженный | 55 | 75 | 30 | ||||
| Нормализованный | 60 | 90 | 20 | ||||
| AISI 4140 | Горячекатаный | 90 | 120 | 15 | 29. 7e6 7e6 | 0,283 | 0,32 |
| Снятие стресса | 100 | 120 | 10 | ||||
| Отожженный | 60 | 80 | 25 | ||||
| Нормализованный | 90 | 120 | 20 | ||||
| АСТМ А242 | 46 | 67 | 18 | 30e6 | 0,282 | 0,3 | |
| АСТМ А302 | Класс А | 45 | 75 | 15 | 29e6 | 0,282 | 0,29 |
| Класс С | 50 | 80 | 17 | ||||
| АСТМ А514 | Закалка и отпуск | 100 | 110 | 18 | 29e6 | 0,283 | 0,3 |
| АСТМ А517 | Марка F | 100 | 115 | 16 | 29e6 | 0,280 | 0,29 |
| АСТМ А533 | Класс 1 | 50 | 80 | 18 | 29e6 | 0,282 | 0,29 |
| Класс 2 | 70 | 90 | 16 | ||||
| Класс 3 | 83 | 100 | 16 | ||||
| АСТМ А572 | 50 класс | 50 | 65 | 18 | 30e6 | 0,283 | 0,3 |
| АСТМ А588 | 50 | 70 | 18 | 29. 7e6 7e6 | 0,280 | 0,28 | |
| АСТМ А633 | Марка Е | 55 | 75 | 18 | 29.7e6 | 0,280 | 0,28 |
| АСТМ А656 | 50 класс | 50 | 60 | 20 | 29e6 | 0,282 | 0,29 |
| Класс 60 | 60 | 70 | 17 | ||||
| Класс 70 | 70 | 80 | 14 | ||||
| Класс 80 | 80 | 90 | 12 | ||||
| Класс 100 | 100 | 110 | 12 | ||||
| АСТМ А710 | Класс А | 80 | 85 | 20 | 29.7e6 | 0,280 | 0,3 |
| ХИ-80 | 80 | — | 18 | 29.7e6 | 0,280 | 0,3 | |
| ХИ-100 | 100 | — | 16 | 29. 7e6 7e6 | 0,284 | 0,3 | |
| ПРИМЕЧАНИЕ : См. нашу базу данных материалов для получения данных, соответствующих спецификациям конкретных материалов. | |||||||
Нержавеющая сталь
| Материал | Класс | Состояние | Предел текучести Прочность [ksi] | Максимальная Прочность [тыс.фунтов/кв.дюйм] | Удлинение % | Эластичность Модуль упругости [psi] | Плотность [фунт/дюйм 3 ] | Коэффициент Пуассона |
|---|---|---|---|---|---|---|---|---|
| AISI 201 | Аустенитный | Отожженный | 40 | 75 | 40 | 28e6 | 0,289 | 0,27 |
| AISI 202 | Аустенитный | Отожженный | 40 | 75 | 40 | 28e6 | 0,289 | 0,27 |
| AISI 302 | Аустенитный | Отожженный | 30 | 75 | 40 | 28e6 | 0,289 | 0,27 |
| AISI 304 | Аустенитный | Отожженный | 30 | 75 | 40 | 28e6 | 0,289 | 0,29 |
| АИСИ 304Л | Аустенитный | Отожженный | 25 | 70 | 40 | 28e6 | 0,289 | 0,28 |
| AISI 316 | Аустенитный | Отожженный | 30 | 75 | 40 | 28e6 | 0,289 | 0,26 |
| AISI 316L | Аустенитный | Отожженный | 25 | 70 | 40 | 28e6 | 0,289 | 0,26 |
| AISI 405 | Ферритный | 25 | 60 | 20 | 29e6 | 0,282 | 0,28 | |
| AISI 410 | Мартенситный | Отожженный | 40 | 70 | 16 | 29e6 | 0,282 | 0,28 |
| Закалка и отпуск | 80 | 100 | 12 | |||||
| AISI 430 | Ферритный | 30 | 60 | 20 | 29e6 | 0,282 | 0,28 | |
| AISI 446 | Ферритный | Отожженный | 40 | 65 | 16 | 29e6 | 0,282 | 0,28 |
| 15-5PH | Мартенситный дисперсионный твердеющий | Х900 | 170 | 190 | 10 | 28. 5e6 5e6 | 0,283 | 0,27 |
| х2025 | 145 | 155 | 12 | |||||
| х2150 | 105 | 135 | 16 | |||||
| 17-4PH | Мартенситный дисперсионный твердеющий | Х900 | 170 | 190 | 10 | 28.5e6 | 0,282 | 0,27 |
| х2025 | 145 | 155 | 12 | |||||
| х2150 | 105 | 135 | 16 | |||||
| 17-7PH | Полуаустенитный дисперсионно-твердеющий | Th2050 | 150 | 177 | 6 | 29e6 | 0,276 | 0,28 |
| А-286 | Аустенитный дисперсионный твердеющий | 95 | 140 | 15 | 29.1e6 | 0,287 | 0,31 | |
| Сплав 2205 | Дуплекс аустенитно-ферритный | 65 | 95 | 25 | 28. 5e6 5e6 | 0,287 | 0,27 | |
| Ферраллий 255 | Дуплекс аустенитно-ферритный | 80 | 110 | 15 | 28.5e6 | 0,287 | 0,27 | |
| ПРИМЕЧАНИЕ : См. нашу базу данных материалов для получения данных, соответствующих спецификациям конкретных материалов. | ||||||||
Чугун
| Материал | Класс | Состояние | Предел текучести Прочность [ksi] | Максимальная Прочность [тыс.фунтов/кв.дюйм] | Удлинение % | Эластичность Модуль упругости [psi] | Плотность [фунт/дюйм 3 ] | Коэффициент Пуассона |
|---|---|---|---|---|---|---|---|---|
| АСТМ А159 | Серый чугун | Г1800 | — | 18 | — | 9.6 – 14e6 | 0,264 | 0,26 |
| G2500 | — | 25 | — | 12 – 15e6 | ||||
| Г3000 | — | 30 | — | 13 – 16. 4e6 4e6 | ||||
| G3500 | — | 35 | — | 14,5 – 17e6 | ||||
| G4000 | — | 40 | — | 16 – 20e6 | ||||
| АСТМ А536 | Ковкий чугун | 60-40-18 класс | 40 | 60 | 18 | 24.5e6 | 0,256 | 0,29 |
| Класс 65-45-12 | 45 | 65 | 12 | 24.5e6 | 0,256 | 0,3 | ||
| Марка 80-55-06 | 55 | 80 | 6 | 24.5e6 | 0,256 | 0,31 | ||
| Марка 100-70-03 | 70 | 100 | 3 | 24.5e6 | 0,256 | 0,3 | ||
| Марка 120-90-02 | 90 | 120 | 2 | 23.8e6 | 0,256 | 0,28 | ||
ПРИМЕЧАНИЕ : См. нашу базу данных материалов для получения данных, соответствующих спецификациям конкретных материалов. | ||||||||
Алюминиевые сплавы
| Материал | Состояние | Предел текучести Прочность [ksi] | Максимальная Прочность [тыс.фунтов/кв.дюйм] | Удлинение % | Эластичность Модуль упругости [psi] | Плотность [фунт/дюйм 3 ] | Коэффициент Пуассона |
|---|---|---|---|---|---|---|---|
| Ал 2014 | Т6, Т651 | 59 | 67 | 7 | 10.5e6 | 0,101 | 0,33 |
| Ал 2024 | Т4 | 40 | 62 | 10 | 10.5e6 | 0,1 | 0,33 |
| Ал 5052 | х42 | 23 | 38 | 9 | 10.1e6 | 0,097 | 0,33 |
| Ал 5083 | х216, х421 | 31 | 44 | 10 | 10.3e6 | 0,096 | 0,33 |
| х42 | 31 | 56 | 12 | ||||
| Ал 6061 | Т4 | 16 | 26 | 16 | 9. 9e6 9e6 | 0,098 | 0,33 |
| Т6 | 35 | 38 | 8 | ||||
| Ал 7075 | Т6, Т651 | 68 | 78 | 6 | 10.3e6 | 0,101 | 0,33 |
| ПРИМЕЧАНИЕ : См. нашу базу данных материалов для получения данных, соответствующих спецификациям конкретных материалов. | |||||||
Никелевые сплавы
| Материал | Состояние | Предел текучести Прочность [ksi] | Максимальная Прочность [тыс.фунтов/кв.дюйм] | Удлинение % | Эластичность Модуль упругости [psi] | Плотность [фунт/дюйм 3 ] | Коэффициент Пуассона |
|---|---|---|---|---|---|---|---|
| Хастеллой С-276 | Отжиг на твердый раствор | 41 | 100 | 40 | 29.8e6 | 0,321 | 0,28 |
| Инконель 625 | 1 класс | 55 | 110 | 30 | 29. 8e6 8e6 | 0,305 | 0,28 |
| Класс 2 | 40 | 100 | 30 | ||||
| Инконель 686 | 1 класс | 85 | 120 | 20 | 29.8e6 | 0,315 | 0,28 |
| Класс 2 | 125 | 135 | 20 | ||||
| Класс 3 | 150 | 160 | 20 | ||||
| Инконель 718 | Отжиг на раствор и состаривание | 120 | 150 | 20 | 29.4e6 | 0,297 | 0,29 |
| Термическая обработка раствором | 150 | 180 | 10 | ||||
| Инконель 725 | Отжиг на твердый раствор | 40 | 75 | 45 | 29.6e6 | 0,3 | 0,31 |
| Отжиг и старение на раствор | 120 | 150 | 20 | ||||
| Монель 400 | Отожженный | 25 | 70 | 35 | 26e6 | 0,319 | 0,32 |
| Горячая обработка | 40 | 75 | 30 | ||||
| Холодная обработка, снятие стресса | 50 | 80 | 20 | ||||
| Монель К-500 | Отожженный и состаренный | 85 | 130 | 20 | 26e6 | 0,306 | 0,32 |
| Холодная обработка и старение | 100 | 140 | 15 | ||||
ПРИМЕЧАНИЕ : См.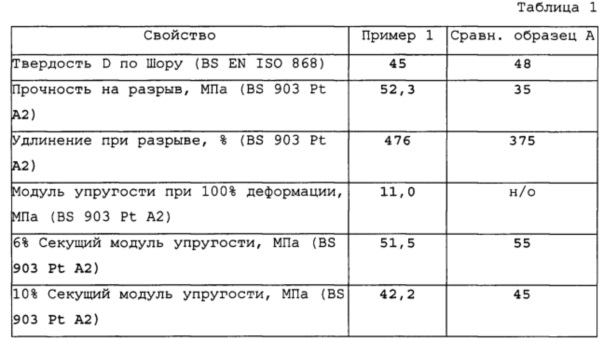 нашу базу данных материалов для получения данных, соответствующих спецификациям конкретных материалов. нашу базу данных материалов для получения данных, соответствующих спецификациям конкретных материалов. | |||||||
Медные сплавы
| Материал | Состояние | Предел текучести Прочность [ksi] | Максимальная Прочность [тыс.фунтов/кв.дюйм] | Удлинение % | Эластичность Модуль упругости [psi] | Плотность [фунт/дюйм 3 ] | Коэффициент Пуассона |
|---|---|---|---|---|---|---|---|
| 70/30 Медно-никелевый сплав | Отожженный | 18 | 45 | 30 | 21.8e6 | 0,323 | 0,3 |
| Холодная обработка | 50 | 65 | 10 | ||||
| 90/10 Медно-никелевый сплав | Отожженный | 15 | 38 | 30 | 20.3e6 | 0,323 | 0,3 |
| Холодная обработка | 30 | 50 | 15 | ||||
| Алюминий Бронза | 32 | 85 | 12 | 15.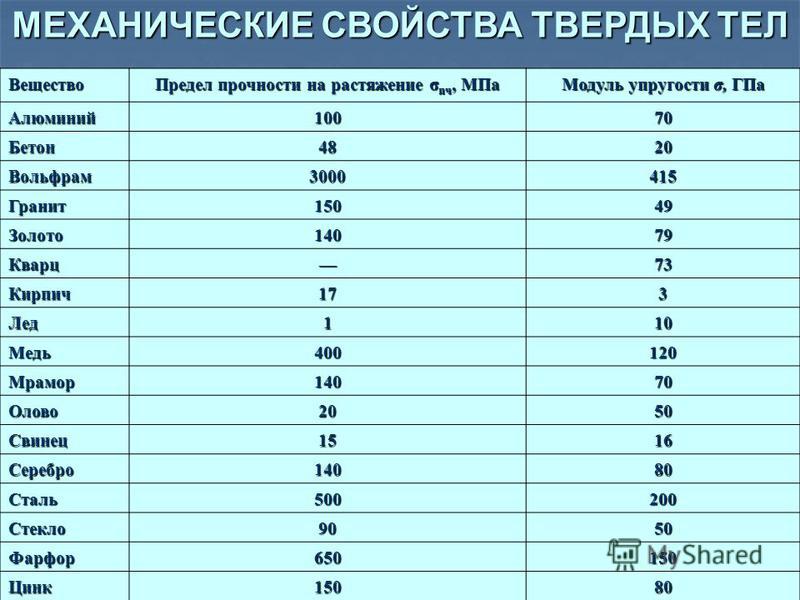 5e6 5e6 | 0,269 | 0,316 | |
| Бериллиевая медь | Термическая обработка раствором | 75 | 85 | 8 | 18.5e6 | 0,298 | 0,27 |
| Термически обработанные осадки | 140 | 165 | 3 | ||||
| Никель Алюминий Бронза 632 | Отожженный | 34 | 90 | 10 | 16.7e6 | 0,274 | 0,32 |
| Закалка | 50 | 90 | 15 | ||||
| ПРИМЕЧАНИЕ : См. нашу базу данных материалов для получения данных, соответствующих спецификациям конкретных материалов. | |||||||
Титановые сплавы
| Материал | Состояние | Предел текучести Прочность [ksi] | Максимальная Прочность [тыс.  фунтов/кв.дюйм] фунтов/кв.дюйм] | Удлинение % | Эластичность Модуль упругости [psi] | Плотность [фунт/дюйм 3 ] | Коэффициент Пуассона |
|---|---|---|---|---|---|---|---|
| Коммерчески чистый | 2 класс | 40 | 50 | 20 | 14.8e6 | 0,163 | 0,34 |
| Ti-5Al-2,5Sn | Отожженный | 110 | 115 | 10 | 15.5e6 | 0,162 | 0,31 |
| Ти-6Ал-4В | 5 класс | 120 | 130 | 10 | 16e6 | 0,16 | 0,31 |
| Ти-6Ал-4В, ЭЛИ | 23 класс | 110 | 120 | 10 | 16.5e6 | 0,16 | 0,31 |
| Ти-5-1-1-1 | 32 класс | 85 | 100 | 10 | 16e6 | 0,16 | 0,31 |
ПРИМЕЧАНИЕ : См.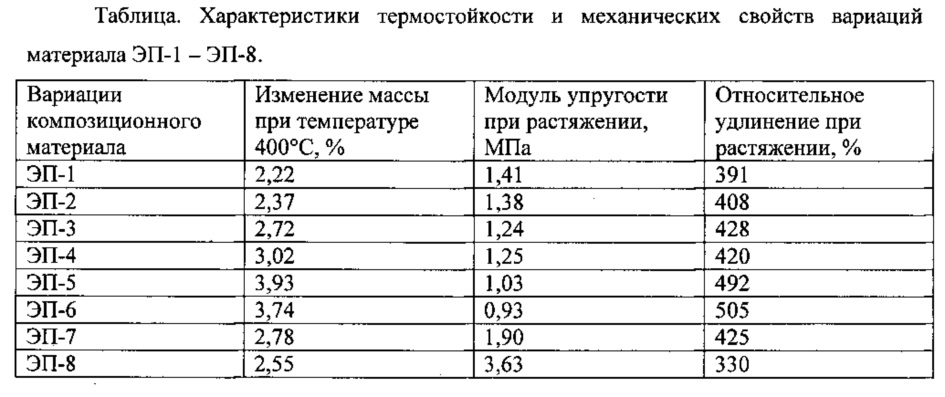 нашу базу данных материалов для получения данных, соответствующих спецификациям конкретных материалов. нашу базу данных материалов для получения данных, соответствующих спецификациям конкретных материалов. | |||||||
Модуль упругости и коэффициент Пуассона для черных металлов
В таблицах ниже приведены значения модуля Юнга (модуля упругости) и коэффициента Пуассона при комнатной температуре для некоторых черных металлов, используемых в технике. Свойства материала выражаются в средних значениях или в диапазонах, которые могут существенно варьироваться в зависимости от обработки и качества материала. Точные значения могут быть измерены с помощью неразрушающих испытаний систем Sonelastic ® при комнатной температуре, а также при низких и высоких температурах.
Чугун
| Материал | Модуль упругости | Коэффициент Пуассона | |
| ГПа | 10 6 фунтов на кв. дюйм | ||
| Чугун | |||
| Серый чугун марки G1800: | 66-97 | 9. 6-14 6-14 | 0,26 |
| Серый чугун марки G4000: | 110-138 | 16-20 | 0,26 |
| Ковкий чугун марки 60-40-18: | 169 | 24,5 | 0,29 |
| Чугун ковкий марки 80-55-06: | 168 | 24,4 | 0,31 |
| Чугун ковкий марки 120-90-02: | 164 | 23,8 | 0,28 |
| Значения только для справки. Для получения точных значений охарактеризуйте материал с помощью систем Sonelastic ® . | |||
Основные области применения:
– Марка G1800: применяется там, где сопротивление не является критическим.
– Марка G4000: блоки и поршни двигателей.
– Марка 60-40-18: детали, работающие под давлением, такие как клапаны и насосы.
– Марка и классы 80-55-06 120-90-02: Зубчатые передачи и детали с высоким сопротивлением.
Серый чугун обладает высоким демпфированием, что является желательным свойством для деталей и конструкций, подверженных вибрации, и высокой износостойкостью, несмотря на то, что он хрупкий. Кроме того, это один из самых дешевых металлических материалов. Чугуны с шаровидным графитом более пластичны и устойчивы, чем серые чугуны, и имеют свойства, аналогичные стали.
Контроль качества и оценка узловатости могут быть выполнены путем измерения демпфирования и вибрации материала. Демпфирование и модули упругости (модуль Юнга, модуль сдвига и коэффициент Пуассона) можно одновременно и точно охарактеризовать с помощью неразрушающих испытаний систем Sonelastic ® при комнатной температуре, а также при низких и высоких температурах.
Знание точных значений жизненно важно для оптимизации использования материала и для надежности моделирования с помощью конечных элементов. Модули упругости и характеристики демпфирования также используются при разработке новых вариантов этих материалов.
Нержавеющая сталь
| Материал | Модуль упругости | Коэффициент Пуассона | |
| ГПа | 10 6 фунтов на кв. дюйм | ||
| Нержавеющая сталь | |||
| Нержавеющий сплав 304: | 193 | 28 | 0,30 |
| Нержавеющий сплав 316 и 316L: | 193 | 28 | 0,30 |
| Нержавеющий сплав 440 A: | 200 | 29 | 0,30 |
| Нержавеющий сплав 17-7PH: | 204 | 29,5 | 0,30 |
Значения только для справки. Для получения точных значений охарактеризуйте материал с помощью систем Sonelastic ® . | |||
Основные области применения:
– Нержавеющая сталь 304: оборудование для пищевой промышленности.
– Нержавеющая сталь 316 и 316L: оборудование, требующее высоконадежных припоев.
– Нержавеющая сталь 440 А: предметы столовых приборов, хирургические инструменты и подшипники.
– Нержавеющая сталь17-7PH: пружины из нержавеющей стали.
Процессы формовки, применяемые к этим материалам, увеличивают модули упругости и демпфирование, что можно точно охарактеризовать с помощью неразрушающих испытаний Sonelastic ® Systems при комнатной температуре, а также при низких и высоких температурах и/или времени отверждения. Знание точных значений жизненно важно для оптимизации использования материала и для надежности моделирования с помощью конечных элементов. Модули упругости и характеристики демпфирования также используются при разработке новых вариантов этих материалов.
Обычные стали и низколегированные стали
| Материал | Модуль упругости | Коэффициент Пуассона | |
| ГПа | 10 6 фунтов на кв.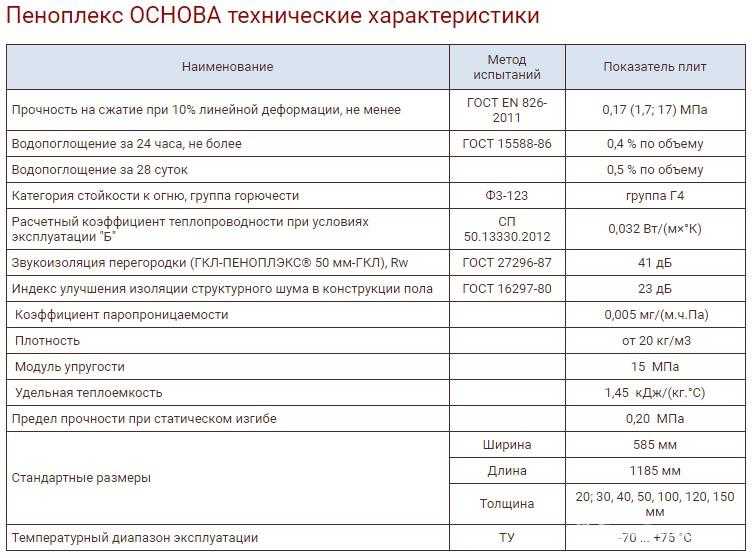 дюйм дюйм | ||
| Нержавеющая сталь | |||
| Сталь А36 | 207 | 30 | 0,30 |
| Нержавеющий сплав 316 и 316L: | 207 | 30 | 0,30 |
| Нержавеющий сплав 440 A: | 207 | 30 | 0,30 |
| Нержавеющий сплав 17-7PH: | 207 | 30 | 0,30 |
| Значения только для справки. Для получения точных значений охарактеризуйте материал с помощью систем Sonelastic ® . | |||
Процессы формовки, применяемые к этим материалам, увеличивают модули упругости и демпфирование, которые можно точно охарактеризовать с помощью неразрушающего Sonelastic ® Испытания систем при комнатной температуре, а также при низких и высоких температурах. Знание точных значений жизненно важно для оптимизации использования материала и для надежности анализа методом конечных элементов (FEA). Модули упругости и характеристики демпфирования также используются при разработке новых вариантов этих материалов.
Знание точных значений жизненно важно для оптимизации использования материала и для надежности анализа методом конечных элементов (FEA). Модули упругости и характеристики демпфирования также используются при разработке новых вариантов этих материалов.
Ссылки
ASM Handbooks, Vol. 1 и 2, Справочник по инженерным материалам, Vol. 1 и 4, Справочник по металлам: свойства и выбор: цветные сплавы и чистые металлы, Vol. 2, 9th edition, и Advance Materials and Processes, Vol. 146, № 4, ASM International, Materials Park, OH.
Откройте для себя системы Sonelastic
® Система Sonelastic® для образцов малого размераСистема Sonelastic® для образцов среднего размера
Система Sonelastic® для образцов среднего размера
Система Sonelastic® для образцов среднего размера
Что такое модуль Юнга материалов? |
Что такое модуль Юнга материалов?
- 10 апреля 2021 г.

Что такое модуль Юнга?
Содержание
Модуль Юнга материала, E также называется модулем упругости или модулем упругости. Это мера жесткости/сопротивления материала растяжению при упругой деформации под действием растягивающей нагрузки. Модуль Юнга — это соотношение между растягивающим напряжением (сила на единицу площади — обычно выражается в МПа) и осевой деформацией (пропорциональная деформация) в области линейной упругости материала, показанной кривой напряжения-деформации.
Когда материал подвергается упругой деформации под действием приложенной нагрузки (сжатия или растяжения), он возвращается к своей первоначальной форме. Однако, если деформация материала чрезмерна, он может подвергнуться пластической деформации, что означает, что он не вернется к своей первоначальной форме.
Единицей модуля Юнга обычно считается гигапаскаль (ГПа), который равен Паскалей x 10 6
Эта концепция была разработана Леонардом Эйлером в 1727 году, хотя она названа в честь Томаса Янга. Однако итальянский ученый по имени Джордано Риккати провел эксперименты, которые в конечном итоге привели к современным расчетам с использованием модуля упругости в современной аэрокосмической, гражданской, строительной и машиностроительной отраслях.
Однако итальянский ученый по имени Джордано Риккати провел эксперименты, которые в конечном итоге привели к современным расчетам с использованием модуля упругости в современной аэрокосмической, гражданской, строительной и машиностроительной отраслях.
Формула модуля Юнга
Уравнение для модуля Юнга E состоит из напряжения растяжения, осевая деформация показана ниже:
Формула модуля Юнга = \(E = \sigma / \varepsilon\)
где E модуль Юнга (модуль упругости или модуль упругости при растяжении) 2 или psi)
\(\varepsilon\) это деформация
Кроме того, уравнение можно разбить на части, чтобы показать приложенную силу, длину и деформацию.
\(E = \sigma / \varepsilon = (F/A) /(\Delta L/L_o) = (FL_o)/(A\Delta L)\)
где F – приложенная сила (натяжение) при единицы измерения в кН или ньютонах
A – площадь поперечного сечения, выраженная в м 2 или в 2
Lo – длина объекта (единицы измерения в м или дюймах)
\(\Delta\ )L — удлинение/прогиб объекта (единицы измерения в м или дюймах)
Уравнение получено из кривой напряжения-деформации материала, которая обычно определяется путем испытания материала путем измерения его деформации под действием растягивающей нагрузки.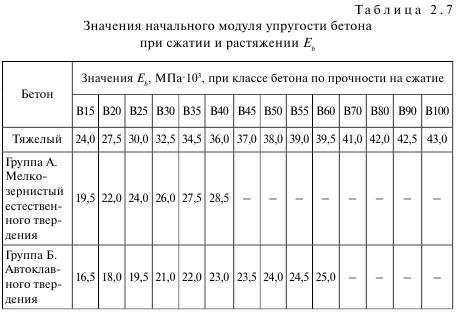
На приведенном ниже графике показана типичная кривая напряжение-деформация, показывающая модуль Юнга как компонент напряжения и деформации.
Кривая напряжение-деформация и модуль ЮнгаДеформация – \(\varepsilon\)
Деформация – это деформация объекта из-за растягивающего напряжения по первоначальной длине объекта. Это безразмерная единица.
Деформация представлена следующим уравнением:
\(\varepsilon =\Delta L/L_0\)
\(\varepsilon\) = деформация (м/м или дюйм/дюйм)
\(\Delta L\) = Удлинение/деформация объекта (единицы измерения в м или дюймах)
\(L_o\) – первоначальная длина объекта (единицы измерения в м или дюймах)
Напряжение – \(\сигма\)
Напряжение представляет собой силу на единицу площади и определяется уравнением ниже0034 2 , фунт/дюйм 2 или фунт/кв. площадь, с единицами измерения в м 2 или в 2
Если мы вернемся к приведенному выше уравнению модуля Юнга, мы увидим, где мы заменили значения деформации и напряжения и упростили его до основных компонентов.
Стресс можно определить в следующих случаях:
- Растягивающее напряжение – Напряжение, вызывающее растяжение и растяжение/удлинение материала – хорошим примером является стальной раскос, который растягивается (т. е. он начинает удлиняться)
- Напряжение сжатия – Напряжение, которое сжимает/укорачивает материал – например, колонна под действием больших осевых нагрузок (также называемая осевым укорачиванием колонны)
- Напряжение сдвига – Напряжение, которое сдвигает материал – оно действует в плоскости, перпендикулярной сжимающему и растягивающему напряжению – хорошим примером является бетонная балка под нагрузкой, и трещины при сдвиге начинают формироваться под углом 45 градусов к опоре и приложенной нагрузке .
Почему модуль Юнга материалов отличается?
Когда мы смотрим на разные материалы, мы замечаем, что модуль Юнга может значительно различаться между ними. Вода имеет модуль Юнга, равный нулю, и мы можем понять это, заметив, что вода не деформируется и не изгибается, поскольку она просто наполняется и принимает форму любого сосуда, в который она помещена. Так почему же модуль Юнга Такие материалы, как сталь, бетон и древесина различаются?
Вода имеет модуль Юнга, равный нулю, и мы можем понять это, заметив, что вода не деформируется и не изгибается, поскольку она просто наполняется и принимает форму любого сосуда, в который она помещена. Так почему же модуль Юнга Такие материалы, как сталь, бетон и древесина различаются?
Причина разницы в модулях упругости определяется прочностью связи между атомами на атомарном уровне. Мы можем представить, что между атомами присутствует жесткость или пружины, а металлические элементы имеют более прочные связи и более высокую жесткость.
Упругая деформация может быть понята через расстояние между атомами, увеличивающееся при растяжении материала, но возвращающееся к своей первоначальной форме при снятии нагрузки.
Пластическая деформация приводит к разрыву связей между атомами, поэтому деформация является постоянной и сохраняется после снятия нагрузки.
Металлические сплавы и элементы имеют сильные межатомные связи между атомами, что приводит к высоким значениям модуля Юнга, тогда как полимеры имеют слабые межмолекулярные связи, что приводит к меньшим значениям модуля Юнга.
Сталь, которая представляет собой металлический сплав (железо, содержащее до 2,14% углерода), и модуль Юнга стали принимается равным 210 ГПа или 205 ГПа, тогда как нейлоновый полимер имеет модуль Юнга около 2,4 ГПа. Разница между этими двумя материалами очень большая.
Изотропные и анизотропные материалы
Материалы можно классифицировать как изотропные или анизотропные, и это влияет на их свойства и то, как они реагируют механически при воздействии нагрузок. Важно определить, является ли материал изотропным или анизотропным, поскольку это повлияет на модели анализа методом конечных элементов.
Эти слова произошли от греческих слов, а слово Iso означает «равный» и тропик относится к «направлению», а и относятся к противоположному, что означает, что анизотропный является полной противоположностью изотропного.
Изотропные материалы имеют одинаковые механические свойства во всех направлениях в каждой заданной точке. Это означает, что при приложении нагрузки к изотропному материалу модуль упругости, напряжение, деформация и прочность одинаковы во всех направлениях (x, y и z).
Это означает, что при приложении нагрузки к изотропному материалу модуль упругости, напряжение, деформация и прочность одинаковы во всех направлениях (x, y и z).
Анизотропные материалы не имеют одинаковых механических свойств во всех направлениях и зависят от ориентации материала. Это означает, что когда к этому типу материала прилагается нагрузка, материал не будет реагировать одинаково вдоль осей x, y и z, и модуль Юнга не будет одинаковым в этих направлениях.
Это связано с атомной структурой этих материалов и тем, как они формируются, и подразделяются на два класса: Одноосные и Двуосные.
Типичными изотропными материалами являются металлы, стекла, блюдца и полимеры.
Типичные анизотропные материалы – это древесина, в которой мы можем видеть, как она формируется с ее сучками и волокнами, образующимися в разных направлениях.
Почему важен модуль Юнга?
Модуль Юнга (модуль растяжения или модуль упругости) является мерой жесткости материала и оказывает большое влияние на конструкцию любой конструкции или транспортного средства, а также на проектирование в целом.
Если взять плиту перекрытия со стальными балками, поддерживающими пол в 3-х этажном доме. На пол будут воздействовать нагрузки от ходьбы людей, собственного веса плиты перекрытия и любой дополнительной отделки. Всю эту нагрузку примет на себя балка, которая затем начнет прогибаться.
Поэтому мы хотим контролировать отклонение балки и следить за тем, чтобы она подвергалась упругой деформации, чтобы при отклонении балка возвращалась в исходное состояние.
Модуль Юнга стали высок (высокая жесткость элемента), что означает, что упругий прогиб стальных балок будет низким при больших нагрузках. Это полезно для зданий, мостов и любой инфраструктуры в машиностроении.
Следует отметить, что сталь является гораздо более пластичным материалом по сравнению с железом или бетоном, которые подвергаются хрупкому разрушению и разрушению без каких-либо предупредительных признаков. Сталь выявит признаки пластической деформации и не разрушится сразу, что позволит всем, кто находится в здании, безопасно эвакуироваться до любого обрушения.
Что такое модуль упругости?
Модуль Юнга часто называют модулем упругости или модулем упругости, но есть и другие способы понимания упругости. Когда мы говорим о модуле упругости, инженеры часто имеют в виду сопротивление/жесткость элемента по отношению к нагрузке на растяжение (отношение напряжения растяжения к деформации растяжения), и это можно измерить с помощью испытания на растяжение.
Другим распространенным термином является объемный модуль, обозначаемый « K ” и является мерой сопротивления материала сжатию.
Другим важным свойством материала является модуль сдвига (также называемый модулем жесткости), который обозначается « G » и является мерой упругой жесткости материала при сдвиге и определяется как отношение напряжения сдвига к деформации сдвига. Единицами СИ для модуля сдвига являются паскали (Па), гигапаскали (ГПа) или фунты на квадратный дюйм (PSI).
Модуль Юнга для материалов Таблицы
| Материал | Гигапаскаль (ГПа) | мегафунтов на квадратный дюйм (Mpsi) |
| Резина (малая деформация) | 0,01–0,1 | 1,45–14,5×10 −3 |
| Полиэтилен низкой плотности | 0,11–0,86 | 1,6–6,5×10 −2 |
| Панцири диатомовых водорослей (в основном кремниевая кислота) | 0,35–2,77 | 0,05–0,4 |
| ПТФЭ (тефлон) | 0,5 | 0,075 |
| ПЭВП | 0,8 | 0,116 |
| Капсиды бактериофагов | 1–3 | 0,15–0,435 |
| Полипропилен | 1,5–2 | 0,22–0,29 |
| Поликарбонат | 2–2,4 | 0,29-0,36 |
| Полиэтилентерефталат (ПЭТФ) | 2–2,7 | 0,29–0,39 |
| Нейлон | 2–4 | 0,29–0,58 |
| Полистирол твердый | 3–3,5 | 0,44–0,51 |
| Полистирол, пенопласт | 0,0025–0,007 | 0,00036–0,00102 |
| Древесноволокнистая плита средней плотности (МДФ) | 4 | 0,58 |
| Древесина (вдоль волокон) | 11 | 1,6 |
| Корковая кость человека | 14 | 2,03 |
| Полиэфирная матрица, армированная стекловолокном | 17,2 | 2,49 |
| Ароматические пептидные нанотрубки | 19–27 | 2,76–3,92 |
| Высокопрочный бетон | 30 | 4,35 |
| Молекулярные кристаллы аминокислот | 21–44 | 3,04–6,38 |
| Пластик, армированный углеродным волокном (50/50 волокон/матрица, биаксиальная ткань) | 30–50 | 4,35–7,25 |
| Пеньковое волокно | 35 | 5,08 |
| Металлический магний (Mg) | 45 | 6,53 |
| Стекло | 50–90 | 7,25–13,1 |
| Льняное волокно | 58 | 8,41 |
| Алюминий | 69 | 10 |
| Перламутр (перламутр, преимущественно карбонат кальция) | 70 | 10,2 |
| Арамид | 70,5–112,4 | 10,2–16,3 |
| Зубная эмаль (в основном фосфат кальция) | 83 | 12 |
| Волокна крапивы двудомной | 87 | 12,6 |
| Бронза | 96–120 | 13,9–17,4 |
| Латунь | 100–125 | 14,5–18,1 |
| Титан (Ti) | 110,3 | 16 |
| Титановые сплавы | 105–120 | 15–17,5 |
| Медь (Cu) | 117 | 17 |
| Пластик, армированный углеродным волокном (70/30 волокно/матрица, однонаправленный, вдоль волокна) | 181 | 26,3 |
| Монокристалл кремния, разные направления | 130–185 | 18,9–26,8 |
| Кованое железо | 190–210 | 27,6–30,5 |
| Сталь (ASTM-A36) | 200 | 30 |
| поликристаллический железоиттриевый гранат (ЖИГ) | 193 | 28 |
| монокристалл железо-иттриевый гранат (ЖИГ) | 200 | 29 |
| Кобальт-хром (CoCr) | 220–258 | 29 |
| Ароматические пептидные наносферы | 230–275 | 33,4–40 |
| Бериллий(Be) | 287 | 41,6 |
| Молибден (Mo) | 329–330 | 47,7–47,9 |
| Вольфрам(W) | 400–410 | 58–59 |
| Карбид кремния (SiC) | 450 | 65 |
| Карбид вольфрама (WC) | 450–650 | 65–94 |
| Осмий(Os) | 525–562 | 76,1–81,5 |
| Одностенная углеродная нанотрубка | 1000+ | 150+ |
| Графен(С) | 1050 | 152 |
| Алмаз(С) | 1050–1210 | 152–175 |
| Динитрид осмия (OsN2) | 1382,7 | 200,5 |
| Динитрид углерода (CN2) | 1555. 3 3 | 225,6 |
Пример 1: Расчет нормального напряжения в стальном стержне
Определите нормальное напряжение в 5-метровом стальном стержне диаметром 40 мм, нагруженном растягивающей нагрузкой 200 кН. Модуль Юнга, E, составляет 210 ГПа. Примечание – измените 200 кН на ньютоны, умножив на 1000. Кроме того, единицами измерения МПа являются Н/мм 2 \(\сигма = P/A\) = 200 000 / (π/4 (40) 2 ) = 159,15 МПа
Пример 2: Рассчитать нормальную деформацию стального стержня
Определить нормальную деформацию стального стержня длиной 5 м и диаметром 40 мм, нагруженного растягивающей нагрузкой 200 кН. Модуль Юнга, E, составляет 210 ГПа.
Примечание – измените 210 ГПа на МПа, умножив на 1000. Кроме того, единицами МПа являются Н/мм 2
\(\varepsilon = \sigma/E\)
= 159,15 / 210 000 7
= 0,0757%
Лучшие сообщения
Гражданское строительство
Этапы РИБА 2020
Что такое план работ RIBA на 2020 год Учрежден Королевским институтом британских архитекторов (RIBA).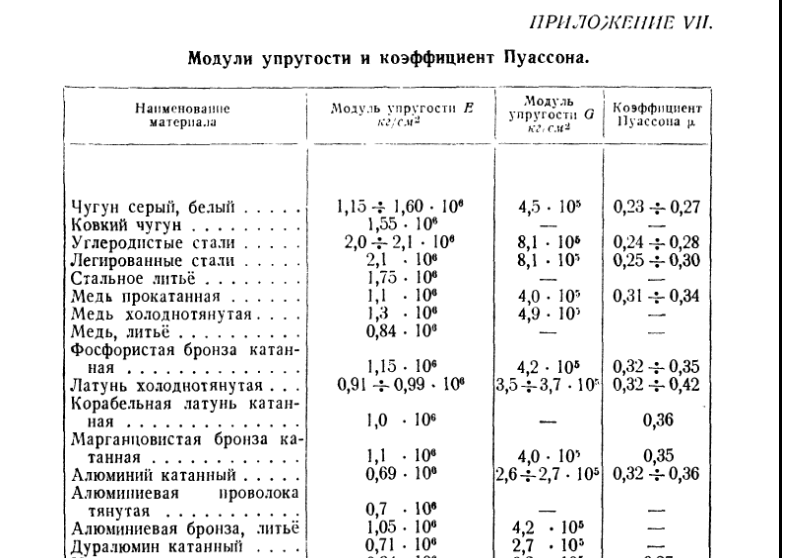 Первоначально запущен в 1963 году в простой матрице
Первоначально запущен в 1963 году в простой матрице
Подробнее »
Объем прямоугольного параллелепипеда – пример расчетов
Объем прямоугольного параллелепипеда Формула объема прямоугольного параллелепипеда — это общее пространство, которое может заполнить эту трехмерную фигуру. Кубоид имеет 6 граней/сторон
Подробнее »
Гражданское строительство
Типы фундаментов для зданий
Типы фундаментов Типы фундаментов, которые обычно используются для зданий или любых других сооружений, представляют собой мелкозаглубленные или глубокие фундаменты.
Подробнее »
Модуль упругости – Модуль Юнга для некоторых общих … / модуль-модуля-упругости-молодого-для-некоторых-общих.pdf / PDF4PRO
Пример: стоматолог-гигиенист
13.02.2014 Модуль из Эластичность – Юнга Модуль для некоторых общий , инструменты и базовая информация для инженерных и 9197s! Поиск “самый эффективный способ навигации инженерных набор инструментов !” Модуль из Эластичность – Юнга Модуль для некоторых обычных Материалов Юнга Модуль (Модуль растяжения ) – Упругие свойства – для некоторых обычных материалов – стали, стекла, дерева и др. Для описания упругих свойств линейных объектов, таких как провода, стержни или колонны, которые растягиваются или сжимаются, удобно Параметр представляет собой отношение напряжения к деформации, параметр, называемый « Модуль Юнга » или « Модуль Эластичность » модуля , может использоваться для прогнозирования удлинения или сжатия. объекта до тех пор, пока напряжение меньше, чем предел текучести материалаMaterialYoung’s Модуль (Модуль из Эластичность ) — E-Ultim
Для описания упругих свойств линейных объектов, таких как провода, стержни или колонны, которые растягиваются или сжимаются, удобно Параметр представляет собой отношение напряжения к деформации, параметр, называемый « Модуль Юнга » или « Модуль Эластичность » модуля , может использоваться для прогнозирования удлинения или сжатия. объекта до тех пор, пока напряжение меньше, чем предел текучести материалаMaterialYoung’s Модуль (Модуль из Эластичность ) — E-Ultim
Модуль Юнга (модуль растяжения) — Свойства упругости — для некоторых распространенных материалов — сталь, стекло, дерево и др. Для описания упругих свойств линейных объектов, таких как проволоки, стержней или колонн, которые растягиваются или сжимаются, удобным параметром является соотношение … Engineering ToolBox – SketchUp Edition – добавление стандартных и настраиваемых параметрических . ..
..
Полноэкранная загрузка
Метки:
Engineering, Material, Common, Some, Toolbox, Engineering toolbox, Для некоторых распространенных материалов
Информация
Домен:
Источник:
Ссылка на эту страницу:
Пожалуйста, сообщите нам, если вы обнаружили проблему с этим документом:
Спасибо за участие!
Подать уведомление
Спасибо за участие!
Отправить уведомление
Другое злоупотребление
Транскрипция модуля эластичности – Молодые модуль для некоторого общего …
13.01.2014 Модуль из Эластичности – Молодой мод. общий , инструменты и базовая информация для проектирования и проектирования технических приложений! Поиск “самый эффективный способ навигации инженерных набор инструментов !” Modulus of Elasticity – Young Modulus for some common MaterialsYoung Modulus (Tensile Modulus ) – Elastic Properties – for some common materials – steel, glass, wood and Для описания упругих свойств линейных объектов, таких как провода, стержни или колонны, которые растягиваются или сжимаются, удобным параметром является отношение напряжения к деформации, параметр, называемый «9». 1974 Young ‘s Modulus ” или “ Modulus of Elasticity ” of Modulus можно использовать для прогнозирования удлинения или сжатия объекта, пока напряжение меньше предела текучести. materialMaterialYoung’s Модуль ( Модуль из Эластичность )
1974 Young ‘s Modulus ” или “ Modulus of Elasticity ” of Modulus можно использовать для прогнозирования удлинения или сжатия объекта, пока напряжение меньше предела текучести. materialMaterialYoung’s Модуль ( Модуль из Эластичность )
2 – E -Предел прочности на растяжение- Su -(106 Н/м2, МПа)Предел текучести- Sy -(106 Н/м2, МПа)(106 фунтов на кв. дюйм) 109 Н/м2, ГПа) АБС-пластики – Арамид70 – 112 Бериллий (Be)42 287 Бериллий Кость компактная 18170(сжатие)Кость губчатая76 Бор 3100 Латунь 102 – 125250 Латунь Naval100 Бронза 96 – Пластик, армированный углеродным волокном 150 Углеродные нанотрубки, одностенные1000+Чугун C, ASTM A-48 170 Целлюлоза, хлопок, древесная масса и регенерированная80 – 240 Ацетат целлюлозы, формованная12 – 58 Ацетат целлюлозы, лист30 – 52 Нитрат целлюлозы, целлулоид50 Хлорированная полиэфир39 Хром36 Кобальт30 Бетон17 Бетон высокой прочности (сжатие) 3040(сжатие)13. 3 Эпоксидные смолы 3-226 – 85 ДВП средней плотности4 Льняное волокно 58 Стекло 50 – 9050 (сжатие) Армированный стекловолокном полиэстер 74 Гранит 52 Графен 1000 Серый чугун 130 Пеньковое волокно 35 Инконель 31 Иридий 75 2 (Mg) Мрамор 15 МДФ – ДВП4 Ртуть Молибден (Mo)40 329 Монель Металл26 Никель31 170 Никель Сталь29 Ниобий (Колумбий)15 Нейлон-6 2 – 445 – 9045 Нейлон-6660 – 80 Дуб (вдоль волокон) 11 Осмий (Os)80 550 Фенольные литые смолы33 – 59Фенолформальдегидные формовочные массы45 – 52 Фосфорная бронза116 Сосна (вдоль волокон) Плутоний14 97 Полиакрилонитрил, – 62 Полиэтилен ПЭВП (высокой плотности) Терефталат, ПЭТФ 2 – , эбонит39 Полиметилметакрилат (ПММА) – , ПП – 228 – 36 Полистирол, ПС 3 – – 100 Политехилен, LDPE (низкая плотность) – из Эластичность – Юнга Модуль для некоторые обычный (ПТФЭ) литая жидкость10 – 20 Полиуретановый эластомер29 – 55 Поливинилхлорид (ПВХ)0004 4 – Родий42 Резина, малая деформация – Кремний16 130 – 185 Карбид кремния Натриевая сталь, высокопрочный сплав ASTM A-514 760690 Нержавеющая сталь AISI 302 180860502 Сталь конструкционная ASTM-A36 200400250 Тантал27 Тефлон. 02.2014 Модуль из Эластичность – Юнг Модуль для некоторые обычные
02.2014 Модуль из Эластичность – Юнг Модуль для некоторые обычные75 (C) 1220 Пихта Дугласа Древесина 1350 (сжатие) 0 Зубная эмаль83 Вольфрам (W) 400–410 Карбид вольфрама (WC) 450–650 Уран24 170 Ванадий19 Кованое железо 190–210 Цинк12 1 Н/м2 = 1×10-6 Н/мм2 = 1 Па = psi1 (фунт/дюйм2) = 144 фунтов на фут (фунт-сила/фут2) = 6, Па (Н/м2) = Н/мм2 Примечание! Используйте конвертер единиц давления на этой странице, чтобы переключить значения на другие значения, которые могут быть выражены как strain = dL / L (1)где strain = (м/м) (дюйм/дюйм)dL = удлинение или сжатие (смещение) объекта (м ) (in)L = длина объекта (м) (in)StressСтресс может быть выражен как стресс = F / A (2)где стресс = (Н/м2) (фунт/дюйм2, psi)F = усилие (Н) (фунт )A = площадь объекта (м2) (дюйм2) 13.02.2014 Modulus of Elasticity – Young Modulus for some common ‘s Modulus (Tensile Modulus ) Young ‘s Modulus or Tensile Modulus can be expressed asE = напряжение / деформация = (F / A) Олово47 Титан16 Титановый сплав 105–120
Олово47 Титан16 Титановый сплав 105–120
5 / (дл / л) (3) где E = Модуль Юнга (Н/м2) (фунт/дюйм2, фунт/кв./96_3.jpg) дюйм)УпругостьУпругость – это свойство объекта или материал , который восстанавливает его первоначальную форму после пружины, является примером упругого объекта – при растяжении он оказывает восстанавливающую силу, которая стремится вернуть его к исходной длине. Эта восстанавливающая сила в общем случае пропорциональна растяжению, описываемому законом Гука. Одно из свойств г. Эластичность заключается в том, что требуется примерно вдвое больше силы, чтобы растянуть пружину в два раза дальше. Эта линейная зависимость смещения от силы растяжения называется законом Гука, который может быть выражен как Fs = -k dL (4)где Fs = сила в пружине (Н)k = постоянная пружины (Н/м)dL = удлинение пружины (м)
дюйм)УпругостьУпругость – это свойство объекта или материал , который восстанавливает его первоначальную форму после пружины, является примером упругого объекта – при растяжении он оказывает восстанавливающую силу, которая стремится вернуть его к исходной длине. Эта восстанавливающая сила в общем случае пропорциональна растяжению, описываемому законом Гука. Одно из свойств г. Эластичность заключается в том, что требуется примерно вдвое больше силы, чтобы растянуть пружину в два раза дальше. Эта линейная зависимость смещения от силы растяжения называется законом Гука, который может быть выражен как Fs = -k dL (4)где Fs = сила в пружине (Н)k = постоянная пружины (Н/м)dL = удлинение пружины (м)
6 Предел текучести Предел текучести, или предел текучести, определяется в машиностроении как величина напряжения, которому может подвергаться материал перед переходом от упругой деформации к пластической.Материал 1974 – это предельное напряжение, при котором материал фактически разрушается с внезапным высвобождением сохраненной упругости. емкость, вязкость и многое другое – для газов, жидкостей и твердых веществДокументы по темеСтресс.
емкость, вязкость и многое другое – для газов, жидкостей и твердых веществДокументы по темеСтресс.
7 Деформация и Модуль Юнга — Напряжение — это сила на единицу площади — деформация — это деформация твердого тела под действием напряжения.1974 общий использование Напряжения в толстостенных трубах или цилиндрах – радиальное и касательное напряжение в толстостенных трубах или цилиндрах с закрытыми концами – внутреннее и внешнее давление их средний предел прочности — сжатие и растяжение. Инженерные материалы — сравнение некоторых типичных свойств обычных материалов машиностроения , таких как сталь, пластик, керамика и композиты. Термические напряжения — напряжение из-за ограничения теплового расширения. болтыКоэффициент Пуассона – Когда материал растягивается в одном направлении, но имеет тенденцию к утончению в двух других направлениях. Формула колонны Эйлера. Потеря устойчивости колонн. Консольные балки. Максимальная реакция, прогиб и момент. термопласты – ABS, PVC, CPVC, PE, PEX.
Потеря устойчивости колонн. Консольные балки. Максимальная реакция, прогиб и момент. термопласты – ABS, PVC, CPVC, PE, PEX.
8 Напряжения PB и PVDFS в телах вращения. Напряжение в дисках или кольцах. Модуль жесткости. Модуль сдвига или Модуль жесткости является коэффициентом Эластичность для силы сдвига или кручения Юнга Модуль из Эластичность для металлов и сплавов – Упругие свойства и Юнгса Модуль для обычных металлов, как металлов и сплавов углеродистая сталь и др. Растяжение болта — растяжение болта в соответствии с законом Гука Пределы выносливости и усталостное напряжение — Пределы выносливости и усталостное напряжение для некоторых сталей 13.02.2014 Модуль из Упругость – Юнга Модуль для некоторые общие Формулы звука – Расчетные формулы для скорости звука – скорости звука – в газах, жидкостях или твердых телах эффективный способ навигации по набору инструментов для проектирования !
9 дюймов набор инструментов для проектирования – SketchUp Edition – 3D-моделирование онлайн! машиностроение набор инструментов — SketchUp Edition — добавление стандартных и настраиваемых параметрических компонентов, таких как балки с полками, пиломатериалы, трубопроводы и т.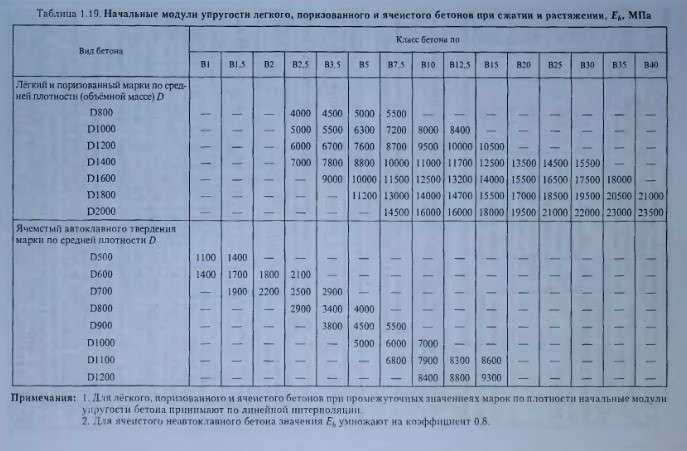 д., в вашу модель SketchUp — возможность использования с потрясающими, увлекательными и бесплатными программами SketchUp Make и SketchUp Pro. Добавьте из Sketchup ExtensionWarehouse!Переведите ToolBoxАрабский – Китайский (упрощенный) – Китайский (традиционный) – Голландский – Французский – Немецкий – Итальянский – Японский – Корейский – Португальский – Русский – Испанский – -Выберите свой язык ..О ToolBoxМы ценим любые комментарии и советы о том, как сделать Engineering ящик для инструментов лучший источник информации.
д., в вашу модель SketchUp — возможность использования с потрясающими, увлекательными и бесплатными программами SketchUp Make и SketchUp Pro. Добавьте из Sketchup ExtensionWarehouse!Переведите ToolBoxАрабский – Китайский (упрощенный) – Китайский (традиционный) – Голландский – Французский – Немецкий – Итальянский – Японский – Корейский – Португальский – Русский – Испанский – -Выберите свой язык ..О ToolBoxМы ценим любые комментарии и советы о том, как сделать Engineering ящик для инструментов лучший источник информации.
10 Пожалуйста, свяжитесь с нами, если вы обнаружите какие-либо ошибки, неточности или иное неприемлемое содержимое в Engineering toolbox . Важная информация всегда должна быть перепроверена в альтернативных источниках. Необходимо строго соблюдать и соблюдать все применимые национальные и местные правила и практики, касающиеся этих аспектов. Психрометрия. Основы. Горение. Инструменты для рисования. 1974 Модуль из Эластичность – Юнга Модуль для некоторые общие СистемыУправление технологическим процессомНасосыСтандартные организацииПар и конденсатТермодинамикаВодные системыЕдиница oC oFConvert!
1974 Модуль из Эластичность – Юнга Модуль для некоторые общие СистемыУправление технологическим процессомНасосыСтандартные организацииПар и конденсатТермодинамикаВодные системыЕдиница oC oFConvert!
Показать больше
Связанные поисковые запросы
Впускной патрубок Инженерный набор инструментов, Проектирование, Узлы водоснабжения, Инженерный набор инструментов, Строить ситуационную осведомленность об окружающей среде, Помощь в проживании, Теплопроводность некоторых распространенных материалов, Набор инструментов, Свойства насыщенного пара – SI, Набор инструментов to Design Inverters for Automotive Applications, STEAM TABLES, инженерное уравнение Бернулли, TOOL BOX TALKS: YEAR’S WORTH
Устойчивость
Абстрактный:
Способность материала поглощать энергию при упругой деформации и возвращать ее при разгрузке называется упругостью. Обычно это измеряется модулем упругости, который представляет собой энергию деформации на единицу объема, необходимую для напряжения материала от нулевого напряжения до предела текучести. Прочность материала — это его способность поглощать энергию в пластическом диапазоне. Способность выдерживать случайные напряжения выше предела текучести без разрушения особенно желательна в таких деталях, как сцепки грузовых вагонов, шестерни, цепи и крюки кранов. Стойкость — это широко используемое понятие, которое трудно определить.
Обычно это измеряется модулем упругости, который представляет собой энергию деформации на единицу объема, необходимую для напряжения материала от нулевого напряжения до предела текучести. Прочность материала — это его способность поглощать энергию в пластическом диапазоне. Способность выдерживать случайные напряжения выше предела текучести без разрушения особенно желательна в таких деталях, как сцепки грузовых вагонов, шестерни, цепи и крюки кранов. Стойкость — это широко используемое понятие, которое трудно определить.
Способность материала поглощать энергию при упругой деформации а вернуть его при выгрузке называется устойчивость . Это обычно измеряется модулем упругости , который представляет собой деформацию энергия на единицу объема, необходимая для напряжения материала, нулевого напряжения к пределу текучести s. Энергия деформации на единица объема при одноосном растяжении
| (1) |
Из приведенного выше определения модуль упругости равен
| (2) |
Это уравнение показывает, что идеальный материал для сопротивления энергии
нагрузки в приложениях, где материал не должен подвергаться постоянным
искажения, такие как механические пружины, имеют высокий предел текучести и
низкий модуль упругости. В таблице 1 приведены некоторые значения модуля
устойчивость к разным материалам.
В таблице 1 приведены некоторые значения модуля
устойчивость к разным материалам.
Таблица 1. Модуль упругости для различных материалов
| Материал | В, psi | с 0 , psi | Модуль упругости, Ur |
| Среднеуглеродистая сталь | 30×10 6 | 45000 | 33,7 |
| Высокоуглеродистая пружинная сталь | 30×10 6 | 140000 | 320 |
| Дюралюминий | 10,5×10 6 | 18000 | 17,0 |
| Купер | 16×10 6 | 4000 | 5,3 |
| Резина | 150 | 300 | 300 |
| Акриловый полимер | 0,5×10 6 | 2000 г. | 4,0 |
Прочность
Прочность материала – это его способность поглощать энергию в
пластиковый ассортимент. Способность выдерживать случайные, сверхвысокие нагрузки.
предел текучести без разрушения особенно желателен в таких частях, как
как сцепки грузовых вагонов, шестерни, цепи и крановые крюки. Прочность – это
общеупотребительное понятие, которое трудно уловить и определить. В одну сторону
рассматривая ударную вязкость, нужно учитывать, что это общая площадь под
кривая напряжение-деформация. Эта область является показателем объема работы
на единицу объема, что можно сделать на материале, не вызывая его
разрыв. На рис. 1.2 показаны кривые напряжения-деформации для высоко- и
малопрочные материалы. Высокоуглеродистая пружинная сталь имеет более высокий предел текучести.
прочность и прочность на растяжение, чем у среднеуглеродистой конструкционной стали.
Однако конструкционная сталь более пластична и имеет большую общую
удлинение.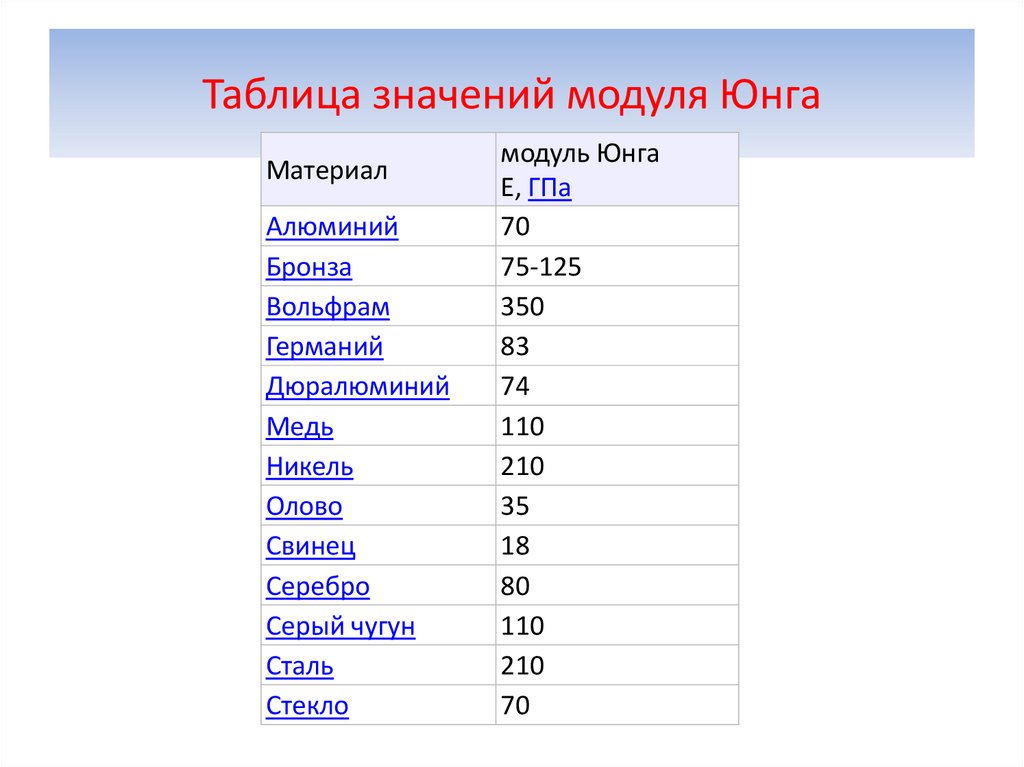 Общая площадь под кривой напряжения больше для
конструкционная сталь, поэтому она является более жестким материалом. Этот
показывает, что ударная вязкость является параметром, который включает оба прочность и пластичность. Заштрихованные области на рис. 1 указывают на
модуль упругости для каждой стали. Из-за более высокой урожайности
прочность, пружинная сталь имеет большую упругость.
Общая площадь под кривой напряжения больше для
конструкционная сталь, поэтому она является более жестким материалом. Этот
показывает, что ударная вязкость является параметром, который включает оба прочность и пластичность. Заштрихованные области на рис. 1 указывают на
модуль упругости для каждой стали. Из-за более высокой урожайности
прочность, пружинная сталь имеет большую упругость.
Несколько математических аппроксимаций для площади напряженно-деформированного состояния.
была предложена кривая. Для пластичных металлов, имеющих напряжение-деформацию
кривой, как у конструкционной стали, площадь под кривой может быть
аппроксимируется одним из следующих уравнений:
| (3) |
| (4) |
Для хрупких материалов кривая напряжение-деформация иногда считается равной быть параболой, а площадь под кривой определяется выражением
| (5) |
Рис. 1. Сравнение кривых напряжение-деформация
1. Сравнение кривых напряжение-деформация
Все эти соотношения являются лишь приближениями к площади под кривыми напряжение-деформация. Кроме того, кривые не отражают истинного поведение в пластическом диапазоне, так как все они основаны на исходной области образец.
Дата публикации: март 2001 г.
Таблица механических свойств металлов: предел прочности при сдвиге, предел прочности при растяжении, предел текучести
В последнее время мы получаем много запросов от читателей о таблицах механических свойств (прочности металла) для различных металлов, таких как предел прочности при сдвиге, предел прочности при растяжении, предел текучести и относительное удлинение стали и др.
Связанное чтение: Тип металла
Чтобы удовлетворить потребности наших читателей, мы составили следующие таблицы механических свойств, в которых перечислены различные черные и цветные металлы.
Связанное чтение: Черные металлы против цветных металлов
Надеюсь, это поможет!
Содержание
(Таблица прочности металла)
| Материал | Марка сплава | Материал Статус | Сдвиг Strength τ(MPa) | Tensile Strength σb(MPa) | Elongation σs(%) | Yield Strength δ(MPa) | Elastic Modulus Е(MPa) |
|---|---|---|---|---|---|---|---|
| Промышленное чистое железо для электриков C> 0,025 | DT1 DT2 DT3 | Отжиг | 180 | 230 | 26 | ||
| Электронный0009 D32、D370 D310~340 S41~48 | annealed | 190 | 230 | 26 | |||
| Ordinary carbon steel | Q195 | unannealed | 260~320 | 315~390 | 28~33 | 195 | |
| Q215 | 270~340 | 335~410 | 26~31 | 215 | |||
| Q235 | 310~380 | 375~460 | 21~ 26 | 235 | |||
| Q255 | 340~420 | 410~510 | 19~24 | 255 | |||
| Q275 | 400~500 | 490~610 | 15~20 | 275 | |||
| Carbon tool steel | 08F | annealed | 220~310 | 280~390 | 32 | 180 | |
| 10F | 260~360 | 330~450 | 32 | 200 | 1 | ||
| 15F | 220~340 | 280~420 | 30 | 190 | |||
| 08 | 260~340 | 300~440 | 29 | 210 | 198000 | ||
| 10 | 250~370 | 320~460 | 28 | — | |||
| 15 | 270~380 | 340~480 | 26 | 280 | 202000 | ||
| 20 | 280~400 | 360~510 | 35 | 250 | 21000 | ||
| 25 | 320~440 | 400~550 | 34 | 280 | 202000 | ||
| 30 | 360~480 | 450~600 | 22 | 300 | 201000 | ||
| 35 | 400~520 | 500~650 | 20 | 320 | 201000 | ||
| 40 | 420~540 | 520~670 | 18 | 340 | 213500 | ||
| 45 | 440~560 | 550~700 | 16 | 360 | 204000 | ||
| 50 | normalized | 440~580 | 550~730 | 14 | 380 | 220000 | |
| 55 | 550 | ≥670 | 43 | 390 | — | ||
| 60 | 550 | ≥700 | 12 | 410 | 208000 | ||
| 65 | 600 | ≥730 | 10 | 420 | — | ||
| 70 | 600 | ≥760 | 9 | 430 | 210000 | ||
| T7~T12 T7A~T12A | annealed | 600 | 750 | 10 | — | — | |
| T8A | cold hardened | 600~950 | 750~1200 | — | — | — | |
| High-quality carbon steel | 10Mn | annealed | 320~460 | 400~ 580 | 22 | 230 | 211000 |
| 65Mn | 600 | 750 | 12 | 400 | 21000 | ||
| Alloy structural steel | 25CrMnSiA 25CrMnSi | low-temperature annealed | 400~560 | 500~700 | 18 | 950 | — |
| 30CrMnSiA 30CrMnSi | 440~6000 | 550~750 | 16 | 1450 850 | — | ||
| Quality spring steel | 60Si2Mn 60Si2MnA 65SiWA | low-temperature annealed | 720 | 900 | 10 | 1200 | 200000 |
| cold hardened | 640~960 | 800~1200 | 10 | 1400 1600 | — | ||
| Stainless steel | 1Cr13 | annealed | 320~380 | 400~ 470 | 21 | 420 | 210000 |
| 2Cr13 | 320~400 | 400~500 | 20 | 450 | 210000 | ||
| 3Cr13 | 400~480 | 500~600 | 18 | 480 | 210000 | ||
| 4Cr13 | 400~480 | 500~600 | 15 | 500 | 210000 | ||
| 1Cr18Ni19 2Cr18Ni19 | ТЕПРАТИРОВАНИЯ | 460 ~ 520 | 580 ~ 640 | 35 | 200 | 200000 | |
. Скалолистые.0044 220 Скалолистые.0044 220 | 200000 | ||||||
| 1Cr18Ni9Ti | Heat-treated softened | 430~550 | 540~700 | 40 | 200 | 200000 |
Shear strength table of steel when heated
| Steel Grade | Heating temperature ℃ | |||||
|---|---|---|---|---|---|---|
| 200 | 500 | 600 | 700 | 800 | 900 | |
| Q195, Q215, 08, 15 | 360 | 320 | 200 | 110 | 60 | 30 |
| Q235, Q255, 20, 25 | 450 | 450 | 240 | 130 | 90 | 60 |
| Q275, 30, 35 | 530 | 520 | 330 | 160 | 90 | 70 |
| 40, 45, 50 | 600 | 580 | 380 | 190 | 90 | 70 |
Примечание: Значение прочности материала на сдвиг следует принимать при температуре штамповки, которая обычно на 150~200℃ ниже температуры нагрева.
Таблица механических свойств цветных металлов.0009 (%)
Strength δ
(MPa)
Modulus Е
(MPa)
Aluminum-magnesium-copper alloy
MB8
Tin-Zinc-Bronze
 5
5 QSn4-3
 5
5Что такое прочность металла?
Прочность металлов относится к способности металлических материалов сопротивляться остаточной деформации и разрушению под действием внешней силы.
Поскольку режимы действия нагрузки включают растяжение, сжатие, изгиб, сдвиг и другие формы, прочность также делится на прочность на растяжение, прочность на сжатие, прочность на изгиб, прочность на сдвиг и так далее.
Часто существует определенная связь между различными сильными сторонами.
Как правило, предел прочности при растяжении (максимальное напряжение при растяжении, которое образец может выдержать до разрушения во время испытания на растяжение) используется в качестве базового показателя прочности.
Что включает в себя прочность металла?
Прочность металла относится к максимальной способности металлических материалов сопротивляться повреждению под действием внешних сил.
Металлы имеют разную прочность.
Например:
Прочность на растяжение:
Код: σ b. Относится к пределу прочности внешней силы при растяжении.
Прочность на сжатие:
Код σbc относится к пределу прочности при сжатии внешней силой.
Прочность на изгиб:
Код σbb относится к предельной прочности на сдвиг, когда внешняя сила перпендикулярна оси материала и заставляет материал изгибаться после воздействия.
Прочность листового металла также включает:
Прочность на сдвиг, предел текучести, ударную вязкость, внутренний и внешний изгиб и т. д.
Что такое прочность на растяжение?
Прочность на растяжение, физический термин, представляет собой критическую величину перехода металла от равномерной пластической деформации к локальной концентрированной пластической деформации, а также максимальную несущую способность металла при статическом растяжении.
Прочность на растяжение – сопротивление максимально равномерной пластической деформации материала.
До того, как образец на растяжение испытает максимальное растягивающее напряжение, деформация носит равномерный характер, но после превышения максимального растягивающего напряжения металл начинает усадку, т. е. концентрированную деформацию;
Для хрупких материалов без (или с очень небольшой) равномерной пластической деформацией отражает сопротивление материала разрушению.
Символ Rm (символ прочности на растяжение, указанный в старом национальном стандарте GB/T 228-1987 – σb), в МПа.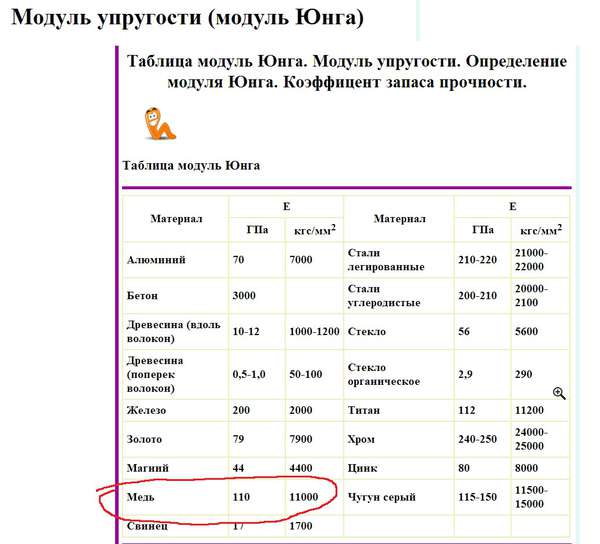
Что такое прочность на сжатие?
Прочность на сжатие, код σ BC, относится к пределу прочности, когда внешняя сила оказывает давление.
Чтобы понять характеристики камня и его применимость в технике, сначала необходимо провести испытание камня на механическую прочность.
Наиболее важным испытанием на прочность является испытание на прочность при сжатии.
Что такое прочность на изгиб?
Прочность на изгиб относится к способности материалов сопротивляться изгибу и непрерывному растрескиванию.
В основном используется для исследования прочности хрупких материалов, таких как керамика.
Как правило, для оценки используется трехточечный или четырехточечный метод испытаний на изгиб.
Четырехточечное испытание требует двух сил нагрузки, что является более сложным; Наиболее часто используется трехточечный тест.
Его значение прямо пропорционально максимальному давлению.
В чем разница между прочностью металла и твердостью
Понятия твердости и прочности разные, но они являются показателями для измерения механических свойств металлических материалов, которые могут быть преобразованы при определенных условиях.
Твердость: это способность металла сопротивляться вдавливанию твердых предметов в его поверхность. Он измеряет твердость и мягкость металла.
Обычно используются следующие показатели твердости: твердость по Бринеллю (HB), твердость по Роквеллу (HRC, HRB и HRA) и твердость по Виккерсу (HV).
Прочность: относится к способности металла противостоять постоянной деформации и разрушению под действием внешней силы. Он измеряет способность металла сопротивляться разрушению после выдерживания нагрузки.
Обычно используемые показатели прочности: предел текучести и предел прочности при растяжении.
Разница между прочностью металла и твердостью:
Твердость в основном используется для проверки и контроля качества термической обработки металлических деталей.
Прочность является важной основой для проектирования и выбора материалов основных деталей.
Какой металл самый прочный?
Самым прочным металлом является вольфрам , за ним следуют титан, тритий, осмий, железо, сталь, цирконий, хром, ванадий и тантал.


 2-е изд., исправл. и доп. / Зубченко А.С., Колосков М.М., Каширский Ю.В. и др. Под ред. А.С. Зубченко. М.: Машиностроение, 2003. 784 с.
2-е изд., исправл. и доп. / Зубченко А.С., Колосков М.М., Каширский Ю.В. и др. Под ред. А.С. Зубченко. М.: Машиностроение, 2003. 784 с.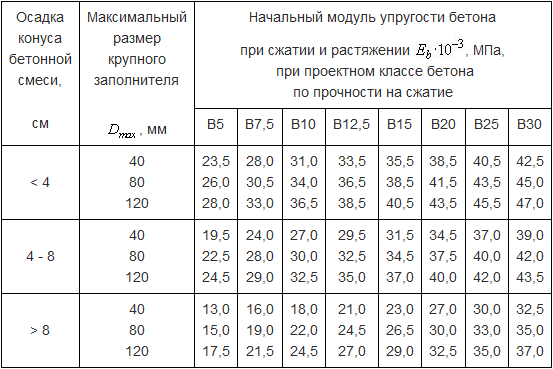 В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств. Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости.
Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости.
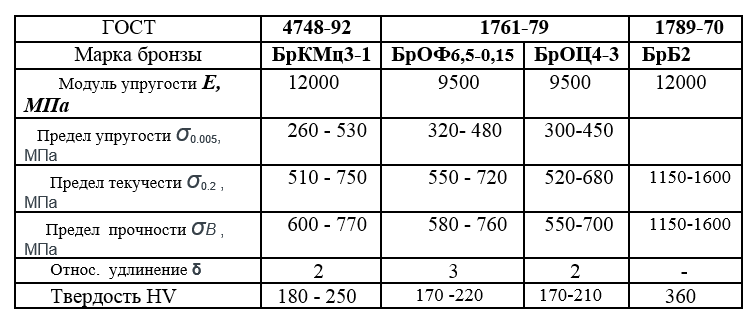

 Для определения вида прочности учитывается 2 критерия — растяжение и сжатие, что влияют на сопротивление нагрузкам.
Для определения вида прочности учитывается 2 критерия — растяжение и сжатие, что влияют на сопротивление нагрузкам.
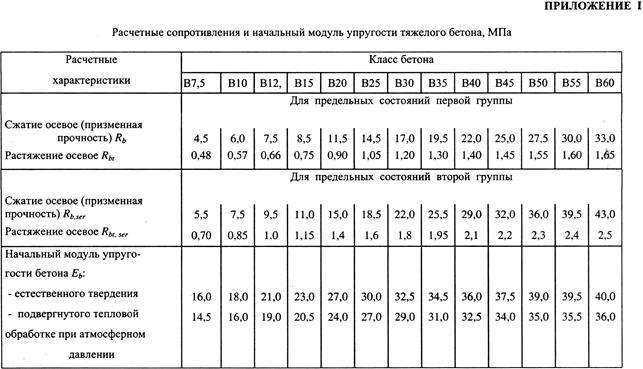 Это свойство учитывают для того, чтобы знать какой из продуктов может быть установлен. При возведении загородных частных домов применяют довольно маленький перечень бетонных растворов, согласно их классности. Чаще всего этот выбор происходит в диапазоне от В7 до В30, а также М100, М150, М200, М250, М300, М350, М400. Однако данного ассортимента полностью хватает для возведения малоэтажных зданий. Это возможно, даже если в строительстве применяются плитные цоколи, а также формируются арки для декорирования.
Это свойство учитывают для того, чтобы знать какой из продуктов может быть установлен. При возведении загородных частных домов применяют довольно маленький перечень бетонных растворов, согласно их классности. Чаще всего этот выбор происходит в диапазоне от В7 до В30, а также М100, М150, М200, М250, М300, М350, М400. Однако данного ассортимента полностью хватает для возведения малоэтажных зданий. Это возможно, даже если в строительстве применяются плитные цоколи, а также формируются арки для декорирования.
 Данное обстоятельство связано с модулем ползучести. Если необходимо точное значение, то она также узнается из соответствующих таблиц. В таком случае во внимание также берутся температура и уровень радиационного фона.
Данное обстоятельство связано с модулем ползучести. Если необходимо точное значение, то она также узнается из соответствующих таблиц. В таком случае во внимание также берутся температура и уровень радиационного фона. В результате пластичной деформации возникают глубокие трещины, являющиеся, в дальнейшем, причиной постепенного разрушения зданий и различных бетонных конструкций.
В результате пластичной деформации возникают глубокие трещины, являющиеся, в дальнейшем, причиной постепенного разрушения зданий и различных бетонных конструкций.