Типы шкал измерений: Шкалы измерений в метрологии | Виды шкал: номинальные, абсолютные, порядка, отношений, интервалов
alexxlab | 26.04.1988 | 0 | Разное
Шкалы измерений в метрологии | Виды шкал: номинальные, абсолютные, порядка, отношений, интервалов
Метрология и стандартизация
Шкала измерений – это совокупность значений, позволяющих количественно или качественно отобразить свойства объекта измерений. Разнообразные проявления (количественные или качественные) любого свойства образуют множества, отображения элементов которых на упорядоченное множество чисел или в более общем случае условных знаков образуют шкалы измерения этих свойств. Шкала измерений количественного свойства является шкалой физической величины. Шкала физической величины – это упорядоченная последовательность значений ФВ, принятая по соглашению на основании результатов точных измерений.
Виды шкал измерений
В практической деятельности необходимо проводить измерения различных величин, характеризующих свойства тел, веществ, явлений и процессов. Некоторые свойства измерительных шкал в метрологии проявляются только качественно, другие – количественно.
Шкала – упорядоченный числовой или символьный ряд значений, отражающий допустимые вариации значений измеряемой величины.
В соответствии с логической структурой проявления свойств различают пять основных видов шкал измерений: шкалы наименований, шкалы порядка, шкалы интервалов, шкалы отношений, абсолютные шкалы.
Номинальная шкала (шкала наименований)
Рисунок – Пример номинальной шкалы (атлас цветов)
Такие шкалы измерений в метрологии используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности эти свойства нельзя считать физическими величинами, поэтому шкалы такого вида но являются шкалами ФВ. Номинальные шкалы, или, как их еще называют шкалы наименований так же называют шкалами измерений, или шкалами классификаций. Это самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имен.
В номинальных шкалах, в которых отнесение отражаемого свойства к тому или иному классу эквивалентности осуществляется с использованием органов чувств человека, наиболее адекватен результат, выбранный большинством экспертов. При этом большое значение имеет правильный выбор классов эквивалентной шкалы – они должны надежно различаться наблюдателями, экспертами, оценивающими данное свойство. Нумерация объектов по шкале наименований осуществляется по принципу: “не приписывай одну и ту же цифру разным объектам”. Числа, приписанные объектам, могут быть использованы для определения вероятности или частоты появления данного объекта, но их нельзя использовать для суммирования и других математических операций.
При этом большое значение имеет правильный выбор классов эквивалентной шкалы – они должны надежно различаться наблюдателями, экспертами, оценивающими данное свойство. Нумерация объектов по шкале наименований осуществляется по принципу: “не приписывай одну и ту же цифру разным объектам”. Числа, приписанные объектам, могут быть использованы для определения вероятности или частоты появления данного объекта, но их нельзя использовать для суммирования и других математических операций.
Поскольку данные шкалы характеризуются только отношениями эквивалентности, то в них отсутствует понятия нуля, “больше” или “меньше” и единицы измерения. Примером номинальных шкал являются широко распространенные атласы цветов, предназначенные для идентификации цвета.
Шкала порядка (рангов)
Если свойство данного эмпирического объекта проявляет себя в отношении эквивалентности и порядка по возрастанию или убыванию количественного проявления свойства, то для него может быть построена шкала порядка. Она является монотонно возрастающей или убывающей и позволяет установить отношение больше/меньше между величинами, характеризующими указанное свойство. В шкалах порядка существует или не существует нуль, но принципиально нельзя ввести единицы измерения, так как для них не установлено отношение пропорциональности и соответственно нет возможности судить во сколько раз больше или меньше конкретные проявления свойства.
Она является монотонно возрастающей или убывающей и позволяет установить отношение больше/меньше между величинами, характеризующими указанное свойство. В шкалах порядка существует или не существует нуль, но принципиально нельзя ввести единицы измерения, так как для них не установлено отношение пропорциональности и соответственно нет возможности судить во сколько раз больше или меньше конкретные проявления свойства.
В случаях, когда уровень познания явления не позволяет точно установить отношения, существующие между величинами данной характеристики, либо применение удобно и достаточно для практики, используют условные (эмпирические) шкалы порядка. Условная шкала – это шкала ФВ, исходные значения которой выражены в условных единицах. Пример шкалы порядка – шкала вязкости Энглера, 12-бальная шкала Бофорта для силы морского ветра.
Рисунок – Пример шкалы порядка (шкала Бофорта)
Широкое распространение получили шкалы измерений порядка с нанесенными на них реперными точками. К таким шкалам, например, относится шкала Мооса для определения твердости минералов, которая содержит 10 опорных (реперных) минералов с различными условными числами твердости: тальк – 1; гипс – 2; кальций – 3; флюорит – 4; апатит – 5; ортоклаз – 6; кварц – 7; топаз – 8; корунд – 9; алмаз – 10. Отнесение минерала к той или иной градации твердости осуществляется на основании эксперимента, который состоит в том, что испытуемый материал царапается опорным. Если после царапанья испытуемого минерала кварцем (7) на нем остается след, а после ортоклаза (6) – не остается, то твердость испытуемого материала составляет более 6, но менее 7. Более точного ответа в этом случае дать невозможно,
К таким шкалам, например, относится шкала Мооса для определения твердости минералов, которая содержит 10 опорных (реперных) минералов с различными условными числами твердости: тальк – 1; гипс – 2; кальций – 3; флюорит – 4; апатит – 5; ортоклаз – 6; кварц – 7; топаз – 8; корунд – 9; алмаз – 10. Отнесение минерала к той или иной градации твердости осуществляется на основании эксперимента, который состоит в том, что испытуемый материал царапается опорным. Если после царапанья испытуемого минерала кварцем (7) на нем остается след, а после ортоклаза (6) – не остается, то твердость испытуемого материала составляет более 6, но менее 7. Более точного ответа в этом случае дать невозможно,
В условных шкалах одинаковым интервалам между размерами данной величины не соответствуют одинаковые размерности чисел, отображающих размеры. С помощью этих чисел можно найти вероятности, моды, медианы, квантили, однако их нельзя использовать для суммирования, умножения и других математических операция. Определение значения величин при помощи шкал порядка нельзя считать измерением, так как на этих шкалах не могут быть введены единицы измерения. Операцию по приписыванию числа требуемой величине следует считать оцениванием. Оценивание по шкалам порядка является неоднозначным и весьма условным, о чем свидетельствует рассмотренный пример.
Операцию по приписыванию числа требуемой величине следует считать оцениванием. Оценивание по шкалам порядка является неоднозначным и весьма условным, о чем свидетельствует рассмотренный пример.
Шкала интервалов (разностей)
Эти шкалы измерений в метрологии являются дальнейшим развитием шкал порядка и применяются для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности. Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. Пример шкалы интервалов – летоисчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо рождество Христово и т.д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов.
Рисунок – Пример шкалы интервалов (Температурные шкалы Цельсия и Фаренгейта)
На шкале интервалов определены действия сложения и вычитания интервалов. Действительно, по шкале времени интервалы можно суммировать или вычитать и сравнивать, во сколько раз один интервал больше другого, но складывать даты каких-либо событий просто бессмысленно.
Шкала интервалов величины Q описывается уравнением Q = Qо + q[Q], где q – числовое значение величины; Qо – начало отсчета шкалы; [Q] – единица рассматриваемой величины. Такая шкала полностью определяется заданием начала отсчета Qо шкалы и единицы данной величины [Q].
Задать шкалу практически можно двумя путями. При первом из них выбираются два значения Qо и Q1, величины, которые относительно просто реализованы физически. Эти значения называются опорными точками, или основными реперами, а интервал (Q1 ~ Qо) – основным интервалом. Точка Qо принимается за начало отсчета, а величина (Q1 -Qо)/n=[Qо] за единицу Q. При этом n выбирается таким, чтобы [Q] было целой величиной.
Рисунок – Пример шкалы отношений
При втором пути задания шкалы единица воспроизводится непосредственно как интервал, его некоторая доля или некоторое число интервалов размеров данной величины, а начало отсчета выбирают каждый раз по-разному в зависимости от конкретных условий изучаемого явления. Пример такого подхода – шкала времени, в которой 1с = 9192631770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. За начало отсчета принимается начало изучаемого явления.
Пример такого подхода – шкала времени, в которой 1с = 9192631770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. За начало отсчета принимается начало изучаемого явления.
Шкала отношений
Шкала отношений описывает свойства эмпирических объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности (шкалы второго рода – аддитивные), а в ряде случаев и пропорциональности (шкалы первого рода – пропорциональные). Пример шкалы отношений – шкала массы (второго рода), термодинамической температуры (первого рода).
В шкалах отношений существует однозначный естественный критерий нулевого количественного проявления свойства и единица измерений, установленная по соглашению. С формальной точки зрения этот вид шкал измерений является шкалой интервалов с естественным началом отсчета. К значениям, полученным по этой шкале, применимы все арифметические действия, что имеет важное значение при измерений физических величин.
Рисунок – Пример абсолютной шкалы (шкала температур Кельвина)
Шкалы отношений – самые совершенные. Они описываются уравнением Q = q[Q], где Q – ФВ, для которой строится шкала, [Q] – ее единица измерения, q – числовое значение ФВ. Переход от одной шкалы отношений к другой происходит в соответствии с уравнением q2 = q1[Q1]/[Q2].
Абсолютные шкалы
Абсолютные шкалы – это шкалы, обладающие всеми признаками шкал отношений, но дополнительно имеющие естественное однозначное определение единицы измерения и не зависящие от принятой системы единиц измерения. Примером абсолютной шкалы могут стать шкалы с относительным величинам: коэффициенту усиления, ослабления и др. Для образования многих производных единиц в системе СИ используются безразмерные и счетные единицы абсолютных шкал.
Отметим, что шкалы наименований и порядка называют неметрическими (концептуальными), а шкалы интервалов и отношений – метрическими (материальными). Метрические и абсолютные шкалы относятся к разряду линейных. Практическая реализация шкал измерений в метрологии осуществляется путем стандартизации как самих шкал и единиц измерений, так и, в необходимых случаях, способов и условий их однозначного воспроизведения.
Метрические и абсолютные шкалы относятся к разряду линейных. Практическая реализация шкал измерений в метрологии осуществляется путем стандартизации как самих шкал и единиц измерений, так и, в необходимых случаях, способов и условий их однозначного воспроизведения.
Изготовление измерительной шкалы своими руками
Видео о том, как самостоятельно сделать шкалу стрелочного прибора на примере изготовления шкалы амперметра.
Похожие материалы
Виды шкал и их особенности
Категория: Стандартизация, метрология, сертификация
Проблема обеспечения высокого качества продукции тесным образом связана с проблемой качества измерений. Между ними явно прослеживается непосредственная связь: там, где качество измерений не соответствует требованиям технологического процесса, невозможно достичь высокого уровня качества продукции. Поэтому качество продукции в значительной степени зависит от успешного решения вопросов, связанных с точностью измерений параметров качества материалов и комплектующих изделий и поддержания заданных технологических режимов. Иными словами, технический контроль качества осуществляется путем замеров параметров технологических процессов, результаты измерений которых необходимы для регулирования процессом.
Иными словами, технический контроль качества осуществляется путем замеров параметров технологических процессов, результаты измерений которых необходимы для регулирования процессом.
Следовательно, качество измерений представляет собой совокупность свойств состояния измерений, обеспечивающих результаты измерений с требуемыми точностными характеристиками, получаемые в необходимом виде за определенный отрезок времени.
Основные свойства состояния измерений:
• точность результатов измерений;
• воспроизводимость результатов измерений;
• сходимость результатов измерений;
• быстрота получения результатов;
• единство измерений.
При этом под воспроизводимостью результатов измерений понимается близость результатов измерений одной и той же величины, полученные в разных местах, разными методами, разными средствами, разными операторами, в разное время, однако в одних и тех же условиях измерений (температуре, давлении, влажности и т. д.).
д.).
Сходимость результатов измерений — это близость результатов измерений одной и той же величины, проведенных повторно с применением одних и тех же средств, одним и тем же методом в одинаковых условиях и с той же тщательностью.
Любое измерение или количественное оценивание чего-либо осуществляется, используя соответствующие шкалы.
Шкала — это упорядоченный ряд отметок, соответствующий соотношению последовательных значений измеряемых величин. Шкалой измерений называется принятая по соглашению последовательность значений одноименных величин различного размера.
В метрологии шкала измерений является средством адекватного сопоставления и определения численных значений отдельных свойств и качеств различных объектов. Практически используют пять видов шкал: шкалу наименований, шкалу порядка, шкалу интервалов, шкалу отношений и шкалу абсолютных значений.
Шкала наименований (номинальная шкала). Это самая простая из всех шкал. В ней числа выполняют роль ярлыков и служат для обнаружения и различения изучаемых объектов. Числа, составляющие шкалу наименований, разрешается менять местами. В этой шкале нет отношений типа «больше—меньше», поэтому некоторые полагают, что применение шкалы наименований не стоит считать измерением. При использовании шкалы наименований могут проводится только некоторые математические операции. Например, ее числа нельзя складывать и вычитать, но можно подсчитывать, сколько раз (как часто) встречается то или иное число.
Числа, составляющие шкалу наименований, разрешается менять местами. В этой шкале нет отношений типа «больше—меньше», поэтому некоторые полагают, что применение шкалы наименований не стоит считать измерением. При использовании шкалы наименований могут проводится только некоторые математические операции. Например, ее числа нельзя складывать и вычитать, но можно подсчитывать, сколько раз (как часто) встречается то или иное число.
Шкала порядка. Места, занимаемые величинами в шкале порядка, называются рангами, а сама шкала называется ранговой, или неметрической. В такой шкале составляющие ее числа упорядочены по рангам (т.е. занимаемым местам), но интервалы между ними точно измерить нельзя. В отличие от шкалы наименований шкала порядка позволяет не только установить факт равенства или неравенства измеряемых объектов, но и определить характер неравенства в виде суждений: «больше—меньше», «лучше—хуже» и т.п.
С помощью шкал порядка можно измерять качественные, не имеющие строгой количественной меры, показатели. Особенно широко эти шкалы используются в гуманитарных науках: педагогике, психологии, социологии. К рангам шкалы порядка можно применять большее число математических операций, чем к числам шкалы наименований.
Особенно широко эти шкалы используются в гуманитарных науках: педагогике, психологии, социологии. К рангам шкалы порядка можно применять большее число математических операций, чем к числам шкалы наименований.
Шкала интервалов. Это такая шкала, в которой числа не только упорядочены по рангам, но и разделены определенными интервалами. Особенность, отличающая ее от описываемой дальше шкалы отношений, состоит в том, что нулевая точка выбирается произвольно. Примерами могут быть календарное время (начало летоисчисления в разных календарях устанавливалось по случайным причинам, температура, потенциальная энергия поднятого груза, потенциал электрического поля и др.).
Результаты измерений по шкале интервалов можно обрабатывать всеми математическими методами, кроме вычисления отношений. Данные шкалы интервалов дают ответ на вопрос «на сколько больше?», но не позволяют утверждать, что одно значение измеренной величины во столько-то раз больше или меньше другого. Например, если температура повысилась с 10 до 20°С, то нельзя сказать, что стало в два раза теплее.
Шкала отношений. Эта шкала отличается от шкалы интервалов только тем, что в ней строго определено положение нулевой точки. Благодаря этому шкала отношений не накладывает никаких ограничений на математический аппарат, используемый для обработки результатов наблюдений.
По шкале отношений измеряют и те величины, которые образуются как разности чисел, отсчитанных по шкале интервалов. Так, календарное время отсчитывается по шкале интервалов, а интервалы времени — по шкале отношений.
При использовании шкалы отношений (и только в этом случае!) измерение какой-либо величины сводится к экспериментальному определению отношения этой величины к другой подобной, принятой за единицу. Измеряя длину объекта, мы узнаем, во сколько раз эта длина больше длины другого тела, принятого за единицу длины (метровой линейки в данном случае) и т.п. Если ограничиться только применением шкал отношений, то можно дать другое (более узкое, частное) определение измерения: измерить какую-либо величину — значит найти опытным путем ее отношение к соответствующей единице измерения.
Шкала абсолютных величин. Во многих случаях напрямую измеряется величина чего-либо. Например, непосредственно подсчитывается число дефектов в изделии, количество единиц произведенной продукции, сколько студентов присутствует на лекции, количество прожитых лет и т.д. и т.п. При таких измерениях на измерительной шкале отмечаются
абсолютные количественные значения измеряемого. Такая шкала абсолютных значений обладает и теми же свойствами, что и шкала отношений, с той лишь разницей, что величины, обозначенные на этой шкале, имеют абсолютные, а не относительные значения.
Результаты измерений по шкале абсолютных величин имеют наибольшую достоверность, информативность и чувствительность к неточностям измерений.
Шкалы интервалов, отношений и абсолютных величин называются метрическими, так как при их построении используются некоторые меры, т.е. размеры, принятые в качестве единиц измерений.
Измерение и шкалы | Современное прогнозирование
Любая система содержит очень много различной информации. Конечно же, не вся она нам нужна, но ту, которая нам нужна, надо как-то измерить и преобразовать. Для этого информации нужно предать какую-нибудь форму, то есть перевести её в данные. Например, общую информацию о том, что потребителям нравится наша продукция, и они согласны покупать её в большем количестве, можно формализовать, проведя исследования и дав оценку удовлетворённости покупателей. В результате этого мы получим данные, с которыми можно уже работать и на основе которых можно принимать решение.
Конечно же, не вся она нам нужна, но ту, которая нам нужна, надо как-то измерить и преобразовать. Для этого информации нужно предать какую-нибудь форму, то есть перевести её в данные. Например, общую информацию о том, что потребителям нравится наша продукция, и они согласны покупать её в большем количестве, можно формализовать, проведя исследования и дав оценку удовлетворённости покупателей. В результате этого мы получим данные, с которыми можно уже работать и на основе которых можно принимать решение.
Во время такого преобразования исследователь явно или неявно выбирает шкалу, в которой он будет измерять данные. Существует много различных классификаций шкал, и даже есть специальный раздел математики, изучающий шкалы и операции с ними — теория измерений. Не вдаваясь в детали это дисциплины, рассмотрим то, что может нам пригодиться в прогнозировании.
Принято считать, что любая шкала может обладать следующими характеристиками:
- описание,
- порядок,
- расстояние,
- естественная точка отсчёта,
- естественная единица измерения.

Последняя характеристика обычно опускается, так как для целей исследования особо полезной информации не несёт. С точки зрения прогнозирования выделение следующих четырёх видов шкал (упорядоченных по уровню) на основе первых четырёх характеристик вполне достаточно для использования по максимуму различных математических и не математических методов:
1. Номинальная шкала
Шкала, в которой есть только характеристика «описание». В ней нет естественного упорядочения, нет расстояния между элементами и тем более нет естественной точки отсчёта. С данными, измеренными в номинальной шкале возможна только одна операция — сравнение в форме «равно» или «неравно». То есть обладает ли объект указанным свойством или нет.
Пример (шутливый). Туристы бывают:
- белые,
- китайцы,
- русские,
- женщины,
- другие.
Из-за ограниченности номинальной шкалы, практически всё, что можно сделать с данными, измеренными в ней — это посмотреть на количество объектов, имеющих указанные признаки. Например, мы можем понять, сколько в нашем распоряжении оказалось китайских туристов, какой процент от всех туристов они составляют. Если в нашем распоряжении несколько величин, измеренных в номинальной шкале, мы можем, например, использовать коэффициент сопряжённости, для того, чтобы оценить, есть ли связь в выборе признака в одной шкале с выбором признака в другой.
Например, мы можем понять, сколько в нашем распоряжении оказалось китайских туристов, какой процент от всех туристов они составляют. Если в нашем распоряжении несколько величин, измеренных в номинальной шкале, мы можем, например, использовать коэффициент сопряжённости, для того, чтобы оценить, есть ли связь в выборе признака в одной шкале с выбором признака в другой.
Для целей анализа номинальную шкалу бывает удобно трансформировать в бинарную, в которой «1» соответствует наличию, а «0» — отсутствию свойства. В случае с нашими туристами мы получим соответственно 5 новых переменных, измеренных в такой бинарной шкале.
2. Порядковая (ранговая) шкала
Это уже более сложная шкала, в ней появляется вторая характеристика — «порядок». Данные, измеренные в этой шкале можно сравнить и упорядочить, однако сказать насколько (и уж тем более во сколько раз) одна величина больше другой нельзя. То есть к операциям с данными, в этой шкале добавляется «больше» и «меньше».
Пример. Туристы бывают:
Туристы бывают:
- грустные,
- нейтральные,
- весёлые.
В этом примере, как видим, туристы упорядочены по настроению, но при этом нет возможности сказать, насколько один может быть веселее другого. К порядковой шкале будет относиться даже шкала, которая на первый взгляд не выглядит как порядковая.
Пример. Туристы бывают:
- от 10 до 15 килограмм,
- от 15 до 20 килограмм,
- от 20 до 100 килограмм,
- больше 100 килограмм.
Измерить расстояние между элементами в такой шкале не представляется возможным, поэтому она порядковая.
Точно так же оценки за экзамен измеряются в порядковой шкале: разница между 5 и 3 формально равна двум, но при этом не имеет смысла, так как в этой шкале двойка — это просто ещё одна оценка. Если по курсу вначале получить 3,а потом — 2, то пятёрки не получится.
В порядковой шкале можно уже использовать некоторые базовые статистические инструменты. Например, можно оценить моду, для того, чтобы понять, туристы какого веса чаще встречаются в выборке. Можно так же рассчитать ранговый коэффициент корреляции (Спирмена либо Кендалла), который может показать, есть ли статистическая линейная связь между весом туристов и их настроением. Расчёт средней величины (а так же медианы и стандартного отклонения) в порядковой шкале возможен, но в этом случае получаемое значение будет просто добавлять в нашу шкалу новые значения, но не более того. Например, если в шкале оценок за экзамены появилась «4.5» (как средняя между «4» и «5»), то это значение просто расширяет нашу шкалу, которая теперь будет содержать: «2», «3», «4», «4.5» и «5». Расстояние между «4» и «4.5», а так же «4.5» и «5» всё так же невозможно адекватно измерить.
Можно так же рассчитать ранговый коэффициент корреляции (Спирмена либо Кендалла), который может показать, есть ли статистическая линейная связь между весом туристов и их настроением. Расчёт средней величины (а так же медианы и стандартного отклонения) в порядковой шкале возможен, но в этом случае получаемое значение будет просто добавлять в нашу шкалу новые значения, но не более того. Например, если в шкале оценок за экзамены появилась «4.5» (как средняя между «4» и «5»), то это значение просто расширяет нашу шкалу, которая теперь будет содержать: «2», «3», «4», «4.5» и «5». Расстояние между «4» и «4.5», а так же «4.5» и «5» всё так же невозможно адекватно измерить.
3. Интервальная шкала
В интервальной шкале добавляется ещё одна характеристика — расстояние, но в ней всё так же отсутствует естественная точка отсчёта. Приемлемые операции в этой шкале (плюс к тем, которые уже были) — сложение и вычитание. Однако операции деления и умножения в этой шкале бессмысленны.
Пример. Температура туриста.
Температура туриста.
Если температура одного туриста — 36.6ºC, а другого — 18.3ºC, то мы можем сказать, что второй турист холоднее первого на 18.3ºC, но сказать, что первый турист горячее второго в два раза нельзя — это не имеет смысла. А всё потому что 0ºC — это не естественная точка отсчёта, а искусственная, привязанная к температуре замерзания воды. Если в качестве точки отсчёта в этой шкале взять, например, абсолютный ноль, то этот бессмысленный эффект «первый в два раза горячее второго» пропадёт.
В интервальной шкале имеют смысл и средняя величина, и медиана, и стандартное отклонение, и квантили распределения. Если очень хочется, то можно рассчитать и коэффициент корреляции Пирсона, который покажет, есть ли линейная связь между показателями.
4. Абсолютная шкала.
Это последний тип шкалы, и он имеет все рассмотренные нами характеристики. Наличие естественной точки отсчёта означает, что когда показатель принимает значение «0», то это говорит о том, что исследуемое свойство у объекта просто отсутствует. В этой шкале возможны все математические операции.
В этой шкале возможны все математические операции.
Пример. Количество туристов в комнате.
Думаю, комментарии к этому примеру излишни.
У шкал есть одно удобное свойство: любые данные, измеренные в шкале более высокого уровня, можно легко преобразовать в данные, измеренные в шкале более низкого уровня.
Если провести ещё одну свёртку данных и избавиться от расстояний между значениями, то можно получить порядковую шкалу, например, следующего вида:
- менее 5 туристов,
- от 5 до 10 туристов,
- более 10 туристов.

Продолжая упрощения, избавляясь от порядка, можно предложить простейшую номинальную шкалу:
- 5 туристов,
- не 5 туристов.
Очевидно, что обратное преобразование невозможно. Если мы изначально собирали данные в номинальной шкале, то получить из них данные, измеренные в шкале более высокого уровня, в принципе невозможно.
И последнее. В случае, если оказывается нужно оценить связь между показателями, измеренными в разных шкалах, нужно использовать коэффициенты, предназначенные для шкал более низкого уровня. Например, для определения связи настроения туриста с его температурой стоит обратиться к ранговому коэффициенту корреляции.
1. Понятие шкалы измерений. Типы шкал измерений, их основные характеристики. Примеры различных типов шкал измерений.
Понятия
физическая величина и измерение тесным
образом связаны с понятием шкалы
физической величины – упорядоченной
совокупностью значений физической
величины, служащей исходной основой
для измерений данной величины. Шкалой
измерений называют порядок определения
и обозначения возможных значений
конкретной величины или проявлений
какого-либо свойства. Понятия шкалы
возникли в связи с необходимостью
изучать не только количественные, но и
качественные свойства природных и
рукотворных объектов и явлений. Различают
несколько типов шкал: 1. Шкала наименований
(классификации) – это самая простая
шкала, которая основана на приписывании
объекту знаков или цифр для их идентификации
или нумерации. Например, атлас цветов
(шкала цветов) или шкала (классификация)
растений Карла Линнея. Данные шкалы
характеризуются только отношением
эквивалентности (равенства) и в них
отсутствуют понятия больше, меньше,
отсутствуют единицы измерения и нулевое
значение. Этот вид шкал приписывает
свойствам объектов определенные числа,
которые выполняют функцию имен. Процесс
оценивания в таких шкалах состоит в
достижении эквивалентности путем
сравнения испытуемого образца с одним
из эталонных образцов. Таким образом,
шкала наименований отражает качественные
свойства.
Шкалой
измерений называют порядок определения
и обозначения возможных значений
конкретной величины или проявлений
какого-либо свойства. Понятия шкалы
возникли в связи с необходимостью
изучать не только количественные, но и
качественные свойства природных и
рукотворных объектов и явлений. Различают
несколько типов шкал: 1. Шкала наименований
(классификации) – это самая простая
шкала, которая основана на приписывании
объекту знаков или цифр для их идентификации
или нумерации. Например, атлас цветов
(шкала цветов) или шкала (классификация)
растений Карла Линнея. Данные шкалы
характеризуются только отношением
эквивалентности (равенства) и в них
отсутствуют понятия больше, меньше,
отсутствуют единицы измерения и нулевое
значение. Этот вид шкал приписывает
свойствам объектов определенные числа,
которые выполняют функцию имен. Процесс
оценивания в таких шкалах состоит в
достижении эквивалентности путем
сравнения испытуемого образца с одним
из эталонных образцов. Таким образом,
шкала наименований отражает качественные
свойства.

 Это наиболее
совершенная и информативная шкала.
Результаты измерений в ней можно
вычитать, умножать и делить. В некоторых
случаях возможна и операция суммирования
для аддитивных величин. Аддитивной
называется величина, значения которой
могут быть суммированы, умножены на
числовой коэффициент и разделены друг
на друга (например, длина, масса, сила и
др.). Неаддитивной величиной называется
величина, для которой эти операции не
имеют физического смысла, например,
термодинамическая температура. Примером
шкалы отношений является шкала масс –
массы тел можно суммировать, даже если
они не находятся в одном месте. 5.
Абсолютные шкалы – это шкалы отношений,
в которых однозначно (а не по соглашению)
присутствует определение единицы
измерения. Абсолютные шкалы присущи
относительным единицам (коэффициенты
усиления, полезного действия и др.),
единицы таких шкал являются безразмерными.
Условные шкалы – шкалы, исходные значения
которых выражены в условных единицах.
К таким шкалам относятся шкалы наименований
и порядка.
Это наиболее
совершенная и информативная шкала.
Результаты измерений в ней можно
вычитать, умножать и делить. В некоторых
случаях возможна и операция суммирования
для аддитивных величин. Аддитивной
называется величина, значения которой
могут быть суммированы, умножены на
числовой коэффициент и разделены друг
на друга (например, длина, масса, сила и
др.). Неаддитивной величиной называется
величина, для которой эти операции не
имеют физического смысла, например,
термодинамическая температура. Примером
шкалы отношений является шкала масс –
массы тел можно суммировать, даже если
они не находятся в одном месте. 5.
Абсолютные шкалы – это шкалы отношений,
в которых однозначно (а не по соглашению)
присутствует определение единицы
измерения. Абсолютные шкалы присущи
относительным единицам (коэффициенты
усиления, полезного действия и др.),
единицы таких шкал являются безразмерными.
Условные шкалы – шкалы, исходные значения
которых выражены в условных единицах.
К таким шкалам относятся шкалы наименований
и порядка. Шкалы разностей, отношений
и абсолютные называются метрическими
(физическими) шкалами.
Шкалы разностей, отношений
и абсолютные называются метрическими
(физическими) шкалами.Характеристики шкал измерений:
Шкала | Характеристики | |||
Нуль ФВ | Возрастание / убывание ФВ | Единица измерения | Применяемые математические операции | |
Наименований | Отсутствует | Отсутствует | Отсутствует | Невозможно |
Порядка | Отсутствует или задан условно | Применимо | Отсутствует | Невозможно |
Интервалов | Произвольно выбранный | Применимо | Имеется | «+», «–», «», «» над интервалами |
Отношений | Естественный | Применимо | Имеется | «+», «–», «», «» над величинами |
Абсолютные | Естественный | Применимо | Естественная | |
ГП
Всероссийский научно-исследовательский институт (ГП ВНИИФТРИ) Зам. ДиректораГП “ВНИИФТРИ” Ю.И. Брегадзе________________ 06 декабря 1995 г. РЕКОМЕНДАЦИЯ Государственная система обеспечения единства измерений Шкалы измерений. Основные положения. Термины и определения МИ 2365-96РЕКОМЕНДАЦИЯГСИ. Термины и определения МИ 2365-96Содержание
В настоящей рекомендации приведены основные положения теории шкал измерений, а также соответствующие термины и определения необходимые для правильного понимания и практического применения шкал измерений метрологами и приборостроителями. Термин “шкала” в метрологической практике
имеет, по крайней мере, два различных значения. Во-первых, шкалой или точнее
шкалой измерений называют принятый по соглашению порядок определения и
обозначения всевозможных проявлений (значений) конкретного свойства (величины)
Во-вторых, шкалой называют отсчетные устройства аналоговых средств измерений, В
настоящей рекомендации термин “шкала” используется только в первом из
приведенных выше значений. В первом разделе настоящей рекомендации даны основные положения теории шкал измерений. Второй раздел содержит термины по метрологии, определения которых учитывают положения теории и опыта практического применения шкал измерений. Измерению подлежат различные проявления свойств тел, веществ, явлений,
процессов. Некоторые свойства при этом проявляются количественно (длина, масса,
температура и т.п.), а другие – качественно (например, цвет, т.к. не имеет
смысла выражение типа “красный цвет больше (меньше) синего”).
Многообразие (количественное или качественное) проявлений любого свойства
образуют множества, отображение элементов которых на упорядоченные множества
чисел или, в более общем случае, на систему условных знаков образуют шкалы
измерения этих свойств. Такими системами знаков являются, например, множество
обозначений (названий) цветов, совокупность классификационных символов или
понятий, множество баллов оценки состояний объекта, множество действительных
чисел и т. В соответствии с логической структурой проявления свойств в теории измерений различают пять основных типов шкал измерений: наименований, порядка, разностей (интервалов), отношений и абсолютные шкалы. Каждый тип шкалы обладает определенными признаками, основные из которых рассматриваются ниже. ШКАЛЫ НАИМЕНОВАНИЙ
отражают качественные свойства. Их элементы характеризуются только
соотношениями эквивалентности (равенства) и сходства конкретных качественных
проявлений свойств. В шкалах наименований нельзя ввести понятия единицы измерения; в них отсутствует и нулевой элемент. Шкалы наименований, по существу, качественны; однако возможны некоторые статистические операции при обработке результатов измерений в этих шкалах, например, можно найти модальный или наиболее многочисленный класс эквивалентности. ШКАЛЫ ПОРЯДКА – описывают
свойства, для которых имеют смысл не только соотношения эквивалентности, но и
соотношения порядка по возрастанию или убыванию количественного проявления
свойства. В этих шкалах также нет возможности ввести единицы измерений из-за того, что они не только принципиально нелинейны, но и вид нелинейности может быть различен и неизвестен на разных ее участках. Результаты измерений в шкалах твердости, например, выражаются в числах твердости по Бринеллю, Виккерсу, Роквеллу, Шору, а не в единицах измерений. Шкалы порядка допускают монотонные преобразования, в них может быть или отсутствовать нулевой элемент. ШКАЛЫ РАЗНОСТЕЙ (ИНТЕРВАЛОВ)
– отличаются от шкал порядка тем, что для описываемых ими свойств имеют смысл
не только соотношения эквивалентности и порядка, но и суммирования интервалов
(разностей) между различными количественными проявлениями свойств. Интервалы времени (например, периоды работы, периоды учебы) можно складывать и вычитать, но складывать даты каких-либо событий бессмысленно. Другой пример, шкала длин (расстояний) – пространственных интервалов определяется путем совмещения нуля линейки с одной точкой, а отсчет делается у другой точки. К этому типу шкал относятся и шкалы температур по Цельсию, Фаренгейту, Реомюру. Шкалы разностей имеют условные (принятые по соглашению) единицы измерений и нули, опирающиеся на какие-либо реперы. В этих шкалах допустимы линейные преобразования, в них применимы процедуры для отыскания математического ожидания, стандартного отклонения, коэффициента ассиметрии и смещенных моментов. ШКАЛЫ ОТНОШЕНИЙ. К
множеству количественных проявлений в этих шкалах применимы соотношения
эквивалентности и порядка – операции вычитания и умножения, (шкалы отношений
1-го рода – пропорциональные шкалы), а во многих случаях и суммирования (шкалы
отношений 2-го рода – аддитивные шкалы). В шкалах отношений существуют условные (принятые по соглашению) единицы и естественные нули. Примерами шкал отношений являются шкалы массы (2-го рода), термодинамическая температурная шкала (1-го рода). Массы любых объектов можно суммировать, но суммировать температуры разных тел нет смысла, хотя можно судить о разности и, отношении их термодинамических температур. Шкалы отношений широко используются в физике и технике, в них допустимы все арифметические и статистические операции. АБСОЛЮТНЫЕ ШКАЛЫ - обладают всеми признаками шкал отношений, но дополнительно в них существует естественное однозначное определение единицы измерений. Такие шкалы используются для измерений относительных величии (отношений одноименных величин: коэффициентов усиления, ослабления, КПД, коэффициентов отражений и поглощений, амплитудной модуляции и т.д.). ЛОГАРИФМИЧЕСКИЕ ШКАЛЫ
– логарифмическое преобразование шкал, часто применяемое на практике, приводит
к изменению типа шкал. Логарифм есть число безразмерное, поэтому перед логарифмированием преобразуемая размерная величина в начале обращается в безразмерную путем ее деления на принятое по соглашению произвольное (опорное) значение той же величины, после чего выполняется операция логарифмирования. В зависимости от типа шкалы, подвергнутой логарифмическому преобразованию, логарифмические шкалы могут быть двух видов. При логарифмическом преобразовании абсолютных шкал получаются абсолютные логарифмические шкалы, называемые иногда логарифмическими шкалами с плавающим нулем, т.к. в них не фиксируется опорное значение. Примерами таких шкал являются шкалы усиления (ослабления) сигнала в дБ. Для значений величин в абсолютных логарифмических шкалах допустимы операции сложения и вычитания. При логарифмическом преобразовании шкал отношений и интервалов
получается логарифмическая шкала интервалов с фиксированным нулем,
соответствующим принятому опорному значению преобразуемой шкалы. БИОФИЗИЧЕСКИЕ ШКАЛЫ. В метрологической практике существует ряд шкал, которыми описываются реакции биологических объектов, прежде всего человека, на воздействующие на них физические факторы. К ним относятся шкалы световых и цветовых измерений, шкалы восприятия звуков, шкалы эквивалентных доз ионизирующих излучений и др. Будем называть такие шкалы биофизическими. Биофизическая шкала – шкала измерений свойств физического фактора
(стимула), модифицированная таким образом, чтобы по результатам измерений этих
свойств можно было прогнозировать уровень или характер реакции биологического
объекта на действие этого фактора. Такая модифицированная шкала стимулов, естественно, по логической структуре приближается к структуре шкалы реакций и приобретает некоторую прогностическую ценность. Однако, как правило, биофизическая шкала стимулов и шкала
соответствующих реакций являются шкалами разных типов, поэтому на
прогностические суждения о реакциях, вызываемых стимулами, нельзя прямо
переносить логические соотношения шкалы стимулов. Так, например, шкала яркостей
с точки зрения стимулов является неограниченной аддитивной шкалой отношений, а
с точки зрения восприятия человеком – шкалой порядка в ограниченном снизу и
сверху диапазоне значений стимулов. Большинство свойств описывается одномерными шкалами, однако имеются свойства, описываемые многомерными шкалами – трехмерные шкалы цвета в колориметрии, двухмерные шкалы электрических импедансов и др. Основные признаки и особенности типов шкал систематизированы в таблице 1. Практическая реализация шкал измерений достигается путем стандартизации как самих шкал и единиц измерений, так и, в необходимых случаях, способов и условий (спецификаций) их однозначного воспроизведения. Шкалы наименований и порядка могут реализовываться и без эталонов (шкала-классификация Линнея, шкала запахов, шкала Бофорта), но если создание эталонов необходимо, то они воспроизводят весь применяемый на практике участок шкалы (пример – эталоны твердости). Внесение любых изменений в спецификацию, определяющую шкалу наименований или порядка, практически означает введение новой шкалы. Шкалы разностей и отношений (метрические шкалы), соответствующие SI, как правило воспроизводятся эталонами. В метрологических НД обычно говорится только об установлении и воспроизведении единиц измерений. На деле даже для величин, соответствующих основным единицам SI (секунда, кельвин, кандела и др.), эталоны кроме единиц хранят и воспроизводят шкалы (атомного и астрономического времени, температурную МТШ-90 и т.д.). При любом варианте построения эталонов поверочными схемами предусматривается воспроизведение всех необходимых для практики участков шкал. Абсолютные шкалы могут опираться на эталоны, воспроизводящие любые их участки (как эталоны метрических шкал), но могут воспроизводится и без них (КПД, коэффициент усиления). Особенности воспроизведения (реализации) шкал систематизированы в таблице 2. Основные признаки классификации шкал измерений
Таблица 2 Особенности реализации шкал измерений
Метрология Наука об измерениях, методах и средствах обеспечения их единства и
способах достижения требуемой точности. Законодательная метрология Раздел метрологии, включающий взаимосвязанные законодательные и научно-технические вопросы, нуждающиеся в регламентации со стороны государства и (или) мирового сообщества, для обеспечения единства измерений. Теоретическая метрология Раздел метрологии, в котором изучаются и разрабатываются ее теоретические основы (теория измерений, теория шкал измерений, проблемы установления систем единиц измерений, вопросы использования в метрологии фундаментальных констант и др.). Практическая (прикладная) метрология Раздел метрологии, в котором изучаются и разрабатываются вопросы практического применения положений теоретической и законодательной метрологии. Единство измерений Состояние измерений, при котором их результаты выражены в узаконенных
единицах или шкалах измерений, а неопределенности (погрешности) результатов
измерений не выходят за установленные границы (с заданной вероятностью). Примечание. Данное определение понятия “единства измерений” не противоречит Закону “Об обеспечении единстве измерений” (статья 1), но распространяет его на шкалы наименований и порядка (см. “шкала измерений”). Шкала измерений (шкала) Отображение множества различных проявлений качественного или количественного свойства на принятое по соглашению упорядоченное множество чисел или другую систему логически связанных знаков (обозначений). Примечания. 1. Понятие шкала измерений (кратко – шкала) не следует отождествлять с отсчетным устройством (шкалой) средства измерений. 2. Различают пять типов шкал: наименований, порядка, разностей (интервалов), отношений и абсолютные. 3.
Примерами систем знаков, образующих шкалы измерений, являются множество баллов
оценки свойств объектов, множество обозначений (названий) цвета объекта,
множество названий состояния объекта, совокупность классификационных символов
или понятий и т. 4. Шкалы разностей и отношений объединяют термином “метрические шкалы”. 5. Различают одномерные и многомерные шкалы измерений. Шкала величины Шкала измерений количественного свойства. Тип шкалы Классификационный признак данной шкалы измерений, характеризующий совокупность присущих ей логических соотношений. Шкала наименований Шкала измерений качественного свойства, характеризующаяся только соотношением эквивалентности различных проявлений этого свойства. Примечания. 1. Множество проявлений (реализации) качественного свойства может быть упорядочено по признаку близости (сходства) и (или) по признаку возможных количественных различий в некоторых подмножествах проявления свойства. Например,
шкалы измерений цвета опираются на трехкоординатную модель цветового
пространства, упорядоченную по цветовым различиям (качественный признак) и
яркости (количественный признак). 2. Отличительные признаки шкал наименований: неприменимость в них понятий: нуля, единицы измерений, размерности; допустимость только изоморфных или гомоморфных преобразований; возможность реализации как с помощью эталонов, так и без них; недопустимость изменения спецификаций, описывающих конкретные шкалы. Чаще всего шкалы наименований определяются рядом “классов эквивалентности”. Шкала порядка Шкала количественного свойства, характеризующаяся соотношениями эквивалентности и порядка по возрастанию (убыванию) различных проявлений свойства. Примечание. Отличительные признаки шкал порядка: неприменимость в них понятий “единица измерений” и “размерность”, необязательность наличия нуля, допустимость любых монотонных преобразований, возможность реализации как с помощью эталонов, так и без них, недопустимость изменения спецификаций, описывающих конкретные шкалы. Шкала разностей (интервалов) Шкала измерений количественного свойства, характеризующаяся
соотношениями эквивалентности, порядка, суммирования интервалов различных,
проявлений свойства. Примечание. Отличительные признаки шкал разностей: наличие устанавливаемых по соглашению нуля и единицы измерений, применимость понятия “размерность”, допустимость линейных преобразований, реализация только посредством эталонов, допустимость изменения спецификаций, описывающих конкретные шкалы. Шкала отношений Шкала измерений количественного свойства, характеризующаяся соотношениями эквивалентности, порядка, пропорциональности (допускающими в ряде случаев операцию суммирования) различных проявлений свойства. Примечания. 1. Отличительные признаки шкал отношений: наличие естественного нуля и устанавливаемой по соглашению единицы измерений, применимость понятия “размерность”, допустимость масштабных преобразований, реализация только посредством эталонов, допустимость изменения спецификаций, описывающих конкретные шкалы. 2.
Шкалы отношений, в которых не имеет смысла операция суммирования, называются
“пропорциональными шкалами отношений”, а шкалы, в которых эта
операция имеет смысл, называют “аддитивными шкалами отношений”. Абсолютная шкала Шкала отношений (пропорциональная или аддитивная) безразмерной величины. Примечания. 1. Отличительные признаки абсолютных шкал: наличие естественных (не зависящих от принятой системы) единиц нуля и безразмерной единицы измерений, допустимость только тождественных преобразований, реализация как с помощью эталонов, так и без них, допустимость изменения спецификаций, описывающих конкретные шкалы. 2. Результаты измерений в абсолютных шкалах могут выражаться не только в безразмерных единицах, но и в процентах, промиллях, децибелах, битах (см. логарифмические шкалы), 3. Единицы абсолютных шкал могут применяться в сочетании с размерными единицами других шкал. Пример – плотность записи информации в бит/см. 4.
Разновидностью абсолютных шкал являются дискретные (целочисленные, счетные,
квантованные) шкалы, в которых результат измерения выражается безразмерным
числом частиц, квантов или других единичных объектов, эквивалентных по
количественному проявлению измеряемого свойства. Например, значение электрического заряда выражается числом электронов, значение энергии монохроматического электромагнитного излучения – числом квантов (фотонов). Иногда за единицу измерений в таких шкалах принимают какое-то определенное число частиц (квантов), например, один моль, т.е. число частиц равное числу Авогадро со специальным названием (Фарадей, Эйнштейн). Абсолютная ограниченная шкала Абсолютная шкала, диапазон значений которой находится в пределах от нуля до единицы (или некоторого предельного значения по спецификации шкалы). Логарифмическая шкала Шкала, построенная на основе систем логарифмов. Примечание. Для построения логарифмических шкал обычно используются системы десятичных или натуральных логарифмов, а также система логарифмов с основанием два. Логарифмическая шкала разностей Логарифмическая шкала измерений, получаемая при логарифмическом
преобразовании величины, описываемой шкалой отношений, или интервала в шкале
разностей, т. Примечание. Выбор опорного значения Х0 определяет нулевую точку логарифмической шкалы разностей. Логарифмическая абсолютная шкала Логарифмическая шкала измерений, получаемая логарифмическим преобразованием абсолютных шкал, когда в выражении L = log X под знаком логарифма X – безразмерная величина, описываемая абсолютной шкалой. Примечание. Другое название этой разновидности шкалы – логарифмическая шкала с плавающим нулем. Биофизическая шкала Шкала измерений свойств физического фактора (стимула), модифицированная
таким образом, чтобы по результатам измерений этих свойств можно было
прогнозировать уровень или характер реакции биологического объекта на действие
этого фактора. Одномерная шкала Шкала, используемая для измерений свойства объекта, характеризуемого одним параметром; результаты измерений в такой шкале выражаются одним числом или знаком (обозначением). Многомерная шкала Шкала, используемая для измерений свойства объекта, характеризуемая двумя или более параметрами; результаты измерений в такой шкале выражаются двумя или более числами или знаками (обозначениями). Примечания. 1. Некоторые свойства, в принципе, невозможно описать одним параметром. Например, импеданс и комплексный коэффициент отражения описываются двумя параметрами, образующими двумерные шкалы; цвет описывается тремя координатами в моделях цветовых пространств, образующими трехмерные шкалы. 2. Многомерные шкалы могут быть образованы сочетанием шкал различных типов. Спецификация шкалы измерений Принятый по соглашению документ, в котором дано определение шкалы и
(или) описание правил и процедур воспроизведения данной шкалы (или единицы
шкалы, если она существует). Примечания. 1. Некоторые метрические шкалы, например, шкалы массы и длины, полностью специфицируются стандартизованными определениями единиц измерений. 2. Спецификации многих, даже метрических шкал, кроме определения единиц измерений содержат дополнительные положения. Например, спецификация шкалы световых измерений содержит не только определение единицы измерений яркости - канделы, но и табулированную функцию относительной спектральной световой эффективности монохроматического излучения для дневного зрения. Элементы шкал измерений Основные понятия, необходимые для определения школ: класс эквивалентности, нуль, условный нуль, условная единица измерений, естественная (безразмерная) единица измерений, диапазон шкалы измерений. Нуль шкалы Элемент шкал порядка (некоторых), интервалов, отношений и абсолютных, их начальная точка. Примечание. Различают
естественный и условный нули шкал. Естественный нуль шкалы Начальная точка шкалы, соответствующая стремящемуся к нулю количественному проявлению измеряемого свойства. Условный нуль шкалы Точка шкалы разностей (интервалов) или шкалы порядка, которой по соглашению присвоено нулевое значение измеряемого свойства (величины). Примечание. Шкала может простираться по обе стороны от точки условного нуля. Например, в наиболее распространенной календарной шкале за условный ноль принят день Рождества Христова. Поэтому общепринято обозначение “…лет до Рождества Христова”. Диапазон шкалы измерений Размер величины Количественная определенность измеряемой величины, присущая конкретному объекту деятельности. Значение величины Оценка размера величины по соответствующей ей шкале в виде некоторого числа принятых для нее единиц, чисел, баллов или иных количественных знаков (обозначений). Примечание. Для
качественных свойств аналогичным термином является “оценка свойства”. Оценка свойства Нахождение местоположения качественного свойства конкретного объекта деятельности на соответствующей шкале наименований. Истинное значение величины Значение величины, которое идеальным образом отражает положение на соответствующей ей шкале реализации количественного свойства конкретного объекта деятельности. Примечание. Для качественных свойств аналогичным термином является “истинная оценка свойства”. Истинная оценка свойства Оценка свойства, которая идеальным образом отражает положение на соответствующей шкале наименований реализации качественного свойства конкретного объекта деятельности. Действительное значение величины Значение величины, настолько близкое к истинному значению, что для данной цели может быть использована вместо нее. Действительная оценка свойства Оценка свойства, настолько близкая к истинной оценке, что для данной
цели может быть использована вместо нее. Единица измерений Величина фиксированного размера, для которой условно (по определению) принято числовое значение, равное 1. Примечания. 1. Термин “единица величины” является синонимом термина “единицы измерений”. 2. Термин “единица физической величины”, обозначающий более узкое понятие, применять не рекомендуется, так как невозможно определить границы его применения. 3. Понятие “единица измерений” не имеет смысла для свойств, описываемых шкалами наименований и порядка. Система единиц (измерений) Совокупность основных и производных единиц измерений, образованная в соответствии с принятыми по договоренности правилами (принципами). Примечание. Термин
“система единиц физических величин” не вполне корректен, так как
известные системы единиц, например, Международная (SI), охватывают не только
физические величины, но и геометрические (плоский и телесный углы), световые и
др. Пределы изменений значений измеряемого свойства, охватываемые данной конкретной реализации шкалы. Измеряемое свойство Проявления общего для объектов деятельности (тел, веществ, явлений, процессов) свойства, выделенного для познания и использования. Примечание. Измеряют количественные и качественные свойства не только физических, но и нефизических объектов (биологических, психологических, социальных, экономических и др.). Измеряемая величина (величина) Измеряемое свойство, характеризуемое количественными различиями. Примечание. Понятие “величина” не применимо к качественным свойствам, описываемым шкалами наименований, поэтому понятие “свойство” является более общим по сравнению с понятием “величина”. Основные единицы системы Единицы величин, размеры и размерности которых в данной системе единиц
приняты за исходные при образовании размеров и размерностей производных единиц. Примечание. Определения и процедуры воспроизведения некоторых основных единиц могут опираться на другие основные и производные единицы, а также на размерные и безразмерные константы. Производные единицы системы Единицы величин, образованные в соответствии с уравнениями, связывающими их с основными единицами или основными и уже определенными производными. Системные единицы Единицы, входящие в одну из принятых систем единиц. Внесистемные единицы Единицы, не входящие в рассматриваемую систему единиц. Примечание. Единица, внесистемная по отношению к некоторой системе, может быть системной по отношению к другой системе. Когерентная производная единица Производная единица, связанная с другими основными и производными единицами системы уравнением, в котором числовой коэффициент равен 1. Когерентная система единиц Система единиц, состоящая из основных и когерентных производных единиц. Примечание. Примером когерентной системы единиц является Международная система единиц – SI. Кратная единица Единица, в целое число раз большая системной или внесистемной единицы. Примечание. В SI образуется с множителем 10 в степени п. Дольная единица измерений Единица, в целое число раз меньшая системной или внесистемной единицы. Примечание. В SI образуется с множителем 10 в степени минус п. Условная единица измерений Единица, размер которой установлен по соглашению. Примечание. Условными единицами измерений, в частности, являются основные единицы Международной системы единиц (SI). Абсолютная единица измерений Единица измерения величины, описываемой абсолютной шкалой, размер которой однозначно определяется безразмерным характером измеряемой величины. Примечания. 1.
В абсолютных единицах измеряются такие величины, как коэффициенты отражения,
пропускания, усиления, ослабления и т. 2. Широко распространено применение дольных абсолютных единиц: процентов, промилле. Логарифмическая единица измерений Единица измерений логарифмической шкалы. Примечание. Получили распространение логарифмические единицы: бел, децибел, лог, децилог, непер, байт и др. Размер единицы Размер величины, принятой за единицу измерения. Измерение Сравнение конкретного проявления измеряемого свойства (измеряемой величины) со шкалой (частью шкалы) измерений этого свойства (величины) с целью получения результата измерения (значения величины или оценки свойства). Объект измерений Объект деятельности (тело, вещество, явление, процесс), одно или несколько конкретных проявлений свойств которого подлежат измерениям. Примечание. Объектами измерений являются как физические, так и нефизические объекты Средство измерений Объект, предназначенный для выполнения измерений, имеющий нормированные
метрологические характеристики, воспроизводящий и (или) хранящий какую-либо
часть (точку) шкалы с установленной погрешностью (неопределенностью) в течение
заданного интервала времени. Мера Средство измерений, воспроизводящее и (или) хранящее одну или несколько точек шкалы измерений. Примечание. Понятие меры применимо в шкалах, описывающих как количественные свойства (величины - “мера величины”), так и качественные свойства, например, “мера цвета” – стандартизованный образец цвета. Однозначная мера Мера, воспроизводящая и (или) хранящая одну точку шкалы. Многозначная мера Мера, воспроизводящая и (или) хранящая две или более точек шкалы. Примечание. Многозначная мера может воспроизводить и (или) хранить некоторый участок шкалы. Пример: градуированный конденсатор переменной емкости. Набор мер Комплект мер, воспроизводящих точки шкалы (шкал), применяемых как в отдельности, так и, если это имеет смысл, в различных сочетаниях. Примеры: набор гирь, набор мер твердости, набор образцов цвета и т.д. Измерительный прибор Средство измерений, предназначенное для получения значения измеряемой
величины или оценки свойства в установленном диапазоне (участке) шкалы
измерений. Примечание. Измерительный прибор, как правило, содержит меру и устройства для преобразования измеряемой величины (измеряемого свойства) в сигнал измерительной информации и его индикации в форме, доступной для восприятия. Стандартный образец (вещества или материала) Мера специфического свойства (величины), в том числе характеризующего состав или значение величины (величин), для измерения которой необходимо учитывать особенности данного вещества (материала). Примечания. 1. Стандартные образцы, в основном, применяются непосредственно при выполнении измерений, но могут применяться и как эталоны при поверке (калибровке) средств измерений. 2. Существуют стандартные образцы неколичественных (качественных) свойств, например, в колориметрии широко применяются наборы стандартных образцов цвета объектов – атласы цветов. Измерительный преобразователь Средство измерений или его часть, служащее для получения и
преобразования информации об измеряемой величине (измеряемом свойстве) в форму,
удобную для обработки, хранения, дальнейших преобразований, индикации или
передачи. Компаратор Устройство, среда, объект, используемый для сравнения хранимых или воспроизводимых средствами измерений участков (точек) шкал измерений. Примечание. Компаратор в совокупности с мерой может использоваться для измерений. Шкала средства измерений Часть отсчетного устройства средства измерений, представляющая собой упорядоченный ряд оцифрованных отметок, соответствующих хранимой и (или) воспроизводимой части шкалы измерений. Принцип измерений Явление или эффект, положенный в основу метода измерений. Метод измерений Прием или совокупность приемов сравнения конкретного проявления измеряемого свойства (измеряемой величины) со шкалой измерений возможных проявлений этого свойства (величины). Результат измерений Значение величины или оценка свойства, полученные путем измерений. Примечания. 1.
За результат измерений в шкалах разностей (интервалов), отношений и абсолютных,
чаще всего принимают среднее арифметическое из ряда результатов равноточных
наблюдений. 2. В шкалах порядка за результат измерений можно принять медиану результатов ряда наблюдений, но нельзя принимать среднее арифметическое 3. Результат измерений в шкалах наименований выражается эквивалентностью конкретного проявления свойства точке или классу эквивалентности соответствующей шкалы. 4. Результат измерений должен также содержать информацию о его неопределенности (погрешности). Неопределенность результата измерений Область (участок) шкалы измерений, в которой предположительно находится истинная оценка свойства или истинное значение измеряемой величины. Погрешность результата измерений (погрешность измерений) Отклонение результата измерения от истинного значения измеряемой величины Примечания. 1. На практике всегда имеют дело с приближенной оценкой погрешности измерений, чаще всего получаемой как отклонение от действительного значения. 2.
Термин “погрешность измерений” неприменим к результатам измерений в
шкалах порядка и наименований, где применяется понятие “неопределенность
результата измерения”. 3. Различают по различным классификационным признакам погрешности измерений и их составляющие: систематические и случайные, инструментальные, метода измерений, абсолютные и относительные и др. Абсолютная погрешность измерений (абсолютная погрешность) Погрешность измерений, выраженная в единицах измеряемой величины. Примечание. Термин “абсолютная погрешность” применим к результатам измерений в шкалах разностей (интервалов), отношений и абсолютных. Относительная погрешность измерений (относительная погрешность) Погрешность измерений, выраженная отношением абсолютной погрешности измерений к значению измеряемой величины. Примечания. 1. Распространено представление относительной погрешности в процентах. 2. Понятие “относительная погрешность” применимо в измерениях
величин по шкалам отношений и абсолютным шкалам, а также к интервалам величин,
описываемых шкалами разностей (интервалов). Неопределенность воспроизведения шкалы Неопределенности результатов измерений, выполняемых при воспроизведении шкалы. Погрешности воспроизведения шкалы Погрешности результатов измерений, выполняемых при воспроизведении точек шкалы. Погрешность воспроизведения единицы измерений Погрешность воспроизведения какой-либо точки шкалы разностей, отношений или абсолютной. Неопределенности передачи шкалы Неопределенности результатов измерений, выполняемых при передаче шкалы. Погрешности передачи шкалы Погрешности результатов измерений, выполняемых при передаче точек шкалы. Погрешность передачи размера единицы измерений Погрешность передачи какой-либо точки шкалы разностей, отношений или
абсолютной. Эталон (шкалы или единицы измерений) Устройство, предназначенное и утвержденное для воспроизведения и (или) хранения и передачи шкалы или размера единицы измерений средствам измерений. Примечание. В Законе РФ “Об обеспечении единства измерений” используется термин “эталон единицы величины”, по смыслу соответствующий термину “эталон шкалы или единицы измерений”. Эталон шкалы измерений Эталон, воспроизводящий всю или какую-либо часть шкалы измерений. Примечания. 1. Эталон может воспроизводить одну точку шкалы (одно фиксированное значение величины) – см. эталон единицы измерений. 2. В шкалах наименований и порядка эталоны обязательно воспроизводят целиком практически используемый участок шкалы. Эталон единицы измерений Эталон, воспроизводящий одно значение измеряемой величины (одну точку шкалы). Примечание.
Воспроизводимое эталоном единицы измерений значение величины может отличаться
от единицы измерений. В настоящее время воспроизводят значение единицы измерений эталоны массы, длины, интервалов времени, электрического напряжения (исключительно или в ряду других значений). Первичный эталон Эталон, предназначенный для передачи шкалы или (и) размера единицы измерений вторичным и (или) рабочим эталонам, а также высокоточным средствам измерений. Вторичный эталон Эталон, которому путем сличения передается шкала или размер единицы от соответствующего первичного эталона для последующей передачи рабочим эталонам и другим средствам измерений. Государственный эталон Эталон, признанный решением уполномоченного на то государственного органа в качестве исходного на территории государства. Примечание. При международных сличениях государственные эталоны и другие, принадлежащие отдельным государствам эталоны, принято называть “национальными эталонами”. Международный эталон Эталон, принятый по международному соглашению в качестве первичного
международного эталона и служащий для согласования с ним шкал и размеров единиц
измерений, воспроизводимых и хранимых национальными эталонами. Рабочий эталон Эталон, предназначенный для передачи шкалы (или размера единицы) рабочим эталонам низших разрядов (образцовым средствам измерений) и рабочим средствам измерений. Примечания. 1. Рабочие эталоны могут по иерархической подчиненности подразделяться на рабочие эталоны 1, 2-го и т.д. разрядов. 2. Рабочие эталоны применяют для поверки и калибровки средств измерений. Эталон сравнения Эталон, применяемый для сличения эталонов, которые не могут быть по разным причинам непосредственно сличены друг с другом. Эталон-переносчик Пригодный для транспортирования эталон, конструктивно предназначенный для передачи шкалы или размера единицы поверяемому или калибруемому рабочему эталону или средству измерений на месте его эксплуатации. Воспроизведение (шкалы или единицы измерений) Совокупность операций, имеющих целью воссоздание шкалы измерений (или
ее участка) или размера единицы, соответствующих их спецификации (определению). Приведение шкалы (или ее участка) или размера единицы, хранимой поверяемым (калибруемым) эталоном или рабочим средством измерений в соответствие со шкалой (размером единицы измерений), воспроизводимой или хранимой более точным (исходным) эталоном. Поверка средств намерений Совокупность операций, выполняемых органами Государственной метрологической службы (другими уполномоченными на то органами, организациями) с целью определения и подтверждения соответствия средства измерений установленным техническим требованиям. Примечания. 1. Поверке подвергают средства измерений, применяемые в сфере распространения государственного метрологического контроля и надзора. 2. Как правило, основной операцией поверки является сравнение
поверяемого средства измерений с более точным эталоном, применяемым при
поверке. Этим самим осуществляется передача шкалы измерений рабочему средству
измерений с регламентированной точностью. Калибровка средства измерений Совокупность операций, выполняемых с целью определения и подтверждения действительных значений метрологических характеристик и (или) пригодности к применению средства измерений, не применяемого в сфере, подлежащей государственному метрологическому контролю и надзору. Примечание. Калибровка является метрологической услугой, основной задачей которой является передача калибруемому средству шкалы измерений в интересующем заказчика (потребителя) диапазоне измерений при приемлемой точности. Градуировка средств измерений (градуировка) Экспериментальное определение градуировочной характеристики средства измерений, т.е. установление соответствия между сигналами измерительной информации (отсчетами) и шкалой измерений. Примечание. Операции градуировки
используются как при поверке, так и при калибровке. В Величина измеряемая Воспроизведение (шкалы или единицы измерения) Г Градуировка средств измерений д Диапазон шкалы измерений Е Единство измерений Единица измерений Единица измерений абсолютная Единица измерений внесистемная Единица измерений дольная Единица измерений кратная Единица измерений логарифмическая Единица измерений производная Единица измерений производная когерентная Единица измерений системная Единица измерений системная основная Единица измерений системная производная Единица измерения условная З Значение величины Значение величины действительное Значение величины истинное И Измерение К Калибровка средств измерений Компаратор М Мера Мера многозначная Мера однозначная Метрология Метрология законодательная Метрология практическая (прикладная) Метрология теоретическая Метод измерения Н Набор мер Неопределенность воспроизведения шкалы Неопределенность передачи шкалы Неопределенность результата измерений Нуль шкалы Нуль шкалы естественный Нуль шкалы условный О Образец стандартный Объект измерений Оценка свойств Оценка свойств действительная Оценка свойств истинная П Передача шкалы (или размера единицы измерения) Поверка средств измерений Погрешность воспроизведения единицы Погрешность воспроизведения шкалы Погрешность измерения абсолютная Погрешность измерения относительная Погрешность передачи размера единицы измерений Погрешность передачи шкалы Погрешность результата измерений Преобразователь измерительный Прибор измерительный Принцип измерений Р Размер величины Размер единицы Результат измерений С Свойство измеряемое Система единиц Система единиц когерентная Спецификация шкалы измерений Средство измерений Т Тип шкалы Ш Шкала абсолютная Шкала абсолютная ограниченная Шкала биофизическая Шкала величин Шкала измерений Шкала логарифмическая Шкала логарифмическая абсолютная Шкала логарифмическая разностей Шкала многомерная Шкала наименований Шкала одномерная Шкала отношений Шкала порядка Шкала разностей (интервалов) Шкала средств измерений Э Эталон Эталон вторичный Эталон государственный Эталон единицы измерений Эталон международный Эталон рабочий Эталон сравнения Эталон первичный Эталон-переносчик Эталон шкалы измерений Элемент шкалы измерений |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 2 из 13Следующая ⇒ Для работы с данными в SPSS важно знать, по шкале какого типа измеряются исследуемые переменные. Это необходимо для выбора метода анализа данных и определения возможности расчета статистических показателей (табл. 2.3). Существует четыре типа шкал измерения переменных: Номинальная шкала. Порядковая шкала. Интервальная шкала. Примеры переменных, измеряемых по шкалам разных типов Относительная шкала.
Номинальная шкала характеризуется самым низким уровнем измерения переменных. Все значения переменной, измеряемой по номинальной шкале, находятся на одном уровне. По этой шкале измеряются, как правило, качественные характеристики объекта исследования. Между значениями переменной, измеряемой по номинальной шкале, не существует логического порядка. Например, в качестве ответа на вопрос анкеты: «Какого производителя продукта «X» вы предпочитаете?» — может быть предложено несколько вариантов: «Производитель А», «Производитель В», «Производитель С» и т.д. В этом случае, с точки зрения исследователей, все предложенные производители являются равнозначными. Числовые коды («1», «2», «3»…) могут присваиваться значениям метки переменной в любом порядке. Переменные, измеряемые по номинальной шкале и имеющие всего два значения (например, «мужчины» и «женщины»), называются дихотомическими. Порядковая шкала является второй по уровню измерения переменных. Значения переменной, измеряемой по порядковой шкале, не являются равнозначными, они находятся на равных уровнях по отношению друг к другу и подчиняются логическому числовому порядку. Порядковая шкала характеризуется низким уровнем измерения переменных, поскольку является шкалой с неравными интервальными отрезками. Совершенно четко можно утверждать, что уровень обслуживания авиапассажиров первого класса выше, чем бизнес-класса, но насколько именно, неизвестно. Также разница в обслуживании между первым и бизнес-клас- сом, между бизнес- и эконом-классом может быть различной (см. табл. 2.3). Низкий уровень измерения переменных по порядковой шкале можно проиллюстрировать на примере переменной «Категории потребителей по уровню дохода». Потребители примерно с одинаковым уровнем дохода (например, 950 и 1050 евро) оказываются в разных категориях, а потребители с существенной разницей по уровню дохода (например, 1050 и 2950 евро) оказываются в одной категории. Интервальная шкала является третьей по уровню измерения переменных. В отличие от порядковой шкалы она является шкалой с равными интервальными отрезками. Это позволяет осуществлять количественное сравнение значений переменной, т.е. можно определить, насколько одно значение больше или меньше (лучше или хуже, длиннее или короче и т.д.) другого. Характерной чертой интервальной шкалы является отсутствие «естественного нуля», т.е. исходная точка измерения является относительной. Примерами интервальной шкалы являются шкала Цельсия и календарь. По шкале Цельсия за «0» принята температура замерзания воды, однако за «0» можно было принять любую другую температуру. Существуют также различные календари с одинаковым количеством дней в году, но разным временем начала года. В маркетинговых исследованиях очень часто используется рейтинговая шкала, когда респондентам предлагается оценить по балльной шкале (например, от 1 до 7 баллов) утверждение, продукт, бренд и т.п. Строго говоря, рейтинговая шкала является порядковой, поскольку балльные оценки субъективны. Очень часто при проведении исследований шкала бапльных оценок рассматривается как интервальная. В основе этого лежит предположение, что интервальные отрезки шкалы балльных оценок одинаковы. Это дает возможность рассчитать соеднее значение переменной (например, средний балл успеваемости студентов). Расчет средней величины (среднеарифметической) для показателя, измеряемого по порядковой шкале, невозможен. Например, не существует показателя «средний класс» полета (см. табл. 2.3). Относительная шкала характеризуется самым высоким уровнем измерения переменных. Ее основное отличие от интервальной шкалы заключается в существовании «естественного нуля», который можно интерпретировать как отсутствие значения переменной. Например, если заработная плата равна нулю, это значит, что ее не выплачивают. По относительной шкале измеряются количественные характеристики. Это могут быть как физические характеристики (объем, вес, скорость и пр.), так и экономические характеристики (доход, издержки, цена и пр.). Относительная шкала получила свое название благодаря возможности сравнения значений переменной по отношению друг к другу, что невозможно при использовании интервальной шкалы измерения. Например, нельзя сказать, что человек, у которого коэффициент интеллекта (iQ) равен 160, в два раза умнее человека у которого этот показатель составляет 80. Но можно сказать, что заработная плата 1000 евро в два раза больше заработной платы 2000 евро. При выборе типа шкалы измерения переменных в SPSS (столбец «Measure» во вкладке редактора данных «Variable View») интервальная шкала и шкала отношений объединяются в один вид — метрическую шкалу (Scale). При построении в SPSS интерактивных графиков номинальная (Nominal) и порядковая (Ordinal) шкалы объединяются в «категориальный» тип (табл.
Чем выше уровень измерения переменной, тем богаче ее информационная содержательность и тем больше возможностей осуществления расчетов и определения статистических показателей. Числовые коды («1», «2», «3»…) значений метки переменной, измеряемой по номинальной или порядковой шкале, не могут рассматриваться как числа, они представляют собой лишь некие числовые символы. Поскольку они не являются числами, с ними нельзя производить никаких арифметических операций (сложение, вычитание, деление, умножение). Что касается статистических показателей, характеризующих распределение величины, измеряемой по номинальной шкале, можно провести частотный анализ (Frequencies) и определить моду (Mode). Частоты показывают, например, сколько респондентов предпочитают того или иного производителя продукта «Л». Мода обозначает самую многочисленную группу респондентов, предпочитающих определенного производителя продукта «Л». Для переменных, измеряемых по порядковой шкале, кроме вышеуказанных статистических показателей можно определить медиану и средневзвешенное. Значения меток переменной, измеряемой по интервальной шкале, рассматриваются как числа. С ними можно производить такие арифметические операции, как сложение и вычитание. Что касается возможности расчета статистических показателей, характеризующих распределение переменной, измеряемой по интервальной шкале, кроме моды и медианы можно также определить стандартное отклонение (Std. deviation) и среднеарифметическое (Mean). (Средневзвешенное значение переменных с интервальной шкалой равно среднему арифметическому.) При расчете статистических показателей, характеризующих распределение переменной, измеряемой по интервальной шкале, не рассчитывается такой показатель, как сумма (Sum). Например, не рассчитывается «суммарный коэффициент интеллекта» для группы студентов, такого показателя не существует. Значения меток переменной, измеряемой по шкале отношений, выражаются в числах, с ними можно производить любые арифметические операции. Также можно определять любые статистические показатели, характеризующие распределение переменной. Возможна трансформация имеющихся данных, измеряемых по шкале более высокого уровня, в данные, измеряемые по шкале более низкого уровня, но не наоборот. На практике, в том числе при применении SPSS, различие между переменными, измеряемыми по интервальной и относительной шкалам, обычно несущественно. Во многих учебниках по SPSS метрические переменные (Scale) определяются как интервальные. ип шкалы измерения переменных определяет возможность применения того или иного метода анализа данных. Все методы статистического анализа делятся на две группы: методы оценки связи между переменными; методы выявления структуры данных. Методы выявления структуры данных характеризуются тем, что исходные данные для проведения анализа не содержат информации (предположений) о существовании взаимосвязей между исследуемыми переменными. Методы оценки связи между переменными устанавливают влияние одной или нескольких независимых переменных на одну или несколько зависимых переменных. С точки зрения теории статистики существуют правила применения того или иного метода оценки связи между переменными в зависимости от типа шкалы их измерения (табл. 2.5).
Применение некоторых основных методов статистического анализа в SPSS будет более подробно рассмотрено в следующих подразделах. КОНТРОЛЬНЫЕ ВОПРОСЫ Что представляют собой таблицы, содержащиеся во вкладках редактора данных SPSS «Свойства переменных» (Variable View) и «Значения переменных» (Data View)? Каким образом осуществляется процедура занесения в исходный файл данных SPSS меток переменных? Чем отличаются пропущенные значения, определяемые системой (system-defined truss, ig values) от пропущенных значений, задаваемых пользователем программы {user-defined missing values)! Какие три типа шкал измерения переменных используются в SPSS и каким образом задается тип шкалы измерения переменной при формировании исходного файла данных? Чем отличаются дихотомическая и категориальная кодировка данных? Почему при занесении в исходный файл данных SPSS ответов ка многовариантные (безальтернативные) вопросы необходимо использовать дихотомическую кодировку данных? С какой целью и в каких случаях применяется двойная запись данных при создании исходного файла SPSS? По шкале какого типа измеряются следующие переменные: а) частота приобретения товара «A» реже 1-го раза в неделю; 1—3 раза в неделю; чаще 3-х раз в неделю; б) семейное положение замужем/женат; не замужем/ холост; разведена/разведен; в) оценка уровня сервисного обслуживания очень высокая; высокая; средняя; низкая; очень низкая; г) возраст (23 года, 24 года, 32 года, 57 лет)? 1. 3. СРАВНЕНИЕ СРЕДНИХ ВЕЛИЧИН ВSPSS Методы сравнения средних величин часто используются в маркетинговых исследованиях для выявления взаимосвязи между исследуемыми переменными. К таким методам относятся T-тесты и дисперсионный анализ. В ходе проведения Т-теста или дисперсионного анализа проверяется исходная (нулевая) гипотеза о равенстве сравниваемых средних величин, которая представляет собой утверждение: «Взаимосвязи между исследуемыми величинами не существует». Например, исходная (нулевая) гипотеза предполагает равенство среднего балла успеваемости студентов — юношей и девушек, что свидетельствует о том, что пол студента не влияет на его успеваемость. По результатам проведения анализа данная гипотеза должна быть подтверждена или опровергнута. Основным результатом T-теста или дисперсионного анализа, выдаваемого SPSS, является величина «Significance» («Значимость»). Результаты проверки исходной (нулевой) гипотезы определяются доверительным интервалом (Confidence Interval), который задается при формировании задания на проведение Г-теста или дисперсионного анализа в SPSS. По умолчанию устанавливается доверительный интервал 95%. SPSS предоставляет возможность сравнения средних величин (Compare Means) при помощи различных методов (рис. 3.2). При запуске процедуры «Средние величины» (Means) (см. рис. 3.2) определяются средние величины зависимых переменных в разных группах, сформированных по разным признакам (независимым переменным), а также вычисляются различные статистические показатели распределения зависимых переменных в группах (например, дисперсия, стандартное отклонение и др.).
Сравнение двух средних величин осуществляется при помощи T-теста. Например, с помощью этого теста можно определить, отличается ли средняя цена на определенный товар в заданной выборке предприятий торговли от средней цены, указанной каким-либо официальным источником. Т-тест для независимых выборок (,Independent Samples T-test) (см. рис. 3.2) производится для сравнения средних величин тестируемого признака в двух группах. При этом каждый респондент может оказаться только в одной из двух групп, например: мужчины и женщины, семейные и несемейные, покупающие или не покупающие товар «X» и т.д. Т-тест для спаренных выборок (Paired-Samples T-test) (см. рис. 3.2) применяется для сравнения средних величин в двух группах, но при этом один и тот же респондент может одновременно оказаться в разных группах. Например, респонденты, покупающие товар А и товар В. Для сравнения средних величин в трех и более группах применяется однофакторныi дисперсионный анализ (One- Way-ANO VA) (см. В данной работе подробно рассматривается Г-тест для независимых выборок и однофакторный дисперсионный анализ. 3.1. Т-ТЕСТ ДЛЯ НЕЗАВИСИМЫХ ВЫБОРОК 3.1.1. ПОСТАНОВКА ЦЕЛИ ИССЛЕДОВАНИЯ И ПРЕДСТАВЛЕНИЕ ИСХОДНЫХ ДАННЫХ ВSPSS Т-тест проводится с целью определения влияния одной (независимой) переменной на другую (зависимую) переменную. По типу шкалы измерения зависимая переменная должна быть метрической, а независимая, как правило, является дихотомической (см. подраздел 2.3 «Типы шкал измерения переменных»). Переменная дихотомического типа может принимать только два значения; следовательно, при помощи этой переменной можно разбить все анализируемые данные на две группы. Именно поэтому независимая переменная называется группирующей, а зависимая переменная — тестируемой. Например, следует определить, влияет ли пол туриста на его удовлетворенность местом отдыха (рис. 3.3). Независимая переменная «пол» является дихотомической, она разделяет всех респондентов на две группы: «мужчины» и «жен щины». В Качестве зависимой переменной выступает переменная, представляющая вопрос анкеты № 34 «Оцените по 5-балльной шкале степень своей удовлетворенности местом отдыха в целом». В файле данных SPSS, сформированном по результатам опроса туристов, отдыхающих в курортной зоне «Баварский лес», эта переменная имеет имя «q_34» и метку переменной «Удовлетворенность» (рис. 3.4). В столбце «Values» таблицы «Свойства переменных» отображаются значения метки переменной «Удовлетворенность» и их числовые коды. Числовые коды значений переменной «Удовлетворенность» содержатся в таблице «Значения переменных» вкладки редактора данных «Data View» (рис. 3.5).
Из данных, представленных на рис. 3.5, видно, что респондент в строке 3525 доволен местом отдыха, респондент в строке 3526 — очень доволен, респондент в строке 3529 — доволен и недоволен одновременно, а респондент в строке 3530 затруднился ответить на поставленный вопрос. Для того чтобы выяснить, влияет ли пол туриста на степень его удовлетворенности местом отдыха, необходимо сравнить средний уровень удовлетворенности мужчин и женщин. Если данные показатели существенно отличаются друг от друга, то можно судить о наличии вышеуказанной взаимосвязи. Т-тест позволяет проверить верность гипотезы, согласно которой средние величины тестируемого показателя в двух группах равны. В рассматриваемом примере исходная (нулевая) гипотеза формулируется следующим образом: «Мужчины и женщины в одинаковой степени довольны (недовольны) местом отдыха, т.е. пол туриста не влияет на его удовлетворенность местом отдыха». В ходе проведения T-теста исходная гипотеза должна быть подтверждена или опровергнута. Для выполнения этого задания последовательно решаются две задачи: Проверяются условия равенства дисперсий тестируемой переменной в двух сравниваемых группах. Выявляются взаимосвязи между исследуемыми переменными, т.е. проверяются неравенства средних значений тестируемой переменной в двух сравниваемых группах. 3.1.2. КОМАНДЫ SPSSНА ВЫПОЛНЕНИЕ Т-ТЕСТА ДЛЯ НЕЗАВИСИМЫХ ВЫБОРОК
При помощи выбора меню «Analyze > Compare Means > Independent Samples T-tesU (см. рис. 3.2) открывается диалоговое окно «T-тест для независимых выборок» (рис. 3.6). В левом поле окна указываются метки всех переменных, занесенных в базу данных. Из данного списка выбирается метка тестируемой переменной (в рассматриваемом примере это «Удовлетворенность») и переносится в поле «Test Variable(s)». Далее из списка выбирается метка группирующей переменной (в рассматриваемом примере это «Пол») и переносится в поле «Group ng Vat able».
руппирующая переменная делит всех респондентов на две группы: мужчины («1») и женщины («2»). Кодировку этих групп необходимо указать во вспомогательном диалоговом окне «Обозначенные группы» (Define Groups), которое открывается нажатием одноименной кнопки в диалоговом окне «Г-тест для независимых выборок» (рис- 3.
Группирующая переменная может быть не только дихотомической (т.е. принимающей только два значения), но и метрической, например переменная «возраст». В этом случае группы обозначаются при помощи указания «точки разрыва» (Cut point), например старше или младше указанного возраста. Путем нажатия кнопки «Продолжение» (Continue) (см. рис. 3.7) снова активируется главное диалоговое окно «T-teст для независимых выборок» (см. рис. 3.6). При нажатии в этом окне кнопки «Опции» (Options) открывается одноименное диалоговое окно (рис. 3.8.). В данном окне устанавливается «доверительный интервал» (Confidence Interval), который по умолчанию задается в размере 95%. Доверительный интервал определяет допустимую вероятность ошибки в случае отклонения исходной (нулевой) гипотезы (см. рис. 3.1). После того как задан доверительный интервал путем нажатия кнопки «Продолжение» (Continue) осуществляется возврат в главное диалоговое окно «Г-тест для независимых выборок» (см рис.
⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Формы дистанционного обучения Передача мяча двумя руками снизу Значение правильной осанки для жизнедеятельности человека Основные ошибки при выполнении передач мяча на месте |
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 3289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. |
Типы данных и шкалы измерения
Данные являются ценным активом настолько, что это самый ценный ресурс в мире. Это делает понимание различных типов данных и роль специалиста по обработке и анализу данных более важными, чем когда-либо. В деловом мире все больше компаний пытаются понять большие числа и то, что они могут с ними сделать. Экспертиза данных пользуется большим спросом. Определение правильных данных и шкал измерения позволяет компаниям организовывать, идентифицировать, анализировать и, в конечном счете, использовать данные для обоснования стратегий, которые позволят им оказывать реальное влияние.
Данные высшего уровня: качественные и количественные
Что такое данные? Короче говоря, это совокупность измерений или наблюдений, разделенных на два разных типа: качественные и количественные.
Качественные данные относятся к информации о качествах или к информации, которую невозможно измерить. Как правило, описательный и текстовый. Примеры включают цвет глаз человека или тип автомобиля, на котором он ездит. В опросах он часто используется для классификации ответов «да» или «нет».
Как правило, описательный и текстовый. Примеры включают цвет глаз человека или тип автомобиля, на котором он ездит. В опросах он часто используется для классификации ответов «да» или «нет».
Количественные данные являются числовыми. Он используется для определения информации, которую можно подсчитать. Некоторые примеры количественных данных включают расстояние, скорость, рост, длину и вес. Легко запомнить разницу между качественными и количественными данными, поскольку одни относятся к качествам, а другие — к количествам.
Книжная полка, например, может иметь 100 книг на полках и иметь высоту 100 сантиметров. Это количественные точки данных. Цвет книжной полки — красный — является качественной точкой данных.
Что такое количественные (числовые) данные?
Количественные или числовые данные можно разделить на два типа: дискретные и непрерывные.
Дискретные данные
Дискретные данные — это целое число, которое нельзя разделить или разбить на отдельные части, дроби или десятичные дроби. Примеры дискретных данных включают количество домашних животных у кого-то — можно иметь двух собак, но не двух с половиной собак. Количество побед чьей-либо любимой команды также является формой дискретных данных, потому что у команды не может быть полувыигрыша — это либо победа, либо поражение, либо ничья.
Примеры дискретных данных включают количество домашних животных у кого-то — можно иметь двух собак, но не двух с половиной собак. Количество побед чьей-либо любимой команды также является формой дискретных данных, потому что у команды не может быть полувыигрыша — это либо победа, либо поражение, либо ничья.
Непрерывные данные
Непрерывные данные описывают значения, которые можно разбить на различные части, единицы, дроби и десятичные дроби. Можно измерять непрерывные точки данных, такие как рост и вес. Время также можно разбить – на полсекунды или на полчаса. Температура — еще один пример непрерывных данных.
Дискретные и непрерывные
Существует простой способ запомнить разницу между двумя типами количественных данных: данные считаются дискретными, если их можно подсчитать, и непрерывными, если их можно измерить. Кто-то может считать студентов, купленные билеты и книги, а кто-то измеряет рост, расстояние и температуру.
Что такое качественные (категориальные) данные?
Качественные данные описывают качество точек данных и не являются числовыми. Он используется для определения информации, а также может быть дополнительно разбит на подкатегории по четырем шкалам измерения.
Он используется для определения информации, а также может быть дополнительно разбит на подкатегории по четырем шкалам измерения.
Свойства и масштабы измерения
Шкалы измерения определяют и классифицируют переменные. Психолог Стэнли Стивенс разработал четыре общепринятые шкалы измерения: .номинал , порядковый номер , интервал и коэффициент . Каждая шкала измерения имеет свойства, которые определяют, как правильно анализировать данные. Оцениваются следующие свойства: идентичность , величина , равные интервалы и минимальное значение, равное нулю .
Свойства измерения
Идентичность: Идентичность относится к каждому значению, имеющему уникальное значение.
Величина: Величина означает, что значения имеют упорядоченное отношение друг к другу, поэтому переменные имеют определенный порядок.

Равные интервалы: Равные интервалы означают, что точки данных вдоль шкалы равны, поэтому разница между точками данных 1 и 2 будет такой же, как разница между точками данных 5 и 6.
Минимальное значение нуля: Минимальное значение нуля означает, что весы имеют истинную нулевую точку. Градусы, например, могут упасть ниже нуля и все еще иметь значение. Но если вы ничего не весите, вы не существуете.
Четыре шкалы измерения
Понимая масштаб измерения своих данных, специалисты по данным могут определить тип статистического теста для выполнения.
1. Номинальная шкала измерения
Номинальная шкала измерения определяет свойство идентичности данных. Эта шкала имеет определенные характеристики, но не имеет числового значения. Данные могут быть помещены в категории, но не могут быть умножены, разделены, добавлены или вычтены друг из друга. Также невозможно измерить разницу между точками данных.
Примеры номинальных данных включают цвет глаз и страну рождения. Номинальные данные можно снова разбить на три категории:
Номинальные данные можно снова разбить на три категории:
Номинал с заказом: Некоторые номинальные данные могут быть разбиты на подкатегории по порядку, например, «холодный, теплый, горячий и очень горячий».
Номинальные без порядка: Номинальные данные также могут быть подразделены на номинальные без порядка, например, мужские и женские.
Дихотомические: Дихотомические данные определяются наличием только двух категорий или уровней, таких как «да» и «нет».
2. Порядковая шкала измерения
Порядковая шкала определяет данные, которые располагаются в определенном порядке. Хотя каждое значение ранжировано, нет информации, которая бы указывала, что отличает категории друг от друга. К этим значениям нельзя ни добавить, ни вычесть.
Примером такого рода данных могут быть точки данных об удовлетворенности в опросе, где «один = счастливый, два = нейтральный и три = несчастный». Когда кто-то финишировал в гонке, также описываются порядковые данные. Хотя первое, второе или третье место показывает, в каком порядке финишировали бегуны, оно не указывает, насколько далеко финишер, занявший первое место, был впереди бегуна, занявшего второе место.
Когда кто-то финишировал в гонке, также описываются порядковые данные. Хотя первое, второе или третье место показывает, в каком порядке финишировали бегуны, оно не указывает, насколько далеко финишер, занявший первое место, был впереди бегуна, занявшего второе место.
3. Интервальная шкала измерения
Интервальная шкала содержит свойства номинальных и упорядоченных данных, но разницу между точками данных можно определить количественно. Этот тип данных показывает как порядок переменных, так и точные различия между переменными. Их можно складывать или вычитать друг из друга, но нельзя умножать или делить. Например, 40 градусов — это не 20 градусов, умноженных на два.
Эта шкала также характеризуется тем, что число ноль является существующей переменной. В порядковой шкале ноль означает, что данные не существуют. В интервальной шкале ноль имеет значение — например, если вы измеряете градусы, ноль имеет значение температуры.
Точки данных на шкале интервалов имеют одинаковую разницу между собой. Разница на шкале между 10 и 20 градусами такая же, как и между 20 и 30 градусами. Эта шкала используется для количественной оценки различий между переменными, тогда как две другие шкалы используются только для описания качественных значений. Другие примеры интервальных шкал включают год выпуска автомобиля или месяцы года.
Разница на шкале между 10 и 20 градусами такая же, как и между 20 и 30 градусами. Эта шкала используется для количественной оценки различий между переменными, тогда как две другие шкалы используются только для описания качественных значений. Другие примеры интервальных шкал включают год выпуска автомобиля или месяцы года.
4. Шкала отношений
Шкалы отношений включают свойства всех четырех шкал измерения. Данные являются номинальными и определяются тождеством, могут быть классифицированы по порядку, содержат интервалы и могут быть разбиты на точные значения. Вес, рост и расстояние — все это примеры переменных отношений. Данные в шкале отношений можно складывать, вычитать, делить и умножать.
Шкалы отношений также отличаются от шкал интервалов тем, что шкала имеет «истинный ноль». Число ноль означает, что данные не имеют точки значения. Примером этого является рост или вес, поскольку кто-то не может быть ростом ноль сантиметров или весить ноль килограммов, или иметь отрицательные сантиметры или отрицательные килограммы. Примерами использования этой шкалы являются расчет акций или продаж. Из всех типов данных на шкалах измерения специалисты по данным могут больше всего сделать с точками данных отношения.
Примерами использования этой шкалы являются расчет акций или продаж. Из всех типов данных на шкалах измерения специалисты по данным могут больше всего сделать с точками данных отношения.
Подводя итог, номинальные весы используются для маркировки или описания значений. Порядковые шкалы используются для предоставления информации о конкретном порядке точек данных, что в основном наблюдается при использовании опросов удовлетворенности. Шкала интервалов используется для понимания порядка и различий между ними. Шкалы отношений дают больше информации об идентичности, порядке и различиях, а также разбивку числовых деталей в каждой точке данных.
Использование количественных и качественных данных в статистике
После того, как специалисты по обработке данных получат исчерпывающий набор данных из своей выборки, они могут начать использовать эту информацию для составления описаний и выводов. Для этого они могут использовать как описательную, так и логическую статистику.
Описательная статистика
Описательная статистика помогает продемонстрировать, представить, проанализировать и обобщить результаты, содержащиеся в выборке. Они представляют данные в простой для понимания и презентабельной форме, например, в виде таблицы или графика. Без описания данные были бы в необработанном виде без пояснений.
Подсчет частоты
Один из способов, которым специалисты по данным могут описать статистику, — это использование подсчета частоты или статистики частоты, которая описывает количество раз, когда переменная присутствует в наборе данных. Например, количество людей с голубыми глазами или количество людей с водительскими правами в выборке можно подсчитать по частоте. Другие примеры включают квалификацию образования, такую как аттестат о среднем образовании, университетский диплом или докторскую степень, а также категории семейного положения, такие как холост, женат или разведен.
Частотные данные представляют собой форму дискретных данных, так как части значений не могут быть разбиты на части. Вместо этого для расчета непрерывных точек данных, таких как возраст, специалисты по данным могут использовать центральную статистику тенденций. Для этого они находят среднее или среднее значение точки данных. Используя пример возраста, это может сказать им средний возраст участников в выборке.
Вместо этого для расчета непрерывных точек данных, таких как возраст, специалисты по данным могут использовать центральную статистику тенденций. Для этого они находят среднее или среднее значение точки данных. Используя пример возраста, это может сказать им средний возраст участников в выборке.
Хотя специалисты по обработке и анализу данных могут делать выводы на основе описательной статистики и представлять их в понятной форме, они не обязательно могут делать выводы. Вот тут-то и приходит на помощь статистика выводов.
Логическая статистика
Логическая статистика используется для выдвижения гипотезы из набора данных. Было бы невозможно получить данные от всего населения, поэтому специалисты по данным могут использовать логическую статистику для экстраполяции своих результатов. Используя эту статистику, они могут делать обобщения и прогнозы в отношении более широкой выборки, даже если они не опросили их всех.
Примером использования логической статистики являются выборы. Еще до того, как вся страна проголосовала, специалисты по данным могут использовать подобную статистику, чтобы делать предположения относительно того, кто может победить на основе меньшего размера выборки.
Еще до того, как вся страна проголосовала, специалисты по данным могут использовать подобную статистику, чтобы делать предположения относительно того, кто может победить на основе меньшего размера выборки.
Использование визуализации данных для обмена идеями
Визуализация данных описывает методы, используемые для создания графического представления образца данных путем кодирования его с помощью визуальных фрагментов информации. Это помогает передавать данные зрителям четким и эффективным способом.
Характеристики эффективных графических дисплеев
Эффективная визуализация может помочь людям анализировать сложные значения данных и делать выводы. Целью этого процесса является максимально четкое изложение результатов. Графический дисплей с эффективным обменом сообщениями будет четко отображать данные и позволит зрителю получить представление и тенденции из набора данных и выявить различные результаты между данными.
Примеры визуализации данных
Наилучшее визуальное представление набора данных определяется отношениями, которые специалисты по данным хотят передать между точками данных. Они хотят представить распределение с выбросами? Они хотят сравнить несколько переменных или проанализировать одну переменную во времени? Представляют ли они тенденции в вашем наборе данных? Вот некоторые из ключевых примеров визуализации данных.
Они хотят представить распределение с выбросами? Они хотят сравнить несколько переменных или проанализировать одну переменную во времени? Представляют ли они тенденции в вашем наборе данных? Вот некоторые из ключевых примеров визуализации данных.
Гистограмма используется для сравнения двух или более значений в категории и того, как несколько фрагментов данных соотносятся друг с другом.
Линейная диаграмма используется для визуального представления тенденций, шаблонов и колебаний в наборе данных. Линейные графики обычно используются для прогнозирования информации.
Точечная диаграмма используется для отображения взаимосвязи между точками данных в компактной визуальной форме.
Круговая диаграмма используется для сравнения частей целого.
Воронкообразная диаграмма используется для представления того, как данные перемещаются по различным шагам или стадиям процесса.

Гистограмма используется для представления данных за определенный период времени или интервал.
Количественные сообщения
Количественные сообщения описывают отношения данных. В зависимости от выборки существуют разные способы передачи количественных данных.
Номинальное сравнение: Подкатегории сравниваются по отдельности в произвольном порядке.
Временной ряд: Индивидуальная переменная отслеживается в течение периода времени, обычно представленного в виде линейной диаграммы.
Ранжирование: Подкатегории ранжируются по порядку, обычно представленному в виде гистограммы.
Часть к целому: Подкатегории представлены в виде соотношения по сравнению с целым, обычно представленным в виде гистограммы или круговой диаграммы.
Отклонение: Подкатегории сравниваются с контрольной точкой, обычно представленной в виде гистограммы.

Частотное распределение: Подкатегории подсчитываются в интервалах, обычно представленных в виде гистограммы.
Корреляция: Два набора мер сравниваются, чтобы определить, движутся ли они в одном и том же или противоположном направлении, обычно представленном на диаграмме рассеивания.
Расширьте свои знания в области обработки данных
Поскольку наука о данных становится все более востребованным навыком, самое время расширить свои знания о самом ценном ресурсе в мире: данных. Степень в области науки о данных позволит вам выявлять, анализировать и представлять сложные и переплетенные сети данных. Затем вы можете использовать эти идеи для прогнозирования и создания стратегий, особенно в бизнес-среде. Магистр наук о данных UNSW может дать вам навыки, необходимые для того, чтобы раскрыть всю мощь данных и помочь компаниям принимать более эффективные решения, позволяя им добиваться значительных изменений и результатов.
7 Типы шкал измерения данных в исследованиях
Шкалы измерений в исследованиях и статистике — это различные способы определения переменных и группировки их в разные категории. Иногда называемый уровнем измерения, он описывает характер значений, присвоенных переменным в наборе данных.
Термин «шкала измерения» происходит от двух ключевых слов в статистике, а именно; измерение и масштаб. Измерение — это процесс записи наблюдений, собранных в рамках исследования.
Масштабирование, с другой стороны, представляет собой присвоение объектам чисел или семантики. Эти два слова, объединенные вместе, относятся к взаимосвязи между назначенными объектами и записанными наблюдениями.
Что такое шкала измерения?Шкала измерения используется для квалификации или количественного определения переменных данных в статистике. Он определяет тип методов, которые будут использоваться для статистического анализа.
Существуют различные виды шкал измерения, и тип собираемых данных определяет вид шкалы измерения, которая будет использоваться для статистических измерений. Этих шкал измерения четыре, а именно; номинальная шкала, порядковая шкала, интервальная шкала и шкала отношений.
Этих шкал измерения четыре, а именно; номинальная шкала, порядковая шкала, интервальная шкала и шкала отношений.
Шкалы измерения используются для измерения качественных и количественных данных. Номинальная и порядковая шкалы используются для измерения качественных данных, а шкалы интервалов и отношений используются для измерения количественных данных.
Характеристики шкалы измерений ИдентичностьИдентичность определяется как присвоение чисел значениям каждой переменной в наборе данных. Рассмотрим вопросник, в котором запрашивается пол респондента, например, с вариантами «Мужской» и «Женский». Значения 1 и 2 могут быть присвоены мужчинам и женщинам соответственно.
Над этими значениями нельзя выполнять арифметические операции, поскольку они предназначены только для целей идентификации. Это характеристика номинальной шкалы.
Величина Величина определяется как размер шкалы измерения, где числа (тождество) имеют неотъемлемый порядок от наименьшего к наибольшему. Обычно они представлены на шкале в порядке возрастания или убывания. Позиция в гонке, например, располагается от 1-го, 2-го, 3-го до наименьшего.
Обычно они представлены на шкале в порядке возрастания или убывания. Позиция в гонке, например, располагается от 1-го, 2-го, 3-го до наименьшего.
Этот пример измеряется в порядковой шкале, потому что он имеет как идентичность, так и величину.
Равные интервалыРавные интервалы определяются как шкала со стандартным порядком. То есть разница между каждым уровнем на шкале одинакова. Это не относится к приведенному выше примеру с порядковой шкалой.
Каждая позиция не имеет одинаковой разницы интервалов. В гонке 1-е место может завершить гонку за 20 секунд, 2-е место – за 20,8 секунды, а 3-е место – за 30 секунд.
Переменная, которая имеет идентичность, величину и равный интервал, измеряется по шкале интервалов.
Абсолютный ноль Абсолютный ноль определяется как характеристика, уникальная для шкалы отношений. Это означает, что на шкале существует ноль, и он определяется отсутствием измеряемой переменной (например, отсутствие квалификации, отсутствие денег, отсутствие принадлежности к какому-либо полу и т. д.
д.
Уровень измерения данного набора данных определяется соотношением между значениями, присвоенными атрибутам переменной данных. Например, связь между значениями (1 и 2), присвоенными атрибутам (мужской и женский) переменной (Пол), является «идентичностью». Это через. пример номинальной шкалы.
Зная различные уровни измерения данных, исследователи могут выбрать лучший метод статистического анализа. Существуют различные уровни измерения данных: номинальная, порядковая, интервальная шкала и шкала отношений 9.0003
Номинальная шкалаНоминальная шкала — это шкала измерения, используемая для целей идентификации. Это самый холодный и самый слабый уровень измерения данных среди четырех.
Иногда называемая категориальной шкалой, атрибутам присваиваются номера для облегчения идентификации. Однако эти числа не являются качественными по своей природе и действуют только как ярлыки.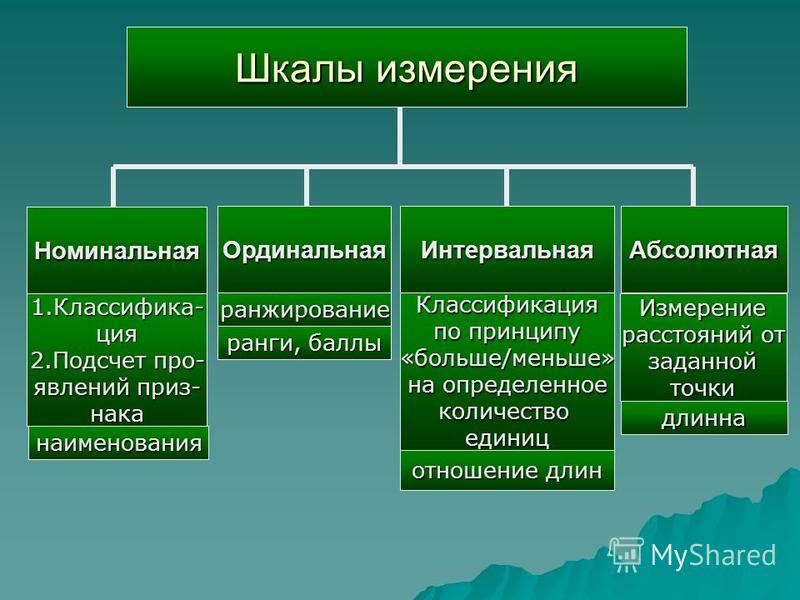
Единственным статистическим анализом, который может быть выполнен на номинальной шкале, является подсчет процентов или частоты. Его можно проанализировать графически, используя гистограмму и круговую диаграмму.
Пример номинальной шкалы
В приведенном ниже примере популярность политической партии измеряется по номинальной шкале.
К какой политической партии вы относитесь?
- Независимый
- Республиканский
- демократ
Обозначение независимых как «1», «республиканцев» как «2» и «демократов» как «3» никоим образом не означает, что какой-либо из атрибутов лучше, чем другой. Они просто используются в качестве идентификатора для удобного анализа данных.
Порядковая шкала Порядковая шкала включает ранжирование или упорядочение атрибутов в зависимости от масштабируемой переменной. Элементы этой шкалы классифицируются в соответствии со степенью встречаемости рассматриваемой переменной.
Атрибуты в порядковой шкале обычно располагаются в порядке возрастания или убывания. Он измеряет степень появления переменной.
Порядковая шкала может использоваться в исследованиях рынка, рекламе и опросах удовлетворенности клиентов. Он использует квалификаторы, такие как очень, очень, больше, меньше и т. д., чтобы описать степень.
Мы можем выполнять статистический анализ, например, медиану и моду, используя порядковую шкалу, но не среднее значение. Однако существуют и другие статистические альтернативы среднему, которые можно измерить с помощью порядковой шкалы.
Пример порядковой шкалы
Например: Компании-разработчику программного обеспечения может понадобиться спросить своих пользователей:
Как бы вы оценили наше приложение?
- Отлично
- Очень хорошо
- Хорошо
- Плохой
- Бедный
Атрибуты в этом примере перечислены в порядке убывания.
Интервальная шкала Интервальная шкала измерения данных представляет собой шкалу, в которой уровни упорядочены и каждые численно равные расстояния на шкале имеют одинаковую интервальную разность. Если это расширение порядковой шкалы, с основным отличием в наличии равных интервалов.
Если это расширение порядковой шкалы, с основным отличием в наличии равных интервалов.
С помощью шкалы интервалов вы не только знаете, что данный атрибут A больше, чем другой атрибут B, но также и степень, в которой A больше, чем B. Кроме того, в отличие от порядковой и номинальной шкалы, арифметические операции могут выполняться на интервальная шкала.
Шкала времени с 5-минутным интервалом
Используется в различных секторах, таких как образование, медицина, инженерия и т. д. Некоторые из этих применений включают расчет CGPA учащегося, измерение температуры пациента и т. д.
Пример интервальной шкалы
Типичным примером является измерение температуры по шкале Фаренгейта. Его можно использовать для расчета среднего значения, медианы, режима, диапазона и стандартного отклонения.
Шкала отношений Ratio Scale — пиковый уровень измерения данных. Это расширение шкалы интервалов, поэтому оно удовлетворяет четырем характеристикам шкалы измерения; идентичность, величина, равный интервал и свойство абсолютного нуля.
Этот уровень измерения данных позволяет исследователю сравнивать как различия, так и относительную величину чисел. Некоторые примеры шкал отношений включают длину, вес, время и т. д.
Применительно к исследованиям рынка распространенными примерами шкал отношений являются цена, количество клиентов, конкуренты и т. д. Она широко используется в маркетинге, рекламе и коммерческих продажах. .
Шкала отношений измерения данных совместима со всеми методами статистического анализа, такими как меры центральной тенденции (среднее, медиана, мода и т. д.) и меры дисперсии (диапазон, стандартное отклонение и т. д.).
Пример шкалы отношений
Например: Опрос, который собирает веса респондентов.
К какой из следующих категорий вы относитесь? Весить
- более 100 кг
- 81 – 100 кг
- 61 – 80 кг
- 40 – 60 кг
- Менее 40 кг
Formplus — лучший инструмент для сбора номинальных, порядковых, интервальных и относительных данных. Это простой в использовании конструктор форм, который позволяет с легкостью собирать данные. Выполните следующие шаги, чтобы собрать данные о Formplus
Это простой в использовании конструктор форм, который позволяет с легкостью собирать данные. Выполните следующие шаги, чтобы собрать данные о Formplus
Мы будем использовать вопросы с несколькими вариантами ответов для сбора данных о конструкторе форм Formplus.
- Зарегистрируйтесь или войдите в свою учетную запись на https://www.formpl.us/
- Перейдите на вкладку «Параметры выбора» в меню конструктора форм.
- Нажмите кнопку «Радио».
- Нажмите кнопку редактирования, чтобы отредактировать форму.
- Отредактируйте вопрос и варианты выбора.
- Нажмите кнопку «Сохранить», чтобы сохранить изменения.
- Повторить Шаг 1 .
- Нажмите кнопку редактирования, чтобы изменить форму.

- Изменить вопрос и варианты выбора
- Присвойте значения параметрам выбора.
- Нажмите кнопку «Сохранить», чтобы сохранить изменения.
- Щелкните значок «+» внизу, чтобы добавить новую страницу.
- Повторить Шаг 1 .
- Нажмите кнопку редактирования, чтобы изменить форму.
- Отредактируйте вопрос и варианты выбора.
- Нажмите кнопку «Сохранить», чтобы сохранить изменения.
Примечание : Параметры интервальных данных не имеют нулевого значения.
Данные соотношения- Повторить Шаг 1 .
- Нажмите кнопку редактирования, чтобы изменить форму.
- Отредактируйте вопрос и варианты выбора.
- Нажмите кнопку «Сохранить», чтобы сохранить изменения.
- Нажмите кнопку «Сохранить» в правом верхнем углу, чтобы сохранить форму.

Примечание: пример данных отношения имеет нулевое значение, что отличает его от шкалы интервалов.
Шаг 3. Настройка и предварительный просмотр формы Типы шкал измеренияСуществует два основных типа шкал измерения, а именно; сравнительные шкалы и несравнительные шкалы.
Сравнительные шкалыПри сравнительной шкале респондентов просят сравнить один объект с другим. При использовании в маркетинговых исследованиях клиентов просят оценить один продукт в прямом сравнении с другими. Сравнительные шкалы можно дополнительно разделить на парное сравнение, ранговый порядок, постоянную сумму и шкалы q-сортировки.
- Шкала парного сравнения
Шкала парного сравнения — это метод масштабирования, который представляет респондентам одновременно два объекта и предлагает им выбрать один в соответствии с заранее определенным критерием. Исследователи продуктов используют его в сравнительных исследованиях продуктов, предлагая покупателям выбрать наиболее предпочтительный для них продукт из двух тесно связанных продуктов.
Исследователи продуктов используют его в сравнительных исследованиях продуктов, предлагая покупателям выбрать наиболее предпочтительный для них продукт из двух тесно связанных продуктов.
Например, в последней версии программного продукта появилось 3 новых функции. Но компания планирует удалить одну из этих функций в новой версии. Поэтому исследователи продукта проводят сравнительный анализ наиболее и наименее предпочтительной функции.
- Какая функция из следующих пар наиболее предпочтительна для вас?
- Фильтр – Диктофон
- Фильтр – Видеорегистратор
- Диктофон – Видеомагнитофон
- Шкала рангов:
В методе ранжирования респондентам одновременно предоставляется несколько вариантов и предлагается ранжировать их в порядке приоритета на основе заранее определенного критерия. Он в основном используется в маркетинге для измерения предпочтения бренда, продукта или функции.
При использовании в конкурентном анализе респондента могут попросить ранжировать группу брендов с точки зрения личных предпочтений, качества продукции, обслуживания клиентов и т. д. Результаты сбора таких данных обычно получают в ходе совместного анализа, поскольку он заставляет клиентов, чтобы различать варианты.
Шкала ранжирования является типом порядковой шкалы, поскольку она упорядочивает атрибуты от наиболее предпочтительных к наименее предпочтительным, но не имеет определенного расстояния между атрибутами.
Например:
Расположите следующие бренды от наиболее предпочтительных до наименее предпочтительных.
- Кока-Кола
- Пепси-кола
- Доктор перец
- Маунтин Дью
- Шкала постоянной суммы
Шкала постоянной суммы — это тип шкалы измерения, в которой респондентов просят распределить постоянную сумму единиц, таких как очки, доллары, фишки или фишки, среди объектов-стимулов в соответствии с определенным критерием. Шкала с постоянной суммой присваивает каждому атрибуту фиксированное количество единиц, отражая важность, которую респондент придает ему.
Шкала с постоянной суммой присваивает каждому атрибуту фиксированное количество единиц, отражая важность, которую респондент придает ему.
Этот тип шкалы измерения можно использовать для определения того, что влияет на решение покупателя при выборе продукта для покупки. Например, вы можете определить, насколько важны цена, размер, аромат и упаковка для покупателя при выборе марки духов для покупки.
Некоторые из основных недостатков этого метода заключаются в том, что респонденты могут быть сбиты с толку и в конечном итоге присвоить больше или меньше баллов, чем указано. Исследователям остается иметь дело с группой данных, которые неоднородны и могут быть трудны для анализа.
Избегайте этого с помощью логической функции Formplus. Эта функция позволяет добавить ограничение, запрещающее респонденту добавлять больше или меньше баллов, чем указано в вашей форме.
- Шкала Q-сортировки
Шкала Q-сортировки — это тип шкалы измерений, в котором используется метод ранжирования для сортировки сходных объектов по некоторому критерию.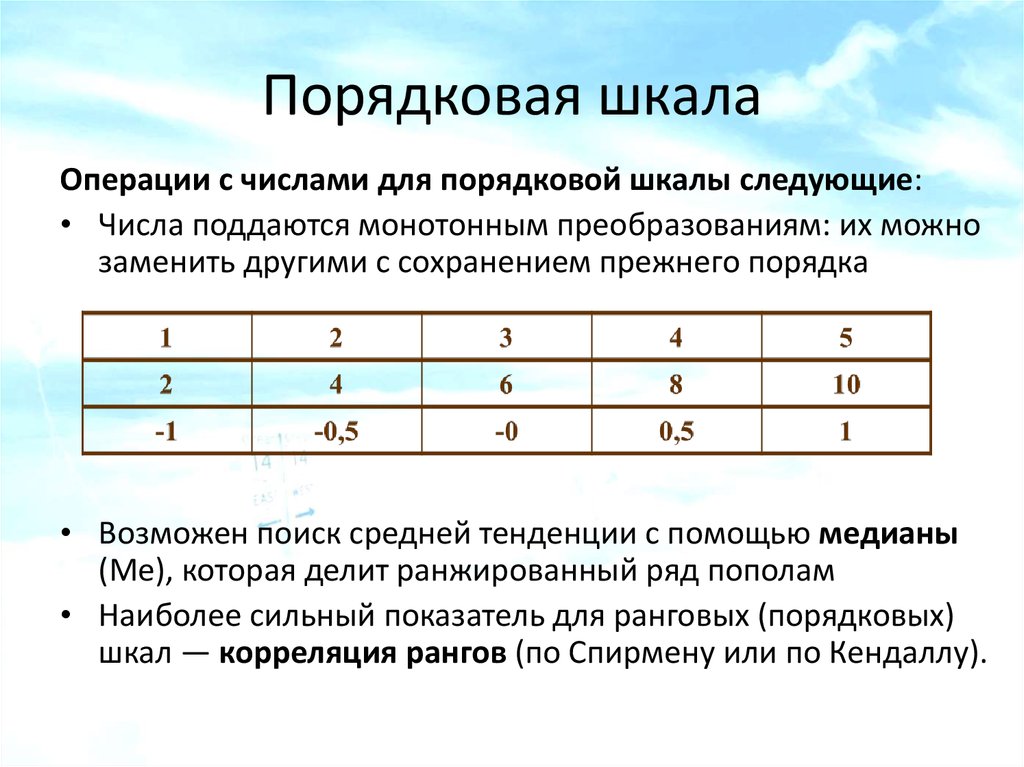 Респонденты сортируют количество утверждений или отношений в стопки, обычно по 11.
Респонденты сортируют количество утверждений или отношений в стопки, обычно по 11.
Масштабирование Q-сортировки помогает присваивать ранги различным объектам в одной группе, и различия между группами (кучками) четко видны. Это быстрый способ облегчить различение среди относительно большого набора атрибутов.
Например, новый ресторан, который только готовит свое меню, может захотеть собрать некоторую информацию о том, что нравится потенциальным клиентам:
Предоставленный документ содержит список из 50 блюд. Пожалуйста, выберите 10 блюд, которые вам нравятся, 30 блюд, к которым вы относитесь нейтрально (ни нравится, ни не нравится) и 10 блюд, которые вам не нравятся.
Несравнительные шкалы При несравнительной шкале клиентов просят оценить только один объект. Эта оценка совершенно не зависит от других исследуемых объектов. Иногда называемая монадической или метрической шкалой, несравнительная шкала может быть далее разделена на непрерывную и детализированную рейтинговые шкалы 9. 0003
0003
- Шкала непрерывной оценки
В непрерывной шкале оценок респондентов просят оценить объекты, поставив соответствующую отметку на линии, идущей от одного крайнего значения критерия к другому переменному критерию. Также называемая графической оценочной шкалой, она дает респонденту возможность поставить оценку в любом месте в зависимости от личных предпочтений.
После получения оценок исследователь делит строку на несколько категорий, а затем присваивает баллы в зависимости от категории, к которой относятся оценки. Этот рейтинг можно визуализировать как в горизонтальном, так и в вертикальном виде.
Несмотря на простоту построения, непрерывная рейтинговая шкала имеет ряд существенных недостатков, что ограничивает ее использование в маркетинговых исследованиях.
- Детализированная рейтинговая шкала
Детализированная рейтинговая шкала — это разновидность порядковой шкалы, в которой каждому атрибуту присваиваются номера. Респондентов обычно просят выбрать атрибут, который лучше всего описывает их чувства по заранее определенному критерию.
Респондентов обычно просят выбрать атрибут, который лучше всего описывает их чувства по заранее определенному критерию.
Детализированная рейтинговая шкала далее делится на 2, а именно; Шкала Лайкерта, шкала Стапеля и семантическая шкала.
- Шкала Лайкерта
Шкала Лайкерта — это порядковая шкала с пятью категориями ответов, которая используется для упорядочивания списка атрибутов от лучшего к наименьшему. В этой шкале используются наречия степени, такие как очень сильно, сильно и т. Д., Для обозначения разных уровней.
- Шкала Stapel:
Это шкала с 10 категориями, обычно от -5 до 5 без нуля. Это вертикальная шкала с 3 столбцами, где атрибуты расположены посередине, а наименьшее (-5) и максимальное (5) — в 1-м и 3-м столбцах соответственно.
- Семантическая дифференциальная шкала
Это семибалльная оценочная шкала с конечными точками, связанными с биполярными метками (например, хороший или плохой, счастливый и т. д.). Его можно использовать для маркетинга, рекламы и на разных этапах разработки продукта.
д.). Его можно использовать для маркетинга, рекламы и на разных этапах разработки продукта.
Если по своей сути исследуется более одного элемента, его можно визуализировать в таблице с более чем 3 столбцами.
ЗаключениеВ двух словах, шкалы измерения относятся к различным мерам, используемым для количественной оценки переменных, которые исследователи используют при проведении анализа данных. Они являются важным аспектом исследований и статистики, поскольку именно уровень измерения данных определяет используемый метод анализа данных.
Понимание концепции шкал измерений является необходимым условием для работы с данными и проведения статистического анализа. Различные шкалы измерения имеют некоторые схожие свойства, и поэтому важно правильно проанализировать данные, чтобы определить их шкалу измерения, прежде чем выбирать метод для анализа.
Существует несколько методов масштабирования для измерения одной и той же шкалы измерения. Поэтому не существует единого способа выбора метода масштабирования для исследовательских целей.
Поэтому не существует единого способа выбора метода масштабирования для исследовательских целей.
Номинальная, порядковая, интервальная, относительная шкалы с примерами
Уровни измерения в статистике
Для выполнения статистического анализа данных важно сначала понять переменные и то, что следует измерять с помощью этих переменных. В статистике существуют различные уровни измерения, и данные, измеренные с их помощью, можно в общих чертах разделить на качественные и количественные данные.
Во-первых, давайте разберемся, что такое переменная. Величина, значение которой меняется в совокупности и может быть измерено, называется переменной. Например, рассмотрим выборку занятых лиц. Переменными для этого набора населения могут быть отрасль, местоположение, пол, возраст, навыки, тип работы, оплачиваемый отпуск и т. д. Значение переменных будет отличаться для каждого сотрудника.
Например, в США практически невозможно рассчитать среднюю почасовую ставку рабочего. Таким образом, выборочная аудитория выбирается случайным образом, чтобы она надлежащим образом представляла большую часть населения. Затем рассчитывается средняя часовая ставка этой выборочной аудитории. Используя статистические тесты, вы можете сделать вывод о средней почасовой ставке для большей группы населения.
Таким образом, выборочная аудитория выбирается случайным образом, чтобы она надлежащим образом представляла большую часть населения. Затем рассчитывается средняя часовая ставка этой выборочной аудитории. Используя статистические тесты, вы можете сделать вывод о средней почасовой ставке для большей группы населения.
Уровень измерения переменной определяет используемый тип статистического теста. Математическая природа переменной или, другими словами, то, как переменная измеряется, рассматривается как уровень измерения.
Что такое номинальная, порядковая, интервальная и пропорциональная шкалы?
Номинальный, порядковый, интервальный и относительный определяются как четыре основных уровня шкал измерения, которые используются для сбора данных в форме опросов и анкет, каждый из которых представляет собой вопрос с несколькими вариантами ответов.
Каждая шкала представляет собой добавочный уровень измерения, то есть каждая шкала выполняет функцию предыдущей шкалы, и все шкалы опросных вопросов, такие как шкала Лайкерта, семантически-дифференциальная, дихотомическая и т. д., являются производными от этих четырех основных уровней переменных. измерение. Прежде чем мы подробно обсудим все четыре уровня шкал измерения с примерами, давайте кратко рассмотрим, что представляют собой эти шкалы.
д., являются производными от этих четырех основных уровней переменных. измерение. Прежде чем мы подробно обсудим все четыре уровня шкал измерения с примерами, давайте кратко рассмотрим, что представляют собой эти шкалы.
Номинальная шкала — это шкала именования, в которой переменные просто «называются» или помечаются без определенного порядка. В порядковой шкале все переменные расположены в определенном порядке, помимо их имен. Шкала интервалов предлагает метки, порядок, а также определенный интервал между каждым из его переменных параметров. Шкала отношений обладает всеми характеристиками интервальной шкалы, кроме того, она также может принимать значение «ноль» любой из своих переменных.
Вот еще четыре уровня измерения в исследованиях и статистике: номинальный, порядковый, интервальный, относительный.
Номинальная шкала, также называемая категориальной шкалой переменных, определяется как шкала, используемая для маркировки переменных по отдельным классификациям, и не включает количественное значение или порядок. Эта шкала является самой простой из четырех шкал переменных измерений. Вычисления, сделанные для этих переменных, будут бесполезны, так как нет числового значения параметров.
Эта шкала является самой простой из четырех шкал переменных измерений. Вычисления, сделанные для этих переменных, будут бесполезны, так как нет числового значения параметров.
В некоторых случаях эта шкала используется для целей классификации – числа, связанные с переменными этой шкалы, являются только тегами для классификации или разделения. Расчеты, сделанные по этим числам, будут бесполезны, поскольку они не имеют количественного значения.
Для таких вопросов, как:
Где вы живете?
- 1- Пригород
- 2- Город
- 3- Город
Номинальная шкала часто используется в исследовательских опросах и вопросниках, где значение имеют только метки переменных.
Например, опрос клиентов с вопросом «Какую марку смартфонов вы предпочитаете?» Варианты: «Apple»-1, «Samsung»-2, «OnePlus»-3.
- В этом опросном вопросе для исследователя, проводящего потребительские исследования или нетнографию, важны только названия торговых марок.
 Для этих марок нет необходимости в каком-либо конкретном заказе. Однако, собирая номинальные данные, исследователи проводят анализ на основе соответствующих меток.
Для этих марок нет необходимости в каком-либо конкретном заказе. Однако, собирая номинальные данные, исследователи проводят анализ на основе соответствующих меток. - В приведенном выше примере, когда респондент выбирает Apple в качестве предпочтительного бренда, введенные и связанные данные будут равны «1». Это помогло дать количественную оценку и ответить на последний вопрос: сколько респондентов выбрали Apple, сколько выбрали Samsung и сколько выбрали OnePlus, и какой из них самый высокий.
- Это основа количественного исследования, а номинальная шкала является самой фундаментальной шкалой исследования.
Данные номинальной шкалы и анализ
Существует два основных способа сбора данных о номинальной шкале:
- Задавая открытый вопрос, ответы на который могут быть закодированы соответствующим номером метки, выбранным исследователем.
- Другой альтернативой сбору номинальных данных является включение вопроса с несколькими вариантами ответов, в котором ответы будут помечены.

В обоих случаях анализ собранных данных будет происходить в процентах или по модулю, т. е. наиболее распространенный ответ, полученный на вопрос. Один вопрос может иметь более одного режима, поскольку в целевой группе могут существовать два общих фаворита.
Примеры номинальной шкалы
- Пол
- Политические предпочтения
- Место жительства
| Ваш пол? | Каковы ваши политические предпочтения? | Где ты живешь? |
|
|
|
Создать бесплатную учетную запись
Номинальная шкала SPSS
В SPSS можно указать уровень измерения в виде шкалы (числовые данные на шкале интервалов или отношений), порядковой или номинальной. Номинальные и порядковые данные могут быть строковыми буквенно-цифровыми или числовыми.
Номинальные и порядковые данные могут быть строковыми буквенно-цифровыми или числовыми.
При импорте данных любой переменной во входной файл SPSS она по умолчанию принимается как масштабируемая переменная, поскольку данные в основном содержат числовые значения. Важно изменить его на номинальный или порядковый или сохранить его в виде шкалы в зависимости от переменной, которую представляют данные.
Порядковая шкала: 2
nd Уровень измеренияПорядковая шкала определяется как шкала измерения переменных, используемая для простого отображения порядка переменных, а не разницы между каждой из переменных. Эти шкалы обычно используются для описания нематематических идей, таких как частота, удовлетворение, счастье, степень боли и т. д. Довольно просто запомнить реализацию этой шкалы, так как «Порядковый номер» звучит похоже на «Порядок», т.е. именно цель этой шкалы.
Порядковая шкала сохраняет описательные качества наряду с внутренним порядком, но лишена происхождения шкалы, поэтому расстояние между переменными нельзя рассчитать.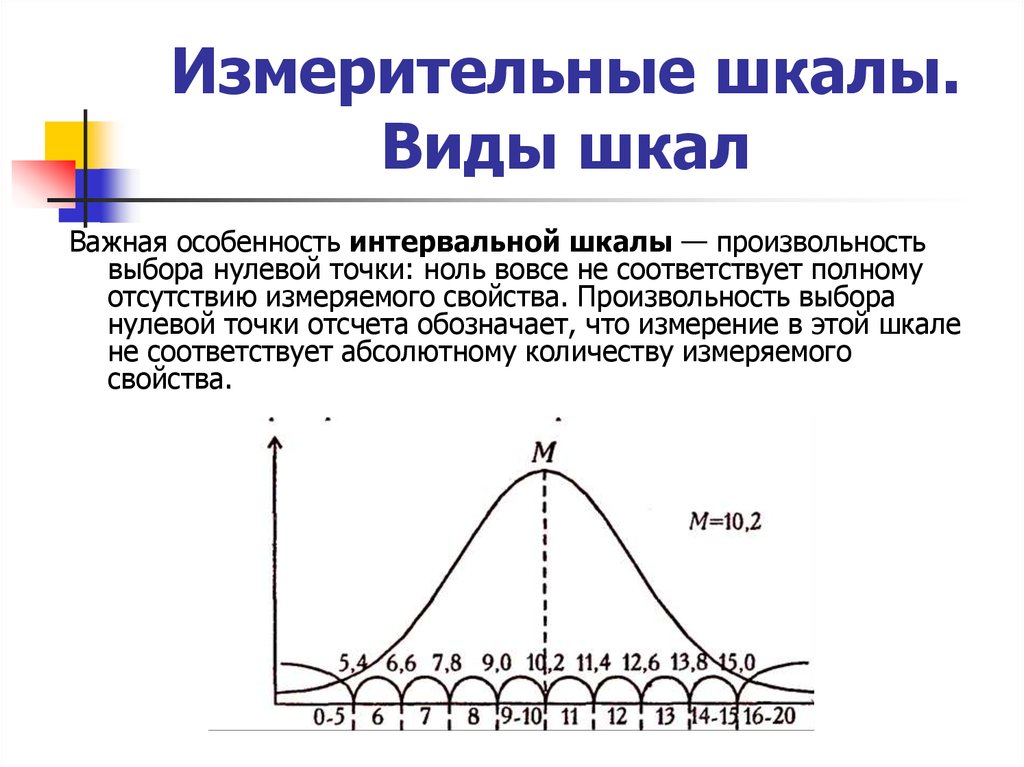 Описательные качества указывают на теговые свойства, аналогичные номинальной шкале, кроме того, порядковая шкала имеет еще и взаимное расположение переменных. Начало этой шкалы отсутствует, в связи с чем нет фиксированного начала или «истинного нуля».
Описательные качества указывают на теговые свойства, аналогичные номинальной шкале, кроме того, порядковая шкала имеет еще и взаимное расположение переменных. Начало этой шкалы отсутствует, в связи с чем нет фиксированного начала или «истинного нуля».
Порядковые данные и анализ
Данные в порядковой шкале могут быть представлены в табличном или графическом форматах, чтобы исследователь мог провести удобный анализ собранных данных. Кроме того, для анализа порядковых данных можно использовать такие методы, как U-критерий Манна-Уитни и H-критерий Крускала-Уоллиса. Эти методы обычно применяются для сравнения двух или более порядковых групп.
В U-критерии Манна-Уитни исследователи могут сделать вывод, какая переменная одной группы больше или меньше другой переменной случайно выбранной группы. В то время как в тесте Крускала-Уоллиса исследователи могут проанализировать, имеют ли две или более порядковые группы одинаковую медиану или нет.
Узнайте о: Номинальная и порядковая шкала
Примеры порядковой шкалы
Статус на рабочем месте, рейтинг команд в турнирах, порядок качества продукции и порядок согласия или удовлетворения — вот некоторые из наиболее распространенных примеров порядковой шкалы. Эти шкалы обычно используются в маркетинговых исследованиях для сбора и оценки относительных отзывов об удовлетворенности продуктом, изменении восприятия при обновлении продукта и т. д.
Эти шкалы обычно используются в маркетинговых исследованиях для сбора и оценки относительных отзывов об удовлетворенности продуктом, изменении восприятия при обновлении продукта и т. д.
Например, вопрос семантической дифференциальной шкалы, такой как:
Насколько вы удовлетворены нашими услугами?
- Очень неудовлетворен – 1
- Не удовлетворен – 2
- Нейтральный – 3
- Доволен – 4
- Очень доволен – 5
- Здесь порядок переменных имеет первостепенное значение, как и маркировка. Очень неудовлетворенный всегда будет хуже, чем неудовлетворенный, а удовлетворенный будет хуже, чем очень довольный.
- Здесь порядковая шкала находится на шаг выше номинальной шкалы – порядок соответствует результатам, как и их наименование.
- Анализ результатов на основе порядка наряду с именем становится удобным процессом для исследователя.
- Если они намерены получить больше информации, чем то, что они могли бы собрать с помощью номинальной шкалы, они могут использовать порядковую шкалу.

Эта шкала не только присваивает значения переменным, но также измеряет ранг или порядок переменных, например:
- Классы
- Удовлетворение
- Счастье
Насколько вы удовлетворены нашими услугами?
- 1- Очень неудовлетворен
- 2- Не удовлетворен
- 3- нейронный
- 4- Удовлетворено
- 5- Очень доволен
Шкала интервалов: 3
rd Уровень измеренияШкала интервалов определяется как числовая шкала, в которой известен порядок переменных, а также разница между этими переменными. Переменные, которые имеют знакомые, постоянные и вычисляемые различия, классифицируются с использованием шкалы интервалов. Также легко запомнить основную роль этой шкалы: «Интервал» указывает на «расстояние между двумя объектами», что помогает достичь шкала интервалов.
Эти весы эффективны, поскольку они открывают двери для статистического анализа предоставленных данных. Среднее значение, медиану или моду можно использовать для расчета центральной тенденции в этой шкале. Единственным недостатком этой шкалы является отсутствие заранее определенной отправной точки или истинного нулевого значения.
Среднее значение, медиану или моду можно использовать для расчета центральной тенденции в этой шкале. Единственным недостатком этой шкалы является отсутствие заранее определенной отправной точки или истинного нулевого значения.
Интервальная шкала содержит все свойства порядковой шкалы, кроме того, предлагает вычисление разницы между переменными. Основной характеристикой этой шкалы является равноудаленная разница между объектами.
Например, рассмотрим температурную шкалу Цельсия/Фаренгейта:
- 80 градусов всегда выше, чем 50 градусов, и разница между этими двумя температурами такая же, как разница между 70 градусами и 40 градусами.
- Кроме того, значение 0 является произвольным, поскольку существуют отрицательные значения температуры, что делает температурную шкалу Цельсия/Фаренгейта классическим примером интервальной шкалы.
- Интервальная шкала часто выбирается в исследовательских случаях, когда разница между переменными является требованием, чего нельзя достичь с помощью номинальной или порядковой шкалы.
 Интервальная шкала количественно определяет разницу между двумя переменными, тогда как две другие шкалы способны связывать только качественные значения с переменными.
Интервальная шкала количественно определяет разницу между двумя переменными, тогда как две другие шкалы способны связывать только качественные значения с переменными. - В отличие от двух предыдущих шкал можно оценить средние и медианные значения в порядковой шкале.
- В статистике часто используется интервальная шкала, так как числовое значение может быть не только присвоено переменной, но и может быть выполнено вычисление на основе этих значений.
Даже если шкалы интервалов замечательны, они не вычисляют «истинное нулевое» значение, поэтому в игру вступает следующая шкала.
Интервальные данные и анализ
Все методы, применимые к анализу номинальных и порядковых данных, применимы и к интервальным данным. Помимо этих методов, существует несколько методов анализа, таких как описательная статистика, корреляционно-регрессионный анализ, которые широко используются для анализа интервальных данных.
Описательная статистика — это термин, используемый для анализа числовых данных, который помогает осмысленно описывать, изображать или суммировать данные, а также помогает в расчете среднего значения, медианы и моды.
Примеры шкалы интервалов
- Существуют ситуации, когда шкалы ориентации считаются шкалами интервалов.
- Помимо температурной шкалы, время также является очень распространенным примером шкалы интервалов, поскольку значения уже установлены, постоянны и поддаются измерению.
- Календарные годы и время также подпадают под эту категорию шкал измерения. Шкала Лайкерта
- , показатель Net Promoter Score, шкала семантического дифференциала, биполярная матричная таблица и т. д. являются наиболее часто используемыми примерами интервальной шкалы.
Следующие вопросы относятся к категории интервальной шкалы:
- Каков доход вашей семьи?
- Какая температура в вашем городе?
Создайте бесплатную учетную запись
Шкала отношений: 4
th Уровень измерения Шкала отношений определяется как шкала измерения переменных, которая не только производит порядок переменных, но также делает различие между переменными известными вместе с информацией на значение истинного нуля. Он рассчитывается, предполагая, что переменные имеют опцию для нуля, разница между двумя переменными одинакова и существует определенный порядок между опциями.
Он рассчитывается, предполагая, что переменные имеют опцию для нуля, разница между двумя переменными одинакова и существует определенный порядок между опциями.
При выборе истинного нуля к переменным можно применять различные методы вывода и описательного анализа. Помимо того, что шкала отношений делает все, что могут делать номинальная, порядковая и интервальная шкалы, она также может устанавливать значение абсолютного нуля. Лучшими примерами шкал отношений являются вес и рост. В маркетинговых исследованиях шкала отношений используется для расчета доли рынка, годового объема продаж, цены будущего продукта, количества потребителей и т. д.
- Шкала отношений предоставляет наиболее подробную информацию, поскольку исследователи и статистики могут рассчитать центральную тенденцию, используя статистические методы, такие как среднее значение, медиана, мода, а также такие методы, как среднее геометрическое, коэффициент вариации или среднее гармоническое. шкала.
- Шкала отношений включает характеристики трех других шкал измерения переменных, т.
 е. маркировку переменных, значимость порядка переменных и вычисляемую разницу между переменными (которые обычно равноудалены).
е. маркировку переменных, значимость порядка переменных и вычисляемую разницу между переменными (которые обычно равноудалены). - Из-за существования истинного нулевого значения шкала отношения не имеет отрицательных значений.
- Чтобы решить, когда использовать шкалу отношений, исследователь должен наблюдать, обладают ли переменные всеми характеристиками шкалы интервалов наряду с наличием абсолютного нулевого значения.
- Среднее значение, моду и медиану можно рассчитать с помощью шкалы отношений.
Данные о соотношениях и анализ
На фундаментальном уровне данные шкалы отношений носят количественный характер, благодаря чему все методы количественного анализа, такие как SWOT, TURF, кросс-табуляция, совместное использование и т. д., могут использоваться для расчета данных о соотношениях. В то время как некоторые методы, такие как SWOT и TURF, будут анализировать данные о соотношении таким образом, чтобы исследователи могли создавать дорожные карты того, как улучшить продукты или услуги, а кросс-таблица будет полезна для понимания того, будут ли новые функции полезны для целевой рынок или нет.
Примеры шкалы соотношений
Следующие вопросы относятся к категории шкалы соотношений:
- Каков текущий рост вашей дочери?
- Менее 5 футов.
- 5 футов 1 дюйм – 5 футов 5 дюймов
- 5 футов 6 дюймов — 6 футов
- Более 6 футов
- Какой у вас вес в килограммах?
- Менее 50 кг
- 51- 70 кг
- 71- 90 кг
- 91-110 кг
- Более 110 кг
Узнайте о: Интервальная и относительная шкала
Резюме — Уровни измерения
Четыре шкалы измерения данных — номинальная, порядковая, интервальная и относительная — довольно часто обсуждаются в академическом обучении. Приведенная ниже простая для запоминания диаграмма может помочь вам в тесте статистики.
| Предложения: | Номинальный | Порядковый номер | Интервал | Соотношение |
| Последовательность переменных установлена | – | Да | Да | Да |
| Режим | Да | Да | Да | Да |
| Медиана | – | Да | Да | Да |
| Среднее | – | – | Да | Да |
| Можно оценить разницу между переменными | – | – | Да | Да |
| Сложение и вычитание переменных | – | – | Да | Да |
| Умножение и деление переменных | – | – | – | Да |
| Абсолютный ноль | – | – | – | Да |
Создать бесплатную учетную запись
лекция1
Лекция
1
Типы весов и уровни измерения
Дискретные и
непрерывные переменные
В тексте Даниэля различаются дискретные и непрерывные переменные. Эти
являются техническими различиями, которые не будут так важны для нас в этом
учебный класс. Согласно тексту, дискретные переменные — это переменные, в которых
промежуточные значения невозможны. Например, количество телефонных звонков.
вы получаете в день. Вы не можете принимать телефонные звонки 6.3. Непрерывные переменные
все остальное; любая переменная, которая теоретически может иметь значения между
баллы (например, от 153 до 154 фунтов). Оказывается, это
не все, что полезно различия для наших целей. Что на самом деле больше
важным для статистических соображений является уровень измерения использовал. Когда я говорю, что это более важно, я действительно преуменьшаю это.
Понимание уровня измерения переменной (или шкалы, или меры)
Первое и самое важное различие, которое необходимо сделать о переменной, когда
занимаюсь статистикой!
Эти
являются техническими различиями, которые не будут так важны для нас в этом
учебный класс. Согласно тексту, дискретные переменные — это переменные, в которых
промежуточные значения невозможны. Например, количество телефонных звонков.
вы получаете в день. Вы не можете принимать телефонные звонки 6.3. Непрерывные переменные
все остальное; любая переменная, которая теоретически может иметь значения между
баллы (например, от 153 до 154 фунтов). Оказывается, это
не все, что полезно различия для наших целей. Что на самом деле больше
важным для статистических соображений является уровень измерения использовал. Когда я говорю, что это более важно, я действительно преуменьшаю это.
Понимание уровня измерения переменной (или шкалы, или меры)
Первое и самое важное различие, которое необходимо сделать о переменной, когда
занимаюсь статистикой!
Уровни
измерения
Статистики часто ссылаются на «уровни измерения»
переменная, мера или шкала, чтобы различать измеряемые переменные, которые
имеют разные свойства. Различают четыре основных уровня: номинальный, порядковый,
интервал и отношение.
Различают четыре основных уровня: номинальный, порядковый,
интервал и отношение.
Номинальная
Переменная, измеренная по «номинальной» шкале,
переменная, которая на самом деле не имеет никакого оценочного различия. Одно значение
на самом деле не больше, чем другой. Хорошим примером номинальной переменной является
пол (или пол). Информация в наборе данных о поле обычно кодируется как 0 или 1, 1.
указывает на мужчину и 0 указывает на женщину (или наоборот – 0 для мужчин, 1
для женского пола). 1 в данном случае является произвольным значением и не больше и не больше.
лучше, чем 0. Между 0 и 1 существует только номинальная разница. При номинальном
переменных, существует качественная разница между значениями, а не количественная
один.
Порядковый номер
Нечто, измеряемое по «порядковой» шкале
имеет оценочный оттенок. Одно значение на больше или больше или лучше
чем другой. Продукт А предпочтительнее продукта Б, поэтому А получает
значение 1, а B получает значение 2. Другим примером может быть оценка вашего
удовлетворенность работой по шкале от 1 до 10, где 10 означает полное
удовлетворение. С порядковыми шкалами мы знаем только, что 2 равно
лучше 1 или 10 лучше 9; мы не знаем, насколько. Это может варьироваться. Расстояние между 1 и 2 может быть короче, чем между 9и 10.
Другим примером может быть оценка вашего
удовлетворенность работой по шкале от 1 до 10, где 10 означает полное
удовлетворение. С порядковыми шкалами мы знаем только, что 2 равно
лучше 1 или 10 лучше 9; мы не знаем, насколько. Это может варьироваться. Расстояние между 1 и 2 может быть короче, чем между 9и 10.
Интервал
Переменная, измеренная на шкале интервалов, дает
информация о большем или лучшем качестве порядкового номера
шкалы делают, но интервальные переменные имеют одинаковое расстояние между каждым значением.
Расстояние между 1 и 2 равно расстоянию между 9 и 10.
Хорошим примером является температура в градусах Цельсия или Фаренгейта.
такая же разница между 100 градусами и 90, как и между 42 и 32.
свойства, которыми обладает интервальная шкала, за исключением того, что при масштабировании отношений
абсолютный нуль. Примером является температура, измеряемая в градусах Кельвина. Здесь нет
возможное значение ниже 0 градусов Кельвина, это абсолютный ноль. вес это другое
например, 0 фунтов. является осмысленным отсутствием веса. Баланс вашего банковского счета составляет
еще один. Хотя у вас может быть отрицательный или положительный баланс счета, существует
определенное и непроизвольное значение счета
остаток 0.
является осмысленным отсутствием веса. Баланс вашего банковского счета составляет
еще один. Хотя у вас может быть отрицательный или положительный баланс счета, существует
определенное и непроизвольное значение счета
остаток 0.
Можно думать о номинальном, порядковом, интервал и отношение как ранжированные по отношению друг к другу. Соотношение более сложный, чем интервал, интервал более сложный, чем порядковый номер, и порядковый более сложный, чем номинальный. Я не знаю, есть ли ранги равноудалены или нет, вероятно, нет. Так что же это за уровень измерения? ранжирование уровней измерения?? Я бы сказал порядковый. В статистике лучше быть немного консервативен, когда сомневаешься.
Два
Общие классы переменных (кого это волнует?)
Хорошо, помните, я сказал, что это первое и самое важное различие
при использовании статистики? Вот почему. В большинстве случаев статистики или
исследователи кончают тем, что заботятся только о разнице между номинальными и всеми
другие. Как правило, существует два класса статистики: те, которые имеют дело с
номинальные зависимые переменные и те, что имеют дело с порядковыми, интервальными,
или относительные переменные. (Сейчас мы сосредоточимся на зависимой переменной и
позже мы обсудим независимую переменную). Когда я описываю эти типы
два общих класса переменных, я (и многие другие) обычно называю их
«категорический» и «непрерывный». (Иногда я буду использовать “дихотомический”
вместо «категорический»). Отметим также, что
«непрерывный» в этом смысле не совсем то же самое, что
«непрерывный» используется в главе 1 текста при различении
между дискретным и непрерывным. Это гораздо более свободный термин. Категоричность и
дихотомические обычно означают, что шкала является номинальной. “Непрерывный”
переменные обычно являются порядковыми или лучше.
(Сейчас мы сосредоточимся на зависимой переменной и
позже мы обсудим независимую переменную). Когда я описываю эти типы
два общих класса переменных, я (и многие другие) обычно называю их
«категорический» и «непрерывный». (Иногда я буду использовать “дихотомический”
вместо «категорический»). Отметим также, что
«непрерывный» в этом смысле не совсем то же самое, что
«непрерывный» используется в главе 1 текста при различении
между дискретным и непрерывным. Это гораздо более свободный термин. Категоричность и
дихотомические обычно означают, что шкала является номинальной. “Непрерывный”
переменные обычно являются порядковыми или лучше.
Порядковые шкалы с несколькими категориями
(2,3 или, возможно, 4), а номинальные меры часто классифицируются как категориальные.
и анализируются с использованием биномиального класса статистических тестов, тогда как порядковые
шкалы со многими категориями (5 или более), интервалом и отношением, как правило,
проанализированы с помощью нормального теоретического класса статистических тестов. Хотя различие несколько размыто
во-первых, это часто очень полезное различие для выбора правильного статистического
тест. Существует ряд специальных
статистика, которая была разработана для работы с порядковыми переменными с
несколько возможных значений, но мы не собираемся рассматривать их в этом классе (см. Агрести, 1984, 1990; ОКоннелл, 2006 г.; Уикенс,
1989 для получения дополнительной информации об анализе порядковых переменных).
Хотя различие несколько размыто
во-первых, это часто очень полезное различие для выбора правильного статистического
тест. Существует ряд специальных
статистика, которая была разработана для работы с порядковыми переменными с
несколько возможных значений, но мы не собираемся рассматривать их в этом классе (см. Агрести, 1984, 1990; ОКоннелл, 2006 г.; Уикенс,
1989 для получения дополнительной информации об анализе порядковых переменных).
Общие классы
Статистика (О, думаю, мне все равно)
Итак, у нас есть эти две общие категории (т. е. непрерывная и категоричная),
что дальше? Ну, это различие (как бы нечетко оно ни звучало) имеет очень важное значение.
последствия для типа используемой статистической процедуры, и мы будем делать
решения, основанные на этом различии на протяжении всего курса . Есть
два общих класса статистики: основанные на биномиальная теория и
те, которые основаны на нормальной теории . Хи-квадрат и логистическая регрессия
с биномиальной теорией или биномиальными распределениями и t-тестами,
ANOVA, корреляция и регрессия имеют дело с нормальной теорией. Итак, вот таблица
обобщить.
Итак, вот таблица
обобщить.
Тип зависимого Переменная (или шкала) | Уровень Измерение | Общий класс
Статистика | Примеры Статистические процедуры |
Категориальный (или дихотомический) | номинальный, порядковый номер с 2, 3 или 4 уровни | бином | хи-квадрат, логистическая регрессия |
Непрерывный | порядковый номер с более чем 4 категории | нормальный | Дисперсионный анализ, регрессия, корреляция, t-критерий |
Опрос
Вопросы и меры: некоторые распространенные примеры
На практике исследователи
и проблемы исследования реальной жизни не говорят вам, как зависимая переменная
должны быть разделены на категории, поэтому я обозначу несколько типов вопросов для опроса или
другие общепринятые меры.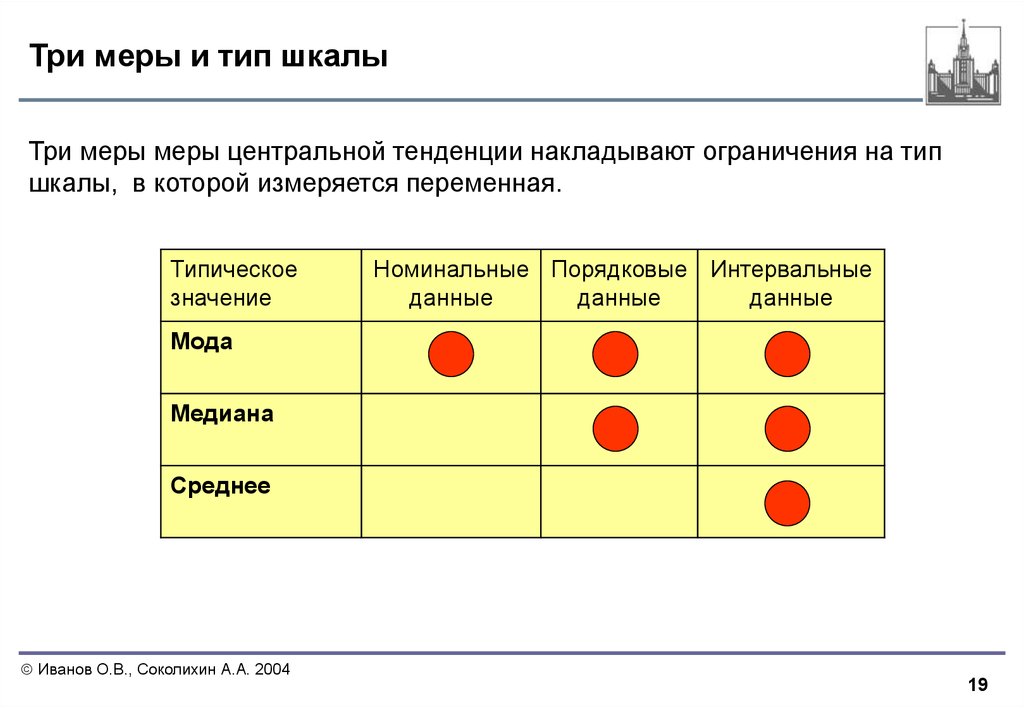
Да/Нет
Вопросы
. Любой вопрос в опросе, на который можно дать ответ «да» или «нет», является номинальным.
и поэтому биномиальная статистика будет применяться всякий раз, когда будет задан один вопрос «да/нет».
служит зависимой переменной или одной из зависимых переменных в
анализ.
Шкала Лайкерта
В опросе особого типа используется набор
ответы, упорядоченные таким образом, что один ответ больше другого.
термин Шкала Лайкерта названа в честь изобретателя,
Ренсис Лайкерт, чье имя
произносится как «Ликерт». Как правило, это
термин используется для любого вопроса, который имеет около 5 или более возможных вариантов. Ан
Примером может быть: «Как бы вы оценили администратора вашего отдела?»
1=очень некомпетентен, 2=несколько некомпетентен, 3=не компетентен, 4=несколько
компетентный или 5 = очень компетентный. шкалы Лайкерта
либо порядковый, либо интервальный, и многие психометристы
утверждал бы, что они являются интервальными шкалами, потому что, когда они хорошо построены,
является равным расстоянием между каждым значением. Итак, если Лайкерт
шкала используется в качестве зависимой переменной в анализе, обычная статистика теории
используются, например, дисперсионный анализ или регрессия.
Итак, если Лайкерт
шкала используется в качестве зависимой переменной в анализе, обычная статистика теории
используются, например, дисперсионный анализ или регрессия.
Физический
Меры
Большинство физических мер, таких как
рост, вес, систолическое артериальное давление, расстояние и т. д., являются интервалом или соотношением
шкалы, поэтому они попадают в общую «непрерывную»
категория. Поэтому статистика типа нормальной теории также используется, когда такая мера служит зависимой переменной в анализе.
анализ.
Подсчеты
Подсчеты сложны. Если переменная измеряется счетом, например, если
Исследователь подсчитывает количество дней, в течение которых пациент находился в больнице.
госпитализации, переменная находится на шкале отношений и рассматривается как непрерывная
переменная. Однако часто рекомендуются специальные статистические данные, т.к.
переменные часто имеют очень асимметричное распределение с
большое количество случаев с нулевым счетом (см. Agresti,
1990, с. 125; Коэн, Коэн, Уэст и Айкен, 2003 г., глава 13). Если исследователь подсчитывает количество
субъектов в эксперименте (или количество случаев в наборе данных), непрерывный
мера типа на самом деле не используется. Подсчет в этом случае действительно
изучение частоты появления некоторого значения переменной. Например,
подсчет количества субъектов в наборе данных, которые сообщают, что
госпитализированных в прошлом году, зависит от дихотомической переменной в наборе данных
что означает пребывание в больнице или отсутствие госпитализации (например, из
например, «были ли вы госпитализированы в течение последнего года?»).
Даже если подсчитать количество случаев на основе вопроса «как
много дней в прошлом году вы были госпитализированы», что является
непрерывная мера, переменная, используемая в анализе, на самом деле не является
непрерывная переменная. Вместо этого исследователь будет фактически анализировать
дихотомическую переменную путем подсчета числа людей, не
госпитализированных в прошлом году (0 дней) по сравнению с теми, кто был (1 или более
дней).
125; Коэн, Коэн, Уэст и Айкен, 2003 г., глава 13). Если исследователь подсчитывает количество
субъектов в эксперименте (или количество случаев в наборе данных), непрерывный
мера типа на самом деле не используется. Подсчет в этом случае действительно
изучение частоты появления некоторого значения переменной. Например,
подсчет количества субъектов в наборе данных, которые сообщают, что
госпитализированных в прошлом году, зависит от дихотомической переменной в наборе данных
что означает пребывание в больнице или отсутствие госпитализации (например, из
например, «были ли вы госпитализированы в течение последнего года?»).
Даже если подсчитать количество случаев на основе вопроса «как
много дней в прошлом году вы были госпитализированы», что является
непрерывная мера, переменная, используемая в анализе, на самом деле не является
непрерывная переменная. Вместо этого исследователь будет фактически анализировать
дихотомическую переменную путем подсчета числа людей, не
госпитализированных в прошлом году (0 дней) по сравнению с теми, кто был (1 или более
дней).
Типы масштабов измерения – номинальные, порядковые, интервал, масштаб с различными вариациями
. присваивается переменным. Назначение той или иной шкалы измерения зависит от числовых свойств переменной, о чем говорилось в прошлой статье «Шкалы измерения».
Операции, применяемые к различным переменным из вопросников в SPSS, зависят от масштаба, присвоенного переменным. Назначение той или иной шкалы измерения зависит от числовых свойств переменной, о чем говорилось в прошлой статье «Шкалы измерения».
В сегодняшней статье обсуждаются различные шкалы, используемые при анализе данных.
Существует 4 шкалы измерения, а именно Номинальная, Порядковая, Интервальная и Относительная, все переменные попадают в одну из этих шкал. Понимание математических свойств и назначение надлежащего масштаба переменным важно, поскольку они определяют, какие математические операции разрешены. Это определяет статистические операции, которые мы можем использовать. Операции, применяемые к различным переменным из Анкет в SPSS, зависят от Масштаба, присвоенного переменным. Назначение той или иной шкалы измерения зависит от числовых свойств переменной, о чем говорилось в прошлой статье «Шкалы измерения».
Это определяет статистические операции, которые мы можем использовать. Операции, применяемые к различным переменным из Анкет в SPSS, зависят от Масштаба, присвоенного переменным. Назначение той или иной шкалы измерения зависит от числовых свойств переменной, о чем говорилось в прошлой статье «Шкалы измерения».
В сегодняшней статье обсуждаются различные шкалы, которые используются при анализе данных. Существует 4 шкалы измерения, а именно Номинальная, Порядковая, Интервальная и Относительная, все переменные попадают в одну из этих шкал. Понимание математических свойств и присвоение надлежащего масштаба переменным важно, поскольку они определяют, какие математические операции разрешены. Это определяет статистические операции, которые мы можем использовать.
4 шкалы расположены в следующем порядке: Номинальная, Порядковая, Интервальная и Относительная шкалы, где Номинальная имеет наименьшие математические свойства, за ней следуют Порядковая и Интервальная, тогда как Относительная имеет самые математические свойства.
Номинальная шкала
Со статистической точки зрения это самый низкий уровень измерения. Номинальная шкала назначается элементам, которые разделены на категории без какого-либо порядка или структуры, например, цвета не имеют назначенного порядка. У нас может быть 5 цветов, таких как красный, синий, оранжевый, зеленый и желтый, и мы можем пронумеровать их от 1 до 5. или 5 – 1, или пронумеровать их в миксе, здесь номера присвоены цветам только для целей идентификации, и порядок их по возрастанию или по убыванию не означает, что цвета имеют порядок. Номер дает нам идентификатор присвоенной категории. Единственная математическая операция, которую мы можем выполнить с номинальными данными, — это подсчет. Еще одним примером из исследовательской деятельности является номинальная шкала ДА/НЕТ. В нем нет порядка и нет расстояния между ДА и НЕТ.
Порядковая шкала
Далее в списке идет порядковая шкала. Порядковая шкала — это ранжирование ответов, например ранжирование велосипедиста в конце гонки на позициях 1, 2 и 3. Это не ранги, а временная дистанция между 1 и 2 вполне может быть не такой же, как между 2 и 3, таким образом, расстояние между точками не то же самое, но присутствует порядок, когда ответы имеют порядок, но расстояние между ответами не обязательно одинаково, элементы рассматриваются или помещаются в порядковую шкалу. Поэтому порядковая шкала позволяет исследователю интерпретировать общий порядок, а не относительные позиционные расстояния.
Это не ранги, а временная дистанция между 1 и 2 вполне может быть не такой же, как между 2 и 3, таким образом, расстояние между точками не то же самое, но присутствует порядок, когда ответы имеют порядок, но расстояние между ответами не обязательно одинаково, элементы рассматриваются или помещаются в порядковую шкалу. Поэтому порядковая шкала позволяет исследователю интерпретировать общий порядок, а не относительные позиционные расстояния.
Переменные порядкового масштаба имеют свойства Идентичность и Величина. Числа представляют собой измеряемое качество (идентичность) и могут сказать нам, имеет ли случай больше измеряемого качества или меньше измеряемого качества, чем другой случай (величина). Расстояние между точками шкалы не одинаково. Ранжированные предпочтения представлены как пример порядковых шкал, встречающихся в повседневной жизни.
Интервальная шкала
Обычная шкала оценки опроса представляет собой интервальную шкалу, например, когда вас просят оценить удовлетворенность обучением по 5-балльной шкале: полностью согласен, согласен, нейтрально, не согласен и полностью не согласен, используется интервальная шкала. Это интервальная шкала, поскольку предполагается, что она имеет одинаковое расстояние между каждым из элементов шкалы, т. е. предполагается, что величина между «Полностью согласен» и «Согласен» такая же, как «Согласен» и «Полностью согласен». Это означает, что мы можем интерпретировать различия в расстоянии по шкале. Мы сравниваем это с порядковой шкалой, где мы можем говорить только о различиях в порядке, а не о различиях в степени порядка, то есть о расстоянии между ответами.
Это интервальная шкала, поскольку предполагается, что она имеет одинаковое расстояние между каждым из элементов шкалы, т. е. предполагается, что величина между «Полностью согласен» и «Согласен» такая же, как «Согласен» и «Полностью согласен». Это означает, что мы можем интерпретировать различия в расстоянии по шкале. Мы сравниваем это с порядковой шкалой, где мы можем говорить только о различиях в порядке, а не о различиях в степени порядка, то есть о расстоянии между ответами.
Свойства интервальных шкал
Интервальные шкалы обладают следующими свойствами:
- Личность
- Магнитуда
- Равное расстояние
В эту шкалу помещаются переменные, отвечающие вышеуказанным свойствам. Равное расстояние между точками шкалы помогает узнать, на сколько единиц больше или меньше один случай отличается от другого. Значение расстояния между 25 и 35 такое же, как расстояние между 65 и 75.
Шкала отношений
Шкала отношений находится на верхнем уровне измерения. Фактор, который четко определяет шкалу отношений, заключается в том, что она имеет истинную нулевую точку. Простейшим примером шкалы отношений является измерение длины (не обращая внимания на какие-либо философские аспекты определения того, как мы можем определить нулевую длину) или денег. Наличие нулевой длины или нулевых денег означает, что нет ни длины, ни денег, но нулевая темпратуэ не является абсолютным нулем, поскольку она, безусловно, имеет свой эффект. Шкалы отношений обладают всеми свойствами абстрактной системы счисления.
Фактор, который четко определяет шкалу отношений, заключается в том, что она имеет истинную нулевую точку. Простейшим примером шкалы отношений является измерение длины (не обращая внимания на какие-либо философские аспекты определения того, как мы можем определить нулевую длину) или денег. Наличие нулевой длины или нулевых денег означает, что нет ни длины, ни денег, но нулевая темпратуэ не является абсолютным нулем, поскольку она, безусловно, имеет свой эффект. Шкалы отношений обладают всеми свойствами абстрактной системы счисления.
Свойства шкалы соотношений
- Личность
- Магнитуда
- Равное расстояние
- Абсолютный/истинный ноль
Эти свойства позволяют применять все возможные математические операции, включая сложение, вычитание, умножение и деление. Абсолютный/истинный ноль позволяет нам узнать, во сколько раз один случай больше другого. Переменные, попадающие в эту категорию и обладающие всеми вышеупомянутыми числовыми свойствами, попадают в шкалу отношений.
Теги:
- SPSS
- Анализ данных
Категория:
- Исследования
Номинальная, порядковая, интервальная и относительная шкалы
Номинальная, порядковая, интервальная и относительная шкалы являются уровнями измерения в статистике. Эти шкалы представляют собой широкие классификации, описывающие тип информации, записанной в значениях ваших переменных. Переменные принимают разные значения в вашем наборе данных. Например, вы можете измерить рост, пол и ранг в классе. Каждая из этих переменных использует отдельный уровень измерения.
Стэнли Смит Стивенс разработал эти четыре шкалы измерений в 1946 году. Аналитики продолжают использовать их и сегодня, потому что то, как вы записываете свои данные, влияет на то, что вы можете узнать из них, и на статистический анализ, который вы можете выполнить.
Номинальная, порядковая, интервальная и относительная шкалы являются четырьмя основными уровнями измерения. Эти уровни перечислены в порядке возрастания подробной информации, которую они предоставляют. Давайте взглянем на эти шкалы измерения!
Эти уровни перечислены в порядке возрастания подробной информации, которую они предоставляют. Давайте взглянем на эти шкалы измерения!
Связанный пост : Что такое переменная?
Номинальные шкалы
Номинальные шкалы просто обозначают категории, к которым могут относиться значения переменной. Номинал = имя. Аналитики также называют номинальные переменные как атрибутивными, так и категориальными данными.
Номинальные шкалы имеют значения, которые можно присвоить счетному числу различных групп на основе характеристики. Вы можете назвать категории, но они не имеют естественного порядка. В некоторых случаях номинальные данные могут определять группы в ваших данных, которые вы хотите сравнить, например экспериментальные условия экспериментальной и контрольной групп.
Примеры номинальных шкал включают пол, семейное положение, специальность колледжа и группу крови.
Двоичные переменные — это тип номинальных данных. Эти данные могут иметь только два значения. Статистики также называют бинарные данные индикаторными переменными и дихотомическими данными. Например, мужчина/женщина, годен/не годен и наличие/отсутствие атрибута — все это двоичные данные.
Статистики также называют бинарные данные индикаторными переменными и дихотомическими данными. Например, мужчина/женщина, годен/не годен и наличие/отсутствие атрибута — все это двоичные данные.
Номинальная шкала — это самый низкий уровень измерения, поскольку вы можете только группировать наблюдения, но не можете упорядочивать группы.
Узнайте больше о номинальных данных: определение и примеры.
Подходящие расчеты для номинальных шкал
Вы не можете рассчитать среднее значение, медиану или стандартное отклонение для номинальных переменных, поскольку у вас есть информация только о категориях. Мода является надлежащей мерой центральной тенденции для номинальных шкал, поскольку она определяет наиболее распространенную категорию.
При использовании номинальных данных вам часто необходимо оценивать относительную частоту категорий. Следовательно, круговые диаграммы и гистограммы являются обычными методами графического отображения этих переменных, поскольку они отображают количество и относительную частоту для каждой группы. Для статистических тестов вы можете использовать тесты пропорций.
Для статистических тестов вы можете использовать тесты пропорций.
Связанные сообщения : Измерения центральной тенденции и относительных частот
Порядковые шкалы
Рейтинговая система, в которой используются звезды, является порядковой шкалой.Порядковые шкалы также именуют группы в ваших данных, но вы можете расположить эти группы в естественном порядке. Хотя порядок имеет решающее значение, различия между значениями могут быть непоследовательными. Другими словами, вы можете ранжировать значения, но не знаете относительную степень различия между ними.
Примеры порядковых шкал включают:
- Уровень образования (начальное, среднее, высшее).
- Доход (низкий, средний и высокий).
- Общее состояние (от плохого до отличного).
- Лайкерта и другие шкалы согласия (полностью не согласен или полностью согласен).
- Ранг (например, спортивные команды и классы).
Порядковые данные имеют комбинацию свойств номинальных шкал и количественных свойств.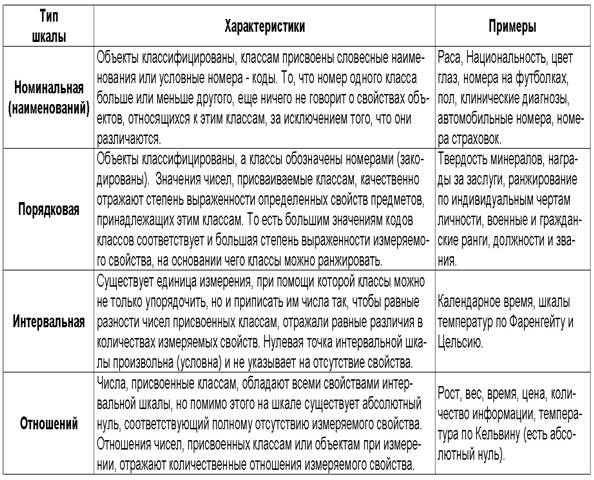 С одной стороны, эти переменные имеют ограниченное число дискретных значений, как и номинальные данные. С другой стороны, различия между значениями предоставляют информацию о порядке, подобно количественным переменным. Однако разница между соседними значениями может быть непостоянной. Например, первое, второе и третье место в гонке являются порядковыми данными. Разница во времени между первым и вторым местом может быть не такой, как между вторым и третьим местом.
С одной стороны, эти переменные имеют ограниченное число дискретных значений, как и номинальные данные. С другой стороны, различия между значениями предоставляют информацию о порядке, подобно количественным переменным. Однако разница между соседними значениями может быть непостоянной. Например, первое, второе и третье место в гонке являются порядковыми данными. Разница во времени между первым и вторым местом может быть не такой, как между вторым и третьим местом.
Порядковые переменные на ступеньку выше номинальных шкал как уровень измерения. Эти шкалы группируют наблюдения, как и номинальные данные, но они также позволяют ранжировать значения.
Узнайте больше об порядковых данных: определение, примеры и анализ.
Подходящие расчеты для порядковых шкал
Аналитики часто представляют порядковые шкалы с помощью чисел, таких как шкала Лайкерта от 1 до 5, которая измеряет удовлетворенность. В числовой форме вы можете рассчитать средние баллы, как и в случае с количественными переменными. Однако полезность этих чисел ограничена, поскольку различия между рангами могут быть непостоянными. Следовательно, многие статистики считают среднее значение неподходящей мерой для порядковых данных.
Однако полезность этих чисел ограничена, поскольку различия между рангами могут быть непостоянными. Следовательно, многие статистики считают среднее значение неподходящей мерой для порядковых данных.
Однако медиана является допустимой мерой центральной тенденции для порядковых переменных, поскольку медиана относится к среднему значению ранжирования , что идеально подходит для ранговых данных.
Если вам нужно измерить дисперсию порядковых данных, используйте диапазон, межквартильный диапазон или разброс между двумя процентилями.
Связанные сообщения : Определение и использование медианы, межквартильный диапазон и процентили: интерпретации и расчеты
Интервальные шкалы и шкалы отношений для непрерывных данных
Непрерывные переменные могут принимать все числовые значения, а шкала может быть разделена на меньшие приращения, включая дробные и десятичные значения. Между любыми двумя значениями находится бесконечное число значений.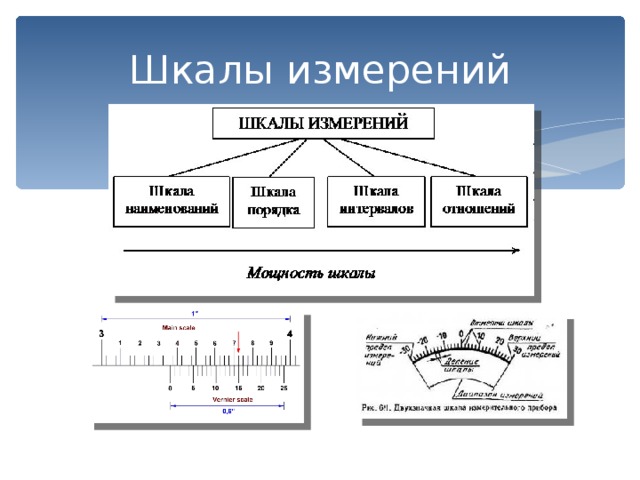 И различия между любыми двумя значениями всегда значимы. Как правило, вы измеряете непрерывные переменные по шкале.
И различия между любыми двумя значениями всегда значимы. Как правило, вы измеряете непрерывные переменные по шкале.
Примеры непрерывных данных включают рост, вес и температуру.
Статистики делят непрерывные данные на два типа, которые вы измеряете, используя шкалы интервалов и отношений.
Интервальные весы
Интервальные весы часто записывают непрерывные данные, но не всегда — кредиты и баллы SAT являются целыми числами. На этих шкалах порядок значений и интервал или расстояние между любыми двумя точками имеют значение. Например, разница в 20 градусов между 10 и 30 градусами Цельсия эквивалентна разнице между 50 и 70 градусами. Однако эти переменные не имеют нулевого измерения, что указывает на отсутствие признака. Например, ноль по Цельсию представляет температуру, а не отсутствие температуры.
Из-за отсутствия истинного нуля коэффициенты измерения недействительны для интервальных шкал. Тридцать градусов Цельсия не в три раза выше температуры, чем 10 градусов Цельсия. Вы можете складывать и вычитать значения на шкале интервалов, но вы не можете их умножать или делить.
Вы можете складывать и вычитать значения на шкале интервалов, но вы не можете их умножать или делить.
Примеры интервальных шкал включают температуру в градусах Цельсия и Фаренгейта, кредитные баллы (300–850), баллы SAT (200–800) и даты в календаре.
Интервальные шкалы являются ступенью выше порядковых данных как уровень измерения. Этот тип позволяет упорядочивать значения, как порядковые данные, но также позволяет оценить степень различия между любыми двумя значениями.
С помощью интервальных шкал можно вычислить среднее значение и стандартное отклонение для показателей центральной тенденции и изменчивости соответственно. Однако медиана и межквартильный диапазон могут быть более подходящими для асимметричных распределений.
Коэффициент вариации недействителен для этого типа измерений, поскольку он включает отношение, которое ведет нас к следующему разделу!
Связанный пост : Несимметричные распределения
Шкалы отношений
Шкалы отношений обычно используют непрерывные данные. Для этого уровня измерений интервалы по-прежнему имеют значение. Кроме того, эти переменные имеют нулевые измерения, что свидетельствует об отсутствии атрибута. Например, ноль килограммов указывает на недостаток веса. Следовательно, измерения 9Для этих весов действует 1461 коэффициент . 30 кг в три раза больше веса 10 кг. Вы можете складывать, вычитать, умножать и делить значения на шкале отношений.
Для этого уровня измерений интервалы по-прежнему имеют значение. Кроме того, эти переменные имеют нулевые измерения, что свидетельствует об отсутствии атрибута. Например, ноль килограммов указывает на недостаток веса. Следовательно, измерения 9Для этих весов действует 1461 коэффициент . 30 кг в три раза больше веса 10 кг. Вы можете складывать, вычитать, умножать и делить значения на шкале отношений.
Примеры шкал отношений включают температуру в градусах Кельвина (с абсолютным нулем, означающим отсутствие температуры), рост, вес, скорость и периоды времени.
Шкалы отношений являются верхним уровнем измерения. Подобно шкалам интервалов, они позволяют упорядочивать наблюдения и определять разницу между любыми двумя значениями. Кроме того, они позволяют оценивать коэффициенты. Высота 4 м в два раза больше 2 м. Период в 10 минут в два раза длиннее 5 минут.
Шкалы отношений позволяют вам рассчитывать те же статистические данные, что и шкалы интервалов, плюс отношения. Следовательно, такое измерение, как коэффициент вариации, допустимо для этого типа измерения.
Следовательно, такое измерение, как коэффициент вариации, допустимо для этого типа измерения.
Связанный пост : Коэффициент вариации
Сводка по номинальным, порядковым, интервальным и относительным шкалам
Знание того, используют ли ваши данные номинальный, порядковый, интервальный или относительный уровень измерения, может помочь вам избежать ошибок анализа. Рассмотрим следующую таблицу, в которой суммированы возможности различных уровней.
| Действительно | Номинальный | Порядковый номер | Интервал | Соотношение |
| Распределение частот | Да | Да | Да | Да |
| Медиана, процентильные диапазоны | № | Да | Да | Да |
| Сложение, вычитание, среднее, стандартное отклонение | № | № | Да | Да |
| Умножение, деление, отношения, коэффициент вариации | № | № | № | Да |
Связанный пост : Частотные распределения
Выбор уровней измерения
Часто данные, которые необходимо собрать, определяют выбор шкалы измерения. Например, если вы записываете пол, цвет глаз и семейное положение, это определенно номинальные данные. Однако, если вы записываете значения времени и температуры, это либо шкалы интервалов, либо шкалы отношений. Если вы ранжируете спортивные команды, это будут порядковые данные.
Например, если вы записываете пол, цвет глаз и семейное положение, это определенно номинальные данные. Однако, если вы записываете значения времени и температуры, это либо шкалы интервалов, либо шкалы отношений. Если вы ранжируете спортивные команды, это будут порядковые данные.
Иногда вам нужно решить, какую шкалу измерения использовать. Например, вы можете сравнить группы с порядковым доходом (низкий, средний, высокий). Вы также можете измерить доход, используя их значения в валюте, которые представляют собой шкалу отношений.
В этих ситуациях вы хотите записывать данные, используя уровень измерения, ближайший к краю отношения, когда это возможно. При желании вы всегда можете перекодировать более высокие уровни до более низких уровней, например, преобразовать шкалы соотношений в порядковые и номинальные данные. Однако предположим, что вы записываете только номинальный или порядковый уровень измерения. В этом случае вы не сможете позже перекодировать его на более высокий уровень, потому что у вас не будет необходимой детализации.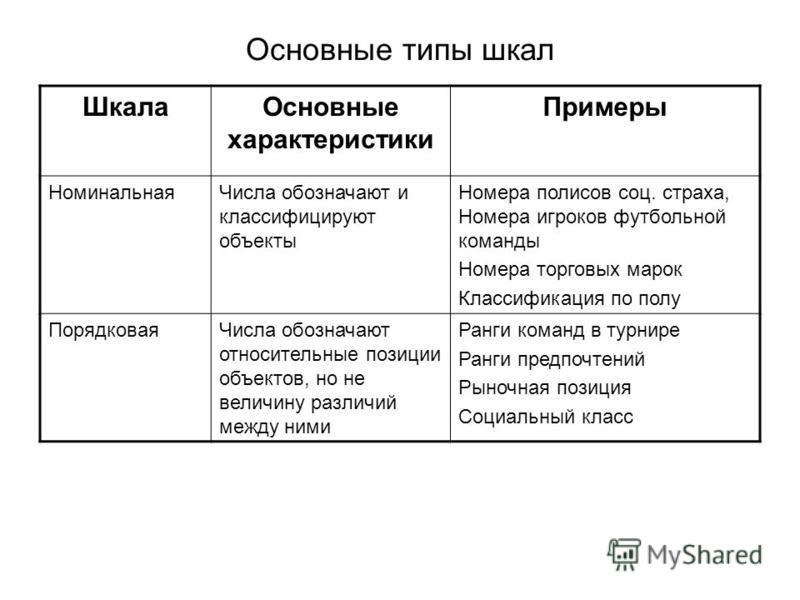




 Шкалы измерений. Основные положения. Термины и определения»
Шкалы измерений. Основные положения. Термины и определения» Шкалы измерений. Основные положения.
Шкалы измерений. Основные положения.
 д. Элементы множеств проявления свойств находятся в определенных
логических соотношениях между собой. Такими соотношениями могут быть
“эквивалентность” (равенство) или “сходство” (близость)
этих элементов, их количественная различимость (“больше”,
“меньше”), допустимость выполнения определенных математических
операций сложения, вычитания, умножения деления с элементами множеств и т.д.
Эти особенности элементов множеств проявления свойств определяют типы
(особенности соответствующих им шкал измерений).
д. Элементы множеств проявления свойств находятся в определенных
логических соотношениях между собой. Такими соотношениями могут быть
“эквивалентность” (равенство) или “сходство” (близость)
этих элементов, их количественная различимость (“больше”,
“меньше”), допустимость выполнения определенных математических
операций сложения, вычитания, умножения деления с элементами множеств и т.д.
Эти особенности элементов множеств проявления свойств определяют типы
(особенности соответствующих им шкал измерений). Примерами таких шкал является шкала классификации (оценки)
цвета объектов по наименованиям (красный, оранжевый, желтый, зеленый и т.д.),
опирающаяся на стандартизованные атласы цветов, систематизированные по
сходству. В таких атласах, выполняющих роль своеобразных эталонов, цвета могут
обозначаться условными номерами (координатами цветами). Измерения в шкале
цветов выполняются путем сравнения при определенном освещении образцов цвета из
атласа с цветом исследуемого объекта и установления эквивалентности их цветов.
Примерами таких шкал является шкала классификации (оценки)
цвета объектов по наименованиям (красный, оранжевый, желтый, зеленый и т.д.),
опирающаяся на стандартизованные атласы цветов, систематизированные по
сходству. В таких атласах, выполняющих роль своеобразных эталонов, цвета могут
обозначаться условными номерами (координатами цветами). Измерения в шкале
цветов выполняются путем сравнения при определенном освещении образцов цвета из
атласа с цветом исследуемого объекта и установления эквивалентности их цветов. Характерным примером шкал порядка являются существующие шкалы чисел
твердости тел, шкалы баллов землетрясений, шкалы баллов ветра, шкала оценки
событий на АЭС и т.п. Узкоспециализированные шкалы порядка широко применяются в
методах испытаний различной продукции.
Характерным примером шкал порядка являются существующие шкалы чисел
твердости тел, шкалы баллов землетрясений, шкалы баллов ветра, шкала оценки
событий на АЭС и т.п. Узкоспециализированные шкалы порядка широко применяются в
методах испытаний различной продукции. Характерный
пример – шкала интервалов времени.
Характерный
пример – шкала интервалов времени.
 Практическое распространение получили логарифмические
шкалы на основе применения систем десятичных и натуральных логарифмов, а также
логарифмов с основанием два.
Практическое распространение получили логарифмические
шкалы на основе применения систем десятичных и натуральных логарифмов, а также
логарифмов с основанием два. В радиотехнике
в качестве опорного чаще всего принимают значения 1 мВт, 1 В, 1 мкВ; в акустике
– 20 мкПа и др. К этим шкалам в общем случае нельзя прямо применять ни одно
арифметическое действие; сложение и вычитание величин, выраженных в значениях
таких шкал, должно проводиться путем нахождения их антилогарифмов, выполнения
необходимых арифметических операций и повторного логарифмирования результата.
В радиотехнике
в качестве опорного чаще всего принимают значения 1 мВт, 1 В, 1 мкВ; в акустике
– 20 мкПа и др. К этим шкалам в общем случае нельзя прямо применять ни одно
арифметическое действие; сложение и вычитание величин, выраженных в значениях
таких шкал, должно проводиться путем нахождения их антилогарифмов, выполнения
необходимых арифметических операций и повторного логарифмирования результата. Такие шкалы строятся по моделям, так
модифицирующим (трансформирующим) результаты измерений свойства стимула, чтобы
было однозначное соответствие между результатом измерений и характеристикой
биологической реакции (гомоморфное отображение множества стимулов на множество
реакций). При этом некоторому подклассу множества стимулов могут
соответствовать эквивалентные реакции.
Такие шкалы строятся по моделям, так
модифицирующим (трансформирующим) результаты измерений свойства стимула, чтобы
было однозначное соответствие между результатом измерений и характеристикой
биологической реакции (гомоморфное отображение множества стимулов на множество
реакций). При этом некоторому подклассу множества стимулов могут
соответствовать эквивалентные реакции.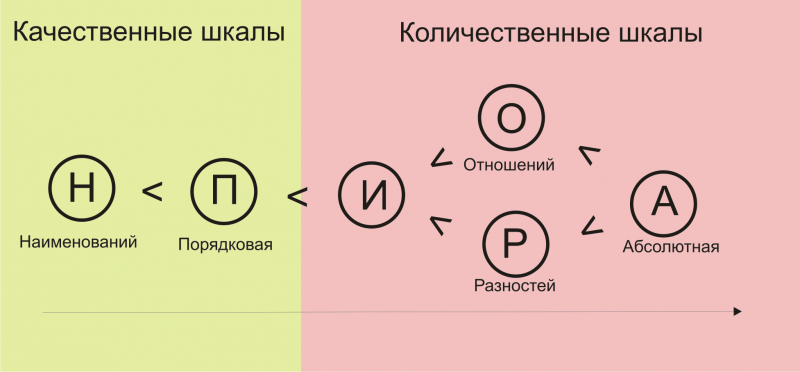
 Эталоны этих шкал измерений могут воспроизводить одну точку шкалы (эталон
массы), некоторый участок шкалы (эталон длины) или практически всю шкалу
(эталон времени).
Эталоны этих шкал измерений могут воспроизводить одну точку шкалы (эталон
массы), некоторый участок шкалы (эталон длины) или практически всю шкалу
(эталон времени).

 п.
п.
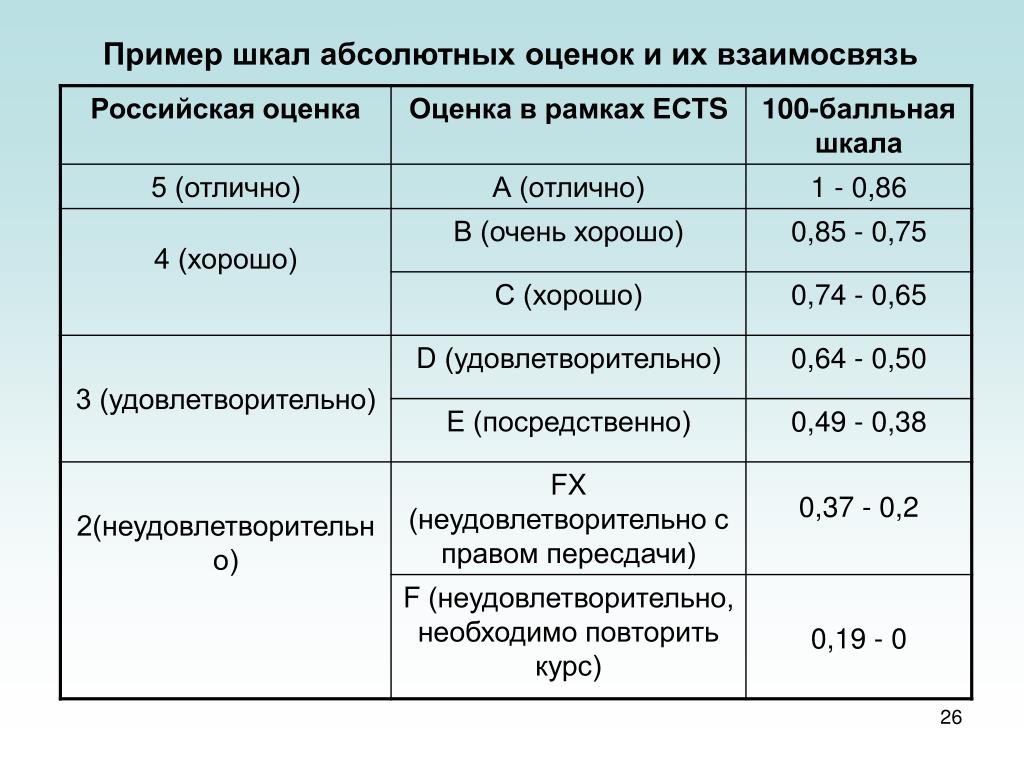
 Например, шкала термодинамических температур – пропорциональная, шкала масс -
аддитивная.
Например, шкала термодинамических температур – пропорциональная, шкала масс -
аддитивная.
 е. шкала, определяемая зависимостью L = log (X/X0), где Х – текущее, а Х0 – принятое по соглашению опорное значение
преобразуемой величины.
е. шкала, определяемая зависимостью L = log (X/X0), где Х – текущее, а Х0 – принятое по соглашению опорное значение
преобразуемой величины.







 п.
п.




 Однако к самим величинам,
описываемым шкалами разностей, это понятие неприменимо. Например, бессмысленно
(невозможно) выражать в процентах погрешность измерений температуры по шкале
Цельсия или погрешность датировки события.
Однако к самим величинам,
описываемым шкалами разностей, это понятие неприменимо. Например, бессмысленно
(невозможно) выражать в процентах погрешность измерений температуры по шкале
Цельсия или погрешность датировки события.


 Передача шкалы (или размера единицы измерений)
Передача шкалы (или размера единицы измерений) Часто при поверке проводится
градуировка поверяемого средства измерений по эталону.
Часто при поверке проводится
градуировка поверяемого средства измерений по эталону. При этом могут
устанавливаться поправки к показаниям градуируемых средств измерений.
При этом могут
устанавливаться поправки к показаниям градуируемых средств измерений.
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
 ..«120»…
..«120»…


 Одинаковые балльные оценки в действительности отображают разный уровень измеряемой переменной. Например, студенты, получившие одинаковые оценки на экзамене, в действительности могут иметь разный уровень знаний.
Одинаковые балльные оценки в действительности отображают разный уровень измеряемой переменной. Например, студенты, получившие одинаковые оценки на экзамене, в действительности могут иметь разный уровень знаний.
 2.4).
2.4).

 Например, значения переменной «Уровень дохода», измеряемой по относительной шкале, можно трансформировать в значения переменной «Категории потребителей по уровню дохода», измеряемой по порядковой шкале (см. табл. 2.3). Подобная трансформация данных, производимая в целях упрощения процедуры анализа и наглядности представления результатов, неизбежно связана с частичной потерей информации и снижением точности расчетов.
Например, значения переменной «Уровень дохода», измеряемой по относительной шкале, можно трансформировать в значения переменной «Категории потребителей по уровню дохода», измеряемой по порядковой шкале (см. табл. 2.3). Подобная трансформация данных, производимая в целях упрощения процедуры анализа и наглядности представления результатов, неизбежно связана с частичной потерей информации и снижением точности расчетов. К таким методам относятся, например, кластерный и факторный анализ.
К таким методам относятся, например, кластерный и факторный анализ.
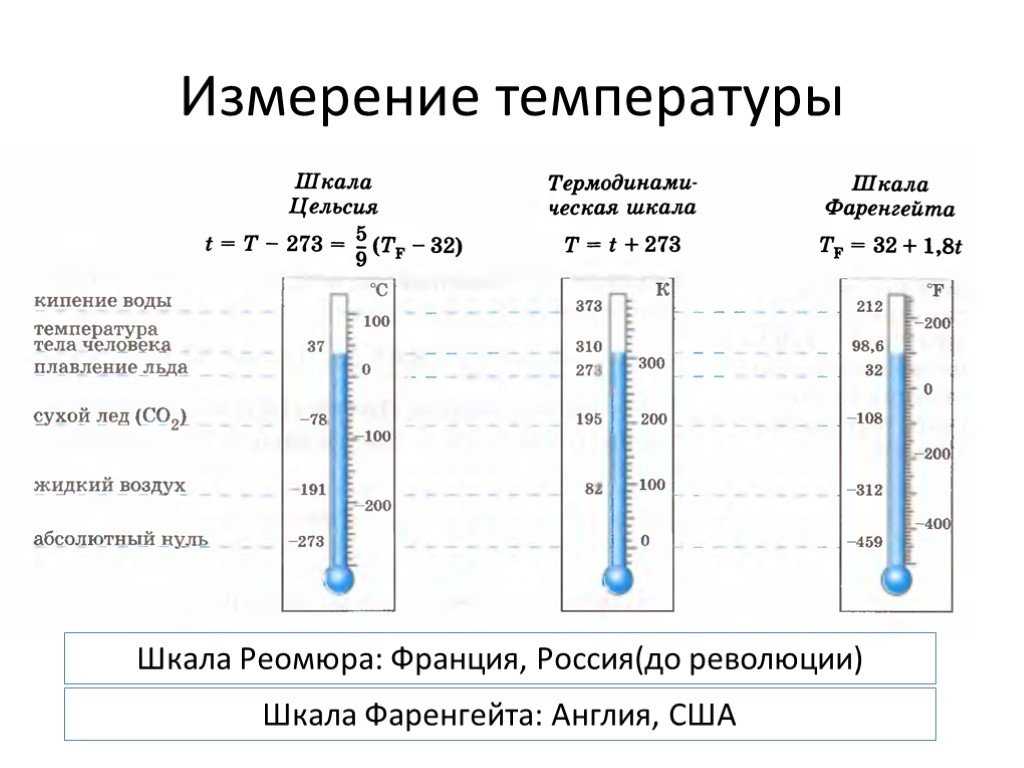 Как отличаются друг от друга переменные, измеряемые по разным типам шкал, относительно возможности произведения арифметических операций и расчета статистических показателей?
Как отличаются друг от друга переменные, измеряемые по разным типам шкал, относительно возможности произведения арифметических операций и расчета статистических показателей? Она характеризует вероятность ошибки, с которой может быть отклонена исходная (нулевая) гипотеза. Если вероятность ошибки мала, исходная гипотеза может быгь отклонена, т.е. ее можно считать неверной (рис. 3.1).
Она характеризует вероятность ошибки, с которой может быть отклонена исходная (нулевая) гипотеза. Если вероятность ошибки мала, исходная гипотеза может быгь отклонена, т.е. ее можно считать неверной (рис. 3.1). При этом Т-тест для одной выборки (One-Sample T-test) используется для сравнения средней величины тестируемого признака в выборке с заданной стандартной величиной.
При этом Т-тест для одной выборки (One-Sample T-test) используется для сравнения средней величины тестируемого признака в выборке с заданной стандартной величиной. рис. 3.2).
рис. 3.2). В файле данных SPSS, сформированном по результатам опроса туристов, отдыхающих в курортной зоне «Баварский лес», эта переменная имеет имя «s_l» и метку переменной «Пол» (см. рис. 2.1,2.3, 2.6).
В файле данных SPSS, сформированном по результатам опроса туристов, отдыхающих в курортной зоне «Баварский лес», эта переменная имеет имя «s_l» и метку переменной «Пол» (см. рис. 2.1,2.3, 2.6).

 6 и 3.7).
6 и 3.7). 3.6.), где нажатием кнопки «ОК» запускается процедура проведения T-теста.
3.6.), где нажатием кнопки «ОК» запускается процедура проведения T-теста. Обратная связь – 161.97.168.212 (0.019 с.)
Обратная связь – 161.97.168.212 (0.019 с.)




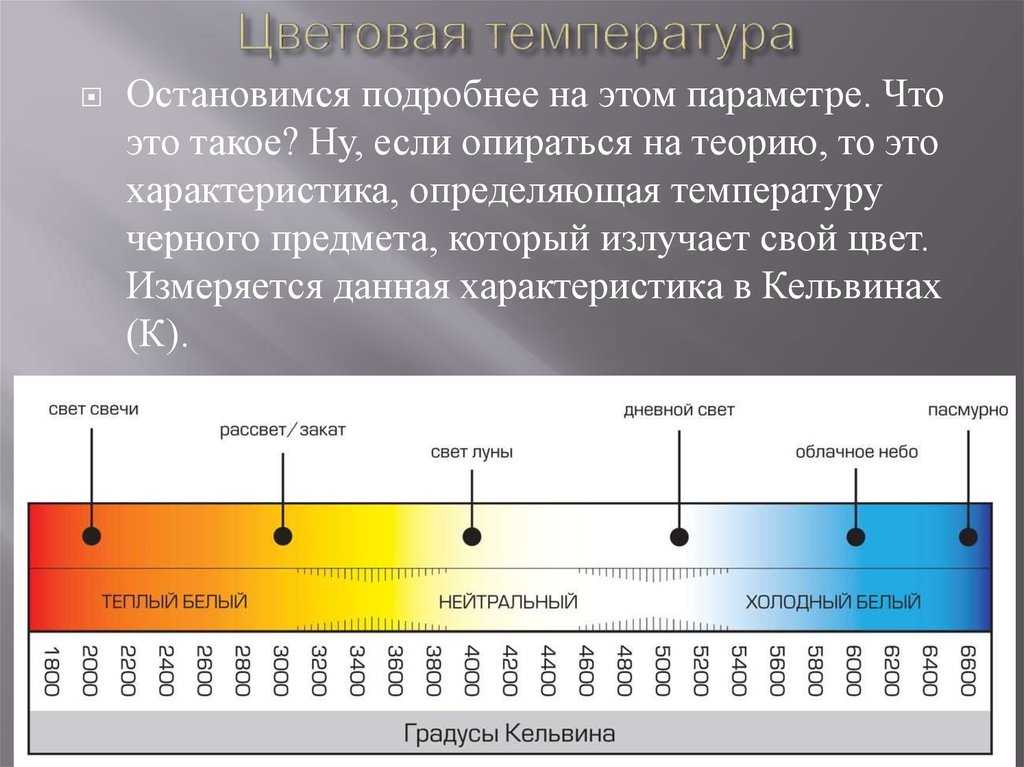 Для этих марок нет необходимости в каком-либо конкретном заказе. Однако, собирая номинальные данные, исследователи проводят анализ на основе соответствующих меток.
Для этих марок нет необходимости в каком-либо конкретном заказе. Однако, собирая номинальные данные, исследователи проводят анализ на основе соответствующих меток.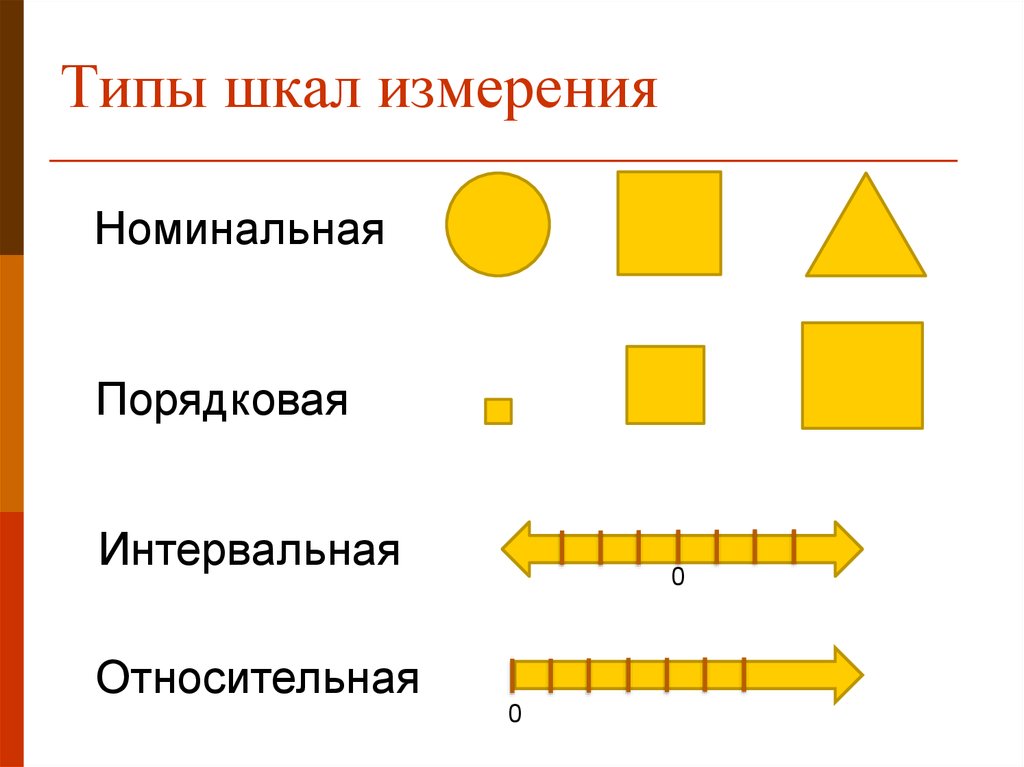

 Интервальная шкала количественно определяет разницу между двумя переменными, тогда как две другие шкалы способны связывать только качественные значения с переменными.
Интервальная шкала количественно определяет разницу между двумя переменными, тогда как две другие шкалы способны связывать только качественные значения с переменными. е. маркировку переменных, значимость порядка переменных и вычисляемую разницу между переменными (которые обычно равноудалены).
е. маркировку переменных, значимость порядка переменных и вычисляемую разницу между переменными (которые обычно равноудалены).