Торус 200 схема: ТОР ТОРУС 200 КЛАССИК схема инструкции

alexxlab | 05.05.2023 | 0 | Разное

schems6

Файл	Краткое описание	Размер
Страницы >>> [17] [16] [15] [14] [13] [12] [11] [10] [9] [8] [7] [6] [5] [4] [3] [2] [1]
Torus200.rar	Описание устройства, а также рекомендации по ремонту инверторного сварочного источника Торус-200, производства компании ТОР. В архиве также содержатся принципиальные схемы, рисунок печатной платы, а также множество фотографий внутренностей источника. Выложил информацию на форуме Power Electronics Valdemar_Br.	14.7 Mb
vuk.pdf	Описание и принципиальная электрическая схема выпрямительного устройства 50ВУК-120. Прислал описание stas yasko.	185 kb
oscillyator_rusich_165. jpg	Принципиальная электрическая схема осциллятора от сварочного аппарата Русич, производства НПО СВАРКА. Исследовал схему и обмоточные данные Wentmiller. Привёл схему в удобочитаемый вид stas yasko.	437 kb
pdg-251.rar	Принципиальная электрическая схема полуавтомата ПДГ-251 в составе сварочного аппарата SELMA производства ОАО Электромашиностроительный завод «Фирма СЭЛМА». Прислал схему Кайсин Андрей.	141 Kb
uvk-7.djvu	Виды внутренностей универсального сварочного осциллятора УВК-7 производства СВАРБИ. Прислал фотографииstas yasko.	50.6Kb
400.TIF	Принципиальная электрическая схема осциллятора от сварочного аппарата “Русич С-400” производства НПО СВАРКА. Прислал схему stas yasko.	50.6Kb
strat200.djvu	Паспорт и принципиальная электрическая схема инверторного сварочного источника СТРАТ-200(160), производства компании ООО Актив, Санкт-Петербург. Прислал документацию Электрод.	188Kb
repgysmi183.pdf	Руководство по ремонту инверторного сварочного источника GYSMI-183, производства французской компании GYS. Руководство на английском языке. Прислал руководство Электрод.	1.31Mb
es1840.djvu	Техническое описание, принципиальные электрические схемы и данные моточных узлов системы электропитания легендарной персоналки ЕС-1840. Прислал документацию Дмитрий.	1.51Mb
feb-150.djvu	Паспорт, техническое описание, а также принципиальные электрические схемы на сварочный полуавтомат типа ФЕБ-150, производства ООО НПО ФЕБ. Прислал документацию Лупандин Семен.	6.79Mb
magma.pdf	Руководство по эксплуатации на для дуговой сварки типа МАГМА-315(У/Р)М, производства ООО НПО ФЕБ. Руководство содержит информацию по техническому обслуживанию и ремонту источника. Прислал документацию Александр Кузьмин.	1.51Mb
feb.rar	Комплект ремонтной технической документации на блоки подачи проволоки ФЕБ-09,(07) и ФЕБ-12,(02), производства ООО НПО ФЕБ. Комплект включает принципиальные электрические схемы, перечни элементов, схемы расположения элементов, а также технические описания. Прислал документацию Борис.	1.69Mb
Service_Manual.pdf	Руководство по ремонту неизвестного китайского UPS мощностью 6-10кВА. Руководство содержит общую блок схему, силовые схемы основных узлов, а также осциллограммы в характерных точках. Сопроводительный текст на английском языке. Прислал руководство Dizel.	394Kb
PCM.rar	Принципиальные электрические схемы, описания, инструкции по ремонту источников бесперебойного питания, производства фирмы PowerCom. Прислал документацию Владимир Анатольевич .	2.22Mb
APC.rar	Принципиальные электрические схемы, описания, инструкции по ремонту источников бесперебойного питания, производства фирмы APC. Перечень схем можно посмотреть здесь. Прислал документацию Владимир Анатольевич.	24.5Mb
POWER_max.rar	Принципиальная электрическая схема инверторного сварочного источника Powermax в форматах PCAD2006 и GIF. Прислал документацию Александр Шевченко. Александр не уточнил производителя этого источника, но, по моим сведениям, аппараты с такими названиями выпускают компании Hypertherm и Castolin Eutectic.	581kb
sm_colt.djvu	Руководство по обслуживанию (Service Manual) и принципиальные электрические схемы инверторных сварочных источников COLT, COLT-1300, PUMA-150, производства итальянской фирмы CEMONT.	612kb
instruykcija_forsag.part1.rar instruykcija_forsag.part2.rar instruykcija_forsag.part3.rar instruykcija_forsag.part4.rar	Очень подробное и качественное описание, а также инструкция по ремонту и настройке сварочных источников постоянного тока Форсаж-315, Форсаж-315М, Форсаж-315GAZ. Документация представлена в формате TGBrowser (браузер прилагается). Прислал документацию Лупандин Семен.	4.74Mb 4.74Mb 4.74Mb 4.74Mb
cemont85a.pdf	Описание и принципиальные электрические схемы инверторного сварочного источника для ручной дуговой сварки CEMONT S1000, производства итальянской фирмы CEMONT. Прислал документацию VladI+.	2.55 Mb
BUSP_2.zip	Качественно нарисованная принципиальная электрическая схема блока управления для полуавтоматической сварки БУСП-2УЗ.1.. Схема представлена в формате программы sPlan 6.0, а также в графическом формате JPG. Нарисовал и прислал схему Leonid Belasheevs’kyy.	538 Kb
Страницы >>> [17] [16] [15] [14] [13] [12] [11] [10] [9] [8] [7] [6] [5] [4] [3] [2] [1]

Инвертор сварочный. Принцип работы. | «СМС». Строительное оборудование по ценам производителей.

Инвертор сварочный получает все большее распространение. Это связано в первую очередь с их высокими характеристиками, малой массой и габаритами, по сравнению с классическими сварочными трансформаторами. При этом принцип действия таких аппаратов для многих специалистов остается загадкой.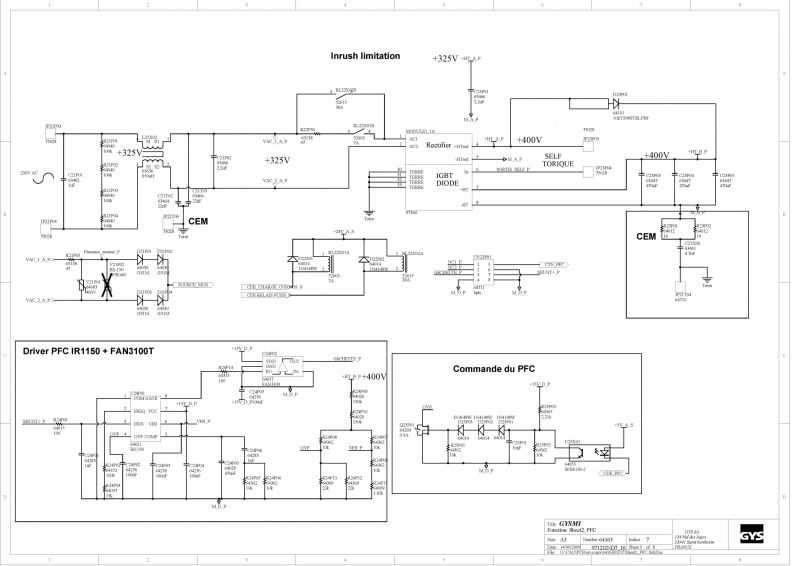

Купить инвертор сварочный

На самом деле работа сварочного инвертора не сильно отличается от классического сварочного аппарата на основе трансформатора и выпрямителя. Для получения больших значений тока в обоих приборах применяется понижающий трансформатор, преобразующий высокое значение входного напряжения в напряжение сварочного электрода. Отличие заключается в том, что на трансформатор инвертора подается не сетевое напряжение с промышленной частотой 50Гц, а более высокочастотное. Обычно частота преобразования находится в районе 400Гц. Использование переменного напряжения такой частоты позволяет уменьшить размеры и массу применяемого трансформатора. Это сказывается и на габаритах всего аппарата. Для получения необходимых характеристик напряжения используется электронная схема, состоящая из двух частей – выпрямителя и инвертора. Первый выполняет функции получения постоянного напряжения. Второй преобразует это напряжение в переменное с нужной частотой. Такой процесс носит название инвертирования.

Для его реализации используются мощные транзисторы, являющиеся последними достижениями электронной техники. Обладая множеством достоинств, такое решение не избежало недостатков. Главным из них является нагрев силовых электронных приборов, который снижает продолжительность непрерывной работы аппарата.

Инвертор Торус-200

Питающая сеть: 165-253 В, 50 Гц

Диапазон регулирования сварочного тока, А: 20-220

Мощность макс, кВт: 7,2

Диаметр электрода, мм: 2-5

Процент времени работы при 200 А, ПВ: 100%

Напряжение холостого хода, В: 65

Сварка TIG: да

Индикатор сварочного тока: Нет

Габаритные размеры, мм: 300х186х125

Масса, кг: 5,1

Быстрый просмотр

Инвертор Торус-165

Питающая сеть: 165…242 В, 50 Гц

Максимальная потребляемая мощность, кВт 4,8: 4,8

Характер сварочного тока: постоянный

Регуляция сварочного тока: плавная

Диапазон сварочного тока, А: 30–165

Процент времени работы при токе до 140 А, ПВ: 100%

Напряжение холостого хода, В: 65

Вес, кг: 4,6

Размеры, мм: 125х190х270

Быстрый просмотр

Сварочный аппарат инверторный САИ 220

Диаметр электрода, мм: 1. 6-5.0

Пределы регул. свар. тока, А: 10-220

Напряжение, В: 220

Вес, кг: 5

Напряжение холостого хода, В: 80

Быстрый просмотр

Сварочный аппарат инверторный САИ 190

Диаметр электрода, мм: 1.6-5.0

Пределы регул. свар. тока, А: 10-190

Напряжение, В: 220

Вес, кг: 4.7

Напряжение холостого хода, В: 80

Быстрый просмотр

Сварочный аппарат инверторный САИ 160

Напряжение сети, В: 220±10%

Максимальный потребляемый ток, А: 22

Напряжение холостого хода, В: 80

Напряжение дуги, В: 26

Диапазон регулирования сварочного тока, А: 10–160

Продолжительность нагружения, %: 40% 160А

Максимальный диаметр электрода, мм: 3,2–4

Класс защиты: IP21

Масса, кг: 4,5

Быстрый просмотр

Master ММА-250

Диаметр электрода, мм: 1. 6 — 5.0

Пределы регул. свар. тока, А: 20-250

Напряжение, В: 380

Мощность, кВт: 9.4

Вес, кг: 19

Сила тока, А:

Напряжение холостого хода, В: 70

Габаритные размеры, мм: 480х204х303

Напряжение, В: 380

Быстрый просмотр

Master 252

Диаметр электрода, мм: 1.6-5.0

Пределы регул. свар. тока, А: 20-250

Напряжение, В: 220

Мощность, кВт: 9.4

Вес, кг: 17.5

Напряжение холостого хода, В: 69

Габаритные размеры, мм: 480х200х300

Быстрый просмотр

Master 202 с комплектом

Диаметр электрода, мм: 1.6-5.0

Пределы регул. свар. тока, А: 30-200

Напряжение, В: 220

Мощность, кВт: 7

Вес, кг: 8

Быстрый просмотр

Master 162 с комплектом без кейса

Напряжение питающей сети, В: 220В ± 15%

Первичный ток, А: 33

Номинальный сварочный ток, А: ПВ % t=25°C

Напряжение холостого хода, В: 62

Плавная регулировка тока, А: 30-160

Степень защиты: IP21

Класс изоляции: Н

Встроенная термозащита: есть

Габариты, мм: 290 x 132 х 203

Масса источника, кг: 5,5

Быстрый просмотр

Master 162 с комплектом

Напряжение питания: 180-240 V50 Hz

Напряжение холостого хода, В: 62

Диапазон сварочного тока, А: 20-160

Номинальное сварочное напряжение: 26,4

Продолжительность нагрузки (ПН, %): 60

Вес, кг: 5,5

Быстрый просмотр

IN 160-230V-160A D=4,0mm в пластиковом кейсе

Диаметр электрода, мм: 1. 6-4.0

Пределы регул. свар. тока, А: 10-160

Напряжение, В: 75

Мощность, кВт: 5

Вес, кг: 4.2

Габаритные размеры, мм: 420х170х370

Напряжение, В: 220

Быстрый просмотр

GYSMI 161

Диаметр электрода, мм: 1.6-4.0

Пределы регул. свар. тока, А: 10-160

Напряжение, В: 75

Мощность, кВт: 3.5

Вес, кг: 4.1

Быстрый просмотр

GYSMI 131 DC

Диаметр электрода, мм: 1.6-3.2

Пределы регул. свар. тока, А: 10-130

Напряжение, В: 80

Мощность, кВт: 5

Вес, кг: 3

Габаритные размеры, мм: 125х240х170

Напряжение, В: 220

Быстрый просмотр

Последним функциональным устройством инвертора является выходной выпрямитель. Его использование обусловлено невозможностью применения высокочастотного напряжения для процессов сварки.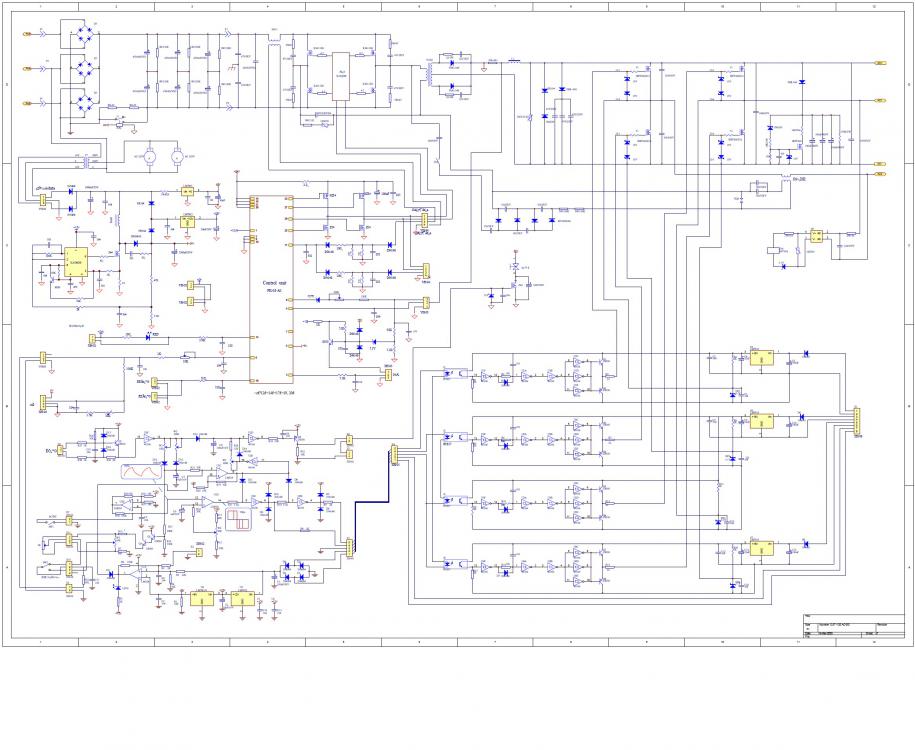 Именно по этому инвертор сварочный относится к классу аппаратов, работающих на постоянном токе. Применение электронной схемы из выпрямителя и инвертора, поначалу кажется усложнением конструкции. Тем не менее, эта связка, кроме выполнения главной задачи – преобразования напряжения, позволяет получить и некоторые дополнительные функциональные возможности. Например, она обеспечивает плавное регулирование сварочного тока, позволяет реализовывать процесс зажигания дуги на малых значениях тока и многое другое. В итоге некоторое усложнение схемы оборачивается уменьшением массы и габаритов и придает новые свойства оборудованию.

Принцип преобразования с использованием инвертора сегодня получает все большее распространение. Подобным образом устроены импульсные блоки питания, автомобильные преобразователи 12/220 вольт и многие другие устройства. Отличаются они лишь некоторыми характеристиками.

Симметричный тор Мэдисона (MST) – Висконсинская лаборатория физики плазмы – UW–Madison

Симметричный тор Мэдисона (MST) производит тороидальную плазму, как правило, либо в пинче с обращенным полем (RFP), либо в геометрии токамака с низким коэффициентом безопасности. Плазма RFP сама по себе представляет собой систему, которая одновременно демонстрирует черты передовых процессов науки о плазме пересоединения, турбулентности, возбуждения частиц, динамо и формирования когерентной структуры. Он также может обеспечить высокотемпературную плазму термоядерного класса с временем удержания, аналогичным токамаку сопоставимого размера. Устройство MST предоставляет пользователям доступ к хорошо охарактеризованной тороидальной плазме с комплексным набором диагностических средств.

Типичная плотность электронов находится в диапазоне 0,5 – 1,5 x10 ¹⁹ m ^-3 с температурой электронов в диапазоне 200 – 1800 эВ в зависимости от типа разряда. Разряды обычно длятся 30–60 мс с интервалом между разрядами около 3 минут. Обычно в течение 4-дневной беговой недели ежедневно делается более 100 снимков.

Конструкция MST уникальна тем, что имеет алюминиевый корпус, который служит как вакуумным сосудом, так и уравновешивающим магнитом (малый и большой радиусы плазмы, a=0,5 м и R=1,5 м). Полоидальное поле создается широким диапазоном тока плазмы (30-500 кА), управляемого индуктивно. Омический нагрев до 10 МВт обеспечивается за счет рассеяния тока плазмы. Внешнее тороидальное поле до 0,3 Тл создается одновитковым током в оболочке.

Плазма обычно заправляется дейтерием с использованием газовой затяжки, но доступны различные виды газа, включая водород и гелий. Для подачи инертных газов, таких как гелий и аргон, доступен отдельный инжектор газовой затяжки. Плазменное взаимодействие с ограничителями, плитками и стенкой сосуда приводит к появлению второстепенных частиц, включая углерод, бор, кислород, азот и алюминий.

Основные параметры, достигнутые в базовой работе МСТ: ρ _i ∼ ρ _s ≈ 0,2-5 см, число Лундквиста S ~ 10 ^4-7  (на основе равновесия B), поток плазмы от 0–20 км/с (самогенерируемый) до 50 км/с (смещенный электрод) со звуковым числом Маха M _s  ∼ 0,5 и альфвеновским числом Маха M _А ∼ 0,1. Добавление внешних источников плазмы, таких как инжекция компактного тора (CT), сможет значительно изменить эти параметры.

Это элемент-гармошка с набором кнопок, которые открывают и закрывают соответствующие панели содержимого.

MST обладает передовым набором средств диагностики плазмы и управления плазмой мирового класса, которые были разработаны в рамках программы проверки работоспособности RFP.

Импульсное параллельное возбуждение тока

PPCD — это метод управления профилем тока, используемый для подавления развития резонансных тиринг-мод в пинчевой плазме с обращенным полем. Время удержания энергии увеличивается на порядок до 10—15 мс, температура электронов достигает 1—2 кэВ, а температура ионов может достигать 1 кэВ (в зависимости от условий запуска). В этих разрядах механизмы переноса больше не связаны со стохастичностью силовых линий, как в стандартных разрядах RFP. Из-за слабого тороидального магнитного поля эффекты тороидальности слабее, что приводит к ионным банановым орбитам порядка радиуса ионного гироскопа. Ионный транспорт, как правило, доминирует над классическим транспортом в ядре. Градиент плотности на краю становится достаточно крутым, чтобы дестабилизировать дрейфовые волны из-за неустойчивости моды захваченных электронов.

Программируемые источники питания

MST имеет новые сильноточные программируемые источники питания для управления током плазмы и работы тороидального поля, поддерживаемые Национальным научным фондом. Эти системы значительно расширяют диапазон достижимых безразмерных параметров плазмы.

Мощный инжектор нейтрального луча

Мощный инжектор нейтрального луча мощностью 1 МВт производит значительное количество быстрых ионов. Нейтралы водорода или дейтерия могут вводиться в плазму по касательной, чтобы создать значительную популяцию быстрых ионов в ядре. Эта инъекция приводит к нагреву, увеличению вращения, производству термоядерных нейтронов и гамма-излучения, а также к стимуляции нестабильности энергичных частиц.

Резонансные магнитные возмущения

Существует также седельная катушка с обратной связью, которая позволяет применять резонансные и нерезонансные магнитные возмущения, влияющие на магнитное пересоединение и поток плазмы. Система используется для блокировки спиральной плазмы в произвольной ориентации, чтобы можно было проводить исследования с использованием оптической, рентгеновской и лучевой диагностики.

MST обладает передовым набором средств диагностики плазмы и управления плазмой мирового класса, которые были разработаны в рамках программы проверки работоспособности RFP.

Томсоновское рассеяние

Диагностика многоточечного рассеяния Томсона обеспечивает измерение температуры электронов в 21 пространственной точке на малом радиусе. Во время каждого разряда MST можно получить тридцать полных профилей температуры электронов с переменной задержкой между каждым профилем. В типичной операции используются лазеры Nd:YAG с двойной импульсной вспышкой для обеспечения частоты дискретизации 2–25 кГц.

Спектроскопия рекомбинации с перезарядкой

Диагностический нейтральный пучок 50 кВ используется для стимуляции излучения ближнего УФ. Спектрометр с высокоэффективной решеткой и детекторами на фотоумножителях обеспечивает измерения CHERS плотности, скорости и температуры примесных ионов с временным разрешением 100 кГц.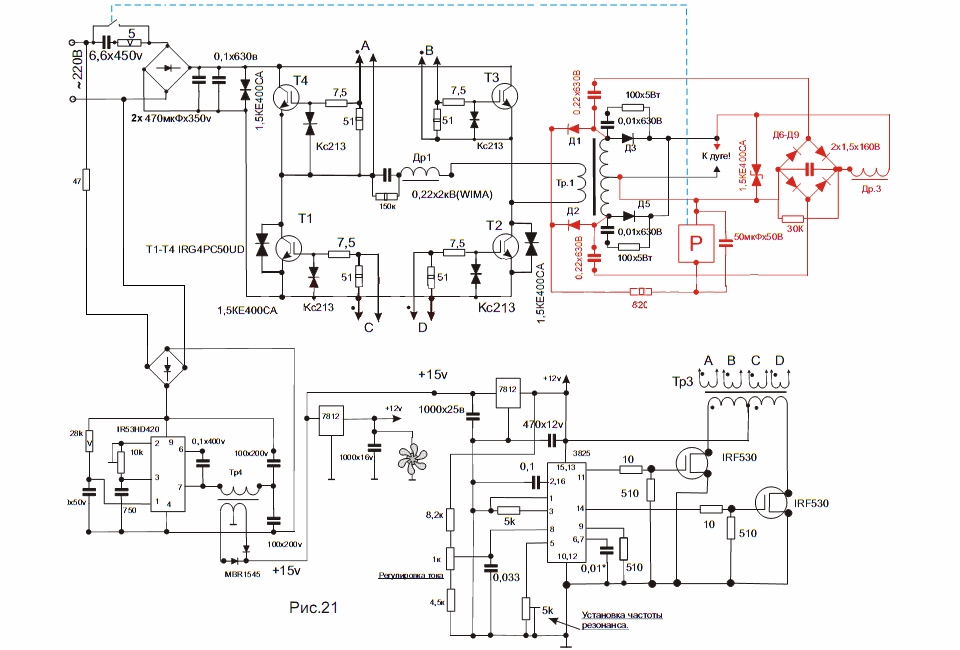 Доступны как полоидальные, так и тороидальные виды.

Движущийся эффект Старка

Эмиссия нейтрального водорода от того же диагностического нейтрального луча используется для измерения магнитного поля ядра с использованием спектральной MSE. Эти измерения обычно используются в ограничивающих расчетах магнитного равновесия.

Мягкая рентгеновская томография

Четыре камеры SXR просматривают 40 линий визирования, охватывающих полоидальную плоскость. Каждая линия обзора включает двухцветные измерения яркости рентгеновского излучения, которые используются для томографической реконструкции профиля температуры электронов и в качестве ограничения магнитного равновесия. Измерения абсолютной яркости в сочетании с отдельными измерениями температуры и плотности электронов и содержания примесей дают достаточную информацию для определения профиля эффективного заряда ионов.

Детектор быстрого рентгеновского излучения

Детектор FXR представляет собой спектрометр мягкого рентгеновского излучения с высоким временным разрешением, который измеряет возбуждение электронов за счет испускаемого тормозного излучения. Детектор представляет собой кремниевый лавинный фотодиод ² размером 10 мм. Выходной сигнал детектора подается на формирующий усилитель Гаусса с временем формирования 20 нс и оцифровывается на частоте 500 МГц.

Рентгеновская спектроскопия

Двенадцать детекторов жесткого рентгеновского излучения с разрешением 2 кэВ и шесть детекторов мягкого рентгеновского излучения с разрешением 0,45 кэВ могут быть установлены на 17 возможных хордах, просматривающих полоидальную плоскость. Обнаружение фотонов использует анализ амплитуды импульса с использованием времени формирования 2,4 микросекунды или 240 наносекунд и оцифровывает на частоте 100 МГц с типичным временным разрешением до 1 кГц. Детекторы используются для подготовки рентгеновской спектроскопии для определения характеристик популяций быстрых электронов, которые развиваются во время событий пересоединения. 92. Система сцинтиллятор-фотоумножитель используется для измерения глобальной скорости нейтронов.

Усовершенствованный анализатор нейтральных частиц

ANPA способен одновременно измерять быстрые нейтралы водорода и дейтерия, которые образуются, когда быстрые ионы, введенные пучком нейтральных частиц мощностью 1 МВт, подвергаются перезарядке с тепловыми ионами. ANPA может измерять быстрые нейтральные энергии в диапазоне от 25 до 50 кэВ с временным разрешением 10 микросекунд.

Датчики

Хотя они ограничены слаботочными разрядами, доступны различные вставные датчики, включая датчики Ленгмюра для измерения краевой плотности и температуры, емкостные датчики для измерения радиального профиля потенциала плазмы и бронированные магнитные датчики, которые позволяют вводить плотный массив кубов с b-точками примерно до половины радиуса тора.

Интерферометрия-поляриметрия

Система интерферометра-поляриметра в дальнем инфракрасном диапазоне (FIR), разработанная в сотрудничестве с Калифорнийским университетом в Лос-Анджелесе, обеспечивает быстрое реагирование и измерения флуктуаций с высоким разрешением. Система гетеродинного детектирования обеспечивает широкую полосу пропускания (до ∼1 МГц) для измерения динамических изменений равновесия плазмы, а также высокочастотных флуктуаций хордовой электронной плотности и угла Фарадея.

Зонд пучка тяжелых ионов

Зонд пучка тяжелых ионов (HIBP), разработанный Xantho Technologies, LLC, вводит пучок однозарядных ионов в плазму. Эти первичные ионы ионизируются до состояния более высокого заряда электронным ударом, что приводит к вторичной популяции двухзарядных ионов, которые отделены от первичных ионов внутренним магнитным полем плазмы. Обнаружение потока вторичных ионов дает информацию о потенциале плазмы ядра, флуктуациях потенциала и флуктуациях электронной плотности.

Мягкая рентгеновская камера Multi-Energy

Мягкая рентгеновская камера Pilatus 3, предоставленная Принстонской лабораторией физики плазмы, в настоящее время установлена ​​на радиальном виде тора. Конструкция камеры с точечным отверстием обеспечивает 487 линий обзора в полоидальном поперечном сечении. Каждый пиксель обеспечивает программируемый в цифровом виде энергетический порог для создания диагностики, чувствительной к нескольким диапазонам рентгеновского излучения. Текущая рабочая схема использует приращения всего 200 эВ, чтобы покрыть энергетические пороги между 2 – 20 кэВ. Камера имеет время интегрирования 1 мс и время считывания 1 мс для частоты кадров 500 Гц.

Конформные блоки тора и уравнения Казимира в канале ожерелья

Конформные блоки тора и уравнения Казимира в канале ожерелья

Скачать PDF

Скачать PDF

• Обычная статья – Теоретическая физика
• Открытый доступ
• Опубликовано: 14 октября 2022 г.

• Константин Алкалаев ¹ ,
• Семен Мандрыгин ¹ и
• Михаил Павлов ¹  

Журнал физики высоких энергий том 2022 , Номер статьи: 91 (2022) Процитировать эту статью

• 49 доступов

• 1 Альтметрика

• Сведения о показателях

Аннотация

Рассматривается конформная блочная декомпозиция в произвольных обменных каналах двумерной конформной теории поля на торе. Каналы описываются диаграммами, построенными из замкнутого контура с внешними ветвями (поддиаграмма ожерелья) и трехвалентными вершинами, образующими трехвалентные деревья, прикрепленные к ожерелью. Тогда конформный блок n -точечного тора в любом канале можно получить, воздействуя рядом операторов OPE на k -точечный блок тора в канале ожерелья на k = 1 , … , n . Сосредоточив внимание на канале ожерелья, мы переходим к режиму больших c , где алгебра Вирасоро усекается до sl (2 , ℝ) подалгебры, и получаем систему уравнений Казимира для соответствующих k -точечный глобальный конформный блок. В плоском пределе, когда модульный параметр тора q → 0, мы явно находим уравнения Казимира на плоскости, которые определяют ( k + 2)-точечный глобальный конформный блок в гребенчатом канале. Наконец, мы формулируем общую схему для нахождения уравнений Казимира для глобальных блоков тора в произвольных каналах.

Скачайте, чтобы прочитать полный текст статьи

Каталожные номера

1. А.А. Белавин, А.М. Поляков и А.Б. Замолодчиков, Бесконечная конформная симметрия в двумерной квантовой теории поля , Nucl. физ. В 241 (1984) 333 [ВДОХНОВЕНИЕ].

   Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

2. Э.П. Verlinde, Правила слияния и модульные преобразования в двумерной конформной теории поля , Nucl. физ. B 300 (1988) 360 [ВДОХНОВЕНИЕ].

   Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

3. Д. Поланд, С. Рычков и А. Вичи, Конформный бутстрап: теория, численные методы и приложения , Ред. Мод. физ. 91 (2019) 015002 [arXiv:1805. 04405] [INSPIRE].

4. С. Кольер, Ю.-Х. Лин и С. Инь, Modular Bootstrap Revisited , JHEP 09 (2018) 061 [arXiv:1608.06241] [INSPIRE].

   Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

5. Т. Хартман, Д. Мазак, Д. Симмонс-Даффин и А. Жибоедов, Белая книга Snowmass: Аналитический конформный бутстрап , in Летнее исследование Snowmass 2022 , Сиэтл, США, 17–26 июля 2022 г. [arXiv:2202.11012] [INSPIRE].

6. А. Бисси, А. Синха и X. Чжоу, Избранные темы в аналитическом конформном бутстрапе: управляемое путешествие , arXiv: 2202.08475 [INSPIRE].

7. Т. Хартман, Энтропия запутывания при большом центральном заряде , arXiv:1303.6955 [INSPIRE].

8. А.Л. Фитцпатрик, Дж. Каплан и М.Т. Уолтерс, . Универсальность физики рекламы на больших расстояниях на базе CFT Bootstrap , JHEP 08 (2014) 145 [arXiv:1403. 6829] [INSPIRE].

   Артикул ОБЪЯВЛЕНИЯ Google Scholar

9. Э. Хиджано, П. Краус и Р. Снайвли, Мировой подход к полуклассическим конформным блокам , JHEP 07 (2015) 131 [arXiv:1501.02260] [INSPIRE].

   Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

10. К.Б. Алкалаев и В.А. Белавин, Классические конформные блоки через соответствие AdS/CFT , JHEP 08 (2015) 049 [arXiv:1504.05943] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

11. Э. Хиджано, П. Краус, Э. Перлмуттер и Р. Снайвли, Новый взгляд на диаграммы Виттена: геометрия конформных блоков AdS , JHEP 01 (2018X) :050arPIRE 146 ].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

12. E. Hijano, P. Kraus, E. Perlmutter and R. Snivel, Полуклассические блоки Virasoro от ADS ₃ Гравита , JHEP 12 (2015) (2015) (2015) (2015) (2015) (2015) (2015) (2015) (2015) (2015). ВДОХНОВЛЯТЬ].

    МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

13. П. Банерджи, С. Датта и Р. Синха, Конформные блоки высших точек и энтропия запутанности в тяжелых состояниях , JHEP 05 (2016) 127 [arXiv:1601.06794] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

14. Дж. Л. Карди, Операторное содержание двумерных конформно-инвариантных теорий , Nucl. физ. B 270 (1986) 186 [ВДОХНОВЕНИЕ].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

15. К. Ициксон и Дж. Б. Зубер, Двумерные конформно-инвариантные теории на торе , Nucl. физ. B 275 (1986) 580 [ВДОХНОВЕНИЕ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

16. Т. Эгучи и Х. Оогури, Конформные и текущие алгебры на общей римановой поверхности , Nucl. физ. B 282 (1987) 308 [ВДОХНОВЕНИЕ].

17. М. Чо, С. Кольер и X. Инь, Рекурсивные представления произвольных конформных блоков Вирасоро , JHEP 04 (2019) 018 [arXiv:1703.09805] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

18. П. Краус, А. Малони, Х. Максфилд, Г. С. Нг и Дж.-к. Wu, Диаграммы Виттена для конформных блоков тора , JHEP 09 (2017) 149 [arXiv:1706.00047] [INSPIRE].

19. К.Б. Алкалаев и В. А. Белавин, Голографические двойники конформных блоков тора большого c , JHEP 10 (2017) 140 [arXiv:1707.09311] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

20. J. Ramos Cabezas, Квазиклассические блоки тора в t-канале , JHEP 08 (2020) 151 [arXiv:2005.04128] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

21. М. Герберсхаген, Методы монодромии для конформных блоков тора и энтропия запутанности при большом центральном заряде

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

22. Дж. Д. Браун и М. Хенно, Центральные заряды в канонической реализации асимптотических симметрий: пример из трехмерной гравитации , Commun. Мат. физ. 104 (1986) 207 [ВДОХНОВЕНИЕ].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

23. Л. Хадаш, З. Яскольский и П. Суханек, Рекурсивное представление одноточечного конформного блока тора , JHEP 01 (2010) 063 [arXiv:0911]INSRE53].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

24. Ф. А. Долан и Х. Осборн, Конформные парциальные волны и разложение операторного произведения , Nucl. физ. B 678 (2004) 491 [hep-th/0309180] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

25. Ф. А. Долан и Х. Осборн, Конформные парциальные волны: дополнительные математические результаты , arXiv:1108.6194 [INSPIRE].

26. Y. Gobeil, A. Maloney, GS Ng and J.-q. Wu, Тепловые конформные блоки , SciPost Phys. 7 (2019) 015 [arXiv:1802.10537] [ВДОХНОВЕНИЕ].

27. К. Алкалаев и В. Белавин, Блоки суперконформного тора Large-c , JHEP 08 (2018) 042 [arXiv:1805.12585] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

28. В. Розенхаус, Многоточечные конформные блоки в гребенчатом канале , JHEP 02 (2019) 142 [arXiv:1810.03244] [ВДОХНОВЕНИЕ].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

29. Ж.-Ф. Фортин, В. Ма и В. Скиба, Конформные блоки высших точек в гребенчатом канале , JHEP 07 (2020) 213 [arXiv:1911.11046] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

30. А. Замолодчиков, Двумерная конформная симметрия и критические четырехспиновые корреляционные функции в модели Ашкина-Теллера , ж. Эксп. Теор. Физ. 90 (1986) 1808.

    Google Scholar

31. А.Л. Фитцпатрик, Дж. Каплан и М.Т. Уолтерс, Конформные блоки Вирасоро и термальность из классических фоновых полей , JHEP 11 (2015) 200 [arXiv:1501.05315] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

32. К.Б. Алкалаев и В.А. Белавина, От глобального к тяжелому-легкому: 5-точечные конформные блоки , JHEP 03 (2016) 184 [arXiv:1512.07627] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

33. К.Б. Алкалаев, Р.В. Гейко и В.А. Раппопорт, Различные квазиклассические пределы конформных блоков тора , JHEP 04 (2017) 070 [arXiv:1612.05891] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

34. E. Perlmutter, Конформные блоки Вирасоро в закрытой форме , JHEP 08 (2015) 088 [arXiv:1502.07742] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

35. Г. Фелдер и Р. Сильвотти, Модульная ковариация минимальных модельных корреляционных функций , Общ. Мат. физ. 123 (1989) 1 [ВДОХНОВЕНИЕ].

36. П. Краус и А. Малони, Формула Карди для трехточечных коэффициентов или откуда у черной дыры появились пятна , JHEP 05 (2017) 160 [arXiv:1608.03284] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

37. Э.М. Брем, Д. Дас и С. Датта, Зондирование термальности за диагональю , Phys. Ред. D 98 (2018) 126015 [arXiv:1804.07924] [INSPIRE].

38. П. Менотти, Классические конформные блоки Тор , Мод. физ. лат. A 33 (2018) 1850166 [arXiv:1805.07788] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

39. M. Piatek, Классический конформный блок, n = 2 ^* Скрученные суперпотенциал и параметр Accessestion уравнения LAMé , JHEP 03 (2014) 124 (2014) 124 (2014) 124 (2014) 124 (2014) 124 (2014) 124 [2014) ].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

40. Ж.-Ф. Фортин, В.-Дж. Ма и В. Скиба, Все глобальные одно- и двумерные конформные блоки высших точек , arXiv: 2009.07674 [INSPIRE].

41. Ж.-Ф. Фортин, В.-Дж. Ма и В. Скиба, Шеститочечные конформные блоки в канале снежинки , JHEP 11 (2020) 147 [arXiv:2004.02824] [INSPIRE].

    Артикул ОБЪЯВЛЕНИЯ Google Scholar

42. Ж. -Ф. Фортин, В.-Дж. Ма и В. Скиба, Семиточечные конформные блоки в расширенном канале снежинки и за его пределами , Phys. Ред. D 102 (2020) 125007 [arXiv:2006.13964] [INSPIRE].

43. Д. Симмонс-Даффин, The Conformal Bootstrap , in Институт перспективных теоретических исследований в физике элементарных частиц: новые границы в полях и струнах , World Scientific (2017), стр. 1–74 [DOI] [ архив: 1602.07982] [ВДОХНОВЕНИЕ].

44. Р. Блюменхаген и Э. Плаушинн, Введение в конформную теорию поля: с приложениями к теории струн , Springer (2009) [DOI].

45. JD Qualls, Lectures on Conformal Field Theory , arXiv:1511.04074 [INSPIRE].

46. Д. Симмонс-Даффин, Проекторы, тени и конформные блоки , JHEP 04 (2014) 146 [arXiv:1204.3894] [INSPIRE].

47. М. Исаченков и В. Шомерус, Суперинтегрируемость d-мерных конформных блоков , Phys. Преподобный Летт. 117 (2016) 071602 [arXiv:1602.01858] [INSPIRE].

48. А. Бхатта, П. Раман и Н. В. Сурьянараяна, Голографические конформные парциальные волны как гравитационные открытые сети Вильсона , JHEP 06 (2016) 119 [arXiv: 119602].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

49. А. Л. Фитцпатрик, Дж. Каплан, Д. Ли и Дж. Ван, Точные блоки Вирасоро из линий Уилсона и независимых от фона операторов , JHEP 07 (2017) 092 [ar2INS.63PIRE] ].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

50. М. Бескен, А. Хегде, Э. Хиджано и П. Краус, Голографические конформные блоки из взаимодействующих линий Вильсона , JHEP 08 (2016) 099 [arXiv:1603. 07317] [ВДОХНОВЕНИЕ].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

51. Ю. Хикида и Т. Уэтоко, Конформные блоки из линий Вильсона с петлевыми поправками , Phys. Ред. D 97 (2018) 086014 [arXiv:1801.08549] [INSPIRE].

52. Ю. Хикида и Т. Уэтоко, Суперконформные блоки из линий Вильсона с петлевыми поправками , JHEP 08 (2018) 101 [arXiv:1806.05836] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

53. К. Алкалаев и В. Белавин, Подробнее о тороидальных сетях Вильсона и торических блоках , JHEP 11 (2020) 121 [arXiv:2007.10494] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

54. А. Кастро, П. Сабелла-Гарнье и К. Жуковски, Гравитационные линии Вильсона в 3D de Sitter , JHEP 07 (2020) 202 [arXiv:2001.09998] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

55. В. Белавин и Дж. Р. Кабесас, Построение линий Вильсона из \( \mathfrak{osp} \)(1 | 2) конформных блоков , arXiv:2204.12149 [INSPIRE].

56. К.Б. Алкалаев и В.А. Белавин, Голографическая интерпретация одноточечного тороидального блока в квазиклассическом пределе , JHEP 06 (2016) 183 [arXiv:1603.08440] [INSPIRE].

    Артикул МАТЕМАТИКА ОБЪЯВЛЕНИЯ Google Scholar

Ссылки на скачивание

Информация об авторе

Авторы и организации

1. И.Е. Тамма Кафедра теоретической физики им. П.Н. Лебедева, 119991, Москва, Россия

   Константин Алкалаев, Семен Мандрыгин и Михаил Павлов

Авторы

1. Константин Алкалаев

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

2. Семен Мандрыгин

   Посмотреть публикации автора

   Вы также можете искать этого автора в PubMed Google Scholar

3. Михаил Павлов

   Посмотреть публикации автора

   Вы также можете искать этого автора в PubMed Google Академия

Автор, ответственный за переписку

Константин Алкалаев.