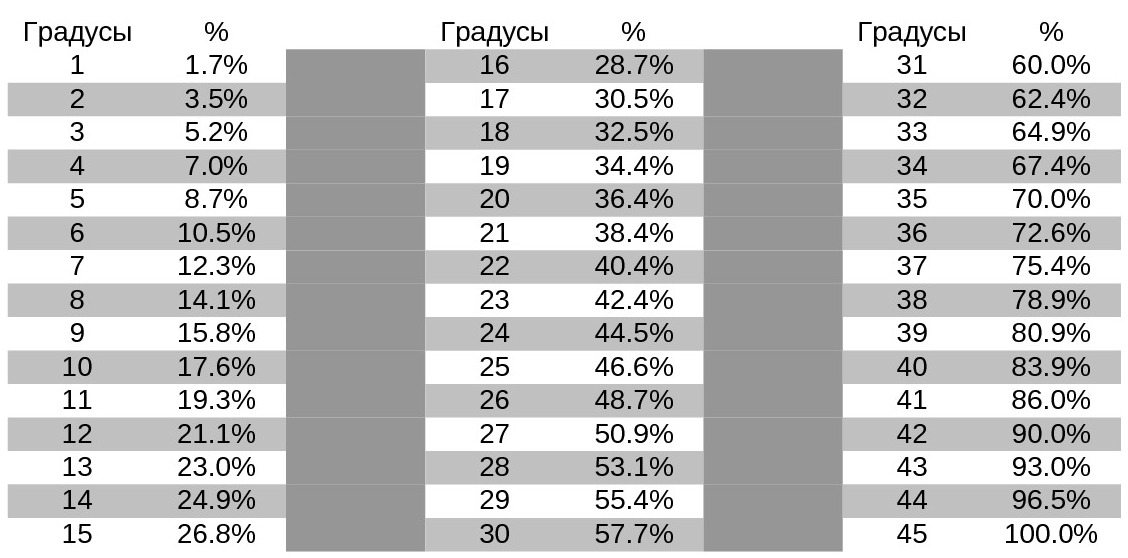
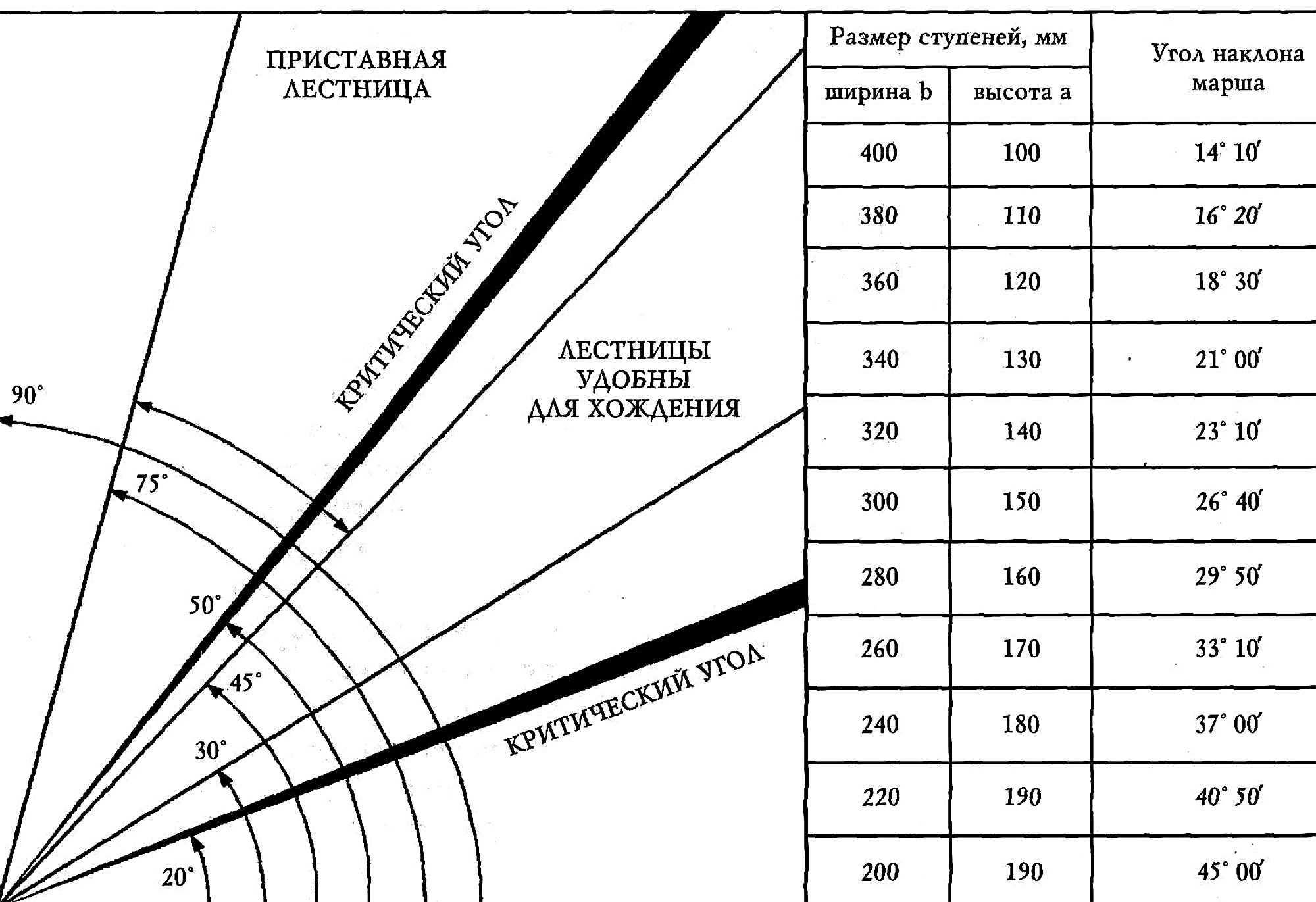
Уклон формула: Калькулятор уклонов – посчитать онлайн

alexxlab | 20.04.2023 | 0 | Разное

29. Допускаемые продольные и поперечные уклоны, формулы определения уклонов.

Проезжей части придают как правило двухскатную пов-ть.

Поперечные уклоны

15 – 20 – 25 %₀ – при монолитных покрытиях

20 – 25 – 30 %₀– при штучных покрытиях

– 40 %₀ – на обочинах

– тысячные доли

i = dh / l = 1/100=10%₀, где dh – превышение, l – заложение (расстояние).

Тротуарам придают односкатную пов-ть с уклоном в сторону лотка. Поперечные уклоны как на проезжей части. Тротуар возвышается над проезжей частью на высоту лотка 15см, в тоннелях 25см, а на мостах, эстакадах, насыпях до 45см.

Газонам придают уклон как на тротуаре в сторону проезжей части.

Для трамвайных путей поперечный уклон 7%₀. При больших продольных уклонах поперечные уменьшают до 5%₀.

Продольные уклоны

П.уклон у проезжей части зависит от категории улицы и скорости движения.

Максимальные уклоны:

Тип дорог	Скорость (км/ч)	Наибольший уклон (%0)
Скоростные дороги	120	40
Магистральные улицы непрерывного движения	100	50
Регулируемого движения	80	50
Районного назначения	80	60
Грузовые дороги	80	40
Жилые улицы	60	80
Пешеходные улицы		40
Проезды	30	80

Минимальные уклоны: 5%_0.

Продольные уклоны трамвайных путей 90-6%_0. На пересечениях путей меньше 40%₀.

Продольные профили про­ектируют в основном по осям проезжих частей улиц и дорог. При­мер продольного профиля городской улицы, совмещенного с гео­логическим разрезом, представлен на рис. 18.

Наиболее часто при детальной планировке применяют масшта­бы для горизонтальных продольных профилей 1 : 1000 и для вер­тикальных 1 : 100. При построении проектного продольного профиля руководствуются следующими условиями.

1. продольные уклоны следует созда­вать при минимально возможном объеме земляных работ по всей ширине улицы

Переломные отметки продольного профили устанавливают с таким расчетом, чтобы при сохранении типовых элементов поперечно­го профиля по возможности сохранить существующие отметки поверхности земли, что исключит необходимость перепланировки рельефа при­легающих территорий). .

2. При местных неровностях рельефа продольные профили улиц и дорог надо проектировать методом секущих линий со срезкой отдельных выступающих участков и засыпкой срезанным грунтом пониженных мест (микропланировка рельефа).

3. Конечные точки проектируемых продольных профилей долж­ны иметь нулевые рабочие отметки, (рабо отметка- разность между красной(проектной) и черной(существующей) отметками)т. е. проектная линия должна сопрягаться с отмотками существующей поверхности. . Положение проектной линии, продольного профили характери­зуется проектными отметками, уклонами и длиной участков между точками . В точках изменения уклонов воэникают углы, образующие выпуКлые и вогнутые переломы продольного профиля. в местах переломов продоль­ного профиля прямолинейные в профиле участки должны согтря-гяться кривыми радиальными вставками (выпуклыми и вогнутыми вертикальными кривыми).

Над каждой существующей (черной) отметки ставят красную (проектную) отметку.над опорными точками-перекрестками надписывают отметки высот.так же указывают расстояние меджу перекрестками и уклоны.они не должны быть меньше 5промилей.

Калькулятор угла уклона пандуса

Калькулятор для пандуса

В соответствии с СП 59.13330.2020 «Доступность зданий и сооружений для маломобильных групп населения. Актуализированная редакция СНиП 35-01-2001» максимальный перепад высот для установки пандуса не должен превышать 6,0 м, а уклон одного марша пандуса — не более 1:12,5 (80‰). В стеснённых условиях допускается увеличение уклона до 1:10 (100‰).

Соотношение	Проценты (%)	Промилле (‰)	Градусы (°)
1:33	3%	30‰	1,7°
1:20	5%	50‰	2,9°
1:12,5	8%	80‰	4,8°
1:10	10%	100‰	5,7°

Введите параметры будущего пандуса, исходя из данных объекта.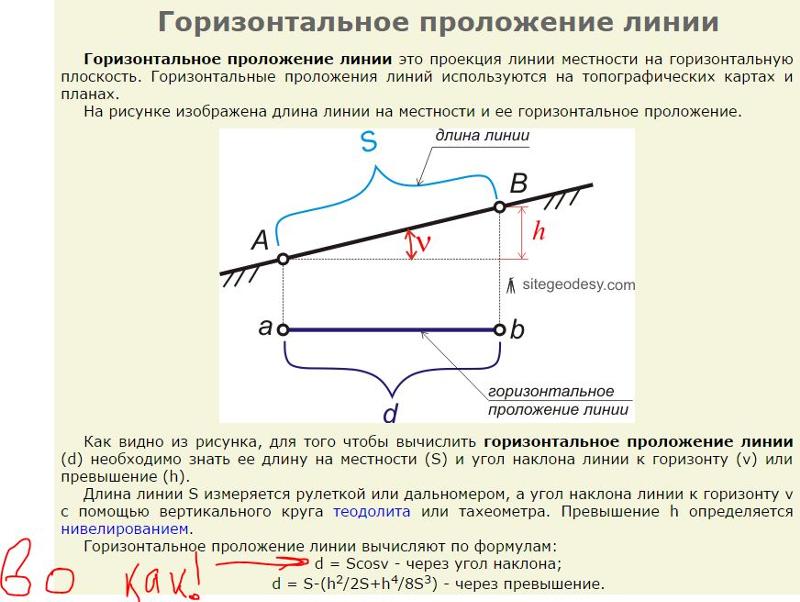 Параметры необходимо вводить в миллиметрах. Нажмите кнопку «Рассчитать». Соответственно, длина наклонной площадки рассчитывается в миллиметрах. Также Вы получите рекомендации относительно параметров, которые у Вас получились.

Основным действующим нормативным документом для определения уклона пандуса и его длины в РФ является СП 59.13330.2020 «Доступность зданий и сооружений для маломобильных групп населения»

Продольный уклон марша пандуса	Длина одного марша пандуса, м,не более	Суммарная длина наклонных поверхностей пандуса, м, не более
От 30 до 40 ‰ (от 1:33 до 1:25) (включительно)	15	110
От 40 до 50 ‰ (от 1:25 до 1:20) (включительно)	12
От 50 до 60 ‰ (от 1:20 до 1:16,7) (включительно)	9
От 61 до 80 ‰ (от 1:16 до 1:12,5) (включительно)	6	36
П р и м е ч а н и я Не допускаются марши пандуса с продольным уклоном более 80 ‰ (1:12,5). В стесненных условиях допускается увеличение уклона марша пандуса до 100 ‰ при длине его наклонных плоскостей до 5,0 м, при этом передвижение людей на кресле-коляске должно быть с помощью сопровождающих лиц.

Пандус – это устройство для адаптации социально-значимых объектов и открытых пространств: вход в здание, сопровождение лестницы, пешеходный переход и т.д. Пандус необходим, чтобы сделать жизнь маломобильных групп населения комфортнее: пожилые люди, с коляской или тяжелой поклажей, с костылями после травм, инвалиды-колясочники.

Активное развитие и продвижение федеральной программы «Доступная среда» сподвигло многие организации установить пандусы на входной группе. Однако зачастую это делается либо для галочки, либо организациями, не владеющими навыками и знаниями существующих нормативов. Поэтому не всегда готовое изделие соответствует государственным стандартам. Как результат – недоступность для людей с ограничениями.

Нормативы для пандусов 2023

По нормативам СП 59.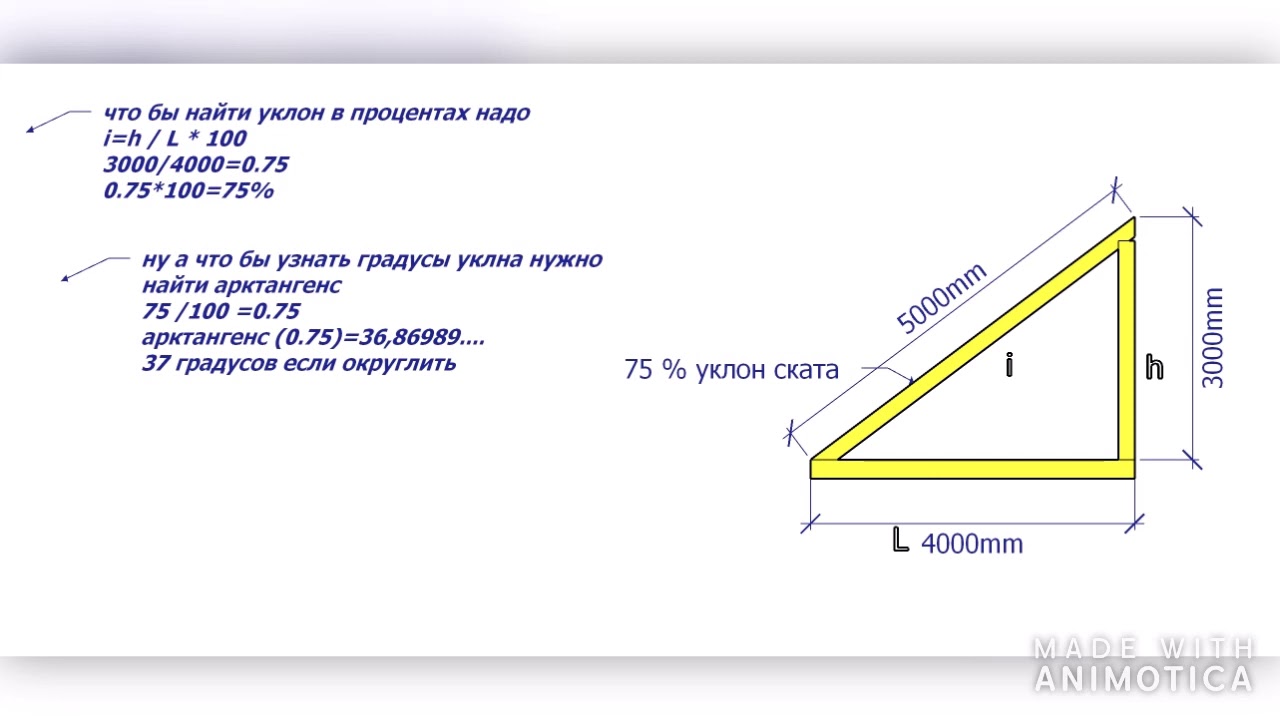 13330.2020 (с учетом вступивших в силу изменений 01 июля 2021 года) пандус должен иметь следующие характеристики:

Список документации, рекомендуемой к ознакомлению:

1. СНиП 35-01-2001 содержит предписания по адаптации жилых домов и социально-значимых объектов для маломобильных групп населения. А так же конкретные ограничения по установке и параметрам пандусов.
2. ГОСТ Р 51261-2022 содержит технические требования к стационарным опорным устройствам.
3. СП 30-102-99 содержит требования к входной площадке.
4. СП 59.13330.2020 содержит предписания по доступности зданий и сооружений для маломобильных групп населения

Угол наклона пандуса не должен превышать уклон в отношении 1:20 (5%). В данном случае очень часто проценты путают с градусами. В результате чего подъем/спуск получается в разы выше. Угол наклона – это соотношение длины к высоте подъема.

Запомните При перепаде высоты от трех метров, вместо пандусов применяются подъемные устройства. В данном случае наличие пандуса будет бесполезным и недоступным для инвалида-колясочника.

Справка! В ряде некоторых случаев допускается небольшое увеличение угла наклона пандуса:

• При временном сооружении пандуса (ремонте или реконструкции здания). Если его высота не превышает 0,5 м, а промежуток между площадками не более 6 м, уклон может быть 8% или 1:12
• Если высота подъема не достигает 0,2 м, уклон допустим в пропорции 1:10 (10%).
• Длина непрерывного движения марша пандуса не должна превышать 9,0 м, далее необходимо организовывать  разворотную площадку или площадку отдыха.
• Длина горизонтальной площадки прямого пандуса должна быть не менее 1,5 м.
• Пандусы должны иметь двухстороннее ограждение с поручнями на высоте 0,9 и 0,7 м.
• Поверхность пандуса должна быть нескользкой текстурой.
• Поверхность марша пандуса должна визуально контрастировать с горизонтальной поверхностью в начале и конце пандуса.

Поручни для пандуса

• В начале и конце поручни должны быть длиннее на 300 мм и иметь закруглённую форму.
• Верхний поручень расположен на высоте 900 мм.
• Расстояние между поручнями 900-1000 мм.
• Перила должны быть круглого сечения с диаметром от 30 до 50 мм.
• Начало и конец маркируются предупредительными полосами.
• Нижний поручень должен быть на высоте 700 мм.
• По продольным краям марша пандуса следует устанавливать бортики высотой не менее 0,05 м.
• Покрытие пандуса должно обладать противоскользящим эффектом.
• Минимальное расстояние от гладкой стены 45 мм, от неровной 60 мм.
• Поручни с внутренней стороны не должны прерываться.
• Поручни изготавливаются из металла и устанавливаются с обеих сторон наклонной площадки.

Если пандус изначально соответствует всем строительным параметрам, то его можно оснастить необходимыми дополнительными устройствами при их отсутствии:

• Опорными поручнями. Расстояние между  поручнями пандуса одностороннего движения должно быть в пределах 0,9-1,0 м, чтобы инвалид-колясочник мог на них подтянуться. Также для удобства и безопасности хвата поручни должны иметь закругленную форму и выступать на 300 мм от края.
• Контрастной тактильной разметкой (для незрячих и слабовидящих людей). Разметкой следует обозначать сами поручни и подстилающую поверхность. С внутренней стороны поручней можно приклеить тактильные наклейки для обозначения начала и конца препятствия.

Если пандус изначально не соответствует конструкторским параметрам в соответствии со сводами правил, то его следует демонтировать, а на его месте организовать доступный пандус.

Вопросы по адаптации
Автопарковка для МГН
Адаптация тротуаров для незрячих
Адаптация лестниц для МГН
Адаптация входной группы
Адаптация холла в помещении
Адаптация санузела для незрячих
Адаптация лифтов для МГН

НАШЕ ПРЕИМУЩЕСТВО – ДОЛГОЛЕТНИЙ ОПЫТ и КАЧЕСТВО!

Наклоны и уравнения прямых

Наклоны и уравнения прямых Наклоны и уравнения линий

Немного полезной информации о линиях

Факт	Вы можете использовать этот факт, если знаете:
Формула уклона:	две точки на прямой
Формула пересечения наклона: y = mx + b	наклон и пересечение оси Y линии
Формула точки-наклона: y – y 1 = m(x – x 1 )	наклон линии и точка на линии
Параллельные линии имеют одинаковый наклон	наклон линии
Наклоны перпендикулярных линий противоположны обратным	наклон линии

Самая сложная часть работы с точками, уклонами и линии определяет, какую формулу использовать при решении конкретных задач. Когда вы пытаетесь решить проблему, задайте себе следующие вопросы:

1. Что я должен найти?
2. Что я уже знаю?
3. Какой метод я буду использовать?

В приведенной ниже таблице показаны методы, использовать при решении конкретных типов задач.

Что вы хотите найти?	Что ты уже знаешь?	Метод использования
Наклон линии	Координаты двух точек на строка	Используйте формулу наклона
Наклон и точка пересечения с осью Y линии	Уравнение прямой в стандарте форма	Запишите уравнение в виде точки пересечения форма
Уравнение прямой	Наклон линии и точка на этой линии	Используйте формулу угла наклона
Уравнение прямой	Наклон и точка пересечения с линией Y	Используйте формулу пересечения наклона
Уравнение прямой	Координаты двух точек на строка	Используйте формулу наклона, чтобы найти наклон линии, затем используйте наклон и одну из точек на формула точка-наклон
Уравнение прямой, параллельной заданная строка	Уравнение заданной параллели линия и точка на вашей линии	Напишите уравнение данного линия в форме пересечения наклона, чтобы определить ее наклон, затем используйте тот же самый уклон и ваша точка в формуле точка-уклон
Уравнение прямой, перпендикулярной на заданную строку	Уравнение заданного перпендикуляра линия и точка на вашей линии	Напишите уравнение данного линия в форме пересечения наклона, чтобы определить ее наклон, затем используйте противоположное величина, обратная этому наклону и вашей точке в формуле точка-наклон

Давайте рассмотрим несколько примеров.

Пример 1 Каков наклон линии, проходящей через точки (2,3) и (4,-5) ?

Что мы хотим найти? Наклон линии

Что мы уже знаем? Две точки на линии

Какой метод мы будем использовать? Используйте формулу наклона

Пример 2 Что такое наклон и точка пересечения с осью Y 2x – 3y = 5?

Что мы хотим найти? Наклон и y-пересечение

Что мы уже знаем? Уравнение прямой в стандартной форме

Какой метод мы будем использовать? Запишите уравнение в форма пересечения наклона

2х – 3у = 5

– 3г = – 2х + 5

у = 2/3 х – 5/3

Поскольку уравнение теперь имеет форму y = mx + b, мы можем определить наклон m=2/3 и точка пересечения с осью y b=-5/3

Пример 3 Каково уравнение прямой с наклон – 2, который проходит через (3,-5)?

Что мы хотим найти? Уравнение прямой

Что мы уже знаем? Наклон и точка на линии

Какой метод мы будем использовать? Используйте формулу “точка-наклон”

м = -2, (х ₁ , у ₁ ) = (3, -5)

у – у ₁ = м(х – х ₁ )

у – -5 = -2(х – 3)

у + 5 = -2х + 6

у = -2х + 1

Пример 4 Каково уравнение прямой с наклон 3/4 и y-пересечение – 3?

Что мы хотим найти? Уравнение прямой

Что мы уже знаем? Наклон и y-пересечение

Какой метод мы будем использовать? Использовать пересечение наклона формула

м = 3/4, б = -3

у = мх + б

у = 3/4 х + -3

у = 3/4 х – 3

Пример 5 Каково уравнение прямой, которая содержит точки (3,4) и (1,-2)?

Что мы хотим найти? Уравнение прямой

Что мы уже знаем? Две точки на линии

Какой метод мы будем использовать? Используйте формулу наклона чтобы найти наклон линии, затем используйте наклон и одну из точек в формуле точка-наклон

Теперь используем одну из точек и наш наклон в точку-наклон формула:

м = 3

у – у ₁ = м(х – х ₁ )

у – 4 = 3(х – 3)

у – 4 = 3х – 9

у = 3х – 5

Пример 6 Найдите уравнение прямой, проходящей через (-1, 4) и параллелен 3x-y=5. Что мы хотим найти? Уравнение прямой

Что мы уже знаем? Точка на нашей линии и уравнение прямой, параллельной нашей прямой

Какой метод мы будем использовать? Напишите уравнение заданную линию в форме пересечения наклона, чтобы определить ее наклон, затем используйте тот же наклон и ваша точка в формуле точка-наклон

3x – у = 5

– у = – 3х + 5

у = 3х – 5

м = 3, б = – 5

Таким образом, наклон данной линии равен 3

Параллельные линии имеют одинаковые наклоны, поэтому наклон нашей линия тоже 3. Наша линия тоже проходит через точку (-1,4), поэтому напишем уравнение с формулой точка-наклон.

у – у ₁ = м(х – х ₁ )

у – 4 = 3(х – – 1)

у – 4 = 3(х + 1)

у – 4 = 3х + 3

у = 3х + 7

Пример 7 Найти уравнение прямой через (4,-1), перпендикулярное 4x+3y=2

Что мы хотим найти? Уравнение прямой

Что мы уже знаем? Точка на нашей линии и уравнение прямой, перпендикулярной нашей прямой

Какой метод мы будем использовать? Напишите уравнение заданную линию в форме пересечения наклона, чтобы определить ее наклон, затем используйте противоположное обратное значение этого наклона и вашей точки в точке-наклоне формула

4х + 3у = 2

3у = – 4х + 2

у = – 4/3 х + 2/3

м = – 4/3, б = 2/3

Перпендикулярные линии имеют наклоны, противоположные обратным, поэтому наклон нашей линии обратно пропорционален -4/3 или 3/4. Наш прямая тоже проходит через точку (4,-1), поэтому напишем уравнение с формула точка-наклон.

у – у ₁ = м(х – х ₁ )

у – – 1 = 3/4(х – 4)

у + 1 = 3/4 х – 3

у = 3/4 х – 4

 

Формула уклона. Что такое формула уклона? Уравнение, примеры, часто задаваемые вопросы

Формула уклона используется для определения крутизны или наклона линии. Координаты x и y точек, лежащих на линии, используются для вычисления наклона линии. Изменение координаты «у» по отношению к изменению координат «х» называется наклоном линии и обычно обозначается буквой «м». Используя формулу наклона, мы можем определить, являются ли две линии перпендикулярными, параллельными или коллинеарными.

Что такое формула уклона?

Формула уклона требуется для расчета наклона линии. Для расчета наклона линии требуются координаты x и y точек на линии. Отношение изменения координаты y к изменению координаты x называется наклоном линии.

Наклон (м) = изменение y/изменение x = Δy/Δx

Формула наклона

В математике наклон линии используется для определения степени наклона линии, т. е. крутизны линия. Чтобы определить наклон линии, нам нужны координаты x и y точек, лежащих на линии. Формула наклона представляет собой чистое изменение координаты «y», деленное на чистое изменение координаты «x». Δy — изменение координаты «y», а Δx — изменение координаты «x». Следовательно, отношение изменения координаты «y» к изменению координаты «x» определяется выражением

Наклон (M) = изменение y/изменение в x = Δy/Δx

M = (Y ₂ – Y ₁ )/(x ₂ – x ₁ )

8)/(x ₂ – x ₁ )8)/(x ₂ – x ₁ ) )/(x ₂ – x ₁ )

, где x ₁ и x ₂ — координаты оси X, а y ₁ и y ₂ — координаты оси Y.

Формула расчета наклона

Координаты x и y линии используются для расчета наклона линии. Чистое изменение координаты y равно Δy, а чистое изменение координаты x равно Δx. Таким образом, изменение координаты y по отношению к изменению координаты x можно записать как

M = ΔY/ΔX

, где,

M -это наклон
ΔY -это изменение в Y-COordinates
Δx IS-изменение в h-coordinates
Δx IS-изменение в Зоне Δx IS-изменение. что тангенс θ также является наклоном линии, где θ — угол, образуемый линией с положительным направлением оси x.

И, тангенс θ = высота/основание

Так как высота/основание между любыми двумя заданными точками = (y ₂ – y ₁ )/(x ₂ – x ₁ )

Таким образом, уравнение наклона: m = tan θ = Δy/Δx

Из графика получаем: y ₁ )
Δx = (x ₂ – x ₁ )
Тогда формула наклона будет следующей: – x ₁ )

 

Наклон линии (прямой линии) Формула

• Мы знаем, что тангенс θ также является наклоном линии, следовательно, наклон линии также может быть представлен в виде положительная ось X,

  Δy = изменение координат «y»,

  Δx = изменение координат «x».

• Мы также можем определить наклон линии как отношение подъема по отношению к пробегу.

Уклон (м) = подъем/пробег

• Пусть ax + by + c = 0 будет общим уравнением прямой. Теперь формула для наклона линии имеет вид используя линейное уравнение, задается как,

y = mx + c

Где m – наклон линии, а c – точка пересечения линии по оси y.

Уравнение наклона

Формула наклона используется для определения наклона линии. Уравнение, используемое для определения наклона, записывается следующим образом:

m = tanθ = Δy/Δx = (y ₂ – y ₁ )/(x ₂ – x ₁ 8 )

где,

м – наклон линии
Δy – разность координат y
Δx – разность координат x ось

Уравнение линии с наклоном m определяется как,

y = mx + c

где,

m – наклон линии
b точка пересечения линии

Решенный пример с формулой наклона

Пример 1. Найдите наклон линии с координатами (3, 7) и (5, 8).

Решение:

Дано, (x ₁ , y ₁ ) = (3,7) и (x ₂ , Y ₂ ) = (5,8)

Формула наклона (M) = (Y ₂ – Y ₁ )/(x ₂ – x ₁ )

5 ⇒ m = (8 – 7)/(5 – 3) = 1/2

Следовательно, наклон данной прямой равен 1/2.

Пример 2. Определите наклон линии с координатами (7, -5) и (2, -3).

Решение:

Дано, (x ₁ , y ₁ ) = (7, -5) и (x ₂ , Y ₂ ) = (2, -3)

Формула наклона (M) = (Y ₂ -Y ₁ )/(x ₂ -x ₁ )

⇒ m = (-3 – (-5))/(2 – 7) = -2/5

Следовательно, наклон данной прямой равен -2/5

Пример 3. Найдите значение a , если наклон прямой, проходящей через точки (-4, а) и (2, 5), равен 3.

Решение:

Дано, (x ₁ , y ₁ ) = (4,а) и (х ₂ , y ₂ ) = (2, 5) и уклон (м) = 3

Мы знаем, что уклон (м) = (y ₂ – y ₁ )/(x ₂ – х ₁ )

⇒ 3 = (5 – а)/(2 – 4)

⇒ 3 = (5 – а)/(-2)

⇒ -6 = 5 – а ⇒ а = 5 + 6 = 11

Следовательно, значение a = 11

Пример 4: Если линия образует угол 60° с положительной осью Y, то каково значение наклона линии?

Решение:

Учитывая данные, Угол, образуемый линией с положительной осью у = 60°

Мы знаем, что если линия образует угол 60° с положительной осью у, то она образует угол (90° – 60° = 30°) относительно оси x.

Следовательно, значение наклона линии (м) = tan 30° = 1/√3

Следовательно, значение наклона линии = 1/√3.

Пример 5: Шила проверяла график и заметила, что рейз составил 12 единиц, а пробег — 4 единицы. Теперь вычислите наклон линии.

Решение:

Учитывая данные, подъем = 12 единиц и пробег = 4 единицы

Мы знаем, что уклон (м) = подъем/бег

⇒ м = 12/4 = 809 3 900 , наклон данной линии равен 3

Пример 6: Найдите наклон прямой 3x – 7y + 8 = 0.

Решение:

Данные, уравнение прямой = 3x – 7y + 8 = 0

Теперь сравним данное с общим уравнением прямой, т. е. ax + by + c = 0

Следовательно, a = 3, b = -7 и c = 8

Мы знаем, что Уклон (м) = – коэффициент x/коэффициент y = -a/b

⇒ m = -3/(-7 ) = 3/7

Следовательно, наклон данной прямой равен 3/7.

Часто задаваемые вопросы о формуле уклона

Вопрос 1: Что такое уклон линии?

Ответ:

Наклон линии — это значение крутизны или наклона линии в плоскости x-y.