В чем измеряется коэффициент упругости: Коэффициент упругости, формула и примеры

alexxlab | 04.05.2023 | 0 | Разное

области применения, формула расчета и единицы измерения

Самым важным показателем, определяющим упругость металлических изделий, предназначенных для различного пользования, считается коэффициент пружинной жесткости. Он определяет устойчивость пружинного механизма к различным трансформациям и воздействиям с другими элементами. Также важно сопротивление пружины при ее взаимодействии с различными телами. Как правило, коэффициент жесткости равняется силе сопротивления.

Содержание:

• Применение и разновидности пружин
• Единицы измерения коэффициента
• Определение жесткости пружины
• Видео

Применение и разновидности пружин

Пружина является упругим изделием, что обеспечивает трансформацию нарастающих двигательных импульсов к приборным и механизменным составляющим собственного звена. Встречается устройство во многих изделиях как в бытовых приборах, так и в производственных элементах. А степень надежности работы механизмов на производстве зависит от коэффициента пружинной жесткости. Эту величину следует соизмерять с усилием, приложенным к пружине, что определяет ее сжатие или растяжение. Пружинное вытяжение зависит от свойств металла, который ее составляет, а не от коэффициента упругости.

Пружинный элемент имеет разнообразные структуры. Все зависит от того, для чего он предназначен. По деформационным особенностям и структурным характеристикам пружина бывает:

• спиральной;
• канонической;
• цилиндрической.

Коэффициентный показатель жесткости определенного элемента зависит от способа деформационной передачи. Параметры деформации подразделяют все механизмы на такие:

• ввинчивающиеся;
• крутящиеся;
• изогнутые;
• растягивающиеся.

При одновременном применении нескольких пружинных механизмов в одном изделии жесткостный показатель будет обусловлен крепежным элементом. Если все соединено параллельным креплением, то показатель будет расти, а последовательное крепление предусматривает уменьшение.

Единицы измерения коэффициента

Показатель жесткости изделия является важной величиной, который имеет свойства определять срок изнашиваемости механизма. Рассчитать требуемый коэффициент можно по такой формуле:

С = (d * G) : ( n * 8 * D³ ср ), где:

• С — коэффициент жесткости;
• d — пружинный диаметр;
• G — модуль сдвига пружины;
• n — количество витков;
• D ср — сила упругости.

Расчет коэффициентного показателя может быть произведен и в электронном вычислении. Для этого применяется калькулятор пружинных расчетов. При этом стоит учитывать, что эксплуатационные характеристики пружинного механизма будут зависеть от качества сборки изделия и от материала, который использовался в производстве прибора.

Коэффициент жесткости в физике зачастую именуют коэффициентом упругости или Гука. Все эти величины отвечают за жесткость пружины. Это механический показатель, применяемый для определения твердых величин. Коэффициент упругости равняется силовому полю, приложенному к пружинному механизму для изменения длины на определенном расстоянии.

Коэффициент Гука рассчитывается путем соотношения силы упругости к длине пружинящего механизма. Эта величина будет зависеть от качества материалов и от размерных составляющих твердого тела. Упругость пружины будет зависеть от ее длины и площади. Эти величины определяются как Модуль Юнги и зависят от составляющих и свойственных параметров материала, из которых изготовлена пружина.

Основные теории упругости – в этом видео.

Определение жесткости пружины

Как и любой другой механизм, пружина может соединяться:

• параллельным соединением;
• последовательным соединением.

Соединяясь в одно целое, несколько механизмов при деформации меняют свою жесткость. Параллельное соединение предусматривает увеличение упругости, а последовательное — уменьшение.

Параллельное соединение вычисляется такой формулой:

k = k 1 + k 2 + k 3 + …+ k n, где:

• k — показатель жесткости системы;
• n — соединение пружинных механизмов.

Последовательное соединение пружин рассчитывается по такой формуле:

1: k = (1: k 1 + 1: k 2 + 1: k 3 + … + 1: k n).

Кроме этого, существует множество расчетов показателей упругости при деформации, но на каждый из них приходится соответствующая формула. Все расчеты ведутся обычно в определенных программных комплексах на предприятиях, изготавливающих механизмы из пружин. Так что формулы уже запрограммированы, а для расчета вводятся только известные данные.

Итак, коэффициент жесткости пружины является постоянной величиной, которая рассчитывается для определения срока эксплуатации прибора на практике. Кроме того, определяются свойства пружинного механизма и его работы в целом, что помогает улучшить качество изготавливаемого изделия.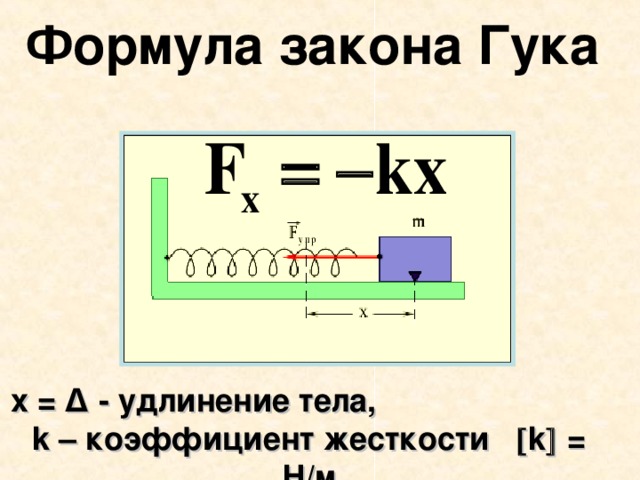

Видео

Из этого видео вы узнаете, как определить жесткость пружины.

Сила упругости и закон Гука

☰

Чем большей деформации подвергается тело, тем значительней в нем возникает сила упругости. Это значит, что деформация и сила упругости взаимосвязаны, и по изменению одной величины можно судить об изменении другой. Так, зная деформацию тела, можно вычислить возникающую в нем силу упругости. Или, зная силу упругости, определить степень деформации тела.

Если к пружине подвешивать разное количество гирек одинаковой массы, то чем больше их будет подвешено, тем сильнее пружина растянется, то есть деформируется. Чем больше растянута пружина, тем большая в ней возникает силы упругости. Причем опыт показывает, что каждая следующая подвешенная гирька увеличивает длину пружины на одну и туже величину.

Так, например, если исходная длина пружины была 5 см, а подвешивание на ней одной гирьки увеличило ее на 1 см (т.

е. пружина стала длиной 6 см), то подвешивание двух гирек увеличит ее на 2 см (общая длина составит 7 см), а трех — на 3 см (длина пружины будет 8 см).

Еще до опыта известно, что вес и возникающая под его действием сила упругости находятся друг с другом в прямопропорциональной зависимости. Кратное увеличение веса во столько же раз увеличит силу упругости. Опыт же показывает, что деформация точно также зависит от веса: кратное увеличение веса во столько же раз увеличивает изменения в длине. Это значит, что, исключив вес, можно установить прямопропорциональную зависимость между силой упругости и деформацией.

Если обозначить удлинение пружины в результате ее растяжения как x или как ∆l (l₁ – l₀, где l₀ — начальная длина, l₁ — длина растянутой пружины), то зависимость силы упругости от растяжения можно выразить такой формулой:

F_упр = kx или F_упр = k∆l, (∆l = l₁ – l₀ = x)

В формуле используется коэффициент k. Он показывает, в какой именно зависимости находятся сила упругости и удлинение. Ведь удлинение на каждый сантиметр может увеличивать силу упругости одной пружины на 0,5 Н, второй на 1 Н, а третьей на 2 Н. Для первой пружины формула будет выглядеть как F_упр = 0,5x, для второй — F_упр = x, для третьей — F_упр = 2x.

Коэффициент k называют жесткостью пружины. Чем жестче пружина, тем труднее ее растянуть, и тем большее значение будет иметь k. А чем больше k, тем больше будет сила упругости (F_упр) при равных удлинения (x) разных пружин.

Жесткость зависит от материала, из которого изготовлена пружина, ее формы и размеров.

Единицей измерения жесткости является Н/м (ньютон на метр). Жесткость показывает, сколько ньютонов (сколько сил) надо приложить к пружине, чтобы растянуть ее на 1 м. Или насколько метров растянется пружина, если приложить для ее растяжения силу в 1 Н. Например, к пружине приложили силу в 1 Н, и она растянулась на 1 см (0,01 м).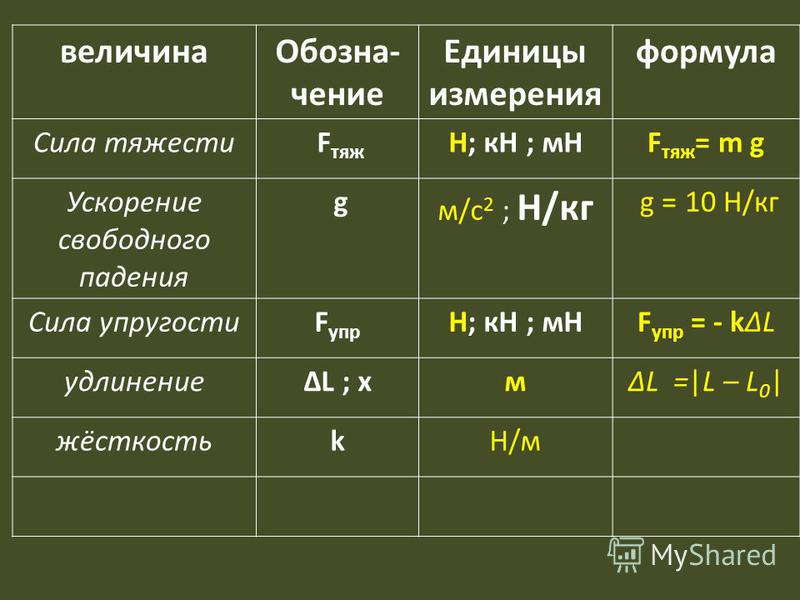 Это значит, что ее жесткость равна 1 Н / 0,01 м = 100 Н/м.

Также, если обратить внимание на единицы измерения, то станет понятно, почему жесткость измеряется в Н/м. Сила упругости, как и любая сила, измеряется в ньютонах, а расстояние – в метрах. Чтобы уровнять по единицам измерения левую и правую части уравнения F_упр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них).

Соотношение между силой упругости и деформацией упругого тела, описываемое формулой F

упр = kx, открыл английский ученый Роберт Гук в 1660 году, поэтому это соотношение носит его имя и называется законом Гука.

Упругой деформацией является такая, когда после прекращения действия сил, тело возвращается в свое исходное состояние. Бывают тела, которые почти нельзя подвергнуть упругой деформации, а у других она может быть достаточно большой. Например, поставив тяжелый предмет на кусок мягкой глины, вы измените его форму, и этот кусок сам уже не вернется в исходное состояние. Однако если вы растяните резиновый жгут, то после того, как отпустите его, он вернет свои исходные размеры. Следует помнить, что закон Гука применим только для упругих деформаций.

Формула F_упр = kx дает возможность по известным двум величинам вычислять третью. Так, зная приложенную силу и удлинение, можно узнать жесткость тела. Зная, жесткость и удлинение, найти силу упругости. А зная силу упругости и жесткость, вычислить изменение длины.

Что нужно знать о коэффициентах эластичности

Обновлено 25 августа 2022 г. Джейкоб Рид
На экзаменах по микроэкономике 2015 и 2016 годов FRQ были сосредоточены на эластичности и расчете коэффициентов эластичности. Некоторые из моих учеников чувствовали себя недостаточно подготовленными к решению этих сложных вопросов. Чтобы убедиться, что это больше не повторится, я создал приведенный ниже обзор эластичности вместе с 15 вопросами Расчеты и интерпретации коэффициента эластичности , чтобы проверить ваши навыки. Если повезет, он предоставит вам все, что вам нужно знать об эластичности, чтобы вы не были застигнуты врасплох, когда в мае начнется экзамен AP.

Основы и эластичность спроса по цене

Эластичность – это степень, в которой одно изменение вызывает другое изменение. Поскольку эластичность спроса по цене проще всего понять, мы начнем с нее. Мы знаем, что когда цены растут, объем спроса уменьшается. Эластичность говорит нам, насколько уменьшается величина спроса.

Когда большое изменение цены вызывает небольшое изменение объема спроса, кривая спроса относительно IN эластична. То есть потребители относительно  IN чувствителен к изменению цены. Относительно неэластичные кривые спроса имеют тенденцию быть более вертикальными, чем горизонтальными. Если потребители требуют одинаковое количество товара независимо от цены, кривая спроса совершенно неэластична; потребители совершенно IN чувствительны к изменению цен. Совершенно неэластичные кривые спроса вертикальны.

Товары с неэластичными кривыми спроса, как правило, являются:

• Товары первой необходимости.
• Товары, у которых мало заменителей.
• Относительно недорогие товары.

Когда небольшое изменение цены вызывает большое изменение объема спроса, кривая спроса является относительно E эластичной. То есть E потребители особенно чувствительны к изменению цены. Кривые относительно эластичного спроса имеют тенденцию быть более горизонтальными, чем вертикальными. Если потребители будут требовать любое количество по одной максимальной цене, кривая спроса будет совершенно эластичной; потребители совершенно чувствительны к изменению цен. Кривые абсолютно эластичного спроса горизонтальны.

Товары, которые имеют эластичные кривые спроса, тогда будут:

• Товары, которые не являются необходимостью.
• Товары, имеющие множество заменителей.
• Относительно дорогие продукты

Существует еще один тип упругости, и он называется единичной эластичностью. Кривая единичной эластичности спроса будет иметь рост цен, вызывающий пропорциональное уменьшение объема спроса.

Примечание. Глядя на форму кривой спроса, нельзя определить эластичность. Эластичность линейной кривой спроса уменьшается по мере увеличения количества (см. тест TR ниже)

Тест общей выручки

Когда речь идет об эластичности спроса по цене, самым простым способом определения эластичности является проверка общей выручки (TR). Формула общего дохода: P x Q. На кривой спроса объемы падают по мере роста цен, а объемы растут по мере снижения цен. Если цена растет, а TR увеличивается (P и TR движутся в одном направлении), кривая спроса неэластична. Если цена падает, а TR уменьшается (опять же P и TR идут в одном направлении, кривая спроса также неэластична. Если цена растет, а TR падает (P и TR идут в противоположных направлениях, кривая спроса эластична. Если цена падает, а TR растет (снова PR и TR движутся в противоположных направлениях, кривая спроса также эластична. Если изменения цены не изменяют TR, кривая спроса является единично эластичной (увеличение или снижение цены сохраняет TR неизменной)9.0004

Прямолинейная кривая спроса имеет эластичный участок вверху, неэластичный участок внизу и точку единичной эластичности в середине. Если на графике есть кривая предельного дохода (вы увидите ее, узнавая о монополиях и фирмах с монополистической конкуренцией), она может помочь вам определить эластичность. Снижение цены увеличивает общий доход по мере увеличения количества, пока предельный доход больше нуля. Участок единичной эластичности кривой спроса находится там, где MR=0. Тогда снижение цены уменьшает общую выручку, поскольку предельная выручка отрицательна. В этом диапазоне кривая спроса неэластична.

Примечание. ТЕСТ ОБЩЕГО ДОХОДА ПРИМЕНЯЕТСЯ ТОЛЬКО К ЭЛАСТИЧНОСТИ СПРОСА ПО ЦЕНЕ.

Коэффициент эластичности

 Другим способом определения эластичности является расчет коэффициента. Коэффициент говорит нам о пропорциях, в которых изменение цены изменяет количество. Например, коэффициент -2 говорит нам о том, что повышение цены на заданный процент вызовет вдвое большее уменьшение количества. С другой стороны, коэффициент -0,5 вызовет уменьшение объема спроса на половину (поскольку 0,5 составляет 1/2) процента повышения цены. Основная формула для расчета коэффициента – это %∆Q/%∆P (∆ означает изменение). После расчета коэффициента абсолютное значение (то есть положительное или отрицательное значение не имеет значения) можно использовать для определения эластичности. Значения эластичности следующие:

• Абсолютное значение коэффициента = 0: совершенно неэластичный
• Абсолютное значение коэффициента <1 (но не ноль): относительно неэластичный
• Абсолютное значение коэффициента = 1: единичная эластичность ∞ или неопределенный): относительно эластичный
• Абсолютное значение коэффициента = ∞ или неопределенный: абсолютно эластичный.

Примечание. Это значения эластичности для всех типов эластичности.

Формулы процентного изменения коэффициента эластичности: Метод конечной точки

Метод конечной точки для расчета процентного изменения является самым простым и прямым. Кроме того, это (пока что) все, что нужно для расчета коэффициентов на опубликованных экзаменах по микроэкономике Advanced Placement Exams. Проблема с этим методом заключается в том, что он не так точен, как формула средней точки, и направление изменения может вызвать у вас проблемы.

Формула конечной точки для %∆

Пример: если количество увеличивается со 100 до 150, это означает увеличение на 50 %, поскольку (150 – 100)/100 x 100 = 50 %. Но если вы пойдете в обратном направлении (от 150 до 100), вы получите изменение на 33 ⅓ %. Эта разница будет означать, что вы получите 2 разных коэффициента в зависимости от того, какие числа вы используете в качестве нового и старого. Хитрость заключается в том, чтобы следовать направлению вопроса. Таким образом, если количество увеличится со 100 до 150 при снижении цены со 100 до 75 долларов, процентное изменение количества составит 50%, а процентное изменение цены составит -25%. И %∆Q/%∆P=50%/-25%=-2, поэтому эта кривая спроса эластична по цене.

Формулы процентного изменения коэффициента эластичности: Метод средней точки

Метод средней точки расчета процентного изменения устраняет проблемы направления, связанные с вычислением процентного изменения. Это связано с тем, что для расчета процентного изменения требуется средняя средняя точка между новой и старой ценой/количеством.

Недостатком этого метода является то, что экзамен AP по микроэкономике не позволяет учащимся использовать калькуляторы, а математические расчеты с помощью этого метода часто более сложны. Какой метод вы предпочитаете, действительно зависит от вас. Но выбирайте с умом.

Формула средней точки для %∆

Ценовая эластичность 

Как упоминалось выше, %∆Q/%∆P даст вам коэффициент ценовой эластичности. Кривые спроса имеют отрицательный коэффициент ценовой эластичности из-за обратной зависимости кривой спроса между ценой и количеством. Кривые предложения имеют положительный коэффициент ценовой эластичности из-за прямой зависимости между ценой и количеством. Эластичность спроса по цене определяется количеством заменителей, тем, насколько необходим товар и какой частью дохода потребителя требуется оплатить этот товар. Эластичность предложения по цене определяется ценами на альтернативные ресурсы, наличием ресурсов, временем, необходимым для производства продукта, и т. д. 

Эластичность по доходу 

Эластичность по доходу показывает, насколько изменение дохода потребителя вызывает изменение величины спроса. Нормальные товары (большинство товаров попадают в эту категорию) — это товары, которые потребители покупают больше, когда их доходы растут, и меньше, когда их доходы падают. Товары низшего качества — это такие товары, как однослойная туалетная бумага, рамен высшего качества или непатентованные брендовые товары. Когда доходы потребителей растут, потребители покупают меньше этих товаров, а когда доходы падают, они покупают больше.

Одним из неценовых определяющих факторов  спроса является изменение дохода. Эластичность дохода говорит нам, насколько изменение дохода изменит спрос на товар или услугу. Формула эластичности дохода: %∆Q/%∆Income. Нормальные товары имеют положительный коэффициент эластичности по доходу, поскольку увеличение доходов вызывает увеличение спроса на нормальные товары. Некачественные товары имеют отрицательный коэффициент эластичности по доходу. Это связано с тем, что рост доходов вызывает снижение спроса на товары низшего качества.

Перекрестная эластичность

Перекрестная ценовая эластичность связана с заменителями и дополнениями. Заменители — это товары, которые можно использовать вместо друг друга; как масло и маргарин, или варенье и желе. Когда цена одного увеличивается, спрос на другой также увеличивается. Дополнения — это товары, которые используются вместе; как хлеб с маслом или зубные щетки и зубная паста. Когда цена одного увеличивается, спрос на другой снижается. Перекрестная ценовая эластичность говорит нам, насколько изменение цены одного товара влияет на спрос на другой.

При изменении цены заменителя или дополнения спрос на данный товар изменится. Формула перекрестной ценовой эластичности: %∆Q/%∆P (P — цена другого товара). Товар-заменитель будет иметь положительный коэффициент, потому что увеличение цены на товар-заменитель вызовет увеличение спроса на рассматриваемый товар. Дополнительные товары будут иметь отрицательный коэффициент, потому что увеличение цены на дополнительные товары вызовет снижение спроса на рассматриваемый товар.

Соединения с несколькими вариантами ответов:
Выпущенный в 2012 году экзамен по микроэкономике AP. Вопросы: 33, 34

Далее: 
Страница обзора содержания: Акцизы

Другое рекомендуется ресурсы : ACDC Video (эластичность спроса, общий доход), ACDC Video (доход, кросс-цена)

Коэффициенты эластичности спроса | Экономика

Последний шанс посетить киносеминар Grade Booster перед экзаменами. Забронировать сейчас →

Изучение экономики

Тематические видео

Уровень:

AS, A-Level, IB, BTEC National, BTEC Tech Award

Плата:

AQA, Edexcel, OCR, IB, Eduqas, WJEC

Последнее обновление 4 ноября 2019 г.

Поделиться :

В этом тематическом видео мы расскажем об актуальности коэффициентов трех различных эластичностей спроса (PED, YED и XED).

Коэффициенты:

Коэффициент означает значение

• Эластичность – это число!
• Коэффициент может быть высоким – эластичный
• Или низким – неэластичный
• Или нулевой – совершенно неэластичный
• Или бесконечность – абсолютно эластичный

Ценовая эластичность спроса

900 02 Формула: Ped = % изменения количества спрос на товар X / % изменения цены товара X

PED обычно будет отрицательным, т. е. обратная зависимость между объемом спроса и изменением цены

ВАЖНО! Новые спецификации требуют, чтобы учащиеся включали знаки «минус» или «плюс» вместе с коэффициентом

• Если PED = 0, спрос абсолютно неэластичен по цене
• Если PED <1, спрос неэластичен по цене
• Если PED > 1, спрос неэластичен по цене
• Если PED = бесконечность, спрос абсолютно эластичен по цене
• Если PED = 1, спрос унитарно эластичен к изменению дохода

  Формула: YED = % изменения количества спроса / % изменения дохода

  • Для товаров первой необходимости: YED положителен, но коэффициент < +1
  • Для обычных предметов роскоши: YED положителен, но коэффициент > +1
  • Для некачественные товары: YED имеет отрицательное значение (YED<0)

  Перекрестная эластичность спроса по цене

  • Перекрестная эластичность спроса по цене (XED) измеряет процентное изменение объема спроса на товар А после изменения цены другого продукт, хорошо B
  • Товары-заменители (при конкурентном спросе) имеют положительную перекрестную эластичность спроса.