В какой зависимости находятся параметры по отношению друг к другу: Параметризация
alexxlab | 13.04.2023 | 0 | Разное
Параметризация
С помощью параметризации осуществляется оценка:
1. Только формы оригинала.
2. Формы, положения оригинала и его частей.
3. Только положения частей оригинала относительно друг друга.
4. Только положения оригинала в пространстве.
Согласно теории параметризации, по отношению друг к другу параметры:
1. Независимы.
2. Находятся в обратно пропорциональной зависимости.
3. Находятся в прямо пропорциональной зависимости.
4. Находятся в экспоненциальной зависимости.
Процесс измерения параметров начинается:
1. Назначения системы параметризации.
2. Изучения работы измерительных приборов.
3.
Определения единиц измерения.
4. Определения необходимых измерительных приборов.
Система параметризации выбирается вне оригинала при определении:
1. Параметров формы.
2. Произвольных параметров.
3. Параметров положения
4. Любых параметров.
На чертежах параметры реализуются:
1. Только условными обозначениями.
2. Только геометрическими условиями.
3. Только размерами.
4. Условными обозначениями, геометрическими условиями, размерами.
Связь между количеством параметров, необходимых для выделения из множества фигур единственной фигуры, количеством параметра формы ПФ, положения ПП, параметров, заменяемых геометрическими условиями ГУ, выражается соотношением:
1. П = ПП + ПФ. 2.
П = (ПП + ПФ)/2 + ГУ.
3. П = ПП + ПФ + ГУ.
4. П = ПП + ПФ – ГУ.
Система параметризации называется связанной с оригиналом при определении:
1. Параметров формы.
2. Произвольных параметров.
3. Параметров положения.
4. Любых параметров.
Количество параметров, позволяющих определить положение произвольной точки в пространстве, носит название:
1. Описание пространства.
2. Определение пространства.
3. Параметр пространства.
4. Размерность пространства.
Классификация аксонометрических изображений на изометрию, диметрию, триметрию производится на основании:
1. Соотношения показателей по всем осям.
2.
Направления проецирующих лучей по
отношению к плоскости проекций.
3. Произвольным образом.
4. Соотношения показателей по осям абсцисс и аппликат.
Основой для вторичной проекции аксонометрии оригинала может служить:
1. Любой из стандартных видов.
2. Только фронтальная проекция.
3. Только горизонтальная проекция.
4. Только профильная проекция.
Показатели искажения по всем осям различны в:
1. Изометрии.
2. Диметрии.
3. Триметрии.
4. Любом виде аксонометрии.
Классификация аксонометрии на прямоугольную и косоугольную производится на основании:
1. Соотношения показателей по всем осям.
2.
Направления проецирующих лучей по
отношению к плоскости проекций.
3. Произвольным образом.
4. Соотношения показателей по осям абсцисс и ординат.
Показатели искажения по всем осям одинаковы в:
1. Изометрии.
2. Диметрии.
3. Триметрии.
4. Любом виде аксонометрии.
Аксонометрический чертеж оригинала получают на:
1. Четырех плоскостях проекций.
3. Двух плоскостях проекций.
4. Одной плоскости проекций.
Вторичной проекцией точки называется:
1. Только проекция проекции точки на плоскость x0y.
2. Проекция проекции точки на любую координатную плоскость.
3. Только проекция точки на плоскость x0y.
4.
Только проекция проекции точки на
плоскость x0z.
Аксонометрические оси – это:
1. Оси натуральной системы координат.
2. Аксонометрические проекции осей натуральной системы координат.
3. Оси системы координат, не связанных с оригиналом.
4. Проекции осей абсцисс и ординат системы, не связанной с оригиналом.
Аксонометрия может быть получена проецированием:
1. Только ортогональным.
2. Только параллельным.
3. Любого вида.
4. Только центральным.
Сущность метода аксонометрии состоит в том, что оригинал относят к некоторой системе координат и затем проецируют на плоскость проекций вместе с:
1. Другими предметами.
2. Координатной системой.
3.
Только с осью абсцисс.
4. Только с осью ординат.
Напряженность электрического поля — как найти? Правила и примеры
Что такое электрическое поле
Долгое время ученые не могли толком объяснить, как именно заряженные тела взаимодействуют друг с другом, не соприкасаясь. Майкл Фарадей первым выяснил, что между ними есть некое промежуточное звено. Его выводы подтвердил Джеймс Максвелл, который установил, что для воздействия одного такого объекта на другой нужно время, а значит, они взаимодействуют через «посредника».
В современной физике электрическое поле — это некая материя, которая возникает вокруг заряженных тел и обусловливает их взаимодействие. Если речь идет о неподвижных объектах, поле называют электростатическим. |
Тела, имеющие одноименные заряды, будут отталкиваться, а разноименные — притягиваться.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Определение напряженности электрического поля
Для исследования электрического поля используются точечные заряды. Давайте выясним, что это такое.
Точечным зарядом называют такой наэлектризованный объект, размерами которого можно пренебречь, поскольку он слишком мал в сравнении с расстоянием, отделяющим этот объект от других заряженных тел. |
Теперь поговорим непосредственно о напряженности, которая является одной из главных характеристик электрического поля. Это векторная физическая величина. В отличие от скалярных она имеет не только значение, но и направление.
Для того, чтобы исследовать электрическую напряженность, нужно в поле заряженного тела q1 поместить еще один точечный заряд q2 (допустим, они оба будут положительными).
Напряженность электрического поля — это показатель, равный отношению силы, действующей на заряд в электрическом поле, к величине этого заряда. |
Напряженность является силовой характеристикой поля. Она говорит о том, как сильно влияние поля в данной точке не только на другой заряд, но также на живые и неживые заряженные объекты.
Важно!
Иногда можно услышать оборот «напряжение электрического поля», но это ошибка — правильно говорить «напряженность».
Единицы измерения и формулы
Из указанного выше определения понятно, как найти напряженность электрического поля в некой точке:
E = F / q, где F — действующая на заряд сила, а q — величина заряда, расположенного в данной точке.
Если нужно выразить силу через напряженность, мы получим следующую формулу:
Направление напряженности электрического поля всегда совпадает с направлением действующей силы. Если взять отрицательный точечный заряд, формулы будут работать аналогично.
Поскольку сила измеряется в ньютонах, а величина заряда — в кулонах, единицей измерения напряженности электрического поля является Н/Кл (ньютон на кулон).
Принцип суперпозиции
Допустим, у нас есть несколько зарядов, которые взаимодействуют. Вокруг каждого существует свое электрическое поле. Тогда существует некая точка или область, в которой одновременно существует электрическое поле нескольких зарядов. Чему равна общая напряженность электрического поля, создаваемого этими зарядами?
Было установлено, что общая сила воздействия на конкретный заряд, расположенный в поле, является суммой сил, действующих на данный заряд со стороны каждого тела.
Из этого следует, что и напряженность поля в любой взятой точке можно вычислить, просуммировав векторно напряженности, создаваемые каждым зарядом в отдельности в той же точке. Это и есть принцип суперпозиции.
Это правило корректно для любых полей, за некоторыми исключениями. Принцип суперпозиции не соблюдается в следующих случаях:
Но задачи с такими данными выходят за пределы школьного курса физики.
Напряженность поля точечного заряда
У электрического поля, создаваемого точечным зарядом, есть одна особенность — ввиду малой величины самого заряда оно очень слабо влияет на другие наэлектризованные тела. Именно поэтому такие «точки» используют для исследований.
Но прежде чем рассказать, от чего зависит напряженность электрического поля точечного заряда, рассмотрим подробнее, как взаимодействуют эти заряды.
Закон Кулона
Предположим, в вакууме есть два точечных заряда, которые статично расположены на некотором расстоянии друг от друга.
В зависимости от одноименности или разноименности они могут притягиваться либо отталкиваться. В любом случае на них действуют силы, направленные вдоль соединяющей их прямой.
Закон Кулона Модули сил, действующих на точечные заряды в вакууме, пропорциональны произведению данных зарядов и обратно пропорциональны квадрату расстояния между ними. |
Силу электрического поля в конкретной точке можно найти по формуле: где q1 и q2 — модули точечных зарядов, r — расстояние между ними.
В формуле участвует коэффициент пропорциональности k, который был определен опытным путем и представляет собой постоянную величину. Он обозначает, с какой силой взаимодействуют два тела с зарядом 1 Кл, расположенные на расстоянии 1 м.
Важно!
Сила взаимодействия двух точечных зарядов остается прежней при появлении сколь угодно большого количества других зарядов в данном поле.
Учитывая все вышесказанное, напряжение электрического поля точечного заряда в некой точке, удаленной от заряда на расстояние r, можно вычислить по формуле:
Итак, мы выяснили, что называется напряженностью электрического поля и от чего зависит эта величина. Теперь посмотрим, как она изображается графическим способом.
Онлайн-подготовка к ОГЭ по физике поможет снять стресс перед экзаменом и получить высокий балл.
Линии напряженности
Электрическое поле нельзя увидеть невооруженным глазом, но можно изобразить с помощью линий напряженности. Графически это будут непрерывные прямые, которые связывают заряженные объекты. Условная точка начала такой прямой — на положительном заряде, а конечная точка — на отрицательном.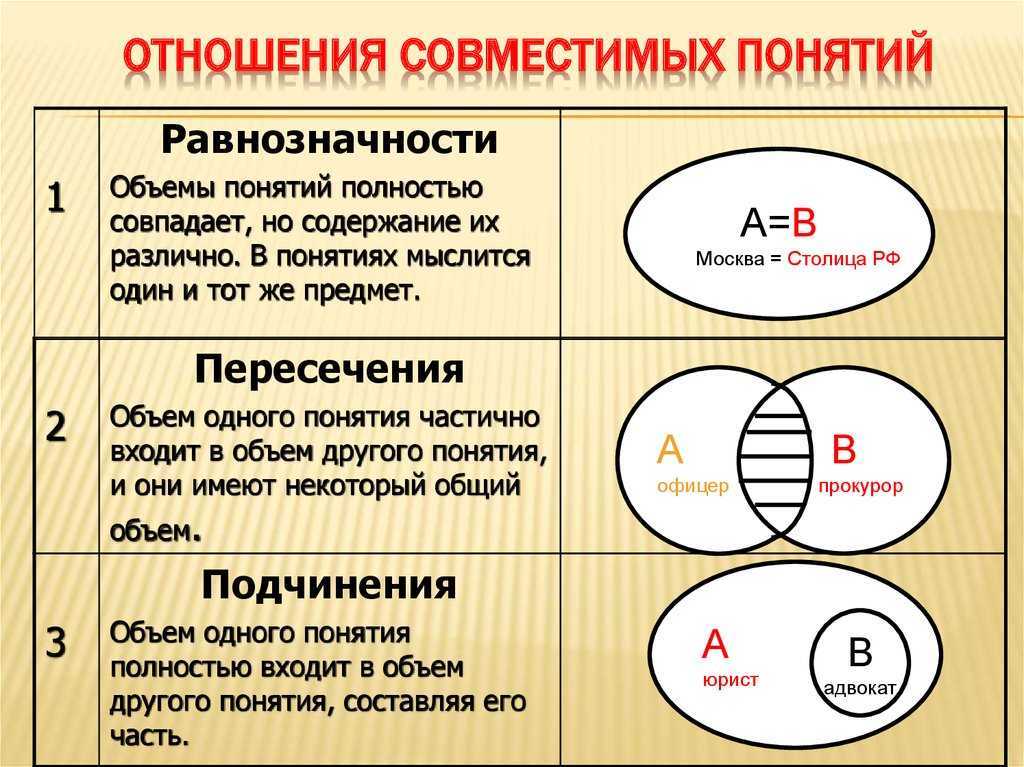
Линии напряженности — это прямые, которые совпадают с силовыми линиями в системе из положительного и отрицательного зарядов. Касательные к ним в каждой точке электрического поля имеют то же направление, что и напряженность этого поля. |
При графическом изображении силовых линий можно передать не только направление, но и величину напряженности электрического поля (разумеется, условно). В местах, где модуль напряженности выше, принято делать более густой рисунок линий. Есть и случаи, когда густота линий не меняется — это бывает при изображении однородного поля.
Однородное электрическое поле создается разноименными зарядами с одинаковым модулем, расположенными на двух металлических пластинах. Линии напряженности между этими зарядами представляют собой параллельные прямые всюду, за исключением краев пластин и пространства за ними.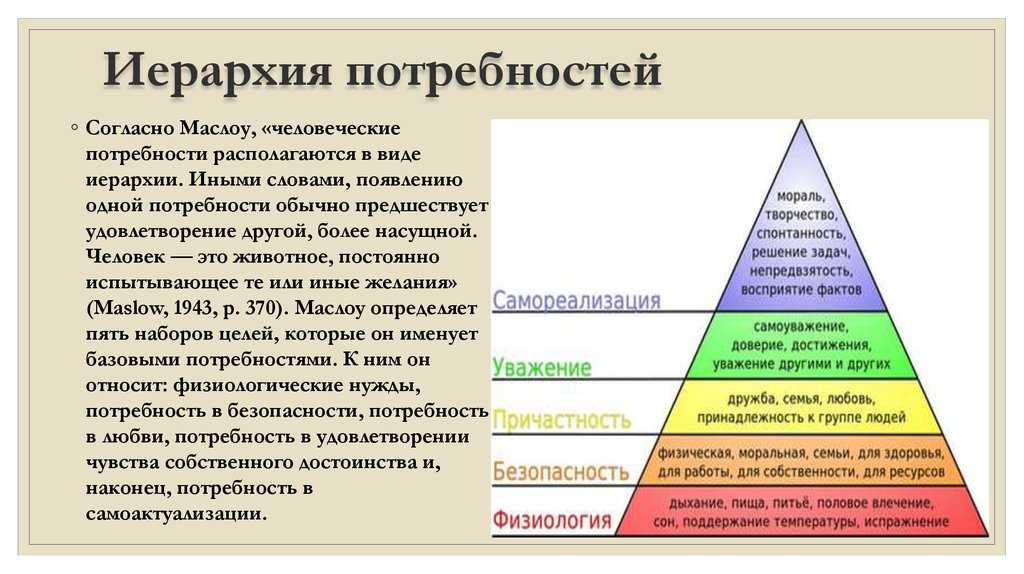
Что такое параметры в математике?
Параметры представляют собой особый тип математических переменных. Параметрическое уравнение содержит одну или несколько параметрических переменных, которые могут иметь несколько возможных значений. Репетиторство по математике может помочь учащимся понять сложные концепции параметров, функций и значений. Значение каждого параметра сохраняется постоянным при использовании функции. В статистических разделах математики параметр представляет собой оценочное числовое значение характеристики совокупности.
Примеры параметрических уравненийКвадратное уравнение — известный пример, который можно записать в виде параметрического уравнения. В форме ax2 + bx + c = 0 a, b и c являются параметрами. Если параметрическим переменным присваиваются значения (например, a = 1, b = 2, c = 3), уравнение перестает быть параметрическим. x2 + 2x + 3 — отдельный член семейства квадратичных функций.
Другим известным примером является уравнение прямой линии, проведенной в декартовой системе координат.
Наиболее общая форма уравнения: y = mx + b. Переменные m и b обычно называют наклоном и точкой пересечения соответственно. Варьируя m и b, можно получить бесконечное число различных прямых линий. Однако уравнение никогда не может дать параболу или окружность, независимо от того, какая комбинация m и b используется. Говорят, что уравнение производит семейство функций, потому что каждая функция дает один и тот же результат — прямую линию.
Параметр может также использоваться для описания системы уравнений. Например, если мяч брошен и его траектория построена в декартовой системе координат, обе компоненты траектории x и y зависят от времени после того, как мяч был брошен, и от начальной скорости мяча. Уравнения могут выглядеть примерно так: x = vt и y = vt – 5t2. В данном случае параметрами являются скорость и время.
Более продвинутым применением параметров является метод вариации параметров, который используется для решения дифференциальных уравнений.
В этом методе параметры фактически являются функциями, которые заменяют неизвестные константы в решении дифференциального уравнения. Решая эти параметрические функции, можно определить неизвестные константы и найти общее и частное решения дифференциального уравнения.
Существует множество способов использования параметров в реальных сценариях, например, в области статистики. В статистике параметр представляет собой оценку данной совокупности. Общие статистические параметры включают среднее значение и стандартное отклонение. Эти оценки используются в уравнениях для расчета тестовой статистики для различных статистических тестов.
Когда в старшей школе изучают параметры? Учащиеся должны иметь четкое представление о параметрах для успеха в предварительном исчислении и исчислении, которые широко преподаются в средних школах. Параметры часто изучаются вместе с другими математическими функциями в предварительном исчислении.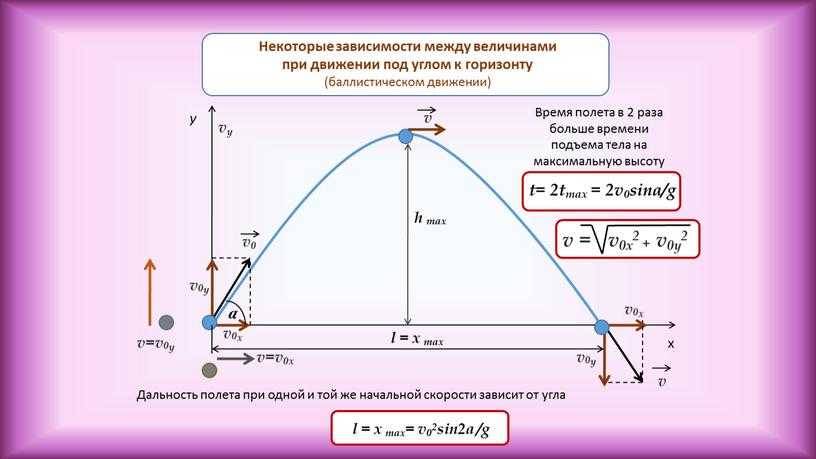
Поскольку параметры преподаются в предварительном исчислении, учащиеся, скорее всего, узнают о них во второй половине своей карьеры в старшей школе.
Старшеклассники обычно изучают алгебру 1 в девятом классе, геометрию в десятом классе, алгебру 2 или тригонометрию в одиннадцатом классе и предварительный анализ или исчисление в двенадцатом классе. Тем не менее, отличники или учащиеся AP, скорее всего, будут изучать алгебру 1 в восьмом классе, геометрию в девятом классе, алгебру 2 или тригонометрию в десятом классе, предварительное исчисление в одиннадцатом классе и исчисление в двенадцатом классе. Это может отличаться от штата к штату, поскольку существуют некоторые различия в руководящих принципах штатов в отношении учебной программы по математике, преподаваемой в средних школах.
Параметрические уравнения часто используются для описания типов кривых, которые могут быть представлены на плоскости, но эти уравнения также используются, когда кривые на декартовой плоскости не могут быть описаны функцией.
Параметры позволяют отображать полное положение объекта во времени.
В повседневной жизни параметрические уравнения полезны для измерения кругового движения и движения снаряда. Например, вы можете использовать параметры для измерения кривой брошенного мяча или вашего положения на движущемся колесе обозрения.
Есть ли параметрические уравнения в SAT? Математический раздел SAT охватывает довольно широкий круг математических тем. Студенты должны понимать такие понятия, как операции, алгебра, функции, геометрия, измерения, анализ данных, статистика и вероятность, чтобы добиться успеха на SAT. Математический раздел SAT включает 19 вопросов по алгебре, 17 вопросов о решении задач и анализе данных, 16 вопросов, связанных с продвинутой математикой (например, решение квадратных уравнений и работа с полиномами), и 6 вопросов, связанных с дополнительными математическими темами (например, тригонометрия). , вычисление площади и объема и использование теорем, связанных с окружностями и линиями).
Вопросы SAT Math, скорее всего, проверят учащихся на их способность создавать и решать линейные уравнения, анализировать количественные данные, применять вероятности в контексте, создавать эквивалентные алгебраические выражения, решать задачи, связанные с площадью и объемом, работать с прямоугольными треугольниками и тригонометрическими функциями, и более. Математический раздел SAT вряд ли будет включать темы предварительного исчисления, такие как параметрические уравнения.
Однако, несмотря на то, что параметрические уравнения не являются основной частью теста SAT по математике, учащиеся должны приложить все усилия, чтобы понять эти концепции. Плохая успеваемость по предварительному исчислению или исчислению может негативно сказаться на успеваемости учащегося и его среднем балле.
Как репетиторы по математике могут помочь учащимся Онлайн-репетитор — отличный способ оказать учащимся поддержку, необходимую им для достижения успеха в математике на любом уровне.
Если учащегося пугают понятия, которые он изучает на уроке математики, репетитор может дать ему дополнительные инструменты и ресурсы для изучения материала в индивидуальной обстановке. Не менее важно и то, что работа с репетитором бесценна для укрепления уверенности учащихся. Точно так же, если учащийся преуспевает в математике, репетитор может предложить ему возможность выйти за рамки основ школьной программы, решить новые задачи и развить навыки критического мышления. Репетиторы по математике для учащихся — отличный способ помочь учащимся раскрыть свой истинный потенциал, независимо от их стиля обучения и академических потребностей.
Learner позволяет легко найти подходящего репетитора для каждого ребенка. Начать работу очень просто, и она полностью сосредоточена на академическом профиле учащегося. Первый шаг для родителей — ответить на вопросы об уникальных потребностях и опыте своего ребенка на веб-сайте Learner. Затем родители могут запланировать звонок академического тренера, чтобы определить цели и задачи обучения.
Наконец, Learner подберет для каждого ребенка подходящего репетитора. Первое занятие с репетитором Learner всегда на 100 % бесплатно, чтобы убедиться, что репетиторство подходит ребенку.
Ищете индивидуальные занятия по математике? Поговорите с нашим академическим консультантом, чтобы получить индивидуальное соответствие с вашим онлайн-репетитором по математике сегодня!
Часто задаваемые вопросы о параметрах Используют ли инженеры параметрические уравнения?Параметрические уравнения используются инженерами для поиска решений проблем. Эти уравнения можно использовать в качестве моделей для визуализации упрощений рассматриваемой системы и реального контекста, в котором работает система.
Можно ли использовать параметрические уравнения в текстовых задачах? Параметрические уравнения можно использовать в текстовых задачах, когда применяется математика параметров. Иногда у фактического параметра будет график, сопровождающий проблему вместе с параметрами.
В математике параметрическое уравнение определяет группу величин как функции одной или нескольких независимых переменных, называемых параметрами.
Что такое позиционные параметры?Позиционный параметр — это параметр, обозначаемый одной или несколькими цифрами, кроме одной цифры 0. Позиционные параметры связаны по положению, а позиционные параметры назначаются, но могут быть переназначены. Позиционные параметры могут называться одноместными параметрами.
Откуда взялся термин «параметр»?Термин «параметр» происходит от древнегреческих слов, означающих «помимо, вспомогательный» и «мера». Параметр определяется как величина, влияющая на результат поведения математического объекта. Он считается постоянным.
В чем разница между параметром и переменной? Переменная — это способ представления атрибута или количества.
Зависимая переменная — это переменная, которая зависит от других факторов. Другими словами, независимая переменная является причиной, а зависимая — следствием. В отличие от переменных параметр является константой в уравнении, описывающем модель.
Примечания к статистике Переменные и параметры
Как и все специальные области, статистика разработала свой собственный язык. Как мы уже отмечали, 1 может возникнуть большая путаница, когда общеупотребительному слову также придается техническое значение. Статистика изобилует такими терминами, включая нормальный, случайный, дисперсионный, значимый и т. д. Двумя часто путаемыми терминами являются переменная и параметр; здесь мы объясняем и противопоставляем их.
Информация, записанная о выборке лиц (часто пациентов), включает такие измерения, как кровяное давление, возраст или вес, а также такие атрибуты, как группа крови, стадия заболевания и диабет. Их значения будут различаться у разных субъектов; в этом контексте кровяное давление, вес, группа крови и т.
д. являются переменными. Переменные – это величины, которые варьируются от человека к человеку.
Напротив, параметры относятся не к фактическим измерениям или атрибутам, а к величинам, определяющим теоретическую модель. На рисунке показано распределение измерений сывороточного альбумина у 481 белого мужчины старше 20 лет со средним значением 46,14 и стандартным отклонением 3,08 г/л. Для эмпирических данных среднее значение и стандартное отклонение называются выборочными оценками. Они являются свойствами совокупности индивидуумов. Также показано нормальное распределение 1 , которое наиболее точно соответствует данным. Он также имеет среднее значение 46,14 и стандартное отклонение 3,08 г/л. Для теоретического распределения среднее значение и стандартное отклонение называются параметрами. Существует не одно нормальное распределение, а множество, называемых семейством распределений. Каждый член семейства определяется своим средним значением и стандартным отклонением, параметры 1 , которые определяют конкретное теоретическое нормальное распределение, с которым мы имеем дело.
В этом случае они дают наилучшую оценку популяционного распределения сывороточного альбумина, если можно предположить, что в популяции сывороточный альбумин имеет нормальное распределение.
Большинство статистических методов, таких как тесты t , называются параметрическими, поскольку они оценивают параметры некоторого основного теоретического распределения. Непараметрические методы, такие как U-критерий Манна-Уитни и логарифмический ранговый критерий для данных о выживании, не предполагают какого-либо конкретного семейства для распределения данных и, следовательно, не оценивают какие-либо параметры для такого распределения.
Другое использование слова «параметр» связано с его первоначальным математическим значением как значения, определяющего одну из групп кривых. Если мы подбираем регрессионную модель, такую как модель, описывающая связь между функцией легких и ростом, наклон и точка пересечения этой линии (более известные как коэффициенты регрессии) являются параметрами, определяющими модель.
Они не имеют значения для отдельных людей, хотя их можно использовать для прогнозирования функции легких человека по его росту.
В некоторых контекстах параметры — это значения, которые можно изменить, чтобы увидеть, что происходит с производительностью некоторой системы. Например, эффективность программы скрининга (такая как положительная прогностическая ценность или экономическая эффективность) будет зависеть от таких аспектов, как чувствительность и специфичность скринингового теста. Если мы посмотрим, как изменится производительность, если, скажем, улучшить чувствительность и специфичность, то мы будем рассматривать их как параметры, а не использовать значения, наблюдаемые в реальном наборе данных.
Параметр — это технический термин, который только недавно стал широко использоваться, но, к сожалению, не сохранил своего правильного значения. В медицинских журналах часто встречаются переменные, неправильно называемые параметрами (но не в BMJ , мы надеемся, 2 ).