Вес теоретический: Теоретический и фактический вес металлопроката

alexxlab | 10.07.2023 | 0 | Разное

Таблицы веса – теоретический вес металлопроката

По таблицам веса металлопроката можно самостоятельно произвести расчет длины или площади металлопроката по его массе – расчет количества метров погонных в 1 тонне сортового и фасонного проката или расчет количества квадратных метров в 1 тонне плоского (листового) проката. В таблицах теоретический веса металлопроката указан в килограммах. 

Таблица 1.

ВЕС МЕТРА АРМАТУРЫ

Теоретический вес метра арматуры. (вес или масса 1 погонного метра арматуры)
Диаметр, мм	масса 1м	Диаметр, мм	масса 1м	Диаметр, мм	масса 1м	Диаметр, мм	масса 1м
6	0,222	14	1,21	22	2,98	36	7,99
8	0,395	16	1,58	25	3,85	40	9,87
10	0,617	18	2,00	28	4,83	45	12,48
12	0,888	20	2,47	32	6,31	50	15,41

Таблица 2.

ВЕС МЕТРА УГОЛКА

Теоретический вес метра уголка. (вес 1 погонного метра уголка)
Размер, мм	масса 1м	Размер, мм	масса 1м	Размер, мм	масса 1м	Размер, мм	масса 1м
20х20х3	0,89	50х50х4	3,05	80х80х7	8,51	140х140х12	25,5
20х20х4	1,15	50х50х5	3,77	80х80х8	9,65	160х160х10	24,7
25х25х3	1,12	63х63х5	4,81	90х90х7	9,64	160х160х11	27
25х25х4	1,46	63х63х6	5,72	90х90х8	10,9	160х160х12	29,4
28х28х3	1,27	70х70х5	5,38	100х100х7	10,8	160х160х14	34
32х32х3	1,46	70х70х6	6,39	100х100х8	12,2	160х160х16	38,5
32х32х4	1,91	70х70х7	7,39	100х100х10	15,1	180х180х11	30,5
35х35х3	1,59	75х75х5	5,8	100х100х12	17,9	180х180х12	33,1
35х35х4	2,12	75х75х6	6,89	125х125х10	19,1	200х200х12	37
40х40х4	2,42	75х75х7	7,96	125х125х12	22,7	200х200х14	42,8
45х45х4	2,97	75х75х8	9,02	125х125х14	26,2	200х200х16	48,7
45х45х5	3,37	80х80х6	7,36	140х140х10	21,5	200х200х20	60,1

Таблица 3.

ВЕС МЕТРА ШВЕЛЛЕРА

Теоретический вес метра швеллера. (вес 1 погонного метра швеллера)
Номер	масса 1м	Номер	масса 1м	Номер	масса 1м	Номер	масса 1м
5/5П	4,84	12/12П	10,4	20/20П	18,4	30/30П	31,8
6,5/6,5П	5,9	14/14П	12,3	22/22П	21	33/33П	36,5
8/8П	7,05	16/16П	14,2	24/24П	24	36/36П	41,9
10/10П	8,59	18/18П	16,3	27/27П	27,7	40/40П	48,3

Таблица 4.

ВЕС СТАЛЬНОГО ЛИСТА

Теоретический вес метра квадратного (м./кв.) стального листа. (Прокат листовой холодно и горячекатаный)
Толщина, мм	1м.кв	Толщина, мм	1м.кв	Толщина, мм	1м.кв	Толщина, мм	1м.кв
0,5	3,925	1,8	14,13	10	78,5	32	251,2
0,55	4,32	2	15,7	12	94,2	36	282,6
0,6	4,71	2,5	19,62	14	109,9	40	314
0,7	5,5	3	23,55	16	125,6	50	392,5
0,8	6,28	4	31,4	18	141,3	60	471
0,9	7,06	5	39,25	20	157	70	549,5
1	7,85	6	47,1	22	172,7	80	628
1,2	9,42	8	62,8	25	196,25	90	706,5
1,5	11,7	9	70,65	30	235,5	100	785

Таблица 5.

ВЕС ПРОФИЛЬНОЙ ТРУБЫ

Теоретический вес метра трубы профильной. (вес 1 метра прямоугольной и вес 1 метра квадратной трубы)
Размер, мм	1метр, кг	Размер, мм	1метр, кг	Размер, мм	1метр, кг	Размер, мм	1метр, кг
15х15х1,0	0,426	60х60х4,0	6,82	15х10х1,0	0,348	40х25х3,0	2,66
15х15х1,5	0,605	60х60х5,0	8,3	15х10х1,5	0,488	40х30х2,0	2,02
20х20х1,0	0,583	60х60х6,0	9,69	20х10х1,0	0,426	40х30х2,5	2,47
20х20х1,5	0,841	70х70х4,0	8,07	20х10х1,5	0,605	50х25х2,0	2,17
20х20х2,0	1,075	70х70х5,0	9,87	20х15х1,0	0,505	50х25х2,5	2,66
25х25х1,5	1,07	80х80х4,0	9,33	20х15х1,5	0,723	50х25х3,0	3,13
25х25х2,0	1,39	80х80х5,0	11,44	25х10х1,0	0,505	60х30х2,5	3,25
25х25х2,5	1,68	80х80х6,0	13,46	25х10х1,5	0,723	60х30х3,0	3,83
30х30х2,0	1,7	90х90х5,0	13	25х15х1,0	0,583	60х30х3,5	4,39
30х30х2,5	2,07	90х90х6,0	15,34	25х15х1,5	0,841	80х40х3,0	5,25
30з30з3,0	2,42	100х100х6,0	17,22	30х10х1,0	0,583	80х40х3,5	6,04
40х40х2,0	2,33	100х100х7,0	19,78	30х10х1,5	0,841	80х40х4,0	6,82
40х40х2,5	2,85	100х100х8,0	22,25	30х15х1,0	0,661	100х50х4,0	8,7
40х40х3,0	3,36	120х120х6,0	20,99	30х15х1,5	0,959	100х50х5,0	10,65
40х40х3,5	3,85	120х120х8,0	27,27	30х15х2,0	1,23	100х50х6,0	12,51
40х40х4,0	4,3	140х140х6,0	24,76	40х20х2,0	1,7	120х60х6,0	15,34
50х50х3,0	5,48	140х140х8,0	32,29	40х20х2,5	2,07	120х60х8,0	19,73
50х50х3,5	6,3	180х180х8,0	42,34	40х20х3,0	2,42	120х80х6,0	17,22
50х50х4,0	7,08	180х180х10,0	52,03	40х25х2,0	1,86	120х80х8,0	22,25
50х50х5,0	8,57	180х180х12,0	61,36	40х25х2,5	2,27	180х100х8,0	32,29

  ВНИМАНИЕ !

В таблицах приведен теоретический вес металлопроката (теоретический вес или масса металлопроката согласно ГОСТ РФ), в реальности, как показывает практика, фактический вес метра погонного арматуры (масса арматуры), стального круга, уголка, швеллера, полосы или трубного металлопроката или вес 1 метра квадратного листового или плоского металлопроката у разных заводов- производителей имеет отклонения в большую или меньшую сторону. Все это необходимо учитывать при расчете массы арматура А3 и А1, массы трубы, или массы любого другого профиля металлопроката.

В ГОСТ РФ на различные профиля и типы металлопроката приведены предельно допустимые отклонения фактического веса от теоретического веса погонного или квадратного метра профиля металлопроката. Например, допуски по отклонению фактического от теоретического веса арматуры или стального круга приведены в ГОСТ 5781-82.
Продукция отгружается по фактическому весу металлопроката, полученному от производителя, а не по теоретическому, который является по сути усредненной справочной величиной.

2007-2023 ГРУППА ВЕГА | ООО “СТК ВЕГА” / “СТРОЙТЕХ”, +7/495/640-21-81; Информация на сайте носит информационный характер и не является публичной офертой – оферта. © Копирование материалов с сайта запрещено.

Коэффициент пересчета веса металла

Теоретический вес проката должен в идеале соответствовать весу фактическому. Разница между теоретическим Gт и фактическим Gф весом выражается величиной, именуемой “Коэффициент пересчета” (Кп). Целью организации поставок продукции по теоретическому весу является экономия металла за счет производства проката с размерами сечения в поле минусовых допусков. Существует “Положение по организации поставок проката по теоретическому весу”, разработанное Харьковским ВНИИОчермет в 1979 году. В настоящее время большинство компаний, как металлоторгующих так и потребляющих металл, испытывают трудности, связанные как с продажей, так и с покупкой металлопроката по теоретическому весу. Исчисляемый теоретический вес должен в идеальном случае – соответствовать весу фактическому. Разница между теоретическим и практическим весом выражается величиной, именуемой “Коэффициент пересчета”. Заводы – производители работают по этому “Положению” и отгружают продукцию по теоретическому весу, вводя коэффициенты пересчета.

Выдержки из “Положения”: 

Пункт 1.1. Целью организации поставок продукции по теоретическому (сдаточному) весу является экономия металла и повышение эффективности его использования в народном хозяйстве за счет производства проката с размерами сечения в поле минусовых допусков».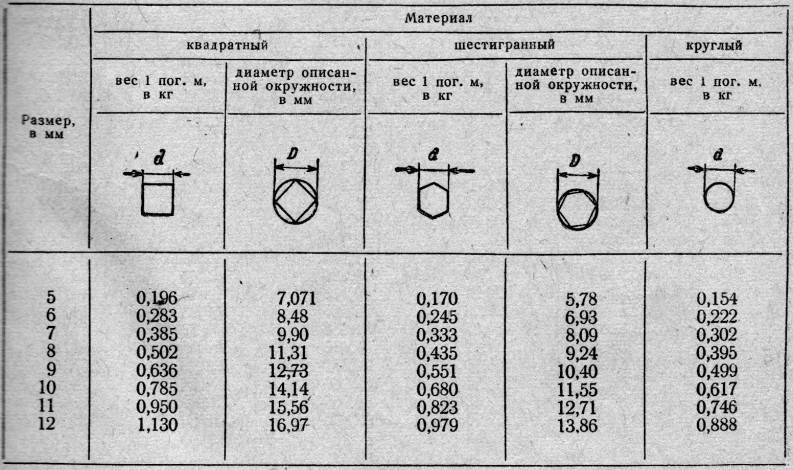 Как известно, за редким исключением допуски на прокатную продукцию двусторонние +. Это обусловлено технологическими особенностями прокатного производства.Пункт 1.5. Теоретическим (сдаточным) весом сортового, фасонного и листового проката считается вес, исчисленный по геометрическим размерам, предусмотренным стандартами для соответствующих видов и профилей проката.

Пункт 1.6. Теоретический вес определяется при двустороннем (плюсовом и минусовом) допусках – по номинальным размерам. При одностороннем плюсовом допуске – по номинальному размеру с прибавлением 50 %-ной величины допуска. При одностороннем минусовом допуске – по номинальному размеру за вычетом 50% величины допуска. Вроде бы все ясно – теоретический вес исчисляют или по номинальным размерам или в середине поля допуска. Но:

Пункт 1.7. При поставках металлопродукции по теоретическому весу, поставщик гарантирует длину сортового (фасонного) или площадь поверхности листового проката, соответствующие его количеству при заказанных размерах сечения.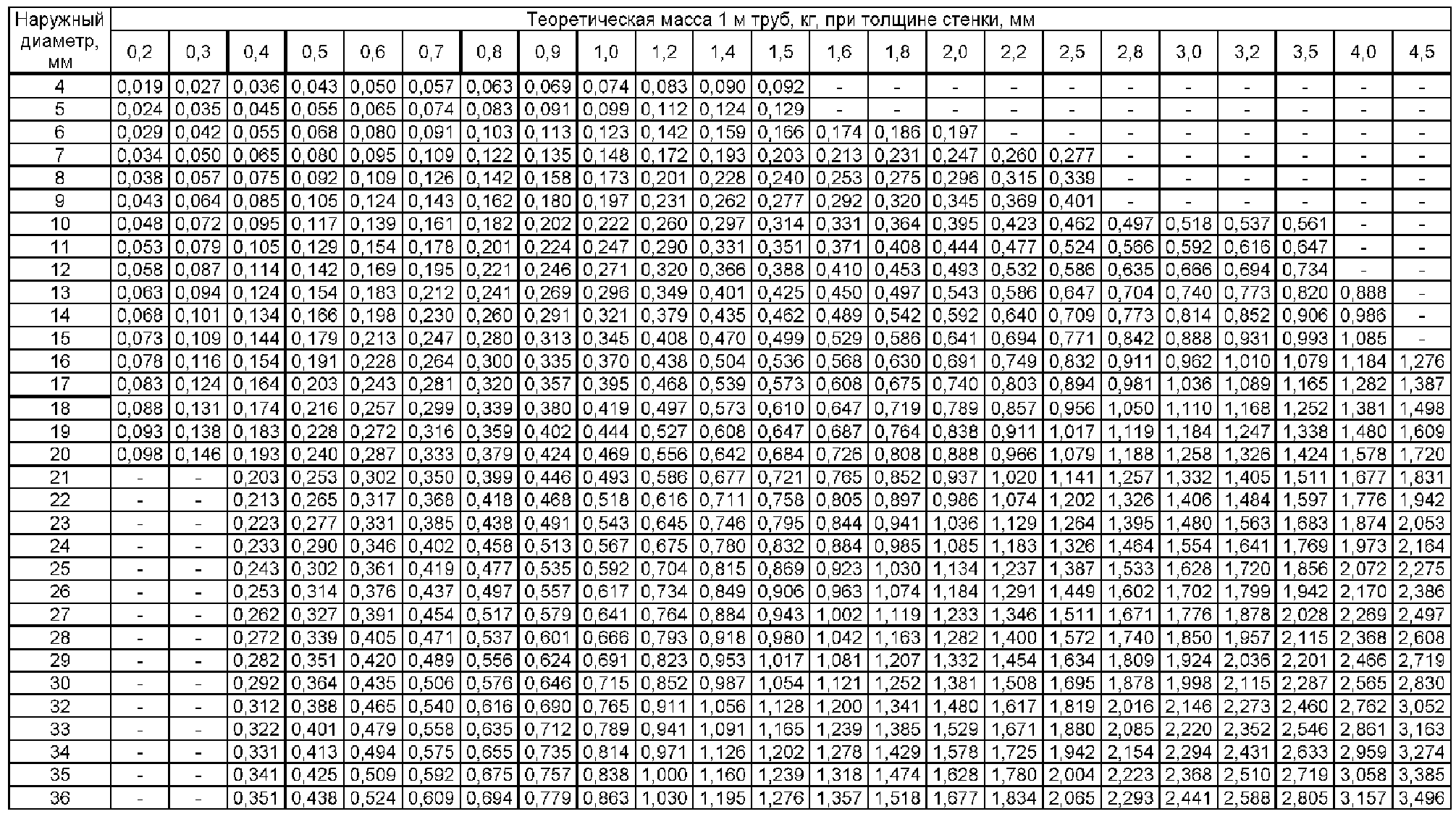 Если поставщик,  гарантирует, то это должно отражаться в сертификате качества, что происходит далеко не всегда.

Пункт 2.1. Для определения теоретического веса партии прокатанного металла, вначале находят его общую длину, а затем умножают ее на теоретический вес единицы длины, который исчисляют исходя из размеров сечения данного профиля и характера  допусков по ГОСТу или ТУ (п. 1.6.).Для листового проката, отгружаемого в пачках (пакетах), теоретический вес может определяться исходя из веса одного листа и количества листов в пачке.

Пункт 2.2. Исходя из необходимости обеспечения равенства заказанной и поставленной длины проката «L», определяют физический (Оф) и теоретический (От) вес партии проката:Gф = L х gф,(2.1).

Gт = L х gт, (2.2). 

где gф и gт – соответственно фактический и теоретический вес 1 м проката, кг.
Тогда длина проката будет исчисляться:
L = Gф/gф,(2.3).
L = Gт/gт, (2.4).

Соответственно теоретический вес металла определяют по формуле.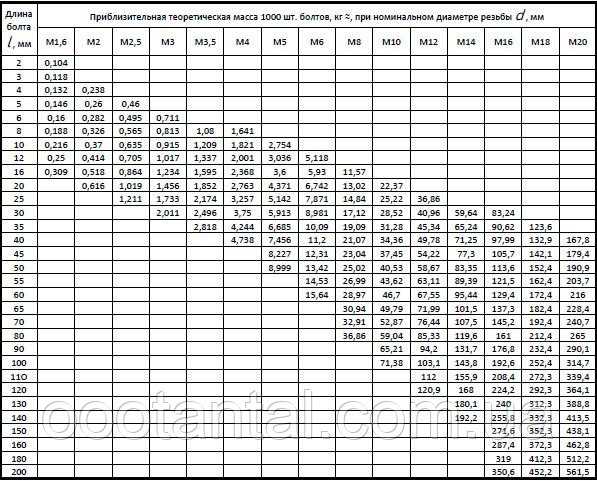
G = Gф х gт/gф (2.5).

Пункт 2.3. Отношение теоретического веса 1 м проката (gт) к его фактическому весу (gф) характеризует использование поля допусков при прокатке и показывает насколько физический вес металла отличается от веса, установленного по размерам сечения, предусмотренного стандартами. Это отношение, называемое коэффициентом использования поля допусков, применяется в качестве коэффициента пересчета (К) для перевода физического веса металла в теоретический.

К = gт/gф.(2.6).
При этом формула (2.5) примет вид:
Gт = К х Gф.(2.7).

Из этого следует – завод – производитель прокатал металлопрокат в минусовом допуске, определил коэффициент пересчета, отправил металл потребителю по теоретическому весу, а металлоторговец должен также отпускать металл по теоретическому весу. Или считать длину сортового проката и умножать на вес 1 м пог. по ГОСТу, или взвесить свой металл, вес умножить на коэффициент пересчета – согласно формуле 2.7.

Коэффициент пересчета веса металлопроката.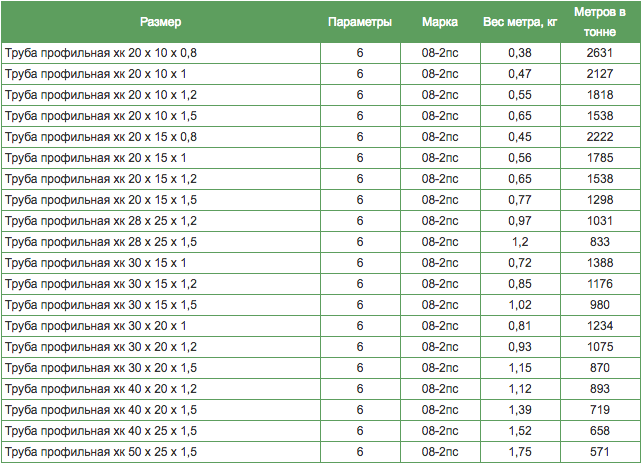  Значение коэффициента пересчета 1.1. “Положения”, который приведен выше, то основная цель поставок продукции по теоретическому весу – “экономия металла и повышение эффективности его использования”.

 

           Gт
Кп = ———
          Gф

 

Пример:
Лист (10х1500х6000мм), Кп = 1,02 
Теоретический вес листа: Gт = V * P , где V – объем,
Р – плотность стали ( 7,85).
Gт = 10 * 1,5 * 6 * 7,85 = 706,5 кг 
Фактический вес листа:
Gф = 706,5 кг / 1,02 = 692,6 кг

Калькулятор теоретической доходности

Создано Джеком Бовотером

Проверено Богной Шик и Стивеном Вудингом

Последнее обновление: 30 декабря 2022 г.

Содержание:

• Определение теоретической доходности Формула теоретического выхода
• Как рассчитать теоретический выход ?
• Примеры расчета доходности
• Часто задаваемые вопросы

Этот калькулятор теоретической доходности ответит на все ваши животрепещущие вопросы относительно как рассчитать теоретическую доходность , например , как найти теоретическую доходность , а также определение теоретической доходности и формулу теоретической доходности .

Перед выполнением любой лабораторной работы вам необходимо выяснить, каков теоретический выход, чтобы вы знали, сколько вашего продукта, будь то молекула или решетка, вы можете ожидать от данного количества исходного материала. Это позволяет вам определить, насколько эффективно вы выполнили свою реакцию (количество, которое вы можете найти на калькуляторе фактического выхода), что делается путем расчета процентного выхода. Вы также можете использовать теоретическое уравнение выхода, чтобы гарантировать, что вы реагируете с равными молями ваших реагентов, чтобы ни одна молекула не тратилась впустую.

ВАЖНОЕ ПРИМЕЧАНИЕ: Выход можно определить только с использованием ограничивающего реагента. Если вы не уверены, какой из ваших реагентов является лимитирующим, подключайте реагенты по одному, и тот из них, который дает наименьшее число молей, будет лимитирующим реагентом. Не забудьте нажать «Обновить» в нижней части калькулятора, чтобы сбросить его.

Определение теоретического выхода

Что такое теоретический выход? Это количество продукта, которое образовалось бы, если бы ваша реакция была эффективной на 100%. Как добиться 100% эффективности? Что ж, это означало бы, что каждая молекула реагировала правильно (то есть не образовывались побочные продукты) на каждом этапе и что ни одна молекула не терялась на стенках стеклянной посуды.

Так как нормальная реакция имеет дело с квинтиллионами молекул или атомов , должно быть очевидно, что некоторые из этих молекул будут потеряны. Следовательно, процентный выход никогда не будет равен 100 %, но его все же полезно знать в качестве показателя эффективности реакции. Чтобы узнать больше об этом, ознакомьтесь с нашим калькулятором процентной доходности (ссылка выше). Узнайте, как рассчитать теоретическую доходность с помощью приведенного ниже уравнения теоретической доходности!

Теоретическая формула выхода

Использование уравнения теоретического выхода поможет вам найти теоретический выход из молей ограничивающего реагента, предполагая эффективность 100%. Итак, чтобы вы не задавались вопросом, как найти теоретический выход, вот формула теоретического выхода:

text{product}}\cdot n _{\text{lim}}\cdot c,mproduct​=ммоль,product​⋅nlim​⋅c,

где:

• mproductm _{\text{product}}mproduct​ — Масса продукта;
• mmol,productm _{\text{mol},\text{product}}mmol,product​ — Молекулярная масса желаемого продукта;
• nlimn_{\text{lim}}nlim​ — моли лимитирующего реагента; и
• ccc — Стехиометрия желаемого продукта.

Количество молей лимитирующего реагента в реакции равно:

nlim=mlmmmol,lim⋅clim,n_{\text{lim}} = \frac{m_{\text{lim}}}{m_ {\text{моль},\текст{lim}}\cdot c_{\text{lim}}},nlim​=ммоль,lim​⋅clim​mlim​​,

где:

• nlimn_{\text{lim}}nlim​ — количество молей лимитирующего реагента;
• mlimm_{\text{lim}}mlim​ — Масса лимитирующего реагента;
• mmol,limm_{\text{mol},\text{lim}}mmol,lim​ — Молекулярная масса лимитирующего реагента; и
• climc_{\text{lim}}clim​ — Стехиометрия лимитирующего реагента.

Стехиометрия определяется как число перед химической формулой в сбалансированной реакции. Если число отсутствует, то стехиометрия равна 1. 9Стехиометрия 0021 необходима для отражения соотношений молекул, которые объединяются для образования продукта .

Преимущество этого калькулятора в том, что его можно использовать как угодно, то есть для нахождения массы реагентов, необходимой для производства определенной массы вашего продукта. Вся эта информация скрыта в молях, которые могут быть получены из молярности или концентрации раствора (вы можете узнать, как это сделать, с помощью нашего калькулятора молярности и калькулятора концентрации).

Как рассчитать теоретический выход?

Формула теоретической доходности может показаться сложной для понимания, поэтому мы покажем вам краткое руководство о том, как рассчитать теоретическую доходность. Необходимые измерения: масса реагентов, их молекулярные массы, стехиометрия реакции (найденная из сбалансированного уравнения) и молекулярная масса желаемого продукта . Не смотрите дальше, чтобы узнать, как найти теоретическую доходность:

1. Сначала рассчитайте моль вашего лимитирующего реагента . Мы делаем это, используя второе уравнение в разделе теоретической формулы доходности (совет: убедитесь, что единицы веса одинаковы для получения правильных результатов: вы можете использовать конвертер веса, если вам нужна помощь с факторами).

2. Выберите реагент с наименьшим числом молей с учетом стехиометрии. Это ваш ограничивающий реагент. Если оба имеют одинаковое количество родинок, вы можете использовать любой из них.

3. Используйте первое уравнение, чтобы найти масса желаемого продукта в любых единицах измерения ваших реагентов.

Ну вот! Если вы все еще боретесь, проверьте приведенные ниже примеры для более практического подхода.

Примеры расчета доходности

Время для некоторых примеров. Допустим, вы проводите реакцию нуклеофильного присоединения, образуя гидроксиацетонитрил из цианида натрия и ацетона.

Реакция с циангидрином и ацетоном (от Rehua — CC BY-SA 3.0, Википедия).

Проигнорируем растворители под стрелкой (они оба будут присутствовать в избытке и, следовательно, не будут лимитирующими реагентами), а также катион натрия цианида натрия, так как это всего лишь ион-наблюдатель. Если мы реагируем 5 г5\ \text{г}5 г ацетона с 2 г2\ \text{г}2 г цианида, каков теоретический выход гидроксиацетонитрила?

1. Сначала нам нужно разработать ограничивающий реагент. Поскольку стехиометрия обоих реагентов равна 1 (т.е. одна молекула ацетона реагирует с одной молекулой цианида), мы можем просто использовать уравнение масса = молекулярная масса × моль , чтобы найти это:

   • Давайте изменим уравнение, чтобы найти родинки. Это дает:
     моль=масса/молекулярная масса\small\text{моль} = \text{масса}/\text{молекулярная масса}моль=масса/молекулярная масса

   • Ацетон имеет молекулярную массу 58 г/моль58\ \text{г}/\text{моль}58 г/моль, поэтому:
     моль=5/58=0,862 моль\small\text{моль} = 5/58 = 0,862\ \text{моль}моль=5/58=0,862 моль

   • Цианид имеет молекулярную массу 26 г/моль26\ \text{г}/\text{моль}26 г/моль, поэтому:
     моль=2/26=0,0769 моль\small\text{моль} = 2/26 = 0,0769\ \text{моль}моль=2/26=0,0769 моль

   • Таким образом, молей цианида меньше, а это означает, что это ограничивающий реагент.

2. Знание ограничивающего реагента и его молей означает знание того, сколько молей образует продукт. Поскольку стехиометрия продукта равна 111, образуется 0,07690,07690,0769 молей.

3. Мы снова можем использовать уравнение масса=молекулярная масса×моль\small\text{масса} = \text{молекулярная масса} \times \text{моль}масса=молекулярная масса×моль для определения теоретической массы продукта. Молекулярная масса гидроксиацетонитрила 85 г/моль85\ \text{г}/\text{моль}85 г/моль:

  mass=85⋅0,0769=6,54 г\quad\ \ \text{mass} = 85 \cdot 0,0769 = 6,54\ \text{g}  mass=85⋅0,0769=6,54 g

Теперь мы знаем, что если выполнить эксперимента мы ожидаем 6,54 г6,54\ \text{г}6,54 г гидроксиацетонитрила. Не так уж плохо, верно?

Допустим, вы пытаетесь синтезировать ацетон для использования в приведенной выше реакции.

Вы реагируете 8 г8\ \text{г}8 г карбоната кальция (100 г/моль100\ \text{г}/\text{моль}100 г/моль) с 9 г9\ \text{g}9 г уксусной кислоты (60 г/моль60\ \text{г}/\text{моль}60 г/моль), сколько образуется ацетона?

1. Еще раз, нам нужно сначала выяснить, какой реагент является ограничивающим. Давайте снова воспользуемся уравнением масса=молекулярная масса⋅моль\small\text{масса} = \text{молекулярная масса}\cdot \text{моль}масса=молекулярная масса⋅мол:

   • Давайте изменим уравнение, чтобы найти родинки. Это дает:
     моль=масса/молекулярная масса\маленький\текст{моль} = \text{масса} / \text{молекулярная масса}моль=масса/молекулярная масса

   • Найдем количество молей уксусной кислоты:
     моль=9/60=0,15 моль\small\text{моль} = 9/60 = 0,15\ \text{моль}моль=9/60=0,15 моль

   • И моль карбоната кальция:
     моль=8/100=0,08 моль\small\text{моль} = 8/100 = 0,08\ \text{моль}моль=8/100=0,08 моль

   • Похоже, лимитирующим реагентом является карбонат кальция. Но ждать! Мы не учитывали стехиометрию. Так как для образования одной молекулы ацетона нам нужно 2 молекулы уксусной кислоты, то надо моли уксусной кислоты разделить на 222:
     моль=0,15/2=0,075 моль\маленький\text{моль} = 0,15 / 2 = 0,075\ \text{моль}моль=0,15/2=0,075 моль

   • Получается, что лимитирующим реагентом является уксусная кислота !

2. Теперь, когда мы знаем предельный реагент и его моли, мы знаем, сколько молей продукта образуется. Поскольку стехиометрия продукта составляет 111, образуется 0,750,750,75 молей.

3. Используйте уравнение масса=молекулярная масса⋅моль\small\text{масса} = \text{молекулярная масса}\cdot\text{моль}масса=молекулярная масса⋅моль для определения теоретической массы продукта. Молекулярная масса ацетона 58 г/моль58\ \text{г}/\text{моль}58 г/моль:

   масса = 58 × 0,075 = 4,35 г \ text {масса} = 58 × 0,075 = 4,35 \ \ text {г} масса = 58 × 0,075 = 4,35 г

Итак, из этой реакции мы должны получить, теоретически говоря, 4,35 г4,35\ \text{г}4,35 г ацетона. Хороший!

А теперь покоряйте мир теоретических расчетов доходности, вы можете это сделать!

Часто задаваемые вопросы

Как узнать теоретическую доходность?

Чтобы найти теоретический выход:

1. Сбалансируйте реакцию.
2. Определите ограничивающий реагент, который представляет собой реагент с наименьшим количеством молей .
3. Разделите наименьшее количество молей реагента на стехиометрию продукта.
4. Умножьте результата шага 3 на молекулярную массу желаемого продукта.

Что такое теоретический выход?

Теоретический выход равен количеству продукта, которое образовалось бы в результате реакции, если бы она была эффективной на 100% . Это максимальная масса продукта, которую могут образовать реагенты, и вы можете сравнить с ней свой выход, чтобы увидеть, насколько успешно вы провели реакцию.

Является ли предельным реагентом теоретический выход?

№ , предельным реагентом не является теоретический выход. Чтобы найти теоретический выход, вы должны найти количество молей лимитирующего реагента. Затем вы можете умножить это число на стехиометрию желаемого продукта, чтобы найти количество образовавшихся молей, а затем использовать это для получения теоретического выхода.

Каков теоретический выход двуокиси углерода?

Теоретический выход CO ₂ зависит от протекающей реакции и количества реагентов. Чтобы найти теоретический выход, выполните следующие действия:

1. Найдите количество молей ограничивающего реагента.
2. Умножьте молей ограничивающего реагента на стехиометрию диоксида углерода в реакции, чтобы получить моли CO ₂ образовавшегося.
3. Умножьте молей CO ₂ на 44, молекулярную массу CO ₂ , чтобы получить теоретический выход вашей реакции.

Джек Боутер

Ограничивающий реагент

Молекулярная масса

г / моль

моль

Стехиометрия

Желаемый продукт

Стехиометрия

моль(и)

Молекулярная масса

г / моль

Теоретический выход

Посмотреть 9 похожих калькуляторов химических реакций 💥

Энергия активацииФактический выходУравнение Аррениуса… Еще 6

Теоретические и фактические выходы – Химия LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

31601

Ключевые термины

• (Избыток реагента, ограничивающий реагент)
• Теоретическая и фактическая доходность
• Процентная или фактическая доходность

Навыки развития

• Используйте стехиометрические расчеты для определения избыточных и ограничивающих реагентов в химической реакции и объясните, почему.
• Рассчитайте теоретические выходы продуктов, образующихся в реакциях с участием лимитирующих реагентов.
• Оценка процентных или фактических выходов из известных количеств реагентов

Теоретические и фактические выходы

Реагенты, не израсходованные полностью, называются избыточными реагентами, а полностью прореагировавший реагент называется лимитирующим реагентом. Эта концепция была проиллюстрирована для реакции:

\[\mathrm{2 Na + Cl_2 \rightarrow 2 NaCl}\]

Количества продуктов, рассчитанные по полной реакции лимитирующего реагента, называются теоретическими выходами, тогда как фактически полученное количество продукта является фактическим выходом. Отношение фактического выхода к теоретическому выходу, выраженное в процентах, называется процентным выходом.

\(\mathrm{проценты\: выход = \dfrac{фактический\: выход}{теоретический\: выход}\times100}\)

Уравнения химических реакций дают идеальное стехиометрическое соотношение между реагентами и продуктами. Таким образом, теоретический выход можно рассчитать по стехиометрии реакции. Для многих химических реакций фактический выход обычно меньше теоретического, что понятно из-за потерь в процессе или неэффективности химической реакции.

Пример \(\PageIndex{1}\)

Метиловый спирт можно получить в реакции высокого давления

\(\mathrm{CO_{\large{(g)}} + 2 H_{2\large{ (g)}} \rightarrow CH_3OH_{\large{(l)}}}\)

Если из 1,2 метрических тонны водорода, реагирующего с избыточным количеством \(\ce{CO}\, получается 6,1 метрических тонны метилового спирта) ), прикиньте теоретическую и процентную доходность?

Раствор

Для расчета теоретического выхода рассмотрим реакцию

\(\begin{alignat}{2}
\ce{&CO_{\large{(g)}} +\, &&2 H_{2\large{(g)}} \rightarrow \, &&CH_3OH_{\large{ (l)}}}\\
&\:28.0 &&\:4.0 &&\:\:\:32.0 \hspace{45px}\ce{(стехиометрический\: массы\: в\: г,\: кг,\ : or\: тонны)}
\end{alignat}\)

\(\mathrm{1.2\: тонны\: H_2 \times\dfrac{32. 0\: CH_3OH}{4.0\: H_2}= 9.6\: тонны \: CH_3OH}\)

Таким образом, теоретический выход из 1,2 метрических тонны (1,2×10 ⁶ г) газообразного водорода составляет 9.6 тонн. Фактический выход указан в задаче, 6,1 метрических тонны. Таким образом, выход в процентах равен

\(\mathrm{\%\: yield =\dfrac{6,1\: тонны}{9,6\: тонны}\times 100 = 64 \%}\)

Благодаря химическому равновесию или закона действующих масс лимитирующий реагент может быть израсходован не полностью. Таким образом, в некоторых случаях ожидается более низкая доходность. Потери в процессе восстановления продукта приведут к еще меньшему фактическому выходу.

Пример \(\PageIndex{2}\)

9+}\)

ОБСУЖДЕНИЕ

Можно также рассчитать теоретический выход \(\ce{AgCl}\) из процентного выхода 98,7% и получить

\(\mathrm{\dfrac{0,1234\: g\ : AgCl}{0,987}= 0,1250\: г\: AgCl}\)

Из 0,1250 г \(\ce{AgCl}\) количество присутствующего \(\ce{Ag+}\) также составляет 0,09409 г.

Проблемы развития навыков

1. В аналитическом эксперименте вас просят определить количество йодид-иона \(\ce{I+}\) в 10,00 мл раствора, который не содержит других ионов, образующих осадок с ионами серебра. Вы узнали, что ионы \(\ce{Ag+}\) осаждают все йодид-ионы в растворе. При проведении эксперимента следует ли рассматривать \(\ce{AgNO3}\) как избыток реагента или лимитирующий реагент? Молярная масса или атомный вес: \(\ce{Ag}\), 107,868; \(\ce{I}\), 126,904 (Вы должны знать, где их найти).

Подсказка: \(\ce{AgNO3}\) – избыточный реагент

Навык –
Применить понятие избыточных и лимитирующих реагентов для работы. Вы можете добавлять \(\ce{AgNO3}\) медленно, пока прозрачная часть раствора не будет давать осадка при добавлении капли раствора \(\ce{AgNO3}\). Это указывает на то, что все ионы \(\ce{I-}\) израсходованы.

2. Из 10,00 мл раствора йодида вы добавили \(\ce{AgNO3}\) раствор или твердое вещество. Как узнать, что вы добавили избыточное количество \(\ce{AgNO3}\) для осаждения иодидов?

Совет: проверьте избыток или ограничивающий реагент.

Навык –
Избыток реагента можно проверить на его наличие, а лимитирующий реагент можно проверить на его отсутствие.

3. В аналитическом опыте из 10,00 мл раствора с избытком нитрата серебра получено 0,1234 г \(\ce{AgI}\). Сколько (в г) йодид-ионов присутствует?

Подсказка: 0,05670 г \(\ce{Ag}\) и 0,06670 г \(\ce{I}\)

Навык –
Рассчитать количество лимитирующего реагента из количества продуктов.

4. В аналитическом эксперименте из 10,00 мл раствора с избытком нитрата серебра было получено 0,1234 г \(\ce{AgI}\). Какова концентрация йодида (моль/л или M) в растворе?

Подсказка: 0,05256 моль/л

Навык –
Рассчитать концентрацию, зная количество растворенного вещества. Понятие концентрации будет рассмотрено в разделе, посвященном раствору, но вы должны уметь конвертировать; см. следующее соотношение.

0,1234 г \(\ce{AgI}\) = 0,0005256 моль = 0,5256 милли-моль \(\ce{AgI}\) или \(\ce{Ag}\) или \(\ce{I}\) .