Вес в погонном метре арматуры: Арматура 25 мм – Вес 1 метра + Калькулятор
alexxlab | 20.05.2023 | 0 | Разное
Масса арматуры А3 – Справочник массы
главная ⇒ строймат ⇒ прокат ⇒ арматура
Масса одного погонного метра рифлёной арматуры диаметром 12 (мм) составляет 0.888 (кг).
Стандартный вес рифлёной арматуры A-III:
Вес погонного метра рифлёной стальной арматуры класса A-III разного диаметра:
- 6 (мм) – 0.222 (кг), 8 (мм) – 0.395 (кг), 10 (мм) – 0.617 (кг), 12 (мм) – 0.888 (кг), 14 (мм) – 1.21 (кг), 16 (мм) – 1.58 (кг), 18 (мм) – 2 (кг), 20 (мм) – 2.47 (кг), 22 (мм) – 2.98 (кг).
Такую арматуру выполняют из низколегированных конструкционных сталей (ГОСТ 5058-65) следующих марок: 35ГС, 25Г2С, 32Г2Рпс.
Технические условияГОСТ 5781-82 определяют параметры рифлёной арматуры класса A-III, используемой для армирования конструкций из железобетона.
Важно: согласно ГОСТ 5781-82 в стали марки 32Г2Рпс можно заменить алюминий титаном или цирконием в равных долях.
| Общая масса арматуры А3 | |||
|---|---|---|---|
| Чертеж Чертеж и параметры типовой модели | d (мм) Предел диаметра арматуры в (мм) | m (кг) Предел массы арматуры в (кг) | Норматив Нормативный документ |
Арматура А1 | от 6 (мм) до 80 (мм) | от 0. 222 (кг) до 39.460 (кг) | ГОСТ 5781-82 |
| Таблица массы арматуры А3 | |||
|---|---|---|---|
| d (мм) Диаметр арматуры в (мм) | m (кг) Предел массы арматуры в (кг) | В тонне (м) Погонных метров арматуры в тонне в (м) | |
| 6 (мм) | 0.222 (кг) | 4504.5 (м) | |
| 8 (мм) | 0.395 (кг) | 2531.65 (м) | |
| 10 (мм) | 0.617 (кг) | 1620.75 (м) | |
| 12 (мм) | 0.888 (кг) | 1126.13 (м) | |
| 14 (мм) | 1.21 (кг) | 826.45 (м) | |
| 16 (мм) | 1.58 (кг) | 632.91 (м) | |
| 18 (мм) | 2 (кг) | 500 (м) | |
| 20 (мм) | 2.47 (кг) | 404.86 (м) | |
| 22 (мм) | 2.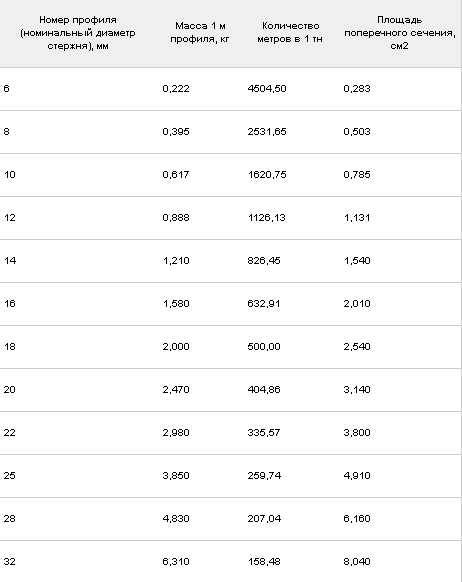 98 (кг) | 335.57 (м) | |
| 25 (мм) | 3.85 (кг) | 259.74 (м) | |
| 28 (мм) | 4.83 (кг) | 207.04 (м) | |
| 32 (мм) | 6.31 (кг) | 158.48 (м) | |
| 36 (мм) | 7.99 (кг) | 125.16 (м) | |
| 40 (мм) | 9.87 (кг) | 101.32 (м) | |
| 45 (мм) | 12.48 (кг) | 80.13 (м) | |
| 50 (мм) | 15.41 (кг) | 64.89 (м) | |
| 55 (мм) | 18.65 (кг) | 53.62 (м) | |
| 60 (мм) | 22.19 (кг) | 45.07 (м) | |
| 70 (мм) | 30.21 (кг) | 33.1 (м) | |
| 80 (мм) | 39.46 (кг) | 25.34 (м) | |
Обзор моделей и методов подбора кривой в LabVIEW
Что такое подбор кривой?Цель подбора кривой – найти функцию f ( x ) в классе функций Φ для данных ( x i , y i 0 8 i
), где , 1, 2,…,
n –1.
Функция f ( x ) минимизирует остаток под весом W . Остаток — это расстояние между выборками данных и ф ( х ). Меньший остаток означает лучшую подгонку. В геометрии подгонка кривой представляет собой кривую y = f ( x ), которая соответствует данным ( x i , y i ), где i 0,9008 …, n –1.В LabVIEW вы можете использовать следующие ВП для расчета функции аппроксимации кривой.
- Линейная посадка VI
- Экспоненциальная аппроксимация VI
- Power Fit VI
- Подгонка пика Гаусса VI
- Подгонка логарифма VI
Эти ВП создают различные типы моделей подбора кривых для набора данных. Обратитесь к справке LabVIEW Help для получения информации об использовании этих ВП. На следующих графиках показаны различные типы моделей фитингов, которые вы можете создать с помощью LabVIEW.
Рисунок 1.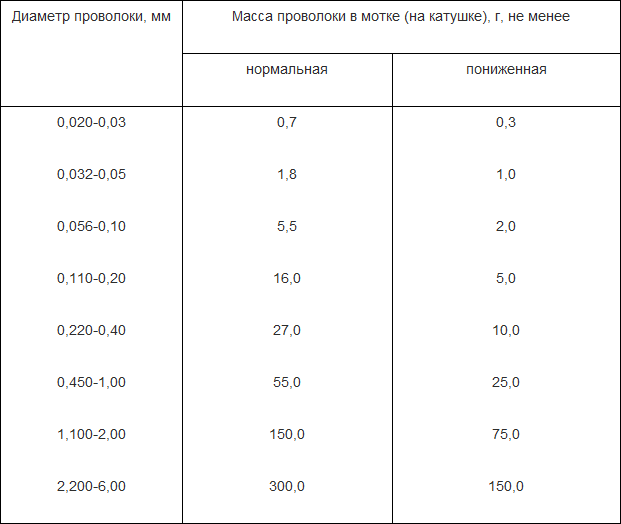
Модели подбора кривых в LabVIEW
Перед подбором набора данных необходимо решить, какую модель подбора использовать. Неправильный выбор, например, использование линейной модели для подбора логарифмических данных, приводит к неправильному результату подбора или результату, который неточно определяет характеристики набора данных. Поэтому сначала необходимо выбрать подходящую модель подгонки на основе формы распределения данных, а затем судить о том, подходит ли модель в соответствии с результатом.
Каждая модель фитинга VI в LabVIEW имеет вход Weight . Ввод Weight по умолчанию равен 1, что означает, что все выборки данных оказывают одинаковое влияние на результат подбора. В некоторых случаях в наборе данных существуют выбросы из-за внешних факторов, таких как шум. Если вы вычисляете выбросы с тем же весом, что и выборки данных, вы рискуете отрицательно повлиять на результат подбора. Таким образом, вы можете настроить вес выбросов, даже установить вес на 0, чтобы исключить негативное влияние.
Вы также можете использовать Curve Fitting Express VI в LabVIEW для разработки приложения для подбора кривой.
Методы подбора кривойРазличные методы подбора могут оценивать входные данные для нахождения параметров модели подбора кривой. Каждый метод имеет свои собственные критерии оценки аппроксимирующей невязки при нахождении аппроксимируемой кривой. Понимая критерии для каждого метода, вы можете выбрать наиболее подходящий метод для применения к набору данных и построения кривой. В LabVIEW вы можете применить метод наименьших квадратов (LS), метод наименьших абсолютных невязок (LAR) или метод двойного квадрата к линейной аппроксимации, экспоненциальной аппроксимации, аппроксимации мощности, пиковой аппроксимации Гаусса или логарифмической аппроксимации VI, чтобы найти функцию ф ( х ).
Метод LS находит F ( x ), минимизируя остаточную в соответствии со следующей формулой:
, где N – это количество образцов данных
W I IS 7 I th элемент массива весов для выборок данных
f ( x i ) является i -м элементом массива y модели0053
y i is the i th element of the data set ( x i , y i )
The LAR method finds f ( x ) путем минимизации остатка по следующей формуле:
Метод бисквадрата находит f ( x ) с помощью итеративного процесса, как показано на следующей блок-схеме, и вычисляет остаток по той же формуле, что и в метод ЛС.
Метод Bisquare вычисляет данные, начиная с итерации 9.0007 к .
Рисунок 2. Блок-схема метода Bisquare
Поскольку методы LS, LAR и Bisquare вычисляют f ( x ) по-разному, вы хотите выбрать метод аппроксимации кривой в зависимости от набора данных. Например, методы подбора LAR и Bisquare являются надежными методами подбора. Используйте эти методы, если в наборе данных существуют выбросы. В следующих разделах подробно описаны методы расчета LS, LAR и Bisquare.
Метод LS
Метод наименьших квадратов начинается с решения линейных уравнений.
AX = B
A – матрица, а X и B – векторы. Ax – b представляет ошибку уравнений.
Следующее уравнение представляет собой квадрат ошибки предыдущего уравнения.
E ( x ) = ( Ax – b ) T ( Ax – b ) = x T A T AX -2 B T A x + B T B
TO MIDISIIZE
7 E
(6.
), вычислить производную предыдущей функции и обнулить результат:
E’ ( x ) = 0
2 A T Ax -2 A T b = 0
A T Ax = A T b
x = ( A T A ) -1 A T б
Из потока алгоритма вы можете увидеть эффективность процесса вычислений, потому что процесс не является итеративным. Приложения, требующие эффективности, могут использовать этот процесс расчета.
Метод LS вычисляет x путем минимизации квадратичной ошибки и обработки данных с гауссовым шумом. Если шум не распределен по Гауссу, например, если данные содержат выбросы, метод LS не подходит. Вы можете использовать другой метод, такой как метод LAR или Bisquare, для обработки данных, содержащих шум, не распределенный по Гауссу.
Метод LAR
Метод LAR минимизирует остаток по следующей формуле:
Из формулы видно, что метод LAR является методом LS с изменяющимися весами. Если выборка данных далека от f ( x ), вес устанавливается относительно ниже после каждой итерации, чтобы эта выборка данных оказывала меньшее негативное влияние на результат подбора. Поэтому метод LAR подходит для данных с выбросами.
Биквадратный метод
Как и метод LAR, метод Bisquare также использует итерацию для изменения весов выборок данных. В большинстве случаев метод Bisquare менее чувствителен к выбросам, чем метод LAR.
Сравнение методов подбора кривой
При сравнении трех методов подбора кривой методы LAR и Bisquare уменьшают влияние выбросов за счет корректировки веса каждой выборки данных с помощью итеративного процесса. К сожалению, корректировка веса каждой выборки данных также снижает эффективность методов LAR и Bisquare.
Чтобы лучше сравнить три метода, проведите следующий эксперимент.
Используйте три метода, чтобы соответствовать одному и тому же набору данных: линейная модель, содержащая 50 выборок данных с шумом. В следующей таблице показано время вычислений для каждого метода:
Таблица 1. Время обработки для трех методов подбора
| Метод подбора | Лар | Биквадрат | |
| Время (мкс) | 3,5 | 30 | 60 |
Как видно из предыдущей таблицы, метод LS имеет наибольшую эффективность.
На следующем рисунке показано влияние выбросов на три метода:
Рисунок 3. Сравнение трех методов подбора
Выборки данных, далекие от подобранных кривых, являются выбросами.
На предыдущем рисунке вы можете рассматривать выборки данных в точках (2, 17), (20, 29).) и (21, 31) как выбросы. Результаты показывают, что выбросы оказывают большее влияние на метод LS, чем на методы LAR и Bisquare.
Из предыдущего эксперимента видно, что при выборе подходящего метода подбора необходимо учитывать как качество данных, так и эффективность вычислений.
LabVIEW Curve Fitting Models
В дополнение к ВП Linear Fit, Exponential Fit, Gaussian Peak Fit, Logarithm Fit и Power Fit, вы также можете использовать следующие VI для расчета функции подбора кривой.
- Общий многочлен VI
- Общая линейная посадка VI
- Посадка на кубические шлицы VI
- Подгонка нелинейной кривой VI
General Polynomial Fit
General Polynomial Fit VI подгоняет набор данных к полиномиальной функции общего вида:
f(x) = a + bx +
18 90 …
На следующем рисунке показана аппроксимация кривой общего полинома с использованием полинома третьего порядка для нахождения действительных нулей набора данных.
Вы можете видеть, что нули встречаются примерно в (0,3, 0), (1, 0) и (1,5, 0).
Рисунок 4. General Polynomial Model
Этот ВП вычисляет среднеквадратичную ошибку (MSE) с помощью следующего уравнения:
Заказ вход. Высокий порядок полинома не гарантирует лучшего результата подгонки и может вызвать колебания. Полином десятого порядка или ниже подходит для большинства приложений. Полиномиальный порядок по умолчанию 2.
Этот ВП имеет вход Coefficient Constraint . Вы можете установить этот ввод, если знаете точные значения полиномиальных коэффициентов. При установке этого входа ВП вычисляет результат, более близкий к истинному значению.
General Linear Fit
The General Linear Fit VI fits the data set according to the following equation:
y = a 0 + a 1 f 1 ( x ) + A 2 F 2 ( x ) +… + A K-1 F K-1 ( x )
Y Y Y Y Y Y Y Y Y Y Y ( x )
9107 Y Y ( x ).
является линейной комбинацией коэффициентов a 0 , a 1 , a 2 , …, a число коэффициентов 900k-13
Следующие уравнения показывают, как расширить понятие линейной комбинации коэффициентов так, чтобы множитель для a 1 является некоторой функцией x .
y = A 0 + A 1 SIN (ω x )
Y = A
y = A 0 + 0708 = . = = A 0 + . y = a 0 + a 1 cos(ω x 2 , где ω – угловая частота. В каждом из предыдущих уравнений y представляет собой линейную комбинацию коэффициентов a 0 и a 1 . у = а 0 + a 1 sin(ω x ) y = a 0 + a 1 x 2 + a 2 cos(ω x 2 ) y = a 0 + a 1 (3sin(ω x )) + a 2 x 3 + ( a 3 / x ) + … В каждом из предыдущих уравнений y может быть как линейной функцией коэффициентов a 0 , a 1 , a 2 2 , 
Для General Linear Fit VI y также может быть линейной комбинацией нескольких коэффициентов. Каждый коэффициент имеет множитель некоторой функции x . Таким образом, вы можете использовать ВП General Linear Fit для расчета и представления коэффициентов функциональных моделей в виде линейных комбинаций коэффициентов.
Построение матрицы наблюдения
При использовании ВП General Linear Fit необходимо построить матрицу наблюдения H . Например, следующее уравнение определяет модель, используя данные датчика.
y = a 0 + a 1 sin(ω x ) + a 2 cos(ω x ) + a 3 x 2
В следующей таблице показаны множители для коэффициентов a j в предыдущем уравнении.
Коэффициент | Множитель |
а или | 1 |
а 1 | sin(ωx) |
а 2 | cos(ωx) |
а 3 | х 2 |
Для построения матрицы наблюдения H , значение каждого столбца в H равно независимой функции или множителю, вычисляемому для каждого значения x , x i .
Если набор данных содержит n точек данных и k коэффициентов для коэффициента A 0 , A 1 ,…, A K – 1 , затем H – N × K. Следовательно, количество строк в H равно количеству точек данных, n . Количество столбцов в H равно количеству коэффициентов, k .
Для получения коэффициентов, a 0 , a 1 , …, a k – 1 , the General Linear Fit VI solves the following linear equation:
H a = y
where a = [ a 0 a 1 … a k – 1 ] T and y = [ y 0 y 1 … г п – 1 ] Т .
Подгонка кубического сплайна
Сплайн — это кусочно-полиномиальная функция для интерполяции и сглаживания. При подгонке кривой сплайны аппроксимируют сложные формы.
Кубический сплайновый Fit Vi подходит наборе данных ( x I , Y I ), минимизируя следующую функцию:
, где P – Parameter 7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7 . I – это I TH Элемент массива для набора данных
Y I – I TH Eleclet of The Data Data Data Data Data Data Data Data 7. . . . i , y i )
x i is the i th element of the data set ( x i , y i )
f ” ( х ) — производная второго порядка функции кубического сплайна, f ( x )
λ( x ) — кусочно-постоянная функция:
й элемент Гладкость входа ВП .
Если параметр Balance Parameter input p равен 0, модель кубического сплайна эквивалентна линейной модели. Если Параметр баланса , вход p равно 1, метод подбора эквивалентен интерполяции кубическим сплайном. p должен находиться в диапазоне [0, 1], чтобы аппроксимированная кривая была как близкой к наблюдениям, так и гладкой. Чем ближе p к 0, тем более плавной будет подобранная кривая. Чем ближе p к 1, тем ближе подобранная кривая к наблюдениям. На следующем рисунке показаны результаты подгонки, когда p принимает разные значения.
Рис. 5. Кубический сплайн , модель
Из предыдущего рисунка видно, что когда p равно 1,0, аппроксимированная кривая наиболее близка к данным наблюдения. Когда p равно 0,0, подобранная кривая является самой гладкой, но кривая не пересекается ни в одной точке данных.
Nonlinear Curve Fit
Nonlinear Curve Fit VI подгоняет данные к кривой, используя нелинейный метод Левенберга-Марквардта в соответствии со следующим уравнением:
y = f ( x ;0107 a 0 , a 1 , a 2 , …, a k )
where a 0 , a 1 , a 2 , …, a k — коэффициенты, k — количество коэффициентов.
Нелинейный метод Левенберга-Марквардта является наиболее общим методом подбора кривой и не требует, чтобы y имели линейную связь с а 0 , а 1 , а 2 , …, а к . Вы можете использовать нелинейный метод Левенберга-Марквардта для подбора линейных или нелинейных кривых. Однако наиболее распространенным применением метода является подбор нелинейной кривой, потому что общий метод линейного подбора лучше подходит для подбора линейной кривой.
LabVIEW также предоставляет ВП Constrained Nonlinear Curve Fit для подгонки нелинейной кривой с ограничениями. Вы можете установить верхний и нижний пределы каждого параметра подбора на основе предварительных знаний о наборе данных, чтобы получить лучший результат подбора.
На следующем рисунке показано использование ВП Nonlinear Curve Fit для набора данных. Нелинейный характер набора данных подходит для применения метода Левенберга-Марквардта.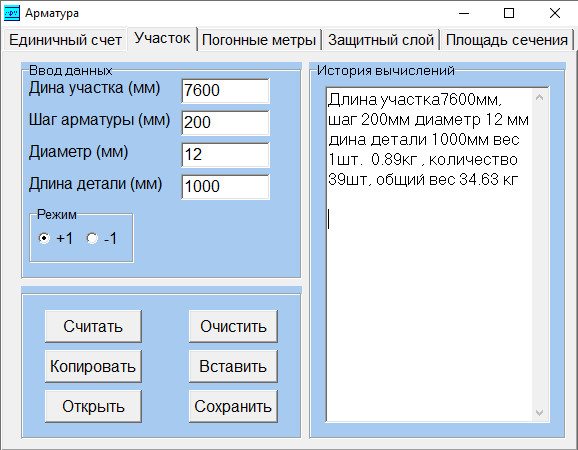
Рисунок 6. Модель нелинейной кривой
Предварительная обработка
ВП Remove Outliers выполняет предварительную обработку набора данных, удаляя точки данных, выходящие за пределы диапазона. VI устраняет влияние выбросов на целевую функцию. На следующем рисунке показан набор данных до и после применения ВП Remove Outliers.
Рисунок 7. Удалить выбросы VI
На предыдущем рисунке график слева показывает исходный набор данных с наличием выбросов. На графике справа показаны предварительно обработанные данные после удаления выбросов.
Вы также можете удалить выбросы, попадающие в указанные вами индексы массива.
Некоторые наборы данных требуют более высокой степени предварительной обработки. Инструмент предварительной обработки медианного фильтра полезен как для удаления выбросов, так и для сглаживания данных.
Постобработка
LabVIEW предлагает ВП для оценки результатов данных после подгонки кривой.
Эти ВП могут определять точность результатов аппроксимации кривой и вычислять доверительные интервалы и интервалы прогнозирования в серии измерений.
Goodness of Fit
Goodness of Fit VI оценивает результат подбора и вычисляет сумму квадратов ошибок (SSE), R-квадрат ошибок (R 2 ) и среднеквадратичную ошибку (RMSE) на основе подбора результат. Эти три статистических параметра описывают, насколько хорошо подобранная модель соответствует исходному набору данных. Следующие уравнения описывают SSE и RMSE соответственно.
где DOF — степень свободы.
SSE и RMSE отражают влияние случайных факторов и показывают разницу между набором данных и подобранной моделью.
Следующее уравнение описывает R-квадрат:
где SST — это общая сумма квадратов согласно следующему уравнению:
R-квадрат — это количественное представление уровня аппроксимации.
Высокий R-квадрат означает лучшее соответствие между подходящей моделью и набором данных. Поскольку R-квадрат представляет собой дробное представление SSE и SST, значение должно быть между 0 и 1.
0 ≤ R-квадрат ≤ 1
Когда выборки данных точно соответствуют аппроксимированной кривой, SSE равно 0, а R-квадрат равен 1. Когда некоторые выборки данных находятся за пределами аппроксимированной кривой, SSE больше 0 и R-квадрат меньше 1. Поскольку R-квадрат нормализован, чем ближе R-квадрат к 1, тем выше уровень аппроксимации и менее гладкая кривая.
На следующем рисунке показаны аппроксимированные кривые набора данных с различными результатами R-квадрата.
Рисунок 8. Результаты подгонки с различными значениями R-квадрата
Из предыдущего рисунка видно, что подобранная кривая с R-квадратом, равным 0,99, лучше соответствует набору данных, но менее гладкая, чем подобранная кривая с R- квадрат равен 0,97.
Доверительный интервал и интервал прогнозирования
В реальном процессе тестирования и измерения, поскольку выборки данных из каждого эксперимента в серии экспериментов различаются из-за ошибки измерения, результаты подбора также различаются. Например, если ошибка измерения не коррелирует и нормально распределяется между всеми экспериментами, вы можете использовать доверительный интервал для оценки неопределенности подгоночных параметров. Вы также можете использовать интервал прогнозирования для оценки неопределенности зависимых значений набора данных.
. -1 , Y N -1 ) для функции линейной подгонки Y = A 0 x + A 1 . Для каждой выборки данных ( x i , y i ) дисперсия ошибки измерения определяется весом,
Вы можете использовать форму функции x = ( A T A ) -1 A T B O F метод LS в соответствии с данными, чтобы соответствовать данных, чтобы соответствовать данных, чтобы соответствовать данных, чтобы соответствовать данных, чтобы соответствовать данных, чтобы соответствовать данных.
следующее уравнение.
where a = [ a 0 a 1 ] T
y = [ Y 0 Y 1 … y N-1 ] TH 9001. , a 0 и a 1 , как следующее уравнение.
где J — матрица Якоби
m количество параметров
n количество выборок данных
В предыдущем уравнении количество параметров m, равно 2. i th диагональный элемент C8
, C ii , – дисперсия параметра a i , .
Доверительный интервал оценивает неопределенность подгоночных параметров на определенном уровне достоверности.
Например, 95% доверительный интервал означает, что истинное значение подгоночного параметра с вероятностью 95% попадает в доверительный интервал. Доверительный интервал параметра подгонки i th составляет:
, где t — обратная кумулятивная функция распределения Стьюдента n — m степеней свободы при вероятности, а — стандартное отклонение параметра a я и равно .
Вы также можете оценить доверительный интервал каждой выборки данных на определенном уровне достоверности. Например, 95% доверительный интервал выборки означает, что истинное значение выборки имеет 95% вероятность попадания в доверительный интервал. Доверительный интервал I TH Образец данных:
, где Diag I ( A ) обозначает I TH Диагональный элемент Matrix A4. В приведенной выше формуле матрица (
JCJ) T представляет собой матрицу A .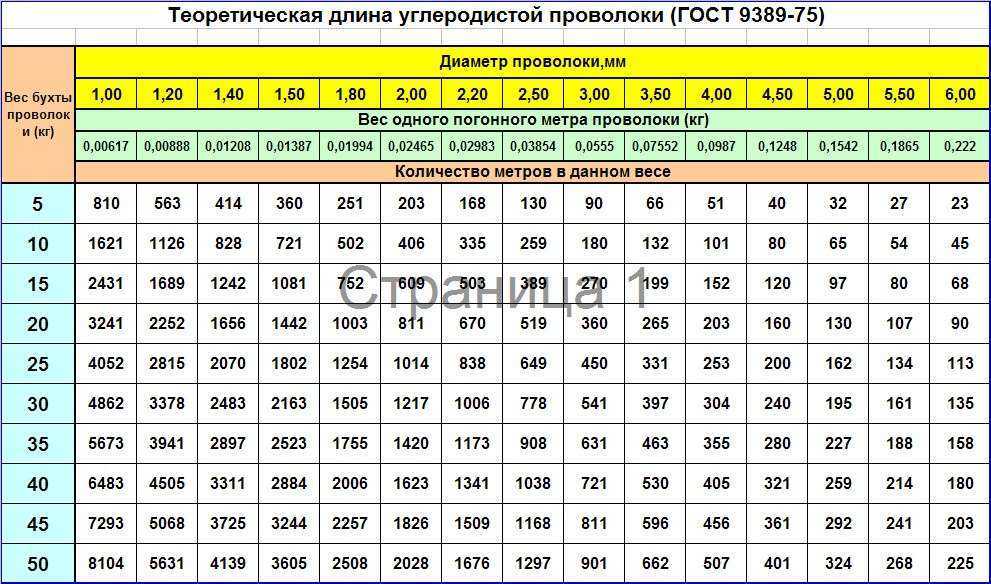
Интервал прогнозирования оценивает неопределенность выборок данных в последующем эксперименте по измерению на определенном уровне достоверности. Например, 95-процентный интервал прогнозирования означает, что выборка данных имеет 95-процентную вероятность попадания в интервал прогнозирования в следующем эксперименте по измерению. Поскольку интервал прогнозирования отражает не только неопределенность истинного значения, но и неопределенность следующего измерения, интервал прогнозирования шире доверительного интервала. Интервал предсказания i th пример:
LabVIEW предоставляет ВП для расчета доверительного интервала и интервала прогнозирования для обычных моделей аппроксимации кривой, таких как линейная аппроксимация, экспоненциальная аппроксимация, аппроксимация пика Гаусса, логарифмическая аппроксимация и модели степенной аппроксимации. Эти ВП вычисляют верхнюю и нижнюю границы доверительного интервала или интервала прогнозирования в соответствии с установленным уровнем достоверности.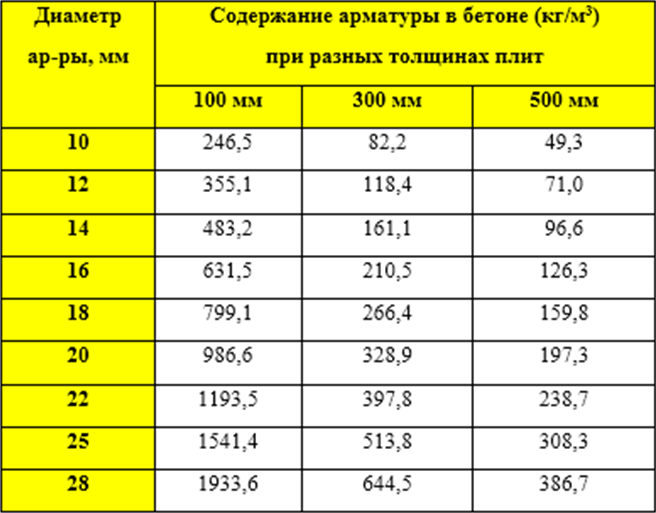
На следующем рисунке показаны примеры графика доверительного интервала и графика Prediction Interval графика соответственно для одного и того же набора данных.
Рисунок 9. Доверительный интервал и интервал предсказания
На графике Доверительный интервал видно, что доверительный интервал узкий. Небольшой доверительный интервал указывает на подобранную кривую, которая близка к реальной кривой. Из графика Prediction Interval можно сделать вывод, что каждая выборка данных в следующем эксперименте по измерению будет иметь 95% шанс попасть в интервал предсказания.
Жесткий кабелепровод из ПВХ — Allied Tube & Conduit
Компания Allied Tube & Conduit предлагает полный ассортимент жестких кабелепроводов и фитингов из ПВХ, а также коммуникационных воздуховодов из ПВХ. Для коммерческого, промышленного и коммунального использования трубы и воздуховоды из ПВХ Allied доказали свою долговечность и эффективность в течение многих лет без обслуживания в подземных, закрытых и открытых применениях в соответствии с Национальным электротехническим кодексом.
- Коммерческое, промышленное и коммунальное использование
- Стойкий к коррозии
- Немагнитный и не гальванический
- Самозатухающий
- Ударопрочный
Коррозионностойкий
Устойчивый к большинству химикатов, ПВХ обычно не подвергается воздействию агрессивных почв или солей.
Немагнитный и негальванический
Свойства Allied PVC Conduit обеспечивают хорошую изоляцию, отсутствие потери мощности или нагрева проводника.
Самозатухающий
Свойства делают ПВХ огнестойким.
Ударопрочный
Прочный, долговечный, с высокой прочностью на растяжение, простой в обращении и простой в установке прямо на стройплощадке.
Системы труб из жесткого ПВХ сортамента 40 и 80 устойчивы к солнечному свету и используются снаружи, в бетоне, скрыто в стенах и непосредственно в грунте, включая системы для:
- Коммунальные услуги
- Кабели, линии передачи данных и связи
- Институциональные, коммерческие, промышленные здания
- Жилые помещения и служебные входы
- Уличные и шоссейные подземные линии
- Транспортные системы – метро, мосты, туннели, аэропорты
- Установки очистки воды и сточных вод
- Марины
- Шахты и мельницы
Коммунальные воздуховоды типов DB-60 и DB-120 предназначены для непосредственного заглубления.
Типы ЭБ-20 и ЭБ-35 предназначены для заглубления в бетон.
Соответствие нормам и стандартам
Жесткие кабелепроводы Allied Schedule 40 и Schedule 80 сертифицированы третьей стороной по UL 651 и разрешены для использования с 90º C проводников в соответствии с Национальным электротехническим кодексом. Они производятся в соответствии с NEMA TC2.
Воздуховоды Allied Type DB и EB изготовлены в соответствии с NEMA TC 6 и 8 и разрешены для использования с проводниками, рассчитанными на 90ºC.
Фитинги Allied из ПВХ производятся в соответствии с NEMA TC3. Стандарт UL для фитингов из ПВХ — UL 651; для коробок UL 514C, для накладок UL 514D и для корпусов UL 50.
Информацию о листинге UL см. на страницах продуктов.
Спецификация
Вся проводка должна быть проложена в жестком кабелепроводе Allied Tube & Conduit из ПВХ и закреплена с помощью соответствующих фитингов. Все фитинги должны быть предложены Allied Tube & Conduit.
Все розетки, тяговые коробки и точки соединения должны быть оснащены выходными коробками, фитингами и соединительными коробками Allied.
Открытый кабелепровод должен быть надежно закреплен и закреплен с помощью хомутов. Ленты должны быть установлены на рекомендуемом расстоянии, как указано в Национальном электротехническом кодексе (NEC). Хомуты должны допускать линейное расширение и сжатие трубы из-за изменения температуры. Если перепад температур превышает 25°F, необходимо установить компенсаторы в соответствии с рекомендациями производителя.
Если труба из жесткого ПВХ встроена в бетон или непосредственно заглублена, поддерживающие хомуты не требуются.
Жесткий кабелепровод из ПВХ Schedule-40, рассчитанный на 90°C для проводки
Allied Schedule-40 устойчив к солнечному свету. Соответствует или превосходит требования NEMA TC-2 и UL-651 для кабелепровода Schedule 40*.
Спецификация 40
| Торговый размер | Средний наружный диаметр (дюймы) | Минимальный средний внутренний диаметр (дюймы) | Минимальная стенка (дюймы) | Вес на фут (фунты) | Количество ящиков 10 футов (футы) |
|---|---|---|---|---|---|
| 1/2 | 0,840 | 0,578 | 0,109 | 0,166 | 60040 | 0
| 3/4 | 1,050 | 0,780 | 0,113 | 0,220 | 4400 |
| 1 | 1,315 | 1,004 | 0,133 | 0,327 | 3600 |
| 1-1/4 | 1,660 | 1,335 | 0,140 | 0,444 | 3300 |
| 1-1/2 | 1,900 | 1,564 | 0,145 | 0,530 | 2250 |
| 2 | 2,375 | 2,021 | 0,154 | 0,749 | 1400 |
| 2-1/2 | 2,875 | 2,414 | 0,203 | 1,187 | 930 |
| 3 | 3,500 | 3,008 | 0,216 | 1,613 | 880 |
| 3-1/2 | 4,000 | 3,486 | 0,226 | 1,952 | 630 |
| 4 | 4,500 | 3,961 | 0,237 | 2,312 | 570 |
| 5 | 5,563 | 4,975 | 0,258 | 3,133 | 380 |
| 6 | 6,625 | 5,986 | 0,280 | 4. |