Вращательное в поступательное движение – Поступательное и вращательное движение
alexxlab | 14.03.2020 | 0 | Разное
Поступательное и вращательное движение
Существует пять видов движения твердого тела:
Первые два называются простейшими движениями твердого тела. Остальные виды движений можно представить как комбинацию основных движений.
Любое прямолинейное движение является поступательным. Однако поступательное движение не следует смешивать с прямолинейным. При поступательном движении тела траектории его точек могут быть любыми кривыми линиями.
Рис.1 Поступательное криволинейное движение кабин колеса обзора
Из теоремы следует, что поступательное движение твердого тела определяется движением какой-нибудь одной из его точки. Следовательно, изучение поступательного движения тела сводится к задаче кинематике точки.
При поступательном движении общую для всех точек тела скорость $\overrightarrow {v}$ называют скоростью поступательного движения тела, а ускорение $\overrightarrow {a}$ – ускорением поступательного движения тела. Векторы $\overrightarrow {v}$ и $\overrightarrow {a}$ можно изображать приложенными в любой точке тела.
Заметим, что понятие о скорости и ускорении тела имеют смысл только при поступательном движении. Во всех остальных случаях точки тела, движутся с разными скоростями и ускорениями, и термины «скорость тела» или «ускорение тела» для этих движений теряют смысл.
Вращательным движением абсолютно твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела движутся в плоскостях, перпендикулярных к неподвижной прямой, называемой осью вращения, и описывают окружности, центры которых лежат на этой оси.
Для определения положения вращающегося тела проведем через ось вращения, вдоль которой направим ось Az, полуплоскость – неподвижную и полуплоскость, врезанную в само тело и вращающуюся вместе с ним (рис. 2).
Рисунок 2. Угол поворота тела
Тогда положение тела в любой момент времени однозначно определится взятым с соответствующим знаком углом $\varphi $ между этими полуплоскостями, который назовем углом поворота тела. Будем считать угол $\varphi $ положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси Az), и отрицательным, если по ходу часовой стрелки. Измерять угол $\varphi $ будем всегда в радианах. Чтобы знать положение тела в любой момент времени, надо знать зависимость угла $\varphi $ от времени t, т.е. ${\mathbf \varphi }$=f(t). Это уравнение выражает закон вращательного движения твердого тела вокруг неподвижной оси.
При вращательном движении абсолютно твердого тела вокруг неподвижной оси углы поворота радиуса-вектора различных точек тела одинаковы.
Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость $\omega $ и угловое ускорение $\varepsilon $.
Уравнения, описывающие вращательное движение, можно получить из уравнений поступательного движения, произведя в последних следующие замены: перемещение s — угловое перемещение (угол поворота) $\varphi $, скорость u — угловая скорость $\omega $, ускорение a — угловое ускорение $\varepsilon $.

spravochnick.ru
Поступательное и вращательное движения абсолютно твердого тела
1. Поступательным называется такое движение абсолютно твердого тела, при котором любая прямая, жестко связанная с телом, перемещается параллельно самой себе. Все точки тела, движущегося поступательно, в каждый момент времени имеют одинаковые скорости и ускорения, а их траектории полностью совмещаются при параллельном переносе. Поэтому кинематическое рассмотрение поступательного движения абсолютно твердого тела сводится к изучению движения любой его точки. В самом общем случае поступательно движущееся твердое тело обладает тремя степенями свободы.
2. Движение абсолютно твердого тела, при котором две его точки А и B остаются неподвижными, называется вращением (вращательным движением) вокруг неподвижной прямой АВ, называемой осью вращения. При вращении твердого тела вокруг неподвижной оси все его точки описывают окружности, центры которых лежат на оси вращения, а плоскости – перпендикулярны к ней. Тело, вращающееся вокруг неподвижной оси, обладает одной степенью свободы: его положение полностью определяется заданием угла f поворота из некоторого начального положения.
3. Угловой скоростью вращения твердого тела называется вектор w, численно равный первой производной от угла поворота по времени,
w = df/dt
и направленный вдоль оси вращения таким образом, чтобы из его конца вращение тела было видно происходящим против часовой стрелки. Направление вектора w совпадает с направлением поступательного движения буравчика, рукоятка которого вращается вместе с телом.
4. Линейная скорость v произвольной точки М вращающегося тела определяется как векторное произведение по формуле Эйлера
v = [wr]
где r – радиус-вектор, проведенный в точку М из произвольной точки О оси вращения тела. Численное значение v линейной скорости точки М прямо пропорционально ее расстоянию R от оси вращения:
v = wr sina = wR
где a – угол между векторами w и r.
5. Периодом обращения Т тела называется время, в течение которого тело поворачивается вокруг неподвижной оси вращения на угол f = 2p.
6. Угловым ускорением называется вектор e, равный первой производной от вектора угловой скорости по времени:
e = dw/dt
Угловое ускорение характеризует быстроту изменения во времени вектора угловой скорости тела. При вращении вокруг неподвижной оси направление вектора w сохраняется и
e = dw/dt = d2f/dt2
причем вектор e совпадает но направлению с w в случае ускоренного вращения (e > 0) и противоположен ему по направлению в случае замедленного вращения (e < 0)
a = dv/dt = d/dt | wr | = | er | + | w | wr ||
www.examen.ru
1. Поступательное движение твердого тела и его свойства.
2. Вращательное движение твердого тела.
3. Частные случаи вращательного движения.
Формула Эйлера.
В кинематике твердого тела, к изложению которой мы приступаем, решаются те же, что и в кинематике точки, две основные задачи:
– задание движения твердого тела;
– определение основных кинематических характеристик этого движения.
Решение первой задачи сводится к определению необходимого числа функций времени (уравнений движения), однозначно определяющих положение каждой точки тела в пространстве. Решение второй задачи заключается в определении зависимостей, позволяющих по известным уравнениям движения определить траекторию, а также скорость и ускорение любой точки тела в любой момент времени.
Различают пять видов движения твердого тела: поступательное, вращательное, плоскопараллельное, сферическое и свободное. Первые два из них (поступательное и вращательное) называют простейшими.
Поступательное движение твердого тела и его свойства.
Поступательным называется такое движение тела, при котором любая прямая, соединяющая две произвольные точки тела, перемещается, оставаясь параллельной своему начальному направлению.
Поступательное движение может быть как прямолинейным, так и криволинейным (рис.2.16).
Рис. 2.16. Примеры поступательного движения твердого тела
Докажем следующие свойства поступательного движения. Если тело движется поступательно, то все его точки в каждый момент времени имеют одинаковые скорости и ускорения, а траектории всех точек при наложении совпадают.
Пусть тело движется поступательно. Тогда (см. рис.2.17) для любых двух его точек А и В, в любой момент времени справедливо следующее векторное выражение:
,
где вектор по определению поступательного движения не изменяется ни по величине, ни по направлению. Это означает, что траектории точекА и В смещены относительно друг друга на постоянный вектор и, следовательно, при наложении совпадут.

Рис. 2.17. К определению свойств поступательного движения
Дифференцируя вышеприведенное векторное выражение по времени, получаем:
, или
так как последняя производная (как производная от постоянного вектора ) равна нулю. Дифференцируя равенство скоростей, получаем равенство ускорений:
.
Доказанные свойства позволяют свести изучение поступательного движения тела к изучению движения любой одной из его точек методами кинематики точки.
Вращательное движение твердого тела
Движение твердого тела, при котором все точки, лежащие на некоторой прямой, принадлежащей телу или неизменно с ним связанной, остаются неподвижными в рассматриваемой системе отсчета, называется вращательным движением. Упомянутая выше прямая называется осью вращения.

Рис. 2.18. Вращение тела вокруг неподвижной оси
Очевидно, что все точки тела, не лежащие на оси вращения, будут двигаться по окружностям, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси.
Положение тела при вращательном движении можно однозначно определить углом между неподвижной полуплоскостью I и подвижной, вращающейся вместе с телом, полуплоскостью II, проходящими через ось вращения. Положительным направлением отсчета угла
Для однозначного определения положения тела в любой момент времени, необходимо располагать зависимостью угловой координаты от времени:
= (t) . (2.25)
Уравнение (2.25) называется уравнением или законом вращательного движения твердого тела.
Введем основные кинематические характеристики вращательного движения – угловую скорость и угловое ускорение . Пусть за промежуток времени t тело повернется на угол. Тогда отношение t называют средней угловой скоростью за этот промежуток времени: ср = t . Предел данного отношения при стремлении t к нулю, называют мгновенной или просто угловой скоростью:
. (2.26)
Аналогичным образом вводится понятие углового ускорения:
. (2.27)
Согласно (2.26) и (2.27) угловая скорость и угловое ускорение измеряются в радианах в секунду (рад/с) и в радианах в секунду за секунду (рад/с2) соответственно. Так как радиан является безразмерной величиной, допустимы и более компактные обозначения – (с -1) и (с -2).
Для того, чтобы использовать угловую скорость и угловое ускорение в векторных выражениях, необходимо рассматривать угловую скорость как вектор, с модулем равным d/dt и направленным вдоль оси вращения в ту сторону, откуда вращения тела видно происходящим против хода часовой стрелки. Вектор углового ускорения, модуль которого равен d/dt, также считают направленным вдоль оси вращения. Он совпадает по направлению с вектором угловой скорости при ускоренном вращении и противоположен ему при замедленном вращении тела (рис. 2.19). Необходимо отметить, что введенные таким необычным способом векторы называют псевдовекторами ( как бы векторами), чтобы подчеркнуть их некоторую “векторную неполноценность”. Тем не менее теперь становится возможна запись следующей векторной формулы:
, (2.28)
правильно отражающей не только количественную связь и, но и взаимосвязь направлений векторови, отображенной на рисунке 2.19.

Рис. 2.19. Взаимосвязь направлений ц и e
Перейдем теперь к определению индивидуальных кинематических характеристик точек вращающегося тела по известному закону вращательного движения . Для этого рассмотрим движение любой точкиМ, не лежащей на оси вращения. Пусть за время dt тело повернется на угол dа точка М переместится по дуге окружности радиуса R на расстояние dS (рис. 2.20).
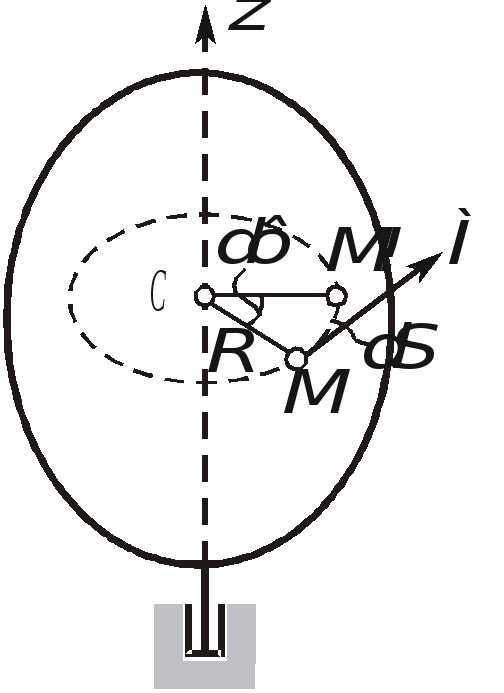
Рис. 2.20. Связь угловой скорости тела с линейными скоростями его точек
Тогда ее скорость будет равна , т.е.(2.29)
Так как всех точки тела вращаются с одной и той же угловой скоростью, то из (2.29) следует, что линейные скорости точек тела пропорциональны их расстояниям от оси вращения. Для определения ускорений воспользуемся формулами (2.19) и (2.20):
, (2.30)
. (2.31)
Полное ускорение точки М будет равно (рис. 2.21) геометрической сумме и:
или . (2.32)
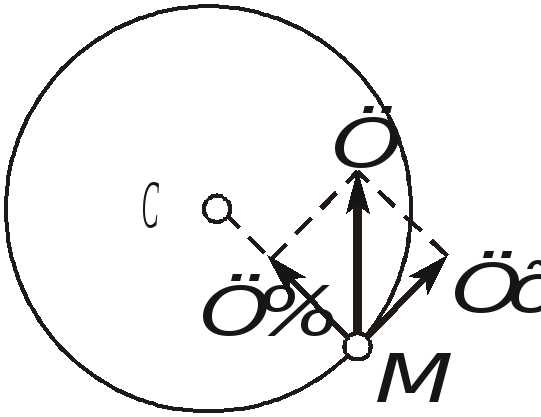
Рис. 2.21. Ускорение точек тела при вращательном движении
Рассмотрим теперь частные случаи вращательного движения
а) Равномерное вращение – вращение с постоянной угловой скоростью
( = const):
, , .
Пусть при t = 0: = 0, тогда С = 0 и мы получаем следующее уравнение или закон равномерного вращения:
. (2.33)
в) Равнопеременное вращение – это вращение с постоянным угловым ускорением ( = const):
, , ,
, ,
.
Пусть при t = 0: и = 0, тогда С1 = , C2 = 0. Подставляя найденные значения констант интегрирования в полученные выше выражения, получаем:
, (2.34)
. (2.35)
В полученном законе изменения угловой скорости (2.34) и в уравнении равнопеременного вращения (2.35), угловое ускорение будет положительным при равноускоренном вращении и отрицательным при равнозамедленным.
В заключение приведем вполне очевидные соотношения, которые часто используются при решении задач:
, (2.36)
где N – число оборотов, n – угловая скорость в оборотах в минуту.
4. Формула Эйлера
В заключение получим векторные формулы для скорости и ускорения точек в круговом движении. Рассмотри движение точки М, не лежащей на оси вращения (рис. 2.22). Покажем, что ее скорость полностью определяется формулой Эйлера : . (2.37)

Рис. 2.22. Иллюстрация формулы Эйлера
Действительно, модуль векторного произведения равенV=r sin = R, что совпадает с выражением (2.29). Формула (2.34) правильно определяет и направление вектора скорости: вектор направлен перпендикулярно плоскости треугольникаОСМ в ту сторону, откуда поворот от квиден происходящим против хода часовой стрелки (т.е. векторнаправлен, как и полагается, по касательной к траектории в направлении вращения тела).
Для вывода векторных формул, определяющих ускорение, продифференцируем формулу Эйлера по времени:
.
Учитывая, что согласно (2.28) и (2.5)
,
получаем:
, (2.38)
где , . (2.39)
В справедливости выражений (2.36) можно убедиться непосредственно, определив модули и направления входящих в них векторных произведений. Так согласно первой формуле (2.39) , что совпадает с уже известным выражением (2.30). Правильно определяется и направление вектора(см. рис.2.22). Вторая формула (2.39) дает[сравните с (2.31)]. Направлен вектор , как и положено, перпендикулярно плоскости, в которой лежат перемножаемы векторывнутрь траектории, откуда поворот отк векторувиден происходящим против хода часовой стрелки.
Лекция 14
Вопросы
studfiles.net
Механизмы преобразования вращательного движения
Наиболее распространенными механизмами преобразования вращательного движения в прямолинейное являются знакомые нам по рис. 1 кривошипно-шатунный и по рис. 7, д — реечный, а также винтовой, эксцентриковый, кулисный, храповой и другие механизмы.
Винтовые механизмы
Винтовые механизмы широко применяются в самых разнообразных машинах для преобразования вращательного движения в поступательное и, наоборот, поступательного во вращательное. Особенно часто винтовые механизмы применяются в станках для осуществления прямолинейного вспомогательного (подача) или установочного (подвод, отвод, зажатие) движения таких сборочных единиц, как столы, суппорты, каретки, шпиндельные бабки, головки и т. д.
Винты, применяемые в этих механизмах, называются ходовыми. Часто также винтовой механизм служит для подъема грузов или вообще для передачи усилий. Примером такого применения винтового механизма является использование его в домкратах, винтовых стяжках и т. д. В этом случае винты будут называться грузовыми. Грузовые винты обычно работают с незначительными скоростями, но с большими усилиями по сравнению с ходовыми винтами.
Основными деталями винтового механизма являются винт и гайка.
Обычно в винтовых механизмах (передачах винт—гайка) движение передается от винта к гайке, т. е. вращательное движение винта преобразуется в поступательное движение гайки, например механизм поперечного перемещения суппорта токарного станка. Встречаются конструкции, когда движение передается от гайки к винту, и винтовые передачи, в которых вращение винта преобразуется в поступательное того же винта, при закрепленной неподвижно гайке. Примером такого механизма может служить винтовая передача верхней части стола (рис. 9, а) фрезерного станка. При вращении рукояткой 6 винта 1 в гайке 2, закрепленной винтом 3 в салазках 4 стола ,5, винт 1 начинает двигаться поступательно. Вместе с ним движется по направляющим салазок стол 5.
Эксцентриковые и кулачковые механизмы
Схема эксцентрикового механизма показана на рис. 9, б. Эксцентрик представляет собой круглый диск, ось которого смещена относительно оси вращения вала, несущего диск. Когда вал 2 вращается эксцентрик 1 воздействует на ролик 3, перемещая его и связанный с ним стержень 4 вверх. Вниз ролик возвращается пружиной 5. Таким образом, вращательное движение вала 2 преобразуется эксцентриковым механизмом в поступательное движение стержня 4.
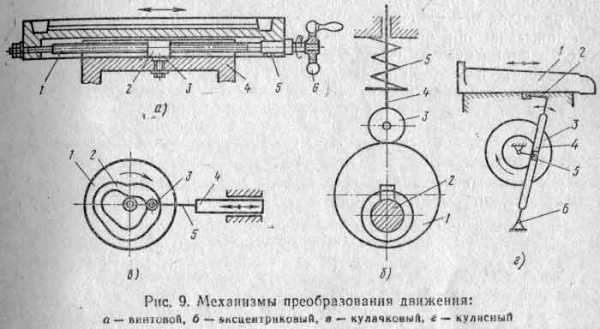
Кулачковые механизмы широко применяются в станках-автоматах и других машинах для осуществления автоматического цикла работы. Эти механизмы могут быть с дисковым цилиндрическим и торцовым кулачками. Показанный на рис. 9, в механизм представляет собой кулачок 1 с канавкой 2 сложной формы на торце, в кoторую помещен ролик 3, соединенный с ползуном 4 посредством стержня 5. В результате вращения кулачка 1 (на разных его участках) ползун 4 получает разную скорость прямолинейного возвратно-поступательного движения.
Кулисный механизм
На рис. 9, г представлена схема кулисного механизма, широко применяемого, например, в поперечно-строгальных и долбежных станках. С ползуном 1, на котором закреплен суппорт с режущим инструментом , шарнирно связана при помощи серьги 2 качающаяся влево и вправо деталь 4, называемая кулисой. Внизу кулиса соединена посредством шарнирного соединения 6, причем своим нижним концом она поворачивается около этой оси во время качаний.
Качания кулисы происходят в результате поступательно-возвратных перемещений в ее пазу детали 5, называемой кулисным камнем и получающей движение от зубчатого колеса 3, с которым она соединена. Зубчатому колесу 3, называемому кулисной шестерней, вращение передается колесом, закрепленным на ведущем валу. Скорость вращательного движения кулисного колеса регулируется коробкой скоростей, связанной с электродвигателем.
Длина хода ползуна зависит от того, в каком виде установлен на кулисной шестерне кулисный камень. Чем дальше от центра шестерни расположен кулисный камень, тем больше окружность, которую он описывает при вращении шестерни, и, следовательно, тем больше угол качания кулисы и длиннее ход ползуна. И наоборот, чем ближе к центру колеса установлен кулисный камень, тем меньше все перечисленные движения.
Храповые механизмы
Храповые механизмы позволяют в широком диапазоне изменять величину периодических перемещений рабочих органов машин. Типы и область применения храповых механизмов разнообразны.
Храповой механизм (рис. 10) состоит из четырех основных звеньев: стойки 1, храповика (зубчатого колеса) 4, рычага 2 и детали 3 с выступом, которая носит название собачки. Храповик со скошенными в одну сторону зубьями насажен на ведомый вал механизма. На одной оси с валом шарнирно закреплен рычаг 2, поворачивающийся (качающейся) под действием приводной штанги 6. На рычаге также шарнирно укреплена собачка, выступ которой имеет форму, соответствующую впадине между зубьями храповика.
Во время работы храпового механизма приходит в движение рычаг 2, Когда он движется вправо, собачка свободно скользит по закругленной части зуба храповика, затем она под действием своей силы тяжести или специальной пружины заскакивает во впадину и, упираясь в следующий зуб, толкает его вперед. В результате этого храповик, а с ним и ведомый вал поворачиваются. Обратный поворот храповика с ведомым валом при холостом ходе рычага с собачкой 3 предотвращается стопорной собачкой 5, шарнирно закрепленной на неподвижной оси и прижатой к храповику пружиной.
Описанный механизм преобразует качательное движение рычага в прерывисто-вращательное движение ведомого вала.
Также Вам будет интересно:
chiefengineer.ru
Кинематика поступательного движения
При поступательном движении тела все точки тела движутся одинаково, и, вместо того чтобы рассматривать движение каждой точки тела, можно рассматривать движение только одной его точки.
Основные характеристики движения материальной точки: траектория движения, перемещение точки, пройденный ею путь, координаты, скорость и ускорение.
Линию, по которой движется материальная точка в пространстве, называют траекторией.
Перемещениемматериальной точки за некоторый промежуток времени называется вектор перемещения∆r=r-r0, направленный от положения точки в начальный момент времени к ее положению в конечный момент.
Скоростьматериальной точки представляет собой вектор, характеризующий направление и быстроту перемещения материальной точки относительно тела отсчета.Вектор ускоренияхарактеризует быстроту и направление изменения скорости материальной точки относительно тела отсчета.
Кинематика вращательного движения.
Вращательным движением твёрдого тела вокруг неподвижной оси называется такое движение, при котором все точки тела движутся _по окружностям, центры которых лежат на одной прямой (ось вращения).
Ось вращения может проходить через тело или лежать за его пределами. Если ось вращения проходит сквозь тело, то точки, лежащие на оси, при вращении тела остаются в покое. Точки твёрдого тела, находящиеся на разных расстояниях от оси вращения за одинаковые промежутки времени проходят различные расстояния и следовательно имеют различные линейные скорости .
Cвязь кинематических величин поступательного и вращательного движения.
Между движением твердого тела вокруг неподвижной оси и движением отдельной материальной точки (или поступательным движением тела) существует тесная и далеко идущая аналогия. Каждой линейной величине из кинематики точки соответствует подобная величина из кинематики вращения твердого тела. Координате sсоответствует уголφ , линейной скоростиv– угловая скоростьw, линейному (касательному) ускорениюа– угловое ускорениеε. Сравнительные параметры движения:
Поступательное движение | Вращательное движение | ||||
Перемещение | S | Угловое перемещение | φ | ||
Линейная скорость | Угловая скорость | ||||
Ускорение | Угловое ускорение | ||||
Масса | m | Момент инерции | I | ||
Импульс | Момент импульса | ||||
Сила | F | Момент силы | M | ||
Таблицу можно продолжать и далее.
Работа:
Кинетическая энергия
Выражения для вращательного движения напоминают соответствующие выражения поступательного движения. Они получаются из последних формальной заменой m → I , v → w , p → L
Выражения имеют не просто формальное сходство. Поступательное движение можно рассматривать, как вращательное, с радиусом вращения, стремящимся к бесконечности, и угловой скоростью, стремящейся к нулю.
Представленная таблица не может претендовать на всю полноту охвата аналогичных значений. Для вращательного и поступательного движений формулируются и аналогичные законы:
Закон сохранения импульса (ЗСИ) ,при Fвнеш = 0 | Закон сохранения момента импульса (ЗСМИ) , при Mвнеш = 0 |
Эти законы формулируются следующим образом:
«Если геометрическая сумма внешних сил, действующих на систему, равна нулю, то импульс системы сохраняется, т.е. не меняется со временем. В частности, это имеет место, когда система замкнута» | «Если момент внешних сил относительно неподвижного начала Оравен нулю, то момент импульса системы относительно того же начала остается постоянным во времени» |
[Д.В.Сивухин. Общий Курс Физики. т.I Механика] | |
Динамика поступательного движения. Законы Ньютона.
Первый закон Ньютона:существуют такие системы отсчета, в которых всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние.Такие системы отсчета называются инерциальными.
Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции.
Второй закон Ньютона–основной закон динамики поступательного движения –отвечает на вопрос, как изменяется механическое движение тела под действием приложенной к нему силы:если на тело действует сила, то это тело приобретает ускорение, прямо пропорциональное действующей силе и обратно пропорциональное массе данного тела:
.
В том случае, если на тела действует не одна, а несколько сил, то приведенная в этой формуле сила является равнодействующей всех действующих на это тело сил и определяется их векторной суммой.
Из уравнения второго закона Ньютона следует: .
В случае неизменности массы тела можно записать:
, где.
Вектор называетсяимпульсом (иликоличеством движения)тела.
Отсюда следует иная формулировка второго закона Ньютона, называемая формулировкой в дифференциальном виде, а именно: скорость изменения импульса тела равна силе, действующей на этр тело,то есть
.
В том случае, если на тела действует не одна, а несколько сил, то приведенная в этой формуле сила является равнодействующей всех действующих на это тело сил и определяется их векторной суммой.
Третий закон Ньютонаопределяет взаимодействие между материальными точками:если первая материальной точка действует на вторую с силой , то вторая точка действует на первую с силой , по модулю равной, а по направлению противоположной силе (силыи направлены по прямой, соединяющей взаимодействующие точки).
Импульс системы тел.Если принять, что импульс системы, состоящей изn тел, можно определить, как векторную сумму импульсов всех n тел, то есть, то из третьего закона Ньютона при условии отсутствия внешних сил (то есть, для замкнутой системы) следует:
, т.е..
Таким образом, импульс замкнутой системы тел не изменяется с течением времени, что являетсязаконом сохранения импульса.
Закон сохранения импульса. Реактивное движение.
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, то такая система называется замкнутой.
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.
Реактивное движение – это движение, которое возникает при отделении от тела некоторой его части с определенной скоростью.
Реактивное движение, например, выполняет ракета. Особенностью этого движения является то, что тело может ускоряться и тормозить без какой-либо внешней взаимодействия с другими телами. Продукты сгорания при вылет получают относительно ракеты некоторую скорость. Согласно закону сохранения импульса, сама ракета получает такой же импульс, как и газ, но направлен в другую сторону. Закон сохранения импульса нужен для расчета скорости ракеты.
Энергия и работа при поступательном движении.
Работа – это физическая величина, характеризующая процесс превращения одной формы движения в другую. В механике принято говорить, что работа совершается силой.
Элементарной работой силы называется величина, равная скалярному произведению силы на элементарное перемещение:
,
где – элементарный путь точки приложения силы за время dt, – угол между векторами и.
Если на систему действуют несколько сил, то результирующая работа равна алгебраической сумме работ, совершаемых каждой силой в отдельности. Работа силы на конечном участке траектории или за конечный промежуток времени может быть вычислена следующим образом:
.
Кинетической энергиейтела называется функция механического состояния, зависящая от массы тела и скорости его движения (энергия механического движения).
Кинетическая энергия поступательного движения
.
Закон сохранения энергии.
Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени
Другими словами, энергия не может возникнуть из ничего и не может в никуда исчезнуть, она может только переходить из одной формы в другую.
Связь силы и потенциальной энергии в консервативной системе.
-Осуществляется по следующей позиции
Работа консервативных сил при элементарном изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком «минус» (работа совершается за счет убыли потенциальной энергии).
Потенциальную энергию тела в каком-то определенном положении считают равной нулю (выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают относительно нулевого уровня.
Для консервативных сил
или в векторном виде .
– градиент скаляра П (,,- единичные векторы координатных осей).
Потенциальная энергия тела массой на высоте вычисляется по формуле .
Потенциальная энергия упруго деформированного тела (пружины):
Типы сил. Упругие силы. Потенциальная энергия упругодеформированного тела
В природе существует четыре типа сил: гравитационные, электромагнитные, ядерные и слабые.
Гравитационные силы, или силы тяготения, действуют между всеми телами. Но эти силы заметны, если хотя бы одно из тел имеет размеры, соизмеримые с размерами планет. Силы притяжения между обычными телами настолько малы, что ими можно пренебречь. Поэтому гравитационными можно считать силы взаимодействия между планетами, а также между планетами и Солнцем или другими телами, имеющими очень большую массу. Это могут быть звёзды, спутники планет и т.п.
Электромагнитные силы действуют между телами, имеющими электрический заряд.
Ядерные силы (сильные) являются самыми мощными в природе. Они действуют внутри ядер атомов на расстояниях 10-13 см.
Слабые силы, как и ядерные, действуют на малых расстояниях порядка 10-15 см. В результате их действия происходят процессы внутри ядра.
-Упругие Силы
Под действием внешних сил возникают деформации (т.е. изменение размеров и формы) тел. Если после прекращения действия внешних сил восстанавливаются прежние форма и размеры тела, то деформация называется упругой. Деформация имеет упругий характер в случае, если внешняя сила не превосходит определенного значения, называемого пределом упругости.
При превышении этого предела деформация становится пластичной, или неупругой, т.е. первоначальные размеры и форма тела полностью не восстанавливаются.
– Деформированное упругое тело(например, растянутая или сжатая пружина) способно, возвращаясь в недеформированное состояние, совершить работу над соприкасающимися с ним телами. Следовательно, упруго деформированное тело обладает потенциальной энергией. Она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина, зависит от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к нерастянутому состоянию, т. е. найдем потенциальную энергию растянутой пружины.
Гравитационные силы. Потенциальная энергия гравитационного взаимодействия.
Все тела в природе взаимно притягиваются друг к другу. Впервые Ньютон доказал, что причина, вызывающая падение камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, одна и та же — это сила всемирного тяготения (гравитационная сила), действующая между любыми телами Вселенной.
Гравитационные силы — это силы центральные, т. е. они направлены вдоль прямой, соединяющей взаимодействующие материальные точки.
Гравитационное взаимодействие осуществляется посредством гравитационного поля. Это поле, наряду с другими полями и веществом, является одной из форм материи.
С каждым телом неразрывно связано гравитационное поле, проявляющееся в том, что на помещенную в поле материальную точку действует гравитационная сила, пропорциональная массе этой точки.
studfiles.net
Поступательное и вращательное движение
Ещё в самом начале курса мы упомянули, что полное описание движения тела является достаточно сложной задачей, если не пользоваться идеализированными моделями такого движения. Одна из таких моделей —поступательное движение — это такое движение, при котором каждая точка тела двигается одинаково.
В этом случае, тело должно быть абсолютно твердым. Например, движение камня или ядра можно назвать поступательным. Движение мяча же, нельзя назвать поступательным, поскольку он немного деформируется в процессе движения.
Очевидно, что движение различных точек этого тела описывается совершенно по-разному. Кроме того, само тело состоит не из однородного материала, поэтому, его ни в коем случае нельзя считать абсолютно твердым. Более подробно деформации и действия сил мы рассмотрим в разделе «динамика».
Поступательное движение тела является самым простым, поскольку, чтобы описать движение тела, достаточно описать движение одной из его точек. Как правило, описывают движение центра тяжести тела.
Строго говоря, если движение тела не является поступательным, то нельзя говорить о скорости или об ускорении тела, поскольку каждая из точек этого тела имеет разную скорость и разное ускорение. Однако, во многих случаях, эти скорости и ускорения настолько мало отличаются друг от друга, что этим можно пренебречь.
Например, поступательным движением можно считать движение поезда на прямых участках, движение колеса обозрения или движение различных поршней.
Примеры поступательного движения
Другой тип движения — это вращательное движение, с которым мы частично познакомились, на прошлом уроке.
Вращательным движением твердого тела называется такое движение, при котором все точки тела двигаются по окружности. При этом, центры этих окружностей лежат на одной прямой, которая называется осью вращения.
Пожалуй, один из самых очевидных примеров такого движения — это вращение Земли вокруг своей оси. Точки Земли двигаются по окружности, причем, вокруг определенной оси. Вместе с этим, движение Земли, строго говоря, нельзя назвать поступательным, поскольку очевидно, что магма внутри Земли двигается совсем не так, как земная кора, например. Но, опять же, в космических масштабах, этим обстоятельством можно пренебречь.
С характеристиками вращательного движения мы уже познакомились: это угловая скорость, период и частота.
Любое движение абсолютно твердого тела можно представить, как сумму поступательного и вращательного движения. Например, если мы примем стальной шар за абсолютно твердое тело и покатим его, то его движение любой его точки можно представить, как сумму поступательного и вращательного движения. Таким образом, точки шара будут двигаться по спирали.
В качестве ещё одного примера можно снова привести движение Земли. Как вы знаете, Земля вращается вокруг Солнца. Но само Солнце двигается по направлению к звезде Вега.
В итоге, Земля совершает витки по спирали. Таким образом, движение земли в космическом пространстве можно представить, как сумму движения Земли вокруг Солнца и движения Солнца к Веге.
Необходимо отметить, что в данном примере, мы упростили движение Солнца, поскольку в действительности оно, конечно, двигается не по прямой, а по определенной орбите.
Примеры решения задач.
Задача 1. Находясь на колесе обозрения, вы заметили, что совершили пол-оборота за 3 минуты. Другой человек, находящийся на этом же колесе обозрения, заметил, что он прошёл расстояние, равное 90 м. Найдите радиус, угловую и линейную скорость колеса обозрения.
В первую очередь, обратим внимание на то, что мы можем считать поступательным движение колеса. А, значит, то, что заметили вы, применимо и к другому человеку, находящемся на этом колесе. И наоборот: его наблюдения тоже могут быть использованы вами. Ведь каждая точка колеса проходит одинаковое расстояние.
Задача 2. Металлический шест начинает двигаться по прямой с постоянным ускорением , при этом вращаясь вокруг своего центра. Длина шеста составляет 4 м, а скорость вращения равна 2 рад/с. Найдите модуль линейной скорости крайней точки после поворота на .
videouroki.net
Поступательное движение твердого тела
Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению.
Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров, движение кабин колеса обозрения относительно Земли (рисунок 1.1) и т.д.
Рис. 1.1
Теорема
При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.
Доказательство
Если выбрать две точки твердого тела А и В (рисунок 1.2), то радиусы-векторы этих точек связаны соотношением
Траектория точки А – это кривая, которая задается функцией rA(t), а траектория точки B – это кривая, которая задается функцией rB(t).
Траектория точки B получается переносом траектории точки A в пространстве вдоль вектора AB, который не меняет своей величины и направления во времени (AB = const). Следовательно, траектории всех точек твердого тела одинаковы.
Продифференцируем по времени выражение
Получаем
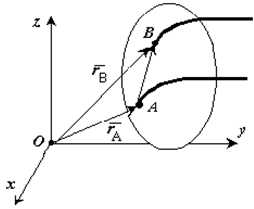
Рис. 1.2
Продифференцируем по времени скорость и получим выражение aB = aA. Следовательно, скорости и ускорения всех точек твердого тела одинаковы.
Для задания поступательного движения твердого тела достаточно задать движение одной из его точек:
isopromat.ru

