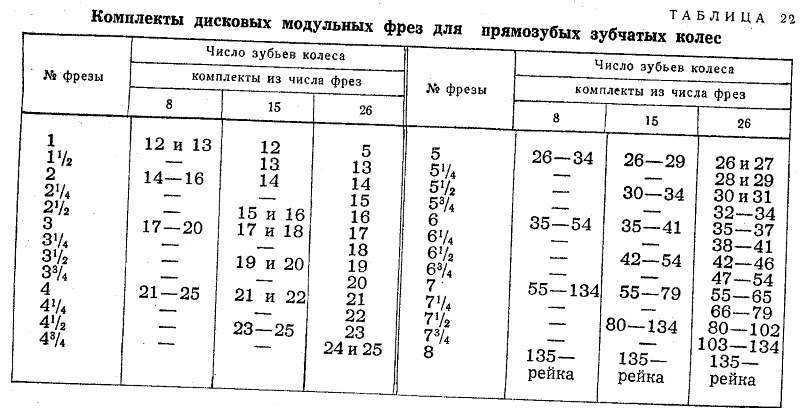
Высота зуба зубчатого колеса: ГОСТ 16531-83 Передачи зубчатые цилиндрические. Термины, определения и обозначения / 16531 83

alexxlab | 21.06.2023 | 0 | Разное

Элементы зубчатого колеса – Теория механизмов машин (Физика)

Лекция 14.

Цилиндрические зубчатые передачи.

Передача непрерывного прошения от одного вала к другому с заданным переда­точным отношением чаще всего осуществляется с помощью зубчатых механизмов. Зубчатые механизмы получили очень широкое применение как в машиностроении, так и в приборостроении благодаря большой надежности и точности в воспроиз­ведения заданного закона движения. Если оси вращения валов параллельны, то применяется цилиндрическая зубчатая передача, аксоидами колес которой являют­ся цилиндры. Такая передача относится к категории плоских механизмов. В лекциях 14-16 излагаются основы синтеза цилиндрической зубчатой передачи по заданному передаточному отношению. Эти основы называются геометрическим расчетом зубчатой передачи.

Элементы зубчатого колеса.

Цилиндрические   зубчатые передачи, как отмечалось ранее, могут быть внешнего и внутреннего зацеплений. Следует также указать реечное зацепление, разграничительное между внешним и внутренним зацеплениями. Простая зубчатая передача имеет два подвижных звена, которыми являются зубчатые колеса. Рассмотрим элементы зубчатого колеса (рис. 14.l).

Поверхность (1), отделяющая зубья от тела зубчатого колеса, называется поверхностью впадин зубьев. Поверхность (2), ограничивающая зубья со стороны, противоположной телу зубчато­го колеса, – поверхность вершин зубьев. Пространство между двумя соседними зубьями (3) – впадина. Поверхность, ограничи­вающая зуб со стороны впадины (4), называется боковой поверхностью зуба.

Боковая поверхность состоит из главной (5) и переход­ной (6) поверхностей. Главная поверхность – это та часть бо­ковой поверхности зуба, которая, взаимодействуя с главной по­верхностью другого зуба, обеспечивает заданное передаточное от­ношение. Переходная поверхность соединяет главную поверхность с поверхностью впадин.

Главной поверхностью чаще всего является эвольвентная по­верхность.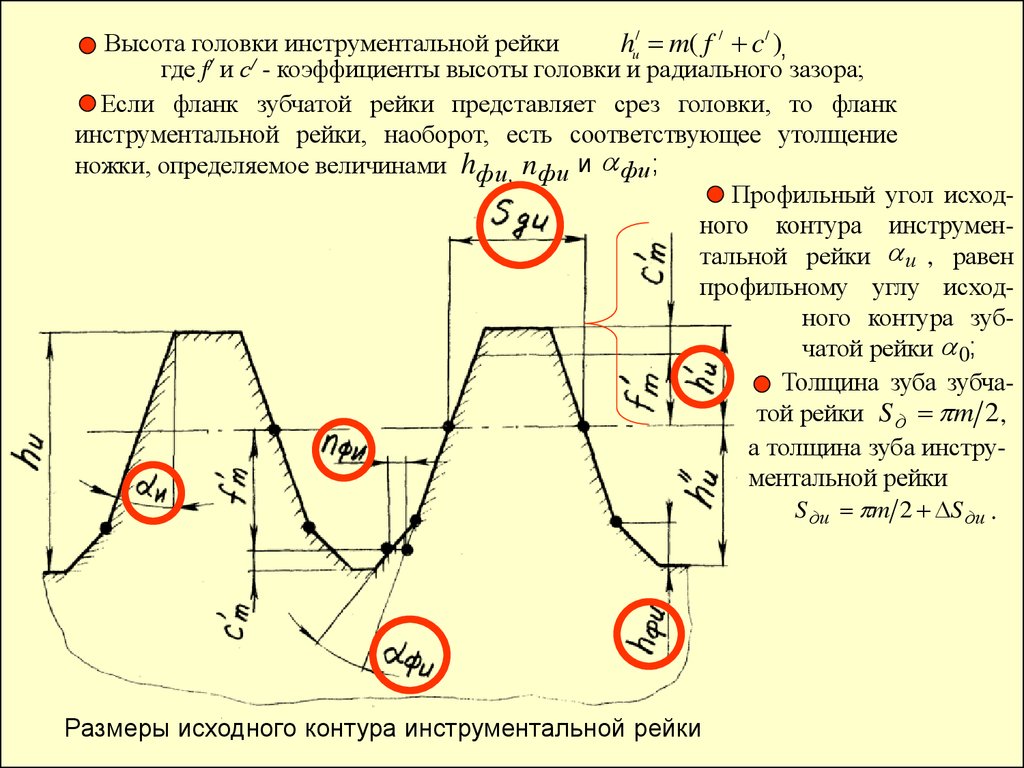 так как среди цилиндрических передач особое рас­пространение получили эвольвентные цилиндрические передачи. Объясняется это тем, что они имеют весьма значительные преиму­щества перед другими передачами. Так, эвольвентные передачи допускают, в определенных пределах, изменение межосевого расстояния, сохраняя при этом по­стоянство передаточного отноше­ния, чего другие передачи не до­пускают, и обладают хорошими эксплуатационными качествами. Изготовление эвольвентных колес и инструмента для их нарезания является наиболее простым, что имеет очень важное практическое значение.

Рассмотрим образование эвольвентных поверхностей, которые будут являться главными поверх­ностями прямого и косого зубьев. На рис. 14.2, а в перспективе по­казана главная поверхность прямого зуба, которую можно пред­ставить как совокупность совершенно одинаковых эвольвент (Э, Э’), расположенных в плоскостях, перпендикулярных оси колеса. Эти эвольвенты являются траекториями точек образующей прямой КК’, принадлежащей плоскости N, которая перекатывается по основ­ному цилиндру 1 без скольжения.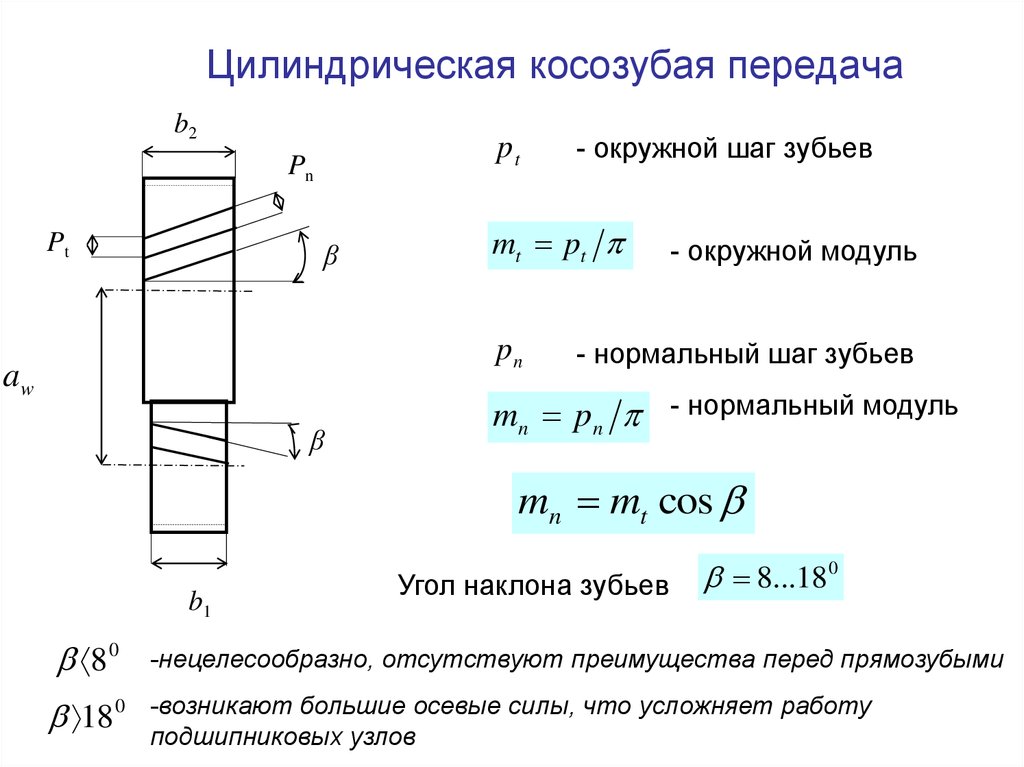 Начальные точки всех эвольвент распола-гаются на образующей K_bK_b^’ основного ци-линдра. Пересе­чение главной поверхности прямого зуба с любым соосным ци­линдром 2 происходит по образующей этого цилиндра (например, прямая КК’). Эта прямая параллельна оси колеса и называется линией прямого зуба. Главная поверхность прямого зуба является эвольвентной линейчатой цилиндрической поверхностью.

Главная поверхность косого зуба (рис. 14.2, б) также может быть представлена как совокупность одинаковых эвольвент (Э, Э’), расположенных в плоскостях, перпендикулярных оси колеса; од­нако в этом случае образующая прямая КК’ расположена на плоскости N под некоторым углом к оси колеса. Благодаря этому при перекатывании плоскости N по основному цилиндру 1 без скольжения начальные точки эвольвент располагаются по винтовой линии K_bK_b^’ на основном цилиндре. В пересечении с любым соос­ным цилиндром 2 главная поверхность косого зуба образует вин­товую линию КК*, называемую линией косого зуба. Главная по­верхность косого зуба является эвольвентной линейчатой винтовой поверхностью.

Таким образом, основное сходство главных поверхностей пря­мого и косого зубьев состоит в том, что в любом торцовом сече­нии, т. е. в сечении плоскостью, перпендикулярной оси колеса, они имеют эвольвенту.

На рис. 14.3, а изображено зубчатое колесо с внешними зубья­ми. Наибольший радиус r_a имеет окружность вершин. На рис. 14,3. б изображено зубчатое колесо с внутренними зубьями. В этом случае тело колеса имеет форму кольца, внутрь полости которого зубья обращены своими вершинами. Поэтому радиус r_a окружности вер­шин внутренних зубьев меньше радиуса r_f окружности впадин, ко­торый является, таким образом, наибольшим. На рис. 14.3 изобра­жены также эвольвентный профиль зуба, основная окружность, на базе которой он построен (радиус r_b), а также делительная окружность радиуса г и окружность произвольного радиуса r_y.

На рис. 14.З буквой  обозначен KON, равный углу профиля зуба в точке K, находящейся на делительной окружности прямозубого колеса. Этот угол стандартизован и ра­вен 20°. Таким образом, делительная окружность прямозубого ко­леса является той окружностью, которая пересекает профиль зуба в точке, для которой угол профиля равен стандартному углу =20°.

Если длину окружностей – делительной, основной и произволь­ного радиуса – поделить на число зубьев z, то получим расстояния между профилями двух соседних зубьев, называемые шагом, т. е. получим шаг по делительной окружности р, шаг по основной ок­ружности p_b и шаг по окружности произвольного радиуса p_y. Дуги р, p_b и p_y соответствуют одному и тому же угловому шагу = p/r = p_b/r_b = p_y/r_y.  Отсюда следует, что шаги пропорциональны радиусам соответствующих окружностей.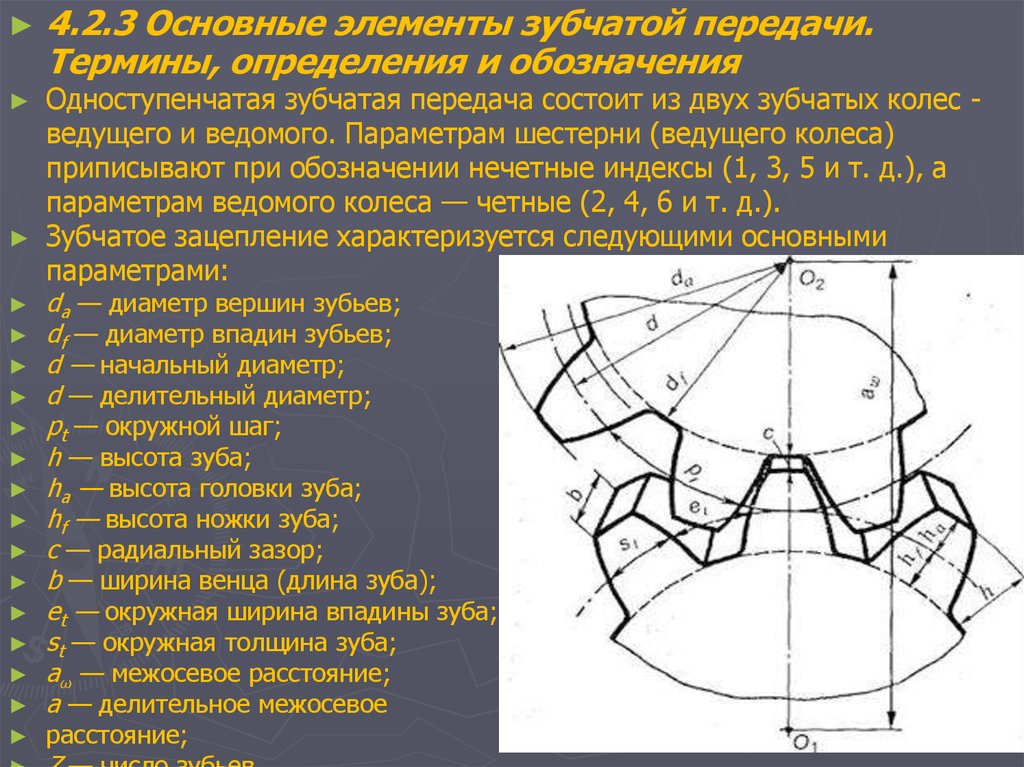 Угловой шаг мож­но выразить и так: = 360°/z.

Важным элементом колеса является шаг по делительной окруж­ности. Выразим длину делительной окружности через шаг р и число зубьев колеса z: 2r = pz. Отсюда диаметр делительной окружности d = (p/)*z = mz. Отношение  p/ обозначают буквой m и называют модулем зубьев колеса (единица модуля – мм). Мо­дуль стандартизован, причем стандарт предусматривает целый ряд значений модуля. Через модуль выражают радиус делительной окружности и все линейные размеры как колеса, так и передачи:

                                                       r = m*z/2 ;                                              (14.1)

                                                       p = *m.                                                (14.2)

         Радиус основной окружности находится из KON (рис. 14.3, а):

                                                                                 (14. 3)

         Радиус произвольной окружности колеса выражается следующим образом:

                                                                              (14.4)

Так как шаги пропорциональны радиусам, то шаг по основной окружности:

а шаг по окружности произвольного радиуса:

                                                                              (14.5)

Основными параметрами колес являются модуль m и число зубьев z. Размеры делительных окружностей характеризуют раз­меры колес и передачи. Поскольку модуль определяется из прочностного расчета, а число зубьев назначает конструктор, то для уменьшения габаритов зубчатой передачи надо уменьшать числа зубьев ее колес [см. уравнение (14.1]

Для колес с внутренними зубьями радиусы основной и дели­тельной окружностей и шаги по этим окружностям определяют но тем же формулам, что и для колеса с внешними зубьями.

Шаг зубьев колеса по любой окружности можно представить как сумму толщины зуба s_y и ширины впадины e_y, т.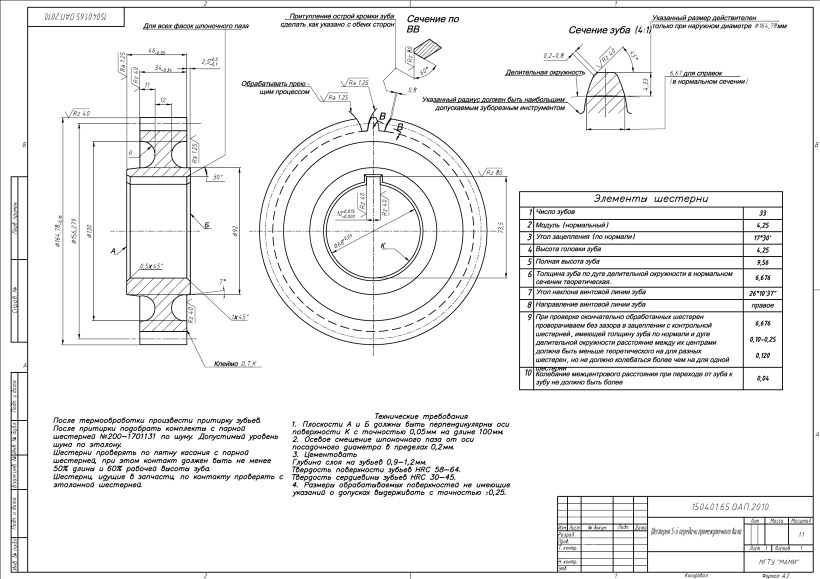 е.

Колеса одного и того же модуля, имеющие одно и то же число зубьев, могут отличаться друг от друга толщиной зуба по дели­тельной окружности.

Различают:

1) колеса с равноделенным шагом, у которых по делительной окружности толщина зуба равна ширине впадины и, следовательно, половине шага

s = e = m/2;

2) колеса, у которых s > е, т. е. s > m/2;

3) колеса, у которых s < е, т. е. s < m/2.

На рис. 14.3, в изображены центральные углы 2 и 2_у, соответствующие дуговым толщинам зуба s и s_у, а также эвольвентные углы inv и inv_y. Из рисунка следует:

_b =  + inv = _y + inv_y

отсюда

_y =  + inv – inv_y

          Выражая угловые толщины через линейные _y = s_y/(2r_y) и = s/(2r) и подставляя из значения в уравнение, ранее составленное для _y, получим формулу для определения толщины внешнего зуба:

                                      s_y = r_y (s/r + 2inv – 2 inv_y)                                 (14.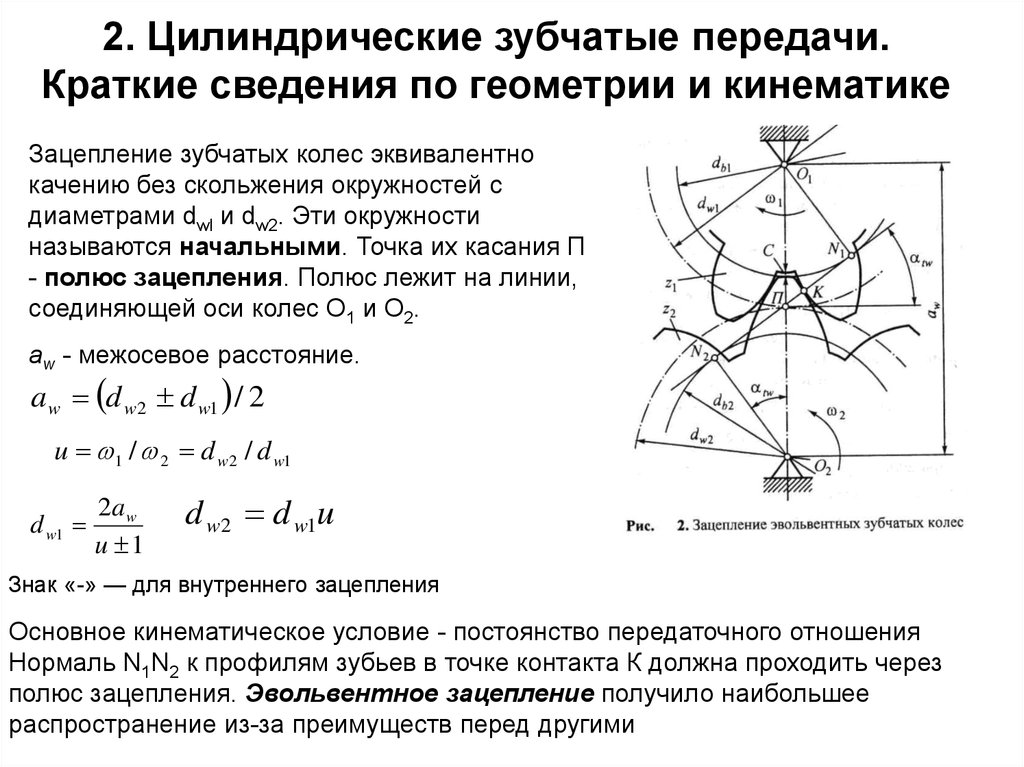 6)

          Аналогично составляется формула для определения толщины s_y внутреннего зуба:

                                      s_y = r_y (s/r – 2inv + 2 inv_y)

Если безгранично увели­чивать число зубьев колеса, а следовательно, и радиусы всех окружностей, то в пре­деле при z =  все окруж­ности преобразуются в па­раллельные прямые, а эвольвентный профиль зуба ста­нет прямолинейным, что имеет очень важное практическое значение. При z =  получим зубчатую рейку (рис. 14.4). В любом месте прямолинейной части зуба рейки профильный угол будет одним и тем же, равным .

Прямая UU, по которой толщина зуба рейки в точности равна ширине впадины, т. е. равна половине шага, называется делитель­ной прямой. Шаг зубьев рейки, измеренный по любой прямой, па­раллельной делительной, имеет одинаковое значение p =m. Шаг рейки, замеренный по нормали n–n к ее профилю, равен mcos, т. е.  равен шагу р_b по основной окружности колеса, модуль которого такой же, как и модуль рейки.

Основные положения станочного зацепления.

Реечное станочное зацепление.

Способы изготовления зубчатых колес. В настоящее время зубчатые колеса изготавливают способами ко­пирования и огибания.

По первому способу изготовляют зубчатые колеса в основном только с равноделенным шагом. При этом большинство их вы­полняется с заведомой погрешностью. Второй способ – способ огибания такими существенными недостатками не обладает: этим спо­собом можно изготовить самые разнообразные зубчатые колеса и притом теоретически точно. Поэтому способ огибания нашел распространение и представляет особый интерес.

При способе огибания заготовке, из которой изготовляют зуб­чатое колесо, и режущему инструменту, имеющему зубчатую форму (червячная фреза, гребенка, долбяк), сообщают на станке такие движения относительно друг друга, которые воспроизводят процесс зацепления. Это зацепление называют станочным.

Помимо движений, воспроизводящих процесс зацепления ин­струменту сообщается еще технологическое движение резания. При этом режущие кромки инструмента описывают по­верхность, называемую производящей. Укажем, что производящая поверхность и изготавливаемая боковая поверхность зуба являются взаимоогибаемыми, откуда сам способ и получил свое наименование.

При расчете геометрических параметров элементов высшей кинематической пары учитывают технологиче­ские возможности изготовления деталей на формообразующих станках (металлорежущих, прокатных станах, прессах и т. д.). Геометрия соответствующего формообразующего инструмента тес­ным образом связана с производящими поверхностями. Для инструментов, осуществляющих процесс формообразова­ния путем срезания стружки, такой производящей поверхностью является воображаемая поверхность, содержащая режущие кромки инструмента или образуемая при их главном движении, необходи­мом для резания. Если режущие кромки – прямые, а главное дви­жение – прямолинейное, то производящей поверхностью является плоскость. Если режущие кромки криволинейные, а главное дви­жение – прямолинейное, то производящей поверхностью является цилиндрическая поверхность (например, эвольвентная поверхность для долбяков).

Зацепление проектируемой поверхности зубьев с производящей поверхностью по аналогии с зацеплением нарезаемого колеса с производящей поверхностью режущего инструмента называют станочным зацеплением. Этот термин был предложен В. А. Гавриленко, крупным ученым, обобщившим и развившим основные положения теории зацепления эвольвентных передач. Сущность станочного зацепления заключается в том, что про­изводящая поверхность (поверхность режущих кромок инструмен­та) и проектируемая поверхность зуба («нарезаемого» колеса) имеют такое же относительное движение, какое имели бы зубчатые колеса при зацеплении друг с другом при взаимодействии аксоидных поверхностей.

При нарезании цилиндрических зубчатых колес оси произво­дящего колеса (т. е. воображаемого зубчатого колеса, у которого боковые поверхности являются производящими поверхностями) и проектируемого («нарезаемого») колеса параллельны между собой и аксоидами являются цилиндры.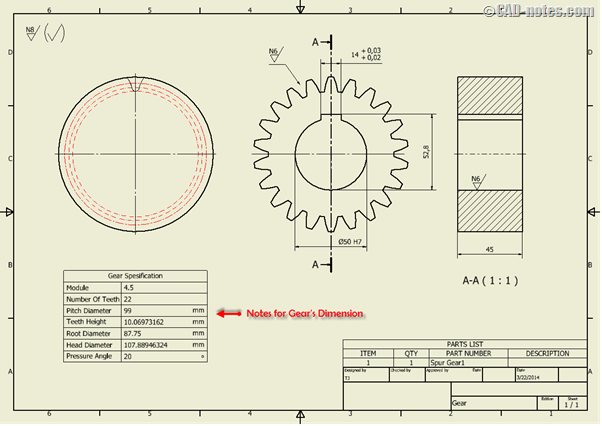 Если производящее колесо имеет конечное число зубьев, то режущими инструментами являются долбяк (рис. 14.5 е), абразивный хон (рис, 14.5 ж), которыми можно обрабатывать боковые поверхности зубьев колес с различными числами зубьев (рис, 14.5, з). При бесконечно большом ра­диусе аксоида производящего колеса инструмент должен иметь бесконечно большое число зубьев, т. е. превратиться в рейку. В этом случае инструментом   обычно   являются   червячная   фреза (рис. 14.5, б) или абразивный червячный круг (рис. 14.5, г), у ко­торых реечный производящий контур (рис. 14.5, д) расположен на винтовой поверхности. Частным случаем является инструмент, называемый зуборезной гребенкой (рис. 14.5, а) или пара тарельчатых шлифовальных кругов (рис. 14.5, в). Главным движением резания у долбяка, гребенки и абразивного хона является поступательное движение, а у червячной фрезы и

шлифоваль­ных кругов – вращательное движение.

В процессе движения огибания (обкатки) основной шаг инстру­мента по профильной нормали соответствует основному шагу про­ектируемого («нарезаемого») колеса. Процесс перехода от формо­образования одного зуба к другому в процессе обкатки осуще­ствляется автоматически при непрерывном относительном движении (рис. 14.5, д. з).

Если производящую поверхность рассечь плоскостью, перпен­дикулярной оси нарезаемого колеса, то в сечении получим ис­ходный производящий контур (ИПК). Станочное зацепление есть зацепление ИПК с профилем зуба нарезаемого колеса.

Рассмотрим реечное станочное зацепление, т. е. такое, когда ИПК имеет очертания зубчатой рейки. Эвольвентные кромки это­го ИПК прямолинейны. Режущий инструмент (чер­вячная фреза или гребенка), образующий своим главным движени­ем эвольвентный реечный ИПК, обладает очень ценным свойством: его можно изготовить, сравнительно дешево и точно. Геометрия зубьев нарезаемого колеса определяется параметрами ИПК реечного инструмента и его расположением по отношению к колесу.

Исходный производящий контур эвольвентного реечного инстру­мента. Форма я размеры ИПК стандартизованы. Эвольвентные части профиля зубьев ИПК (рис. 14.6, а) прямолинейны и на­клонены к оси зуба под углом . Переходы от прямолинейной части зуба к основанию впадины и к вершине осуществлены по дуге радиусом _t. Точки сопряжения отмечены на ИПК буквами А, С, D, Е. Прямолинейная часть CD является эвольвентной, а скругления АС и DE – неэвольвентной частью контура. Прямая, разделяющая зуб по высоте на две равные части, называется делительной. На ИПК отмечаются еще четыре линии, параллельные делительной прямой и проходящие по основаниям впадин зубьев, по их вер­шинам и через точки сопряжения С и О. Расстояния между этими прямыми выражают размеры зуба исходного производящего кон­тура по высоте и измеряются соответственно величинами h_a = h_a^*m и C = c^*m, где h_a^* – коэффициент высоты зуба, с^* – коэффициент радиального зазора.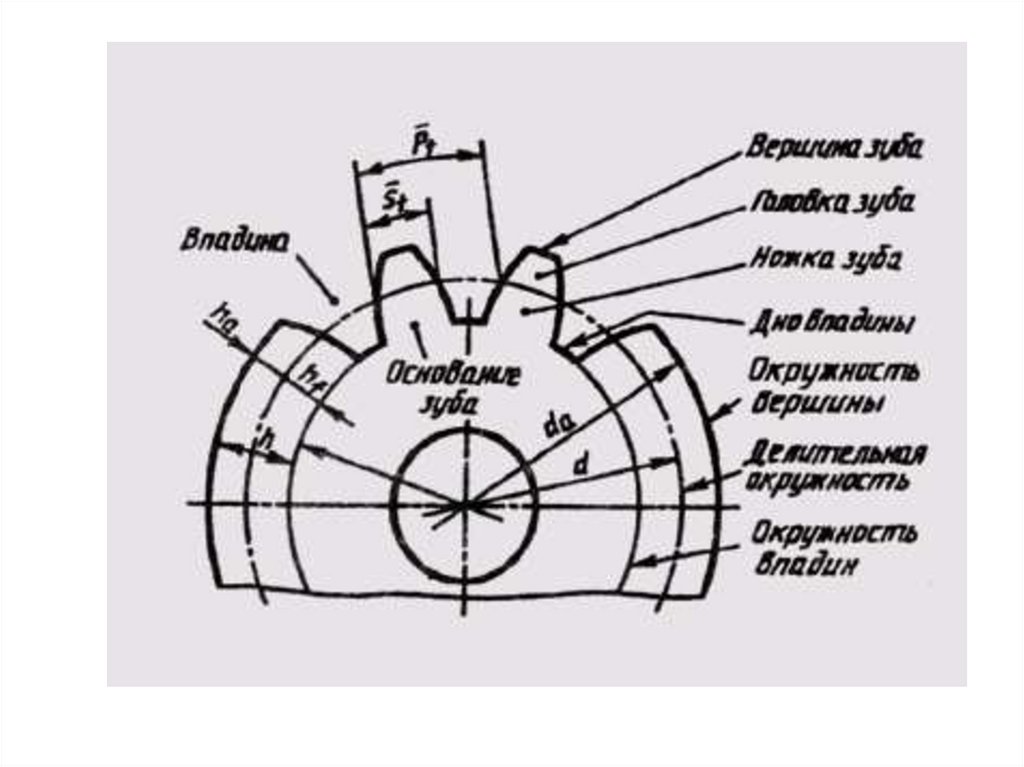 Согласно стандарту: h_a^* = 1,0 ; с^* = 0,25. Прямые, проходящие через точки С и D, называются пря­мыми граничных точек.

Размерами вдоль делительной прямой являются шаг, толщина зуба н ширина впадины. Шаг р исходного производящего контура, измеренный по любой прямой, параллельной делительной, есть ве­личина постоянная, равная m, где m – стандартный модуль. Тол­щина зуба ИПК по делительной прямом равна ширине впадины s₀ = e₀ = m/2, а вместе они составляют шаг. Угол профиля зуба стандартизован:  = 20°. Радиус скругления (дуги DE)

                                                                                     (14.7)

Таким образом. ИПК реечного инструмента характеризуется четырьмя стандартными параметрами: m, , h_a^*, c^*.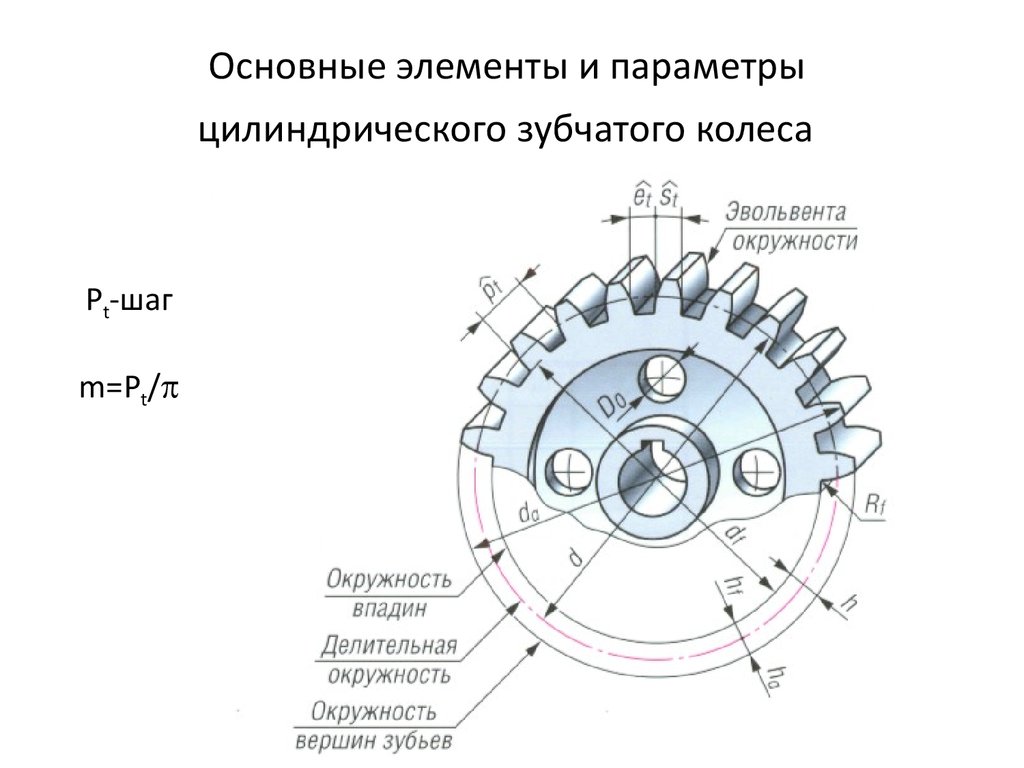

Реечное станочное зацепление и коэффициент смещения. Рееч­ное станочное зацепление, как и всякое зацепление, имеет началь­ные линии. Ими являются станочно-начальная прямая рейки и станочно-начальная окружность колеса, которые катятся друг по другу без скольжения. Можно показать, что в реечном станочном зацеплении радиус r_w0 станочно-начальной окружности равен радиусу делительной окружности r.

Угол реечного станочного зацепления _w0 равен профильному углу а исходного производящего контура (как углы с взаимно перпендикулярными сторонами). Отметим также, что угол профиля зуба колеса в точке, находящейся на делительной окружности, равен профильному углу  исходного производящего контура.

На станке инструмент можно расположить по-разному относи­тельно нарезаемого колеса. Поэтому в станочном зацеплении де­лительная прямая ИПК может располагаться различным образом по отношению к делительной окружности колеса: I) она может касаться делительной окружности – нулевая установка инструмен­та; 2) быть отодвинутой от нее — положительная установка; 3) пе­ресекать ее—отрицательная установка.

Расстояние между делительной прямой и делительной окруж­ностью называется смещением инструмента. Его выражают в виде произведения модуля m на коэффициент смещения х и ему присваивают знак. При нулевой установке смещение mх > 0, х > 0. При положительной установке mх > 0, х> 0. При отрицательной установке смещением является стрелка сегмента, которую делитель­ная прямая отсекает от делительной окружности; в этом случае mx < 0, x < 0.

На рис. 14.6, а изображено реечное станочное зацепление при нарезании зубчатого колеса с положительным смещением и указаны все элементы производящего исходного контура, нарезаемого коле­са и станочного зацепления.

Линия реечного станочного зацепления начинается в точке N и через полюс P₀ уходит в бесконечность. Длина ее активной части ограничена точками В₁^’ и B^’’, находящимися на пересечении линии станочного зацепления с прямой QQ граничных точек и окруж­ностью вершин (рис.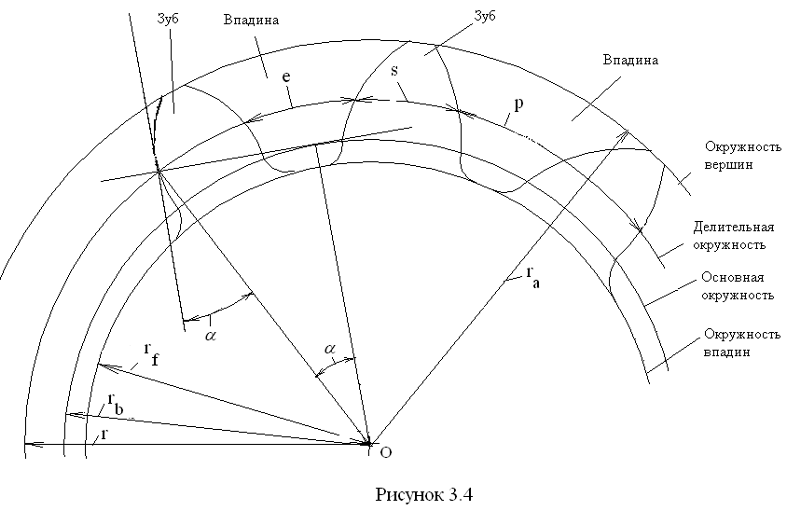 14.6, а)

         Профиль зуба колеса имеет эвольвентную и неэвольвентную части. Переход эвольвснтного профиля в неэпольвентиый находится на окружности граничных точек колеса, радиус которой r_l = OB₁^‘.

Расстояние между окружностью вершин зубьев колеса и прямой впадин ИПК представляет собой станочный зазор С₀. Величина его складывается из двух частей: с^*m, ym, где у — коэффи­циент уравнительного смещения.

Размеры изготовляемого зубчатого колеса с внешними зубьями. Диаметр вершин прямозубого колеса (рис. 14.6, а):

                                                                     (14.8)

     Высота зуба из того же рисунка:

                                                                                  (14.9)

Если x = 0 (смещения инструмента нет) и у = 0, то d_a = m(z + 2h_a^*),        h = m(2h_a^* + с^*), и при стандартных значениях h_a^* = 1,0 и с^* = 0,25 получим      d_a = m(z+2) и h = 2,25m.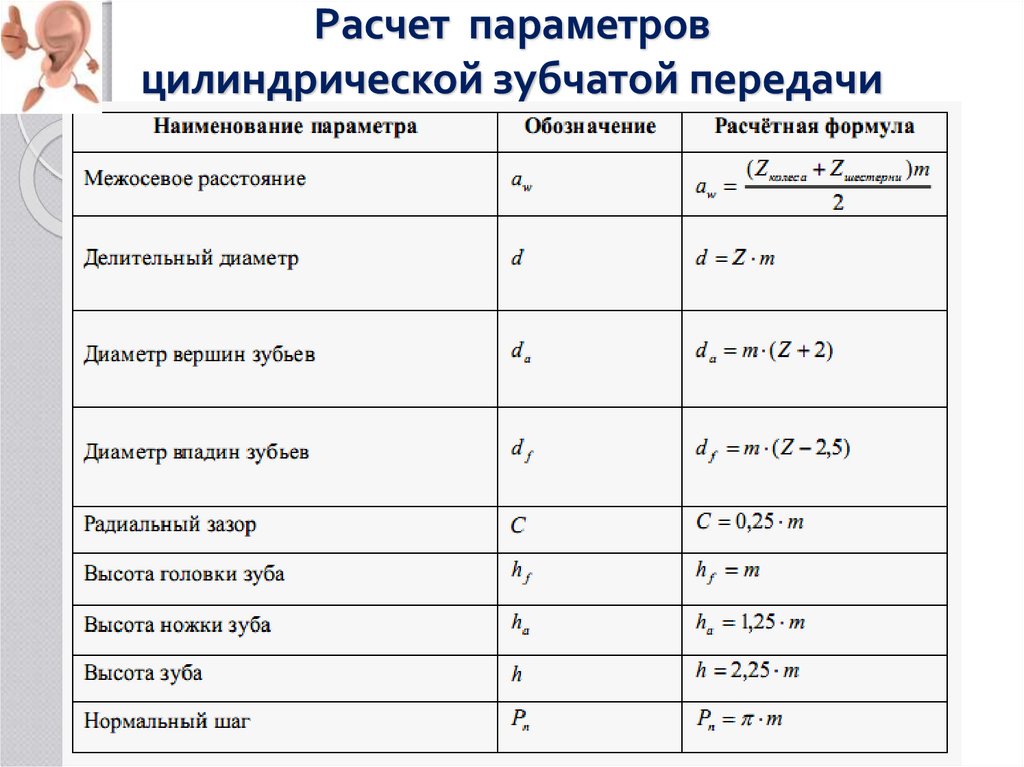

Стачочно-начальная прямая перекатывается по станочно-начальной окружности (она же делительная) без скольжения. По­этому толщина зуба s по делительной окружности нарезаемого колеса равна ширине ММ впадины по станочно-начальной прямой ИПК (рис. 14.6, б).

Отрезок ММ складывается из ширины впадины ИПК по де­лительной прямой e₀ = m/2 и двух катетов, каждый из которых равен xm tg, поэтому:                                   

                                           s = m/2 + 2 xm tg                                        (14.10)

Если инструмент установлен относительно колеса без смещения (xm = 0), то s = m/2; значит, толщина зуба s по делительной ок­ружности колеса равна ширине впадины е, так как s + е =m. В этом случае получается колесо с равноделенным шагом s = e, Если xm > 0, то s > m/2 и, следовательно, s > e. Если xm  < 0, то s < m/2, и поэтому s < e.

При нарезании косозубых колес применяется тот же инструмент 1, что для прямозубых, но устанавливается он наклонно под углом  по отношению к торцовой плоскости t – t колеса (заготовки) (рис. 14.6, в). На этом рисунке показана развертка 2 делительного цилиндра косозубого колеса, в результате чего винтовые линии косого зуба преобразо­вались в прямые линии. В торцовой плоскости t – t косозубого колеса вследствие наклона инструмента шаг увеличивается и становится равным p/cos, а следова­тельно, и модуль в торцовой плоскости будет нестандарт­ным, равным m/cos. По­этому при расчете линейных размеров косозубого колеса по формулам, в которые входит стандартный модуль, вместо m следует подставлять m/cos, например делительный диаметр косозубого колеса d = zm/ cos.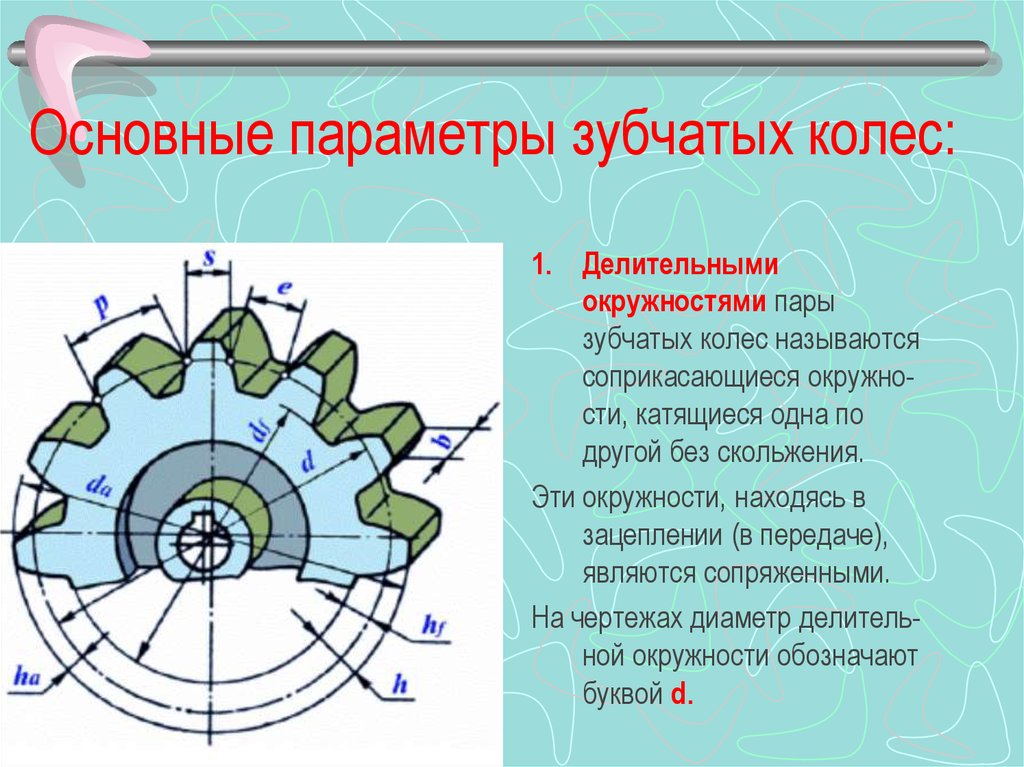

Обратим внимание на размеры h_a^*m, c^*m, xm, y*m, перпенди­кулярные делительной прямой (рис. 14.6, а), которые принято назы­вать размерами по высоте. На рис. 14.6 в эти размеры расположены перпендикулярно плоскости рисунка. Поэтому при повороте инстру­мента на угол  размеры по высоте не изменяются. А отсюда следует, что когда в уравнениях встречаются произведения h_am, cm, xm, ym, то их при расчете косозубой передачи можно под­ставлять в эти уравнения без всякого пересчета сомножителей. Так, например, формула диаметра вершин косозубого колеса может быть записана следующим образом: d_a = d + 2(h_a^*m + xm – y*m).

Угол профиля исходного производящего контура при нарезании косозубого колеса увеличивается по сравнению со стандартной величиной  = 20°, поскольку размеры по высоте не изменяются, а шаг в торцовом сечении увеличивается. Расчетный угол профиля _t исходного производящего контура при нарезании косозубых ко­лес определяют по формуле:

На рис. 14.7 сравниваются профили зубьев трех колес, имею­щих одинаковые числа зубьев, нарезанные одним и тем же ин­струментом, но с различными смещениями: x₁ < x₂ < x₃. Колеса имеют одинаковые радиусы делительных и основных окружностей; следовательно, профили зубьев всех трех колес очерчены по одной и той же эвольвенте. Но толщины зубьев s₁, (дуга ab), s₂ (дуга ас), s₃ (дуга af) и радиусы окружностей вершин r_a1, r_a2, r_a3, у колес будут разные. По мере увеличения х толщина зуба у основания увеличивается, а у вершины уменьшается, т.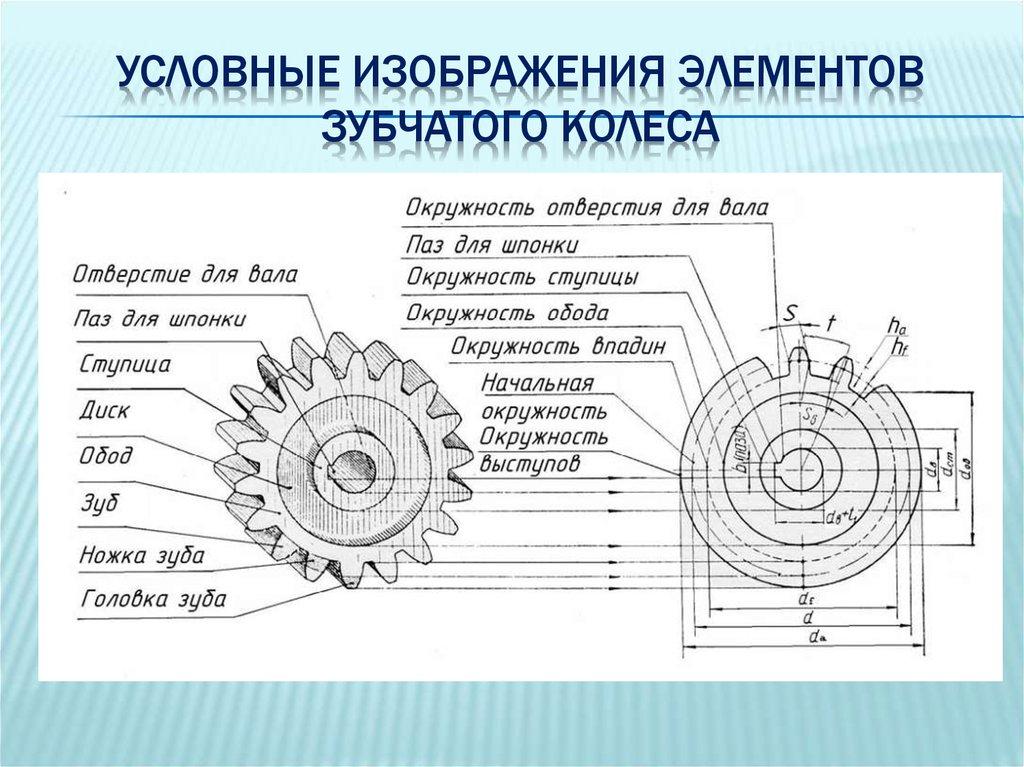 е. коэффициент сме­щения существенно влияет на форму зуба. Следовательно, назначая при проектировании тот или иной коэффициент смещения, можно влиять на форму зубьев колёс и на качество зубчатой передачи, наделяя её желательными свойствами.

Контрольные вопросы к лекции N14

1. Что называют зубчатым колесом?

Информация в лекции “Воля как волевое действие” поможет Вам.

2. Расскажите об основных элементах зубчатого колеса.

3. Запишите формулы окружного и углового шагов эвольвентного зубчатого колеса.

4. Какие методы изготовления зубчатых колёс Вы знаете?

5. В чём заключается сущность изготовления эвольвентных колёс методом огибания?

6. Дайте определение станочного зацепления.

7. Выведите формулы для определения основных размеров зубчатого колеса () используя схему станочного зацепления.

Червячная фреза с непостоянными полными высотами для нарезания зубьев зубчатого колеса

Изобретение относится к зубофрезерному приспособлению для изготовления зубчатого колеса из заготовки.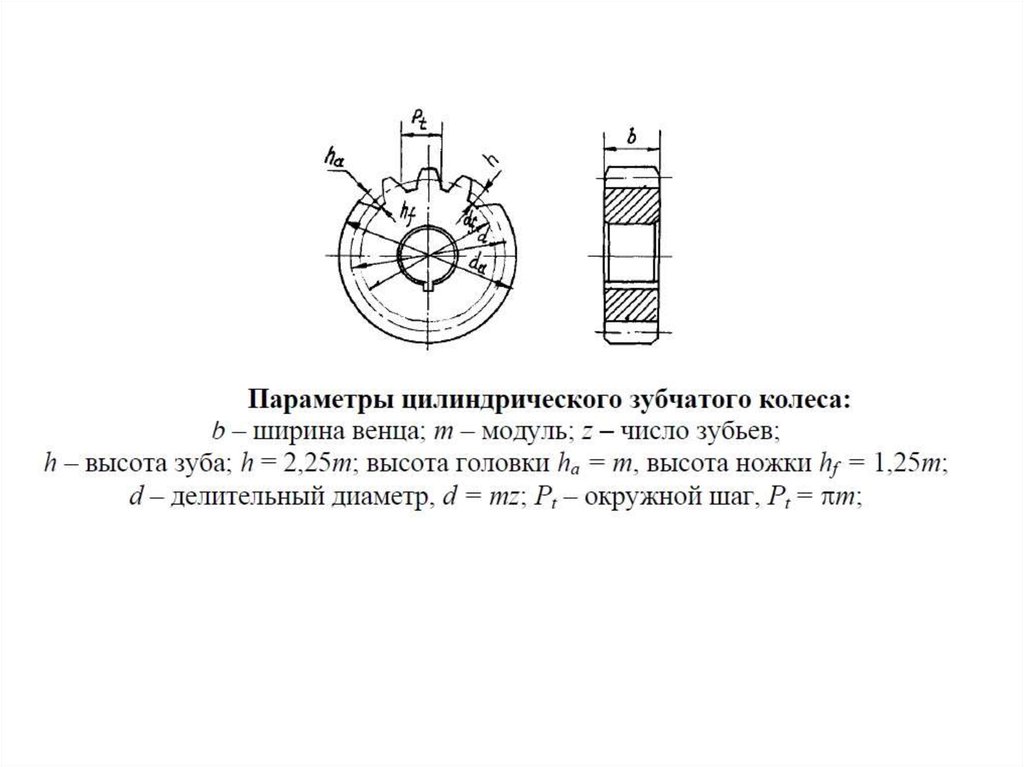 Согласно изобретению приспособление содержит червячную фрезу, имеющую цилиндрическое тело, от которого отходят зубья первой группы и, чередуясь с ними, зубья второй группы. Полная высота зубьев первой группы отличается от полной высоты зубьев второй группы, обеспечивая образование из заготовки зубчатого колеса со смежными зубьями, имеющими разные наружные диаметры. В результате обеспечивается повышение качества резки за счет наличия разных точек зацепления на сопряженных зубьях. 3 н. и 16 з.п. ф-лы, 7 ил.

 

Область техники

Изобретение относится к зуборезным инструментам и, в частности, к зубофрезерному приспособлению для изготовления зубчатого колеса из заготовки.

Уровень техники

Зубчатые колеса обычно изготавливаются посредством резки обрабатываемой детали или заготовки в процессе операции изготовления зубьев, называемой зубофрезерованием. Червячная фреза предназначена для изготовления профиля зуба с заданными высотой зуба, углом зацепления и толщиной зуба.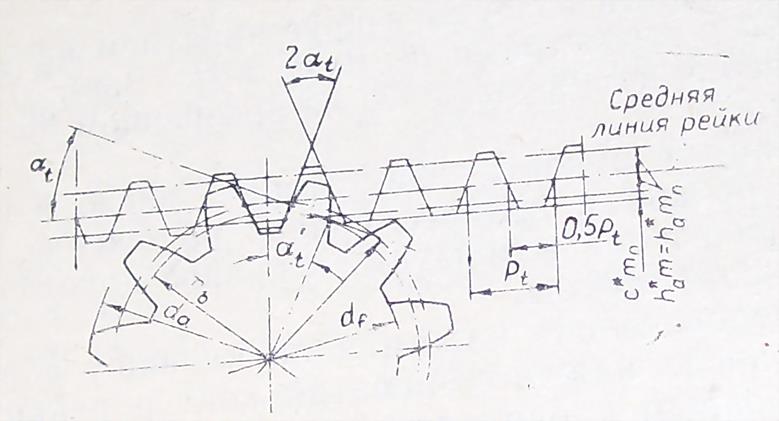 Все зубья, изготовленные стандартной червячной фрезой, имеют одинаковые высоту, угол зацепления и толщину. Эти параметры характеризуют профиль зуба. Стандартная червячная фреза имеет цилиндрическую форму и содержит винтовые режущие зубья. Эти зубья содержат канавки, которые проходят по длине червячной фрезы. Канавки способствуют резанию заготовки и облегчают удаление стружки. Во время использования зубья червячной фрезы последовательно врезаются в обрабатываемую деталь посредством ряда резов, выполняемых червячной фрезой.

Раскрытие изобретения

Зубофрезерное приспособление для изготовления зубчатого колеса из заготовки согласно изобретению содержит червячную фрезу с первой и второй группами зубьев. Червячная фреза имеет цилиндрическое тело. Зубья первой группы отходят от цилиндрического тела и имеют первую полную высоту. Зубья второй группы отходят от цилиндрического тела поочередно с зубьями указанной первой группы и имеют вторую полную высоту. Первая и вторая полные высоты отличаются друг от друга, обеспечивая образование из заготовки зубчатого колеса со смежными зубьями, имеющими разные наружные диаметры.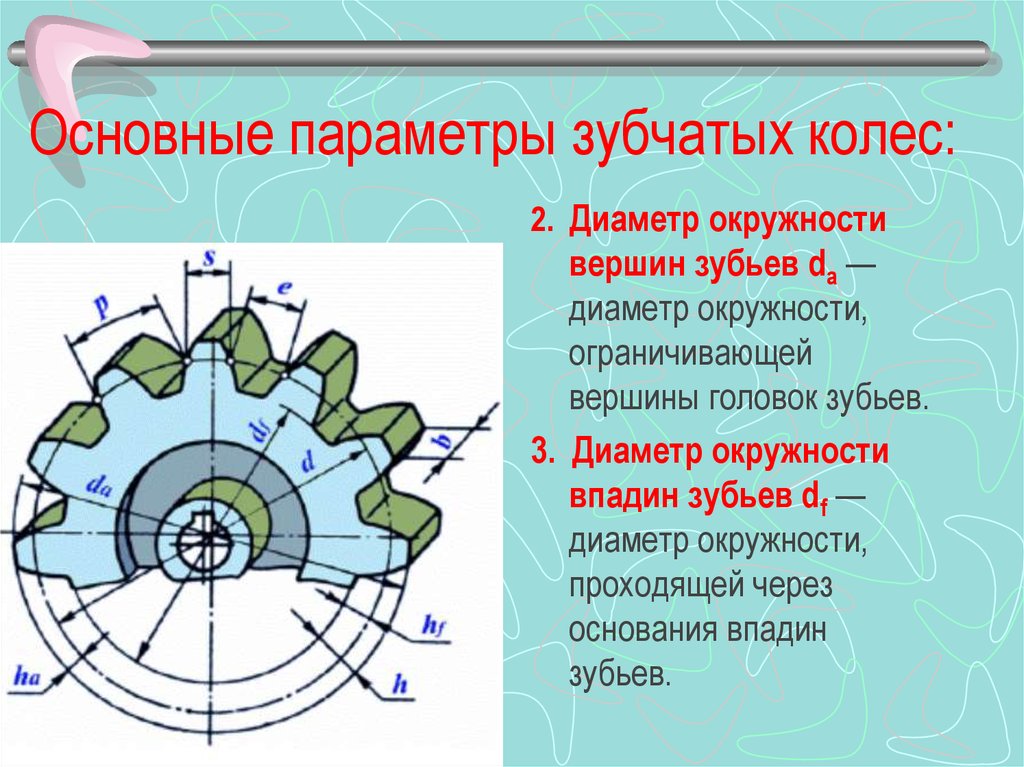

Червячная фреза может быть однозаходной или многозаходной.

Червячная фреза может иметь первый виток с первым зубчатым профилем, и второй виток со вторым зубчатым профилем, при этом первый и второй витки отличаются друг от друга. Первый и второй зубчатые профили также могут отличаться друг от друга. Червячная фреза может иметь три или более витков с тремя или более зубчатыми профилями.

Согласно другому варианту осуществления изобретения зубофрезерное приспособление для изготовления зубчатого колеса из заготовки содержит червячную фрезу с первым и вторым зубьями. Червячная фреза имеет цилиндрическое тело с осью. Первый зуб отходит от цилиндрического тела и определяет первый диаметр, измеряемый от указанной оси, и первую полную высоту зуба. Второй зуб отходит от цилиндрического тела смежно с первым зубом и определяет второй диаметр, измеряемый от указанной оси, и вторую полную высоту зуба. Первый и второй диаметры равны по величине, а первая и вторая полные высоты отличаются друг от друга. В результате Червячная фреза обеспечивает образование из заготовки зубчатого колеса со смежными зубьями, имеющими разные наружные диаметры.

Зубофрезерное приспособление также может содержать поочередно отходящие от цилиндрического тела зубья первой группы червячной фрезы с первой полной высотой и зубья второй группы червячной фрезы со второй полной высотой.

Червячная фреза может быть однозаходной или многозаходной. Червячная фреза может иметь первый виток с первым зубчатым профилем и второй виток со вторым зубчатым профилем. Первый и второй витки могут отличаться друг от друга. Первый и второй зубчатые профили также могут отличаться друг от друга.

Изобретению относится также к способу изготовления зубчатого колеса из заготовки, имеющей ось. Согласно этому способу обеспечивают наличие червячной фрезы, содержащей цилиндрическое тело с осью, первую группу зубьев, отходящих от указанного цилиндрического тела и имеющих первую полную высоту, и вторую группу зубьев, отходящих от цилиндрического тела поочередно с зубьями указанной первой группы и имеющих вторую полную высоту, причем первая и вторая полные высоты отличаются друг от друга.

Указанную червячную фрезу поступательно перемещают поперек окружной поверхности заготовки зубчатого колеса. При этом червячную фрезу и заготовку вращают вокруг своих собственных осей. Заготовку зубчатого колеса подвергают резанию посредством зубьев первой и второй групп червячной фрезы. Первые и вторые зубья червячной фрезы выполнены с возможностью образования зубчатого колеса со смежными зубьями, имеющими разные наружные диаметры.

Червячная фреза может быть однозаходной или многозаходной; может иметь первый виток с первым зубчатым профилем, и второй виток со вторым зубчатым профилем. Первый виток и второй виток могут отличаться друг от друга. Первый и второй зубчатые профили могут отличаться друг от друга.

Изобретение станет более понятным из дальнейшего описания со ссылками на чертежи.

Краткое описание чертежей

На фиг. 1 показаны червячная фреза согласно первому варианту ее выполнения и формирование зубьев в заготовке зубчатого колеса, вид сбоку;

на фиг. 2 – место 2 на фиг. 1, вид в сечении в увеличенном масштабе;

на фиг. 3 – червячная фреза, показанная на фиг. 1, вид вдоль оси;

на фиг. 4 – червячная фреза, показанная на фиг. 1, вид с другого бока;

на фиг. 5 – один из зубьев червячной фрезы, показанной на фиг. 4, вид в увеличенном масштабе;

на фиг. 6 – сечение червячной фрезы с изображением смежных полных высот, ограниченных соседними зубьями;

фиг. 7 – готовое зубчатое колесо, образованное червячной фрезой по фиг. 1 и зацепляющееся с соседним вторым зубчатым колесом согласно изобретению.

Осуществление изобретения

На фиг. 1 и 2 показано зубофрезерное приспособление или червячная фреза, выполненная согласно одному из вариантов осуществления изобретения и обозначенная общей позицией 10. Червячная фреза 10 предназначена для изготовления зубчатого колеса 20 из обрабатываемой детали или заготовки 22. Червячная фреза 10 выполнена с возможностью вращения вокруг оси вала 30.

Червячная фреза 10 имеет цилиндрическое тело 32, ось 36 которого совпадает с осью вращения вала 30. Червячная фреза 10 содержит зубья 40, между которыми в продольном направлении вдоль цилиндрического тела 32 образованы впадины.

Как будет подробно описано ниже, червячная фреза 10 используется для образования зубчатого колеса 20 из заготовки 22. Зубчатое колесо 20 по его окружности будет иметь зубья 50. Заготовка 22 приспособлена для вращения вокруг своей оси 56 и установлена на валу 60. Как будет подробно описано ниже, зубчатое колесо 20 будет образовано червячной фрезой так, что не все зубья 50 зубчатого колеса будут иметь одинаковый наружный диаметр.

Червячная фреза 10 выполнена так, что зубья 50 с разными наружными диаметрами могут быть образованы за одну операцию без последующей механической обработки. Во время изготовления или зубофрезерования зубчатого колеса 20 может быть использована первая группа зубьев 40A с полной высотой 70 и одновременно вторая группа зубьев 40B с полной высотой 72.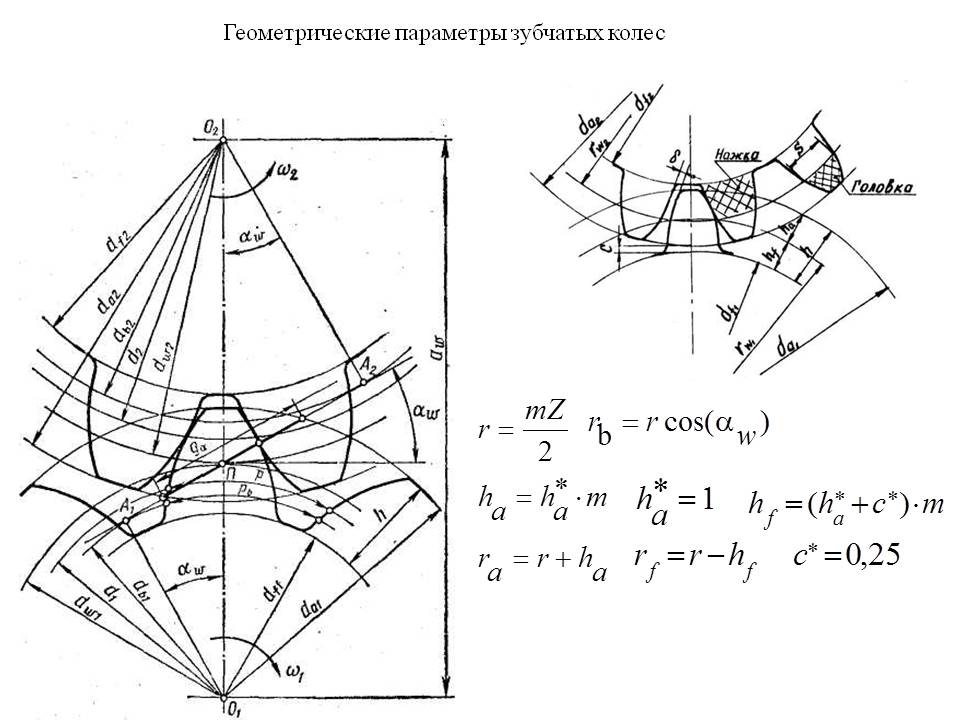 Первая полная высота 70 ограничена выемкой 74 и вершиной 76 первого зуба 40A. Аналогично, полная высота 72 ограничена выемкой 77 и вершиной 78 второго зуба 40B. Полные высоты 70 и 72 отличаются друг от друга. Кроме того, поскольку выемки 74 и 77 находятся в разных местах, диаметры оснований первой группы зубьев 40A и второй группы зубьев 40B варьируется. Изменяющийся диаметр основания позволяет выполнять нарезание зубьев 50 зубчатого колеса 20 разной высоты.

В показанном примере полная высота 72 меньше полной высоты 70. В результате зубья 50 зубчатого колеса, которые образуются посредством червячной фрезы 10, будут иметь первую группу зубьев 50A и вторую группу зубьев 50B. Диаметр 80 зубьев 50A первой группы, измеряемый от оси 56 зубчатого колеса, больше диаметра 82 зубьев 50B второй группы, измеряемого от оси 56 зубчатого колеса.

Со ссылками на фиг. 3 – 5 будут описаны дополнительные особенности червячной фрезы 10. На этих фигурах позицией 100В обозначен диаметр отверстия, выполненного в цилиндрическом теле 32 червячной фрезы 10; позицией 110 обозначен наружный диаметр червячной фрезы 10; а позицией 120 обозначено угловое расстояние между смежными выемками 74 и 78. Каждый зуб 40 червячной фрезы включает в себя радиальную режущую поверхность 122 и криволинейную поверхность 124.

Кроме того, позицией 130 обозначен диаметр делительной окружности червячной фрезы 10; позицией 132 – ступица червячной фрезы; позицией 134 – ширина режущей поверхности; а позицией 136 – длина червячной фрезы. Угол зацепления, ограниченный зубьями 40 червячной фрезы, обозначен позицией 140. Шаг зубьев, определяемый смежными зубьями 40, обозначен позицией 144. Позициями 150 и 152 (фиг. 6) обозначены первый и второй витки червячной фрезы 10. На фиг. 5 толщина зуба 40 червячной фрезы обозначена позицией 160; радиус закругления вершины зуба – позицией 162; головка зуба червячной фрезы – позицией 164; а модификация профиля головки – позицией 168. Полная высота резания 170 ограничена каждым зубом 40.

На фиг. 6, на показаны первый виток 150 и второй виток 152 на цилиндрическом корпусе 32 червячной фрезы 10. Витки 150 и 152, в целом, ограничивают угол подъема в процессе резания, выполняемого червячной фрезой 10.

Как показано на фиг. 7, червячная фреза 10 выполнена с возможностью образования зубчатого колеса 20, имеющего смежные зубья 50 (например, зубья 50A и 50B), имеющие разные диаметры 80 и 82. В представленном примере диаметр 80 больше диаметра 82. Поскольку зубья 50A и 50B, поочередно образованные по окружности зубчатого колеса 20, имеют разные диаметры, они будут иметь разные точки зацепления на сопряженных зубьях 200 соответствующего стандартного зубчатого колеса 220, у которого зубья 200 имеют одинаковые диаметры. Зацепление может сопровождаться возникновением различных резонансных частот, обеспечивая плавное зацепление между соответствующими зубьями 50 зубчатого колеса 20 и зубьями 200 зубчатого колеса 220.

Изготовление зубчатого колеса 20 с использованием червячной фрезы 10 согласно изобретению осуществляется следующим образом.

Сначала выбирают червячную фрезу 10 с характеристиками, пригодными для изготовления требуемого зубчатого колеса 20. Выбирается червячная фреза 10 с определенными параметрами: диаметром 130 делительной окружности, шириной 134 режущей поверхности, длиной 136 червячной фрезы, углом 140 зацепления, толщиной 160 зуба, радиусом 162 закругления вершины, головкой 164 зуба червячной фрезы, модификацией профиля 168 головки и полной высотой резанья 170 для каждого готового зуба. Полная высота 70 зубьев 40A первой группы больше полной высоты 72 чередующихся зубьев 40B второй группы.

Вал 30 червячной фрезы установлен с возможностью вращения вокруг оси 36 и может вращаться приводным двигателем (не показан). Вал 60 обрабатываемой детали установлен с возможностью вращения вокруг оси 56 зубчатого колеса. Червячная фреза 10 движется поступательно поперек окружной поверхности обрабатываемой детали 22, вращаясь при этом вокруг оси 36, а обрабатываемая деталь 22 вращается вокруг оси 56. Первая и вторая группы зубьев 40A и 40B червячной фрезы, имеющие разные полные высоты 70 и 72, режут обрабатываемую деталь 22, образуя зубчатое колесо 20 с чередующимися зубьями 50A и 50B, имеющими разные наружные диаметры.

Представленное выше описание приведено в качестве примера осуществления изобретения и не ограничивает это изобретение. Отдельные элементы или особенности конкретного варианта выполнения, в целом, не ограничиваются этим конкретным вариантом выполнения и, по возможности, являются взаимозаменяемыми и могут использоваться в выбранном варианте выполнения, даже если они специально не показаны или не описаны.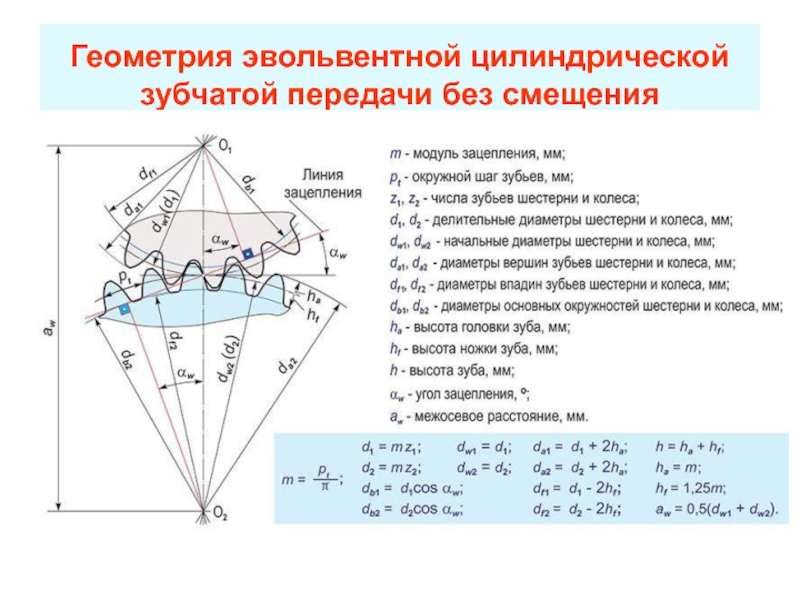 Эти же отдельные элементы или особенности могут изменяться различными способами, не выходя за объем изобретения.

1. Зубофрезерное приспособление для изготовления зубчатого колеса из заготовки, содержащее

червячную фрезу с цилиндрическим телом,

первую группу зубьев червячной фрезы, отходящих от цилиндрического тела и имеющих первую полную высоту, и

вторую группу зубьев червячной фрезы, отходящих от цилиндрического тела поочередно с зубьями указанной первой группы и имеющих вторую полную высоту, при этом

первая и вторая группы зубьев червячной фрезы выполнены с возможностью формирования зубчатого колеса, имеющего чередующиеся по окружности первые и вторые зубья таким образом, что первые зубья зубчатого колеса определяют первый наружный диаметр, а вторые зубья зубчатого колеса определяют второй наружный диаметр, который меньше указанного первого наружного диаметра.

2. Приспособление по п. 1, в котором червячная фреза является однозаходной.

3. Приспособление по п. 1, в котором червячная фреза является многозаходной.

4. Приспособление по п. 1, в котором червячная фреза имеет первый виток с первым зубчатым профилем и второй виток со вторым зубчатым профилем, при этом первый и второй витки отличаются друг от друга.

5. Приспособление по п. 4, в котором первый и второй зубчатые профили отличаются друг от друга.

6. Приспособление по п. 1, в котором каждый зуб червячной фрезы из первой и второй групп имеет закругленную вершину.

7. Приспособление по п. 1, которое дополнительно содержит

первые выемки, определяющие первый диаметр основания и образованные между смежными зубьями червячной фрезы первой и второй групп, и

вторые выемки, определяющие второй диаметр основания, который больше первого диаметра основания, и образованные между смежными зубьями червячной фрезы первой и второй групп, при этом

первые выемки упрощают формирование первых зубьев зубчатого колеса, а вторые выемки упрощают формирование вторых зубьев зубчатого колеса.

8. Приспособление по п. 7, в котором второй диаметр основания больше, чем первый диаметр основания.

9. Приспособление по п. 7, в котором первые и вторые выемки выполнены с возможностью чередования вдоль длины цилиндрического тела червячной фрезы.

10. Зубофрезерное приспособление для изготовления зубчатого колеса из заготовки, содержащее

червячную фрезу, имеющую цилиндрическое тело с осью,

первую группу зубьев, отходящих от цилиндрического тела и определяющих первый диаметр, измеряемый от указанной оси,

вторую группу зубьев, отходящих от цилиндрического тела и определяющих второй диаметр, измеряемый от указанной оси,

третью группу зубьев, отходящих от цилиндрического тела и определяющих третий диметр, измеренный от указанной оси, при этом зубья второй группы расположены между зубьями первой и третьей групп,

первые выемки, образованные между зубьями первой и второй групп и определяющие первый диаметр основания, измеренный от указанной оси, и

вторые выемки, образованные между зубьями второй и третьей групп и определяющие второй диаметр основания, измеренный от указанной оси, при этом

первые выемки и первая, и вторая группы зубьев выполнены с возможностью формирования первых зубьев зубчатого колеса, определяющих первый наружный диаметр, а вторые выемки и вторая, и третья группы зубьев выполнены с возможностью формирования вторых зубьев зубчатого колеса, определяющих второй наружный диаметр, который меньше указанного первого наружного диаметра.

11. Приспособление по п. 10, в котором червячная фреза является однозаходной.

12. Приспособление по п. 10, в котором червячная фреза является многозаходной.

13. Приспособление по п. 10, в котором червячная фреза имеет первый виток с первым зубчатым профилем и второй виток со вторым зубчатым профилем, при этом указанные первый и второй витки отличаются друг от друга.

14. Приспособление по п. 13, в котором первый и второй зубчатые профили имеют разные формы.

15. Способ изготовления зубчатого колеса из заготовки, имеющей ось, включающий в себя этапы, на которых

обеспечивают наличие червячной фрезы, содержащей цилиндрическое тело с осью, первую группу зубьев, отходящих от цилиндрического тела и имеющих первую полную высоту, и вторую группу зубьев, отходящих от цилиндрического тела поочередно с зубьями указанной первой группы и имеющих вторую полную высоту, при этом первая и вторая полные высоты отличаются друг от друга,

поступательно перемещают червячную фрезу поперек окружной поверхности заготовки зубчатого колеса, при этом червячную фрезу и заготовку вращают вокруг своих собственных осей, и

режут заготовку зубчатого колеса посредством зубьев первой и второй групп червячной фрезы таким образом, что указанные первые и вторые зубья образуют зубчатое колесо, имеющее чередующиеся первые и вторые зубья, при этом первые зубья зубчатого колеса определяют первый наружный диаметр, а вторые зубья зубчатого колеса определяют второй наружный диаметр, который меньше указанного первого наружного диаметра.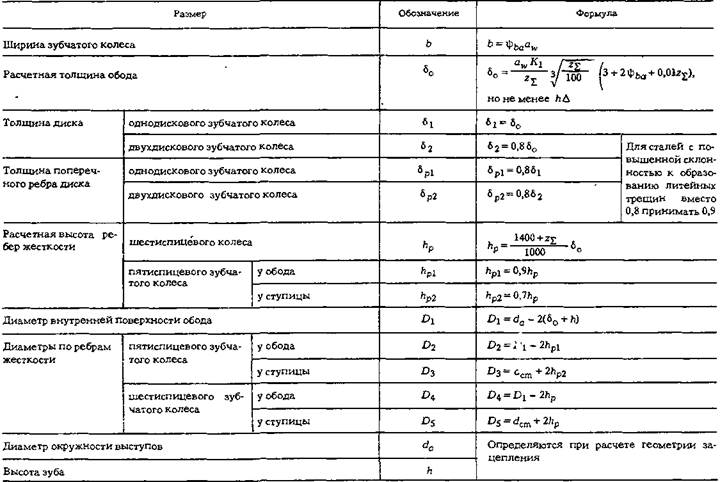

16. Способ по п. 15, в котором червячная фреза является однозаходной.

17. Способ по п. 15, в котором червячная фреза является многозаходной.

18. Способ по п. 15, в котором червячная фреза имеет первый виток с первым зубчатым профилем и второй виток со вторым зубчатым профилем, при этом указанные первый и второй витки отличаются друг от друга.

19. Способ по п. 18, в котором первый и второй зубчатые профили имеют разные формы.

Высота зуба шестерни – Grindel Gears

• А
• Б
• С
• Д
• Е
• Ф
• г
• ЧАС
• я
• Дж
• К
• л
• М
• Н
• с
• О
• п
• Вопрос
• р
• С
• Т
• U
• В
• Вт
• Икс
• Д
• Z

Вернуться к списку

Это радиальное расстояние между внешним диаметром и диаметром основания.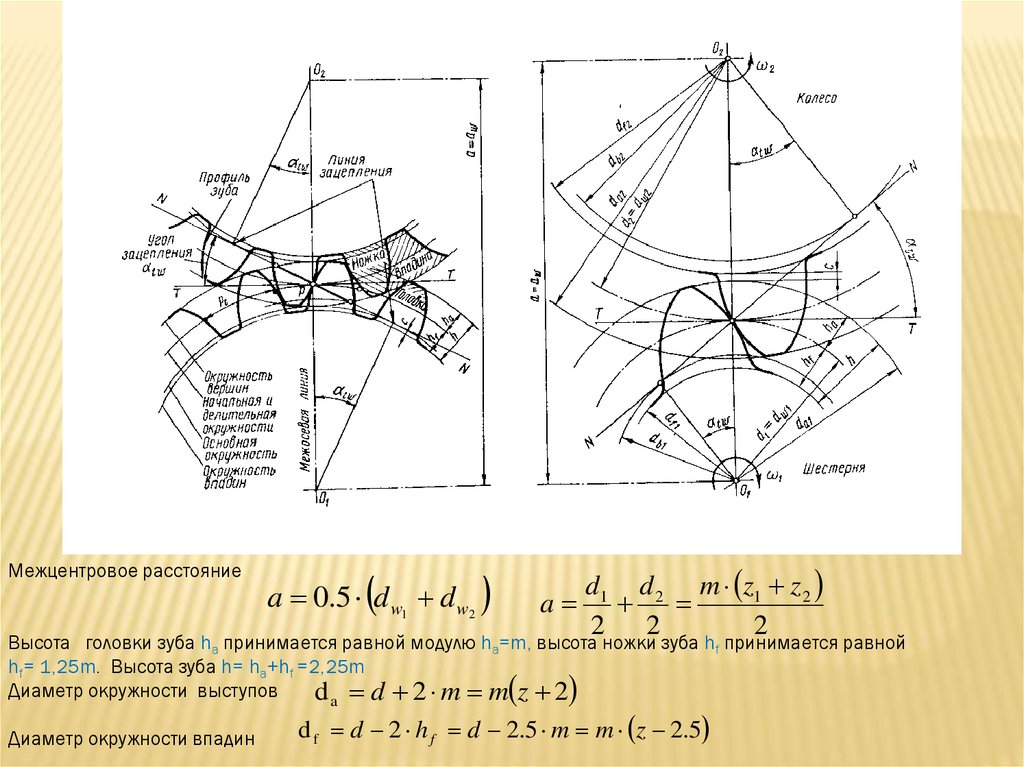

Дизайн зубчатой ​​передачи — RepRap

Содержимое

• 1 Дизайн зубчатой ​​передачи Art of Illusion
  • 1.1 Индекс
  • 1.2 Основы проектирования редукторов
    • 1.2.1 форма зубьев
    • 1.2.2 Количество зубьев
  • 1.3 Ограничения FDM
  • 1.4 Проектирование зубчатых передач в Art Of Illusion
  • 1,5 отверстие в середине шестерни
  • 1.6 Ссылки
• 2 Дальнейшее чтение

Art of Illusion Cog Gear Design

Алфавитный указатель

• Основы проектирования зубчатых колес
• Ограничения FDM
• Проектирование зубчатых передач в Art of Illusion
• Ссылки

При проектировании зубчатых колес для изготовления FDM в ArtOfIllusion необходимо помнить о двух важных вещах: основах обычного проектирования зубчатых колес и точности или ее отсутствии в производственном процессе. Итак, прежде чем мы углубимся в повседневность AoI, вот краткое руководство по дизайну снаряжения.

Вернуться к оглавлению

Основы проектирования зубчатых колес

Если вы инженер, это, вероятно, старая шляпа, но все равно прочтите ее, чтобы исправить мои ошибки. Шестерни обычно круглые, с зубьями. Количество зубов и их форма важнее, чем кажется на первый взгляд.

Форма зубьев

Они должны совпадать и иметь одинаковую высоту. Входящие зубья шестерни должны соприкасаться в нужном месте, и только в нужном месте, поэтому они имеют забавную «эвольвентную» форму, а не квадрат или маленькие треугольники.

Кончики зубьев шестерни не должны полностью опускаться в противоположный желоб. Если это произойдет, вершина следующего входящего зуба ударится о вершину противоположного зуба. Контакт между зубами теоретически происходит в точке чуть более половины пути (обычно с разделением 1: 1,25) вверх по зубам, и это называется «линией шага». Бит над линией поля называется «дополнением», бит ниже – «дедендумом». Угол наклона поверхностей зубов называется «угол давления» и обычно составляет около 20 градусов.

Расстояние между центром одного кончика зуба и центром следующего называется шагом. Вы хотите, чтобы шаг касания передач был как можно ближе. В идеале шаг должен быть в 2,25 раза больше высоты зубьев. Если высота одинакова на обеих шестернях, то и шаг одинаков, а если ширина, высота и шаг одинаковы, то разве они не должны быть одинакового диаметра?

Усилия между соприкасающимися зубьями должны быть равномерными и постоянными, иначе возникнет вибрация. Как и шум и износ. Эти проблемы усугубляются изгибанием зубов, поэтому с относительно мягким пластиком у нас будут интересные проблемы.

Количество зубьев

Для обеспечения механических преимуществ контактные шестерни имеют разное количество зубьев. Маленькая шестерня, приводящая в движение большую шестерню, увеличит крутящий момент и замедлит скорость вращения. Шестерни обычно имеют простые (или, по крайней мере, взаимно простые) числа зубьев. Это сделано для того, чтобы одни и те же зубья не всегда прижимались друг к другу, поэтому износ, грязь, масло, сплющенные пальцы и т. д. распределялись равномерно по всем задействованным зубьям шестерни.

Плохой: 15 и 25 зубьев . Удар на большой шестерне всегда задевает одни и те же 3 зуба на маленькой шестерне, вызывая неравномерный износ; в этом же примере удар маленькой шестерни всегда попадает в одни и те же 5 зубьев большой шестерни. Чтобы рассчитать это, сначала найдите наибольший общий делитель (НОД) числа зубьев каждой шестерни. например НОД(15,25)=5; затем разделите этот результат на количество рассматриваемых зубов. Например. 15/5=3 и 25/5=5.

Хорошо: 16 и 25 зубьев. Удар на большой шестерне (в конце концов) ударяет по каждому зубу маленькой шестерни, изнашивая их все одинаково.

Равномерный равномерный износ шестерни достигается за счет того, что количество зубьев двух шестерен, зацепляющихся друг с другом, является «относительно первичным» друг к другу; это происходит, когда наибольший общий делитель (GCD) каждого количества зубьев шестерни равен 1.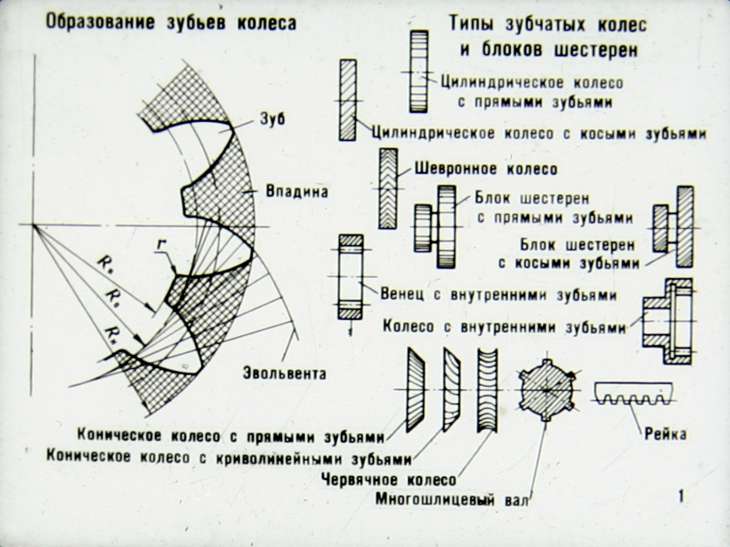 например. НОД(16,25)=1

Вернуться к оглавлению

Ограничения FDM

Механизмы, изготовленные из АБС-пластика или полиморфа, должны иметь прочную конструкцию, чтобы выжить. Маленькие острые кусочки скоро отломаются, когда механизм (неизбежно) заклинит. Износ — это жизненный факт, поэтому требуется много дополнительного материала. Короче говоря, ваши шестерни будут коренастыми и неточными.

Мы делаем шестерни достаточно толстыми, так как большая площадь контакта снижает контактное давление и, следовательно, износ. Мы используем гладкие кривые, а не угловые скачки, отчасти потому, что машина FDM не может быть достаточно точной, а отчасти потому, что они приведут к появлению точек износа.

Чтобы уменьшить массу используемого пластика, мы сделали стратегические вырезы в шестерне для создания спиц. Все по-прежнему остается красивым и коренастым, чтобы не сгибаться. Изгиб приводит к износу и шуму.

Хотя доступные процессы FDM обеспечивают теоретическую точность 0,1 мм, наименьший отдельный элемент, который можно надежно воспроизвести, составляет 0,6 мм.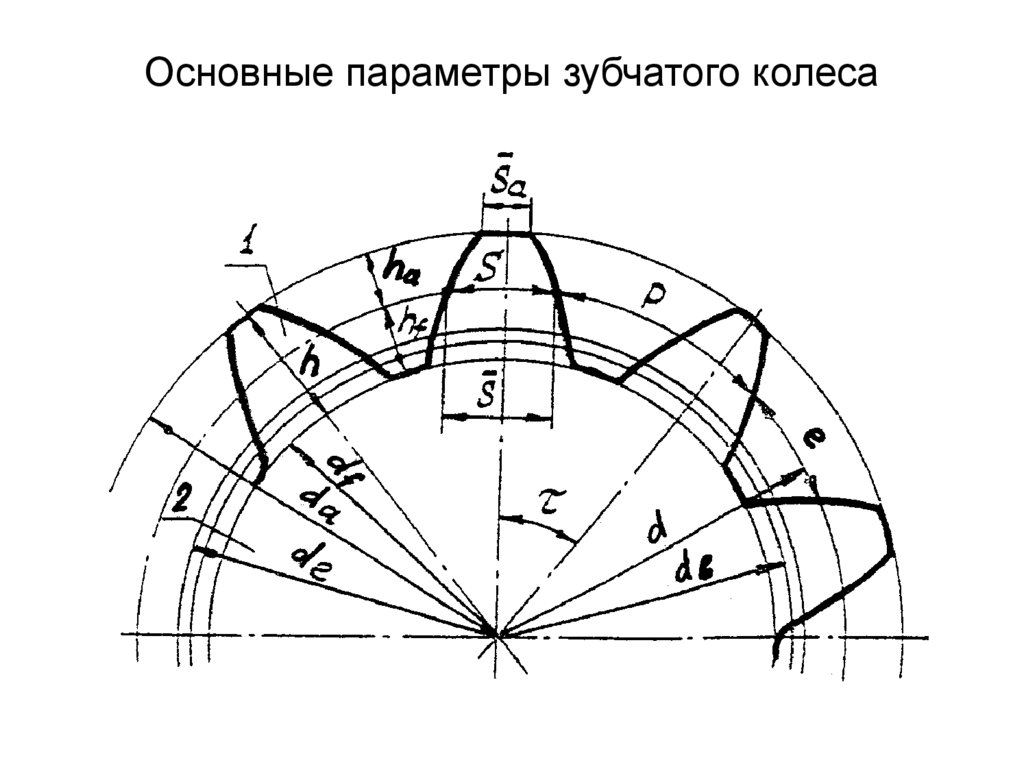 Так что это устанавливает абсолютную минимальную ширину зуба шестерни без какой-либо формы.

Наконец, нам нужно прикрепить некоторые шестерни к валу. Поскольку пластик не такой прочный, для него нужны большие коренастые кольца для удержания больших винтов с резьбой или, в случае этого примера, углубление для удержания гайки.

Вернуться к оглавлению

Создание зубчатых передач в Art Of Illusion

Описанные здесь шестерни используются для подъема и опускания проигрывателя. Большие шестерни крепятся к шпильке, которая поднимается и опускается при вращении в накидной гайке на каретке RepRap. Меньшая шестерня надевается на вал шагового двигателя и одновременно вращает остальные 3 шестерни. Поскольку точность, обеспечиваемая резьбой, очень высока, а величина люфта в шестернях приводит к относительно небольшой ошибке смещения платформы, некоторый люфт в шестернях допустим. В других ситуациях это может быть большой проблемой, и требуются хитрые решения, известные как безлюфтовые шестерни.

Чтобы облегчить жизнь, в AoI есть сценарий “Cog”, который я (ВикОлливер) адаптировал из сценария “Star”, любезно созданного для меня Франсуа Гийе.

Чтобы загрузить его, перейдите в меню «Инструменты» AoI и выберите «Диспетчер скриптов и плагинов». На вкладке «Установить» есть много полезной информации. В Scripts/Tools вы найдете скрипт Cog. Если его там нет, возможно, он уже установлен.

Чтобы спроектировать шестерни, нужно хорошенько подумать. Вам нужно выяснить, насколько большими они будут, и определить подходящий размер зуба. Зубья в примере имеют шаг 3,85 мм. Большая шестерня имеет 79зубья, у меньшей шестерни 16 зубьев; 79 очень плохо делится на 16, поэтому износ должен быть распределен равномерно. Используйте элементарную геометрию, чтобы выяснить диаметр шестерен.

Высота зубьев должна быть чуть больше половины шага, а их высота составляет 2 мм. Таким образом, при вводе параметров сценария Cog внешний диаметр на 2 мм больше внутреннего диаметра.

Конусность стороны зубьев определяется в сценарии Cog как отношение. Процесс слепых экспериментов показал, что значение 0,12–0,13 кажется правильным. После того, как все параметры введены, шестерня может быть создана. В результате получается 2D-путь, который очень похож на шестеренку.

Создав базовую форму шестеренки, нам нужно придать форму довольно квадратным зубьям. Это делается путем редактирования формы шестеренки. Для этого щелкните правой кнопкой мыши шестеренку в окне объектов и выберите “Редактировать объект”. Когда появится окно Curve Object, вытащите меню «Edit» и нажмите «Select All». Затем вытащите меню «Кривая». Когда появится элемент управления «Установить гладкость для выбранных точек», установите ползунок на значение 0,5 и нажмите «ОК». Вы ясно увидите, что периметр вашего зубчатого колеса приобретает красивый сглаженный вид. Если это подходит для ваших целей, нажмите «ОК» в окне «Объект кривой», и вы вернетесь в главное окно дисплея. Затем шестеренку можно выдавить с помощью Tools/Extrude до необходимой толщины; 6 мм казались подходящими для этого, поскольку центральная шестерня была более чем в два раза выше.

После того, как они будут вытянуты и преобразованы в треугольную сетку, отредактируйте сетку, используя режим редактора Edge, и закройте концы. Просто перетащите мышь, чтобы выбрать все края на одном конце, затем используйте Инструменты/Закрыть выбранную границу.

File:GearDesignInAoI-turntable gears.jpg

AoI Визуализация готового набора шестерен для подъема и опускания поворотного стола RepRap

Большие шестерни на приведенном выше рисунке проколоты для экономии пластика, а центральное отверстие позволяет вставить в них часть шпильки M5. Добавлен прочный хомут с шестигранным колодцем, который удерживает гайку М5. Добавление большой шайбы M5 и гайки с другой стороны и затяжка гайки надежно фиксируют шестерню на месте.

В меньшей шестерне имеется отверстие диаметром 4 мм, в которое вставляется кусок трубки из ПВХ. Затем шестерня надевается на 3-миллиметровый вал шагового двигателя, сжимая трубку и образуя плотную центрированную фрикционную посадку. Вот так они выглядели после изготовления. Они используются в обратном порядке вплоть до иллюстрации моделирования, быстрее изготавливать шестерни с их плоской поверхностью, ориентированной вниз:

File:GearDesignInAoI-fdmd повышающие шестерни sml.jpg

Вернуться к оглавлению

отверстие в середине шестерни

Обычно через центр шестерни проходит какой-то вал.

Иногда нам нужно, чтобы шестерня вращалась на валу (например, когда у нас есть “сложенные шестерни” [1], [2]). Итак, гладкое отверстие — возможно, отверстие достаточно большое для подшипника.

Но в большинстве случаев мы хотим, чтобы шестерня была жестко прикреплена к валу, чтобы они вращались вместе. В настоящее время самыми популярными занятиями в центре передач являются:

• Отверстие и прорезь, удерживающие барашковую гайку «внутри» шестерни. Редукторный экструдер Adrian’s # Шестеренчатый привод, универсальный мини-экструдер RepRap, [3]
• шестигранный колодец, в который запирается шестигранная гайка или головка болта с шестигранной головкой; добавьте шайбу и гайку с другой стороны, чтобы жестко закрепить гайку на болте. Редукторный экструдер Уэйда, драйвер экструдера «елочкой», файл: GregFrostPrusa3ImprovedWadesGears.jpg, [4], файл: Hub-gear.bmp, файл: Build67.jpg
Установочный винт
• … Файл:GregFrostPrusa1Pulleys.jpg, [5], Файл:Drive-gear.bmp, Файл:Pulley.bmp
• Что я вижу в файле: Universal Paste Extruder.jpg ? или в [6] ? Файл:Build135.jpg ?

(я уверен, что умные исследователи RepRap продолжат предлагать альтернативы).

Каталожные номера

Базовые формулы передач http://www.pic-design.com/tech/gear_form/gear_form1.htm

Как работают шестерни http://auto.howstuffworks.com/gear.htm — Main.SvendSrensen — 16 ноября 2005 г.

Вернуться к оглавлению

— Main.ForrestHiggs — 06 сентября 2006 г.

Дополнительная литература

• Шестерни
• Эвольвентный профиль1
• шестерня
• РБС/Шестерни
• Шестерни ручной работы
• Параметрические эвольвентные конические и прямозубые шестерни

Михал Залевски.