Юнг модулі: Модуль Юнга, коэффициент Пуассона презентация, доклад

alexxlab | 09.03.1989 | 0 | Разное

Содержание

Модуль Юнга, коэффициент Пуассона презентация, доклад

Слайд 1Текст слайда:

Модуль Юнга, коэффициент Пуассона и пр.

Щеголев Максим
Консультант по бурению

Слайд 2Текст слайда:

Коэффициент Пуассона

Коэффициент Пуассона (коэффициент поперечной деформации) – показывает зависимость между продольными и поперечными деформациями элемента, характеризует упругие свойства материала.
Определяется отношением относительных поперечных εпоп и продольных εпр деформаций элемента:

Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец.

Слайд 3Текст слайда:

Коэффициент Пуассона

Цилиндрический образец до нагружения:

здесь
h0 – начальный продольный размер;
d0 – начальный поперечный размер (в данном случае – диаметр).

Слайд 4Текст слайда:

Коэффициент Пуассона

h2=h0 – Δh
d1=d0 + Δd
здесь Δh и Δd соответственно абсолютные продольные и поперечные деформации.
Отношение абсолютных деформаций к соответствующим начальным размерам покажет относительные деформации:

а их отношение в свою очередь определяет коэффициент Пуассона материала цилиндра.

Значение коэффициента принимается по модулю, т.к. продольная и поперечная деформации всегда имеют противоположные знаки.

Слайд 5Текст слайда:

Коэффициент Пуассона

Для абсолютно хрупкого материала коэффициент Пуассона равен 0, для абсолютно эластичного — 0,5.

Для сталей, в зависимости от марки, этот коэффициент принимает значения от 0,27 до 0,32, для резины он примерно равен 0,5.

Слайд 6Текст слайда:

Модуль Юнга

Физическая величина, характеризующая свойства материала сопротивляться растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси. Она показывает степень жесткости материала и расчитывается следующим образом:

где:
E — модуль упругости,
F — сила,
S — площадь поверхности, по которой распределено действие силы,
l — длина деформируемого стержня,
x — модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина l).

Слайд 7Текст слайда:

Модуль Юнга

Учитывая то, что практически все конструкционные материалы имеют значение E высокого порядка (как правило 109 Па), его размерность часто записывают с помощью кратной приставки «гига» (гигапаскаль [ГПа])

Коэффициент Пуассона и модуль Юнга полностью характеризуют упругие свойства изотропного материала.

Слайд 8Текст слайда:

Предел текучести (σт)

В общем смысле – механическая характеристика материала, характеризующая напряжение, при котором деформации продолжают расти без увеличения нагрузки.

Диаграмма растяжения пластичного материала

Обычно диаграмма растяжения является зависимостью приложенной нагрузки P от абсолютного удлинения Δl.
Современные машины для механических испытаний позволяют записывать диаграмму в величинах напряжения σ (σ = P/A0, где A0 — исходная площадь поперечного сечения) и линейной деформации ε (ε = Δl/l0 ).
Такая диаграмма носит название диаграммы условных напряжений, так как при этом не учитывается изменение площади поперечного сечения образца в процессе испытания.

Слайд 9Текст слайда:

Предел текучести (σт)

Начальный участок является линейным (т. н. участок упругой деформации)

В этом случае модуль Юнга равен отношению нормальных напряжений к соответствующим относительным деформациям, на участке диаграммы до предела пропорциональности σпц (тангенсу угла α наклона участка пропорциональности к оси деформаций ε).

E=σ/ε=tgα

Слайд 10Текст слайда:

Предел текучести (σт)

Следующий участок диаграммы описывает упругое поведение образца иного рода: после снятия нагрузки образец приобретает начальную форму медленнее скорости звука.

Конец указанного участка диаграммы – предел текучести.
Затем образуется площадка предела текучести в пределах которой дальнейшая деформация происходит без роста напряжения .

Слайд 11Текст слайда:

Предел текучести (σт)

После достижения конца площадки текучести (деформация порядка 2 — 2,5 %) начинается деформационное упрочнение (участок упрочнения), видимое на диаграмме, как рост напряжения с ростом деформации.

После достижения точки предела прочности начинает образовываться т. н. «шейка» — область сосредоточенной деформации. Расположение «шейки» зависит от однородности геометрических размеров образца и качества его поверхности. Как правило, «шейка» и, в конечном счёте, место разрушения расположено в наиболее слабом сечении.

Слайд 12Текст слайда:

Предел текучести (σт)

Соответствующий (последний) участок диаграммы называют зоной местной текучести, так как пластические деформации продолжают интенсивно развиваться только в области шейки (за счёт локального уменьшения площади поперечного сечения образца).

Последняя точка на диаграмме – точка разрушения образца.

Слайд 13Текст слайда:

Предел текучести (σт)

Основные точки, пределы и зоны.

σпц – Предел пропорциональности
σпц – Предел текучести (конец зоны упругой деформации). В реальности значения предела текучести выше, чем предел упругости примерно на 5%.
1 – Площадка предела текучести (начало зоны пластической деформации)
2 – Область деформационного упрочнения
3 – Предел прочности (временное сопротивление разрушению) 4 – Образование шейки на образце
5 – Точка разрушения

Скачать презентацию

Модуль Юнга (упругости) для стали и других материалов: определение, смысл

Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.

Модуль Юнга

Содержание

Основные сведения

Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м² или в Па.

Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (10¹²Па)

Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.

Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.

График теста на растяжение

E- это частное от деления нормальных напряжений σ на относительное удлинение ε.

E=α/ε

Закон Гука также можно сформулировать и с использованием модуля Юнга.

Физический смысл модуля Юнга

Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.

Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.

Виды деформации

Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.

В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:

Δl = α * (lF) / S

Величину, обратную α, и называют модулем Юнга:

1/α = E

Относительная деформация:

ε = (Δl) / l = α * (F/S)

Отношение растягивающей силы F к S называют упругим напряжением σ:

ε=α σ

Закон Гука, записанный с использованием модуля Юнга, выглядит так:

σ = ε/α = E ε

Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.

В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.

Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l

Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.

Значения модуля юнга для некоторых материалов

В таблице показаны значения E ряда распространенных веществ.

Материал	модуль Юнга E, ГПа
Алюминий	70
Бронза	75-125
Вольфрам	350
Графен	1000
Латунь	95
Лёд	3
Медь	110
Свинец	18
Серебро	80
Серый чугун	110
Сталь	200/210
Стекло	70

Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.

Предел прочности материала

Это предел возникающего напряжения, после которого образец начинает разрушаться.

Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.

Инструмент для определения предела прочности

Кроме того, существуют пределы прочности на сжатие материала и на растяжение. Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления. В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.

Допускаемое механическое напряжение в некоторых материалах при растяжении

Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.

Испытание на растяжение

Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.

Значения σ_раст в МПа:

Материалы	σ_раст
Бор	5700	0,083
Графит	2390	0,023
Сапфир	1495	0,030
Стальная проволока	415	0,01
Стекловолокно	350	0,034
Конструкционная сталь	60	0,003
Нейлон	48	0,0025

Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия.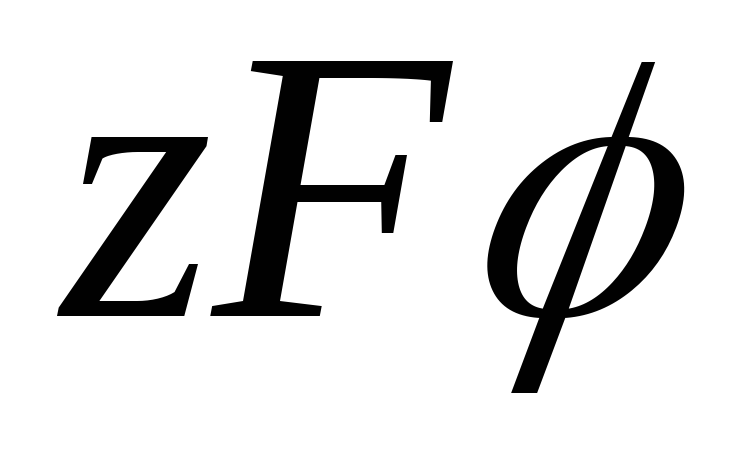 С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.

Запасы прочности, закладываемые в ответственные конструкции, также многократны.

Коэффициент запаса прочности

Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.

Запас прочности

Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.

Связь с другими модулями упругости

Модуль Юнга связан с модулем сдвига, определяющим способность образца к сопротивлению против деформации сдвига, следующим соотношением:

E связан также и с модулем объёмной упругости, определяющим способность образца к сопротивлению против одновременного сжатия со всех сторон.

Қатты денелердің механикалық қасиеттері – ҰБТ, Қорытынды аттестаттау және ОЖСБ сынақтарына дайындайтын онлайн жаттықтырғыш құралы

Есте сақтау

Құпиясөзді қалпына келтіру

Тіркелу

Конспект

Қатты денелер сұйықтар сияқты өзінің көлемін ғана сақтап қоймайды, сонымен қатар пішінін де сақтайды. Олардың пішіні дұрыс болу себебі қатты денелердің атомдары немесе молекулалары кеңістікте белгілі орын алып реттеліп орналасқан кристаллдар құрайды.

Физикалық қасиеттердің кристалл ішіндегі бағыттарға тәуелділігі анизотропия деп аталады (грек сөзі «анизос»- бірдей емес, «тропос» – бағыт).

Кейбір заттар әртүрлі жағдайда аморфтық және кристаллдық қасиеттер білдіреді.

Қатты денелер өзіне түсірілген күштің әсерінен пішіндерін өзгертеді, яғни деформацияланады. Сыртқы күштер әсері тоқталғаннан кейін толық жойылатын деформациялар серпімді деформация (созылу, сығылу) деп аталады.

Созылу деформацияның сипаттамалары:

\(\bigtriangleup I\)‒ абсолюттік ұзару, салыстырмалы ұзару,

\(\bigtriangleup I=I-I_0 \)-; механикалық кернеу \([Па]\), мұндағы

\(F_C\)– серпімділік күші, \(S\) -дененің көлденең қимасының ауданы.

Созылу диаграммасы

\(OA\) ‒ абсолюттік серпімді деформация аймағы

(Гук заңы орындалады),

\(\sigma_{П.Ш.}\)- пропорционалдық шегі; серпімділік шегі;

\(BC\) ‒ материалдың аққыштық аймағы;

беріктілік шегі.

Тәжірибе нәтижелері бойынша салынған созылу диаграммасынан шамалы деформацияларда σ-кернеу салыстырмалы ұзаруға тура пропорционал. Бұл тәуелділік

Гук заңы деп аталады \(\boxed{\sigma=E\mid\varepsilon\mid}\) .

Мұндағы \(E\) – пропорционалдық коэффициент, Юнг модулі немесе серпімділік модулі деп аталады (материалдың деформацияға қарсылығын сипаттайды), [Па].

Гук заңынан \(F=\sigma S=E\varepsilon\cdot S=E\frac{\bigtriangleup l}{l_0}S=k\cdot \bigtriangleup1,\) олай болса \(\boxed{k=\frac{ES}{l_0}}\) – қатаңдық коэффициенті дененің көлденең қимасының ауданына және бастапқы ұзындығына байланысты. Гук заңы орындалатын кездегі максимум кернеу пропорционалдық шек деп аталады. Кернеу \(\sigma_{б.Ш.}\)беріктік шегі деп аталатын өзінің максимум шамасына жеткеннен кейін үзілу болады.

Дене қабаттарының бір біріне қатысты ығысуына байланысты деформацияның түрі

ығысу деформациясы деп аталады. Тіреу нүктелерінде барлық бөренелер, детальдарды біріктіріп ұстап тұратын тойтарма шегелер мен бұрандалар ығысу деформациясына ұшырайды.

Деформацияның күрделірек түрлеріне иілу және бұралу жатады. Мысалы, жүк салынған бөрене иілуге ұшырайды. Болттарды бұрағанда, машина біліктері, бұрғылар айналғанда бұралу деформациясы орын алады.

Сұрақтар

Кристалл қатты денелерге жатпайтыны
Егер болат таяқшаның диаметрі – \(d=2\) см, ал оның Юнг модулі \(E=2\cdot10^{11}\) Па болса, онда \(F=3,14\cdot10^5\) H күшпен қысылған болат таяқшаның салыстырмалы қысқаруы
Ұзындығы \(2\) м болатын алюминий сымды созғанда \(35\) МПа механикалық кернеу пайда болды. 2)\)
Ұзындығы – \(\ell=50\) см, диаметрі \(d=2\) см мыс таяқшаға массасы \(m=1\) т жүк ілінді. Таяқшаның салыстырмалы ұзаруы \((E=118\) ГПа\()\)
Егер массалары \(500\) кг және \(1000\) кг болатын екі дененің өзара әрекеттесу күші \(33, 35\) Н-ға тең болса, онда денелердің арақашықтығы
Қатаңдығы \(200\) Н/м серіппеге \(25\) Н күш әсер еткенде оның деформациясының шамасы
Егер сымның жүктемесін материалын өзгертпей, ұзындығы мен диаметрін \(2\) есе үлкейтсек, онда оның абсолют ұзаруы неше есе өзгереді?
Қатаңдықтары \(k\) және \(2 \ k\) болатын бір-біріне параллель қосылған екі серіппеге жүк ілінген. 2\)сым \(100\) Н күштің әсерінен \(1\) мм-ге ұзарған. Сымдағы кернеуді және Юнг модулін анықта.

Қате туралы хабарландыру

Модуль Юнга трабекулярного и кортикального костного материала: ультразвуковые и микрорастяжные измерения

. 1993 февраль; 26 (2): 111-9.

doi: 10.1016/0021-9290(93)

Дж И Ро ¹ , Р. Б. Эшман, Ч. Х. Тернер

принадлежность

¹ Отделение ортопедической хирургии, Университет штата Нью-Йорк, Буффало.

PMID: 8429054

DOI: 10.

1016/0021-9290(93)

-д

Дж. И. Ро и соавт. Дж. Биомех. 1993 фев.

. 1993 февраль; 26 (2): 111-9.

дои: 10.1016/0021-9290(93)

Авторы

Дж И Ро ¹ , Р. Б. Эшман, Ч. Х. Тернер

принадлежность

¹ Отделение ортопедической хирургии, Университет штата Нью-Йорк, Буффало.

PMID: 8429054

DOI: 10.1016/0021-9290(93)

-д

Абстрактный

Для определения модуля Юнга отдельных трабекул и микропрепаратов кортикальной кости, вырезанных до размеров, аналогичных размерам отдельных трабекул, использовали ультразвуковую технику и тест на микрорастяжение. Средний трабекулярный модуль Юнга, измеренный ультразвуковым и механическим способом, составил 14,8 ГПа (стандартное отклонение 1,4) и 10,4 (стандартное отклонение 3,5), а средний модуль Юнга микрообразцов кортикальной кости, измеренный ультразвуковым и механическим способом, составил 20,7 ГПа (стандартное отклонение 1,9).) и 18,6 ГПа (стандартное отклонение 3,5). При любом методе тестирования было обнаружено, что средний трабекулярный модуль Юнга значительно меньше, чем у кортикальной кости (p < 0,0001). Однако образцы были высушены перед испытанием на микрорастяжение, поэтому значения модуля Юнга могли быть выше, чем у трабекул in vivo. Используя измерения модуля Юнга, полученные для 450 кубов губчатой кости и 256 кубов кортикальной кости, была проверена гипотеза Вольфа о том, что кортикальная кость представляет собой просто плотную губчатую кость. Множественный регрессионный анализ, который контролировал принадлежность к группе, показал, что модуль Юнга кортикальной кости не может быть экстраполирован из зависимости модуля Юнга от плотности губчатой кости, однако модуль Юнга трабекул можно предсказать путем экстраполяции зависимости между модулем Юнга и плотностью кости. губчатая кость. Эти результаты позволяют предположить, что при механическом рассмотрении кортикальная и трабекулярная кости не являются одним и тем же материалом.

Цитируется

Оценка эффективности межтелового слияния и биосовместимости клетки из полиэфирэфиркетона/силиката кальция/пористого тантала на модели козы.
Юань К, Чжан К, Ян И, Линь И, Чжоу Ф, Мэй Дж, Ли Х, Вэй Дж, Ю З, Чжао Дж, Тан Т. Юань К. и др. J Ортоп перевод. 2022 31 августа; 36: 109-119. doi: 10.1016/j.jot.2022.06.006. электронная коллекция 2022 сент. J Ортоп перевод. 2022. PMID: 360 Бесплатная статья ЧВК.
Бесцементный изогнутый стержень эндопротеза для реконструкции дистального отдела бедренной кости у китайцев: комбинированное анатомо-биомеханическое исследование.
Ху С, Лу М, Ван И, Вэнь И, Тан Л, Ду Г, Чжоу И, Луо И, Мин Л, Ту С. Ху Х и др. BMC Расстройство опорно-двигательного аппарата. 2022 8 сентября; 23 (1): 849. doi: 10.1186/s12891-022-05801-z. BMC Расстройство опорно-двигательного аппарата. 2022. PMID: 36071516 Бесплатная статья ЧВК.
Вклад свойств суставной ткани в развитие остеоартрита, вызванного нагрузкой.
Ayobami OO, Goldring SR, Goldring MB, Wright TM, van der Meulen MCH. Айобами О.О. и соавт. Bone Rep. 2022 Jul 19;17:101602. doi: 10.1016/j.bonr.2022.101602. электронная коллекция 2022 дек. Кость Респ. 2022. PMID: 35899096 Бесплатная статья ЧВК.
Обзор анодированных сплавов TiNbSn для улучшения качества слоя и применения в ортопедических имплантатах.
Мори Ю., Масахаши Н., Айзава Т. Мори Ю. и др. Материалы (Базель). 2022 июль 22;15(15):5116. дои: 10.3390/ma15155116. Материалы (Базель). 2022. PMID: 35897548 Бесплатная статья ЧВК. Обзор.
Определение E-модуля губчатой кости, полученной из плечевой кости человека, и проверка нанесенных на график одиночных трабекул: разработка стандартизированной модели плечевой кости.
Кун Ф., Клаусинг Р.Дж., Стиллер А., Фонсека Уллоа К.А., Фельш К., Рикерт М., Янке А. Кун Ф. и др. Дж Ортоп. 2022 11 июля; 33:48-54. doi: 10.1016/j.jor.2022.07.003. eCollection 2022 сен-окт. Дж Ортоп. 2022. PMID: 35855729

Просмотреть все статьи “Цитируется по”

Типы публикаций

термины MeSH

вещества

Грантовая поддержка

AM36257/AM/NIADDK NIH HHS/США

Вдавливание в сравнении с измерениями модуля Юнга на растяжение для мягких биологических тканей

1. Самани А. Плевес Д. Решение обратной задачи для измерения модуля упругости интактных опухолей ткани молочной железы ex vivo. физ.-мед. биол. 2007; 52:1247. [PubMed] [Google Scholar]

2. Крускоп Т.А. Уилер Т.М. Калель Ф. Гарра Б.С. Холл Т. Модули упругости тканей молочной железы и предстательной железы при сжатии. Ультразвуковая визуализация. 1998;20:260. [PubMed] [Google Scholar]

3. Пашек М.Дж., Захир Н. Джонсон, К.Р. Лакинс Дж.Н. Розенберг Г.И. Гефен А. и др. Напряженный гомеостаз и злокачественный фенотип. Раковая клетка. 2005; 8:241. [PubMed] [Google Scholar]

4. Фаррар Д.Дж. Зеленый Х.Д. Бонд М.Г. Вагнер В.Д. Гобби Р.А. Скорость, эластичность и состав пульсовой волны аорты в модели атеросклероза у нечеловеческих приматов. Цирк Рез. 1978;43:52. [PubMed] [Google Scholar]

5. Hasegawa M. Watanabe Y. Реологические свойства грудной аорты у здоровых и белых кроликов. Биореология. 1988;25:147. [PubMed] [Google Scholar]

6. Хаяши К. Идэ К. Мацумото Т. Стенки аорты у кроликов с атеросклерозом — механическое исследование. J Биомех Инж. 1994; 116:284. [PubMed] [Google Scholar]

7. Имура Т. Ямамото К. Сато Т. Миками Т. Ясуда Х. Артериосклеротические изменения брюшной аорты человека in vivo в связи с ишемической болезнью сердца и факторами риска. Атеросклероз. 1988;73:149. [PubMed] [Google Scholar]

8. Richter H.A. Миттермайер С. Объемная эластичность, модуль упругости и податливость нормальной и артериосклеротической аорты человека. Биореология. 1984;21:723. [PubMed] [Google Scholar]

9. Matsumoto T. Abe H. Ohashi T. Kato Y. Sato M. Локальный модуль упругости атеросклеротических поражений грудной аорты кролика, измеренный методом пипеточной аспирации. Физиол Изм. 2002; 23:635. [PubMed] [Google Scholar]

10. Claridge M.W. Bate G.R. Хоскинс П.Р. Адам Д.Дж. Брэдбери А.В. Вильминк А.Б. Измерение жесткости артерий у пациентов с сосудистыми заболеваниями: являются ли изменения сосудистой стенки более чувствительными, чем увеличение толщины комплекса интима-медиа? Атеросклероз.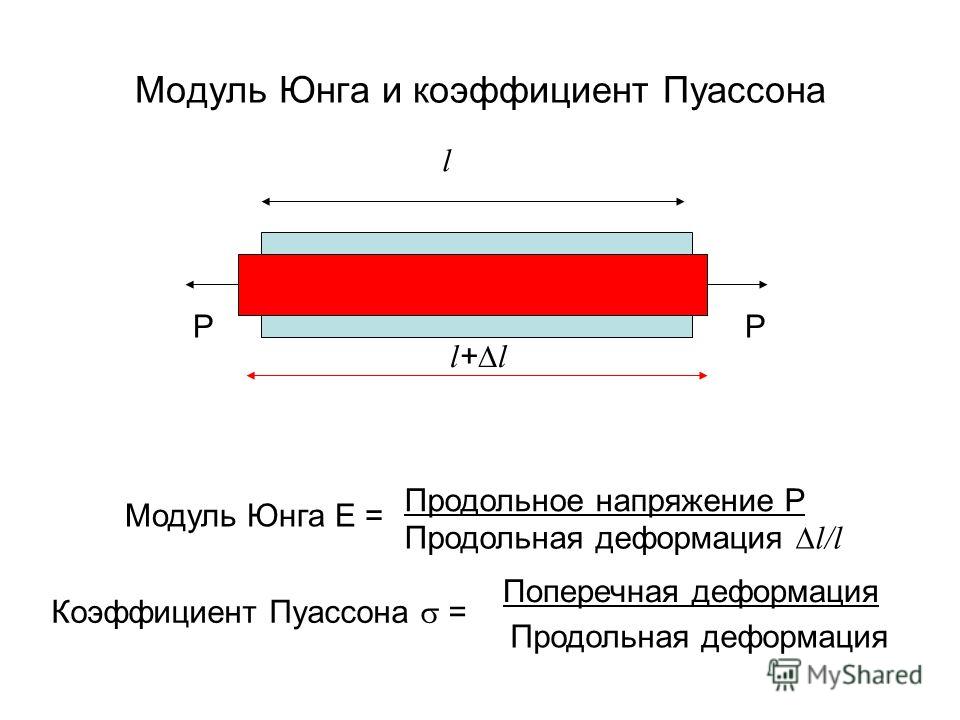 2009 г.;205:477. [PubMed] [Google Scholar]

11. Wuyts F.L. Ванхейс В.Дж. Лангевоутерс Г.Дж. Декремер В.Ф. Раман Э. Р. Байл С. Эластические свойства аорты человека в зависимости от возраста и атеросклероза: структурная модель. физ.-мед. биол. 1995;40:1577. [PubMed] [Google Scholar]

12. Yeh W.C. Ли П.К. Дженг Ю.М. Хсу Х.К. Куо П.Л. Ли М.Л. и соавт. Измерения модуля упругости печени человека и корреляция с патологией. Ультразвук Медицина Биол. 2002; 28:467. [PubMed] [Академия Google]

13. Последний Дж.А. Тингруи П. Южэ Д. Рейли К.М. Келлер К. Акотт Т.С. и соавт. Определение модуля упругости нормальной трабекулярной сети человека с глаукомой. Invest Ophthalmol Vis Sci. [Epub перед печатью.] [Бесплатная статья PMC] [PubMed] [Google Scholar]

14. Chou S.Y. Ченг С.М. LeDuc PR Композитные полимерные системы с контролем локальной эластичности субстрата и их влияние на цитоскелетные и морфологические характеристики адгезивных клеток. Биоматериалы. 2009;30:3136. [PubMed] [Академия Google]

15. Изенберг Б.К. Димилла П.А. Уокер М. Ким С. Вонг Дж.Ю. Дуротаксис гладкомышечных клеток сосудов зависит от силы градиента жесткости субстрата. Биофиз Дж. 2009;97:1313. [Бесплатная статья PMC] [PubMed] [Google Scholar]

16. Ляо С.В. Ю Т.Б. Гуан З. Разработка de novo сахаридно-пептидных гидрогелей в качестве синтетических каркасов для адаптированных клеточных ответов. J Am Chem Soc. 2009;131:17638. [PubMed] [Google Scholar]

17. Субраманиан А. Лин Х.Ю. Сшитый хитозан: его физические свойства и влияние жесткости матрикса на морфологию и пролиферацию клеток хондроцитов. J Biomed Mater Res A. 2005; 75:742. [PubMed] [Академия Google]

18. Лейпциг Н.Д. Шойхет М.С. Влияние жесткости субстрата на поведение взрослых нервных стволовых клеток. Биоматериалы. 2009;30:6867. [PubMed] [Google Scholar]

19. Хаджипанайи Э. Мудера В. Браун Р.А. Тесная зависимость пролиферации фибробластов от жесткости матрикса коллагенового каркаса. J Tissue Eng Regen Med. 2009;3:77. [PubMed] [Google Scholar]

20. Ghosh K. Pan Z. Guan E. Ge S. Liu Y. Nakamura T., et al. Адаптация клеток к физиологически релевантному имитатору ВКМ с различными вязкоупругими свойствами. Биоматериалы. 2007; 28:671. [Бесплатная статья PMC] [PubMed] [Google Scholar]

21. Чен К.С. Се П.Ч.Х. Ван Г.М. Чен В.К. Йе М.Л. Влияние морфологии поверхности и жесткости субстрата на подвижность клеток. Матер Летт. 2009;63:1872. [Google Scholar]

22. Pelham R.J., Jr. Wang Y. Движение клеток и фокальные спайки регулируются гибкостью субстрата. Proc Natl Acad Sci U S A. 1997; 94:13661. [Бесплатная статья PMC] [PubMed] [Google Scholar]

23. Чен Ю.М. Огава Р. Какуго А. Осада Ю. Гонг Дж. П. Динамическое поведение клеток на синтетических гидрогелях с различной плотностью заряда. Мягкая материя. 2009 г.;5:1804. [Google Scholar]

24. Вонг Дж.Ю. Веласко А. Раджагопалан П. Фам К. Направленное движение гладкомышечных клеток сосудов на гидрогелях, совместимых с градиентом. Ленгмюр. 2003; 19:1908. [Google Scholar]

25. Грей Д. С. Тьен Дж. Чен К. С. Изменение положения клеток за счет механотаксиса на поверхностях с микроструктурным модулем Юнга. J Biomed Mater Res A. 2003;66A:605. [PubMed] [Google Scholar]

26. Клоксин А.М. Бентон Дж.А. Ансет К.С. Модуляция эластичности in situ с помощью динамических субстратов для управления клеточным фенотипом. Биоматериалы. 2010;31:1. [Бесплатная статья PMC] [PubMed] [Google Scholar]

27. Муссаллем М.Д. Оленыч С.Г. Скотт С.Л. Келлер Т.С., 3-й Шленофф Дж. Б. Модуляция и сокращение фенотипа гладкомышечных клеток на нативных и сшитых полиэлектролитных мультислоях. Биомакромолекулы. 2009;10:3062. [Бесплатная статья PMC] [PubMed] [Google Scholar]

28. Banerjee A. Artha M. Choudhary S. Ashton R.S. Бхатия С.Р. Шаффер Д.В. и соавт. Влияние модуля гидрогеля на пролиферацию и дифференцировку инкапсулированных нейральных стволовых клеток. Биоматериалы. 2009 г.;30:4695. [Бесплатная статья PMC] [PubMed] [Google Scholar]

29. Discher D.E. Джанми П. Ван Ю.Л. Тканевые клетки чувствуют и реагируют на жесткость своего субстрата. Наука. 2005;310:1139. [PubMed] [Google Scholar]

30. McKee C.T. Вуд Дж.А. Шах Н.М. Фишер М.Е. Рейли С.М. Мерфи С.Дж. и соавт. Влияние биофизических свойств трабекулярной сети глаза, связанных с глаукомой, на клеточный ответ на терапевтические агенты. Биоматериалы. 2011;32:2417. [Бесплатная статья PMC] [PubMed] [Google Scholar]

31. Клейнман Х.К. Мартин Г.Р. Матригель: матрица базальной мембраны с биологической активностью. Семин Рак Биол. 2005; 15:378. [PubMed] [Google Scholar]

32. Семлер Э.Дж. Рануччи К. С. Моге П. В. Механохимические воздействия на агрегацию гепатоцитов могут избирательно индуцировать или подавлять специфическую функцию печени. Биотехнология Биоинж. 2000;69:359. [PubMed] [Google Scholar]

33. Zaman M.H. Трапани Л. М. Симинский А. Л. Маккеллар Д. Гонг Х. Камм Р. Д. и др. Миграция опухолевых клеток в трехмерных матрицах регулируется жесткостью матрицы, а также адгезией клеток к матрице и протеолизом. Proc Natl Acad Sci U S A. 2006; 103:10889. [Бесплатная статья PMC] [PubMed] [Google Scholar]

34. Alcaraz J. Xu R. Mori H. Nelson C.M. Мроу Р. Спенсер В.А. и соавт. Ламинин и биомиметическая внеклеточная эластичность усиливают функциональную дифференцировку эпителия молочных желез. EMBO J. 2008; 27:2829. [Бесплатная статья PMC] [PubMed] [Google Scholar]

35. Soofi S.S. Last J.A. Лилиенсик С.Дж. Нили П.Ф. Мерфи С. Дж. Модуль упругости матригеля, определенный с помощью атомно-силовой микроскопии. J Struct Biol. 2009;167:216. [Бесплатная статья PMC] [PubMed] [Google Scholar]

36. Хьортдал Й.О. Региональные эластические характеристики роговицы человека. Дж. Биомех. 1996; 29:931. [PubMed] [Google Scholar]

37. Schwartz NJ Mackay R.S. Сакман Дж. Л. Теоретическое и экспериментальное исследование механического поведения роговицы применительно к измерению внутриглазного давления. Бык Математика Биофиз. 1966; 28:585. [Google Scholar]

38. Последний J.A. Лилиенсик С. Дж. Нили П.Ф. Мерфи С. Дж. Определение механических свойств базальных мембран роговицы человека с помощью атомно-силовой микроскопии. J Struct Biol. 2009 г.;167:19. [бесплатная статья PMC] [PubMed] [Google Scholar]

39. Нэш И.С. Грин П. Р. Фостер К. С. Сравнение механических свойств кератоконуса и нормальной роговицы. Эксп. Разр. 1982; 35:413. [PubMed] [Google Scholar]

40. Джаясурия А.К. Гош С. Шейнбейм Дж.И. Лубкин В. Беннет Г. Крамер П. Исследование пьезоэлектрической и механической анизотропии роговицы человека. Биосенс Биоэлектрон. 2003; 18:381. [PubMed] [Google Scholar]

41. Sjontoft E. Edmund C. Invivo определение модуля Юнга для роговицы человека. Бык Математика Биол. 1987;49:217. [PubMed] [Google Scholar]

42. Гамильтон К.Е. Пай, модуль Юнга в нормальных углах и влияние на аппланационную тонометрию. Optom Vis Sci. 2008;85:445. [PubMed] [Google Scholar]

43. Liu J. Roberts C.J. Влияние биомеханических свойств роговицы на измерение внутриглазного давления — количественный анализ. J Катаракта рефракта Surg. 2005; 31:146. [PubMed] [Google Scholar]

44. Эльшейх А. Ван Д.Ф. Пай Д. Определение модуля упругости роговицы человека. J преломление Surg. 2007; 23:808. [PubMed] [Академия Google]

45. Ву С.Л. Кобаяши А.С. Шлегель В. А. Лоуренс К. Нелинейные свойства материала интактной роговицы и склеры. Эксп. Разр. 1972;14:29. [PubMed] [Google Scholar]

46. Джу Б. Морис Д.М. Механические свойства роговицы кролика и человека. Дж. Биомех. 1986; 19:847. [PubMed] [Google Scholar]

47. Эльшейх А. Альхассо Д. Рама П. Оценка вклада эпителия в биомеханику роговицы. Эксп. Разр. 2008;86:445. [PubMed] [Google Scholar]

48. Джонсон М. В. Хан Д. П. Хоффман К.Э. Влияние пломбирования склеры на ригидность глаза. Офтальмология. 1990;97:190. [PubMed] [Google Scholar]

49. Уайт О.В. Глазная эластичность? Офтальмология. 1990;97:1092. [PubMed] [Google Scholar]

50. Пурслоу П.П. Карватовский В.С. Глазная эластичность. Является ли инженерная жесткость более полезным параметром характеристики, чем жесткость глаза? Офтальмология. 1996; 103:1686. [PubMed] [Google Scholar]

51. Fung Y.C.B. Эластичность мягких тканей при простом растяжении. Am J Physiol. 1967; 213:1532. [PubMed] [Google Scholar]

52. Ehlers W. Karajan N. Markert B. Расширенная двухфазная модель заряженных гидратированных тканей с применением к межпозвонковому диску. Биомех Модель Механобиол. 2009 г.;8:233. [PubMed] [Google Scholar]

53. Шадвик Р.Е. Накопление упругой энергии в сухожилиях: механические различия, связанные с функцией и возрастом. J Appl Physiol. 1990;68:1033. [PubMed] [Google Scholar]

54. Вайнман А. Нелинейные вязкоупругие тела — обзор. Математические механические тела. 2009;14:300. [Google Scholar]

55. Фатеми М. Гринлиф Дж. Ф. Визуализация вязкоупругих свойств ткани. Отображение сложных сред акустическими и сейсмическими волнами. Top Appl Phys. 2002; 84:257. [Академия Google]

56. Салачински Х.Дж., Голднер С. Джудисандреа, А. Гамильтон, Г. Сейфалян, А.М. Эдвардс А. и др. Механическое поведение сосудистых трансплантатов: обзор. J Биоматер Appl. 2001; 15:241. [PubMed] [Google Scholar]

57. Taylor D.C. Dalton J.D., Jr. Seaber A.V. Garrett WE, Jr. Вязкоупругие свойства мышечно-сухожильных единиц. Биомеханические эффекты растяжения. Am J Sports Med. 1990;18:300. [PubMed] [Google Scholar]

58. Нассери С. Билстон Л.Е. Фан-Тьен Н. Вязкоупругие свойства свиной почки при сдвиге, экспериментальные результаты и моделирование. Реол Акта. 2002; 41:180. [Академия Google]

59. Кристенсен М.С. Харгенс К.В., 3-я ночь С. Ганс Э.Х. Вязкоупругие свойства неповрежденной кожи человека: инструменты, эффекты гидратации и вклад рогового слоя. Джей Инвест Дерматол. 1977; 69:282. [PubMed] [Google Scholar]

60. Бисплингхофф Дж.А. МакНалли К. Манукян С.Дж. Дума С.М. Динамические свойства материала склеры человека. Дж. Биомех. 2009;42:1493. [PubMed] [Google Scholar]

61. Поцелуй М.З. Дэниэлс М. Дж. Варгезе Т. Исследование температурно-зависимых вязкоупругих свойств термических поражений в ткани печени животных ex vivo.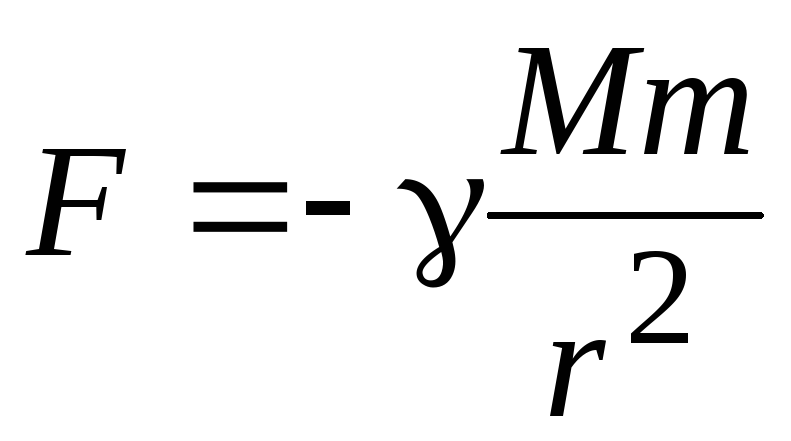 Дж. Биомех. 2009 г.;42:959. [Бесплатная статья PMC] [PubMed] [Google Scholar]

62. Green M.A. Bilston L.E. Синкус Р. Вязкоупругие свойства мозга in vivo, измеренные с помощью магнитно-резонансной эластографии. ЯМР Биомед. 2008;21:755. [PubMed] [Google Scholar]

63. Сантос Н.К. Кастаньо М.А. Обзор биофизических приложений атомно-силовой микроскопии. Биофиз хим. 2004; 107:133. [PubMed] [Google Scholar]

64. Бриско Б. Дж. Фиори Л. Пелильо Э. Наноиндентирование полимерных поверхностей. J Phys D. 1998;31:2395. [Google Scholar]

65. Эбенштейн Д.М. Прюитт Л.А. Наноиндетация биологических материалов. Нано сегодня. 2006; 1:26. [Google Scholar]

66. Саксена Т. Гилберт Дж. Л. Хазенвинкель Дж. М. Универсальная система мезоиндентирования для оценки микромеханических свойств мягких гидратированных субстратов на клеточном уровне. J Biomed Mater Res A. 2009; 90:1206. [PubMed] [Google Scholar]

67. Радмахер М. Изучение механики клеточных процессов методом атомно-силовой микроскопии. Клеточная механика, серия книг. Метод Cell Biol. 2007; 83:347. [PubMed] [Академия Google]

68. Ченг Ю.-Т. Ченг К.-М. Масштабирование, анализ размеров и измерение отступов. Mater Sci Eng R. 2004; 44:91. [Google Scholar]

69. Боуэн В. Р. Ловитт Р. В. Райт К. Дж. Применение атомно-силовой микроскопии к изучению микромеханических свойств биологических материалов. Биотехнологическая лат. 2000;22:893. [Google Scholar]

70. Lin D.C. Horkay F. Наномеханика полимерных гелей и биологических тканей: критический обзор аналитических подходов в режиме Герца и за его пределами. Мягкая материя. 2008;4:669. [Google Scholar]

71. Oliver W.C. Фарр Г.М. Усовершенствованный метод определения твердости и модуля упругости с использованием экспериментов по вдавливанию с измерением нагрузки и смещения. J Mater Res. 1992; 7:1564. [Google Scholar]

72. Hertz H. Uber die beruhrung fester elastischer korper. J Reine Angew Математика. 1882; 92:156. [Google Scholar]

73.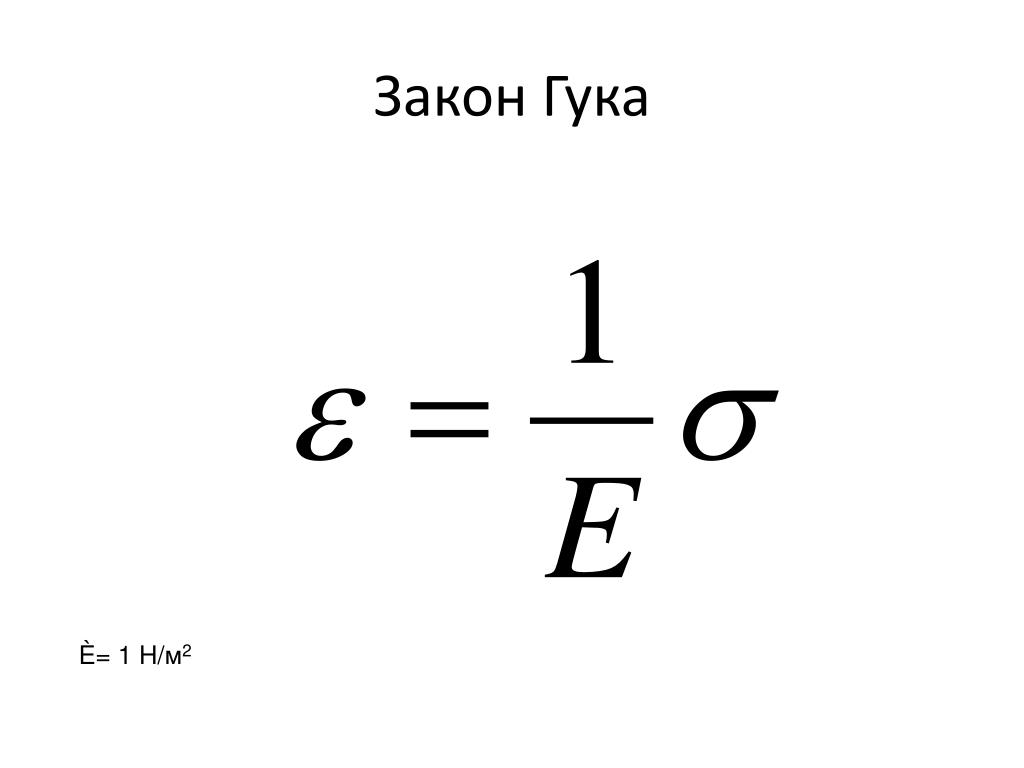 Boussinesq J. Application des Potentiels a Petude de l’equilibre et du Mouvement des Solides Elastiques. Париж: Готье-Вилларс; 1885. [Google Scholar]

74. Любовь А.Э.Х. Задача Буссенгеска для жесткого конуса. Дж Матем. 1939; 10:161. [Google Scholar]

75. Хардинг Дж.В. Снеддон И.Н. Упругие напряжения, возникающие при вдавливании жесткого штампа в плоскую поверхность полубесконечного упругого тела. Proc Camb Philol Soc. 1945;41:16. [Google Scholar]

76. Снеддон И.Н. Задача Буссинеска для цилиндра с плоским торцом. Proc Camb Philol Soc. 1946;42:29. [Google Scholar]

77. Снеддон И.Н. Задача Буссинеска для жесткого конуса. Proc Camb Philol Soc. 1948;44:492. [Google Scholar]

78. Снеддон И.Н. Связь между нагрузкой и проникновением в осесимметричной задаче Буссинеска для штампа произвольного профиля. Int J Eng Sci. 1965; 3:47. [Google Scholar]

79. Махаффи Р.Е. Ши С.К. Макинтош ФК Кас Дж. Частотно-зависимая микрореология полимерных гелей и биологических клеток на основе сканирующего зонда. Phys Rev Lett. 2000;85:880. [PubMed] [Google Scholar]

80. Thormann E. Pettersson T. Claesson P.M. Как измерить силы с помощью атомно-силовой микроскопии без существенного влияния нелинейной оптической чувствительности рычага. Преподобный Научный Инструм. 2009 г.;80:093701. [PubMed] [Google Scholar]

81. Цуй Т.Ю. Оливер В.К. Фарр Г.М. Тонкие пленки: напряжения и механические свойства VI. Питтсбург, Пенсильвания: Mater. Рез. соц. Симп. проц.; 1997. [Google Scholar]

82. Рико Ф. Рока-Кьюсакс П. Гавара Н. Фарре Р. Ротгер М. Навахас Д. Исследование механических свойств живых клеток с помощью атомно-силовой микроскопии с затупленными концами пирамидального кантилевера. Phys Rev E Stat Nonlin Soft Matter Phys. 2005;72:021914. [PubMed] [Google Scholar]

83. Коста К.Д. Инь ФК Анализ вдавливания: значение для измерения механических свойств с помощью атомно-силовой микроскопии. J Биомех Инж. 1999;121:462. [PubMed] [Google Scholar]

84. Na S. Sun Z. Meininger G. A. Хамфри Дж. Д. Об атомно-силовой микроскопии и конститутивном поведении живых клеток. Биомех Модель Механобиол. 2004; 3:75. [Бесплатная статья PMC] [PubMed] [Google Scholar]

85. Домке Дж. Радмахер М. Измерение упругих свойств тонких полимерных пленок с помощью атомно-силового микроскопа. Ленгмюр. 1998;14:3320. [Google Scholar]

86. Клиффорд К.А. Сиа М.П. Вопросы количественной оценки при идентификации наноразмерных областей гомополимеров с использованием измерения модуля посредством наноиндентирования АСМ. Appl Surf Sci. 2005;252:1915. [Google Scholar]

87. Огден Р. В. Большие деформации изотропной упругости — корреляция теории и эксперимента для несжимаемых резиноподобных твердых тел. Proc R Soc Lon Ser A. 1972; 326:565. [Google Scholar]

88. Джонсон К.Л. Кендалл К. Робертс А.Д. Поверхностная энергия и контакт упругих тел. Proc R Soc Lond A Math. 1971; 324:301. [Google Scholar]

89. Лоттерс Дж. К. Олтуис В. Велтинк П. Х. Бергвельд П. Механические свойства резинового эластичного полимера полидиметилсилоксана для датчиков. J Micromech Microeng. 1997;7:145. [Google Scholar]

90. Цукрук В.В. Хуан З. Чижик С.А. Горбунов В.В. Исследование микромеханических свойств податливых полимерных материалов. J Mater Sci. 1998; 33:4905. [Google Scholar]

91. Лутольф М.П. Хаббелл Дж.А. Синтетические биоматериалы как инструктивное внеклеточное микроокружение для морфогенеза в тканевой инженерии. Нац биотехнолог. 2005; 23:47. [PubMed] [Google Scholar]

92. Хоффман А.С. Гидрогели для биомедицинских применений. Adv Drug Deliv Rev. 2002; 54:3. [PubMed] [Академия Google]

93. Чон Б. Ким С.В. Бэ Ю.Х. Термочувствительные золь-гель обратимые гидрогели. Adv Drug Deliv Rev. 2002; 54:37. [PubMed] [Google Scholar]

94. Гриффит Л.Г. Полимерные биоматериалы. Acta Mater. 2000;48:263. [Google Scholar]

95. Jen A.C. Wake M.C. Микос А.Г. Обзор: гидрогели для иммобилизации клеток. Биотех Биоинж. 1996; 50:357. [PubMed] [Google Scholar]

96. Вонг Дж.Ю. Лич Дж. Б. Браун XQ Баланс химии, топографии и механики на границе раздела клетка-биоматериал: вопросы и задачи для оценки роли механики субстрата на реакцию геля. Наука о серфинге. 2004;570:119. [Google Scholar]

97. Ирвин Э.Ф. Саха К. Розенблут М. Гэмбл Л.Дж. Кастнер Д.Г. Хили К.Э. Модульно-зависимая адгезия и поведение макрофагов. J Biomater Sci Polym Ed. 2008;19:1363. [PubMed] [Google Scholar]

98. Саха К. Кеунг А.Дж. Ирвин Э.Ф., Ли Ю., Литтл Л., Шаффер Д.В., и соавт. Модуль субстрата направляет поведение нервных стволовых клеток. Биофиз Дж. 2008; 95:4426. [Бесплатная статья PMC] [PubMed] [Google Scholar]

99. Лич Дж. Б. Браун X.Q. Жакот Дж.Г. Димилла П.А. Вонг Дж.Ю. Рост нейритов и ветвление клеток pc12 на очень мягких субстратах резко снижается ниже порога жесткости субстрата. Дж. Нейронная инженерия. 2007; 4:26. [PubMed] [Академия Google]

100. Коричневый X.Q. Оокава К. Вонг Дж.Ю. Оценка полидиметилсилоксановых каркасов с физиологически значимыми модулями упругости: взаимодействие механики субстрата и химии поверхности влияет на реакцию гладкомышечных клеток сосудов. Биоматериалы. 2005; 26:3123. [PubMed] [Google Scholar]

101.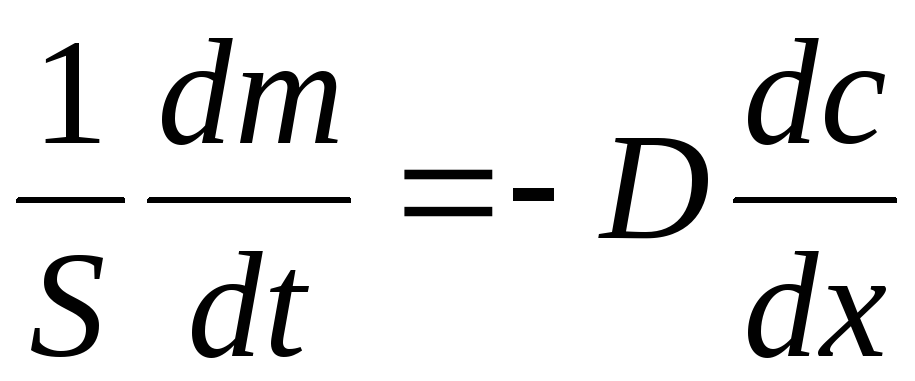 Discher D.E. Муни Д.Дж. Зандстра П.В. Факторы роста, матрицы и силы объединяются и контролируют стволовые клетки. Наука. 2009; 324:1673. [Бесплатная статья PMC] [PubMed] [Google Scholar]

102. Асейчик-Видличка М. Сродка Д.В. Каспрзак Х. Пирсченек Б.К. Моделирование упругих свойств переднего отдела глаза и их вклад в поддержание качества изображения: роль лимба. Глаз (Лондон) 2007; 21:1087. [PubMed] [Академия Google]

103. Амини Р. Барокас В. Х. Открытие угла передней камеры при корнеосклеральном вдавливании: механизм деформации всего глазного яблока и значение лимба. Invest Ophthalmol Vis Sci. 2009;50:5288. [PubMed] [Google Scholar]

104. Srodka W. Pierscionek B.K. Влияние свойств материала оболочки глазного яблока на оптическую стабильность изображения. J Биомед Опт. 2008;13:054013. [PubMed] [Google Scholar]

105. Тейлор З. Миллер К. Переоценка эластичности мозга для анализа биомеханизмов гидроцефалии. Дж. Биомех. 2004; 37:1263. [PubMed] [Академия Google]

106. Ченг Т. Ган Р.З. Экспериментальное измерение и модельный анализ механических свойств сухожилия, напрягающего барабанную перепонку. мед. инж. физ. 2008;30:358. [PubMed] [Google Scholar]

107. Chanthasopeephan T. Desai JP Lau A.C. Измерение сил при разрезании печени: новое оборудование и экспериментальные результаты. Энн Биомед Инж. 2003; 31:1372. [PubMed] [Google Scholar]

108. Хольцапфель Г.А. Гассер Т.К. Огден Р. В. Новая конститутивная основа механики артериальных стенок и сравнительное исследование моделей материалов. Дж Эласт. 2000;61:1. [Академия Google]

109. Ахтар Р. Шварцер Н. Шеррат М. Дж. Уотсон Р. Э. Б. Грэм Х.К. Траффорд А.В. и др. Наноиндентирование гистологических препаратов: картирование упругих свойств мягких тканей. J Mater Res. 2009;24:638. [Бесплатная статья PMC] [PubMed] [Google Scholar]

110. Johnson K.L. Связаться с Механик. Кембридж: Издательство Кембриджского университета; 1985. [Google Scholar]

111. Картер Ф.Дж. Франк Т. Г. Дэвис П. Дж. Маклин Д. Кушери А. Измерения и моделирование соответствия органов человека и свиньи. Мед имидж анал. 2001; 5:231. [PubMed] [Академия Google]

112. Константинидес Г. Кальджиоглу З.И. Макфарланд М. Смит Дж. Ф. Ван Влит К.Дж. Исследование механических свойств полностью гидратированных гелей и биологических тканей. Дж. Биомех. 2008;41:3285. [PubMed] [Google Scholar]

113. Чен Э.Дж. Новакофски Дж. Дженкинс В.К. OBrien WD Измерение модуля Юнга мягких тканей с применением к визуализации эластичности. IEEE Trans Ultrason Ferrolectr Freq Control. 1996; 43:191. [Google Scholar]

114. Барнс С.Л. Лыщик А. Вашингтон М.К. Гор Дж. К. Мига М.И. Разработка метода механического тестирования фиброзной мышиной печени. мед. физ. 2007;34:4439. [Бесплатная статья PMC] [PubMed] [Google Scholar]

115. Tay B.K. Ким Дж. Сринивасан М.А. Механическое поведение внутрибрюшных органов in vivo. IEEE Trans Biomed Eng. 2006;53:2129. [PubMed] [Google Scholar]

116. Эбенштейн Д. М. Прюитт Л.А. Наноиндентирование мягких гидратированных материалов для нанесения на ткани сосудов. J Biomed Mater Res A. 2004; 69:222. [PubMed] [Google Scholar]

117. Жакот Дж.Г. Дианис С. Шналль Дж. Вонг Дж.Ю. Простой метод микроиндентирования для картирования микромасштабной податливости мягких гидратированных материалов и тканей. J Biomed Mater Res A. 2006; 79:485. [PubMed] [Google Scholar]

118. Лундквист А. Лиллеодден Э. Зикхаус В. Кинни Дж. Прюитт Л. Балуч М. Вязкоупругие свойства здоровой артерии человека, измеренные в солевом растворе методом вдавливания на основе АСМ. В: Герберих В.В., редактор; Гао Х., редактор; Сундгрен Ж.-Э., редактор; Бейкер С.П., редактор. Тонкие пленки: напряжения и механические свойства VI. Питтсбург: Mater Res Soc; 1997. [Google Scholar]

119. Oie T. Murayama Y. Fukuda T. Nagai C. Omata S. Kanda K. et al. Визуализация локальной эластичности сосудистых тканей с помощью системы тактильного картирования. Джей Артиф Органс. 2009 г.;12:40. [PubMed] [Google Scholar]

120. Энглер А.Дж. Ричер Л. Вонг Дж.Ю. Пикарт К. Дишер Д.Э. Измерения эластичности срезов ткани, тонких гелей и полиэлектролитных многослойных пленок с помощью поверхностного зонда: корреляция между жесткостью подложки и адгезией клеток. Наука о серфинге. 2004; 570:142. [Google Scholar]

121. Юань Ю.Х. Верма Р. Измерение микроэластических свойств рогового слоя. Коллоидная поверхность Б. 2006; 48:6. [PubMed] [Google Scholar]

122. Кендалл М.А.Ф. Чонг Ю.-Ф. Кок А. Механические свойства эпидермиса кожи в отношении адресной доставки генов и лекарств. Биоматериалы. 2007;28:4968. [PubMed] [Google Scholar]

123. Леунг С.-Ф. Чжэн Ю. Чой CYK Мак С.С.С. Чиу С.К.В. Зи Б. и др. Количественное измерение фиброза шеи после облучения на основе модуля Юнга. Рак. 2002;95:656. [PubMed] [Google Scholar]

124. Линг Х.Ю. Чой П.К. Чжэн Ю.П. Лау К.Т. Извлечение механических свойств подошвенных тканей стопы с помощью ультразвукового индентирования, связанного с генетическим алгоритмом. J Mater Sci Mater Med. 2007;18:1579. [PubMed] [Академия Google]

125. Pailler-Mattei C. Bec S. Zahouani H. Измерения in vivo эластичных механических свойств кожи человека с помощью испытаний на вдавливание. мед. инж. физ. 2008;30:599. [PubMed] [Google Scholar]

126. Мак А.Ф.Т. Джордж Х.В. Лю Б.С. Ли Б.Д. Биомеханическая оценка остаточной ткани конечности ниже колена. J Rehabil Res Dev. 1994; 31:188. [PubMed] [Google Scholar]

127. Чжэн Ю.П. Чой Ю.К.К. Вонг К. Чан С. Мак A.F.T. Биомеханическая оценка подошвенной ткани стопы у больных сахарным диабетом с помощью системы ультразвукового индентирования. Ультразвук Медицина Биол. 2000; 26:451. [PubMed] [Академия Google]

128. Самани А. Бишоп Дж. Лугинбуль К. Плевес Д.Б. Измерение модуля упругости небольших образцов ткани ex vivo. физ.-мед. биол. 2003;48:2183. [PubMed] [Google Scholar]

129. Han L. Noble J.A. Берчер М. Новая система ультразвукового индентирования для измерения биомеханических свойств мягких тканей in vivo. Ультразвук Медицина Биол. 2003; 29:813. [PubMed] [Google Scholar]

130. Чен Э.Дж. Новакофски Дж. Дженкинс В.К. О’Брайен В. Д. Измерение модуля Юнга мягких тканей с применением к визуализации эластичности. IEEE Trans Ultrason Ferrolectr Freq Control. 1996;43:191. [Google Scholar]

131. Элькин Б.С. Азелоглу Э.У. Коста К.Д. Моррисон Б., 3-я Механическая неоднородность гиппокампа крысы, измеренная с помощью вдавливания на атомно-силовом микроскопе. J Нейротравма. 2007;24:812. [PubMed] [Google Scholar]

132. Азизи Э. Халенда Г.М. Робертс Т.Дж. Механические свойства апоневроза икроножной мышцы диких индеек. Интегр Комп Биол. 2009;42:51. [Бесплатная статья PMC] [PubMed] [Google Scholar]

133. Cui L. Maas H. Perreault E.J. Сандеркок Т.Г. In situ оценка свойств материала сухожилий: различия между мышцами задних конечностей кошек. Дж. Биомех. 2009 г.;42:679. [Бесплатная статья PMC] [PubMed] [Google Scholar]

134. de Almeida F.M. Томиоссо Т.С. Накагаки В.Р. Гомес Л. Матиелло-Роса С.М. Пиментель Э.Р. Влияние пассивного растяжения на биохимические и биомеханические свойства пяточного сухожилия крыс. Подключить тканевый рез. 2009; 50:279. [PubMed] [Google Scholar]

135. Vogel H.G. Влияние созревания и возраста на механические и биохимические параметры соединительной ткани различных органов у крыс. Подключить тканевый рез. 1978; 6:161. [PubMed] [Академия Google]

136. Рен Т.А. Йерби С.А. Бопре Г.С. Картер Д.Р. Механические свойства ахиллова сухожилия человека. Clin Biomech (Бристоль, Эйвон) 2001; 16:245. [PubMed] [Google Scholar]

137. Buchanan C.I. Марш Р.Л. Влияние длительных упражнений на биомеханические свойства ахиллова сухожилия цесарок. J Appl Physiol. 2001; 90:164. [PubMed] [Google Scholar]

138. Озязган И. Лиман Н. Дурсун Н. Гюнеш И. Влияние овариэктомии на механические свойства кожи у крыс. Зрелые. 2002;43:65. [PubMed] [Академия Google]

139. Герберт Л.А. Чен В.К. Хартманн А. Гарансис Дж. К. Механические свойства капсулы почки собаки. J Appl Physiol. 1976; 40:164. [PubMed] [Google Scholar]

140. Hollenstein M. Nava A. Valtorta D. Snedeker J.G. Mazza E. Механическая характеристика капсулы и паренхимы печени. Лекционные заметки Comput Sci. 2006; 4072:150. [Google Scholar]

141. Снедекер Дж.Г. Нидерер П. Шмидлин Ф.Р. Фаршад М. Деметропулос К.К. Ли Дж. Б. и др. Зависящие от скорости деформации свойства материала капсулы почки свиньи и человека. Дж. Биомех. 2005;38:1011. [PubMed] [Академия Google]

142. Джаясурия А.К. Шейнбейм Дж.И. Лубкин В. Беннет Г. Крамер П. Пьезоэлектрические и механические свойства бычьей роговицы. J Biomed Mater Res A. 2003; 66A: 260. [PubMed] [Google Scholar]

143. Райхель Э. Миллер Д. Бланко Э. Мастандуно Р. Модуль упругости центральной и перилимбальной роговицы крупного рогатого скота. Энн Офтальмол. 1989; 21:205. [PubMed] [Google Scholar]

144. Wollensak G. Iomdina E. Долговременные биомеханические свойства роговицы кролика после фотодинамического кросслинкинга коллагена. Акта Офтальмол. 2009 г.;87:48. [PubMed] [Google Scholar]

145. Wollensak G. Spoerl E. Seiler T. Измерение стресс-деформации роговицы человека и свиньи после перекрестного связывания, индуцированного рибофлавином-ультрафиолетовым альфа-излучением. J Катаракта рефракта Surg. 2003; 29:1780. [PubMed] [Google Scholar]

146. Downs CJ Frasncis Suh J.-K. Томас К.А. Беллеза А.Дж. Бургойн К.Ф. Харт Р.Т. Вязкоупругая характеристика перипапиллярной склеры: свойства материала по квадранту в глазах кролика и обезьяны. Транс ASME. 2003; 125:124. [Бесплатная статья PMC] [PubMed] [Google Scholar]

147. Жирар М. Су Ж.-К.Ф. Харт Р.Т. Бургойн К.Ф. Даунс Дж. К. Влияние времени хранения на механические свойства перпапиллярной склеры кролика после энуклеации. Curr Eye Res. 2007; 32:465. [PubMed] [Google Scholar]

148. Schultz D.S. Lotz JC Lee S.M. Тринидад М.Л. Стюарт Дж. М. Структурные факторы, опосредующие жесткость склеры. Invest Ophthalmol Vis Sci. 2008;49:4232. [PubMed] [Google Scholar]

149. Downs JC Suh J.K. Томас К.А. Беллеза А.Дж. Харт Р.Т. Бургойн К.Ф. Свойства вязкоупругого материала перипапиллярной склеры в нормальных глазах и глазах обезьян с ранней глаукомой. Invest Ophthalmol Vis Sci. 2005;46:540. [PubMed] [Академия Google]

150. Phillips J.R. McBrien N.A. Близорукость депривации формы: эластические свойства склеры. Офтальмологический физиол опт. 1995;15:357. [PubMed] [Google Scholar]

151. Майкос Дж.Т. Элиас Р.А. Шрейбер Д.И. Механические свойства твердой мозговой оболочки головного и спинного мозга крыс. J Нейротравма. 2008;25:38. [PubMed] [Google Scholar]

152. Веларди Ф. Фратернали Ф. Анджелилло М. Анизотропные определяющие уравнения и экспериментальное поведение ткани головного мозга при растяжении. Биомех Модель Механобиол. 2006; 5:53. [PubMed] [Академия Google]

153. Билстон Л.Е. Тибо Л.Э. Механические свойства шейного отдела спинного мозга человека in vitro. Энн Биомед Инж. 1996;24:67. [PubMed] [Google Scholar]

154. Миллер К. Чинзей К. Механические свойства ткани головного мозга при растяжении. Дж. Биомех. 2002; 35:483. [PubMed] [Google Scholar]

155. Ассул Н. Флауд П. Шауа М. Летурнер Д. Батай И. Механические свойства грудной и брюшной аорты крыс. Дж. Биомех. 2008;41:2227. [PubMed] [Google Scholar]

156. Редди К.Г. Возрастное перекрестное связывание коллагена связано с жесткостью матрикса стенки аорты в патогенезе лекарственного диабета у крыс. Микроваск Рез. 2004; 68:132. [PubMed] [Академия Google]

Модуль Юнга – GeeksforGeeks

Модуль Юнга назван в честь Томаса Янга , британского физика. Связь между напряжением (силой на единицу площади) и деформацией (пропорциональной деформацией объекта) определяется модулем Юнга. Когда к жесткому материалу добавляется определенная нагрузка, он деформируется. Когда груз снимается с эластичного материала, тело возвращается в свою первоначальную форму. За пределами минимальной степени деформации материалы часто не являются линейными и эластичными. Только линейные упругие поверхности имеют устойчивый модуль Юнга.

Подобно объемному модулю, коэффициенту Пуассона и модулю сдвига, модуль Юнга также является константой упругости. Поэтому, прежде чем понять концепцию модуля Юнга, давайте сначала узнаем о константах упругости.

Постоянные упругости

Постоянные упругости – это константы, определяющие деформацию, вызываемую данной системой напряжений, действующих на материал. Существует много типов констант упругости, таких как объемный модуль, модуль Юнга или модуль упругости, коэффициент Пуассона и модуль сдвига или модуль жесткости. Когда деформирующая сила действует на объект, она вызывает сдвиг исходного размера твердого тела. В таких ситуациях связь между константами упругости может быть использована для определения степень деформации .

Ниже приведены основные константы упругости, которые необходимо изучить:

1. Объемный модуль: Он определяется отношением давления (P), приложенного к соответствующему относительному уменьшению объема или объемной деформации ( ∈ _V ) материала. Математически это определяется как:
K = P / ∈ _V = P / -(∆V/V ₀ )
где ∆V — изменение объема материала в результате сжатия и В ₀ Начальный объем материала.
Значение обозначается символом K и имеет размерность силы на единицу площади.
Выражается в единицах на квадратный дюйм (psi) в английской системе и в ньютонах на квадратный метр (Н/м ² ) в метрической системе.
2. Модуль Юнга: Это мера жесткости твердого тела или сопротивления упругой деформации под нагрузкой. Он связывает напряжение (силу на единицу площади) с деформацией (пропорциональной деформацией) вдоль оси или линии. Математически это определяется как:
Y = (F/A) / -(∆L/L ₀ )
где ∆L — изменение длины материала в результате сжатия, а L ₀ — начальная длина материал.
Значение обозначается символом Y и имеет размерность силы на единицу площади.
Единицей СИ для модуля Юнга является Паскаль (Па), значения чаще всего выражаются в мегапаскалях (МПа) или ньютонах на квадратный миллиметр (Н/мм ² ).
3. Модуль сдвига или модуль жесткости: T Отношение касательного напряжения (или) касательного напряжения и касательной деформации (или) касательной деформации называется модулем жесткости. Математически это определяется как:
η = (F/A) / ∅
, где F — сила, приложенная к единице площади поверхности тела A, а ∅ — деформация при сдвиге.
Значение обозначается символом η.
Выражается в Паскалях (Па) в системе СИ.

Теперь давайте обсудим модуль упругости Юнга более подробно:

Модуль упругости Юнга

Модуль Юнга является математической константой. Он был назван в честь Томаса Янга , английского врача и ученого 18-го века. Он определяет упругие характеристики твердого тела, которое подвергается растяжению или сжатию только в одном направлении. В качестве примера рассмотрим металлический стержень, который возвращается к своей первоначальной длине после растяжения или сжатия в продольном направлении.

Измерение способности материала выдерживать изменения длины при продольном растяжении или сжатии. Он также известен как модуль упругости. Мы вычисляем его путем деления. Он рассчитывается как продольное напряжение, деленное на деформацию. В случае натянутого металлического стержня можно указать как напряжение, так и деформацию.

Модуль Юнга, также известный как Модуль упругости или Модуль упругости при растяжении , представляет собой измерение механических свойств линейных упругих твердых тел, таких как стержни, проволока и т. д. Существуют и другие числа, которые дают нам меру упругих характеристик материала. Объемный модуль и модуль сдвига являются двумя примерами. Однако чаще всего используется значение модуля Юнга. Это связано с тем, что он предоставляет информацию об эластичности материала при растяжении.

Когда материал сжимается или растягивается, он испытывает упругую деформацию и возвращается к своей первоначальной форме при снятии нагрузки. Когда гибкий материал деформируется, он деформируется больше, чем когда деформируется жесткое вещество. Другими словами, это можно интерпретировать как:

Твердое тело с низким значением модуля Юнга упруго.
Твердое тело с высоким значением модуля Юнга является неупругим или жестким.

Модуль Юнга описывается как механическая способность материала выдерживать сжатие или удлинение относительно его начальной длины.

Формула модуля Юнга:

Математически модуль Юнга определяется как отношение напряжения, приложенного к материалу, и деформации, соответствующей приложенному напряжению в материале, как показано ниже:

Модуль Юнга = Напряжение / Деформация

или

Y = σ / ϵ

где Y — модуль Юнга материала, σ — напряжение, приложенное к материалу, а ε — деформация, соответствующая приложенному напряжение в материале.

Единицы модуля Юнга:

Единицей модуля Юнга в системе СИ является Паскаль (Па) .

Размерная формула для Y: [ML ^-1 T ^-2 ] .

Значения чаще всего выражаются в мегапаскалях (МПа), ньютонах на квадратный миллиметр (Н/мм ² ), гигапаскалях (ГПа) или килоньютонах на квадратный миллиметр (кН/мм ² ).

Модуль Янга из некоторых материалов следующим образом:

		Модул Янг (Y) в NM ^–	‘s Modulus (Y).0003	Rubber	5 × 10 ⁸
2.	Bone	1.4 × 10 ¹⁰
3.	Lead	1.6 × 10 ¹⁰
4.	Aluminum	7. 0 × 10 ¹⁰
5.	Brass	9.0 × 10 ¹⁰
6.	Copper	11.0 × 10 ¹⁰
7.	Iron	19,0 × 10 ¹⁰

Математическая интерпретация молодых: по его длине, т. е. по нормали к поверхности провода, как показано на рисунке. Если △L — изменение длины проволоки, то растягивающее напряжение (σ = F/A), где A — площадь поперечного сечения проволоки, и продольная деформация (ϵ = △L/L).

Таким образом, модуль Юнга для этого случая определяется как:

Y = (F/A) / (△L/L)

= (F × L) / (A × △L)

Если растяжение производится грузом массой m, то Сила F равна mg , где m — масса, а g — ускорение свободного падения.

А площадь поперечного сечения провода, А равна πr ² где r — радиус провода.

Таким образом, приведенное выше выражение можно записать как:

Y = (m × g × L) / (πr ² × △L)

Таким образом, Факторы, от которых зависит модуль Юнга материала: :
Большее значение Юнга модуля материала, тем больше значение силы , необходимой для изменения длины материала .
Модуль Юнга объекта зависит от природы материала объекта .
Модуль Юнга объекта не зависит от размеры (т. е. длина, ширина, площадь и т. д.) объекта.
Модуль Юнга вещества уменьшается с повышением температуры .
Модуль упругости Юнга абсолютно твердого тела бесконечен.

Следовательно, из приведенного выше выражения наклон, построенный для изменения длины (△L) и массы объекта (м), показан ниже как:

График между △L и m.

Примеры задач

Задача 1. Кабель обрезан наполовину. Почему это изменение не влияет на опору кабины при максимальной нагрузке?

Решение:

Максимальная нагрузка, которую может выдержать кабель, определяется по формуле:
F = (YA△L) / L
Здесь Y и A постоянные, значение △ не изменяется. л/л.
Следовательно, не влияет на на максимальную нагрузку.

Задача 2. Чему равен модуль Юнга абсолютно твердого тела?

Решение:

Модуль Юнга для материала:
Y=(F/A) / (△L/L)
Здесь △L = 0 для твердого тела. Следовательно, модуль Юнга равен бесконечным .

Проблема 3. Модуль Юнга стали намного больше, чем у резины. Если продольная деформация одинакова, какой из них будет иметь большее растягивающее напряжение?

Решение:

Поскольку растягивающее напряжение материала равно произведению модуля Юнга (Y) на продольную деформацию.

TOP HEADLINES