Закон юнга: Модуль Юнга (упругости) для стали и других материалов: определение, смысл
alexxlab | 30.10.2017 | 0 | Разное
Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.

 Модуль Юнга
Модуль ЮнгаОсновные сведения
Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м2 или в Па.
Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (1012Па)
Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.
Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.


График теста на растяжение
E- это частное от деления нормальных напряжений σ на относительное удлинение ε.
E=α/ε
Закон Гука также можно сформулировать и с использованием модуля Юнга.
Физический смысл модуля Юнга
Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.
Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.


Виды деформации
Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.
В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:
Δl = α * (lF) / S
Величину, обратную α, и называют модулем Юнга:
1/α = E
Относительная деформация:
ε = (Δl) / l = α * (F/S)
Отношение растягивающей силы F к S называют упругим напряжением σ:
ε=α σ
Закон Гука, записанный с использованием модуля Юнга, выглядит так:
σ = ε/α = E ε
Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.
В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.
Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l
Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.
Значения модуля юнга для некоторых материалов
В таблице показаны значения E ряда распространенных веществ.
| Материал | модуль Юнга E, ГПа |
| Алюминий | 70 |
| Бронза | 75-125 |
| Вольфрам | 350 |
| Графен | 1000 |
| Латунь | 95 |
| Лёд | 3 |
| Медь | 110 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 200/210 |
| Стекло | 70 |
Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.
Предел прочности материала
Это предел возникающего напряжения, после которого образец начинает разрушаться.
Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.


Инструмент для определения предела прочности
Кроме того, существуют пределы прочности на сжатие материала и на растяжение. Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления. В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.
Допускаемое механическое напряжение в некоторых материалах при растяжении
Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.


Испытание на растяжение
Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.
Значения σраст в МПа:
| Материалы | σраст | |
| Бор | 5700 | 0,083 |
| Графит | 2390 | 0,023 |
| Сапфир | 1495 | 0,030 |
| Стальная проволока | 415 | 0,01 |
| Стекловолокно | 350 | 0,034 |
| Конструкционная сталь | 60 | 0,003 |
| Нейлон | 48 | 0,0025 |
Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.
Запасы прочности, закладываемые в ответственные конструкции, также многократны.
Коэффициент запаса прочности
Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.


Запас прочности
Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.
Связь с другими модулями упругости
Модуль Юнга связан с модулем сдвига, определяющим способность образца к сопротивлению против деформации сдвига, следующим соотношением:
E связан также и с модулем объёмной упругости, определяющим способность образца к сопротивлению против одновременного сжатия со всех сторон.
Коллоидная химия. Шпаргалка (С. В. Егоров, 2009)
22. Смачивание. Закон Юнга (силовой и энергетический выводы)
Смачивание – это поверхностное явление, заключающееся во взаимодействии жидкости с твердым телом при наличии одновременного контакта трех несмешивающихся фаз. Смачивание часто рассматривают как результат межмолекулярного (вандерваальсова) взаимодействия, однако во многих случаях (например, при соприкосновении жидких металлов с твердыми металлами) смачивание обусловлено скорее, образованием химических соединений, твердых и жидких растворов и диффузионными процессами в поверхностном слое смачиваемого тела.
Смачивание – самопроизвольный процесс, идущий с уменьшением поверхностной энергии. Поэтому при смачивании выделяется теплота. Чем лучше твердое тело смачивается жидкостью, тем выше теплота смачивания. Тепловой эффект, сопровождающий соприкосновение жидкости со смачиваемой поверхностью, называется теплотой смачивания.
Мерой смачивания является краевой угол смачивания Θ между смачиваемой поверхностью и поверхностью жидкости на периметре. Угол Θ отсчитывают со стороны жидкости. Точка, соответствующая краевому углу смачивания 90°, называется точкой инверсии. При статическом (равновесном) смачивании угол Θ связан с поверхностным натяжением жидкости (σж), поверхностным натяжением твердого тела (σ) и межфазным натяжением на границе «твердое тело – жидкость» (σтж) уравнением Юнга:
cosΘ = (σт – σтж) / σж.
Величиной угла Θ оценивают лиофильность и лиофобность поверхностей по отношению к различным жидкостям. На лиофильной поверхности жидкость растекается, т. е. имеет место частичное (0° <
Wa = σж (1 + cosΘ) и Wk = 2σж.
При Wa < WK всегда Θ > 0°, причем с увеличением отношения Wa < Wk улучшается С.
Работа адгезии характеризует работу по отрыву от твердой поверхности. Оценивается она по уравнению Дюпре-Юнга: Wа=σ(1 + cos х).
Разность S = Wa – Wk называется коэффициентом растекания. Часто наблюдаемая задержка в установлении равновесных краевых углов называется гистерезисом смачивания. Различают кинетический (динамический) и статический гистерезис смачивания.
Причинами гистерезиса могут быть шероховатость поверхности, особенности структуры поверхностного слоя, релаксационные процессы в жидкой фазе и др.
Если твердое тело соприкасается одновременно с двумя несмешивающимися жидкостями, происходит избирательное смачивание. Эффективные регуляторы смачивания – поверхностно-активные вещества, которые могут как улучшать, так и ухудшать его.
В узких каналах, цилиндрических капиллярах образуется вогнутый мениск – полностью искривленная поверхность жидкости (рис. 1).
Рис. 1.
Модуль Юнга — Вікіпедія
Матеріал з Вікіпедії — вільної енциклопедії.
Мо́дуль Ю́нга (модуль пружності першого роду або модуль пружності під час розтягу) — фізична величина, що характеризує пружні властивості ізотропних речовин, один із модулів пружності.
За ДСТУ 2825-94[1]: Модуль пружності під час розтягу — відношення нормального напруження до відповідної лінійної деформації за лінійного напруженого стану до границі пропорційності.
Позначається латинською літерою E (від англ. Elasticity), вимірюється в Н/м² (ньютонах на метр в квадраті) або Па (паскалях), переважно в гігапаскалях. Названо на честь англійського фізика XIX століття Томаса Юнга. Часто ще цю фізичну величину називають модулем пружності першого роду.
Модуль Юнга для випадку розтягу-стискання стрижня осьовою силою розраховується наступним чином:
- E = F / S Δ l / l = F l S Δ l , {\displaystyle E={\frac {F/S}{\Delta l/l}}={\frac {Fl}{S\Delta l}},}
де: F — осьова сила;
- S — площа поверхні (перерізу), по якій розподілена дія сили;
- l — довжина стрижня, що деформується;
- Δ l {\displaystyle \Delta l} — модуль зміни довжини стрижня в результаті пружної деформації.
Модуль Юнга встановлює зв’язок між деформацією розтягу й механічним напруженням направленим на розтяг.
- σ = F S = E Δ l l = E ϵ {\displaystyle \sigma ={\frac {F}{S}}=E{\frac {\Delta l}{l}}=E\epsilon } ,
де: σ — механічне напруження, визначається, як сила, що припадає на одиницю площі поперечного перерізу тіла,
- ϵ = Δ l l {\displaystyle \epsilon ={\frac {\Delta l}{l}}} — величина відносної деформації (відносне видовження).
Наведена формула справедлива при малих пружних деформаціях.
В теорії пружності використовуються кілька різних модулів, виходячи із міркувань зручності. Всі вони зв’язані між собою простими співвідношеннями. Пружні властивості ізотропного середовища повністю характеризуються двома незалежними коефіцієнтами, наприклад, модулем Юнга й модулем зсуву, або модулем Юнга й коефіцієнтом Пуассона. Модуль Юнга зручно використовувати при одновісній деформації.
Існують такі формули зв’язку між модулями пружності
- E = 9 K μ 3 K + μ {\displaystyle E={\frac {9K\mu }{3K+\mu }}} ,
де K — модуль всебічного стиску, μ — модуль зсуву.
- E = 3 K ( 1 − 2 ν ) {\displaystyle E=3K(1-2\nu )} ,
де ν — коефіцієнт Пуассона.
- E = 2 μ ( 1 + ν ) {\displaystyle E=2\mu (1+\nu )} ,
де μ — модуль зсуву.
Коефіцієнт Ламе λ виражається через модуль Юнга й коефіцієнт Пуассона:
- λ = E ν ( 1 − 2 ν ) ( 1 + ν ) {\displaystyle \lambda ={\frac {E\nu }{(1-2\nu )(1+\nu )}}}
Значення модуля Юнга для деяких матеріалів[ред. | ред. код]
- ↑ ДСТУ 2825-94 Розрахунки та випробування на міцність. Терміни та визначення основних понять.
Закон Гука, модуль Юнга (сопромат)

Для большинства конструкционных материалов между напряжением (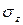
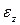 ) до определенного предела нагружения существует линейная зависимость
) до определенного предела нагружения существует линейная зависимость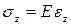
Закон Гука: Напряжение пропорционально деформации.
Впервые Закон Гука был опубликован в виде анаграммы английским ученым Робертом Гуком (1635 – 1703 гг.). При правильной расстановке букв анаграмма читается: «Каково удлинение, такова и сила».
К такому же заключению в 1680 г., независимо от Гука, пришел французский ученый Эдмон Мариотт.
Коэффициент пропорциональности (E) в формуле закона Гука 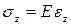
Необходимо отметить, что некоторые материалы не подчиняются закону Гука, например, кожа, ткани. Такие материалы, как, например, чугун, только с некоторым приближением можно считать подчиняющимся закону Гука. Но даже и те материалы, которые подчиняются закону Гука, перестают ему следовать при достижении деформации определенного значения.
Из закона Гука видно: чем больше модуль Юнга, тем меньше (при том же значении напряжения) деформация материала. Следовательно, модуль продольной упругости характеризует жесткость материала при растяжении (сжатии). Из формулы закона Юнга видно, что модуль Юнга измеряется в тех же единицах, что и нормальное напряжение (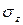 ).
).
Так, например, для всех марок сталей 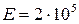 МПа.
МПа.
Модуль Юнга — Википедия
Материал из Википедии — свободной энциклопедии
Мо́дуль Ю́нга (модуль продольной упругости) — физическая величина, характеризующая способность материала сопротивляться растяжению, сжатию при упругой деформации[1]. Обозначается большой буквой Е.
Назван в честь английского физика XIX века Томаса Юнга.
В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал деформируемой среды и процесса.
В Международной системе единиц (СИ) измеряется в ньютонах на квадратный метр или в паскалях. Является одним из модулей упругости.
Модуль Юнга рассчитывается следующим образом:
- E = F / S Δ l / l = F l S Δ l , {\displaystyle E={\frac {F/S}{\Delta l/l}}={\frac {Fl}{S\Delta l}},}
где:
Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне:
- c = E ρ , {\displaystyle c={\sqrt {\frac {E}{\rho }}},}
где ρ {\displaystyle \rho } — плотность вещества.
Связь с другими модулями упругости
В случае изотропного тела модуль Юнга связан с модулем сдвига G {\displaystyle G} и модулем объёмной упругости K {\displaystyle K} соотношениями
- G = E 2 ( 1 + ν ) {\displaystyle G={\frac {E}{2(1+\nu )}}}
и
- K = E 3 ( 1 − 2 ν ) , {\displaystyle K={\frac {E}{3(1-2\nu )}},}
где ν {\displaystyle \nu } — коэффициент Пуассона.
Температурная зависимость модуля Юнга
Температурная зависимость модуля упругости простых кристаллических материалов объясняется исходя из того, что модуль упругости M ( T ) {\displaystyle M(T)} определяется как вторая производная от внутренней энергии W ( T ) {\displaystyle W(T)} по соответствующей деформации E ( T ) = d 2 W ( T ) d ε 2 {\displaystyle E(T)={d^{2}W(T) \over d\varepsilon ^{2}}} . Поэтому при температурах T ≤ Θ D {\displaystyle T\leq \Theta _{D}} ( Θ D {\displaystyle \Theta _{D}} — температура Дебая) температурная зависимость модуля упругости определяется простым соотношением
- M ( T ) = M 0 − M 1 T − M 2 T 2 {\displaystyle M(T)=M_{0}-M_{1}T-M_{2}T^{2}}
где M 0 {\displaystyle M_{0}} — адиабатический модуль упругости идеального кристалла при T ⟶ 0 K {\displaystyle T\longrightarrow 0K} ; M 1 T {\displaystyle M_{1}T} — дефект модуля, обусловленный тепловыми фононами; M 2 T 2 {\displaystyle M_{2}T^{2}} — дефект модуля, обусловленный тепловым движением электронов проводимости[2]
Значения модуля Юнга для некоторых материалов
Значения модуля Юнга для некоторых материалов приведены в таблице
См. также
Примечания
- ↑ Модули упругости — Статьи в Физическом энциклопедическом словаре и Физической энциклопедии.
- ↑ Л.Н. Паль-Валь, Ю.А. Семеренко, П.П. Паль-Валь, Л.В. Скибина, Г.Н. Грикуров. Исследование акустических и резистивных свойств перспективных хромо-марганцевых аустенитных сталей в области температур 5-300 К // Конденсированные среды и межфазные границы. — 2008. — Т. 10, вып. 3. — С. 226—235.
- ↑ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 Анурьев В. И. Справочник конструктора-машиностроителя в 3т. Т. 1/В. И. Анурьев; 8-е изд., перераб и доп. Под ред. И. Н. Жестковой — М.: Машиностроение, 2001. — С. 34. ISBN 5-217-02963-3
- ↑ Галашев А. Е., Рахманова О. Р. Устойчивость графена и материалов на его основе при механических и термических воздействиях // Успехи физических наук. — М.: РАН, ФИАН, 2014. — Т. 184, вып. 10. — С. 1051.
- ↑ В.Д. Нацик, П.П. Паль-Валь, Л.Н. Паль-Валь, Ю.А. Семеренко. Низкотемпературный a-пик внутреннего трения в ниобии и его связь с релаксацией кинков на дислокациях // ФНТ. — 2001. — Т. 27, вып. 5. — С. 547—557.
- ↑ П.П. Паль-Валь, В.Д. Нацик, Л.Н. Паль-Валь, Ю.А. Семеренко. Нелинейные акустические эффекты в монокристаллах ниобия, обусловленные дислокациями // ФНТ. — 2004. — Т. 30, вып. 1. — С. 115—125.
Литература
- Волькенштейн В. С. Сборник задач по общему курсу физики / В. С. Волькенштейн. — СПб.: Лань, 1999. — 328 с.
Ссылки
Модуль Юнга (синонимы: модуль упругости I рода, модуль продольной упругости) – механическая характеристика материалов, определяющая их способность сопротивляться продольным деформациям. Показывает степень жесткости материала.
Назван в честь английского ученого Томаса Юнга.
Обозначается латинской прописной буквой E
Единица измерения – Паскаль [Па].
В сопротивлении материалов модуль продольной упругости участвует в расчетах на жесткость при растяжении-сжатии и изгибе, а также в расчетах на устойчивость.
Учитывая то, что практически все конструкционные материалы имеют значение E высокого порядка (как правило 109 Па), его размерность часто записывают с помощью кратной приставки «гига» (гигапаскаль [ГПа])
Для всех материалов его величину можно определить в ходе эксперимента по определению модуля упругости I рода.
Приближенно значение модуля можно определить по диаграмме напряжений получаемой при испытаниях на растяжение.
Рис. 1 Начальный фрагмент диаграммы напряжений
В этом случае модуль Юнга равен отношению нормальных напряжений к соответствующим относительным деформациям, на участке диаграммы (рис. 1) до предела пропорциональности σпц (тангенсу угла α наклона участка пропорциональности к оси деформаций ε).
E=σ/ε=tgα
В таблице 1 приведены сравнительные значения модуля для некоторых наиболее часто используемых материалов
Таблица 1
Материал | Модуль Юнга |
Сталь | 200 |
Чугун | 120 |
Серый чугун | 110 |
Алюминий | 70 |
Дюралюминий | 74 |
Титан | 120 |
Бронза | 100 |
Латунь | 95 |
Медь | 110 |
Олово | 35 |
Хром | 300 |
Никель | 210 |
Кремний | 110 |
Свинец | 18 |
Бетон | 20 |
Дерево | 10 |
Стекло | 70 |
Модуль упругости I рода служит коэффициентом пропорциональности в формуле описывающей закон Гука:
σ=Eε
Связка модуля Юнга с геометрическими характеристиками поперечных сечений бруса показывает их жесткость:
EA – жесткость поперечного сечения при растяжении-сжатии,
где A – площадь поперечного сечения стержня;
EI – жесткость поперечного сечения при изгибе,
где I – осевой момент инерции сечения балки.
Модуль упругости II рода (модуль сдвига) >
Примеры решения задач >
Модуль Юнга и его основной физический смысл
Модулем продольной упругости конструкционного материала, или модулем Юнга, называют физическую величину, которая характеризует свойство материалов, обеспечивающее их сопротивление деформациям, действующим в продольном направлении.

Параметр характеризует степень жесткости конкретного материала.
Название модуля соответствует фамилии Томаса Юнга – известного английского физика и ученого, который занимался исследованием процессов сжатия и растяжения для твердых материалов. Обозначается данная физическая величина латинской буквой E. Измеряется модуль Юнга в Паскалях.
Параметр модуль Юнга, или модуль продольной упругости, используется при различных расчетах при испытаниях материалов на степень деформации при растяжении-сжатии, а также при изгибе.
Надо сказать, что большинству используемых конструкционных материалов свойственен показатель модуля Юнга достаточно больших значений, которые, как правило, имеют порядок 109 Па. Поэтому для удобства расчетов и записи используют кратную приставку «гига» (ГПа).
Ниже приведены показатели модуля Юнга для некоторых конструкционных материалов, которые достаточно часто используются для различных практических целей. Именно от их свойств прочности зависит долговечность строительных сооружений и других объектов.
Согласно приведенной таблице, максимальный показатель модуля принадлежит стали, а минимальный – дереву.
| Название материала | Показатель E, [ГПа] | Название материала | Показатель E, [ГПа] |
| хром | 300 | латунь | 95 |
| никель | 210 | дюралюминий | 74 |
| сталь | 200 | алюминий | 70 |
| чугун | 120 | стекло | 70 |
| хром | 110 | олово | 35 |
| серый чугун | 110 | бетон | 20 |
| кремний | 110 | свинец | 18 |
| бронза | 100 | дерево | 10 |
 Графическое определение модуля Юнга возможно с помощью специальной диаграммы напряжений, на которой изображена кривая, получаемая при многократных испытаниях одного и того же материала на прочность.
Графическое определение модуля Юнга возможно с помощью специальной диаграммы напряжений, на которой изображена кривая, получаемая при многократных испытаниях одного и того же материала на прочность.В этом случае физический смысл модуля Юнга заключается в нахождении математического отношения нормальных напряжений к соответствующим показателям деформации на определенном участке диаграммы до конкретно заданного предела пропорциональности σпц.
В виде математического выражения модуль Юнга выглядит следующим образом: E=σ/ε=tgα
Следует также сказать о том, что модуль Юнга является еще и коэффициентом пропорциональности в математическом описании закона Гука, который выглядит следующим образом: σ=Eε

Поэтому непосредственная связь модуля продольной упругости с измеряемыми характеристиками поперечных сечений материалов, участвующих в испытаниях на жесткость, выражается с помощью таких показателей, как ЕА и Е1.
EA – это показатель жесткости при растяжении-сжатии материала в его поперечном сечении, где А – значение площади сечения стержня.
Е1 – это показатель жесткость при изгибе материала в его поперечном сечении, где 1 – значение осевого момента инерции, который возникает в сечении ипытываемого материала.
Таким образом, модуль Юнга – это универсальный показатель, который позволяет с нескольких сторон характеризовать прочностные свойства материала.
Ил-Юнг Юнг | Гарвардская юридическая школа

Ил-Юнг Юнг
S.J.D. Кандидат
аспирант, написание TA для коротких проектов
ijung at sjd.law.harvard.edu
Диссертация
Конституционные ограничения на военную мощь и «Конституция мира»
Это исследовательское предложение сфокусировано на так называемой «Конституции мира» Японии, которая представляет собой уникальный случай в повествовании о конституционном ограничении военных действий.Не все войны запрещены даже в рамках международного публичного права. Справедливые причины войны ( jus bellum iustum ), такие как принцип самообороны, до сих пор признаются, и любой участвующий в них государственный деятель попытается узаконить свои действия этими словами. Но статья 9 Конституции Японии делает шаг вперед от других, заявляя, что «навсегда отказаться от войны как суверенного права нации и угрозы или применения силы как средства урегулирования международных споров». Согласно общему мнению ученых-конституционистов в Японии, благодаря статье 9 Япония полностью отказалась от своего права на войну ( jus ad bellum ), даже включая свое право на самооборону.Тем не менее, существует несоответствие между теорией и реальностью, поскольку в Японии действительно есть вооруженные силы во имя Сил самообороны, и они также являются одними из крупнейших в мире. Следовательно, исследование планирует выяснить, действительно ли такое отречение от войны имеет сдерживающую функцию в процессе принятия решений государством. Другими словами, стоит спросить, может ли явное конституционное положение иметь существенный эффект, чтобы удержать национальное государство от участия в военных действиях, даже в войнах самообороны, против другой нации.
Области исследований и супервизоров
- Конституционное право и теория с профессором Ноем Фельдманом, Гарвардская юридическая школа, главный научный руководитель факультета
- Японское право и общество с профессором Марком Рамсиером, Гарвардская юридическая школа
- Международные отношения в Восточной Азии с профессором Уильямом Алфордом, Гарвардская юридическая школа
Дополнительные научные интересы
- Международное публичное право
- Юридическая история
- Закон и Политика
- Восточноазиатские юридические исследования
Образование
- Гарвардский юридический факультет, S.Кандидат юридических наук 2015-настоящее время
- Гарвардская юридическая школа, магистр права Программа 2014-2015 (выполнено требования, отказ от степени)
- Сеульский национальный университет, магистр права, 2013
- Сеульский национальный университет, бакалавр права, 2004
академических назначений и стипендий
- Гарвардская юридическая школа, 2018-2019 гг., Стипендиат программы обучения, написание ТП для коротких проектов
- Гарвардский юридический факультет, 2016–2017 годы, стипендиат программы магистратуры, магистр права.М. Советник
- Сеульский национальный университет, юридический факультет, 2011–2014 годы, ассистент по конституционному праву
- Национальный Корейский Институт Криминологии, 2013, Ассистент-исследователь
- Корейское общество правовой истории, 2010-2013, помощник редактора журнала
Представитель Публикации
- Земельная реформа в Корее при военном правительстве США, Гарвардская школа права LL.M. Бумага, 2015 (награждена премией Ён К. Кима, , 2015, ),
- Формирование государства с помощью теории естественного права. Самуэль Пуфендорф, Сеульский национальный университет, 2013
Дополнительная информация
- Языки: корейский, японский, немецкий
Последнее обновление: 12 августа 2018 г.
,
