Жесткость единицы измерения пружины: Жесткость пружины, теория и онлайн калькуляторы

alexxlab | 16.05.2023 | 0 | Разное

формула, как найти, коэффициент, обозначение

Содержание:

• От чего зависит жесткость
  • Геометрия пружины
  • Тип материала
  • Коэффициент
  • Срок эксплуатации
• В чем измеряется жесткость
  • Как обозначается
• Коэффициент жесткости пружины
  • Формула расчета через массу и длину
• Как можно измерить жесткость
  • Измерительные приборы
  • Практическая задача
• Альтернативные способы определения жесткости

Содержание

• От чего зависит жесткость
  • Геометрия пружины
  • Тип материала
  • Коэффициент
  • Срок эксплуатации
• В чем измеряется жесткость
  • Как обозначается
• Коэффициент жесткости пружины
  • Формула расчета через массу и длину
• Как можно измерить жесткость
  • Измерительные приборы
  • Практическая задача
• Альтернативные способы определения жесткости

 

Определение

Жесткость — способность твёрдого тела, конструкции или её элементов сопротивляться деформации от приложенного усилия вдоль выбранного направления в заданной системе координат.

Сила жесткости — сила, возникающая в теле в результате его деформации и стремящаяся вернуть его в исходное состояние.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

От чего зависит жесткость

Жесткость пружины зависит от нескольких параметров:

• геометрии пружины;
• типа материала;
• коэффициента;
• срока эксплуатации.

Геометрия пружины

На жесткость витой пружины влияет:

• количество витков;
• их диаметр;
• диаметр проволоки.

Диаметр намотки измеряется от оси пружины. Так как длина проволоки в пружине значительно больше длины упругого стержня, сопротивляемость внешней деформации многократно возрастает.

Волновые пружины состоят из металлических лент, навитых ребром по окружности заданного диаметра.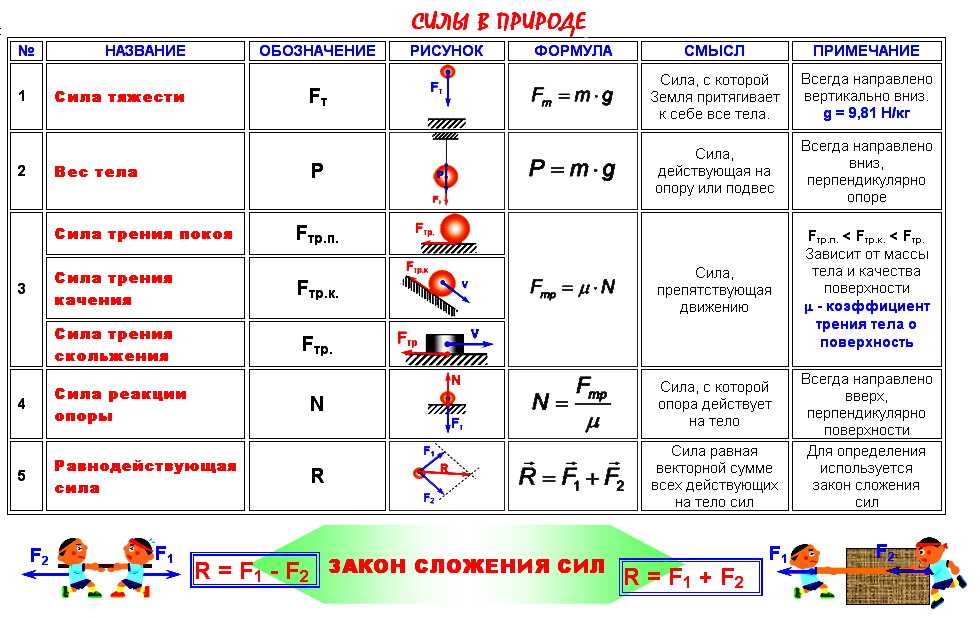

Их основные геометрические параметры:

• количество витков;
• количество волн на виток;
• сечение ленты.

Тип материала

У каждого материала есть условный предел упругости, характеризующий его способность восстанавливаться после деформации. Если этот предел превышается, в структуре материала возникают необратимые изменения.

Определение

Предел упругости — механическая характеристика материала, показывающая максимальное напряжение, при котором имеют место только упругие, обратимые деформации.

Предел упругости измеряют в паскалях и определяют по формуле:

\(\sigma_{у\;}=\;\frac FS\)

где F — действие внешней силы на исследуемый образец, приводящее к повреждениям, а S — его площадь.

Кроме предела упругости, существуют такие характеристики упругости материалов, как модули упругости (модуль Юнга) и сдвига, коэффициент жесткости и другие.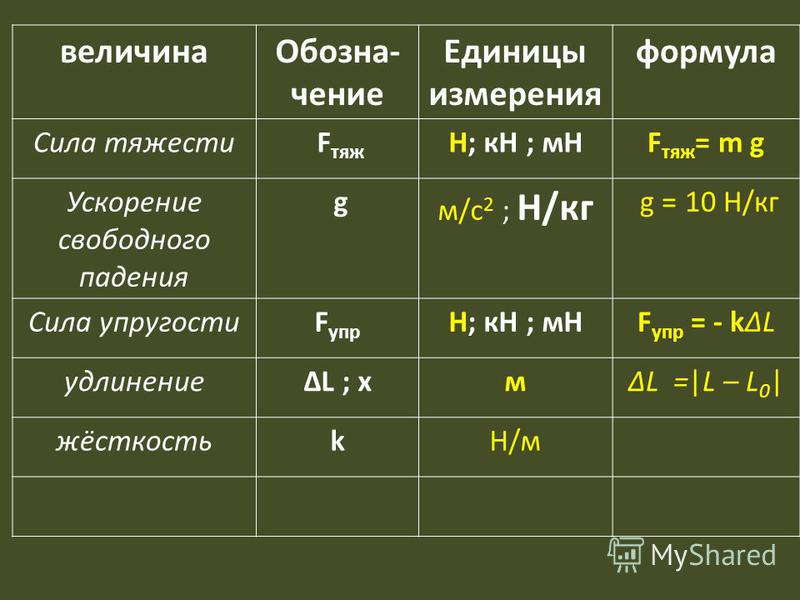 Все они взаимосвязаны, поэтому, выяснив значение одной из величин с помощью справочной таблицы, можно вычислить другие.

Коэффициент

Определение

Согласно закону Гука, при малой деформации абсолютная величина силы упругости прямо пропорциональна величине деформации.

Эта линейная зависимость описывается формулой:

\(F=\;k\;\times\;x\)

где k — коэффициент жесткости, а х — величина, на которую сжалась или растянулась пружина.

Примечание

Деформация считается малой в том случае, когда изменение размеров тела значительно меньше его первоначальных размеров.

Срок эксплуатации

Нахождение под напряжением приводит к постепенной необратимой деформации, называемой ослаблением пружины.

Жесткость пружины влияет на срок ее эксплуатации, как и сила воздействия. Конструкторы пружин, предварительно рассчитав эти параметры, проводят тесты на прототипах, прежде чем начать массовое производство.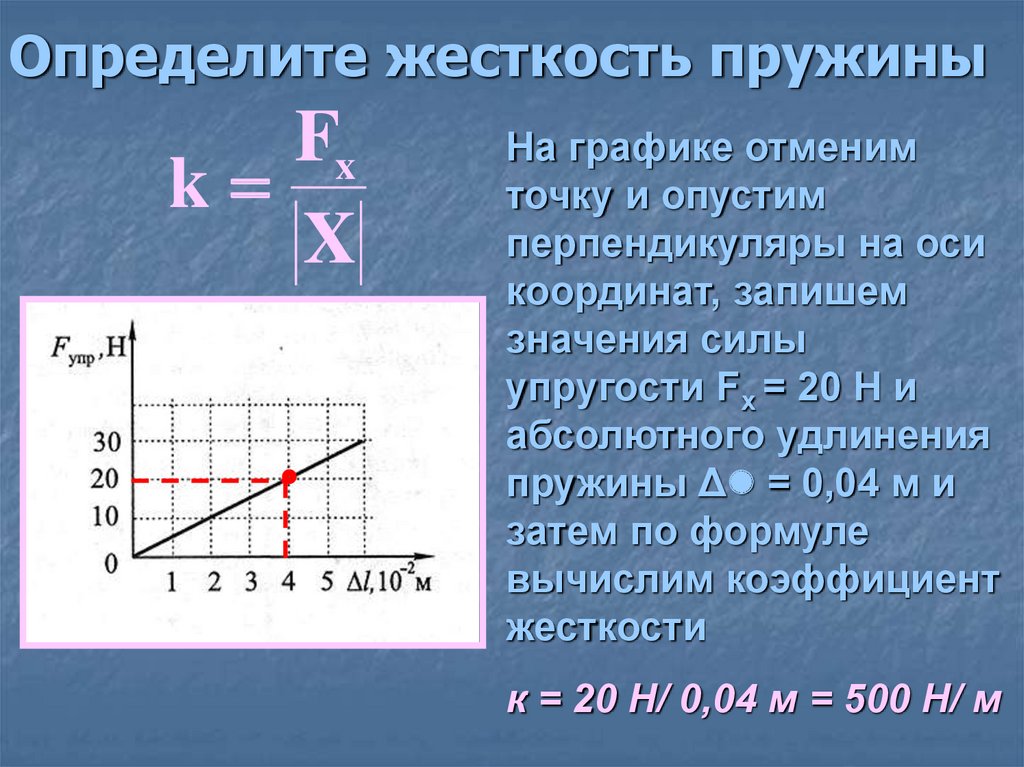

В специальных установках для испытания на усталость материала их сжимают и отпускают определенное количество циклов, отдельно проверяя поведение пружин при максимальной и минимальной нагрузке.

В чем измеряется жесткость

Жесткость пружины в системе СИ измеряется в ньютонах на метр, Н/м. Также встречается единица измерения ньютон на миллиметр, Н/мм. Численно жесткость равна величине силы, изменяющей размер пружины на метр длины.

Как обозначается

Коэффициент жесткости пружины обозначают буквой k.

Коэффициент жесткости пружины

Определение

Коэффициент жесткости — коэффициент, связывающий в законе Гука удлинение упругого тела и возникающую вследствие этого удлинения силу жесткости.

Применяется в механике твердого тела в разделе упругости.

Формула расчета через массу и длину

Используя закон Гука, коэффициент жесткости можно вычислить по формуле:

\(k\;=\;\frac Fx\)

Чтобы выяснить силу тяжести, воздействующую на пружину, нужно воспользоваться формулой:

\(F\;=\;m\;\times\;g\)

где m — масса подвешенного на пружине тела, а g — величина свободного ускорения, равная 9,8.

Чтобы найти х, нужно дважды измерить длину пружины и вычислить разницу между этими двумя значениями.

При соединении нескольких пружин общая жесткость системы меняется. Коэффициенты каждой из пружин суммируются при параллельном соединении. При последовательном соединении общая жесткость вычисляется по формуле:

\(\frac1k\;=\;(\frac1{k_1}\;+\;\frac1{k_2}\;+\;…\;+\;\frac1{k_n})\)

Как можно измерить жесткость

Измерительные приборы

Приборы для испытания пружин на сжатие-растяжение контролируют приложенное усилие с помощью тензометрического датчика, а также изменение их длины, выводя показатели на дисплей. Без специального прибора измерить осевую жесткость можно, используя динамометр и линейку.

Существуют приборы и для измерения поперечной жесткости пружин. Для этого нужно измерить смещение нескольких точек пружины, определив расстояние и угол между ними.

Практическая задача

Самый простой способ измерить жесткость пружины — провести стандартный школьный опыт со штативом и подвешенными на пружине грузиками.

Для измерения осевой жесткости спиральной пружины используют:

• штатив, на котором закрепляют пружину;
• крючок, который крепят на свободный ее конец;
• грузики с известной массой, которые подвешивают на свободный конец пружины;
• линейку, чтобы измерить длину пружины с грузом и без груза.

Проведя несколько измерений с грузиками разной массы и вычислив силу тяжести, воздействовавшую на пружину в каждом из них, можно построить график зависимости длины пружины от приложенного усилия и узнать среднее значение коэффициента жесткости.

Альтернативные способы определения жесткости

Жесткость пружины можно определить и через период ее колебания, воспользовавшись формулой:

\(Т\;=\;2\mathrm\pi\sqrt{\frac{\mathrm m}{\mathrm k}}\)

Или через частоту колебаний по формуле:

\(\omega=\;\sqrt{\frac{\mathrm k}{\mathrm m}}\)

Проводя опыт с пружиной, закрепленной на штативе, и грузиками с известной массой, можно не измерять длину пружины, а привести ее в колебательное движение и сосчитать количество колебаний в период времени.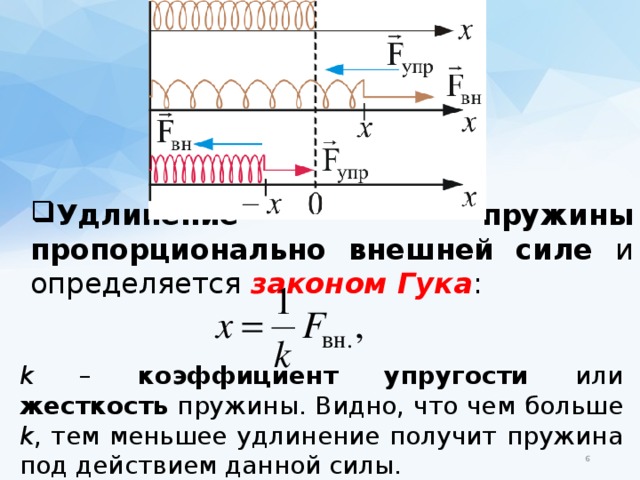

3\;\times\;25}\)

\(k = 100 \frac Нм\)

Жесткость при деформации кручения существенно отличается от жесткости сжатия-растяжения. Предел прочности при кручении у любого материала будет меньше, чем предел прочности при сжатии-растяжении или изгибе. Торсионная жесткость, также называемая крутильной, в системе СИ измеряется в ньютон-метрах на радиан, сокращенно Н-м/рад. Ее можно определить по формуле:

\(k\;=\;\frac M\alpha\)

где \(М\) — крутящий момент, приложенный к телу, а \(\alpha\) — угол закручивания тела по оси приложения крутящего момента.

Насколько полезной была для вас статья?

Рейтинг: 3.80 (Голосов: 5)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Лабораторная работа № 2 «Измерение жесткости пружины»

Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести

уравновешивающей силу упругости на основе закона Гука:

В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F_упр от модуля удлинения |x|. При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле

Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины k_ср.

Результат измерения обычно записывается в виде выражения k = = k_cp±Δk, где Δk — наибольшая абсолютная погрешность измерения. Из курса алгебры (VII класс) известно, что относительная погрешность (ε_k) равна отношению абсолютной погрешности Δk к значению величины k:

откуда Δk — ε_kk. Существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. В данной работе

Поэтому

Средства измерения: 1) набор грузов, масса каждого равна m₀ = 0,100 кг, а погрешность Δm₀ = 0,002 кг; 2) линейка с миллиметровыми делениями.

Материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.

Порядок выполнения работы

1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком — рис. 176).

2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.

3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.

4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.

5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. По результатам измерений заполните таблицу:

Номер опыта	m, кг	mg1, Н	|х|, м

6. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k_cp.

7. Рассчитайте наибольшую относительную погрешность, с которой найдено значение k_ср (из опыта с одним грузом). В формуле (1)

так как погрешность при измерении удлинения Δx=1 мм, то

8. Найдите

и запишите ответ в виде:

¹ Принять g≈10 м/с².

Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».

Закон Гука

Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:

где F – приложенная к пружине сила, а х – изменение длины пружины под ее действием. Средства измерения: набор грузов, масса каждого равна m₀ = (0,1±0,002) кг.

Линейка с миллиметровыми делениями (Δх = ±0,5 мм). Порядок выполнения работы описан в учебнике и комментариев не требует.

№ опыта	масса, кг		удлинение |х|,	К, Н/м
			м
1	0,1	1	0,036	27,78
2	0,2	2	0,074	27,03

3	0,3	3	0,112	26,79
4	0,4	4	0,155	25,81

* Ускорение свободного падения примем равным 10 м/с².

Вычисления:

Вычисление погрешности измерения:

ε_х максимально когда х – наименьшее, т.е., в нашем случае, для опыта с одним грузом

Можно записать результат измерений как:

или округляя:

т.к. в нашем случае отклонения вычисленных R₁; R₂; R₃; R₄ от R_ср велики из-за разности условий опытов принимаем

Источник:

Решебник по физике за 9 класс (И.К.Кикоин, А.К.Кикоин, 1999 год),
задача №2
к главе «ЛАБОРАТОРНЫЕ РАБОТЫ».

Все задачи

← Лабораторная работа № 1 «Измерение ускорения тела при равноускоренном движении»

Лабораторная работа № 3 «Измерение коэффициента трения скольжения» →

Что такое пружинная постоянная?

Постоянная пружины — это математический параметр, присутствующий в законе Гука , математическом законе, описывающем накопленную потенциальную энергию свернутой или растянутой пружины. Закон Гука, названный в честь английского естествоиспытателя Роберта Гука, который впервые сформулировал этот принцип, гласит, что расстояние, на которое пружина растягивается или сжимается, прямо пропорционально приложенной силе. Закон Гука может быть выражен как:

F _с = -kx

Где F _с   – требуемая сила, а x – расстояние. Постоянная пружины, записанная как k в уравнении, может рассматриваться как мера того, насколько трудно растянуть пружину. Константа пружины говорит вам, какое усилие пружина оказывает на единицу расстояния от состояния равновесия пружины (состояния, в котором она не сжимается и не растягивается). Следовательно, постоянную пружины можно рассматривать как меру жесткости пружины: какую силу нужно приложить, чтобы растянуть или сжать пружину и вывести ее из равновесия. Единица жесткости пружины k  –  ньютона на метр (Н/м).

Предположим, что сила 1000 Н удлиняет покоящуюся пружину на 3 метра. Какова жесткость пружины в этом случае? Постоянную пружины можно определить с помощью простого алгебраического анализа:

1000 Н = -k(3 м)

1000 Н/3 м = -k

-k = 333,33 Н/м

k= -333,33 Н/м

То есть , пружина, растянутая на 3 метра при приложении силы 1000 Н, имеет значение постоянной пружины -333,33 Н/м. Это значение в основном означает, что для перемещения такой пружины на расстояние 1 метр требуется 333,33 ньютона. Значение отрицательное, потому что сила, действующая на пружину, направлена ​​в противоположную сторону от внешней силы, растягивающей пружину.

Точное значение жесткости пружины зависит от конкретной пружины. Очень гибкие пружины будут иметь небольшую жесткость и легко растягиваться или сжиматься, в то время как толстые тяжелые пружины будут иметь гораздо более высокую жесткость пружины, и их будет труднее растягивать или сжимать. В дополнение к фактическим пружинам закон Гука применим (до некоторой степени) в большинстве случаев, когда упругое тело деформируется под действием некоторой силы: дергание гитарной струны, ветер, дующий и сгибающий высокие здания, и засыпка упругой вечеринки. воздушный шар.

Наглядное представление закона Гука: расширение пропорционально силе. Предоставлено: Svjo через WikiCommons CC BY-SA 3.0

Простые примеры пружинной константы в действии

Допустим, у нас есть блок, прикрепленный к пружине, ориентированной горизонтально, и пружина находится в состоянии покоя. В этом положении приложенная сила равна 0, а смещение равно 0. Теперь предположим, что мы прикладываем некоторую силу F, чтобы сжать пружину на расстояние ∆x, а затем вернуть пружину обратно в равновесие. Теперь предположим, что мы прикладываем такое же усилие F, чтобы растянуть пружину на то же расстояние ∆x. Закон Гука говорит нам, что зависимость между смещением пружины Δx и приложением силы F при сжатии и растяжении может быть выражена как:

|Ф| = к|Δх|

где k — жесткость пружины. Другими словами, жесткость пружины — это математическая величина, которая определяет взаимосвязь между приложенной силой и растяжением и сжатием пружины.

Приведем несколько реальных чисел к ранее описанному сценарию. Допустим, у нас есть пружина длиной 40 см, которая сжимается до 35 см под действием силы 3 Н. Какова жесткость такой пружины?

В этом случае Δx равно 5 см (0,05 м) и F равно 3 Н. Подстановка этих значений в наше уравнение дает нам:

|3| = к|0,05|

|3|/|0,05| = k

k = 60 Н/м.

То есть пружина имеет жесткость k, равную 60 Н/м. Чтобы сжать или растянуть пружину на один метр, потребуется усилие в 60 ньютонов.

Аналогичным образом работа с заданной жесткостью пружины может помочь вам предсказать, насколько пружина будет растягиваться или сжиматься под действием заданной силы. Допустим, у нас есть пружина с жесткостью 87 Н/м, и мы попытались растянуть ее с усилием 212 Н. Насколько растянется пружина?

И снова подстановка этих значений в наше уравнение дает нам:

|212| = 87 Н/м|Δx|

|212|/87 Н/м = Δx

Δx = 2,43 метра

Таким образом, приложение силы 212 ньютонов к пружине с жесткостью пружины 87 Н/м растянет пружину на 2,43 метра.

Наконец, если мы знаем постоянную пружины и желаемое смещение, мы можем определить, какое усилие нужно приложить к пружине, чтобы сместить ее на это расстояние. Скажем, у нас есть пружина, которую нужно сжать на 13 см (0,13 м), и известная жесткость пружины 57 Н/м. Сколько сил нам потребуется для выполнения этой задачи? Подстановка значений дает нам:

|Ф| = 57 Н/м|0,13|

F = 7,41 Н

Потребуется сила 7,41 ньютона, чтобы сместить пружину с жесткостью 57 Н/м на длину 13 см.

Закон Гука в системе с двумя пружинами

Допустим, у нас есть объект, прикрепленный к двум параллельным друг другу пружинам , каждая из которых имеет разную жесткость. Как мы должны моделировать комбинированные свойства двух пружин и как они влияют на растяжение и сжатие всей системы?

К счастью, для описания такой системы существует простое правило. В системе с двумя параллельными пружинами, каждая из которых имеет разную жесткость пружины, жесткость пружины всей системы представляет собой просто сумму индивидуальных жесткостей пружины.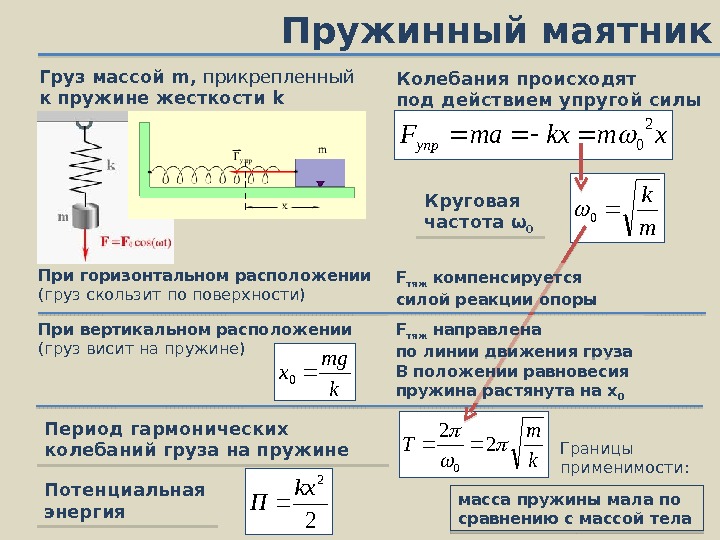 То есть в системе с 2 пружинами и 2 жесткостями k ₁ и k ₂ общая жесткость этой установки составляет всего

k _total = k ₁ + k ₂

Системы параллельных пружин могут быть математически представлены как одна пружина, жесткость которой равна сумме постоянных пружин.

Итак, у нас есть блок, прикрепленный к двум пружинам, установленным параллельно друг другу, первая с жесткостью пружины k ₁ = 100 Н/м, а вторая с константой k ₂ = 200 Н/м. Какая сила потребуется, чтобы сместить всю пружинную систему на 5 см?

Поскольку мы знаем константы отдельных пружин, мы можем просто сложить два значения вместе, чтобы получить константу для всей системы. Подстановка этих значений в наше уравнение дает:

|F| = (к ₁ +k ₂ )(Δx)

|F| = (100 Н/м + 200 Н/м)(0,05 м)

|F| = (300 Н/м)(0,05 м) =  15 Н

Таким образом, для смещения всей пружинной системы на 5 см потребуется сила 15 ньютонов. Линейный характер взаимосвязи между силой и сжатием/растяжением позволяет нам комбинировать свойства двух пружин для моделирования поведения всей системы из двух пружин.

Ограничения закона Гука

Закон Гука является аппроксимацией первого порядка поведения упругих материалов и применим не во всех областях. Закон Гука работает только для определенных диапазонов растяжения/сжатия, потому что существует максимальное расстояние, на которое эластичный материал может быть растянут или сжат, прежде чем он окончательно деформируется. Таким образом, закон Гука применим к относительно небольшому масштабу сил. Несмотря на это ограничение, закон Гука чрезвычайно полезен для инженеров и лежит в основе дисциплин, изучающих подобные пружинам явления, таких как сейсмология и акустика.

Закон Гука применим только для определенных степеней растяжения/сжатия. Предоставлено: «Закон Гука для пружин» Svjo через WikiCommons CC BY-SA 3.0.

В более общем случае сжатия/растяжения упругих тел математическая форма закона Гука точна, но его конкретные параметры могут быть неточны. В более сложных системах напряжения и деформации имеют независимые компоненты, поэтому было бы неправильно представлять их одним действительным числом, а тензором , который отображает несколько векторов в одну точку материала.

Физическое значение жесткости пружины

Все эти уравнения хороши, но что именно означает жесткость пружины в контексте физики? Другие параметры закона Гука, такие как сила и смещение, явно относятся к какой-то физической вещи (силе) или свойству (смещению), так к какому объекту или свойству относится упругая постоянная?

Можно думать об этом так: жесткость пружины относится к физическому свойству пружины, в частности к силе пружины сам проявляет себя в ответ на сжатие или растяжение. Согласно третьему закону динамики Ньютона, каждое действие имеет равное и противоположное противодействие. Таким образом, когда вы тянете за пружину, она оттягивается назад с равной силой. Когда вы нажимаете на пружину, она отталкивается с такой же силой. Тогда постоянная пружины является просто мерой отношения между этой приложенной силой и расстоянием, на которое перемещается пружина; количество силы, действующей на пружину на единицу смещения.

В качестве альтернативы, можно рассматривать константу пружины как меру того, сколько потенциальной энергии сжатая или растянутая пружина накопила в своих витках. Сжатие или растяжение пружины за пределы ее точки равновесия создает напряжение в материалах пружины, напряжение, которое математически представляется как сила, направленная в направлении, противоположном направлению толкания или вытягивания. Когда пружина освобождается, эта накопленная энергия преобразуется в кинетическую энергию, и пружина возвращается в свое равновесное состояние. Таким образом, закон Гука можно рассматривать как частный случай более общих принципов, регулирующих связь между кинетической и потенциальной энергиями.

Spring Constant – Введение, определение, формула и решенные проблемы

Дата последнего обновления: 21 апр 2023

•

Всего просмотров: 307,5 ​​тыс.

•

Просмотров сегодня: 4,76 тыс. М есть действительно интригующий тип движения. Он постоянно применяется в колебательном движении объектов. Пружины вообще имеют ШМ. Пружины имеют свои собственные «постоянные пружины», которые определяют их жесткость. Закон Гука — печально известный закон, который объясняет SHM и дает формулу для силы, приложенной с использованием жесткости пружины.

Например, спросите, не постучится ли к вам в дверь группа автомобильных дизайнеров и не поможет ли разработать систему подвески. «Конечно, — говорите вы. Говорят, что автомобиль весит 1000 килограммов и требует использования четырех амортизаторов, каждый длиной 0,5 метра. Насколько сильными должны быть перья? Предполагая, что в этих амортизаторах используются пружины, каждый из них должен выдерживать вес не менее 250 кг:

 F = мг = (250 кг) (9,8 м/с ² ) = 2450 Н

Где F — сила, м — масса объекта, g ускорение свободного падения, 9. 8 м/с ² . Пружина в амортизаторе должна, как минимум, дать вам усилие в 2450 ньютонов при максимальном сжатии 0,5 метра. Что это означает, что жесткость пружины должна быть? Чтобы выяснить, как рассчитать жесткость пружины, мы должны вспомнить, что говорит закон Гука:

F = –kx

Теперь нам нужно переработать уравнение, чтобы мы вычисляли недостающую метрику, которая равна жесткость пружины, или k.

Пружины, используемые в амортизаторах, должны иметь жесткость не менее 4,900 ньютонов на метр.

Единицы жесткости пружины

Определение жесткости пружины связано с простыми гармоническими движениями и законом Гука. Итак, прежде чем мы попытаемся определить постоянную пружины и понять ее работу, нам нужно взглянуть на закон Гука. Согласно теории упругости, когда к пружине прикладывается нагрузка, она естественным образом растягивается пропорционально, пока приложенная нагрузка меньше предела упругости.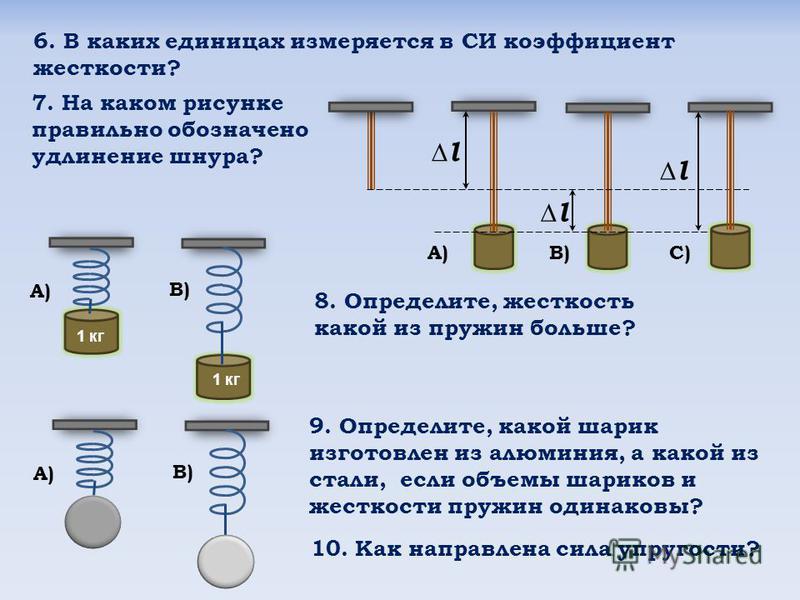 Теперь мы знаем, что когда к объекту прикладывается сила, он каким-то образом деформируется.

Рассмотрим пружину, когда мы прикладываем усилие к одной стороне пружины, она сжимается, так как пружина упругая. В это время пружина прилагает силу в направлении, противоположном приложенной силе, чтобы расшириться до своего первоначального размера. Поэтому, чтобы определить жесткость пружины, мы сначала определяем закон Гука. Закон Гука определяется как сила, необходимая пружине, чтобы вернуться к своему размеру, прямо пропорциональна расстоянию сжатия пружины.

(Изображение будет добавлено в ближайшее время)

На изображении показано движение пружины при приложении силы к одной стороне.

Определение постоянной пружины

Чтобы понять определение постоянной пружины, мы рассмотрим формулу закона Гука. Формула закона Гука также известна как формула жесткости пружины. Формула приведена ниже.

Формула	F = -kx
Единицы измерения пружины0210	Нм-1

Где F — восстанавливающая сила пружины, x — смещение пружины, а k — жесткость пружины. Единицы жесткости пружины указаны в ньютонах на метр.

Теперь, когда мы знаем, что k — это жесткость пружины, мы рассмотрим ее определение. Мы определяем жесткость пружины как жесткость пружины. Другими словами, когда смещение пружины составляет одну единицу, мы можем определить постоянную пружины как силу, приложенную для того, чтобы вызвать указанное смещение. Поэтому ясно, что чем жестче пружина, тем выше будет ее жесткость. 9{-2}}{L}]\]

k= – [MT-2]

Единица жесткости пружины выражается в ньютонах на метр (Н/м).

Решенные задачи

Вопрос 1) Пружина растянулась на 40 см, если к ней добавить груз массой 5 ​​кг. Найдите жесткость пружины.

Ответ 1) Дано,

Масса m = 5 кг,

Перемещение x = 40 см = 0,4 м

Чтобы найти постоянную пружины, сначала нужно найти силу, действующую на пружину.

Мы знаем, что F = m * x

Следовательно, F = 5 * 0,4

F = 2 Н

Нагрузка действует на пружину с силой 2 Н. Следовательно, пружина приложит равную и противоположную силу – 2 Н.

Теперь, подставляя значения в формулу жесткости пружины, получаем

k = -F/x

k = \[\frac{-2}{0,4}\]

k = 5 Н/м

Следовательно, жесткость пружины равна 5 Н/м

Вопрос 2) Рассмотрим пружину с жесткостью 14000 Н/м. К пружине приложена сила 3500 Н. Каким будет смещение пружины?

Ответ 2) Дано,

Сила F = 3500 Н,

Постоянная пружины k = 14000 Н/м,

Мы можем рассчитать смещение пружины, используя формулу постоянной пружины.

x= \[\frac{-F}{k}\]

Нагрузка действует на пружину с силой 3500 Н. Следовательно, пружина приложит равную и противоположную силу – 3500 Н.

Таким образом,

x = \[-(\frac{-3500}{14000})\]

x = 0,25 м

x = 25 см

Следовательно, пружина смещена на расстояние 25 см.