Жесткость пружин соединенных последовательно: Физика и математика для школьников

alexxlab | 13.01.1986 | 0 | Разное

Содержание

Закон Гука, сила упругости — определение, формулы

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Сила — это физическая векторная величина, которая является мерой действия одного тела на другое.

Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат действия этой силы.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой.

Запишитесь и участвуйте в розыгрыше 8 уроков

Деформация

Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил

Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.

На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу сил. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.

По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:

Деформация растяжения
Деформация сжатия
Деформация сдвига
Деформация при кручении
Деформация при изгибе

Сила упругости: Закон Гука

Давайте займемся баскетболом. Начнем набивать мяч о пол, он будет чудесно отскакивать. Этот удар можно назвать упругим. Если при ударе деформации не будет совсем, то он будет называться абсолютно упругим.

Если вы перепутали мяч и взяли пластилиновый, он деформируется при ударе и не оттолкнется от пола. Такой удар будет называться абсолютно неупругим.

Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не может вернуться в исходное состояние).

При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.

Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.

Какой буквой обозначается сила упругости?

Закон Гука

—сила упругости [Н]

k — коэффициент жесткости [Н/м]

х — изменение длины (деформация) [м]

Важно раз

Изменение длины может обозначаться по-разному в различных источниках.

Варианты обозначений: x, ∆x, ∆l.

Это равноценные обозначения — можно использовать любое удобное.

Важно два

Поскольку сила упругости всегда направлена против деформации (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.

Задачка

На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при равномерном (без ускорения) поднятии вверх рыбы весом 300 г?

Решение:

Сначала определим силу тяжести. Не забываем массу представить в единицах СИ – килограммах.

СИ — международная система единиц.

«Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».

m = 300 г = 0,3 кг

Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :

F = mg = 0,3*10 = 3 Н.

Вспомним закон Гука:

И выразим из него модуль удлинения лески:

Так как одна сила уравновешивает другую, мы можем их приравнять:

Подставим числа, жесткость лески при этом выражаем в ньютонах:

= 0,01 м = 1 см

Ответ: удлинение лески равно 1 см.

Учёба без слёз (бесплатный гайд для родителей)

Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.

Параллельное и последовательное соединение пружин

В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.

Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.

Последовательное соединение системы пружин

Последовательное соединение характерно наличием одной точки соединения пружин.

При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:

Коэффициент жесткости при последовательном соединении пружин

k — общая жесткость системы [Н/м]

k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м]

i — общее количество всех пружин, задействованных в системе [-]

Параллельное соединение системы пружин

Последовательное соединение характерно наличием двух точек соединения пружин.

В случае когда пружины соединены параллельно величина общего коэффициента жесткости системы будет увеличиваться. Формула для расчета будет выглядеть так:

Коэффициент жесткости при параллельном соединении пружин

k — общая жесткость системы [Н/м]

k₁, k₂, …, k_i — отдельные жесткости каждого элемента [Н/м]

i — общее количество всех пружин, задействованных в системе [-]

Задачка

Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?

Решение:

а) Рассмотрим параллельное соединение пружин.

При параллельном соединении пружин общая жесткость

k = k₁ + k₂ = 100 + 200 = 300 Н/м

б) Рассмотрим последовательное соединение пружин.

При последовательном соединении общая жесткость двух пружин

66,7 Н/м

Очень-очень важно!

Не забудь при расчете жесткости при последовательном соединении в конце перевернуть дробь.

График зависимости силы упругости от жесткости

Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.

Задачка 1

Определите по графику коэффициент жесткости тела.

Решение:

Из Закона Гука выразим коэффициент жесткости тела:

F = kx

Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.

Например, возьмем вот эту точку.

В ней удлинение равно 2 см, а сила упругости 2 Н.

Переведем сантиметры в метры:

2 см = 0,02 м

И подставим в формулу:

=100 Н/м

Ответ:жесткость пружины равна 100 Н/м

Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!

Задачка 2

На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра.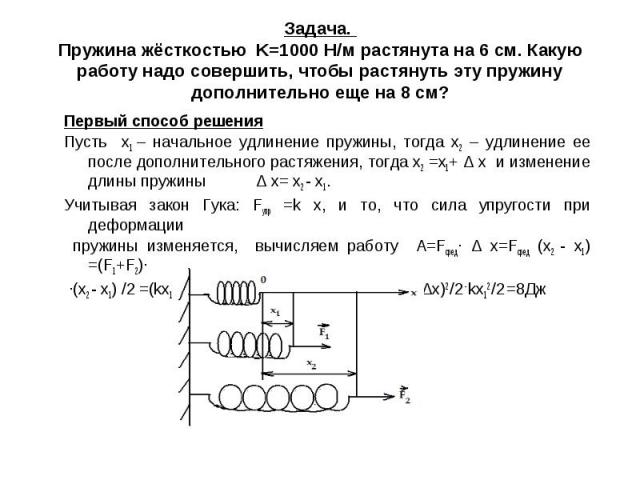

Сравнить жесткости проволок.

Решение:

Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.

Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.

Значит жесткость стальной проволоки больше.

Ответ: жесткость стальной проволоки больше медной.

Как найти жесткость пружин соединенных последовательно?

Содержание

– Как найти жесткость системы пружин?
– Какой формулой определяется коэффициент жесткости соединения из двух последовательно соединенных пружин?
– Какой формулой определяется коэффициент жесткости соединения из двух параллельных пружин?

– Как рассчитать емкость конденсатора при последовательном соединении?
– Как определить жесткость пружины по массе?
– В чем обозначается жесткость пружины?
– В чем измеряется жесткость?
– Почему при параллельном соединении пружин?
– Как рассчитать жесткость?
– Чем отличается последовательное соединение от параллельного?
– Что происходит при последовательном соединении конденсаторов?
– Чему равны IUR при последовательном соединении проводников?
– Что называется последовательным соединением конденсаторов?
– Как найти емкость конденсатора по схеме?
– Как рассчитывается электрическая емкость конденсатора?

Как найти жесткость системы пружин?

¯F=kΔl(1), где в коэффициент пропорциональности называется жесткостью пружины (коэффициентом упругости) k.

Жесткость (как свойство) – это характеристика упругих свойств тела, которое деформируют.

Какой формулой определяется коэффициент жесткости соединения из двух последовательно соединенных пружин?

Жесткость соединений пружин

При последовательном соединении N пружин жесткость соединения вычисляется при помощи формулы: 1k=1k1+1k2+⋯=N∑ i=11ki(2). Если пружины соединены параллельно, то результирующая жесткость равна: k=k1+k2+⋯+N∑i=1ki(3).

Какой формулой определяется коэффициент жесткости соединения из двух параллельных пружин?

Параллельное соединение системы пружин

В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так: k = k1 + k2 + … + ki.

Как рассчитать емкость конденсатора при последовательном соединении?

Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / (U1 + U2 + U3), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов.

Как определить жесткость пружины по массе?

В итоге этих экспериментов появилась такая формула: kx=mg, где k – некий постоянный для данной пружины коэффициент, x – изменение длины пружины, m – ее масса, а g – ускорение свободного падения (примерное значение – 9,8 м/с²).

В чем обозначается жесткость пружины?

Обозначается буквой k, иногда D или c.

В чем измеряется жесткость?

В системе СИ коэффициент механической жёсткости измеряется в ньютонах на метр (Н/м).

Почему при параллельном соединении пружин?

Довольно часто встречается и параллельное соединение пружин. В этом случае смещение тела, которому передается сила, равна деформации каждой из них. … Построенная схема указывает на то, что жесткость пружин при параллельном соединении остается неизменной, но общий показатель возрастает в два раза.

Как рассчитать жесткость?

Определение коэффициента жесткости растяжения

Измеряется длина пружины в вертикальном подвесе с одной свободной стороной изделия – L1;
Измеряется длина пружины с подвешенным грузом – L2. …
Вычисляется разница между последним и первым показателем длины – L;
Рассчитывается коэффициент упругости по формуле: k = F/L.

Чем отличается последовательное соединение от параллельного?

При последовательном соединении проводников сила тока во всех проводниках одинакова. При этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников. При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов.

Что происходит при последовательном соединении конденсаторов?

При последовательном соединении конденсаторов уменьшается общая емкость и увеличивается общее напряжение конденсаторов. А общее напряжение будет равняться сумме напряжений всех конденсаторов. Например: мы имеем три конденсатора по 30 мкФ x 100 В каждый.

Чему равны IUR при последовательном соединении проводников?

Проводники в электрических цепях могут соединяться последовательно и параллельно. При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова: I1 = I2 = I.

Что называется последовательным соединением конденсаторов?

Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).

Как найти емкость конденсатора по схеме?

По формуле С = t/3R, где t – время падения напряжения, вычисляем ёмкость конденсатора в фарадах, если единицы измерения сопротивление резистора выразили в омах, а время в секундах.

Как рассчитывается электрическая емкость конденсатора?

Его значение вычисляется по формуле: E=14πεε0qr2 E = 1 4 π ε ε 0 q r 2 , где q обозначают заряд внутренней сферы, r=R1+x r = R 1 + x – расстояние от центра сферы. Нахождение заряда предполагает применение определения емкости конденсатора С: q=CU q = C U .

Интересные материалы:

Какие фрукты называются цитрусовыми?
Какие глаголы называются личными?
Какие города меняли свои названия?
Какие города Поволжья меняли названия?
Какие языки называется родственными?
Какие языки называются родственными как возникают родственные языки?
Какие имена существительные называются нарицательными?
Какие источники и волны называются когерентными?
Какие контуры называются взаимно независимыми?
Какие крестьяне назывались Владельческие?

Сила упругости – формула, определение, таблица по теме

4.4

Средняя оценка: 4. 4

Всего получено оценок: 240.

4.4

Средняя оценка: 4.4

Всего получено оценок: 240.

Сила упругости всегда является результатом деформации тела. Данная сила всегда пытается вернуть деформированное тело в исходное положение. Что же такое сила упругости, и при каких условиях она возникает?

Общая характеристика силы упругости

Сила упругости возникает при деформации тел, например, при растяжении или сжатии пружины. Деформация – это изменение формы и размеров тела.

Рис. 1. Сила упругости при деформации пружины.

Если исчезнет деформация тела, то сила упругости тоже исчезнет

Причиной возникновения сил упругости являются силы притяжения и отталкивания между частицами (молекулами или атомами), из которых состоят все тела. Если слегка увеличить расстояние между частицами, то силы взаимодействия оказываются силами притяжения между ними. Если же расстояние между частицами немного уменьшить, они становятся силами отталкивания. Сила упругости, действующая на тело, связана с деформацией тела следующим образом:

$F упр=-kx$,

где F упр. – модуль силы упругости, х – удлинение тела (расстояние, на которое изменяется первоначальная длина тела), k – коэффициент пропорциональности, называемый жесткостью пружины, измеряемый в Н/м. Данная формула силы упругости служит выражением закона Гука. Определение закона Гука выражается следующим образом: сила упругости, возникающая при деформации тела, пропорциональна удлинению тела и направлена противоположно перемещению частиц тела относительно других частиц при деформации.

Рис. 2. Формула закон Гука.

Прямую пропорциональную зависимость между силой упругости и удлинением используют в динамометрах – приборах для измерения силы. Силы упругости работают в технике и природе: в часовых механизмах, в амортизаторах на транспорте, в канатах и тросах, в человеческих костях и мышцах.

Растяжение пружины

Рассмотрим подробнее деформацию растяжения на примере пружины.

Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина $L_{0}$ пружины.

Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение

Подвесим теперь к пружине груз. Пружина будет иметь длину $L$, указанную на рисунке справа.

Сравним длину нагруженной пружины с длиной свободно висящей пружины.

\[ \large L_{0} + \Delta L = L \]

Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину $L_{0}$.

\[ \large \boxed{ \Delta L = L — L_{0} }\]

$ L_{0} \left(\text{м} \right) $ – начальная длина пружины;

$ L \left(\text{м} \right) $ – конечная длина растянутой пружины;

$ \Delta L \left(\text{м} \right) $ – кусочек длины, на который растянули пружину;

Величину $ \Delta L $ называют удлинением пружины.

Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.

Примечание: Отношение – это дробь. Относительное – значит, дробное.

\[ \large \boxed{ \frac{\Delta L }{ L_{0}} = \frac{ L — L_{0}}{L_{0} } = \varepsilon } \]

$ \varepsilon $ – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.

Свойства силы упругости

К силам упругости относятся сила реакции опоры и веса тела. Сила реакции (N) со стороны опоры на тело возникает, когда тело кладут на какую-нибудь поверхность (опору).

Если тело подвешивают на нити, то эта же самая сила называется силой натяжения нити (Т).

Силы упругости имеет ряд особенностей:

возникают при деформации
возникают одновременно у двух тел
перпендикулярны поверхности
противоположны по направлению смещению.

Вес тела (P) – это сила, с которой тело действует на горизонтальную опору или вертикальный подвес, вследствие своего притяжения к Земле.

Вес тела обозначается буквой P и измеряется в Ньютонах.

Если опора тела горизонтальна и неподвижна, то вес такого тела численно равен силе тяжести, действующей на это тело и равен P=mg

Если же тело движется вверх с ускорением а, то вес этого тела больше веса покоящегося тела и равен $P=(g+a)m$

А если же тело с ускорением а движется вниз, то его вес $P =(g-a)m$

При равенстве ускорения тела и ускорения свободного падения вес тела равен нулю. Это состояние невесомости.

Рис. 3. Таблица сравнение силы упругости с другими силами.

Соединяем две одинаковые пружины

В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.

Параллельное соединение пружин

На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину $\Delta L$. Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины

Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом $mg$.

Одна пружина:

\[ \large k_{1} \cdot \Delta L = m \cdot g \]

Две параллельные пружины:

\[ \large k_{\text{параллел}} \cdot \Delta L \cdot \frac{1}{2}= m \cdot g \]

Так как правые части уравнений совпадают, левые части тоже будут равны:

\[ \large k_{\text{параллел}} \cdot \Delta L \cdot \frac{1}{2}= k_{1} \cdot \Delta L \]

Обе части уравнения содержат величину $\Delta L $. Разделим обе части уравнения на нее:

\[ \large k_{\text{параллел}} \cdot \frac{1}{2}= k_{1} \]

Умножим обе части полученного уравнения на число 2:

\[ \large \boxed{ k_{\text{параллел}} = 2k_{1} } \]

Коэффициент жесткости $k_{\text{параллел}}$ двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной

Последовательное соединение пружин

Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину $\Delta L$. Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.

Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.

На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину $\Delta L$.

Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины

Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом $mg$.

Одна пружина:

\[ \large k_{1} \cdot \Delta L = m \cdot g \]

Две последовательные пружины:

\[ \large k_{\text{послед}} \cdot \Delta L \cdot 2 = m \cdot g \]

Так как правые части уравнений совпадают, левые части тоже будут равны:

\[ \large k_{\text{послед}} \cdot \Delta L \cdot 2 = k_{1} \cdot \Delta L \]

Обе части уравнения содержат величину $\Delta L $. Разделим обе части уравнения на нее:

\[ \large k_{\text{послед}} \cdot 2 = k_{1} \]

Разделим обе части полученного уравнения на число 2:

\[ \large \boxed{ k_{\text{послед}} = \frac{k_{1}}{2} } \]

Коэффициент жесткости $k_{\text{послед}}$ двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной

Потенциальная энергия сжатой или растянутой пружины

Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину $\Delta L $ обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. {2} }\]

$ E_{p} \left( \text{Дж} \right)$ – потенциальная энергия сжатой или растянутой пружины;

$ \Delta L \left(\text{м} \right) $ – удлинение пружины;

$ \displaystyle k \left(\frac{H}{\text{м}} \right) $ – коэффициент жесткости (упругости) пружины.

Таблица

Большинство материалов имеют значение E очень высокого порядка, поэтому они записываются при помощи «гигапаскалей» ([ГПа]; ).

Материал	Модуль Юнга E, [ГПа]
Алмаз	1220
Алюминий	69
Дерево	10
Кадмий	50
Латунь	97
Медь	110
Никель	207
Резина	0,9 (≈ 1 МПа, мегапаскаль)
Сталь	200
Титан	107

Принципы деформации

Когда сила воздействует на материал, он растягивается или сжимается в ответ. В механике сила, приложенная на единицу площади, является тем, что называется напряжением. Степень растяжения и сжатия, возникающая, когда материал реагирует на напряжение, называется деформацией. Напряжение измеряется отношением разницы в длине к исходной длине в направлении напряжения.

Каждый материал по-разному реагирует на стресс, и детали этой реакции важны для инженеров, выбирающих материалы для своих конструкций и машин, которые должны вести себя предсказуемо при ожидаемых напряжениях.

Для большинства материалов нагрузка, испытываемая при приложении небольшого напряжения, зависит от плотности химических связей. То же самое относится к жёсткости материала, которая напрямую связана с его химической структурой.

Происходящее при снятии напряжения зависит от того, насколько далеко перемещены атомы.

В целом существует два типа деформации:

Упругая. После снятия напряжения материал возвращается к размеру, который был до приложения нагрузки. Деформация обратима, непостоянна.
Пластическая. Напряжение настолько велико, что при снятии нагрузки материал не возвращается к своему предыдущему размеру. Минимальное значение напряжения, вызывающего пластическую деформацию, известно как предел упругости материала.

Любая пружина должна быть спроектирована точно таким образом, чтобы она испытывала только упругую деформацию при установке в машину при нормальной эксплуатации.

Помощь студентам в учёбе от Людмилы Фирмаль

Здравствуйте!

Я, Людмила Анатольевна Фирмаль, бывший преподаватель математического факультета Дальневосточного государственного физико-технического института со стажем работы более 17 лет. На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.

Срок выполнения разный: возможно онлайн (сразу пишите и сразу помогаю), а если у Вас что-то сложное – то от двух до пяти дней.

Для качественного оформления работы обязательно нужны методические указания и, желательно, лекции. Также я провожу онлайн-занятия и занятия в аудитории для студентов, чтобы дать им более качественные знания.

Моё видео:


Вам нужно написать сообщение в Telegram . После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
Сколько может стоить заказ?Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения заказа?Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказ?Сначала пришлите задание, я оценю, после вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Какие гарантии и вы исправляете ошибки?В течение 1 года с момента получения Вами заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Качественно сфотографируйте задание, или если у вас файлы, то прикрепите методички, лекции, примеры решения, и в сообщении напишите дополнительные пояснения, для того, чтобы я сразу поняла, что требуется и не уточняла у вас. Присланное качественное задание моментально изучается и оценивается.
Теперь напишите мне в Telegram или почту  и прикрепите задания, методички и лекции с примерами решения, и укажите сроки выполнения. Я и моя команда изучим внимательно задание и сообщим цену.
Если цена Вас устроит, то я вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.
После выполнения отправлю Вам заказ в чат, если у Вас будут вопросы по заказу – подробно объясню. Гарантия 1 год. В течении 1 года я и моя команда исправим любые ошибки в заказе.



<noscript><img loading='lazy' src='/800/600/http/generator98.ru/wp-content/uploads/koefficient-zhestkosti-pri-posledovatelnom-soedinenii-pruzhin20.png' /></noscript> youtube.com/embed/FTtp-vAv3lI&#8221; frameborder=&#8221;0&#8243; allow=&#8221;accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture&#8221; allowfullscreen=&#8221;&#8221;/>





<noscript><img loading='lazy' src='/800/600/http/xn----7sbapcyiojdlglffl.xn--p1ai/img-file2/img-43052622897.jpg' /></noscript> youtube.com/embed/7LD4euDcivY&#8221; frameborder=&#8221;0&#8243; allow=&#8221;accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture&#8221; allowfullscreen=&#8221;&#8221;/>




<noscript><img loading='lazy' src='/800/600/http/generator98.ru/wp-content/uploads/koefficient-zhestkosti-pri-posledovatelnom-soedinenii-pruzhin21.jpg' /></noscript> youtube.com/embed/ZfNUaigadEY&#8221; frameborder=&#8221;0&#8243; allow=&#8221;accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture&#8221; allowfullscreen=&#8221;&#8221;/>
Можете смело обращаться к нам, мы вас не подведем. Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.
В заключение хочу сказать: если Вы выберете меня для помощи на учебно-образовательном пути, у вас останутся только приятные впечатления от работы и от полученного результата!
 Жду ваших заказов!
 С уважением
Пользовательское соглашение
Политика конфиденциальности

 Калькулятор комбинированной жесткости трех пружин, соединенных последовательно 
 ✖Жесткость 1-й пружины — это сила на единицу длины, необходимая для отклонения первой пружины.ⓘ Жесткость 1-й пружины [K ₁ ]
9 09 0 Килоньютон на метрКилоньютон на миллиметрМиллиньютон на метрМиллиньютон на миллиметрНьютон на метрНьютон на миллиметрФунт-сила на дюйм  +10%
 -10%
 ✖Жесткость 2-й пружины — это сила на единицу длины, необходимая для отклонения второй пружины. ⓘ Жесткость 2-й пружины [K ₂ ]  Килоньютон на метрМиллиньютон на миллиньютон на миллиньютон на миллиметр Миллиметр-фунт-сила на дюйм  +10%
 -10%
0007 3  ]  Kilonewton per MeterKilonewton per MillimeterMillinewton per MeterMillinewton per MillimeterNewton per MeterNewton per MillimeterPound-Force per Inch  +10%
 -10%
 ✖Эквивалентная жесткость пружины — это индивидуальная жесткость пружины, полученная путем комбинирования различных жесткостей пружины.ⓘ Комбинированная жесткость трех пружин, соединенных последовательно [K _экв. ]  Килоньютон на метрКилоньютон на миллиметрМиллиньютон на метрМиллиньютон на миллиметрНьютон на метрНьютон на миллиметрФунт-сила на дюйм  ⎘ Копировать
 👎
 Формула
 Перезагрузить
 👍
 Суммарная жесткость трех пружин, соединенных последовательно Решение 
 ШАГ 0: Итоги предварительного расчета
 ШАГ 1: Преобразование входных данных в базовые единицы
 Жесткость 1-й пружины: 15 ньютон на миллиметр –> 15000 ньютон на метр (проверьте преобразование здесь) 
 Жесткость 2-й пружины: 12 ньютон на миллиметр –> 12000 Ньютон на метр (проверьте преобразование здесь) 
 Жесткость третьей пружины: 30 ньютон на миллиметр –> 30000 ньютон на метр (проверьте преобразование здесь) 
 ШАГ 2: Оцените формулу
 ШАГ 3: Преобразуйте результат в единицу измерения
 5454,54545454546 Ньютон на метр –> 5,45454545454546 Ньютон на миллиметр (Проверьте преобразование здесь)
< 
 Калькуляторы 4 последовательных и параллельных соединений Суммарная жесткость трех пружин, соединенных последовательно Формула 
 Эквивалентная жесткость пружины = жесткость 1-й пружины * жесткость 2-й пружины * жесткость 3-й пружины/(жесткость 1-й пружины * жесткость 2-й пружины + жесткость 2-й пружины * жесткость 3-й пружины + жесткость 3-й пружины * жесткость 1-й пружины) 
 K _{Уравнение} = K ₁ *K ₂ *K ₃ /(K ₁ *K ₂ +K ₂ *K ₃ +K ₃ *K ₁ )
 Дайте определение механической пружине? 
 Пружина из металлической проволоки, функционирующая в пружинном механизме, который сжимает, растягивает, вращает, скользит, тянет и оказывает усилие при приложении равной или большей силы. Пружинный механизм может оказывать давление, вращательную силу или тяговое усилие различными способами.
 Как рассчитать совокупную жесткость трех пружин, соединенных последовательно? 
 Калькулятор комбинированной жесткости трех пружин, соединенных последовательно, использует эквивалентную жесткость пружины  = жесткость 1-й пружины * жесткость 2-й пружины * жесткость 3-й пружины/(жесткость 1-й пружины * жесткость 2-й пружины + жесткость 2-й пружины * жесткость 3-й пружины +Жесткость 3-й пружины*Жесткость 1-й пружины)  для расчета эквивалентной жесткости пружины. Формула комбинированной жесткости трех пружин, соединенных последовательно, определяется как мера сопротивления деформации упругого тела. Эквивалентная жесткость пружины обозначается цифрой 9.0143 K _экв.  символ.
 Как рассчитать комбинированную жесткость трех последовательно соединенных пружин с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для комбинированной жесткости трех пружин, соединенных последовательно, введите жесткость 1-й пружины  (K ₁ )  , жесткость 2-й пружины  (K ₂ )  и жесткость 3-й пружины  (k ₃ )  и нажмите кнопку расчета. Вот как можно объяснить расчет комбинированной жесткости трех пружин, соединенных последовательно, с заданными входными значениями ->  5.454545 = 15000*12000*30000/(15000*12000+12000*30000+30000*15000)  .
 Часто задаваемые вопросы 
 Что такое комбинированная жесткость трех пружин, соединенных последовательно?
 Формула комбинированной жесткости трех пружин, соединенных последовательно, определяется как мера сопротивления деформации упругого тела и представляется как  K _eq = K ₁ *K ₂ *k ₃ /(К ₁ *K ₂ +K ₂ *k ₃ +k ₃ *K ₁ )  или  Эквивалентная жесткость пружины = Жесткость пружины 3*1й 2й пружины*Жесткость /(Жесткость 1-й пружины*Жесткость 2-й пружины+Жесткость 2-й пружины*Жесткость 3-й пружины+Жесткость 3-й пружины*Жесткость 1-й пружины)  . Жесткость 1-й пружины — это сила на единицу длины, необходимая для отклонения первой пружины, жесткость 2-й пружины — это сила на единицу длины, необходимая для отклонения второй пружины, а жесткость 3-й пружины — это сила на единицу длины, необходимая для отклонения третьей пружины. весна.
 Как рассчитать совокупную жесткость трех пружин, соединенных последовательно?
 Формула комбинированной жесткости трех пружин, соединенных последовательно, определяется как мера сопротивления деформации упругого тела, рассчитанная по формуле  Эквивалентная жесткость пружины = жесткость 1-й пружины * жесткость 2-й пружины * жесткость 3-й пружины/ (Жесткость 1-й пружины*Жесткость 2-й пружины+Жесткость 2-й пружины*Жесткость 3-й пружины+Жесткость 3-й пружины*Жесткость 1-й пружины)  . Для расчета совокупной жесткости трех пружин, соединенных последовательно, вам потребуется жесткость 1-й пружины  (K ₁ )  , жесткость 2-й пружины  (K ₂ )  и жесткость 3-й пружины  (k ₃
) 
  . С помощью нашего инструмента вам нужно ввести соответствующее значение для жесткости 1-й пружины, жесткости 2-й пружины и жесткости 3-й пружины и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
 Сколько существует способов расчета эквивалентной жесткости пружины?
 В этой формуле эквивалентная жесткость пружины использует жесткость 1-й пружины, жесткость 2-й пружины и жесткость 3-й пружины. Мы можем использовать 3 других способа (способов) для расчета того же самого, которые заключаются в следующем:
 Эквивалентная жесткость пружины = жесткость 1-й пружины * жесткость 2-й пружины / (жесткость 1-й пружины + жесткость 2-й пружины)
 Эквивалентная жесткость пружины = жесткость 1-й пружины + жесткость 2-й пружины
 Эквивалентная жесткость пружины = жесткость 1-й пружины + жесткость 2-й пружины + жесткость 3-й пружины
 Доля
 Скопировано!
 Энергия, накопленная в последовательных пружинах, по сравнению с энергией, запасенной в параллельных пружинах 
 Заданный вопрос  5 лет, 8 месяцев назад 
 Изменено
 4 года, 7 месяцев назад
 Просмотрено
 14 тысяч раз
 $\begingroup$
 92$.
 Итак, представьте, что у нас есть две одинаковые пружины с жесткостью каждой ($k$) 85 Нм ^-1
 В одной системе они параллельны, выдерживая нагрузку 15 Н. В другой они находятся в серия, также поддерживающая 15 Н.
 Таким образом, общая жесткость пружины в параллельной системе равна $2k$, что составляет 170 Нм ^-1 .
 Суммарная жесткость пружины в последовательной системе равна $\frac{k}{2}$, что составляет 42,5 Нм ^-1 .
 Используя приведенное выше уравнение энергии, энергия, запасенная в пружинах, различна для обеих систем, поскольку $k$ отличается, а значит, и $\Delta l$.
 Я понимаю это с математической точки зрения, но с точки зрения передачи энергии я не понимаю, почему упругая потенциальная энергия меняется. Некоторая часть энергии, конечно, теряется в виде тепловой энергии, но почему обе системы не теряют одинаковое количество энергии или даже не приобретают одинаковое количество энергии?
 потенциальная энергия
 пружина
 упругость
 $\endgroup$
 2
 $\begingroup$
 92$
 Используя приведенное выше уравнение энергии, энергия, запасенная в пружинах, различна для обеих систем, поскольку $k$ различно, а значит, и $\Delta l$.
 Если бы $k$ было другим, тогда да: запасенная энергия тоже должна быть другой.
 Если $\Delta l$ было другим, то да: запасенная энергия тоже должна быть другой.
 Если  и  разные, то вы не знаете. Тогда вы не можете заключить, что энергия другая. $k$ уменьшится вдвое, а что, если $\Delta l$ будет в $\sqrt 2$ больше? Затем сохраняется та же энергия.
  Параллельные пружины  помогают друг другу выдерживать вес. Вместе они могут в сумме оказывать  двойных  силы. Следовательно, вы можете рассматривать эту двухпружинную систему как  одну  эквивалентную пружину с  двойной  жесткостью (поскольку сила пружины $F=kx$ удваивается с двойной жесткостью $k$, если вы сожмете ее так же сильно):
$$k_{параллельно}=2k$$
Поскольку каждый из них несет половину нагрузки, каждый из них сжимается только на 90 293 наполовину 90 294 больше, чем мог бы быть в одиночку:
$$\Delta l_{parallel}=\frac12\Delta l$$
  Пружины серии  не помогают друг другу. Если вы поместите пружину на жесткий стол или на другую пружину, не имеет значения, так как вы смотрите на конечную ситуацию (после того, как будет выполнено сжатие). Следовательно, верхняя пружина несет всю нагрузку,  и  вторая также несет всю нагрузку (плюс вес верхней пружины, но обычно предполагается, что масса меньше). Каждый сжат $\Delta l$, поэтому в сумме эквивалентное сжатие составляет  двойных 9.2=2E_{одна\;пружина}$
 Да, энергии действительно разные. Поскольку смещения   различны – вы накапливаете энергию в пружине, сжимая / растягивая ее, поэтому различное сжатие / растяжение означает различную накопленную энергию.
 $\endgroup$
 4
 $\begingroup$
 Постараюсь максимально подробно ответить на вопрос.
Энергия, запасенная в пружине, НЕ равна $\frac{k\Delta l}{2}$.
Пружина моделируется как источник простого гармонического движения. 2}{2}\\
$$
Разница между последовательной системой и параллельной системой заключается в смещении каждой пружины. Предположим, у вас есть система из двух последовательно соединенных пружин $k_1$ и $k_2$. Тогда смещение каждой пружины до силы $F$ будет равно $\frac{F}{k_1}$ и $\frac{F}{k_2}$ соответственно, а полное смещение, являющееся суммой двух смещений, моделируется как $F/K_{eff}$. Вот откуда вы получаете свою версию $k_{eff}$ в серийной системе.
$$\frac{F}{k_1}+\frac{F}{k_2}=\frac{F}{k_{eff}}$$
Теперь для параллельной системы смещение, через которое проходит каждая пружина, чтобы уравновесить силу, ОДИНАКОВО. Итак, уравнение выглядит так, как показано ниже.
$$k_1x+k_2x=k_{eff}x$$.
Теперь, поскольку $K_{eff_p}$ и $k_{eff_s}$ (параллельные и последовательные пружинные константы для двух пружин) различны. Перемещение, необходимое для уравновешивания подобных сил, будет другим.
$$F=k_{eff_p}x_p=k_{eff_s}x_s\\
\text{iff}\quad k_{eff_p}\neq k_{eff_s}\\
\Rightarrow x_p \neq x_s$$.
Эта разница в смещениях вызывает разницу в гравитационных потенциальных энергиях тел в подвешенном состоянии. (Помните, что тело на высоте $h$ имеет гравитационную потенциальную энергию относительно Земли, равную приблизительно $U=mgh$). При разных значениях $h$ из-за $x_p\neq x_s$ разница гравитационной потенциальной энергии отражается в разнице ваших потенциальных энергий пружинения из-за сохранения энергии.
 $\endgroup$
 $\begingroup$
 Математика была объяснена очень хорошо, но вы сказали, что уже поняли математику, и вас беспокоило только очевидное концептуальное противоречие о передаче энергии.
 Проблема очень тонкая и интересная. Если вы изложите свою «инстинктивную реакцию» словами, она, вероятно, скажет, что, поскольку поддерживаемая сила 15 Н одинакова для обоих пружинных механизмов, они выполняют одинаковую работу. Но в то же время ваш физически подготовленный ум знает лучше. Он знает, что работа или передача энергии происходит только тогда, когда сила действует на расстоянии.
 Когда вы неподвижно держите книгу на расстоянии вытянутой руки перед собой, над книгой не совершается никакой работы. Тем не менее, через минуту ваше тело чувствует, что оно выполняет большую работу, что энергия передается, и это происходит в ваших мышечных клетках. Так что ваше тело не ошибается. Но никакая энергия не передается книге.
 Эти «здравые смыслы», которые наши тела и чувства говорят нам об окружающем нас мире, тысячи раз подкрепляются повседневным опытом, прежде чем мы изучаем физику. От них трудно избавиться. В идеи Аристотеля о том, что тяжелые предметы падают быстрее, чем легкие, и что сила руки остается на камне после того, как вы его бросите, многие верили примерно за 2000 лет до того, как вмешался Галилей.2}{2k’}$, где $k’$ — эффективная жесткость пружины. Параллельная комбинация пружин  жестче  и имеет более высокую эффективную жесткость пружины $k’=2k$, чем последовательная комбинация $k’=\frac12k$. Последовательная комбинация сохраняет в 4 раза больше энергии, чем параллельная комбинация. ($k$ — жесткость каждой отдельной пружины.)
 $\endgroup$
 Твой ответ 
 Зарегистрируйтесь или войдите в систему 
 Зарегистрируйтесь с помощью Google
 Зарегистрироваться через Facebook
 Зарегистрируйтесь, используя электронную почту и пароль
 Опубликовать как гость 
 Электронная почта
 Обязательно, но не отображается
 Опубликовать как гость 
 Электронная почта
 Требуется, но не отображается
 Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
. Достижение произвольной пространственной жесткости с помощью параллельно соединенных пружин | Дж. Мех. Дес. 
 Пропустить пункт назначения навигации
 Научно-исследовательские работы
 С. Хуанг,
 Дж. М. Шиммельс
 Информация об авторе и статье
  Дж. Мех. Дез  . Dec 1998, 120(4): 520-526 (7 страниц)
 https://doi.org/10.1115/1.2829309
  Опубликовано в Интернете:  1 декабря 1998 г.
 История статьи
 Получено:
 1 апреля 1997 г.
 Исправлено:
 1 августа 1997 г.98
 Онлайн:
 11 декабря 2007 г.
 Просмотры Содержание артикула
 Рисунки и таблицы
 Видео
 Аудио
 Дополнительные данные
 Экспертная оценка
 Делиться MailTo
 Твиттер
 LinkedIn
  Иконка Цитировать  Цитировать
 Разрешения
 Поиск по сайту
 Цитирование
 Хуанг С. и Шиммельс Дж. М. (1 декабря 1998 г.). «Достижение произвольной пространственной жесткости с помощью пружин, соединенных параллельно». КАК Я.  Дж. Мех. Дез  . декабрь 1998 г.; 120(4): 520–526. https://doi.org/10.1115/1.2829309
 Скачать файл цитаты:
 Рис (Зотеро)
 Менеджер ссылок
 EasyBib
 Подставки для книг
 Менделей
 Бумаги
 Конечная примечание
 РефВоркс
 Бибтекс
 Процит
 Медларс
 панель инструментов поиска Расширенный поиск
 В этой статье рассматривается синтез произвольной пространственной матрицы жесткости. Ранее мы показали, что произвольная матрица жесткости не может быть достигнута с помощью обычных поступательных пружин и вращательных пружин (простых пружин), соединенных параллельно, независимо от количества используемых пружин или геометрии их соединения. Для получения произвольной пространственной матрицы жесткости с параллельно соединенными пружинами требуются упругие устройства, связывающие поступательную и вращательную составляющие. Устройства, обладающие этими характеристиками, определяются здесь как винтовые пружины. Проиллюстрированы конструкции двух таких устройств. Показано, что существуют некоторые матрицы жесткости, для реализации которых требуется 3 винтовые пружины, и что для реализации полноранговых пространственных матриц жесткости требуется не более 3 винтовых пружин. Кроме того, представлены две процедуры синтеза произвольной пространственной матрицы жесткости. С помощью одной процедуры любая положительно полуопределенная матрица ранга m реализуется с m пружинами, все из которых могут быть винтовыми пружинами. При другом способе любая положительно определенная матрица реализуется с 6 пружинами, из которых не более 3 винтовых пружин.
 Раздел выпуска:
 Исследовательские статьи
 Темы:
 Пружины,
 Жесткость,
 Винты,
 Геометрия
 1.
 Болл, Р. С.,  Договоры по теории винтов , Cambridge University Press, 1900.
 2.
 Баркер Г. П. и Карлсон Д., Конусы диагонально доминирующих матриц.  Pacific Journal of Mathematics  , Vol. 57, № 1, 1975.
 3.
 Бедфорд А. и Фаулер В.,  Инженерная механика — статика , Addison Wesley Publishing Company, Inc., 1995.
 4.
 Диментберг Ф. М., «Винтовое исчисление и его приложения». в механике. Подразделение иностранных технологий», база ВВС Райт-Паттерсон, штат Огайо. Документ № FTD-HT-23-1632-67, 1965.
 5.
 Голуб, Г. Х., и Лоан, К. Ф. В.,  Матричные вычисления , Издательство Университета Джона Хопкинса, (3-е изд.) 1996.
 6.
 Гриффис, М. и Даффи, Дж., «Кинестатическое управление: новая теория для одновременного регулирования силы и смещения», Журнал ASME по механическому дизайну, Vol. 113, № 2, 1991.
 7.
 Хилл, Р. Д., и Уотерс, С. Р., «О конусе положительно-полуопределенных матриц», Линейная алгебра и ее приложения, 90, 1987.
 8.
 Хауэлл , Л.Л., и Мидха, А., «Метод проектирования податливых механизмов с изгибными шарнирами малой длины», Журнал механического проектирования ASME, Vol. 116, № 1, 1994.
 9.
 Хауэлл, Л. Л., и Мидха, А., «Теория замыкания цикла для анализа и синтеза податливых механизмов», ASME Journal of Mechanical Design, Vol. 118, № 1, 1996.
 10.
 Хуанг, К., и Рот, Б., «Размерный синтез замкнутых связей для соответствия характеристикам силы и положения», ASME Journal of Mechanical Design, Vol. 115, № 2, 1993.
 11.
 Хуанг, С., «Анализ и синтез пространственного соответствия», докторская диссертация, Университет Маркетт, Милуоки, Висконсин, 1998.
 12.
 Хуанг С. и Шиммельс Дж. М., «Границы и реализация пространственной жесткости, достигаемые с помощью простых пружин, соединенных параллельно»,  IEEE Transactions on Robotics and Automation , Vol. 14, № 3, 1998.
 13.
 Лонкарик, Дж., «Геометрический анализ податливых механизмов в робототехнике», докторская диссертация. Гарвардский университет, Кембридж, Массачусетс, 1985.
 14.
 Лонкарик, Дж., «Нормальные формы матриц жесткости и податливости»,  IEEE Journal of Robotics and Automation  , Vol. 3, No. 6, 1987.
 15.
 Мэтью, Г.К., и Тезар, Д., Синтез параметров пружины для удовлетворения заданных уровней энергии в планарных механизмах, Журнал ASME Journal of Engineering for Industry, май, 1977.
 16.
 Паттерсон Т. и Липкин Х. Структура соответствия роботов. Журнал механического проектирования ASME, Vol. 115, № 3, 1993.
 17.
 Шиммельс
 Дж. М.
, «
 Линейное пространство законов управления допуском, гарантирующих силовую сборку с трением
,
 IEEE Transactions on Robotics and Automation
, Vol.
 13
, №
 5
, стр.
 656
 –
 667
,
 1997
.
 18.
 Шиммельс, Дж. М., и Хуанг, С., «Пассивный механизм, улучшающий роботизированное позиционирование за счет соответствия и ограничения»,  Робототехника и компьютеризированное производство  , Vol. 12, № 1, 1996.
 19.
 Schimmels
 J. M.
 и
 Пешкин
 M. A.
, «
 Matrix Design for Force Guided Assembly
»
 IEEE Робототехника и автоматизация
, Vol.
 8
, №
 2
, стр.
 213
 –
 227
,
 1992
.
 20.
 Schimmels
 J. M.
 и
 Пешкин
 M. A.
, «
 Force-Assembly с трением
»,
 IEEE Transactions на Robotics и Automation
99.,
 IEEE.
 10
, №
 4
, стр.
 465
 –
 479
,
 1994
.
 21.
 Стерджес, Р. Х., и Лаоваттана, С., «Проектирование ортогонального соответствия для многоугольной вставки штифта», ASME Journal of Mechanical Design, Vol. 118, № 2, 1996.
 Этот контент доступен только в формате PDF.
 В настоящее время у вас нет доступа к этому содержимому.
 25,00 $
 Покупка
 Товар добавлен в корзину.
 Проверить
 Продолжить просмотр  Закрыть модальный 
 27 Важные факторы, связанные с этим – Lambda Geeks 
 Определение жесткости пружины:  Постоянная пружины является мерой жесткости пружины. Пружины с более высокой жесткостью, скорее всего, труднее растянуть. пружины – эластичные материалы. при приложении внешних сил пружина деформируется и после снятия усилия вновь принимает исходное положение. Деформация пружины представляет собой линейную упругую деформацию. Линейной является кривая зависимости между силой и смещением.
 Формула жесткости пружины:  F= -Kx
 Где
 F= приложенная сила,
 K= жесткость пружины
 x = смещение из-за приложенной нагрузки от нормального положения.
 Изображение предоставлено: AndrewDressel, Жесткость винтовой пружины, CC BY-SA 4.0
 Единицы постоянной пружины:  постоянная пружины, представленная как K, и ее единицей измерения является Н/м.
 Как найти жесткость пружины? 
 Уравнение жесткости пружины:   Постоянная пружины определяется в соответствии с законом Гука, указанным ниже:
 Сила, приложенная к пружинам, прямо пропорциональна смещению пружины от положения равновесия.
  Постоянная пропорциональности — это постоянная пружины. Сила пружины противоположна силе. Таким образом, между отношением силы и перемещения отрицательный знак.
 F= -Kx
 Следовательно,
 K= -F/x(Н/м) 9-2]
 Пружина постоянной силы:  Пружина постоянной силы — это пружина, которая не подчиняется закону Гука. Пружина имеет усилие, которое она оказывает в диапазоне своего движения, является постоянной и никоим образом не изменяется. Как правило, эти пружины сконструированы как пружины, свернутые таким образом, что пружина расслабляется, когда полностью свернута, и после раскручивания возникает восстанавливающая сила, поскольку геометрия остается постоянной при развертывании пружины. Пружина постоянной силы оказывает постоянную силу для развертывания из-за постоянного изменения радиуса кривизны.
 Applications of constant spring force:   Brush springs for motors 
  Constant force motor springs  
  Counterbalance springs for window 
  Carriage returns springs of typewriters  
  Timers  
  Кабельные ретракторы  
  Кинокамеры  
  Пружины растяжения  
 Постоянная сила пружины не всегда обеспечивает постоянную силу. Первоначально она имеет конечное значение и после отклонения пружины в 1,25 раза от своего диаметра достигает полной нагрузки и сохраняет постоянную силу в пружине, несмотря на деформацию. Эти пружины изготовлены из металлических полос, а не из проволоки. Пружины изготовлены из таких материалов, как нержавеющая сталь, высокоуглеродистая сталь и т. д. Пружины создают натяжение в линейном направлении.
 Производительность, коррозия элементов, температура влияют на усталость таких пружин. Скорее всего, они будут иметь срок службы от 2500 циклов до более одного миллиона в зависимости от размера и приложенной нагрузки.
 Примеры жесткости пружины 
 Жесткости резиновой ленты:  Резиновая лента действует как пружина с определенными ограничениями. Когда кривая закона Гука рисуется для резиновых лент, график оказывается не совсем линейным. Но если мы будем растягивать ленту медленно, она может подчиняться закону Гука и иметь значение постоянной пружины. Резиновая лента может растягиваться только до предела эластичности, который
 также зависит от размера, длины и качества.
 Значения постоянной пружины:  Значение постоянной пружины определяется по закону Гука. Согласно закону Гука, при растяжении пружины приложенная сила прямо пропорциональна увеличению длины по сравнению с исходным положением.
 Как определить жесткость пружины?  F=-Kx
 K=-F/x
 Пружинные константы материалов:  Пружинные константы для 
 Сталь   =21000 кг/м ³  Жесткость пружины для 
 Медь = 12000 кг/м ³ 
 Как найти жесткость пружины по графику? 
 График жесткости пружины:  Изображение предоставлено: Kolossos, Federkennlinie, CC BY-SA 3.0
 Может ли жесткость пружины быть отрицательной?  Не может быть отрицательным.
 Формула постоянной пружины с массой:  T=[латекс]2\pi \sqrt{\frac{k}{m}}[/latex]
 где,
 T= период пружины
 m=масса
 k=постоянная пружины
 Эффективная постоянная пружины:  Параллельно: Когда две невесомые пружины подчиняются закону Гука и соединены тонкими вертикальными стержнями концы пружин, соединяющие два конца пружин, называются параллельными соединениями.
 Направление постоянной силы перпендикулярно направлению силы.
 Постоянная пружины K записывается как
 K=K1+K2
 Серия:
 Когда пружины соединены друг с другом последовательно таким образом, что комбинация полного растяжения является суммой полного растяжения и постоянной комбинации всех пружин.
 Сила прикладывается к концу торцевой пружины. Направление силы в обратном направлении, поскольку пружины сжаты.
 Закон Гука,
 F1=k1x1
 F2=k2x2
 x 1+ x 2 =[латекс](\frac{F1}{k1}+\frac{F2}{k2})[/latex]
 Эквивалентная жесткость пружины:  K = [латекс](\frac{1}{k1}+\frac{1}{k2})[/latex]
 Жесткость кручения:  Торсион пружина закручена вдоль оси пружины. При закручивании она создает крутящий момент в противоположном направлении и пропорционален углу закручивания.
 Торсионный стержень представляет собой прямой стержень, который подвергается скручиванию и создает напряжение сдвига вдоль оси с крутящим моментом, приложенным к его концу.
 Примеры:  Винтовая торсионная пружина, торсион, торсионное волокно
 Применение:  Часы-часы имеют пружину, свернутую вместе в спираль. Это форма винтовой торсионной пружины.
 формула постоянной пружины при кручении | Коэффициент кручения  В пределах предела упругости пружины кручения подчиняются закону Гука, поскольку они скручиваются в пределах предела упругости,
 Крутящий момент, представленный как,
 τ = -Kθ
 τ = − κ θ
 K — смещение, называемое коэффициентом торсионной пружины. 92
 Торсионные балансы:   Изображение предоставлено:  Шарль-Огюстен де Кулон, Bcoulomb, помечено как общественное достояние, более подробная информация на Викискладе. Торсионные балансы — это крутильный маятник. Он работает как простой маятник.
 Чтобы измерить силу, сначала нужно узнать постоянную пружины. Если сила мала, трудно измерить константу сохранения. Необходимо измерить период резонансных колебаний весов.
 Частота зависит от Момента Инерции и упругости материала. Таким образом, частота выбрана соответственно.
 После расчета инерции определяется константа пружины,
 F=Kδ/L
 Гармонический осциллятор:  Гармонический осциллятор представляет собой простой гармонический осциллятор, когда он подвергается деформации из исходного положения равновесия и испытывает восстанавливающую силу F непосредственно пропорциональна смещению х.
 Математически записывается следующим образом:
 F= -Kx
 Жесткость пружины при кручении:  Жесткость пружины при кручении — это сила пружины, перемещаемая на 360 градусов. Это может быть дополнительно рассчитано путем деления силы на 360 градусов.
 Факторы, влияющие на жесткость пружины:   Диаметр проволоки: Диаметр проволоки пружины 
  Диаметр витка: Диаметры витков в зависимости от жесткости пружины. 
  Длина в свободном состоянии: Длина пружины от равновесия в состоянии покоя 
  Количество активных витков: Количество витков, которые сжимаются или растягиваются. 
  Материал: Материал пружины, использованный для изготовления. 
 Пружина с постоянным крутящим моментом:  Пружина с постоянным крутящим моментом представляет собой пружину с постоянным усилием, перемещающуюся между двумя золотниками. После отпускания сжатой пружины крутящий момент рассчитывается по выходному золотнику, когда пружина возвращается в исходное положение равновесия в накопительном золотнике. /  δ  ,
 K Варьируется от
 Минимум = 0,9 Н/м
 Максимум = 4,8 Н/м
 Постоянная пружины зависит от числа витков n.
 Идеальная жесткость пружины:  Жесткость пружины является мерой жесткости пружины. Чем больше значение k, тем жестче пружина и ее труднее растянуть. Любая пружина, которая подчиняется уравнению закона Гука, называется идеальной пружиной   .
 Пружина постоянной силы в сборе:  Пружина постоянной силы устанавливается на барабан путем наматывания ее на барабан. Пружина должна быть плотно закручена. Затем к свободному концу пружины прикладывается нагрузочная сила, например, в противовесе или наоборот.
  Диаметр барабана должен быть больше внутреннего диаметра. 
  Диапазон: 10–20 % диаметра барабана > внутреннего диаметра. 
  Полуторавитковая пружина должна находиться на барабане в крайнем положении. 
  Лента будет неустойчивой на больших участках, поэтому рекомендуется делать ее меньшего размера. 
  Диаметр шкива должен быть больше исходного диаметра. 
 Часто задаваемые вопросы: 
 Почему важна жесткость пружины?  Жесткость пружины важна, поскольку она показывает основные свойства материала. Это точно определяет, какая сила требуется для деформации любой пружины из любого материала. Более высокая постоянная пружины показывает, что материал более жесткий, а более низкая постоянная пружины показывает, что материал менее жесткий.
 Можно ли изменить константу пружины?  Да. жесткость пружины может изменяться в зависимости от приложенной силы и растяжения материала.
 Может ли жесткость пружины быть равной 0?  Нет. Постоянная пружины не может быть равна нулю. Если он равен нулю, жесткость равна нулю.
 Может ли жесткость пружины иметь отрицательное значение?  Нет. Spring-константа всегда имеет положительное значение.
 Когда модуль Юнга и жесткость Гука равны?  Когда отношение длины к площади пружины равно единице, тогда модуль Юнга и постоянная величина пружины будут равны.
 Постоянная пружины представлена как, K=-F/x,
 Вышеупомянутое уравнение показывает связь между жесткостью пружины и удлинением пружины при той же приложенной силе
 Почему пружину разрезают пополам, ее постоянные изменения пружины?  Это обратно пропорционально растяжению пружины. когда пружина разрезается пополам, длина пружины уменьшается, следовательно, постоянная пружины удваивается. 9-2)
    = 5 Н/м
 Постоянная пружины 5 Н/м.
 Q2) К пружине с жесткостью 15 кН/м приложена сила 25 кН. Определите смещение пружины.  Приведено:
 Прикладная сила = 2,5KN
 Пружина -констант = 15 кН/м
 Решение:
 1. Выключить смещение пружины
. Весна будет применяться равным и противоположным силой -2,5 кН.
              F=-Kx
 X=-F/K
    = – 2,5/15
    = 0,167 м
 Следовательно, пружина смещена на 16,67 см.
 Q3) Пружина с постоянной силы 5,2 Н/м имеет длину в расслабленном состоянии 2,45 м, а перпендикулярную длину пружины 3,57 м. Когда груз прикреплен к концу пружины и ему разрешено отдыхать. Чему равна потенциальная упругая энергия, запасенная пружиной?  Решение:
 Дано:
 Постоянная силы = 2,45 м
 x = 2,45 м
{2})}{k}[/latex]
 =0,02J
 Жесткость пружины с несколькими пружинами 
 Пружина разрезана на 4 равные части, 2 из которых параллельны Какова новая эффективная жесткость этих пружин части?  Пружинные постоянные четырех пружин k1, k2, k3, k4
 соответственно,
 Параллельные:
 Эквивалентная жесткость пружины (k5) = k1 + k2
 Серия;
 Общая эквивалентная жесткость системы: 9-2
   =-1 Н
 Сила пружины направлена в противоположную сторону
 Следовательно, сила пружины = 1 Н.
 Предмет массой 5,13 кг, помещенный на пружину, сжимает ее на 25 м. Какова постоянная силы пружины На какую высоту поднимется этот предмет, когда пружина высвободит свою энергию.
  Для получения дополнительных статей по теме нажмите здесь       
                    
 Закон Гука и простое гармоническое движение 
 Объектив 
 •
 измерить жесткость пружины по закону Гука
 •
 исследовать статические свойства упругих предметов и пружин, соединенных последовательно и параллельно
 •
 изучить простой гармонический осциллятор, построенный из пружин и масс
 •
 чтобы убедиться, что период СГМ пропорционален квадратному корню из массы и не зависит от амплитуды
 •
 для измерения динамической жесткости пружины
 •
 проверить выполнение закона сохранения энергии
 Оборудование 
 Часть I: 
 •
 две почти одинаковые пружины
 •
 длинная резинка
 •
 опорная стойка с метровой палкой
 •
 50-граммовая вешалка
 •
 набор гирь от 100 г до 600 г
 •
 весы баланса
 •
 Интерфейс научной мастерской с датчиком силы и детектором вращательного движения, используемыми в качестве линейного датчика
 Часть II: 
 •
 тележка для столкновения с известной массой на горизонтальной дорожке динамики, колеблющаяся с помощью параллельных пружин
 •
 датчик движения и фотодатчик, подключенные к интерфейсу Science Workshop
 •
 нелинейные пружинящие объекты (резинки)
 •
 две прямоугольные гири по ~0,5 кг каждая для изменения массы системы
 Введение и теория 
 Закон Гука 
 Сила упругости возникает в пружине, когда пружина растягивается/сжимается или деформируется (Δx) под действием внешней силы. Сила упругости действует в направлении, противоположном внешней силе. Он пытается привести деформированный конец пружины в исходное (равновесное) положение. См. рис. 1.
  Рисунок 1 
 Если растяжение относительно невелико, величина силы упругости прямо пропорциональна растяжению Δx в соответствии с законом Гука:
 ( 1 )
 F _el = −kΔx
 где  k  — константа, обычно называемая жесткостью пружины, а Δx — растяжение (разница между новым ( x ) и положением равновесия). Знак минус перед жесткостью пружины в
 уравнение 1 F _el = −kΔx
 показывает, что сила упругости и растяжение действуют в противоположном направлении.
 Простое гармоническое движение 
 Если подвесную массу сместить из положения равновесия и отпустить, то произойдет простое гармоническое движение (ГДД). SHM означает, что положение изменяется с синусоидальной зависимостью от времени.
 ( 2 )
 x = X _max cos(  ω  t)
 Ниже приведены уравнения для скорости и ускорения.
 (3)
 V = −x _MAX  ω  SIN ( ω  T)
 (4)
 A = −x _MAX  ω  ^{2 _COS  ω  ²8. )} Подставляя уравнения0293 ω  t)
 и
 1 F _el = −kΔx
 во Второй закон Ньютона можно вывести уравнение для угловой резонансной частоты колебательной системы:
 ( 5 )
  ω  =
  
 где  k  — жесткость пружины, а  m  — масса системы, совершающей простое гармоническое движение. Единица угловой частоты
 радиан в секунду = рад/с.
 Собственную резонансную частоту генератора можно изменить, изменив либо постоянную пружины, либо колеблющуюся массу. Использование более жесткой пружины увеличило бы частоту колебательной системы. Добавление массы к системе уменьшит ее резонансную частоту.  Двумя другими важными характеристиками колебательной системы являются период ( T ) и линейная частота ( f ). Период колебаний – это время, за которое тело совершает одно колебание. Линейная частота – это количество колебаний в одну секунду. Период обратно пропорционален линейной частоте.
 ( 6 )
 Т =  
 Единицей периода является секунда (с), а единицей частоты является Герц или с ^–1 (Гц = 1/с).  Угловая частота связана с периодом и линейной частотой в соответствии со следующим выражением.
 ( 7 )
  ω  = 2  π  f =  
 Энергия 
 Чтобы возникло колебание, энергия должна быть передана в систему. Когда тело выходит из равновесия, в системе накапливается упругая потенциальная энергия. После освобождения объекта потенциальная энергия переходит в кинетическую и обратно. В гармоническом осцилляторе происходит непрерывный обмен между потенциальной и кинетической энергией.  Для колеблющейся пружины ее потенциальная энергия (  E  _p ) в любой момент времени равна работе (  W  ) при растяжении пружины до соответствующего перемещения  x  .
 ( 8 )
 E _p = W = kx ²  
 Кинетическая энергия (  E  _k ) осциллятора для любого момента времени будет подчиняться хорошо известному уравнению:
 ( 9 )
 E _k = mv ² .
 Соответственно можно рассчитать максимальную потенциальную энергию и максимальную кинетическую энергию.
 (10)
 E _P = KX _MAX ²
 (11)
 E _K = KV _MAX ²
 Согласно закону сохранения энергии: «Механическая энергия сохраняется (не уничтожается и не создается) в колебательной системе без трения».
 Процедура 
 Пожалуйста, распечатайте рабочий лист для этой лабораторной работы. Этот лист понадобится вам для записи ваших данных.
 Часть I. Закон Гука 
 Измерение жесткости пружины, метод 1 
 Цель этой части лабораторной работы – найти жесткость пружины. Постоянная пружины представляет собой коэффициент пропорциональности между силой упругости и смещением в соответствии с законом Гука (
 уравнение 1 F _el = −kΔx
 ).
 1
 Подвесьте пружину к опоре, добавьте груз, измерьте исходное положение равновесия с помощью измерительной линейки и запишите его.
 2
 Добавляйте гири с шагом от 100 г до 600 г и измеряйте соответствующее положение.
 3
 Обсудите с членами вашей группы столбцы, которые необходимо подготовить в GA для записи данных. Составьте набросок таблицы и уточните его у своего ТА. Подготовьте столбцы в GA.
 4
 Создайте новый расчетный столбец для данных силы упругости (ДАННЫЕ → НОВЫЙ РАСЧЕТНЫЙ СТОЛБЦ → уравнение:  F  = переменные “ м ” *  г  , где  м  в кг).
 5
 Создайте новую расчетную колонку для перемещения (ДАННЫЕ → НОВАЯ РАСЧЕТНАЯ СТОЛБЦА → уравнение = переменные «позиция» — начальное положение равновесия).
 6
 Постройте график зависимости силы от перемещения.
 7
 Запишите наклон графика и его неопределенность в рабочий лист лабораторной работы 8. Вы будете использовать значение наклона и его неопределенность, чтобы найти постоянную пружины и ее ошибку.
 Измерение жесткости пружины, метод 2 
 Установка аппарата, показанная на рис. 2 будет использоваться для определения жесткости пружины 2.
  Рисунок 2   :  Установка для эксперимента по закону Гука
 1
 Откройте предварительно установленный файл эксперимента: desktop\pirt-labs\phy 113\PreSetUpFiles\Springs.
 2
 Прежде чем снимать фактические данные, откалибруйте датчик силы. Нажмите кнопку «Настройка» на панели инструментов. Затем щелкните значок датчика силы и нажмите кнопку «Калибровать датчики». Это вызовет панель калибровки, показанную на рис. 3.
  Рисунок 3   :  Калибровка датчика силы в Data Studio
 Опция «2 точки» должна быть выбрана в качестве «Типа калибровки». При отсутствии нагрузки на датчик силы введите 0 в окне стандартного значения «Точка калибровки 1». Нажмите кнопку «Тара» на датчике усилия. Это действие обнуляет показания датчика силы. Нажмите кнопку «Считать с датчика». Затем повесьте груз весом 1 кг на датчик и введите 9,8 в окне стандартного значения «Точка калибровки 2». Нажмите на кнопку «Чтение с датчика». Нажмите «ОК», чтобы сохранить эту калибровку. Закройте окна «Калибровка датчиков» и «Настройка». Теперь вы готовы к фактическим измерениям жесткости пружины.
 3
 Замените груз весом 1 кг на пружину. Прикрепите к нему кусок веревки. Оберните шнур вокруг большого  шкива  детектора вращательного движения против часовой стрелки, как показано на рис. 2. Датчик вращательного движения был откалиброван для считывания линейного расстояния.
 4
 Нажмите кнопку «Пуск», чтобы начать сбор данных. Осторожно потяните за веревку, наблюдая за окном отображения силы. Начинайте отпускать струну, когда усилие достигает 10 Н.
 5
 Примените линейную аппроксимацию к хорошей части вашей записи (см. рис. 4), которая представляет собой график зависимости силы упругости от смещения. Наклон этой линии дает постоянную пружины.
 6
 Запишите наклон графика зависимости силы от зелья и его неопределенность в рабочем листе лабораторной работы 8. Вы будете использовать значение наклона и его неопределенность, чтобы найти постоянную пружины и ее ошибку.
 7
 Повторите эту процедуру для системы пружин последовательно и параллельно.
 8
 Запишите наклон графика зависимости силы от положения и его неопределенность в рабочем листе лабораторной работы 8. Вы будете использовать значение наклона и его неопределенность, чтобы найти постоянную пружины и ее ошибку. В разделе «Обсуждение» вам нужно будет сравнить значение жесткости пружины для системы пружин со значением каждой жесткости пружины.
  Рисунок 4   :  Образец файла эксперимента в DataStudio
 Исследование нелинейного пружинящего объекта.
 1
 В экспериментальной установке с рис. 2, замените пружину длинной резинкой.
 2
 Запишите силу в зависимости от положения для движений вниз (увеличение силы) и вверх (уменьшение силы).
 3
 Используйте эти данные, чтобы узнать, соответствует ли резинка закону Гука (
 уравнение 1 F _el = −kΔx
 ).
 Часть II – Простое гармоническое движение 
 В этой части эксперимента вы проверите, зависит ли период от амплитуды; рассчитать резонансную частоту и жесткость пружины системы. Вы будете записывать собранные данные в рабочий лист лабораторной работы 8.
 1
 Настройте эксперимент, как показано на рисунках ниже. Откройте предварительно установленный файл эксперимента: desktop\pirt-labs\phy 113\PreSetUpFiles\SHM.
  Рисунок 5 
  Рисунок 6 
 2
 Без дополнительной массы измерьте период колебаний для начальных амплитуд 4 см и 12 см. Сбор данных автоматически прекратится через 5 секунд. Пример записи показан на рис. 2. Период измеряется фотодатчиком и заносится в таблицу 1 слева от графика.
 3
 Без дополнительной массы сместите тележку из положения равновесия примерно на 8 см и начните запись. Снова запишите период колебаний тележки, измеренный фотодатчиком. Запишите все три периода колебаний в рабочий лист лабораторной работы 8.
  Рисунок 7   :  Образец файла для эксперимента SHM в DataStudio
 4
 Сопоставьте запись положения и времени с синусоидальной волной. Параметр А – амплитуда (максимальное смещение) колебаний. Параметр B дает вам период колебаний. Вы можете сравнить его значение со значением периода, измеренного фотодатчиком. Параметр D — положение равновесия. Используйте параметр B для расчета резонансной частоты и жесткости пружины системы с помощью уравнений 9.0009 7
  ω  = 2  π  F =
 и
 5  ω  =
914
914
914.
 5
 Сопоставьте запись скорости и времени с синусоидальной волной. Запишите параметр А — амплитуду (максимальное значение) графика зависимости скорости от времени.
 Обратите внимание, что оба графика, положение относительно времени и скорость относительно времени, представляют собой периодические волны одной и той же частоты, только сдвинутые на 90° или
 рад.
 Максимальное и минимальное значения положения достигаются, когда скорость равна нулю, а также максимальное и минимальное значения скорости достигаются, когда положение находится в равновесии. С точки зрения энергии системы это означает, что когда потенциальная энергия максимальна (максимальное смещение), кинетическая энергия равна нулю. В этот момент вся энергия является потенциальной. Точно так же в момент, когда пружина не растянута (объект проходит точку равновесия), вся энергия является кинетической.  Чтобы проверить теорему о сохранении энергии для колеблющейся тележки, достаточно сравнить ее максимальную потенциальную энергию с максимальной кинетической энергией, найдя процентную разницу потерь энергии.
 (12)
 % Потеря =
 PE _I – KE _F
 PE _I
 · 100 %
 Отношения между периодом и MASS 
9414941494149414941494149414141414141414941494149414
.  Это часть эксперимента, в которой вы убедитесь, что период СГМ пропорционален квадратному корню из массы. 
 1
 Загрузите тележку тяжелыми грузами (по одному) и измерьте период SHM, сохраняя постоянную амплитуду, например. 8 см.
 2
 Включая данные из предыдущей части эксперимента, у вас будет три точки, чтобы построить график зависимости периода от
 м
 .
 Согласно теории (уравнения
 5  ω  =
 и
 7  ω  = 2  и
  ω  = 2  и
  ω  = 2  и
  ω  = 2  и
  ω  = 2  и
  ω  = 2  и
  ω  = 2
) линия.
 3
 Запишите наклон графика T vs
 m
  
 в лист лабораторной работы 8.
 4
 Используйте значение наклона и его неопределенность, чтобы найти постоянную пружины.
 5
 На основе наклона графика рассчитайте динамическую жесткость системы.
  Подсказка:  Замена
  ω  =  
 в
  ω  =
  
 дает
 =
 .
  
 Решение для T дает следующее.
 T =
 2  π 
 k
 m
  
 Обсуждение 
 Укажите цель лаборатории. Сравните экспериментальные результаты пружинной жесткости для одиночной пружины из методов 1 и 2 с их теоретическими значениями. Каков процент расхождения? Как жесткость пружины системы из двух последовательно соединенных пружин связана с жесткостью отдельных пружин? Как жесткость пружины системы из двух параллельных пружин связана с жесткостью отдельных пружин? Все ли пружинящие объекты подчиняются закону Гука?  Какой вывод можно сделать о связи между периодом и амплитудой на основе собранных данных? Соответствуют ли измерения жесткости пружины друг другу? Соблюдался ли в вашем эксперименте закон сохранения энергии? На основании ваших экспериментальных данных, какова связь между периодом колебаний и массой в системе пружина-масса? Объясните, какую физическую величину можно принять за характеристику колебательной системы. Назовите основные характеристики простого гармонического движения.
 Заключение 
 Вы достигли цели лаборатории?
 Пружинные константы: уравнения и расчеты | Научный проект 
 Научный проект 
 Силы заставляют объекты двигаться или каким-либо образом деформироваться.  Третий закон Ньютона  гласит, что для каждой силы существует равная и противоположная сила. Это верно для пружин, которые накапливают и используют механическую энергию для выполнения работы.
 Пружины  эластичны  , что означает, что после деформации (при нагрузке или сжатии) они возвращаются к своей первоначальной форме. Пружины есть во многих предметах, которые мы используем ежедневно. Они в шариковых ручках, матрасах, батутах и поглощают удары в наших велосипедах и автомобилях. Согласно третьему закону движения, чем сильнее вы тянете пружину, тем сильнее она тянется назад. Пружины  подчиняются закону Гука  , открытому Робертом Гуком в 17  веке. Закон Гука описывается:
 Скачать проект
  F = -kx 
 Где  F  — сила, действующая на пружину в ньютонах (Н),
  k  — постоянная пружины в ньютонах на метр (Н/м),
 и  х  — смещение пружины от положения равновесия.
 Постоянная пружины,  k  , показывает, насколько жесткой является пружина. Более жесткие (труднее растягиваемые) пружины имеют более высокие коэффициенты упругости. Смещение объекта — это измерение расстояния, описывающее это изменение относительно нормального или равновесного положения.
 Рассчитайте жесткость пружины по закону Гука.
 Как вы думаете, какая пружина имеет наибольшую жесткость? Наименьшая жесткость пружины? Почему?
 Весы (измеряют граммы или килограммы)
 Линейка (для измерения сантиметров)
 Различные винтовые пружины
 Малый груз
 Деревянная доска
 Стол или столешница
 Книги или другие предметы, которые можно штабелировать
 С помощью взрослого прикрепите один конец каждой пружины к одной стороне деревянной доски. Не забудьте оставить пару дюймов между каждой пружиной.  Зачем фиксировать один конец пружины? 
 Разложите несколько книг на столе или столешнице в две стопки длиной примерно с деревянную доску.
 Поместите деревянную доску на стеллажи так, чтобы пружины свисали вниз. Убедитесь, что между нижней частью пружин и столом остается пространство.
 Используя сантиметровую сторону линейки, измерьте  положение равновесия  каждой пружины.
 Взвесьте гирю на весах и запишите ее массу в килограммах.  Почему масса должна быть в килограммах? 
 Прикрепите груз к каждой пружине по одному и используйте линейку для измерения смещения    .  Самый простой способ сделать это — измерить длину пружины, а затем вычесть длину равновесия.
 Рассчитайте силу тяжести, действующую на пружину.
  F _г = мг 
 Где  F _г  — сила тяжести в ньютонах, m — масса груза в килограммах, а g — гравитационная постоянная Земли, равная 9,81. м/с ² .
 Установить силу тяжести (  F _г  ) равной силе пружины (  F)  .  Почему вы можете сделать эти две переменные эквивалентными?  Используйте закон Гука для расчета постоянной пружины  k  для каждой пружины.
 Пружины с большей жесткостью пружины будут иметь меньшие смещения, чем пружины с меньшей жесткостью пружины при одинаковой добавленной массе.
 Закон Гука представляет собой  линейную упругую  деформацию. Эластичность означает, что пружина вернется в свою первоначальную форму, как только внешняя сила (масса) будет удалена. Линейный описывает связь между силой и смещением. Тот факт, что жесткость пружины является константой (это свойство самой пружины), показывает, что зависимость является линейной.
 Конечно, закон Гука остается верным только тогда, когда материал эластичен. Если пружина постоянно деформирована (что-то вроде сдавливания или чрезмерного растяжения), она больше не вернется в исходное положение. Если вы когда-нибудь играли со слинки и случайно слишком сильно растянули его или согнули, вы знаете, что после этого он не работает так, как должен.
 Чтобы закон Гука работал правильно, части уравнения должны быть выражены в правильных единицах. Без последовательных единиц уравнение бессмысленно.
 Вы можете установить силу тяжести, действующую на пружину, равной силе, действующей на пружину, в соответствии с Третьим законом движения Ньютона, который гласит, что силы действуют парами. Каждая сила имеет равную и противоположную силу.
  Заявление об отказе от ответственности и меры предосторожности 
 Education.com предоставляет идеи проекта научной ярмарки для ознакомления
только цели. Education.com не дает никаких гарантий или заявлений
относительно идей проекта научной ярмарки и не несет ответственности за
любые убытки или ущерб, прямо или косвенно вызванные использованием вами таких
Информация. Получая доступ к идеям проекта научной ярмарки, вы отказываетесь и
отказаться от любых претензий к Education.com, возникающих в связи с этим.