Жесткость пружины что такое: Что такое жесткость пружины и как ее рассчитать

alexxlab | 27.03.1991 | 0 | Разное

Содержание

Жесткость пружины. Размышления

Размышления о жёсткости

Посчитал нужным вывесить сей опус на форуме для повышения уровня общего технического развития гуманитарной его части.

Сразу скажу – я не профи и не спортсмен – я просто люблю водить машину и люблю, когда машина едет правильно. Подвеска – моя страсть и моя слабость. Именно от подвески, а не от мощности двигателя зависит средняя скорость по типичной российской дороге, а также безопасность – и моя, и окружающих. Еще очень важны тормоза, но о них как-нибудь позже. В силу того, что я не профи и не спортсмен, и даже не знаком ни с одним профессиональным спортсменом-кольцевиком (о раллистах разговор особый), то всё, что я знаю по этой теме, добывалось по крупицам самостоятельно отовсюду, откуда только возможно. С миру по нитке, как говорится. Увы, получившаяся картина не является полной и исчерпывающей – т.е. копать и копать еще. Но область предстоящих раскопок – это уже нюансы и детали настройки, типа точнейших углов установки колес и влияния жесткости сайлентблоков.

Основа уже накопана и опробована на собственном опыте, что позволяет ею поделиться.

Подразумевается, что перед изменением настройки подвески уже куплены и установлены хорошие диски с правильным вылетом и хорошей правильной резиной. Для Сивиков это 195/50 R16, 205/50 R16 или хотя бы штатные сировские/интегровские 195/55 R15. Для Интегры пойдет еще 215/45 R16 – это штатный размер Интегры Type R 98spec. Для Аккорда – 205/55 R16 и 215/45 R17. Если же вы катаетесь на батонах с профилем 60 или 70, то о какой подвеске вообще может идти речь? Шутка. Батоны тоже имеют право на жизнь.

Подразумевается также, что правильная подвеска увеличивает нагрузку на позвоночник. wink.gif Не всегда сильно увеличивает, но увеличивает по-любому. Тренируйте спину.

Первый шаг (опциональный, т.е. на любителя) – занизить машину. На самом деле эффект от этого очень большой. Даже если вы не измените ничего, кроме как чуть-чуть подрежете свои штатные пружины – буквально на пару витков – то результат не замедлит сказаться.

Но лучше, конечно, поставить правильные пружины. Правильные пружины – это такие пружины, которые соответствуют определенному принципу. Принцип этот очень прост: если вы занижаете машину, сокращая рабочий ход подвески на сжатие на 20%, то вы должны поставить пружины, на 20% более жесткие. Если на 50% – то на 50%. Машина не должна ложиться на отбойники чаще, чем она ложилась до изменений. Езда на отбойниках – это нонсенс. На самом деле из Японии очень часто приходят машины, тюненые там, и тюнены они порой как раз в таком стиле, что по российским дорогам они передвигаются, преимущественно лежа на отбойниках. Такой принцип нам не подходит. Он и для Японии-то по-хорошему не подходит – только если ездить медленно и печально. Впрочем, подобный тюнинг там обычно служит совсем иным целям – чтоб смотрелось круто. Но мы не об этом. Нам-то нужна управляемость.

Подобрав правильные пружины, не вздумайте их ставить со штатными амортизаторами. Дело в том, что пара пружина+амортизатор должна иметь определенный баланс, который позволяет им правильно работать вместе.

При ходе сжатия основное сопротивление этому ходу оказывает пружина. Именно ее жесткость определяет, на сколько она сожмется при приложении определенной силы. Например, штатные пружины ВАЗ 2108 имеют жесткость в пределах 17-18 кг/см. Амортизатор при ходе сжатия тоже вносит свою лепту в общее сопротивление этому ходу, но весьма небольшое, составляющее, полагаю, не больше 10-20%.

После хода сжатия рано или поздно начинается ход отбоя. И вот при ходе отбоя начинается самое интересное – сжатая на ходе сжатия пружина стремится распрямиться. И помешать ей это сделать может только амортизатор. И сила сопротивления амортизатора на отбой должна быть сбалансирована с жесткостью пружины. Эта сила может быть приблизительно равна, она может быть существенно больше (это когда тюнинговый амортизатор установлен вместе со штатной пружиной), но она ни в коем случае не должна быть меньше.

Если амортизатор вяло сопротивляется пружине на ходе отбоя, получается лягушачья подвеска – машина скачет как лягушка. Потому что сильная пружина “плюет” на слабый амортизатор и распрямляется, “выстреливает”. Ей никто в этом почти не мешает. Потом, уже под действием веса автомобиля, она сжимается, потом все идет по кругу. Никакой стабильности, об управляемости же говорить вообще не приходится – какая тут к черту управляемость, если машина просто не в состоянии проехать по обычной дороге, не раскачиваясь.

Следовательно, из этого вытекает правило номер два: если вы ставите более жесткую пружину, то вы обязаны поставить более жесткий амортизатор. И их жесткость должна быть сбалансирована.

Отсюда, в свою очередь вытекает правило номер два-с-половиной: если вы собираетесь занизить машину, то вам по-любому надо тренировать спину. Если вы собираетесь занизить машину очень сильно, то не исключено, что ваша спина будет болеть неделю. Но потом привыкнет – проверено. В серьезной трактовке правило номер два-с-половиной выглядит так: при занижении машины вам не обойтись без замены не только пружин, но и амортизаторов.

Немного цифр

Жесткость пружин, пригодных для повседневной езды, находится обычно в пределах 10-12 кг/мм для передка. Надо заметить, что на передке пружины (и амортизаторы) почти всегда существенно жестче, чем сзади. Мне известны лишь два исключения из этого среди японских машин – это Nissan Skyline GT-R и Honda Integra DC5. Поэтому я обычно говорю о передке, подразумевая, что сзади пружины в 1.5-2 раза мягче.

Жесткость пружин также зависит от веса автомобиля, для которого они предназначены. Скажем, стандартные пружины из комплекта TEIN Type HR для Прелюда – 12/8 кг/мм (перед/зад). Тот же комплект для Аккорда – 10/6. Для Сивика, если память мне не врет – 8/6 или 8/5 кг/мм.

Могу сказать, что езда на Аккорде (точнее, Ascot Innova) с пружинами на передке 12 кг/мм и соответсвующими амортизаторами TEIN Type HR – это большая нагрузка на позвоночник. А ведь в продаже можно встретить комплекты и в 16 кг, и в 20. Но это уже явно чисто кольцевые комплекты, на дорогу на них выезжать просто небезопасно. Почему?

Потому что чрезмерно жесткая подвеска пригодна только для очень хороших дорог. Чем жестче – тем лучше должна быть дорога. На волнистой или разбитой дороге жесткая подвеска работает плохо. Машина просто летит над ямками, постоянно теряя сцепление с дорогой. Если дело происходит в повороте – можно “уплыть” за его пределы. Трассовый опыт показал, что для машины класса Аккорда, жесткость в 12 кг/мм на передке – это предел. Больше – не надо. Лучше даже меньше. Скажем, 8-10 кг/мм – оптимально.

Например, такая тяжелая машина, как Скайлайн GT-R BNR32, на комплекте OHLINS с жесткостью 8/6 кг/мм (перед/зад) на обычных дорогах показал себя великолепно. Совершенно не ощущалась жесткость, позвоночник не трясло – и при этом машина отменно управлялась. Конечно, здесь следует сделать поправку на то, что это – не семейный седан, пусть даже если он и made by Honda – это все-таки чистопородный спортивный автомобиль, созданный для того, чтобы прекрасно управляться. Но тем не менее.

А вот если сравнить Ascot Innova с 12 кг/мм и Torneo SiR с 5 кг/мм (TEIN Type Wagon), то сравнение получается неоднозначное. Неоднозначность заключается в том, что 12 кг – это чуть-чуть больше, чем надо, а вот 5 кг – это заметно меньше, чем надо. На трассе SiR всплывает на волнах и раскачивается ничуть не меньше, чем на стоковой подвеске. И кренится он все-таки сильно. Так что, наверное, для класса Аккорда оптимально будет 8-10 кг/мм.

Еще пару слов о том, о чем мы обычно забываем – о стабилизаторах поперечной устойчивости. Честно говоря, о чем о чем, а об этих прутках стали недостаток информации практически абсолютный. Нигде ничего не найдешь. В двух словах если – то их тоже надо ужесточать. И принцип там тоже простой – чем жестче передний (или, соответственно, мягче задний) стабилизатор, тем выше недостаточная поворачиваемость (understeer). Если наоборот – то растет избыточная поворачиваемость (oversteer). Вероятно, следует ужесточать оба стабилизатора, сохраняя между ними баланс.

Вот где-то так обстоят дела.

Определение идеальной жесткости пружины для боковых опор стержней, неустойчивых при изгибе

В случае, если стержень имеет боковую опору для ограничения продольного изгиба при действии сжимающей осевой силы, необходимо обеспечить, чтобы боковая опора действительно могла предотвратить потерю устойчивости при изгибе. Вследствие этого, в нашей статье мы определим идеальную жесткость пружины для боковой опоры с помощью модели Винтера.

По Джорджу Винтеру, идеальная жесткость пружины – это минимальная жесткость, которая необходима для полного предотвращения неустойчивости при продольном изгибе основного стержня с учетом критической нагрузки, и, соответственно, действует в качестве полноценной опоры. Винтер говорит о «полном придании жесткости». В соответствии с этим, прохождение через нулевую точку кривой потери устойчивости при изгибе должно быть в точке данной опорной пружины, таким образом, чтобы сама кривая потери устойчивости была двух- или многоволновой вместо одноволновой.

В модели Винтера рассматривается идеально прямой сжатый стержень с шарнирами на обоих концах, который поддерживается в середине опорной пружиной. Чтобы определить идеальную жесткость пружины, Винтер разработал идеализированную модель, показанную на рисунке 01.

Идеализированная модель Винтера
Связь между жесткостью пружины и критической нагрузкой
Модель: Стабилизированный стержень с потерей устойчивости
Формы колебаний 1 и 2 из модуля RF-STABILITY

Условный шарнир основан на предположении о наличии точки перегиба на кривой потери устойчивости при изгибе, если расстояния между опорами одинаковы. Если в качестве осевой сжимающей силы применить критическую нагрузку P

e, а стержень при этом перемещается на расстояние w в области опорной пружины, то после разреза на условном шарнире и установки равновесия моментов мы получим идеальную жесткость пружины C_ideal.

Идеальная жесткость пружины

Cideal = 2 ⋅ PeL

C_{идеально}	Идеальная жесткость пружины
P_e	Критическая нагрузка
[LinkToImage03]	Расстояние между опорой и опорной пружиной

На основе зависимости между жесткостью пружины и критической нагрузкой мы получим функцию, показанную на рисунке 02. Таким образом, при жесткости пружины меньшей, чем C_ideal возникает форма потери устойчивости с боковым смещением в области опорной пружины.

Связь между жесткостью пружины и критической нагрузкой
Идеализированная модель Винтера
Модель: Стабилизированный стержень с потерей устойчивости
Формы колебаний 1 и 2 из модуля RF-STABILITY

Критическую нагрузку P_e можно определить с помощью дополнительных модулей RSBUCK и RF-STABILITY или вручную следующим образом.

Критическая нагрузка

Pe = π² ⋅ E ⋅ IL²

P_e	Критическая нагрузка
E	модуль упругости
i	момент инерции сечения
[LinkToImage03]	Расстояние между опорой и опорной пружиной

Определение идеальной жесткости пружины на конкретном примере

В модели (рисунок 03) сжатый стержень (IPE 400), шарнирно опертый с обеих сторон, с параметрами E = 21 000 кН/см², I_z = 1318 см⁴ и L = 5 м, поддерживается в середине опорной пружиной.

Модель: Стабилизированный стержень с потерей устойчивости
Идеализированная модель Винтера
Связь между жесткостью пружины и критической нагрузкой
Формы колебаний 1 и 2 из модуля RF-STABILITY

В результате, критическая нагрузка Р_е равна 1089 кН, а идеальная жесткость пружины C_ideal – 436 кН/м для опорной пружины, заданной в середине стержня.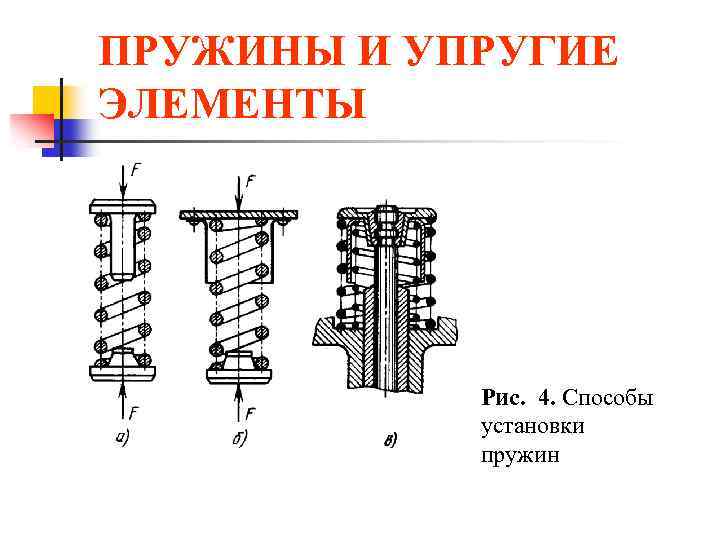

Нахождение стабилизирующей силы в опорной пружине на примере стержня, неустойчивого при изгибе, с несовершенством

После выполнения, в дополнение к выше изложенной теории, испытаний колонн на предельную нагрузку при продольном изгибе, было обнаружено, что теоретически идеальная жесткость пружины недостаточна для колонн с геометрическими несовершенствами.

Поэтому деформация w на рисунке 01 дополняется предварительной деформацией w₀ для получения w_tot.

w_tot = w + w₀

После установления равновесия моментов вокруг условного шарнира (рисунок 01) мы получим:

P ⋅ (w + w₀ ) = C ⋅ w ⋅ L / 2

В результате:

Общая деформация

wges = w01 – 2 · PC · L

w_tot	Общая деформация от прогиба и строительного подъема
w₀	Предварительная деформация от строительного подъема из-за несовершенства геометрии
P	Существующая нормальная сила сжатия в стержне с потерей устойчивости
C	Жесткость пружины у боковой опоры
L	Расстояние между опорой и опорной пружиной

При C_ideal = 2 ⋅ P_e/ L:

Общая деформация

wges = w01 – PPe

w_tot	Общая деформация от прогиба и строительного подъема
w₀	Предварительная деформация от строительного подъема из-за несовершенства геометрии
P	Существующая нормальная сила сжатия в стержне с потерей устойчивости
P_e	Критическая нагрузка на стержень с потерей устойчивости

Стабилизирующая сила F_c находится по данным уравнениям:

Стабилизирующая сила

Fc = C · w = 2 · PL · w01 – PPe

F_c	Боковая стабилизирующая сила
C	Жесткость пружины у боковой опоры
W	Боковой прогиб стержня с потерей устойчивости в его середине
P	Нормальная сила сжатия в стержне с потерей устойчивости
L	Расстояние между опорой и опорной пружиной
w₀	Предварительная деформация от строительного подъема из-за несовершенства геометрии
P_e	Критическая нагрузка на стержень с потерей устойчивости

Таким образом, стабилизирующую силу F_c можно определить на основе следующих параметров:

Действительная сжимающая сила P = 500 кН
Расстояние между опорой и опорной пружиной L = 5,00 м
Несовершенство в виде предварительного изгиба w₀ = L_total / 300 = 10 / 300 = 0,0333 м
Критическая нагрузка P_e = 1089 кН

В результате мы получим стабилизирующую нагрузку F_c = 12,3 кН.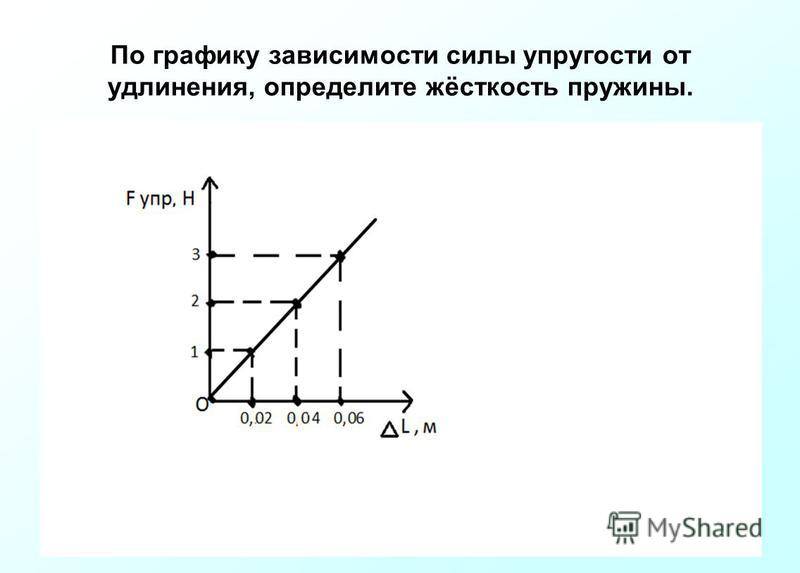 В RFEM получим 11,7 кН.

Заключение

Чтобы проверить правильность полученной жесткости пружины, можно посмотреть на результаты в модуле RF-STABILITY. Первая собственная форма соответствует двухволновой кривой потери устойчивости при изгибе с переходом через нулевое значение на уровне опорной пружины, в то время как вторая собственная форма представляет собой одноволновую кривую потери устойчивости, с опиранием на опорную пружину (рисунок 04). Обе формы имеют примерно одинаковую критическую нагрузку, вызывающую потерю устойчивости при изгибе.

Формы колебаний 1 и 2 из модуля RF-STABILITY
Идеализированная модель Винтера
Связь между жесткостью пружины и критической нагрузкой
Модель: Стабилизированный стержень с потерей устойчивости

[1]	Krahwinkel, M.: Zur Beanspruchung stabilisierender Konstruktionen im Stahlbau. Düsseldorf: VDI, 2001

Пружина. Виды и применение. Жесткость и нагрузка. Особенности

Пружина – упругий, обычно витой элемент механизмов, отвечающий за возврат приложенного усилия. В зависимости от способа навивки работает в направлении сжатия или растяжения.

По конструктивному признаку осуществляется классификация пружин на несколько разновидностей:

Винтовые.
Торсионные.
Спиральные.
Тарельчатые.
Волновые.

Винтовые являются самыми широко распространенными. Они имеют форму трубки. Элемент получают методом навивки проволоки или прута на цилиндрический шаблон. После чего заготовка поддается закалке и отпуску. В зависимости от способа навивки зависит направление работы пружины. Наличие зазоров между витками позволяет ее использовать как элемент сжатия. Примером являются пружины в шариковых ручках, подвесках автомобилей, мототранспорта. При плотной навивке пружина срабатывает на растяжения. Такие элементы имеют на краях проушины зацепы. Их используют в механизмах автоматического закрывания двери.

Торсионные имеют аналогичное устройство, что и винтовые. Однако они устроены так, чтобы срабатывать на кручение и изгиб. Концы таких пружин сделаны удлиненными для зацепа при установке. При воздействии на скручивание элемент противодействует. Торсионные пружины, к примеру, используются в сложных механизмах закрывания дверей.

Спиральные имеют форму ленты закрученной в спираль. Этот элемент применяется для накопления энергии. При установке в механизм он закручивается, накапливая за счет своей упругости энергию на раскручивание. Именно такие пружины применяются в часовых механизмах, работающих на заводе без использования электрического источника энергии. Также их используют в ручных стартерах бензопил, мотокос для возврата шнура обратно и т.п.

Тарельчатая пружина имеет вид шайбы выгнутой под конус. За счет упругости металла она противодействует сжатию. Они постоянно подпирают гайки или другие комплектующие. Это достаточно редко применяемый элемент, однако он получил широкое распространение в механизмах рулевых реек большинства автомобилей.

Волновые представляют собой ленту уложенную по синусоиде, то есть волной. Она навивается по кругу, как и винтовые изделия. Однако благодаря волнообразной укладки при сжатии, она воздействует обратно одинаково по всей плоскости без стремления уйти в сторону. Такое ее качество важно при изготовлении точных механизмов. Волновой элемент также может изготавливаться в виде незамкнутого кольца или тарельчатой пружины с синусоидой.

Классификация пружин по способу нагрузки

Более важным параметром, чем само устройство пружины, является способ ее нагрузки. При изготовлении различных механизмов возможно предусмотреть установку в него пружины практически любого устройства, главное чтобы она подходила по способу нагрузки.

Выполняется классификация пружин на следующие разновидности по воздействию:

Изгиб.
Кручение.
Растяжение.
Сдавливание.

Пружины изгиба противодействуют на усилие, нацеленное на их изгиб. Это качество используется для поджатия деталей механизмов между собой. Примером являются тарельчатые пружины.

Кручения оснащаются удлиненными ровными краями зацепами, которые фиксируются в механизмах. При попытке изменения их нормального положения в любую сторону они за счет упругости навивки основного тела возвращаются обратно. Примером таких элементов выступают торсионные пружины в бельевых прищепках.

Сжатия и растяжения имеют похожее устройство и отличаются только величиной зазора между витками навивки. Элемент сжатия при сдавливающем воздействии оказывает противодействие. Именно такой тип пружин используется в прижимных клавишах. Пружина растяжения наоборот стремится принять свою нормальную форму на действие направленное на ее удлинение. Она используется в конструкции кроватей раскладушек, спусковых механизмах огнестрельного оружия.

Из чего сделана пружина

Для производства пружин применяется специализированная проволока, имеющая повышенные параметры упругости. Из нее делают все виды пружин, кроме тарельчатых. Последние изготавливаются путем штамповки по листовой стали.

Пружинная проволока производится методом проката из определенного стального сплава. Благодаря специализированному составу, после термообработки, готовое изделие не ломается при механическом воздействии в приделах расчетных нагрузок. Также оно приобретает повышенную устойчивость к снижению упругости после многократной деформации. Однако все пружины без исключения поддаются износу. Он проявляется в виде потери упругости. Со временем они перестают принимать, после деформации, свое изначальное положение, поэтому нуждаются в замене.

Жесткость пружин

Рабочая жесткость пружины зависит от ряда параметров:

Химического состава металла.
Способа термической обработки.
Диаметра применяемой проволоки.
Числа витков.
Частоты витков.

Одним из самых важных параметров при выборе пружины является коэффициент ее жесткости. Он определяет, какое усилие требуется для сжатия или растяжения готового изделия. Этот параметр является следствием сложных инженерных расчетов, учитывающих множество показателей механизма, в который необходима установка пружины. Для рядового пользователя более привычной выступает оценка по уровню стойкости измеряемой в единицах веса. Большинство пружин просто оценивают по тому, какой массы груз может ее полностью деформировать.

Если пружина будет подходить к механизму по длине и диаметру, но при этом для ее деформации нужно значительно большее усилие, чем требуется, то система не сможет работать. По сути, развиваемое прижимное усилие не способно вызвать отклик упругости. Если же наоборот жесткости пружины окажется недостаточно, то растянувшись под нагрузкой, она не вернется обратно. Аналогичная ситуация будет и при сжатии.

Жесткость всех видов пружин зависима от температуры. При их подборе оптимально проводить оценку жесткости в той температуре, в которой она будет использоваться. Чем теплее, до определенного порога устойчивости металла, тем выше упругость. При охлаждении структура металла меняется, и пружины приобретают меньший ход и повышенную хрупкость. При эксплуатации в обычных условиях это почти незаметно. Однако такое качество явно проявляется в случае использования тонких пружин в условиях Севера.

Как сделать пружину в домашних условиях

Практически в каждом механизме, где применяется пружина, она имеет свои параметры диаметра и высоты. Вследствие этого после ее износа возникают трудности с заменой. Для достаточно современных механизмов пружины можно заказать у поставщика запчастей, но для старых уже снятых с производства это невозможно.

В таком случае пружину можно изготовить самостоятельно. Для ее производства в домашних условиях требуется наличие пружинной проволоки. Так как она чаще продается на вес от 1 кг, то этого излишне много для получения одной пружины. В таком случае можно приобрести в хозяйственном или автомагазине любую пружину сделанную из проволоки нужного диаметра. Используя ее как источник материала можно изготовить изделие требуемых параметров повторив фабричную технологию в упрощенном варианте. При термообработке пружин на производстве их нагрев и охлаждение делается с точным контролем температуры измерительным оборудованием. В домашних условиях можно приблизительно контролировать нагрев металла по цвету побежалости. При разной температуре тот меняет свой цвет. Сначала он сереет, потом синеет, краснеет, желтеет и становится почти белым.

Пружина донор разогревается любым доступным способом. Можно использовать горн, газовую или бензиновую горелку. Она греется до темно-красного цвета побежалости, после чего оставляется остывать на воздухе. Такая термообработка называется отжиг. Структура металла пружины меняется, и он становится податливым.

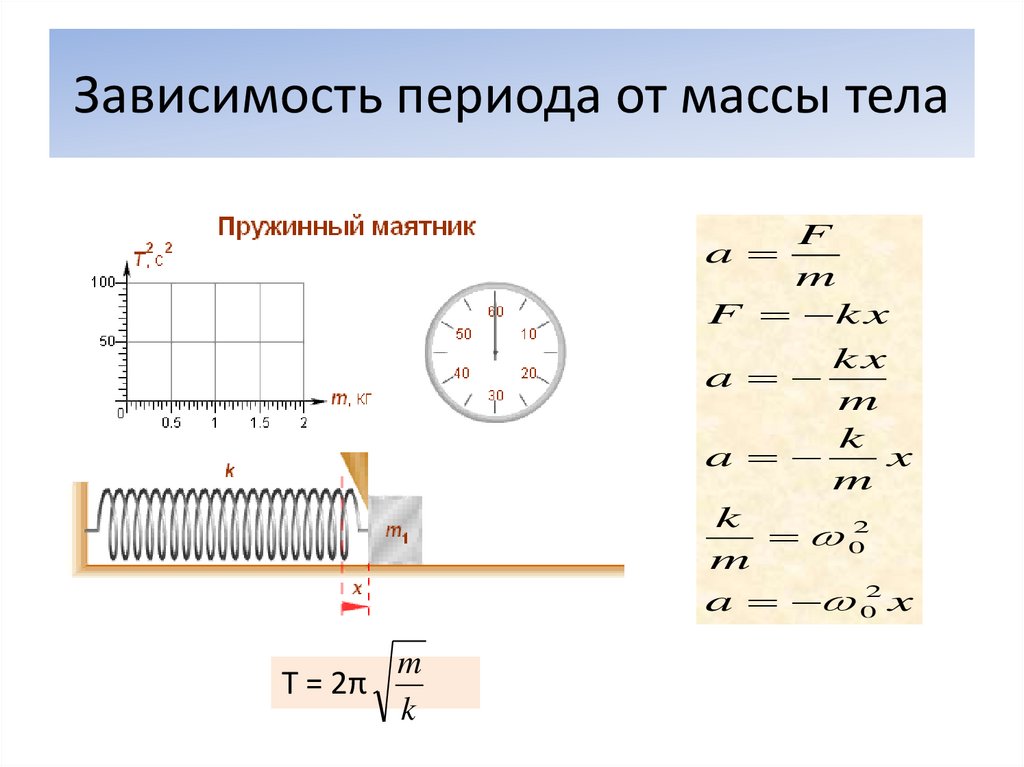Благодаря этому она легко разматывается на проволоку.

Далее проволока наматывается на шаблон нужного диаметра. В его качестве может использоваться прут, болт и т.д. Витки делаются вплотную. Затем заготовка снимается с бланка и из нее формируется необходимая пружина. Если она должна работать на сжатие, то витки разводятся. При изготовлении пружины растяжения в ней формируются проушины. Если же изготавливается торсионное изделие, то края оставляются длинными и ровными.

После этого заготовка снова разогревается до темно-красного цвета и остужается в машинном масле. Это закаляет металл, делая его снова твердым, упругим, но хрупким. Затем изделие снова греется горелкой, но уже до светло-серого цвета и оставляется остужаться на воздухе. В результате металл отпускается. Он сохраняет упругость, но теряет хрупкость. В таком виде изделие уже может использоваться по назначению.

Формы витых пружин

Витые пружины бывают:

Цилиндрические.
Конические.

Навитые на бланк пружины могут иметь не только правильную цилиндрическую форму, но и коническую. В ней каждый новый виток уже предыдущего. Такое изделие применяется в том случае, если на него дополнительно ложиться поддерживающая функция. Оно не только срабатывает на возврат при деформации, но и работает как опора. Конические пружины можно встретить на дорожных классических велосипедах, где они поддерживают сидение.

Цилиндрические и конические пружины могут быть обычными или составными. Составные являются сдвоенными. Это соединенные вместе 2 пружины разного диаметра. Одна располагается снаружи, а вторая ставится между ее витками. Таким образом, они работают вместе, обеспечивая необходимый уровень жесткости.

Механические пружины – типы, жесткость и рабочие расчеты

Мы разработали множество типов механических пружин для различных применений. И все эти типы имеют свои расчеты и характеристики. Если мы должны использовать тип в инженерном приложении, выбор и конструкция этой механической пружины должны быть выполнены на инженерном уровне.

Спиральные пружины

Спиральные пружины, используемые в механических системах пожарной сигнализации.

Мы производим спиральные типы в виде полос, которые мы обычно изготавливаем из металлов. Эти металлические полосы намотаны на ось, которую мы прикрепляем к одной стороне полосы. Провисшая сторона полосы обычно несет нагрузку или усилие. И эта спиралевидная полоса передает нагрузки на оси.

Обычно мы используем спиральные аккумуляторы для хранения энергии. Наиболее важным применением спиральных пружин является часовой механизм. В часовых механизмах мы используем спиральные как в качестве накопителя энергии с настройкой часового механизма. Они используют энергию, запасенную в спиральном типе, для работы часового механизма. Мы используем спиральные также для движущихся действий внутри часовых механизмов. Кроме того, существует множество видов инженерных приложений, в которых мы используем спиральные типы.

Расчет максимального изгибающего напряжения в спиральных пружинах

Если вы думаете об общем механизме спиральных пружин, мы применяем к оси напряжение кручения. Таким образом, действующий тип нагрузки – напряжение изгиба. Вы можете использовать приведенный ниже калькулятор, чтобы рассчитать максимальное напряжение изгиба, возникающее в системе механической пружины и оси.

Максимальное изгибающее напряжение на спиральной пружине

Использовать приведенный выше калькулятор очень просто. Вам просто нужно ввести необходимые значения в данные скобки и нажать на кнопку «Рассчитать!». Результат появится в последней скобке. Если вы хотите сделать другой расчет, просто нажмите кнопку «Сброс», а затем введите новые значения в скобках.

Первый член — это нагрузка. Нагрузка представляет собой полную силу, действующую на слабую сторону спиральной.

Второе слагаемое – это радиус приложения к ним этой нагрузки. Это радиальное расстояние между осью и провисающей стороной.

Ширина – это ширина полосы спирального типа, а толщина – толщина этой полосы.

В скобках мы рекомендуем некоторые единицы измерения. Если вы введете значения в этих единицах, вы получите результат в единицах, указанных в скобках результата. 94)):

Суммарная энергия деформации (Джоули):

Угол отклонения (радианы):

Использование калькулятора выше также очень просто. Здесь значение «длина» представляет собой общую длину полосы спиральной пружины. Модуль упругости — это модуль упругости материалов. Нам нужно рассчитать момент инерции для площади поперечного сечения полосы спиральной пружины.

Как вы видите выше, мы добавили в калькулятор еще и угловое отклонение типа спирали. Вы также можете увидеть результат углового отклонения вашей спиральной системы.

Механические листовые рессоры

Пример применения листовой рессоры (Источник изображения: www.

ttnews.com/articles/leaf-spring-vs-air-ride-opinions-differ-suspensions).

Листовые известны также как многослойные механические рессорные в общей механике. Обычно мы используем пластинчатые системы в тяжелых механизмах, таких как грузовые автомобили, поезда, автобусы и т. д. Из-за отклонения пластин, которые изгибаются, мы получаем демпфирующий эффект.

Обычно мы производим механические листовые рессоры трех типов; эллиптические, полуэллиптические и консольные. В общих типах машин наиболее часто используемым типом листовой рессоры является полуэллиптическая.

Общая механика пружин

Чтобы понять механику и конструктивные характеристики листовых типов, вам необходимо знать некоторую терминологию и информацию об общих классах.

Иногда инженеры используют термин доказательство упругости , который означает максимальную энергию деформации, которую может выдержать механическая пружина. Рассчитываем t модуль упругости как максимальная энергия деформации для единицы объема.

В этих системах в механизмах конструкторы используют их способность к упругой деформации. Механическая пружина на самом деле представляет собой специально разработанные механические элементы, способные выдерживать динамические или статические нагрузки более эффективно, чем объемные формы.

В общем случае они должны выдерживать статическую или динамическую нагрузку в пределах эластичности. Мы не хотим видеть пластическую деформацию в рабочих условиях. Таким образом, должна существовать величина нагрузки, которую механическая пружина может выдерживать в пределах упругости, которую мы называем пробная нагрузка. И мы рассчитываем соответствующее напряжение, используя это значение пробной нагрузки, называемое пробное напряжение.

Их жесткость из них является еще одним важным значением. Мы определяем это как минимальное значение напряжения, которое может вызвать их единичную деформацию.

Требуемое их отклонение должно быть линейным, потому что мы используем механическую пружину в упругой области. После упругой области начинается пластическая область, в которой деформационно-напряженное поведение их носит нелинейный характер.

Описание механических листовых рессор на технической основе

Структура листовых механизмов очень проста. Первый слой системы представляет собой самую длинную пластину, изогнутую с обоих концов. Также мы прикрепляем эти кривые к осям. Мы размещаем другие пластины ниже первой пластины, которая имеет ту же толщину, что и первая пластина.

Мы также называем эту первую пластину основным листом, остальные листы которого короче этого. Но мы можем изготовить второй и третий листы той же длины, что и главный лист, чтобы получить более жесткую структуру.

Зажимаем все эти листья из центра листьев. Этот зажим также несет нагрузку и передает нагрузку на створки.

Между грузом и осями действуют пластины, которые амортизируют динамические нагрузки и воспринимают статические нагрузки.

Расчет напряжения при изгибе механических листовых рессор

Чтобы рассчитать прогиб полуэллиптической листовой системы, нам нужно знать некоторые символические и геометрические переменные листовой системы;

Иллюстрация системы полуэллиптических листовых рессор (Источник изображения: Д.

К. Сингх — Прочность материалов-Springer, 2020, стр. 370).

Как вы видите в представлении листовой системы выше, мы обозначаем диапазон самого большого листа как «l».

Как мы уже говорили выше, толщина каждой пластины одинакова, и мы обозначили это как «t».

Количество пластин, которые мы используем в листовой системе, равно «n».

Возникновение напряжения изгиба в листовой системе — «σ».

Обозначим отклонение эталонной пластины буквой «θ».

Опять же, мы заявили, что кривизна каждой пластины в листовой системе одинакова. Обозначим радиус кривизны листовой системы как «r».

Каждая пластина в листовой системе имеет одинаковую ширину. Мы обозначаем это значение ширины буквой «w».

Нагрузка, действующая на лепестковую систему, которую мы обозначаем буквой «W».

Зная все эти значения, относящиеся к системе механических листовых рессор, вы можете с помощью этого калькулятора рассчитать общее напряжение изгиба в системе пружин;

Калькулятор напряжения при изгибе для листовых рессор

Использовать приведенный выше калькулятор очень просто.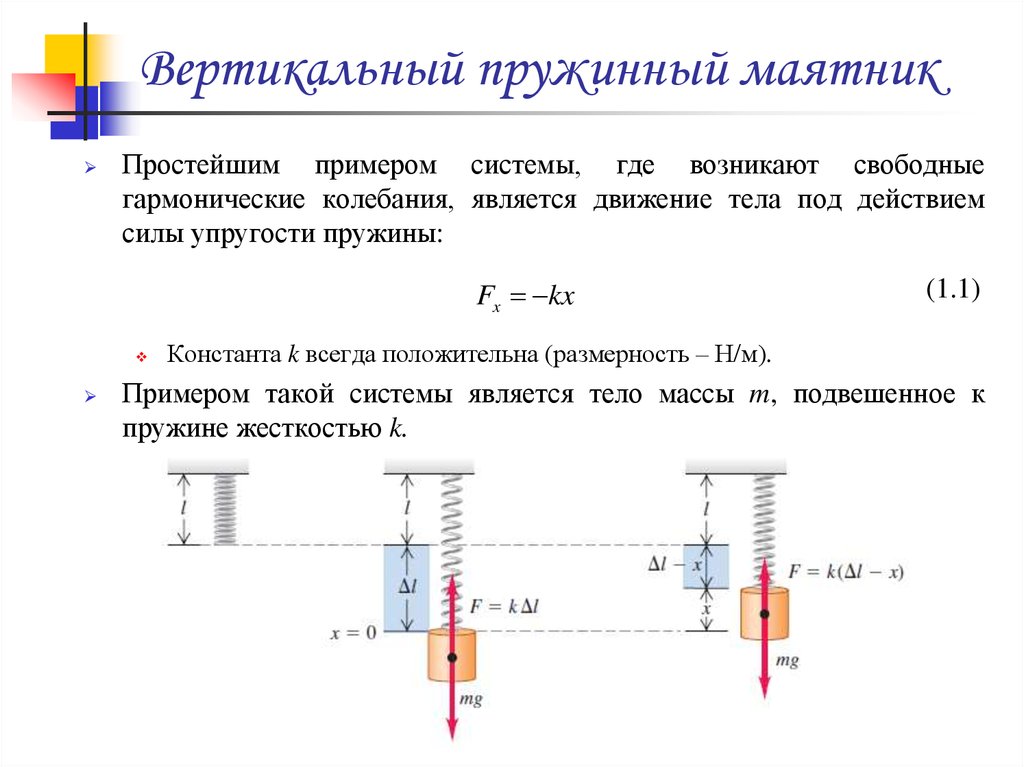 Просто введите нужные значения в скобках. Затем нажмите кнопку «Рассчитать!», чтобы рассчитать напряжение изгиба. Если вы хотите выполнить другой расчет, просто нажмите кнопку «Сброс», а затем снова введите все значения.

Расчет прогиба для механических листовых рессор

Также мы можем легко рассчитать общий прогиб листовой системы. Как и выше, используйте калькулятор ниже, чтобы рассчитать общее отклонение вашей системы створок;

Калькулятор прогиба листовых рессор

Введите нагрузку (N orlbf):

Толщина (мм или дюйм):

Длина (мм пр. дюйм):

Ширина (мм или дюймы):

Количество листьев:

Модуль упругости (ГПа или фунтов на квадратный дюйм):

Напряжение при изгибе:

В этом калькуляторе есть дополнительная переменная — модуль упругости материала механической пружины.

Расчет энергии деформации для механических листовых рессор

Иногда накопленная энергия деформации может быть очень важным параметром для инженеров. Вы можете рассчитать общую накопленную энергию деформации в листовых системах, используя приведенный ниже калькулятор;

Калькулятор энергии деформации для листовых рессор

Введите нагрузку (N orlbf):

Толщина (мм или дюйм):

Длина (мм пр. дюйм):

Ширина (мм или дюймы):

Количество листьев:

Модуль упругости (ГПа или фунтов на квадратный дюйм):

Энергия деформации:

Четвертьэллиптические механические листовые рессоры

Мы также называем четвертьэллиптические листовые рессоры консольными листовыми рессорами. Поэтому мы можем провести их численный анализ при рассмотрении консольных систем. Но нам нужно определить некоторые переменные и геометрические параметры;

Схематическое изображение четвертьэллиптических листовых рессор (Источник изображения: Д. К. Сингх — Прочность материалов-Springer, 2020, стр. 375).

Наш первый параметр — это нагрузка на четвертьэллиптическую листовую систему, которую мы выше обозначили буквой «W».

‘l’ — длина самой длинной пластины в четвертьэллиптической листовой системе.

‘t’ — толщина каждого листа в системе. Считаем каждый лист одинаковой толщины.

‘w’ — ширина каждого листа. Все листья одинаковой толщины.

Количество листьев в четвертьэллиптической системе листьев, которую мы обозначаем как «n».

«E» — модуль упругости материала механической листовой пружины.

Максимальное напряжение изгиба на четвертьэллиптической механической листовой рессоре

Вы можете рассчитать максимальное напряжение изгиба на четвертьэллиптическом листе с помощью калькулятора ниже.

Калькулятор напряжения изгиба для четвертьэллиптических рессорных систем

Введите нагрузку (Н или фунт-сила):

Толщина (мм или дюйм):

Длина (мм или дюймы):

Ширина (мм или дюймы):

Количество листьев:

Максимальное напряжение изгиба:

Использовать приведенный выше калькулятор очень просто. Вам просто нужно ввести необходимые значения в скобках. Затем нажмите кнопку «Рассчитать!», чтобы рассчитать максимальное значение напряжения изгиба. Если вы хотите сделать другой расчет, просто нажмите «Сброс», а затем снова введите каждое значение.

Вы можете ввести свои значения в скобках в единицах, рекомендованных в скобках.

Расчет прогиба четвертьэллиптических механических листовых рессор

Калькулятор прогиба для четвертьэллиптических систем листовых рессор

Введите нагрузку (N orlbf):

Толщина (мм или дюйм):

Длина (мм пр. дюйм):

Ширина (мм или дюймы):

Количество листьев:

Модуль упругости (ГПа или фунтов на квадратный дюйм):

Напряжение при изгибе:

Расчет радиуса кривизны

Под действием определенной нагрузки четвертьэллиптическая листовая система испытывает определенный изгиб. И каждый лист внутри четвертьэллиптической листовой системы будет иметь одинаковый радиус кривизны из-за напряжения изгиба. Вы можете рассчитать это значение радиуса кривизны четвертьэллиптических листовых систем.

Калькулятор радиуса кривизны для четвертьэллиптических рессор

Введите нагрузку (N orlbf):

Толщина (мм или дюйм):

Длина (мм пр. дюйм):

Ширина (мм или дюймы):

Количество листьев:

Модуль упругости (ГПа или фунтов на квадратный дюйм):

Радиус кривизны:

Жесткость механических пружин

Иллюстрация винтовой пружины с тесным витком (Источник изображения: Микелл П. Грувер; Основы современного производства, 4-е издание, стр. 382).

Спиральные механические пружины являются одним из наиболее часто используемых типов в большинстве инженерных приложений. И в различных приложениях на эти винтовые механические пружины действуют осевые силы. Мы определяем значения жесткости в соответствии с этими осевыми силами. И эти значения жесткости имеют формулу;

В этой формуле;

«G» — модуль жесткости материала.
‘d’ – это диаметр проволоки, в которой делаем спираль.
‘R’ – радиус спирали.
‘n’ — количество витков всей геометрии винтовой механической пружины.

Как вы видите выше, расчет коэффициента жесткости механической пружины очень прост, когда на винтовые механические пружины действуют осевые силы.

Что такое угловая жесткость?

Сплошные винтовые пружины могут подвергаться действию углового кручения. Как правило, мы не используем это свойство винтовых пружин в общих механических приложениях. Но в некоторых случаях мы должны учитывать этот физический факт.

С помощью этого скручивающего действия мы должны определить значение «угловой жесткости» механических пружин. Мы определили это значение угловой жесткости с помощью приведенного ниже уравнения;

С этой новой формулой;

«Е» — модуль упругости материала механической пружины.

Параллельные и последовательные комбинации механических пружин

Механические пружины обычно комбинируются последовательно и параллельно. И это сочетание необходимо учитывать в общей величине жесткости этой системы.

Здесь объясняется, как рассчитать жесткость параллельных и последовательных комбинированных пружин.

Расчет жесткости в комбинациях механических пружин

Как уже говорилось выше, эти системы считаются последовательными или параллельными. А рассчитать коэффициенты пружины, которые также называют жесткостью, очень просто.

Параллельные комбинированные механические пружины

Параллельные комбинированные пружины (Источник изображения: socratic.org/questions/what-is-the-spring-constant-in-parallel-connection-and-series-connection).

Параллельные системы в целом аналогичны приведенным выше. Если вы считаете, что эти две механические пружины объединены как параллельные, общая жесткость этой параллельной системы рассчитывается ниже;

Как вы понимаете из этого уравнения, напрямую суммируются жесткости отдельных механических пружин параллельной системы. Это означает, что если вы хотите получить более жесткую систему в своей физической модели, вы можете объединить несколько пружин параллельно.

Серийные комбинированные механические пружины

Комбинация последовательных пружин (Источник изображения: socratic.org/questions/what-is-the-spring-constant-in-parallel-connection-and-series-connection).

Если отдельные механические пружины объединены, как указано выше, вся система называется последовательными пружинами. Расчет общей жесткости последовательных систем отличается от расчета параллельной системы.

Как видно из расчета, обратная общая жесткость последовательной системы относительно умножения равна сумме обратных индивидуальных жесткостей механических пружин относительно умножения снова.

Комбинации сложных механических пружин

С помощью этих двух принципов расчета можно легко рассчитать общую жесткость сложных систем. При расчете этих систем вы должны начать расчет от маленькой системы к большей системе. Выберите маленькую систему внутри всей системы, которая находится далеко от нагрузки или нагрузок.

Расчет работы механической пружины

Во-первых, работа механической пружины — это разновидность механической работы , который вы рассчитываете как разницу между первым и вторым расстоянием сжатия механической пружины. Вы можете высвободить часть энергии, чтобы совершить работу, например, толкая тело или коробку вперед. А также, посчитайте работу с приведенной ниже формулировкой;

Таким образом, в этой формуле «k» – это коэффициент жесткости механической пружины, который измеряется в Н·м или фунт-фут в английских единицах. «x1» и «x2» — первое и второе расстояния, на которые сжимается пружина. Единицами этих расстояний являются м или футы. Единицей механической работы, которую мы рассчитываем для механических пружин, является Вт или фут-фунт-сила/с).

Мы используем их во многих машинах. А также часовые механизмы являются важнейшими примерами использования энергии. А затем накопленная энергия высвобождается контролируемым образом с помощью часового механизма, чтобы дать возможность работать и показывать правильное время. Итак, делаем строгие расчеты работы при проектировании часовых механизмов.

Пока вы выполняете строгие расчеты с механическими пружинами в механических конструкциях, вы, вероятно, будете много раз использовать рабочие расчеты. Чтобы избавиться от этой нагрузки и трудоемких ручных вычислений, мы подготовили простой в использовании и полезный калькулятор работы.

Калькулятор работы пружины

Х ₁ :

х ₂ :

Коэффициент жесткости:

Механическая работа пружины =

Использование калькулятора работы очень просто. Вам просто нужно ввести коэффициент жесткости механической пружины и расстояния сжатия внутри скоб. И нажмите на кнопку «Рассчитать!», чтобы увидеть результат работы.

Если вы хотите произвести другой расчет, просто нажмите кнопку «Сброс» и повторно введите новые значения.

Заключение по механическим пружинам

Выше мы объяснили всю важную информацию о механических пружинах. Вы можете найти все важные моменты о расчетах механических пружин. И у вас не возникнет никаких проблем при расчете механических пружин.

Это основные точки механических пружин. Наконец, не забудьте оставить свои комментарии и вопросы ниже о механических пружинах. Ваши драгоценные отзывы очень важны для нас.

Пружинная постоянная – введение, определение, формула и решенные задачи

Простое гармоническое движение, т.е. SHM, является поистине интригующим типом перемешивания. Он постоянно применяется в колебательном движении объектов. Пружины вообще имеют ШМ. Пружины имеют свои собственные «постоянные пружины», которые определяют их жесткость. Закон Гука — печально известный закон, который объясняет SHM и дает формулу для силы, приложенной с использованием жесткости пружины.

Например, спросите, не постучится ли к вам в дверь группа автомобильных дизайнеров и не поможет ли разработать систему подвески. «Конечно, — говорите вы. Говорят, что автомобиль весит 1000 килограммов и требует использования четырех амортизаторов, каждый длиной 0,5 метра. Насколько сильными должны быть перья? Если предположить, что в этих амортизаторах используются пружины, каждый из них должен выдерживать вес не менее 250 кг:

F = mg = (250 кг) (9,8 м/с ² ) = 2,450 Н

Где F – сила, м – масса объекта, g – ускорение свободного падения, 9,8 м/с ² . Пружина в амортизаторе должна, как минимум, дать вам усилие в 2450 ньютонов при максимальном сжатии 0,5 метра. Что это означает, что жесткость пружины должна быть? Для того, чтобы понять, как рассчитать жесткость пружины, мы должны вспомнить, что говорит закон Гука:

F = –kx

Теперь нам нужно переработать уравнение, чтобы мы вычисляли недостающую метрику, то есть жесткость пружины, или k.

Пружины, используемые в амортизаторах, должны иметь жесткость не менее 4900 ньютонов на метр.

Единицы жесткости пружины

Определение жесткости пружины связано с простыми гармоническими движениями и законом Гука. Итак, прежде чем мы попытаемся определить постоянную пружины и понять ее работу, нам нужно взглянуть на закон Гука. Согласно теории упругости, когда к пружине прикладывается нагрузка, она естественным образом растягивается пропорционально, пока приложенная нагрузка меньше предела упругости. Теперь мы знаем, что когда к объекту прикладывается сила, он каким-то образом деформируется.

Рассмотрим пружину, когда мы прикладываем силу к одной стороне пружины, она сжимается, так как пружина упругая. В это время пружина прилагает силу в направлении, противоположном приложенной силе, чтобы расшириться до своего первоначального размера. Поэтому, чтобы определить жесткость пружины, мы сначала определяем закон Гука. Закон Гука определяется как сила, необходимая пружине, чтобы вернуться к своему размеру, прямо пропорциональна расстоянию сжатия пружины.

(Изображение будет добавлено в ближайшее время)

На изображении показано движение пружины при приложении силы к одной стороне.

Определение постоянной пружины

Чтобы понять определение постоянной пружины, мы рассмотрим формулу закона Гука. Формула закона Гука также известна как формула жесткости пружины. Формула приведена ниже.

Формула	F = -kx
Константы пружины 30398	Нм-1

Где F — восстанавливающая сила пружины, x — смещение пружины, а k — жесткость пружины. Единицы жесткости пружины указаны в ньютонах на метр.

Теперь, когда мы знаем, что k — это жесткость пружины, мы рассмотрим ее определение. Мы определяем жесткость пружины как жесткость пружины. Другими словами, когда смещение пружины составляет одну единицу, мы можем определить постоянную пружины как силу, приложенную для того, чтобы вызвать указанное смещение. Поэтому ясно, что чем жестче пружина, тем выше будет ее жесткость. 9{-2}}{L}]\]

k= – [MT-2]

Единица жесткости пружины выражается в ньютонах на метр (Н/м).

Решенные задачи

Вопрос 1) Пружина растянулась на 40 см, если к ней добавить груз массой 5 кг. Найдите жесткость пружины.

Ответ 1) Дано,

Масса m = 5 кг,

Перемещение x = 40 см = 0,4 м

Чтобы найти постоянную пружины, сначала нужно найти силу, действующую на пружину.

Мы знаем, что F = m * x

Следовательно, F = 5 * 0,4

F = 2 Н

Нагрузка действует на пружину с силой 2 Н. Следовательно, пружина приложит равную и противоположную силу – 2 Н.

Теперь, подставляя значения в формулу жесткости пружины, получаем

k = -F/x

k = \[\frac{-2}{0,4}\]

k = 5 Н/м

Следовательно, жесткость пружины равна 5 Н/м

Вопрос 2) Рассмотрим пружину с жесткостью 14000 Н/м. К пружине приложена сила 3500 Н. Каким будет смещение пружины?

Ответ 2) Дано,

Сила F = 3500 Н,

Постоянная пружины k = 14000 Н/м,

Мы можем рассчитать смещение пружины, используя формулу постоянной пружины.

x= \[\frac{-F}{k}\]

Нагрузка действует на пружину с силой 3500 Н. Следовательно, пружина приложит равную и противоположную силу – 3500 Н.

Таким образом,

x = \[-(\frac{-3500}{14000})\]

x = 0,25 м

x = 25 см

Следовательно, пружина смещена на расстояние 25 см.

Заключение

Так определяется и рассчитывается жесткость пружины. Формула определяется с использованием терминов для определения различных физических величин. Понять, как эта константа используется при решении различных задач из приведенных примеров.

Как рассчитать жесткость пружин – Как отрегулировать и настроить – Секреты подвески

Цилиндрические пружины

Цилиндрические пружины являются наиболее распространенным применением пружин в автоспорте. По этой причине и для получения дополнительной информации о винтовых пружинах обязательно ознакомьтесь с нашей статьей «Винтовые пружины».

Существует два основных способа расчета жесткости пружины. Один из них заключается в расчетах, основанных на осмотре и измерении пружины. Другой – практическим измерением. Практические измерения являются наиболее точными, если они выполняются с использованием правильного оборудования. Оба способа показаны ниже.

Маршрут расчета

На приведенной ниже диаграмме показана цилиндрическая пружина вместе со следующими важными параметрами, которые необходимы для расчета жесткости пружины.

Важными параметрами являются:

L = свободная длина ненагруженной пружины (м)
G = Модуль сдвига жесткости материала
d = диаметр проволоки (м)
D = средний диаметр (м)
N = количество активных катушек (активная катушка проходит один полный круг)

Где:

Длина в свободном состоянии — это расстояние от верхней поверхности пружины до нижней поверхности пружины, когда на нее не действует нагрузка.
Модуль жесткости при сдвиге зависит от типа материала, из которого изготовлена пружина. Значение можно найти в таблице ниже. Все, что вам нужно, это выяснить, из какого материала сделана ваша пружина. Если вы не уверены, наиболее распространенный материал выделен в таблице жирным шрифтом.

Материал	Модуль жесткости при сдвиге (G)
Пружинная сталь ANSI 1095	79 300 000 000 Па
Холоднокатаная сталь	75 000 000 000 Па
Нержавеющая сталь	77 200 000 000 Па

Диаметр проволоки – толщина металла рулона, наиболее точно измеряемая штангенциркулем
Средний диаметр показан на диаграмме и представляет собой расстояние между центрами цилиндрической пружины. Самый простой способ получить это число — использовать приведенное ниже уравнение.
- Средний диаметр = общий диаметр пружины – диаметр проволоки
Число активных витков все еще не определено в отрасли относительно того, как применять точное число для типа пружины. На приведенной ниже диаграмме показаны 4 распространенных типа винтовых пружин на концах.

- Закрытые концы
- Закрытые и шлифованные концы
- Плоские концы, заземленные
- Плоские концы

В настоящее время отраслевым стандартом является то, что пружина с закрытыми концами или закрытыми и шлифованными концами имеет по одному неактивному витку на каждом конце, что означает, что из общего количества витков для параметра «количество активных витков» необходимо убрать два витка.

Однако считается, что пружины с гладкими концами не имеют неактивных витков, поэтому каждый отдельный виток учитывается в параметре «количество активных витков».

Наконец, считается, что пружины с гладкими шлифованными концами имеют половину неактивного витка на каждом конце, что означает, что для параметра «количество активных витков» удаляется всего 1 виток.

Очень важно понимать, как обрабатываются ваши пружины, поскольку параметр количества активных витков может иметь большое влияние на расчетную жесткость пружины.

Уравнение

Когда ваши измерения завершены, пришло время рассчитать жесткость винтовой пружины с помощью приведенного ниже уравнения.

Следовательно:

Таким образом, используя цифры примера:

G = 79,3 ГПа
д = 10,3 мм
Н = 6
Д = 68,5 мм

Практический метод

Если у вас есть доступ к некоторому испытательному оборудованию, то практический метод является наиболее точным вариантом для расчета жесткости пружины. Машина, такая как Тинниус-Олсен, показанная ниже, является идеальной частью оборудования для этого теста. Если у вас есть доступ к одному или чему-то подобному, вставьте пружину в машину и сожмите ее на 10 мм. Запишите усилие, необходимое для его сжатия в этой точке. Затем сжимайте пружину поэтапно по 10 мм, записывая необходимое усилие в каждой точке. Если к концу испытания пружина начинает перенапрягаться, не сжимайте ее, так как это может повредить пружину.

Со всеми вашими результатами в формате, аналогичном приведенному ниже примеру, конвертируйте все ваши миллиметровые показания в метры. Затем разделите требуемую силу на пройденное расстояние в каждом случае. Если все ответы на этот вопрос выглядят одинаково, то у вас есть пружина с постоянной скоростью. Теперь вы можете сложить все ответы и разделить его на количество результатов, чтобы получить среднее значение, которое является вашей скоростью весны.

Если ответы постепенно уменьшаются или увеличиваются на заметную величину, то у вас есть прогрессивная пружина скорости. Если это так для вас, было бы лучше построить график ваших результатов n excel, отслеживая жесткость пружины в зависимости от мм сжатия. Это очень важная информация, которую необходимо знать при применении предварительной нагрузки к пружине. Кроме того, если вы знаете, насколько ваш автомобиль опускается, когда он сидит на колесах, вы можете рассчитать статическую жесткость ваших пружин при дорожном просвете для использования в будущем.

Листовые рессоры

Расчет коэффициента жесткости листовой рессоры намного сложнее, чем для винтовой пружины. Это связано с количеством переменных, которые могут применяться к листовым рессорам, таким как; толщина листа, ширина и конусность, вариации торцевых ограничений или нагрузка, приложенная не по центру и т. д. Таким образом, наиболее точным способом измерения жесткости листовой рессоры является практический. Однако для точного ответа вы также можете использовать маршрут расчета, где необходимо сделать некоторые приближения.

Путь расчета

В автомобилестроении используются листовые рессоры двух основных типов. Они бывают «одностворчатые параболические» и «многослойные рессорные». Последнее более распространено в современных приложениях. На изображениях ниже показаны различные типы.

Однолистовая параболическая

Многослойная листовая рессора

Для листовых рессор применяются два уравнения. Одним из них является формула напряжения изгиба, чтобы гарантировать, что максимальная нагрузка не приведет к чрезмерному напряжению материала. Другое дело жесткость пружины. Именно эта цифра важна для дальнейших расчетов. Уравнения для однолистовой параболической рессоры:

И:

Где:

L = половина общей длины самой длинной листовой рессоры (м)
F = Сила, приложенная к каждой точке крепления к шасси (обычно половина нагрузки, приложенной к точке оси) (м)
b = ширина листовой рессоры в центральной точке (м)
t = высота листовой рессоры по вертикали в центральной точке крепления к оси (м)
E = модуль Юнга для материала (Па) (см. таблицу ниже)
X = смещение пружины по вертикали (м)

Уравнения для ламинированной листовой рессоры немного различаются:

И:

Где:

L = половина общей длины самой длинной листовой рессоры (м)
F = Сила, приложенная к каждой точке крепления к шасси (обычно половина нагрузки, приложенной к точке оси) (м)
b = ширина листовой рессоры в центральной точке (м)
n = количество листов в стопке
n’ = количество лепестков непосредственно на концах пружины
t = высота листовой рессоры по вертикали в центральной точке крепления к оси (м)
E = модуль Юнга для материала (Па) (см. таблицу ниже)
X = смещение пружины по вертикали (м)

Таблица модуля Юнга для обычных материалов

Материал	Модуль Юнга (E)
АНСИ 1095 Пружинная сталь	207 000 000 000 Па
Холоднокатаная сталь	186 000 000 000 Па
Мягкая сталь	210 000 000 000 Па

Практический маршрут

Более точный способ измерения жесткости листовых рессор — это их практические испытания, если у вас есть правильное оборудование для приложения нагрузки. Чтобы проверить нагрузку, вам нужно отсоединить ось от пружины и отодвинуть ее от непосредственно под пружиной. Затем необходимо приложить нагрузку с помощью устройства, которое будет измерять величину прилагаемой нагрузки в ньютонах силы. Листовую пружину необходимо отклонять с шагом в 10 мм с регистрируемой силой, необходимой для перемещения пружины. Для каждого шага силу можно разделить на смещение, чтобы получить жесткость пружины, используя приведенное ниже уравнение. Если числа имеют большой разброс и увеличиваются каждый раз после использования приведенного ниже уравнения, то пружина имеет прогрессивную скорость, и следует построить график в Excel, чтобы показать, какая скорость присутствует в каждой точке смещения, так как это будет более точным. чем с помощью уравнения.

Где:

F = приложенная сила (Н)
x = водоизмещение (м)

Как преобразовать метрические единицы в британские

Если вы предпочитаете, чтобы жесткость пружины выражалась в фунтах и дюймах, вы можете использовать приведенное ниже уравнение преобразования, чтобы преобразовать результат из ньютонов на метр в фунты на дюйм.

Аналогичным образом, если вы хотите преобразовать фунты на дюйм в ньютоны на метр, введите значение фунтов на дюйм в приведенном ниже примере, и я выдам ответ в ньютонах на метр.

Как добавить жесткость пружины для нескольких пружин

Существует две конфигурации, в которых используются несколько пружин. Одна из них — это последовательные пружины, а другая — параллельные. Можно считать, что автомобиль имеет параллельные пружины, потому что, если вы посмотрите на переднюю ось автомобиля, каждое колесо как собственная пружина, действующая на переднюю часть автомобиля, что в сумме дает две пружины, работающие бок о бок. Это делает их параллельными.

Пружины серии

Ниже показано несколько примеров, когда пружину можно рассматривать последовательно.

Когда две или более пружин накладываются друг на друга, общая жесткость пружины всегда становится меньше, чем у самой мягкой пружины. Это связано с тем, что вы фактически добавили еще больше витков к более мягкой пружине (N), что снижает общую жесткость пружины. Прежде чем можно будет использовать приведенное ниже уравнение для расчета общей жесткости последовательно соединенных пружин, необходимо знать жесткость каждой отдельной пружины. Если две пружины используются последовательно, можно использовать следующее уравнение:

Где:

Всего K = Суммарная жесткость пружины
K1 = жесткость нижней пружины
K2 = Максимальная жесткость пружины

Если более двух пружин соединены последовательно, то следующая пружина может продолжать добавляться к уравнению для всех пружин; например, в случае 4 пружин, установленных друг на друга, уравнение будет выглядеть следующим образом:

Параллельные пружины

Параллельные пружины также можно получить несколькими способами. На изображениях ниже показано несколько примеров, когда пружины можно рассматривать параллельно.

Пружины называются параллельными, если они всегда разделяют нагрузку. Суммарную жесткость параллельных пружин рассчитать гораздо проще, чем последовательно соединенных пружин, поскольку жесткости пружин просто складываются. Приведенное ниже уравнение можно использовать для расчета общей эффективной жесткости параллельных пружин:

И так далее.