Жесткость пружины при последовательном соединении: Физика и математика для школьников

alexxlab | 06.03.2022 | 0 | Разное

Содержание

1.1-01. Закон Гука. – Лабораторная экспериментальная площадка для школьников

В данной работе Вы изучите упругое растяжение нескольких пружин под действием силы тяжести. Проведёте серию экспериментов для нахождения коэффициента жёсткости этих пружин. В ходе эксперимента увидите влияние массы пружины на растяжение и как его можно учесть при проведении эксперимента. Дополнительным заданием будет определение коэффициента жёсткости системы пружин при параллельном и последовательном соединении.

Теоретический минимум: закон Гука, сила, сила упругости, сила тяжести, ускорение свободного падения, масса, коэффициент жёсткости, деформация, упругая деформация, неупругая деформация.

Лабораторная работа рекомендуется для учащихся 8, 9 классов.

Краткое методическое описание.

Цель работы:

Познакомиться с законом Гука на примере деформации пружин. Определить жёсткость двух или более пружин, проверить линейную зависимость силы упругости от удлинения пружины. Научиться проводить измерения и обрабатывать экспериментальные данные.

Порядок выполнения лабораторной работы:

Задание. Измерение жёсткости пружин №1 и №2.

Закрепить пружину №1 на стержне с крючком и отметить на шкале с помощью курсора нижний край пружины.
Подобрать начальную массу груза, и измерить его массу вместе с держателем для груза.
Подвесить держатель с грузом на нижний край пружины.
Отметить вторым курсором положение нижнего края пружины после её растяжения под действием силы тяжести.

Определить растяжение пружины и внести измеренные величины в таблицу.

Таблица 1. Экспериментальные данные.
№	m, г	F_т, Н	x₀, мм	x’, мм	l, 10^-3м
. ..	…	…	…	…	…

Добавить груз на держатель и повторить пункты 3-5. Провести измерения для 5 разных масс.
Построить график зависимости силы от удлинения пружины.
По графику определить жёсткость пружины.
Оценить погрешность измерений и полученной величины.
Закрепить пружину №2 и повторить пункты 1-9 для второй пружины.

Дополнительное задание. Параллельное и последовательное соединение пружин.

Закрепить параллельно пружины №1 и №2 и повторить задание «Измерение жёсткости пружин №1 и №2» для параллельного соединения пружин.
Закрепить последовательно пружины №1 и №2 и повторить задание «Измерение жёсткости пружин №1 и №2» для последовательно соединения пружин.
Провести расчёт жёсткости систем при последовательном и параллельном соединении пружин и сравнить результаты с экспериментальными данными.

Метки: 8 класс, 9 класс

Комбинированная жесткость двух последовательно соединенных пружин Калькулятор

✖Жесткость первой пружины — это сила на единицу длины, необходимая для отклонения первой пружины.ⓘ Жесткость 1-й пружины [K₁]

Килоньютон на метрКилоньютон на миллиметрМиллиньютон на метрМиллиньютон на миллиметрНьютон на метрНьютон на миллиметрфунт-сила на дюйм

+10%

-10%

✖Жесткость второй пружины — это сила на единицу длины, необходимая для отклонения второй пружины.ⓘ Жесткость 2-й пружины [K₂]

+10%

-10%

✖Эквивалентная жесткость пружины — это единая жесткость пружины, полученная путем объединения различных констант пружины.

ⓘ Комбинированная жесткость двух последовательно соединенных пружин [K_eq]

⎘ копия

👎

Формула

сбросить

👍

Комбинированная жесткость двух последовательно соединенных пружин Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Жесткость 1-й пружины: 15 Ньютон на миллиметр –> 15000 Ньютон на метр (Проверьте преобразование здесь)
Жесткость 2-й пружины: 12 Ньютон на миллиметр –> 12000 Ньютон на метр (Проверьте преобразование здесь)

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

6666.66666666667 Ньютон на метр –>6.66666666666667 Ньютон на миллиметр (Проверьте преобразование здесь)

< 4 Последовательные и параллельные соединения Калькуляторы

Комбинированная жесткость двух последовательно соединенных пружин формула

Эквивалентная жесткость пружины = Жесткость 1-й пружины*Жесткость 2-й пружины/(Жесткость 1-й пружины+Жесткость 2-й пружины)
K_eq = K₁*K₂/(K₁+K₂)

Определить механическую пружину?

Пружина из металлической проволоки, которая функционирует в пружинном механизме, который сжимает, расширяет, вращает, скользит, тянет и прикладывает силу при приложении равной или большей силы. Пружинный механизм может оказывать давление, вращающую силу или силу натяжения различными способами.

Copied!

Какова жесткость пружины при параллельном и последовательном соединении?

Ответ

Проверено

161,1 тыс.+ просмотров

Подсказка: Говорят, что две невесомые пружины, подчиняющиеся закону Гука, соединены параллельно, если они соединены тонким вертикальным стержнем, как показано на диаграмме ниже. Формула для конденсаторов, соединенных параллельно в электрической цепи, может быть использована для нахождения значения k.

Полный ответ:
Для параллельных:

Две невесомые пружины, подчиняющиеся закону Гука, называются параллельными, если они соединены тонким вертикальным стержнем.
$k_{1}$ и $k_{2}$ — жесткость пружины 1 и 2. На стержень действует постоянная сила $F$, которая удерживает его перпендикулярно направлению действия силы. Чтобы пружины были одинаковой длины. Пружины также могли быть сжаты, если сила была изменена на противоположную.
Одна пружина Гука с жесткостью $k$ эквивалентна этой системе из двух параллельных пружин. Формула для параллельных конденсаторов в электрической цепи может быть использована для расчета значения $k$.
$k=k_{1}+k_{2}$
Для серии

Здесь эквивалентная жесткость пружины будет равна
$k=\dfrac{{{k}_{1}}{{k}_{2 }}}{{{k}_{1}}+{{k}_{2}}}$
Если одни и те же пружины соединены последовательно, как показано на схеме ниже, это называется последовательным соединением. . К пружине 2 приложена постоянная сила F. В результате пружины удлиняются, а общее удлинение комбинации равно сумме удлинений каждой пружины. В качестве альтернативы пружины можно сжать, изменив направление силы на противоположное.
Одна пружина с жесткостью k эквивалентна этой системе из двух последовательно соединенных пружин.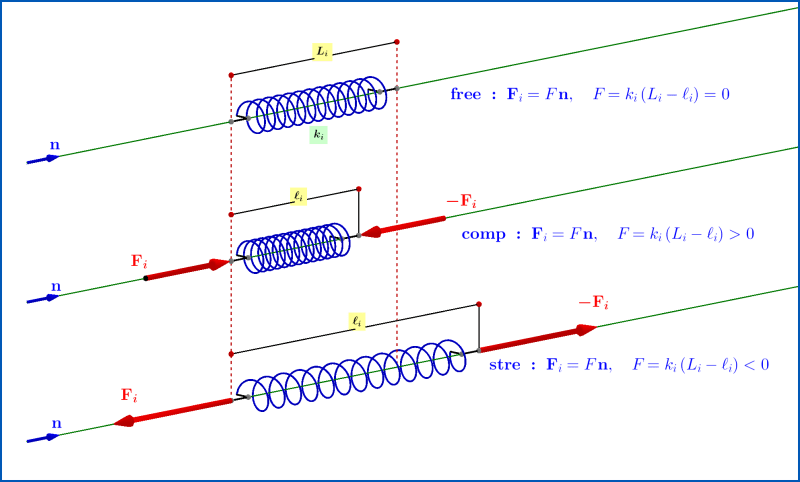 Формула для конденсаторов, соединенных последовательно в электрической цепи, может быть использована для расчета значения k.

Примечание: Если в механике две или более пружины соединены встык или точка-в-точку, говорят, что они соединены последовательно, а когда они соединены бок о бок, говорят, что они быть параллельным; в обоих случаях они действуют как одна пружина.

Недавно обновленные страницы

Какой элемент обладает наибольшим радиусом атомов А 11 класс химии JEE_Main

Высокоэффективный метод получения бериллия 11 класс химии JEE_Main

Какой из следующих сульфатов имеет наибольшую растворимость 11 класс химии JEE_Main

Среди металлов Be Mg Ca и Sr группы 2 химии класса 11 JEE_Main

Какой из следующих металлов присутствует в зеленой маркировке класса 11 химии JEE_Main

Для предотвращения окисления магния в электролите химии класса 11 JEE_Main

Какой элемент обладает наибольшим радиусом атомов А 11 класс химии JEE_Main

Высокоэффективный метод получения бериллия 11 класс химии JEE_Main

Какой из следующих сульфатов имеет наибольшую растворимость 11 класс химии JEE_Main

Среди металлов Be Mg Ca и Sr группы 2 химии класса 11 JEE_Main

Какой из следующих металлов присутствует в зеленой маркировке класса 11 химии JEE_Main

Для предотвращения окисления магния в электролите химии класса 11 JEE_Main

Трендовые сомнения

Две пружины соединены последовательно и прикреплены к блоку массой $ m $, который находится в равновесии.

Постоянные пружины и растяжения в пружинах показаны на рисунке, тогда сила, действующая пружиной на блок, равна (A) $ \dfrac{{{k_1}{k_2}}}{{{k_1} + {k_2} }}\left( {{x_1} + {x_2}} \right) $ (B) $ {k_1}{x_1} + {k_2}{x_2} $ (C) $ {k_1}{x_1} $ (D) Ничего из этого

Ответ

Подтверждено

205,8 тыс.+ просмотров

Подсказка: По закону Гука общая сила, действующая на блок, будет равна натяжению обеих струн и эффективной жесткости пружины. Пружины соединены последовательно, эффективная постоянная силы является обратной суммой обратной величины отдельной жесткой постоянной или обратная эффективная постоянная силы равна сумме обратной величины каждой из пружинных постоянных.

Используемая формула В этом решении мы будем использовать следующие формулы;
$F = ke$, где $F$ — сила пружины, $k$ — постоянная силы, $e$ — удлинение пружины.
$ \dfrac{1}{{{k_{eqs}}}} = \dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}} $, где $ {k_{eqs }} $ — это эквивалентная жесткость двух последовательно соединенных пружин, $ {k_1} $ — жесткость одной пружины, а $ {k_2} $ — жесткость другой.

Полное пошаговое решение:
Чтобы решить этот вопрос, отметим, что две пружины соединены последовательно. И что сила, создаваемая такой пружиной, может рассматриваться как произведение эффективной постоянной пружины и полного удлинения пружин. Как правило, сила, действующая на пружину, равна
$F = ke$, где $F$ — сила пружины, $k$ — постоянная силы, $e$ — удлинение пружины.
Тогда для последовательно соединенных пружин имеем
$ F = {k_{eqs}}e $, где $ {k_{eqs}} $ — эффективная силовая постоянная сети. Само по себе это определяется как
$ \dfrac{1}{{{k_{eqs}}}} = \dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}} $ где $ {k_{eqs}} $ — эквивалентная жесткость двух последовательно соединенных пружин, $ {k_1} $ — жесткость одной пружины, а $ {k_2} $ — жесткость другой.
Фактически сложив их, мы имеем
$ \dfrac{1}{{{k_{eqs}}}} = \dfrac{{{k_1} + {k_2}}}{{{k_1}{k_2}}} $
$ \Rightarrow {k_{eqs}} = \dfrac{{{k_1}{k_2}}}{{{k_1} + {k_2}}} $

Следовательно, приложенная сила будет равна
$ F = \dfrac{{ {k_1}{k_2}}}{{{k_1} + {k_2}}}\left( {{x_1} + {x_2}} \right) $
Правильный вариант A.

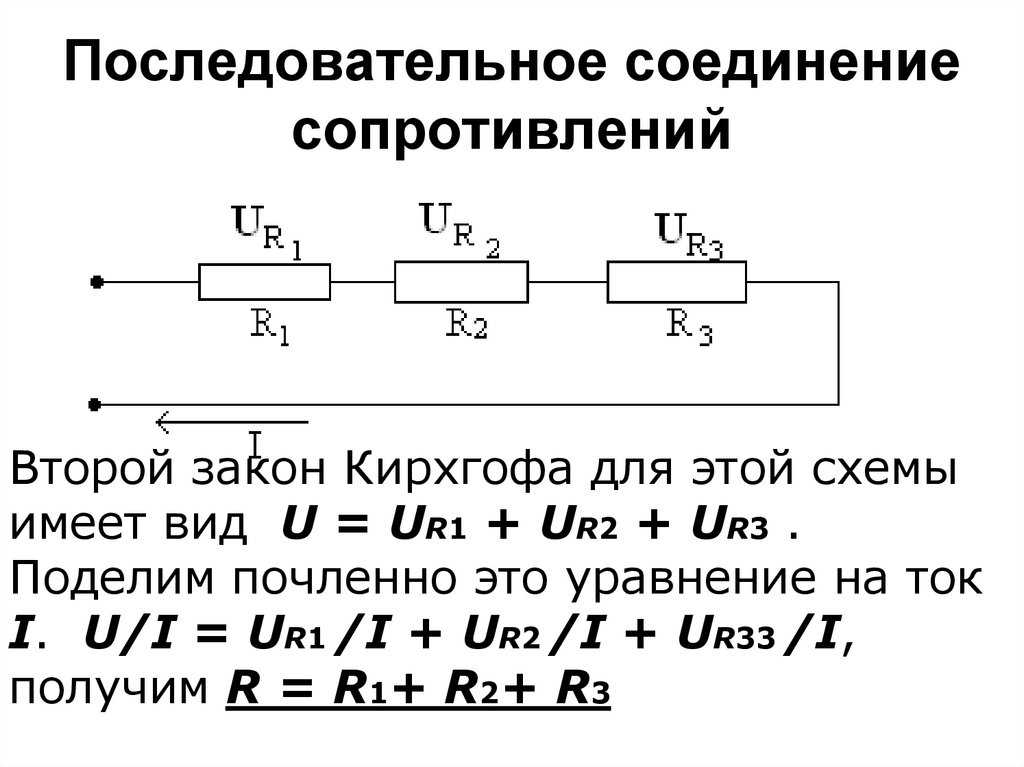TOP HEADLINES