Зубчатое колесо коническое чертеж: ГОСТ 2.405-75 ЕСКД. Правила выполнения чертежей конических зубчатых колес
alexxlab | 10.01.2020 | 0 | Разное
Чертеж – коническое зубчатое колесо
Чертеж – коническое зубчатое колесо
Cтраница 1
Чертежи конических зубчатых колес с прямолинейным профилем исходного контура выполняются по ГОСТ 2.405 – 75 в части указания параметров зубчатого венца и по другим стандартам ЕСКД. [1]
Чертеж конического зубчатого колеса ( см. рис. 21) начинают тонкими линиями с проведения горизонтальной оси. [2]
На чертежах конических зубчатых колес кроме размеров, определяющих форму и габариты детали, приводят размеры венца ( рис. 22.26, а, б): внешние диаметры dae и dae; угол 8а конуса вершин зубьев; угол 8 делительного конуса; угол ( 90 – 5) внешнего дополнительного конуса. Звездочкой обозначены размеры для справок. [3]
На чертеже конического зубчатого колеса обозначают внешний диаметр вершин зубьев до притупления кромки dae и внешний диалгетр вершин зубьев после притупления кромки d ae, поскольку конус вершин зубьев и внешний делительный дополнительный конус на поверхности колеса не пересекаются. Наличие этой поверхности обусловлено тем, что часть цилиндрической поверхности заготовки длиной 1 х сохраняется при обработке по конусу вершин зубьев и внешнему делительному дополнительному конусу. Величину 1 х для мелкомодульных конических зубчатых колес принимают равной 0 1 мм. [4]
На чертеже конического зубчатого колеса помещают таблицу параметров зубчатого венца, которая должна состоять из трех частей, отделенных друг от друга сплошными основными линиями: первая часть – основные данные; вторая – данные для контроля; третья – справочные данные. [5]
На чертеже конического зубчатого колеса на изображении или в технических требованиях допускается приводить данные о форме, расположении и поведении зоны касания.
В какой последовательности выполняется чертеж конического зубчатого колеса. [8]
В какой последовательности выполняют чертеж конического зубчатого колеса. Какие данные указывают на изображении конического зубчатого колеса. [9]
Примеры простановки размеров на чертежах конических зубчатых колес приведены на фиг. Кроме основных значений, в штампе нужно указать еще и межосевой угол. [10]
Пример указания параметров зубчатого венца на чертеже прямозубого конического зубчатого колеса со стандартным исходным контуром приведен на рис. 5.5. На чертеже помещается таблица параметров зубчатого венца, состоящая из трех частей, отделяемых сплошными основными линиями. [11]
На рис. 16.44 приведен в качестве примера чертеж конического зубчатого колеса, из которого видно также и содержание таблицы для нарезания зубьев. [12]
На рис. 268, в, г, д показана последовательность построения чертежа конического зубчатого колеса. Начинают с вычерчивания двух делительных конусов, имеющих общую образующую, нижний конус принадлежит колесу, верхний – сопряженной с ним шестерне. [14]
Размеры толщины зуба s и высоты его головки hx по зубомеру ( рис. 149, а) определяют, зная модуль и число зубьев, используя соответствующие справочники, и проставляют в таблице параметров, обычно на чертежах конических зубчатых колес. [15]
Страницы: 1 2Краевая научно-техническая олимпиада обучающихся | ГБУ ДО “Краевой Центр развития творчества детей и юношества им.
Ю.А. Гагарина”Подведены итоги краевой научно-технической олимпиады обучающихся
В краевой научно-технической олимпиаде обучающихся приняли участие 1025 обучающихся из 119 образовательных организаций края.
Определены победители и призеры:
среди обучающихся 8-9 классов
1 место – Кириченко Екатерина, МБОУ СОШ №10 с. Крымгиреевского Андроповского муниципального округа, руководитель Тучина Наталья Николаевна;
2 место – Майлубаев Юсуф, МОУ СОШ №2 им. Н.Д. Терещенко с. Иргаклы Степновского муниципального округа, руководитель Грянкина Алла Альбиновна;
3 место – Таранишина Ирина, МКОУ СОШ № 4 с. Петропавловское Арзгирского муниципального округа, руководитель Смирнова Елена Алексеевна;
среди обучающихся 10-11 классов
1 место – Бурец Юлия, МКОУ СОШ №2 с. Левокумского Левокумского муниципального округа, руководители Богданова Н.С., Коробченко Т.В.;
1 место – Аукина Валерия, МКОУ СОШ №4 с. Петропавловского Арзгирского муниципального округа, руководитель Смирнова Елена Алексеевна;
2 место – Майлубаев Ясин, МОУ СОШ №2 им. Н.Д. Терещенко с. Иргаклы Степновского муниципального округа, руководитель Майлубаева Румяна Хабибуллаевна;
2 место – Низамединов Малик, МОУ СОШ №2 им. Н.Д. Терещенко с. Иргаклы Степновского муниципального округа, руководитель Науманова Радмила Арифуллаевна;
3 место – Агаев Бекхан, МКОУ «СОШ №6» Изобильненского городского округа, руководитель Хан Ирина Ивановна;
3 место – Докторов Илья, учащийся МОУ СОШ №1 имени Героя Советского Союза И.И. Тенищева с. Александровского Александровского муниципального округа, руководитель Аполохова Ирина Васильевна;
среди студентов 1 курса
профессиональных образовательных организаций
1 место – Бурляев Дмитрий, ГБПОУ «Невинномысский энергетический техникум», руководитель Чумакова Юлия Владимировна;
2 место – Стрельникова Татьяна, ГБПОУ «Георгиевский региональный колледж «Интеграл», руководитель Серкова Наталья Алексеевна;
3 место – Грицынчук Анна, ГБПОУ «Александровский сельскохозяйственный колледж», руководитель Чернышова Юлия Петровна.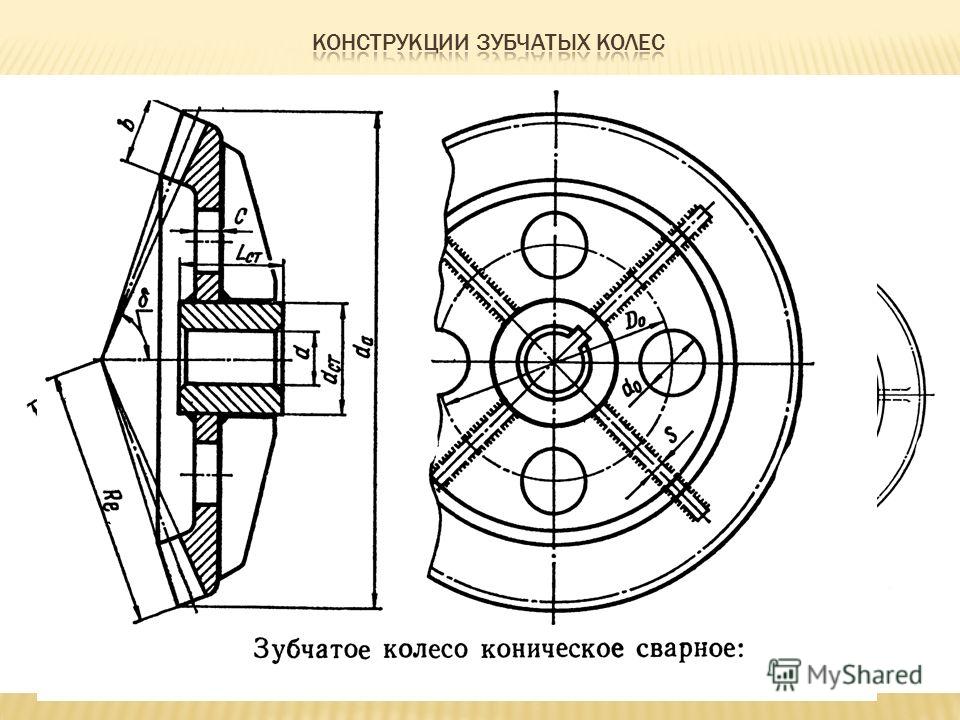
Победители и призеры Олимпиады награждаются дипломом оргкомитета.
Предыдущее
Определены победители регионального этапа Всероссийского литературного конкурса «Класс!»
Коническое зубчатое колесо Чертеж № ПКО-10033.02
Предназначен для передачи крутящего момента
Число зубьев 16 шт.; модуль 2,25; Диаметр 55,17 мм; Длина 220 мм. Тип зубьев: конические круговые
Place of delivery:
Self-delivery
Product delivery order:
Self-delivery
List of documentation transmitted with the product:
Справка с органа сертификации
Product completeness:
1 деталь
Warranty and maintenance:
12 month
Requirements for the shelf life of the product:
5 year
Хранить в закрытых помещениях без отопления
Presence of the comformity certificate for the product:
Чертежи зубчатого колеса: обозначение, оформление, правила выполнения
Конструкция и параметры зубчатого колеса
Оно содержит венец с зубьями, диск и ступицу.
Имеется три наиболее важных его параметра: модуль, диаметр делительной окружности и количество зубьев. Какую же делительную окружность имеет зубчатое колесо? Чертеж цилиндрического колеса с типовыми эвольвентными зубьями показан ниже.
pmd
m = d/z= p/3,14, мм.
Например, зубчатое колесо с 22 зубьями и диаметром 44 мм имеет модуль m = 2 мм. Сцепленные шестерни должны обе иметь один модуль. Значения их стандартизованы, и как раз на делительной окружности модуль данного колеса принимает свое стандартное значение.
Высота головки зуба одного колеса меньше высоты ножки зуба второго, зацепляющегося с ним, благодаря чему образуется радиальный зазор c.
Для обеспечения бокового зазора δ между двумя сцепленными зубьями сумма их толщин принимается меньше их окружного шага p. Радиальный и боковой зазоры предусматриваются для создания необходимых условий смазки, нормальной работы передачи при неизбежных неточностях изготовления и сборки, тепловом увеличении размеров передачи и т. п.
Цилиндрические зубчатые колеса(шестерни):
Цилиндрические зубчатые колеса используются в передачах, где оси валов располагаются параллельно относительно друг друга. При этом они могут располагаться как горизонтально, так и вертикально.
В зависимости от формы продольной линии зуба зубчатые колеса бывают: прямозубые, косозубые и шевронные.
Рис. 1. Цилиндрические зубчатые колеса: прямозубые, косозубые и шевронные
Прямозубое колесо. Этот вид шестерен ввиду своей простой конструкции является наиболее внедряемым в различных системах. В таком виде зубья шестерен располагаются в плоскости, которая перпендикулярна оси вращения. В отличии от косозубых и шевронных колес у данного вида предельный крутящий момент ниже.
Косозубое колесо. Зубья для данного вида колес выполняются под определенным углом к оси вращения шестерен, а по форме образуют часть винтовой линии. По сравнению с прямозубым колесом при работе зубьев данного вида зацепление зубьев происходит плавнее, а за счет увеличенной площади контакта предельный крутящий момент выше.
Но для работы колес с косым зубом приходится применять упорные подшипники, так как возникает механическая сила, направленная вдоль оси. В основном косозубые колёса используются там, где нужны передачи большого крутящего момента на высоких скоростях.
Шевронное колесо. Этот вид имеет зубья, которые выполнены в форме буквы V на плоскости вращения колеса. Главной особенностью шевронных колес является то, что силы на осях обеих половин компенсируются, вследствие чего отпадает необходимость в использовании упорных подшипников. Различают шевронное и многошевронное цилиндрическое зубчатое колесо, состоящее соответственно из двух и более полушевронов, а также шевронное цилиндрическое зубчатое колесо со сплошным венцом и разделенными полушевронами.
В отдельные виды выделяются: цилиндрическое колесо с круговыми зубьями, цилиндрическое колесо со смещением (без смещения), циклоидальное, эвольвентное и цевочное цилиндрическое колеса.
Колесо с круговыми зубьями. Передачу с такими колесами называют передачей Новикова. При такой передаче контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс. Зубья данного вида колеса выполнены в виде полукруга, радиус которого подбирается под нужные требования. Колеса с круговыми зубьями в сравнении с косозубыми обладают более высокой нагрузочной способностью зацепления, высокой плавностью и бесшумностью работы, но при тех же условиях работы у них снижен КПД и ресурс работы, что не позволяет их применять широко.
Колесо со смещением либо без смещения. Это зубчатое колесо, зубья которого образованы при номинальном положении исходной производящей рейки, характеризуемом отсутствием касания (касанием) делительных поверхностей исходной производящей рейки и обрабатываемого зубчатого колеса.
Циклоидальное колесо. В данном виде профили зубьев шестерни выполнены по циклоидальной кривой. Однако при таком способе зацепления шестерен имеется большой недобор чувствительности из-за изменения расстояния между осями.
Циклоидальное колесо применяется в основном в приборостроении. Колесо сложно в изготовлении, поскольку при его создании требуется использование очень многих специальных зуборезных инструментов.
Цевочное колесо. В данном случае зубья одного из колес имеют вид пальцев в форме цилиндра. Такой вид шестерен образовался на базе циклоидального колеса и получил более широкое применение как в машиностроении, так и в приборостроении.
Коническое зубчатое колесо чертеж, зацепление
Конические зубчатые колёса
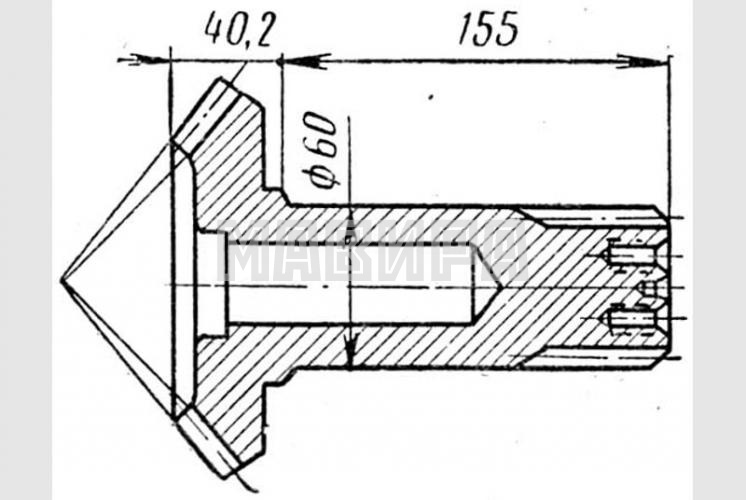
При изготовлении чертежа конического зубчатого колеса с натуры, по аналогии с цилиндрическими колёсами, измеряют наружный диаметр окружности выступов De, затем определяют модуль m и угол внешнего конуса по выступам зубцов (фиг. 363).
Для этого ставят зубчатое колесо торцом ступицы на разметочную плиту и измеряют высоту зубца h по наружному его торцу. Откладывают от окружности выступов по торцу зубца размер, равный h/2.2, и
наносят рейсмасом на всех зубцах риску. Риска пройдёт по начальному диаметру колеса d. Измерив d и поделив его на число зубцов z, определяют модуль m. Полученный модуль может несколько отличаться от стандартного вследствие неточности измерений, и поэтому его округляют до ближайшего стандартного значения модуля. Затем производят вычисление и обмер всех элементов колеса. Диаметр начальной окружности определяют по формуле d = mz. Если известно передаточное число зубчатой пары, т. е. отношение числа зубцов большого колеса z2 к числу зубцов малого z1 то половина угла при вершине начального конуса ?2 большого колеса определится (при угле между осями валов 90°) по формуле
tg?2=z2/z1 = i
где i —передаточное число.
Если передаточное число неизвестно, то угол начального конуса можно получить измерением при помощи угломера, использовав для этого ранее проведённую риску. Так же может быть измерен и угол конуса впадин.
При вычерчивании конического зацепления необходимо, чтобы: вершины начальных конусов обоих колёс находились на пересечении их осей; в этой же точке пересекались линии, соответствующие начальным окружностям зубчатых колёс.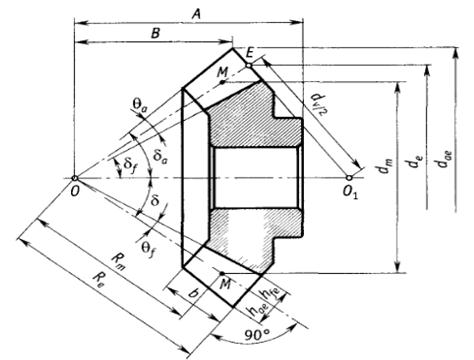
Чертёж конического колеса и пример нанесения размеров, конструктивных и технологических надписей показан на фиг. 354.
Основные способы изготовления
Заготовки для рассматриваемых изделий получаются методом ковки или литьем, в некоторых случаях при применении технологии резания. Технологический процесс изготовления зубчатого колеса довольно сложен, так как нужно получить рабочую поверхность сложной формы с определенными геометрическими параметрами. Проводится нарезание косозубых колес и других изделий при использовании двух основных технологий:
- Метод копирования предусматривает фрезерование, при котором прорез между впадинами зубьев образуются при применении, дисковых, модульных или концевых фрез. После образования каждой впадины заготовка поворачивается ровно на один зуб. Сред особенностей подобной технологии можно отметить то, что форма применяемого режущего инструмента повторяет форму впадины.
- Метод обкатки сегодня встречается намного чаще. В этом случае механическая обработка предусматривает имитирование зацепления зубчатой пары, одним элементом которой становится червячная фреза. При изготовлении инструмента используется металл повышенной прочности, за счет чего и происходит резка. Обработка методом копирования предусматривает применение не только червячной фрезы, но также и долбяка и гребенки.
Довольно большое распространение получили червячные фрезы. Подобный инструмент представлен рейкой, на момент работы заготовка вращается вокруг своей оси. Применяется инструмент для изготовления исключительно шестерен с внешним расположением зубьев.
Технология накатывания используется для получения больших зубчатых колес, а также крупных партий. В подобном случае проводится горячее накатывание, за счет нагрева степень обрабатываемости материала повышается. Венец получается методом выдавливания. Для существенного повышения точности может проводится механическая обработка.
Изготовление вал шестерней также должно проводится с учетом условий эксплуатации.
На этот элемент оказывается высокая нагрузка, поэтому в качестве основы применяется заготовка из каленой стали высокой прочности. Шестерня зубчатая, изготовление которой проводится с учетом диаметра вала, насаживается методом прессования, фиксация обеспечивается шпонкой.
Конструкция зубчатого колеса
Встречается просто огромное количество разновидностей шестерен, все они характеризуются своими определенными особенностями. Среди конструкционных особенностей отметим следующие моменты:
- При изготовлении цилиндрических и конических шестерен с прямым зубом рабочая часть создается заодно целое с валом. Это связано с тем, что размеры конструкции существенно уменьшаются. За счет создания такой конструкции можно получить деталь с высокой точностью и износостойкостью.
- Встречаются и шестерни насадного типа. Они весьма распространены в случае, когда диаметр рабочей части большой. За счет установки насадного варианта исполнения есть возможность проводить обслуживание конструкции.
- При диаметре менее 500 мм изделие получается методом ковки и отливки, а также при применении технологии сварки. Вариант исполнения более 500 мм изготавливаются методов отливки и сварки.
- Клепанные или свертные колеса могут устанавливаться в случае, если есть необходимости в экономии используемого материала.
Конструктивными особенностями подобного варианта исполнения можно назвать:
- В качестве заготовки применяется диск определенной толщины.
- В центральной части есть посадочное отверстие с прорезью для шпонки. Как правило, оно имеет достаточно большую кайму.
- Рабочая часть представлена зубьями, которые могут быть расположены прямо или под углом. При этом геометрия зуба может существенно отличаться, все зависит от области эксплуатации.
Изготовление цилиндрических зубчатых колес проводится при применении специального оборудования. Примером можно назвать зубонарезные станки, которые работают по методу обкатки.
Стоит учитывать, что процесс изготовления конических зубчатых колес существенно отличается.
Чертеж шестерни
Чертеж шестерни должен выполняться в соответствии с требованиями ЕСКД, содержать главный вид и всю необходимую информацию:
- диаметр вершин зубьев (внешний) до притупления кромки
- диаметр вершин зубьев (внешний) после притупления кромки
- расстояние от базовой до внешней плоскости окружности верхней кромки зубьев
- угол конусности зубьев
- угол дополнительного конуса
- ширина венца
- расстояние базовое
- радиусы кривизны и размеры фасок
- положение сечения
В правом углу чертежа, размещают таблицу, состоящую из трех частей, в которой указывают основные параметры:
- основные данные – верхняя часть
- контрольные данные – центральная часть
- справочные данные – нижняя часть
Справка:Неиспользуемые строки в таблице исключаются или ставится прочерк.Подробнее о каждой величине прописано в ГОСТ 2.405-75.
Чертеж конического колеса.
Чертеж червячного колеса.
Шестерня.
Чертеж шестерни.
Конструктивное отличие зубчатых колес определяется:
- по геометрии зуба в поперечном сечении (форма) и способов контакта между собой: прямой – контактирует по точке; вогнутый – контактирует по линии; роликовый – контактирует с гребневым роликом.
- по типам колес: полное – когда оно постоянно вращается; сектор – когда оно поворачивается на определенный угол; сектор с роликом – когда рабочая длина контактируемого ролика уменьшена, по сравнению с контактируемой поверхностью глобоидального червяка.
Заказать чертеж
Документы
Шестерня m=4, Z=30
| Дата добавления: | 15.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 42.22 Кбайт |
| Скачиваний: | 974 |
Шестерня используется в станке 16А812.
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Шестерня m=4, Z=22
| Дата добавления: | 02.11.2010 |
| Дата изменения: | 02.11.2010 |
| Размер файла: | 36.1 Кбайт |
| Скачиваний: | 878 |
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Шестерня m=4, Z=21
| Дата добавления: | 28.05.2010 |
| Дата изменения: | 26.10.2010 |
| Размер файла: | 58.19 Кбайт |
| Скачиваний: | 911 |
Шестерня цилиндрическая прямозубая, m=4, Z=21, с посадкой на шлицы, зуб имеет затыловку, на ступице наружная резьба. Применяется в токарно – винторезном станке 1А64.
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Шестерня m=4, Z=17
| Дата добавления: | 03.11.2010 |
| Дата изменения: | 03.11.2010 |
| Размер файла: | 41.51 Кбайт |
| Скачиваний: | 842 |
Шестерня используется в станке ГФ2171
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Шестерня m=3.5, Z=16
| Дата добавления: | 09.06.2010 |
| Дата изменения: | 19.08.2010 |
| Размер файла: | 51.59 Кбайт |
| Скачиваний: | 860 |
Чертеж шестерни. Используется в станке 2Н57.
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Шестерня m=3, Z=60
| Дата добавления: | 01.11.2010 |
| Дата изменения: | 01.11.2010 |
| Размер файла: | 37.58 Кбайт |
| Скачиваний: | 883 |
Шестерня применяется в станке 2С163
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Шестерня m=3, Z=50
| Дата добавления: | 20. 08.2010 |
| Дата изменения: | 20.08.2010 |
| Размер файла: | 42.49 Кбайт |
| Скачиваний: | 938 |
Шестерня m=3, Z=50 используется в станке 2С550
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Шестерня m=3, Z=50
| Дата добавления: | 01.11.2010 |
| Дата изменения: | 01.11.2010 |
| Размер файла: | 40.79 Кбайт |
| Скачиваний: | 876 |
Шестерня применяется в станке 2С163
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Шестерня m=3, Z=42
| Дата добавления: | 03.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 50.13 Кбайт |
| Скачиваний: | 870 |
Чертеж шестерни цилиндрической с посадкой на шпонку. Применяется в станке 1М63ДФ101.
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Шестерня m=3, Z=42
| Дата добавления: | 20.08.2010 |
| Дата изменения: | 20.08.2010 |
| Размер файла: | 36.34 Кбайт |
| Скачиваний: | 863 |
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
★ Чертеж зубчатого колеса | Информация
Пользователи также искали:
черчение зубчатого колеса, чертеж зуба шестерни, как начертить зубчатое колесо, параметры зубчатого колеса, построение чертежа зубчатого колеса, зубчатое колесо обозначение,
Создание деталировочного чертежа зубчатого колеса.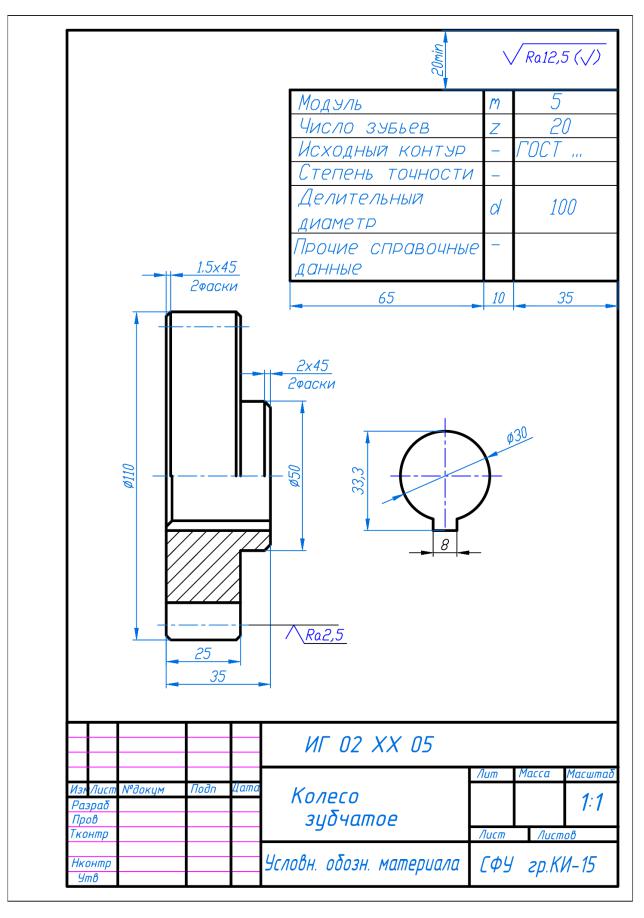 КОМПАС. ПРАВИЛА ВЫПОЛНЕНИЯ ЧЕРТЕЖЕЙ КОНИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС. Unified system design documentation. Rules for making drawings of bevel. .. Видеоуроки Компас.18 Зубчатое колесо в Компасе YouTube. Зубчатое колесо меньшим числом зубьев называется шестерней, а с На чертеже помещают изображение зубчатого колеса и таблицу параметров.. .. Правила выполнения рабочих чертежей конических зубчатых. Предлагается параметрический подход к построению 3D модели зубчатого колеса в пакете Autodesk Inventor с применением параметрической. .. ГОСТ 2.403 75 ЕСКД. Правила выполнения чертежей. выполнения чертежа цилиндрического зубчатого необходимо знать Если чертеж колеса выполняют с натуры, то для определения модуля. .. ГОСТ 2.405 75 Единая система конструкторской документации. ПРАВИЛА ВЫПОЛНЕНИЯ ЧЕРТЕЖЕЙ ЦИЛИНДРИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС Unified system design documentation. Rules for making drawings of spur. .. Эскиз зубчатого колеса YouTube. Зубчатые колеса вычерчивают на чертежах условно., по ГОСТ 2.402 68. Зубчатый венец изображают тремя окружностями рис. 8.6, в.. .. Чертежи муфты, сверла, зубчатого колеса в Компасе. Убедитесь, что текущим является вид Зубчатое колесо. Нажмите сочетание клавиш Ctrl V и вставьте изображение колеса в чертеж, привязав его к. .. Видеоуроки Компас 3D V18 Зубчатое колесо учебный чертеж. 8 апр 2017 Эти правила устанавливает ГОСТ 2.403–75. Зубчатое колесо на чертеже может быть изображено в двух видах. Если для выявления. .. зубчатые передачи. элементы расчета и контруирования. 21 апр 2014 Видеоуроки Компас.18 Зубчатое колесо в Компасе Выложите пожалуйста фотографию самой задачи, т.е. чертежа из книги.. .. ГОСТ 2.403 75 Единая система конструкторской документации. 22 май 2015 Работа по теме: Ковалева,Гаврилюк Инженерная графика ч. Глава.2.3 Выполнение рабочего чертежа зубчатого колеса. ВУЗ: АГУ..
|
Правила выполнения рабочих чертежей цилиндрических. 28 окт 2015 ГОСТ 2.422 70 Правила выполнения рабочих чертежей цилиндрических зубчатых колес передач Новикова с двумя линиями. .. Чертеж цилиндрического зубчатого колеса. чертежей. Методы простановки размеров. Выполнение чертежа детали вращения, листовой, литейной деталей, зубчатого колеса,. .. Вычерчивание цилиндрических зубчатых колес Техническое. ПРАВИЛА ВЫПОЛНЕНИЯ ЧЕРТЕЖЕЙ ЦИЛИНДРИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС. ГОСТ 2.403 75 СТ СЭВ 859 78. ИПК ИЗДАТЕЛЬСТВО СТАНДАРТОВ.. .. Инженерная графика Лекции Чертежи деталей. Сборочный. 24 апр 2017 Эскиз зубчатого колеса. ПНГК ТВ. Loading. Видеоуроки Компас 3D V18 Зубчатое колесо учебный чертеж Duration: 16:51.. .. Правила выполнения рабочих чертежей цилиндрических. муфты, сверла, зубчатого колеса Компасе. Присылайте свои материалы чертежи, 3d модели, изображения для размещения их в Галерее.. .. Как читать чертежи шестерен и зубчатых колес YouTube. 6 мар 2019 Процесс создания зубчатого колеса в Компас 3D V18 на примере учебного чертежа. .. Выполнение эскиза зубчатого колеса, Определение модуля и. 9 апр 2019 Моя группа ВК присоединяйся Мой блог: ⚫ Поддержать Веселого. .. Параметрический подход к построению 3D модели и чертежа. Шестерня – зубчатое передачи с меньшим числом зубьев. Колесо выполнении рабочего чертежа зубчатого колеса при заданных.. .. 94. Специальные соединения деталей. Общий порядок выполнения эскиза зубчатого следующий: определяют модуль Когда выполняют чертеж колеса, не имея натуры, эти размеры. .. .2.3 Выполнение рабочего чертежа зубчатого колеса. НА РАБОЧИХ ЧЕРТЕЖАХ ЗУБЧАТЫХ КОЛЕС. 1. Конический венец с.
|
Цилиндрическое зубчатое колесо чертеж
Правила оформления чертежей гласят, что наименование детали, включаемое в основную надпись чертежа, должно соответствовать принятой технической терминологии иметь логическое соответствие и быть по возможности кратким.
Если наименование состоит из двух слов, то на первое место ставят имя существительное – «колесо зубчатое».
Сведения о том, где должно располагаться изделие или какое у него назначение обычно в наименование не включается.
Наименование
Цилиндрическое зубчатое колесо
Формат файла
*.dwg
Файл архива
*.rar
Размер файла
42,6 кб
Именно колесо зубчатое из машиностроения является самой распространенной и известной деталью. Это изделие представляет собой диск с цилиндрической или конической поверхностью, на котором располагаются зубья. На конструкторских документах колесо зубчатое изображается графически, при соблюдении определенных правил.
В настоящее время зубчатые колеса практически всех разновидностей можно спроектировать с помощью компьютерных программ. Это расширяет возможности творческого процесса, ведь благодаря этим программам расчеты становятся более легкими.
Цилиндрические зубчатые колеса являются одной из разновидностей зубчатых колес.
Этот тип колес применяется во многих отраслях, самых разных машинах и механизмах, которые находят применение в разнообразных отраслях машиностроения и промышленности. Часто их используют для того, чтобы передать вращение между двумя валами, которые расположены параллельно.
Цилиндрические зубчатые колеса бывают с зацеплением внутренним или внешним, косозубые или прямозубые. Встречаются также зубчатые колеса с круговыми зубьями, шевронные и реечные.
В процессе проектирования цилиндрических зубчатых колес обязательно должны быть учтены некоторые технологические требования:
• Конструкция детали должна быть такой, чтобы было обеспечено ее надежное и неподвижное базирование при зубонарезании. Торцовая поверхность при этом должна находиться перпендикулярно к оси отверстия, так как она является базой.
• Зубчатое колесо должно быть расположено так, чтобы все обрабатываемые и связанные между собой поверхности можно было обработать за один раз.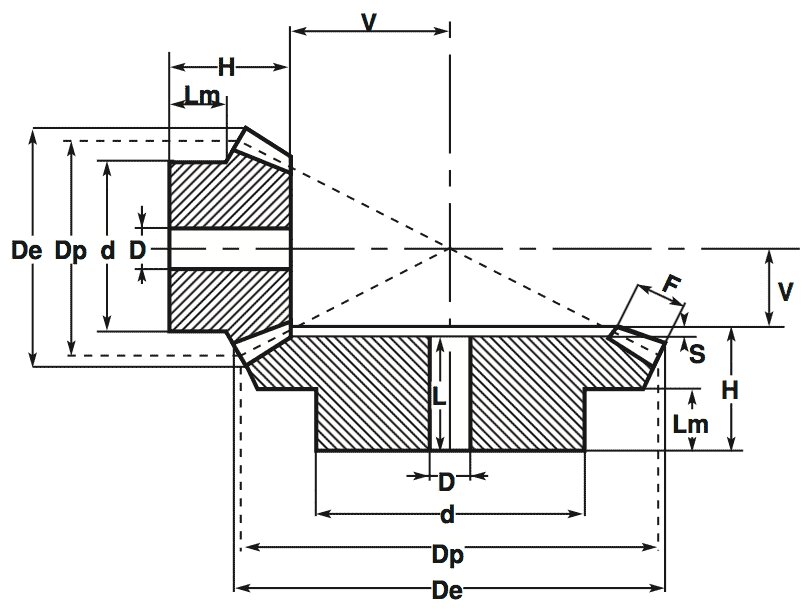
• Не следует применять конструктивные решения, которые могут затруднять технологический выход режущего инструмента.
• Использовать зубошлифование целесообразно только в том случае, если другими методами нельзя добиться похожей точности.
• Для того, чтобы улучшить условия обработки и обеспечить возможность использования многозаходных червячных фрез, в режиме чистовой обработке под шевингование не теряя точности, следует стремиться чтобы не было общих множителей между числом фрезовых заходов и зубьев детали, а также – чтобы они не были кратны числу заходов.
• Стоит выбирать максимально возможное число зубьев долбяка, чтобы повысить точность обработки зубчатого колеса, обладающего внутренними венцами, и обеспечить стойкость инструмента. В противном случае, если число зубьев долбяка будет ограниченно, попытка увеличить число зубьев зубчатого колеса способно навредить – срезать вершины зубьев выполняющегося колеса.
По возможности следует применять шлицевые соединения, которые центрируются по внутреннему диаметру во всех случаях, особенно, если колеса будут вырезаться из закаленных сталей центрируемых сталей, также следует поступать, если сталь зубчатого колеса будет впоследствии закаляться.
Конструирование зубчатых колес
При конструировании зубчатого колеса учитывают материал, из которого оно будет изготовлено, требуемый диаметр и способ получения заготовки.
Стальные зубчатые колеса
Зубчатые колеса диаметром до 150 мм в единичном и мелкосерийном производстве обычно изготовляют из круглого проката; в средне-, крупносерийном и массовом производстве предпочтительнее применять кованые или штампованные заготовки, имеющие более высокие механические характеристики.
Шестерни изготовляют за одно целое с валом (вал-шестерня) (рис. 1, а, б) или делают съемными, если расстояние χ от впадины зуба до шпоночного паза (рис.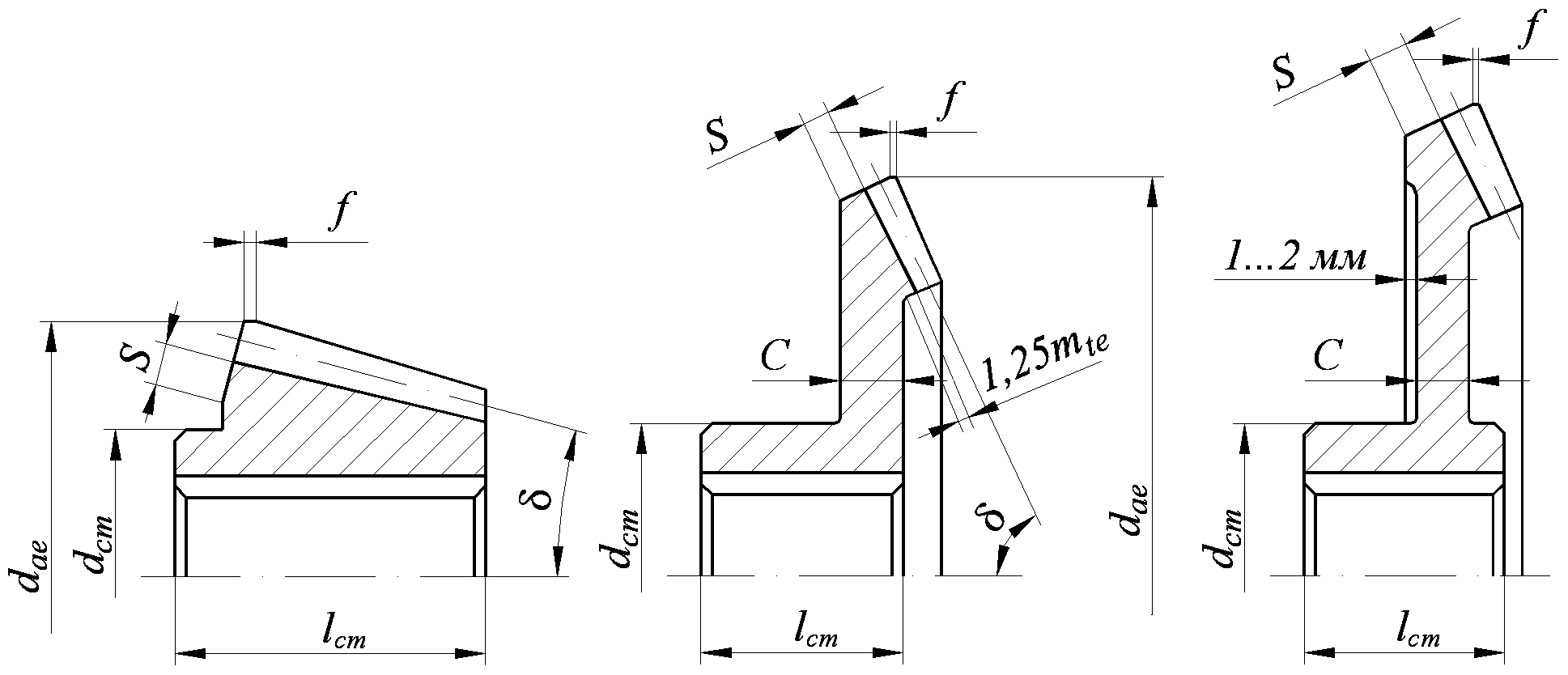
2) больше 2,5 mn для цилиндрических шестерен и 1,8 me для конических. В случае цельной конструкции увеличивается жесткость вала и уменьшается общая стоимость вала и шестерни. Разъемная конструкция позволяет выполнить шестерню и вал из разных материалов, а при поломке одной детали вторую оставить без замены. На рис. 1, а показана конструкция вала-шестерни, когда диаметр впадин зубьев df1 превышает диаметр вала dб.п. (диаметр буртика подшипника), что обеспечивает свободный выход инструмента при нарезании зубьев. При df1 < dб.п. (рис. 1, б) выход фрезы lвых определяют прочерчиванием по ее наружному диаметру Dф, который принимают по табл. 1 в зависимости от mn и степени точности передачи.
Цилиндрические зубчатые колеса диаметром до 400… 500 мм (в отдельных случаях до 600 мм) можно выполнять коваными, штампованными, литыми или сварными.
Конструктивные элементы зубчатых колес показаны на рис. 3.
Типовые конструкции зубчатых колес и основные соотношения их элементов даны на рис. 4—8. Кованые заготовки для зубчатых колес применяют при наружном диаметре колеса 4,df < 200 мм или при нешироких колесах (ψba < 0,2) диаметром da до 400 мм. Операция штамповки отличается высокой производительностью и максимально приближает форму заготовки к форме готового колеса. Для облегчения заполнения металлом и освобождения от заготовки штамп, а следовательно, и заготовка должны иметь радиусы закруглений r ≥ 5 мм и штамповочные уклоны γ ≥ 5° (рис. 4). Внутреннюю поверхность обода, наружную поверхность ступицы и поверхности диска штампованных колес обычно не обрабатывают. Конструкция литого колеса дана на рис. 5.
| Степень прочности передачи | Номинальный модуль mn, мм | |||||
|---|---|---|---|---|---|---|
2. ..2,25 | 2,25…2,75 | 3…3,75 | 4…4,5 | 5…5,5 | 6…7 | |
| 7 8…10 | 90 70 | 100 80 | 112 90 | 125 100 | 140 112 | 160 125 |
Рис. 2. Элемент шестерни при шпоночном соединении
Рис. 3. Конструктивные элементы колес:
a — цилиндрического; б — конического; в — червячного
Рис. 4. Цилиндрические зубчатые колеса при da≤ 500мм:
а —штампованное; б— кованое; dст= 1,6dв; lст≥ bпри соблюдении условия
lст= (0,8…1,5)dв; δ o= 2,5mn+2 , но не менее 8…10 мм; n = 0,5mn для обода, n для ступицы в зависимости от диаметра dв; Dотв= 0,5(Do+dст); dотв= 15…25 мм; c = (0,2…0,3)b для штампованных и c = (0,2…0,3)b для кованых колес
Рис. 5. Литое цилиндрическое зубчатое колесо при da= 400…1000 мм: b ≤ 200 мм dст= 1,6dв — для стального литья; dст= 1,8dв для чугунного литья; lст≥ b
при соблюдении условия lст= (0,8…1,5)dв; δ o= 2,5mn+ 2 ≥ 8 мм;
n = 0,5mn для обода n для ступицы; c = H/5, но не менее 10 мм;
S = H/5, но не менее 10 мм; e = 0,8δ o; H= 0,8dв; H1= 0,8H; R — вписанная дуга окружности
Рис. 6. Бандажированное зубчатое колесо при dв свыше 600 мм: dст= 1,6dв — для стального литья; dст= 1,8dв – для чугунного;lст≥ b
при соблюдении условия lст= (0,8.
..1,5)dв;
c = 0,15b; δ o= 4mn, но не менее 15 мм; t = δ o; e = 0,8δ o; d1= (0,05…0,1)dв; l1= 3d1;b ≥ 300 мм Рис. 7. Сварное зубчатое колесо:
lст= (0,8…1,5)dв≥ b; dст= 1,6dв; δ o= 2,5mn, но не менее 8 мм;s = 0,8c ; Dотв= 0,5 (Do+ dст); dотв= 15…20 мм. Катеты швов: Ka= 0,5dв; Kь= 0,1dв но не менее 4 мм. Ребра приваривают швом Kб Рис. 8. Шевронное зубчатое колесо с канавкой посередине:
lст= b + a; c = (0,3…0,35)(b + a); δ o= 4mn+ 2; h = 2,5mn; a — в зависимости от модуля. Остальные размеры см. рис. 4, 5
Размеры ступицы выбирают по рекомендациям, приведенным под рисунками. Длину ступицы lст по возможности принимают равной ширине венца колеса b, что обеспечивает наименьшую ширину редуктора. Отношение длины ступицы к диаметру вала должно быть не меньше 0,5. При отношении меньше 0,8 на валу предусматривают буртик, исключающий торцевое биение колеса, к которому будет прижиматься торец ступицы колеса. Если по условиям расчета (см. расчет шпоночного и шлицевого соединений) lст> b, то ступицу желательно сместить по оси колеса до совпадения одного ее торца с торцом венца (см. рис. 3, а), что дает возможность нарезать зубья сразу на двух колесах. Реже (для одноступенчатых редукторов) колеса изготовляют со ступицей, выступающей в обе стороны относительно венца (рис. 3, в), при этом зубья можно нарезать только на одном колесе.
При одинаковой длине ступицы и ширине венца можно одновременно нарезать зубья на нескольких колесах.
С целью экономии материала, при больших диаметрах колес, для соединения ступицы с венцом колеса вместо сплошного диска применяют спицы. Зубчатые колеса большого диаметра (при внешнем диаметре da≥ 600 мм) иногда делают бандажированными (рис. 6): венец — стальной кованый (бандаж), а колесный центр — из стального или чугунного литья. Венец сопрягается с колесным центром посадкой с гарантированным натягом. Для большей надежности в плоскости соединения венца с центром ставят винты; соединения проверяют на смятие по материалу колесного центра: при стальном колесном центре [σ] см≥ 0,3σ т, при чугунном [σ] см≥ 0,4σ в.и, где σ т — предел текучести; σ в.и — предел прочности чугуна на изгиб.
При индивидуальном изготовлении колёса иногда делают сварными (рис. 7). При диаметре da≥ 1500 мм для удобства сборки зубчатые колеса делают разъемными — из двух половин.
На торцах зубьев и обода выполняют фаски n = 0,5mn, размер которых округляют до стандартного значения 1; 1,2; 1,6; 2; 2,5; 3; 4; 5.
Острые кромки на торцах ступицы притупляют фасками n x 45, размер которых принимают в зависимости от диаметра вала d:
| d, мм n, мм | 20…30 1 | 30…40 1,2 | 40…50 1,6 | 50…80 2 |
| Продолжение | ||||
| d, мм n, мм | 80…120 2,5 | 120…150 3 | 150…250 4 | 250…500 5 |
Шевронные зубчатые колеса (рис. 8) отличаются от других цилиндрических колес большей шириной. Наиболее часто шевронные колеса изготовляют с канавкой посередине, предназначенной для выхода червячной фрезы, нарезающей зубья.
При известных размерах фрезы ширину канавки a определяют прочерчиванием. Приближенно размер а можно определить в зависимости от модуля m:
| m, мм a, мм | 1,5 27 | 2 32 | 2,5 37 | 3 42 | 3,5 47 | 4 53 | 5 60 | 6 67 | 7 75 | 8 85 | 10 100 |
Остальные конструктивные элементы шевронных колес принимают по соотношениям, указанным под рис. 8.
Конические зубчатые колеса изготовляют коваными, штампованными, литыми или из круглого проката (рис. 9—11).
Конические колеса с внешним диаметром вершин зубьев dae< 120 мм конструируют, как показано на рис. 9. В том случае, когда угол делительного конуса σ < 30 °, колесо выполняют по рис. 9, а, при σ < 45 ° — по рис. 9, б. Если 30° ≤ σ ≤ 45° , можно использовать обе формы. Штампованные колеса (рис. 10, а) применяют в серийном производстве. При внешнем диаметре вершин dae≥ 300 мм используют также литые конические колеса с ребрами жесткости.
Ступицу в зубчатых конических колесах необходимо располагать так, чтобы при закреплении колеса на оправке для нарезания зубьев обеспечивался зазор а> 0,5 mte для свободного выхода инструмента, где т,е внешний окружной модуль (рис. 11).
Рис. 9. Конические зубчатые колеса при dae< 120 мм:a — при δ < 30° ; б— при 5 >45°; диаметр ступицы dст= 1,6dв; lст= (0,9…1,2)dв;
δ o= 2,5mn+ 2, но не менее 10 мм; n = 0,5mn Рис. 10. Конические зубчатые колеса при dae до 500 мм: а — штампованное; б — кованое dст= 1,6dв; lст= (0,9.
..1,2)dв., но не менее 10 мм; c = (0,1…0,17)Re; n = 0,5mn; размеры Dотв и dотв определяют конструктивно
Рис. 11. Крепление конического колеса при нарезании зубьев
Рис. 12. Зубчатое колесо из пластмассы со стальной втулкой (ступицей), установленной при формовании колес
Рис. 13.13. Зубчатое колесо (шестерня) из пластмассы со стальной сборной ступицейВ дисках цилиндрических и конических зубчатых колес предусматривают отверстия диаметром dотв, используемые для закрепления при обработке на станках и при транспортировке. При больших размерах отверстий они служат для уменьшения массы колес, а в литых колесах также для выхода литейных газов при отливке.
Неметаллические зубчатые колеса.
Неметаллические зубчатые колеса. Зубчатые колеса из пластмасс (текстолит, древопластики, полиамиды и т. п.) работают более бесшумно, чем металлические, что имеет особое значение при больших скоростях. Чтобы понизить коэффициент трения между зубьями, одно зубчатое колесо делают из пластмассы, а второе выполняют металлическим. Пластмассы имеют сравнительно небольшие сопротивления срезу и смятию, поэтому в большинстве случаев для передачи момента применяют стальную втулку-ступицу, прочно соединяемую с телом колеса. В небольшие колеса ступицу устанавливают при формовании. Для лучшего сцепления наружную поверхность ступицы делают рифленой (накатанной) (рис. 12). Чтобы предотвратить выкрашивание и откалывание отдельных слоев пластмассы, края зубьев защищают стальными дисками (рис. 13). Толщину диска рекомендуется принимать равной половине модуля, но не более 8 мм и не менее 2 мм. Материал дисков —сталь Ст.2, Ст.З.
Зубчатые колеса больших размеров обычно делают сборными из отдельных секций.
Ширину зубчатого колеса из пластмасс принимают равной ширине зацепляющегося с ним металлического колеса или несколько меньше во избежание местного износа и выработки зубьев
Проектирование конических зубчатых колес в SOLIDWORKS с использованием эскизных блоков и лофтов
Недавно я столкнулся со сценарием, в котором мне нужно было разработать несколько зубчатых колес нестандартного размера, и я нашел творческий способ создания зубчатого колеса со скосом, которым, как я думал, я должен поделиться. Существуют уравнения для расчета характеристик фаски, таких как углы конуса шестерен, зуб, ширина торца и расстояния конуса. Я хотел использовать SOLIDWORKS и производить как можно более простые вычисления. Первым шагом было получить желаемое передаточное число, которое в данном примере составляет 20/40 или 1/2.
Создание эскизов
Для начала я сделал два ортогональных эскиза с шагом диаметра каждой шестерни (20 мм и 40 мм). На верхней плоскости был нарисован 40-миллиметровый круг, а 20-миллиметровая шестерня – на плоскости, параллельной правой плоскости и касательной к краю 40-миллиметрового круга. Эскиз с кругом диаметром 20 мм имел вертикальное отношение к центру большего круга, а края кругов касались друг друга.
Чтобы получить углы конуса, на передней плоскости был создан эскиз с 3 линиями, образующими прямоугольный треугольник.У каждого круга была линия, начинающаяся в центральной точке и продолжавшаяся до пересечения с другой линией. Затем была создана третья линия от этой точки пересечения до места, где соединялись два делительных круга. Эта третья линия представляет собой поверхность зацепления между двумя шестернями, и инструмент интеллектуального измерения может использоваться для определения углов конуса обеих конических шестерен. На рисунке ниже показан эскиз, используемый для определения углов конуса конических шестерен. 20-миллиметровая шестерня имеет угол конуса 26.57 градусов и шестерня 40 мм 63,43 градуса.
Эскиз компоновки конической шестерни
Уравнение первое: угол конуса, рассчитанный с использованием передаточного числа
Уравнение 1 вычисляет угол конуса (δ) для конических зубчатых колес на основе числа зубьев (z) на двух зацепляющих шестернях. Когда мы решаем это уравнение, мы получаем те же значения, которые мы измерили с помощью SOLIDWORKS.
Включение эскизных блоков
Для этой специальной зубчатой передачи я сделал серию эскизных блоков для различных шестерен первого модуля.Я использовал макетную модель, которая содержит уравнения и отношения, чтобы построить мне любую шестерню, где входными данными являются количество зубьев, модуль и угол давления. Единственная ручная часть в этой модели – это сохранение эскиза как эскизного блока. Я также использовал таблицу параметров для быстрого создания всех необходимых мне конфигураций, но я сохраню эту историю для другого блога. Для этих конических зубчатых колес используются два эскизных блока: 20 мм и 40 мм.
Для конической шестерни я использовал полноразмерный блок эскиза и блок эскиза половинного размера и поднял лофт между ними, чтобы создать шестерню.Мне просто нужно было выяснить, как далеко их разнести, чтобы получить угол конуса. У меня было два варианта для этого: тригонометрия и ручные вычисления, или позволить SOLIDWORKS сделать эту работу за меня. Первое, что мне нужно было сделать, это выбрать значение для масштабирования блока эскиза, которое было приемлемым вводом в диспетчере свойств блока. Для простоты я выберу коэффициент 0,5, а это означает, что мой радиус будет вдвое меньше.
Эскиз, используемый для вычисления расстояния от масштабированного блока эскиза
Как видно выше, вертикальная вспомогательная линия представляет собой радиус 20-миллиметрового круга и измеряется на 10 мм.Мы хотим найти горизонтальное расстояние, на котором эта вертикальная линия будет составлять половину длины. Для этого я нарисовал вертикальную линию эскиза, которая совпадала с линией конуса и центральной линией делительной окружности. Затем я измерил его так, чтобы он составлял половину длины вертикальной линии, используя уравнение. Этой информации было достаточно, чтобы полностью определить линию и определить ее горизонтальное положение. Затем я создал контрольный размер, чтобы измерить длину смежной стороны прямоугольного треугольника. Поскольку они похожи на треугольники, я мог бы просто использовать соотношение, чтобы определить положение новой линии, но этот метод фиксирует замысел проекта и автоматически обновляется, если я решу изменить свое передаточное число.
Блоки эскиза, размещенные по конической линии для лофтинга
Solid Body Created by Loft
С помощью этой новой линии я создал плоскость, на которую я поместил масштабированный блок эскиза. Как вы можете видеть на скетче выше, делительная окружность каждой шестерни идеально совпадает с конической линией. Это идеально подходит для хорошего зацепления шестерен. Эти два эскиза затем используются для создания чердака, как показано выше.
Изометрический вид конических зубчатых колес
Крупным планом зацепление зубьев зубчатых колес
Процесс был повторен для 40-миллиметровой шестерни, чтобы создать пару зацепляющихся конических зубчатых колес, как показано на рисунке выше.Изначально зубья имели некоторый взаимный натяг, но инструмент «Отступ» вырезал необходимый зазор, чтобы обеспечить плавное зацепление. На рисунке выше после использования инструмента «Отступ» вы можете увидеть зазор 0,1 мм, который был добавлен, чтобы шестерни не заедали во время работы.
Использование глобальных переменных
Такой подход к созданию конических зубчатых колес позволяет мне легко получить схему для любого передаточного числа с использованием глобальных переменных. Все, что мне нужно сделать, это изменить глобальные переменные, представляющие диаметры шага, как показано ниже, и автоматизация приведет меня к этапу добавления блоков профиля зубчатого колеса.На изображениях ниже представлены различные передаточные числа, показывающие перемещение плоскостей эскиза и пересчет угла конуса.
Equation Manager, отображающий глобальные переменные, используемые для автоматизации новых проектов
Макет с диаметром шага по горизонтали 10 мм и диаметром по вертикали 40 мм
Макет с диаметром шага по горизонтали 18 мм и шагом по вертикали 12 мм Диаметр
Макет с диаметром шага по горизонтали 30 мм и диаметром вертикального шага 25 мм
Макет с диаметром шага по горизонтали 50 мм и диаметром по вертикали 43 мм
Для получения дополнительной информации о SOLIDWORKS или при наличии таковых вопросы, свяжитесь с нами в Hawk Ridge Systems сегодня.Спасибо за прочтение!
Коническая зубчатая передача в SolidWorks – Упражнение 5 в SolidWorks
В этом руководстве вы найдете пошаговое руководство по созданию конического зубчатого колеса в SolidWorks с использованием трехмерных элементов. Я рекомендую вам поиграться и попробовать создать разные винтики и шестерни. Поскольку почти во всех механических конструкциях используются шестерни и шестерни, их очень полезно знать. Коническая шестерня может быть не самым обычным зубчатым колесом, но все же очень важной частью.
Требуемое время: 60 минут
Уровень сложности: Начинающий
Программное обеспечение: SolidWorks
В этом учебном пособии нет специального упражнения, оно само по себе является упражнением.
Ищете еще упражнения? Кликните сюда!
1. Откройте SolidWorks.
2. Откройте новый файл , часть .
- Click новый
- Дважды щелкните деталь на новой вкладке, чтобы создать новый документ детали.
3. Выберите правую плоскость и щелкните эскиз
- Чтобы получить нормальный вид на выбранной плоскости, выберите перпендикулярно из параметров щелчка.
- Вы также можете нажать пробел на клавиатуре, чтобы увидеть панель ориентации. Затем выберите нормальный на .
4. На вкладке эскиза щелкните инструмент линия .
5. Используя инструмент линия , щелкните начало координат и нарисуйте следующие геометрические линии, используя горизонтальные, вертикальные, параллельные и нормальные направляющие SolidWorks.
6. Нажмите умные размеры
7.Измерьте геометрию в соответствии с примером. Убедитесь, что он полностью определен.
8. Сохраните и выйдите из режима эскиза.
9. Выберите панель инструментов features .
10. Выберите s ketch2 в дереве деталей.
11. Щелкните вращающийся бобышек / основание . Появится окно вращения.
12. Щелкните вкладку оси вращения , затем выберите L1 в качестве оси вращения.
13.Убедитесь, что ваш угол установлен на 360 градусов, и нажмите ok .
14. Выберите переднюю плоскость и щелкните эскиз .
15. На вкладке эскиза щелкните инструмент линия .
16. Выберите опцию осевая линия .
17. Используя инструмент осевой линии, нарисуйте линию, проходящую через начало координат.
18. Проведите еще одну линию в соответствии с примером.
19.Выберите линию L2 и E1 , удерживая одновременно клавишу ctrl . Откроется окно диспетчера свойств.
- Окно диспетчера свойств позволяет вам устанавливать различные ограничения и отношения между объектами.
20. В окне свойств выберите коллинеар в качестве отношения между ними.
21. Нажмите ok .
22.Сохраните и выйдите из режима эскиза.
23. Щелкните , вставьте на главную панель инструментов
24. Пройдите Вставка -> справочная геометрия и выберите плоскость
25. В диспетчере свойств щелкните , первую ссылку , затем выберите на экране грань 1 в качестве касательной грани.
26. В диспетчере свойств щелкните вторую ссылку и выберите L2 в качестве перпендикулярной линии на экране.
27. Выберите plane1 (плоскость была создана на предыдущих шагах) и щелкните эскиз .
28. Нажмите ok , чтобы вставить геометрическую плоскость.
29. На вкладке эскиза щелкните инструмент линия . Выберите опцию осевая линия .
30. Используя инструмент осевая линия , нарисуйте линию, которая почти перекрывает предыдущую осевую линию.
31. На вкладке эскиза щелкните инструмент линия .
32. Используя инструмент line , нарисуйте следующую геометрию.
- Инструмент «Линия» можно использовать для рисования различных кривых. Для этого щелкните на экране для начальной точки, а затем вернитесь к начальной точке и начните рисовать кривую.
33. Щелкните Умные размеры .
34. Обозначьте геометрические размеры в соответствии с примером.
35. Щелкните зеркальных объектов
- Зеркальное отражение объектов – зеркальное отображение существующих объектов 2D-эскиза на плоскости вокруг выбранной линии / объекта осевой линии.
36. В диспетчере свойств выберите центральную линию в качестве зеркала относительно . Выберите нарисованные линии и кривые как объекты для зеркального отражения .
37. Нажмите введите , чтобы разместить зеркальную форму.
38. Сохраните и выйдите из режима эскиза.
39. Выберите панель инструментов функций.
40. Щелкните Extruded-Cut Появится окно Extrude-Cut.
- Extruded-Cut – это 3D-функция, которая помогает удалять материалы из 3D-модели.Вы можете резать в обоих направлениях, и вы можете резать экструзией под углом, выбрав опцию уклона .
41. Использовать предыдущий эскиз как выбранных контуров
42. Выберите от до следующего в качестве глубины резания
.43. Проверьте чертёж и установите угол 4 градуса.
44. Нажмите введите .
45. На вкладке «Элементы» щелкните список панели инструментов линейного массива и выберите Круговой массив
- 3D-узор – это функция SolidWorks, которая помогает вам переделывать элементы по заранее заданному шаблону, например линиям, окружностям, кривым и т. Д.
- Трехмерный круговой массив – это элемент трехмерного массива, который позволяет вам создавать круговой массив, используя элемент, который вы выбираете в качестве исходного элемента.
46. В диспетчере свойств выберите выдавливание как элементы для массива .
47. Установите для параметра угла значение 360 градусов.
48. Установите количество шаблонов с на 25.
49. Проверьте коробку с равным интервалом .
50. Нажмите введите .
51. Щелкните на верхней поверхности диска и выберите эскиз .
52. Используя инструмент круга, нарисуйте круг с центром в исходной точке.
53. Измерьте круг с помощью интеллектуального размера соответственно.
54. Сохраните и выйдите из режима эскиза.
55. Щелкните вырезать-выдавить . Появится окно экструдированного выреза.
56. Выберите предыдущий эскиз как выбранных контуров.
57. Выберите от до следующего в качестве глубины резания
.58. Нажмите введите , теперь вы должны увидеть законченную коническую шестерню в 3D!
59. Щелкните файл .
60. Щелкните , чтобы сохранить .
Упражнение 5 – Создание конической шестерни
СПЕЦИАЛЬНАЯ СЕРИЯ | Руководства по компоновке, часть 2: Спиральные и конические зубчатые колеса с нулевым зазором
Это вторая из трех частей инструкций, призванных помочь инженерам-проектировщикам и деталям правильно расположить конические и гипоидные зубья шестерни.Каждое руководство предполагает, что основная информация о конструкции зуба шестерни уже имеется (угол вала, диаметры шага шестерни и шага шестерни, расстояние внешнего конуса, ширина торца, углы шага шестерни и зубчатого колеса, углы торца, корневые углы и внешняя шестерня, а также дополнения к шестерне. и дендендумы). См. Определения этих элементов в приложении в конце и в Части 1. Эта основная информация обычно доступна в виде «габаритной таблицы» зубчатой передачи, которая могла быть рассчитана вашим собственным инженером. Как компания, занимающаяся разработкой и производством зубчатых передач, Nissei предоставляет нашим клиентам информацию о размерах зубчатых колес в рамках наших услуг.Публикации по этой теме также доступны в AGMA (Американская ассоциация производителей шестерен) или в Gleason Works.
Для создания размерного листа обычно требуется определенная информация. Эта информация включает приложенные нагрузки, скорость, угол вала, смещение, материалы шестерен, термообработку, метод смазки, рабочую температуру, требуемый срок службы и рабочие условия, влияющие на ведущую и ведомую нагрузки. Выбирается начальный размер с шагом, шириной грани, углом давления зуба и углом спирали, и рассчитываются напряжения изгиба и контактные напряжения для полученной конструкции.Полученный расчетный срок службы сравнивается с требованием. Это может быть итеративная процедура, включающая несколько испытаний размеров до того, как будет окончательно оформлен размерный лист.
Ключевым следующим шагом является преобразование данных, перечисленных в таблице размеров шестерни, в чертеж. Это связующий этап между конструкцией зуба шестерни и созданием остальной конструкции – заготовки шестерни, ее подшипникового узла, входных или выходных элементов и, в конечном итоге, самого корпуса.
Спирально-конические шестерни имеют изогнутые зубья, которые установлены под углом, обычно 35 градусов, к оси шестерни и шестерни.Можно сравнить косозубые шестерни, у которых зубья также установлены под углом к их осям. В то время как косозубые шестерни характеризуются прямыми зубьями, установленными под углом на цилиндре с воображаемым шагом, спиральные конические зубчатые колеса характеризуются изогнутыми зубьями, установленными под углом на конусе с воображаемым шагом. Цилиндрические шестерни теоретически могут быть представлены двумя касательными цилиндрами, которые катятся вместе без проскальзывания. Подобным образом спирально-конические шестерни представляют собой два касательных конуса, катящихся друг по другу без проскальзывания.Конические зубчатые колеса ZerolÆ представляют собой особый случай спирально-конических зубчатых колес. Изогнутые зубцы установлены под углом от нуля до 10 градусов.
Шаг первый при рисовании любой конической зубчатой передачи – это расположить оси шестерни и шестерни под желаемым углом вала. Подавляющее большинство конических зубчатых колес рассчитаны на угол вала 90 градусов, который мы будем использовать в наших примерах. Точка пересечения осей – это «вершина шага» (рис. 1).
Рисунок 1Следующим шагом является определение «делительной линии», нарисованной как продолжение общего элемента касательного конуса для зубчатой передачи.Угол между осью шестерни и делительной линией – это «угол наклона шестерни»; угол между осью шестерни и линией шага – это «угол шага шестерни». Сумма угла шага шестерни и угла шага шестерни и есть «угол вала» (Рисунок 2).
Рисунок 2Затем расположите точку наклона вдоль линии наклона с размером, указанным для расстояния внешнего конуса. Эта точка одновременно определяет делительный диаметр шестерни и шестерни (Рисунок 3). Постройте нормаль к линии тангажа через точку тангажа.Так вы найдете пятку зубов (рис. 4). Постройте еще одну нормаль на расстоянии вдоль делительной линии, равном ширине лица, чтобы найти кончик зуба с носка (рис. 5). По нормали снаружи измерьте внешние выступы шестерни и шестерни, а также внешние выступы шестерни и шестерни (Рисунок 6).
Рисунок 3Рисунок 4Рисунок 5Рисунок 6От внешнего дополнения шестерни и при заданном угле передней поверхности шестерни проведите линию, соединяющую нормаль на пятке с нормалью на носке.Теперь у вас есть лицевая поверхность шестерни для заготовки. Аналогичным образом проведите линию под углом передней части шестерни от внешнего выступа шестерни, соединяющего нормали пятки и носка, чтобы установить поверхность передней поверхности шестерни. Таким же образом нарисуйте линии под углами шестерни и корня шестерни от внешних точек выточки шестерни и шестерни, соединяя нормали, чтобы создать линии корня шестерни и зубца шестерни (рис. 7).
Рисунок 7Зубы могут сужаться по глубине от пятки до носка или нет, как в случае зубных конструкций с «параллельной глубиной».Корневые линии при удлинении обычно не проходят через вершину питча. Точки пересечения осей можно найти на размерной таблице как размер «вершина корня за точкой пересечения». Конструкция также должна демонстрировать еще одну характеристику конических и гипоидных передач в целом: параллельный зазор. Лицевая линия одной детали должна лежать параллельно корневой линии сопрягаемой детали.
Теперь, когда стандартизованная теоретическая форма зубьев правильно определена, можно приступить к детализации остальной части шестерни и заготовки шестерни.Обратите внимание, что традиционные расчеты номинальной мощности редуктора (не по методике конечных элементов) обычно всегда основываются на этой стандартизированной теоретической форме. Следовательно, заготовки, которые сильно отличаются от этой стандартизированной формы, могут иметь напряжения, значительно отличающиеся от предполагаемых расчетами. В зависимости от модификации детали могут быть слабее или прочнее, чем предполагалось (Рисунок 8).
Рисунок 8Нередко для деталей с мелким шагом можно увидеть заготовки с конструктивными изменениями в стандартизированной форме, такими как те, что показаны на следующих рисунках.Часто внешний диаметр зубчатой передачи обрезается до делительного диаметра. В следующем примере внешний диаметр шестерни показан обрезанным до теоретического внешнего диаметра зубьев. При высоком передаточном числе нежелательно обрезать внешний диаметр шестерни до размера делительного диаметра, как это иногда делается для прохода через подшипник малого диаметра. В таком случае может быть удалена большая часть рабочей области зуба шестерни, что отрицательно скажется на конструкции (Рисунок 9). Обрезка пробелов, как показано, увеличивает ширину поверхности корневой линии.Это может обеспечить некоторую дополнительную прочность на изгиб.
Рисунок 9Предупреждение при изменении формы заготовки связано с практикой независимого вытягивания шестерни и шестерни. При внесении изменений в теоретическую форму зубья шестерни и шестерни должны быть сведены вместе, чтобы оценить влияние на положение взаимного контакта зубьев. В следующем примере заготовки обрезаются, и стыковка зубцов приводит к дилемме размещения рисунка контакта. Рисунок находится в середине ширины поверхности шестерни, но на носке ширины поверхности шестерни.Достижение обычно желаемого контакта «центрального пальца стопы» на обоих элементах невозможно. Проблема размещения контактов для этой зубчатой передачи не была обнаружена до тех пор, пока детали не были изготовлены и запущены вместе на испытательной машине (Рисунок 10).
Рисунок 10Вероятность возникновения этого несоответствия не очевидна, если шестерня и шестерня нарисованы отдельно. Несоответствие приводит к неправильному расположению нагрузки на одном элементе. Обычно локализованный контакт зубьев располагается «центральным носком» как шестерни, так и шестерни.Если бы локализованный контакт зубьев был размещен на центральном носке на этом примере элемента шестерни, контакт сошел бы с концов зубьев зубчатого колеса. Обычно это нежелательно из-за шума, вибрации и концентрации нагрузки.
Мы надеемся, что эта статья помогла вам при проектировании ваших конических зубчатых колес. Как было сказано в выпуске за прошлый месяц, мы надеемся, что теперь вы сможете продолжить разработку остальной части своего приложения и более эффективно сообщать о своих потребностях поставщикам оборудования.Окончательная компоновка гипоидной передачи, которая будет представлена в этой серии, будет опубликована в мартовском номере журнала Gear Solutions .
Приложение
Терминология конического редуктора: спиральная рука
Левая шестерня всегда сопрягается с правой шестерней. Правая шестерня всегда сопрягается с левой шестерней. Показанное здесь «правило кривизны большого пальца» может применяться как к шестерне, так и к шестерне, и работает для скоса Zerol, спиральных скосов и гипоидов. Шестерня или шестерня расположены так, чтобы вы смотрели вниз по оси зубьями к себе и ладонью вниз.(Подробнее в части 1.)
Есть ли лучший способ нарисовать коническую шестерню? – Rhino для Windows
Привет, Бас, скоро посмотрю на твою модель. Судя по скриншотам, все нормально. Тем не менее, я вижу, что, как бы вы ни определили свой модуль или диаметральный шаг (один является обратным другому), они не являются обычными, потому что вы установили исходный профиль где-то посередине вдоль поверхности шестерни.
Я вставил здесь урезанную версию части, которую я написал пару месяцев назад о том, как модуль обычно определяется для конической передачи; начиная с нескольких цитат.
Радзевич 2012, Справочник Дадли по практическому проектированию и производству зубчатых колес: Что касается конических зубчатых колес «Указанные размеры указаны для большого конца зуба. Зуб конической шестерни, имеющий 12 модулей на большом конце, может быть только около 10 модулей на малом конце ». (Стр.26)
SDP / SI 2019, Элементы технологии метрических зубчатых колес: «Поскольку элементы с коническими зубьями имеют коническую форму, размеры зуба и делительный диаметр относятся к внешнему концу (пятке)». (стр. T62)
Maitra 1994 Справочник по проектированию шестерен, 2-е изд.: Что касается конических зубчатых колес, «Все данные о зубьях конических зубчатых колес даны со ссылкой на большой конец [/ цвет]». (Раздел 5.1)
Oberg 1920 Прямозубые и конические зубчатые колеса: «Говоря о шаге конической зубчатой передачи, мы всегда имеем в виду шаг больших или внешних концов зубьев [/ цвет]». (стр. 202)
Это соглашение используется не менее 100 лет. Все производители стандартных шестерен, такие как KHK и Boston Gear, используют одно и то же соглашение при указании модуля своих шестерен.
На самом деле, это соглашение не произвольно, а напрямую основано на основной концепции конической шестерни. Как объясняет превосходный SDP / SI Elements of Metric Gear Technology: «Конические зубчатые колеса имеют конические элементы, потому что они образуются и работают, теоретически, на поверхности сферы. Диаметры шага сопрягаемых конических зубчатых колес относятся к усеченным конусам, как показано на Рисунке 8-2а ». (На цифру стоит посмотреть). Итак, модуль нарисован на поверхности теоретической сферы, являющейся внешней границей шестерен.Этот «задний конус» или «скошенная задняя поверхность», которую можно увидеть на «большом конце» конических шестерен, является коническим приближением этой сферической поверхности и также пересекает делительный диаметр.
Теоретически шестерни могут заходить прямо в центр сферы, но, конечно, это не так. То, где вы отрезаете этот внутренний конец торца шестерни, теоретически не установлено, но это результат экспериментов с нагрузкой и так далее. Таким образом, вы не можете установить модуль «на полпути» вдоль лица шестерни в качестве значимого стандарта, потому что он стал бы зависеть от произвольного выбора ширины лица.Итак, очевидно, что модуль в теории конических зубчатых колес расположен только на «большом конце» зубчатого колеса, где все ожидают его и могут очень легко найти.
Коническая шестерня – SolidFace 3D CAD
Знакомство с зубчатыми колесами и коническими зубчатыми колесами SolidFace
Чтобы лучше понять конические шестерни, нам нужно понять, что такое обычная шестерня. Шестерни являются важной частью различных машин и двигателей с механическим приводом, которые помогают нам выполнять работу.
Основная функция зубчатой передачи состоит в том, чтобы помочь изменить скорость, крутящий момент и направление источник энергии, чтобы создать механическое преимущество для машины или двигателя, в котором он используется для.
Комбинация шестерен может производить различные виды движений, например вращательные движения, поступательные и простые гармонические движения и т. Д.
Также шестерни сделаны в разных размерах, и эти разные размеры можно комбинировать, производя механическое преимущество с различными диаметрами и скоростями вращения.
Конические зубчатые колеса – это один из нескольких типов зубчатых колес, которые помогают передавать вышеупомянутый тип движения с одного конца механической системы на другой.
Один сильный Причина, по которой коническая зубчатая передача предпочтительнее большинства других типов зубчатых колес, заключается в том, что в то время как другие типы шестерен передают свое движение вбок, конические шестерни переключаются направление этих движений, которое мы увидим по мере продолжения.
Что такое шестеренка?
Шестерня – это тип элемента машины, который построен с вырезанными или вставленными зубьями, которые находятся вокруг поверхность цилиндрической или конической формы с одинаковым расстоянием между ними. В зубья, вставленные в шестерню, позволяют им соединяться, вращаться и передавать крутящий момент, находясь в движении.
Крутящий момент сила, которая вызывает вращение в машинах или электродвигателях. Этот крутящий момент обычен в движущихся механических системах, таких как мотоциклы, лодки и автомобили.
Так же, как и в конических зубчатых колесах, сам Gears практически не стоит отдельно и обычно комбинируется с двумя, тремя или более шестернями для создания зацепления. Зубчатая передача – это две или более шестерен, работающих вместе в последовательности, образуя трансмиссию или зубчатую передачу.
Также известны шестерни как винтики или зубчатые колеса.
История шестерен
Шестерни были примерно в течение некоторого времени, самое раннее их использование было в 4 -й Век до нашей эры в Китае, во времена династии Чжоу.
Кроме того, шестерни были использовался в птолемеевском Египте в 3 г. г. до н.э. в Великом Александрийская школа и библиотека, ведущая историческая школа прошлого, основал множество классических и современных научных теорий и был известным наставником греческими философами, такими как Полимат, Архимед и Аджора.
Однако в новейшей истории самым старым механизмом использовался механизм в соборных часах Солсбери 1386 года, которые являются одними из старейших механических часов в мире, а также во многих других готических соборах и их часовом оборудовании.
Детали зубчатой системы
Зубья
Зубы шестерня – это часть, которая контактирует с другими шестернями при контакте во время сетки. Зубья позволяют двум или более шестерням соединяться вместе, в то время как они в сетке.
Также поле уравнивает расстояния и точки, и когда они правильно сцепляются, они несут ответственность для удержания шестерен вместе, предотвращения их соскальзывания и может показывать КПД до 98%.
Радиус
Радиус шестерни Система может быть в двух формах: радиус корня или радиус дополнения. Корневой радиус шестерни – это расстояние от центра шестерни до основание зубов.
В то время как аддендум радиус или продольный радиус – это расстояние от внешней стороны зубьев до центр шестерни.
Типы шестерен
Все шестерни подразделяются на внутренние и внешние, причем внешние шестерни более заметны и распространены, чем внутренние шестерни.Даже наши конические зубчатые колеса являются частью этих внешних зубчатых колес, на самом деле, внутренние зубчатые колеса не имеют многих типов и считаются планетарными.
Тем не менее, Рассматриваемые здесь типы шестерен – это внешние шестерни. Эти внешние шестерни включают следующие шестерни, перечисленные ниже:
- Внутренние шестерни
- Цилиндрические шестерни
- Цилиндрические шестерни
- Двойные косозубые шестерни
- Конические шестерни
- Гипоидные шестерни
- Венечные шестерни
- Червячные шестерни
- Зубчатые шестерни 25 Винт
- Прямые конические шестерни
- Гипоидные конические шестерни
- Спиральные конические шестерни
- Конические шестерни Zerol
- Вид работ
- Ударопрочность
- Способ изготовления
- Допустимое напряжение
- Периферийная скорость
- Требуемые габариты и масса привода
- Требуемая степень точности
- Коническая шестерня является основным механизмом ручной дрели, поскольку коническая шестерня изменяет вращение патрона с вертикального на горизонтальное.
- Кроме того, конические шестерни очень полезны в системах привода винтокрылых машин. Спирально-конические шестерни помогают перенаправить вал с горизонтального газотурбинного газа на более вертикальный ротор.
- Кроме того, конические шестерни также используются в дифференциальных приводах, поскольку они передают мощность на две оси, вращающиеся с разной скоростью.Этот дифференциальный привод также используется в автомобилях.
- Наконец, конические шестерни также используются в строгальном станке с конической зубчатой передачей, который является металлообрабатывающим станком.
- Передача мощности при перпендикулярные углы (90 o ) наклонов.
- Конические шестерни очень эффективны на 98,5% по сравнению с червячными передачами.
- Плавная и бесшумная мощность коробка передач.
- Хорошая гибкость, т.к. имеют регулируемые углы срабатывания и возможность изменения силы выход, просто изменив количество зубьев конической шестерни.
- Может изготавливаться из разных материалы
- Регулируемое механическое преимущество
- Больший крутящий момент при по сравнению с другими передачами, такими как червячные передачи того же размера.
- Соотношение совместимости.
- Коническая шестерня не предназначена для работают независимо, а скорее как дополнительное колесо к другим механизмам.
- Их сложно собрать и должен быть точно установлен, чтобы быть полностью работоспособным.
- Подшипники вала конической шестерни не может противостоять значительной силе.
- Имеют ограниченное передаточное число менее 5.
- Выберите новый SolidFace документ, чтобы создать новую рабочую страницу, продолжите, выбрав «Сборка» и нажмите «ОК».
- Выберите «Библиотека дизайна».
- Откройте набор инструментов и выберите стандарт, выберите стандарт по вашему выбору e.g Стандарт ISO
- Из пунктов, перечисленных в ISO стандарт, выберите Power Transmission.
- В Power Transmission вы найдите еще два варианта: Цепное колесо и Шестерня. Выберите Gear.
- Снова внутри Gear вариант, вы найдете множество вариантов для типа шестерни, например, косозубая шестерня, внутренняя Прямозубая шестерня, различные типы конической шестерни и т. Д.
- Выберите коническую шестерню Пример вашего выбора выберите прямую коническую шестерню.
- Щелкните и перетащите прямую коническая передача из библиотеки дизайна на рабочую страницу, и у вас будет черновая Коническая передача готова.
- После щелчка и перетаскивания процесс из предыдущей записи, это займет короткое время у вашего программного обеспечения SolidFace в то время как для расчета конической шестерни, но сразу после этого открывается окно для «Настроить компонент».
- Внутри «Настроить Компонент », список« Свойства »доступен для изменения и вы сделаете это, просто введя в них свои значения.
- Но для этого примера нажмите «Модуль» и выберите «5», и SolidFace выполнит расчет.После этого вы наблюдайте за изменениями, которые могут повлиять на конический редуктор.
- Затем выберите количество зубьев, например, выберите 30.
- Затем щелкните число шестерни зубов, он будет рассчитывать медленно, а затем влиять на изменения.
- Угол давления должен быть на 20, что является стандартом.
- Затем выберите ширину грани и установите его на 30. Вы заметите, что ширина лица вашего конического зубчатого колеса будет выросла.
- Затем для диаметра задайте его при 50, а не 100, он рассчитает и продолжит.
- Также для монтажа расстояние установите на 50.
- Кроме того, для вала диаметр, наведите указатель мыши на 30 и выберите его, и ваша программа SolidFace будет вычислить введенные значения.
- После этого наведите указатель мыши на непосредственно под полосой, где написано «Настроить компонент», и вы увидите зеленую галочку и красный «х», нажмите зеленую галочку, чтобы «ок» все, что вы ваши уже сделанные настройки, а затем SolidFace рассчитает их, затем Продолжать.
- Программа SolidFace спросит если вам требуется более одной конической шестерни, просто нажмите на любую область рабочую страницу, чтобы получить точную копию конического зубчатого колеса, с которым вы только что работали.
- Этот процесс создания нового конические шестерни будут работать до тех пор, пока вы не отмените его в области «вставки компонента».
- Продолжайте и экономьте, но не делайте этого сохраните файл как сборку, вместо этого измените «Сохранить как тип» на «Деталь» и введите имя файла и затем Сохранить.
- SolidFace предоставляет дизайнерам Дизайн Gears с любым обязательным навыком рисования.
- Автоматически предоставляет несколько стандарты на выбор и выбрать тот, с которым работать.
- Все блоки гибкие и регулируемый и может быть изменен дизайнером или любым другим человеком, которому нужно использовать рисунок.
- Чертеж можно создать в всего 5 минут или меньше, что намного быстрее, чем при использовании рук.
- Моделирование и тестирование можно выполняется на конической передаче.
- Несколько конических зубчатых колес могут быть создается из оригинальной конической шестерни, без необходимости начинать рисунок процесс с самого начала.
- Это удобный список вариантов для редактирования расположены последовательно, вы можете легко перейти от одного вариант к следующему.
Шестерни прямозубые самые простые и распространенные типы зубчатых колес, которые также называются прямозубыми шестерни.Прямозубая шестерня представляет собой цилиндр с радиально выступающими зубьями. Зубы шестерня сделана прямой и выровненной параллельно оси вращения, так что они могут правильно сцепляться вместе.
Одна основная причина незаинтересованности в цилиндрических зубчатых колесах, которые не очень хорошо работают на высоких скорости, потому что они имеют тенденцию быть слишком шумными и не имеют осевой тяги необходим для переноски грузов.
Винтовая шестерня
Винтовая передача использует те же параллельные валы, что и в прямозубых шестернях и заводном зубе линии также вставляются вокруг цилиндрических шестерен.Но у них лучше зубья входят в зацепление и могут передавать более высокие нагрузки, чем их прямозубые шестерни.
Так как их Линии зубьев расположены под углом, они могут создавать силу тяги в осевом направление, которое помогает в их несущей способности и полезно в высокоскоростных Приложения.
Гипоидная передача
Гипоидная передача разработан с гиперболическим шагом, что делает гипоидные шестерни подходящими для работать с валами под углом 90 o . Гипоидные шестерни имеют сходство с гипоидные конические шестерни и спирально-конические шестерни.
Конические шестерни
Конические шестерни – это компоненты, используемые в основном для передачи мощности, для регулировки или изменения вращения вала, направления и уменьшения скорости, а также увеличения крутящего момента между непараллельно вращающимися валами.
Используется на валах с пересекающимися осями, а также на валах, оси которых не пересекаются в особых случаях. Коническая шестерня классифицируется по форме зуба и бывает разных типов.
Типы конической шестерни
Как раньше Заявлено, что конические шестерни классифицируются по форме их зуба.Хотя инженеры и конструкторы могут не соглашаться по поводу различных типов конической шестерни. доступны, это наиболее приемлемые.
Следующие – это типы конических зубчатых колес, доступные конструкторам.
Прямые конические шестерни
Прямая фаска шестерни являются наиболее распространенным типом конических зубчатых колес, и это связано с тем, что их конструкция это просто.Имеют прямые зубья, напоминающие прямозубую шестерню, за исключением их коническая поверхность.
Гипоидные конические шестерни
С гипоидным скосом зубчатых колес, поверхность деления должна быть гиперболической, а не конической. Гипоидный имеют больший диаметр шестерни, более гладкую сетку и более длительный срок службы.
Гипоидный скос шестерня похожа на спирально-конические шестерни, и главное отличие состоит в том, что оси ответной шестерни не пересекаются. Гипоидные конические шестерни часто использовались. в задних мостах автомобилей.
Спирально-коническая шестерня
Спиральная фаска зубчатые передачи имеют линии зубьев, сформированные по спиральным линиям, что делает их зубья угловой. Спирально-конические шестерни обычно очень удобны и имеют типичный угол наклона 35 или .
Есть очень полезно, так как здесь задействуют силу более постепенно, чем обычно конические шестерни, что означает менее мгновенную передачу усилия внутри механизма, поэтому будет меньше шума и стресса.
Zerol коническая шестерня
Фаска Zerol шестерни – это еще один тип конической шестерни, которая является скорее промежуточным звеном между прямая коническая шестерня и спирально-коническая шестерня, поскольку они сочетают в себе функции обоих.
Имя Зерол выводится из того факта, что он имеет нулевой угол спирали. Шестерни Zerol могут поворачиваться в любом направлении без особого труда.
Как изготавливаются конические шестерни
С фаской шестерни широко используются в различных типах техники, они стали очень популярными. важны для инженеров, так же как их производство и их изготовление дизайн, материалы и процесс.
Материалы использованные для их производства:
Сталь
Сталь очень намного предпочтительнее из-за его прочности и устойчивости к износу истирание.
Чугун
Также чугун широко используется из-за его хороших износостойких свойств, обрабатываемости и пластичность, то есть способность превращаться в очень сложные формы в процессе ковки и литья. Единственная серьезная проблема с актерским составом железо такое, что оно очень бедно коррозией.
Литая сталь
Стальное литье на с другой стороны, сочетает в себе простоту изготовления из чугуна и теплоизоляции. стойкость стальных металлов к производству материала, который используется для создания фаски шестерни, выдерживающие высокие нагрузки.
Алюминий
Алюминиевые конические шестерни довольно популярны в областях, где коррозия вызывает серьезную озабоченность. Тем не мение, Алюминиевые конические шестерни также имеют небольшой вес и поэтому очень хорошо подходят для низкая инерция вращающейся массы. Что является важным преимуществом этих типов шестерни есть.
Легированная сталь
Кроме того, с Сплавы Стали возможности для производителей безграничны, поскольку они могут комбинировать уникальные свойства нескольких металлов, чтобы получить лучший тип, подходящий для их потребности.
Однако сплав Стали используются там, где требуется низкий износ зубьев и высокая прочность зубьев. коническая шестерня.
Неметаллические материалы
Неметаллический Материалы, подходящие для изготовления конических зубчатых колес, бесшумны в своей работе. операций, даже на высоких периферийных скоростях.
Обычная углеродистая сталь
Наконец, равнина углеродистая сталь очень предпочтительна в качестве материалов с высокой вязкостью и высокой прочностью. нужны силы, это включает в себя основные отрасли промышленности и т. д.
Соображения, сделанные перед выбором материалов
Материалы, используемые для работы конических зубчатых колес и других зубчатых колес, не выбраны случайным образом, но, как указано в предыдущей записи, сделаны на основе некоторых причины. При выборе типа материалов учитываются следующие факторы: следующее:
Использование конических шестерен
Конические шестерни использовались для выполнения множества различных функции и промышленные приложения в различных категориях отраслей и форм основные компоненты нескольких готовых изделий и оборудования.
Промышленное и механическое применение конических шестерен
Конические зубчатые колеса очень полезны в машиностроении и особенно в машиностроении, где они широко используются. Некоторые из их механических применений:
Конические шестерни имеют много преимуществ. ко всем машинам, в которых они используются.Некоторые из них включают следующее.
Недостатки использования Bevel Шестерни
Как и любая деталь машины, конические шестерни в какой-то момент выходят из строя. Ниже приведены недостатки использования конических зубчатых колес.
Стандартизация конических зубчатых колес
Стандартизация конических шестерен сделано, чтобы помочь обеспечить точность передачи. Эти стандарты считаются классом точности и устанавливаются ISO, JIS, AGMA, DIN и т. д.
В результате этого класса точности конструкторы могут гарантировать, что их конические шестерни могут иметь максимальная мощность, минимальный размер, минимальный шум и точное вращение.
Эти стандарты очень полезно для рисования ручной работы.Как JIS определяет ошибку шага, биение погрешность, погрешность профиля зуба, отклонение спирали и т. д.
Как использовать SolidFace при создании конических зубчатых колес
Чтобы создать и спроектировать коническое зубчатое колесо с помощью SolidFace, мы используем Toolbox для их рисования. Следующие ниже шаги четко объясняют процесс вовлечения.
Форматирование конических шестерен SolidFace
Преимущества использования SolidFace Bevel Gear Creation
Последние слова
Конические шестерни имеют был частью человеческого механизма с древних, классических времен и сформировал критически важная часть нашего производственного процесса с самого начала недавнего промышленного возраст. Тем не менее, трудно увидеть будущее без конической шестерни и шестерен в в целом, поэтому важно их лучше производить.
С ведущими CAD программное обеспечение, такое как SolidFace, это может сделать почти любой, и прежде долгий, утомительный процесс свелся к серии шагов.
Теперь дизайнеры во всем мире могут с легкостью создавать сложное оборудование с опорой на зубчатые передачи, поэтому производители, в свою очередь, могут также создавать передовые технологические устройства, такие как космические ракеты, роботы и т. Д. Возможности сейчас безграничны.
Проектирование прямозубых, косозубых и конических зубчатых колес с использованием CATIA V5. : Skill-Lync
AIM: – Создавайте различные типы Gear с помощью панели инструментов Catia V5 Knowledge.
ЦЕЛЬ: – Расчет зуба с расчетом эвольвентного профиля для различных типов шестерен.
ВВЕДЕНИЕ: –
Зубчатая передача – это вращающаяся круглая часть машины, имеющая нарезанные зубья или, в случае зубчатого колеса или зубчатого колеса, вставленные зубья (называемые зубцами ), которые зацепляются с другой зубчатой частью для передачи крутящего момента. Шестерня может также неофициально называться винтиком. Редукторные устройства могут изменять скорость, крутящий момент и направление источника питания. Шестерни разных размеров изменяют крутящий момент, создавая механическое преимущество за счет своего передаточного числа и, таким образом, могут считаться простой машиной.Скорости вращения и крутящие моменты двух зацепляющих шестерен различаются пропорционально их диаметрам. Зубья на двух зубчатых колесах имеют одинаковую форму.
Две или более зубчатых передачи, работающих последовательно, называются зубчатой передачей или трансмиссией . Шестерни в трансмиссии аналогичны колесам в системе перекрестных ременных шкивов. Преимущество шестерен в том, что зубья шестерни предотвращают проскальзывание. В трансмиссиях с несколькими передаточными числами, таких как велосипеды, мотоциклы и автомобили, термин «шестерня» (напр.g., «первая передача») относится к передаточному отношению, а не к реальной физической передаче. Этот термин описывает аналогичные устройства, даже если передаточное число является непрерывным, а не дискретным, или когда устройство фактически не содержит шестерен, как в бесступенчатой трансмиссии.
ТИПЫ: –
1. Отвод: –
Цилиндрические зубчатые колеса или Прямые зубчатые колеса являются простейшими зубчатыми колесами. Они состоят из цилиндра или диска с радиально выступающими зубьями.Хотя зубья не являются прямыми (но обычно имеют особую форму для достижения постоянного передаточного числа, в основном эвольвентного, но реже циклоидального), край каждого зуба прямой и выровнен параллельно оси вращения. Эти шестерни правильно зацепляются друг с другом только в том случае, если они установлены на параллельных валах. [18] Нагрузки на зубья не создают осевое усилие. Прямозубые шестерни превосходны на средних скоростях, но имеют тенденцию к шуму на высоких скоростях.
2.СПРАВОЧНЫЙ: –
Цилиндрическая зубчатая передача или «сухая фиксированная» шестерня является более совершенной по сравнению с цилиндрической шестерней. Передние кромки зубьев не параллельны оси вращения, а расположены под углом. Поскольку шестерня изогнута, этот наклон делает зуб в форме сегмента спирали. Цилиндрические зубчатые колеса могут быть зацеплены в ориентациях параллельно или перекрещенных . Первое относится к случаям, когда валы параллельны друг другу; это наиболее распространенная ориентация. В последнем случае валы не параллельны, и в этой конфигурации шестерни иногда называют «косыми шестернями».
Угловые зубья входят в зацепление более плавно, чем зубья прямозубой шестерни, благодаря чему они работают более плавно и тихо. В параллельных косозубых зубчатых колесах каждая пара зубьев сначала входит в контакт в одной точке на одной стороне зубчатого колеса; затем движущаяся кривая контакта постепенно нарастает по поверхности зуба до максимума, а затем отступает, пока зубцы не прервут контакт в одной точке на противоположной стороне. В цилиндрических зубчатых колесах зубья внезапно встречаются на линии контакта по всей своей ширине, вызывая напряжение и шум.Прямозубые шестерни на высоких оборотах издают характерный вой. По этой причине прямозубые цилиндрические шестерни используются в низкоскоростных приложениях и в ситуациях, когда снижение шума не является проблемой, а косозубые шестерни используются в высокоскоростных приложениях, при передаче большой мощности или там, где важно снижение шума. Скорость считается высокой, если скорость продольной оси превышает 25 м / с.
Недостатком косозубых шестерен является возникающая в результате осевая нагрузка вдоль оси шестерни, которая должна компенсироваться соответствующими упорными подшипниками.Однако этот недостаток можно превратить в преимущество при использовании шестеренчатой шестерни или двойной косозубой шестерни , которая не имеет осевой тяги – а также обеспечивает самовыравнивание шестерен. Это приводит к меньшей осевой нагрузке, чем у сопоставимой цилиндрической зубчатой передачи.
Вторым недостатком косозубых зубчатых колес является также большая степень трения скольжения между зубьями зацепления, что часто устраняется добавками в смазку.
3. BEVEL: –
Коническая шестерня имеет форму правильного кругового конуса, большая часть которого срезана.Когда две конические шестерни входят в зацепление, их воображаемые вершины должны находиться в одной точке. Их оси валов также пересекаются в этой точке, образуя произвольный непрямой угол между валами. Угол между валами может быть любым, кроме нуля или 180 градусов. Конические шестерни с одинаковым количеством зубьев и осями валов под углом 90 градусов называются косыми (США) или косыми (Великобритания) шестернями.
1. Простая коническая передача 2.Шестерня коническая спирально-цилиндрическая
4. WORM: –
Червяки напоминают винты. Червяк находится в зацеплении с червячным колесом , которое похоже на прямозубое колесо.
Червячные передачи – это простой и компактный способ достижения высокого крутящего момента и низкого передаточного числа. Например, косозубые шестерни обычно ограничиваются передаточным числом менее 10: 1, в то время как червячные передачи варьируются от 10: 1 до 500: 1. Недостатком является возможность значительного скольжения, что приводит к низкой эффективности.
Червячная передача – это разновидность косозубой шестерни, но ее угол наклона винтовой линии обычно несколько велик (около 90 градусов), а ее корпус обычно довольно длинный в осевом направлении. Эти атрибуты придают ему черты винта. Различие между червяком и косозубой шестерней состоит в том, что по крайней мере один зуб остается для полного вращения вокруг спирали. Если это происходит, то это «червь»; в противном случае это «косозубая шестерня». У червя может быть всего один зуб. Если этот зуб сохраняется в течение нескольких оборотов по спирали, на поверхности кажется, что у червя больше одного зуба, но на самом деле вы видите тот же зуб, который появляется снова через определенные промежутки времени по длине червя.Применяется обычная номенклатура винтов: однозубый червяк называется с одинарной резьбой или с одинарной резьбой ; червяк с более чем одним зубом называется с несколькими резьбами или с несколькими зацепами . Угол наклона спирали червяка обычно не указывается. Вместо этого указывается угол подъема, равный 90 градусам минус угол наклона спирали.
В червячной передаче червяк всегда может приводить в движение шестерню. Однако, если шестерня пытается запустить червяк, это может или не может быть успешным.В частности, если угол опережения небольшой, зубья шестерни могут просто сцепиться с зубьями червяка, потому что составляющая силы по окружности червяка недостаточна для преодоления трения. Однако в традиционных музыкальных шкатулках шестерня приводит в движение червяк, имеющий большой угол наклона спирали. Эта сетка приводит в движение лопатки ограничителя скорости, установленные на валу червяка.
Червячные передачи, которые действительно блокируются, называются самоблокирующимися , что может быть использовано с пользой, например, когда желательно установить положение механизма, повернув червяк, а затем заставить механизм удерживать это положение.Примером может служить головка станка на некоторых типах струнных инструментов.
Если зубчатая передача в червячной передаче представляет собой обычную косозубую передачу, достигается только одна точка контакта. Если требуется передача мощности от средней до высокой, форма зуба шестерни изменяется для достижения более тесного контакта, заставляя обе шестерни частично охватывать друг друга. Для этого они должны быть вогнутыми и соединяться в седловой точке; это называется конусным приводом или «двойным охватом».
Червячные передачи могут быть правосторонними или левосторонними, в соответствии с давно установившейся практикой для резьбовых соединений.
ТЕРМИНОЛОГИЯ ШЕСТЕРНЯ: –
МЕТОДОЛОГИЯ: –
1. Добавьте новый параметр
м = 2 см
г = 32
Угол давления (a) = 20 градусов
Rp (радиус делительной окружности) = м * z / 2
Ro (Радиус дополнительной окружности) = Rp + м
Rb (радиус основной окружности) = Rp * Cos (a)
Rr (радиус окружности Dedendum) = Rp – 1.25 * м
2. Перейдите в Эскиз и нарисуйте полукруг с Rb, используя формулу редактирования.
3. Постройте центральную ось.
4. Поверните эту ось с числом моментов (чем больше число шаблонов оси, тем более гладкий профиль вы получите, здесь у нас 8).
5. Затем убедитесь, что точка нашей оси совпадает с точкой начала координат.
6. Затем угловой интервал по формуле
т.е. 2 * 1-й угол
3 * 1-й угол
4 * 1-й угол…Скоро.
7. Обрежьте удлиненную осевую линию так, чтобы она совпадала с базовой окружностью.
8. Проведите касательную линию от каждой точки.
9. длина этой точки
Rb * этот угол * `Rbxx angle xx pi / 180`
10. Соединитесь с этой точкой с помощью шлицевого соединения.
11. Выйдите из верстака и нарисуйте круг Rp, Rb, Rr, Ro, используя формулу редактирования.
12. Разверните эвольвентную кривую = 2 * м .
13. Теперь создайте радиус угла = 0,39 * м.
14. мы получаем одну кривую, для отражения этой кривой с другой стороны нам нужна плоскость в правильном положении, мы используем симметрию.
15. Для этого нам нужно создать точку пересечения эвольвентной кривой с делительной окружностью.
, затем создайте точку на делительной окружности, используя длину команды создания точки, используя формулу = 1 / z / 4.
и ссылка = точка пересечения.
, эта точка создает плоскость в перпендикулярном направлении.
16. Создайте эвольвентную кривую симметрии и выполните обрезку таким образом, чтобы вторая кривая, первая кривая и дополнительная окружность.
17. у тебя один зуб
18. Затем сделайте круговой узор с количеством зубцов по формуле.
19. Обрезать нижнюю часть окружности. и скрыть базовую окружность и делительную окружность, плоскость.
20. Выйдите из верстака, проложите его на глубину размера шестерни.
ДЛЯ СПИРАЛЬНОЙ ШЕСТЕРНИ
1. Плоскость смещения на 250 мм от начала координат
2.Затем мы проецируем тот же профиль, что и на эскизе первой шестерни
3. Скрыть основной эскиз, затем изолировать второй. и повернуть на угол винтовой линии (25 градусов).
4. Затем покажите основной эскиз, теперь у нас есть два эскиза, просто разделите его. мы получили косозубую шестерню.
ДЛЯ КОНИЧЕСКОЙ ШЕСТЕРНИ: –
1. Смещение плоскости от основной плоскости на 250 мм.
2. Спроецируйте основной эскиз и изолируйте его.
3. Теперь выберите второй эскиз, просто отмасштабируйте его до 80% (мы ставим 0.8)
4. Затем покажите основной эскиз и разделите его с точной точкой закрытия.
ДЛЯ СПИРАЛЬНОЙ КОНИЧЕСКОЙ ШЕСТЕРНИ: –
1. Нам нужно сместить 2 плоскости на 125 мм, 250 мм от основной плоскости.
2. выберите первую плоскость и эскиз.
3. Масштабируйте основной эскиз на 80% и поверните на 15 градусов.
4. Выходной рабочий стол
5. выберите вторую плоскость смещения и эскиз.
6. Выберите основной эскиз, масштабируйте его на 50% и поверните на 30 градусов.
7. Выходной рабочий стол
8. Теперь у нас есть 3 эскиза, просто разделите их на части с подходящей точкой закрытия.
Заключение: – Таким образом, мы создаем различную шестерню с помощью панели инструментов знаний на всю жизнь.
Как сделать: конические шестерни для 3D-печати (Fusion 360): 7 ступеней
Изображение 1.
На первом изображении мы видим печатную плату малой шестерни. Я решил сделать зубы высотой 8 мм (для более плавного движения, я думаю, вы действительно хотите, чтобы ваши зубы были близки к равнобедренным).Это означает, что внутренний и внешний круги, упомянутые в шаге 1, находятся на 4 мм внутри и снаружи печатной платы. Здесь я просто продлил линию, вместо того, чтобы рисовать отдельные диаметры, надеюсь, это все еще ясно!
Основание зуба определяется по касательной в обе стороны до совпадения с линией ширины зуба. Отсюда точку зуба можно найти, проведя до внешнего диаметра, где он пересекает ось симметрии.
Здесь вы реализуете первую теорию эвольвентной кривой, гарантируя, что в основании она соприкасается с линиями угла ширины зуба, а на вершине – с осью симметрии.
Image 2
С этого момента мы будем называть конец конуса PC.D большой шестерни «точкой схода». Мы протягиваем вдоль эскиза плоскости пересечения две линии, представляющие внутренний и внешний диаметры, от маленькой шестерни P.C.D до точки схода. Мы назовем их «Зубной конус».
Теперь обратите внимание на линию, упомянутую ранее и проведенную между местом, где внутренний диаметр большой шестерни встречается с линиями угла ширины зуба. На плоскости пересечения вы хотите отметить место пересечения этой линии.Здесь мы хотим нарисовать ВНУТРЕННИЙ профиль зуба. Вытяните эту линию до осевой линии маленькой шестерни.
Теперь, перпендикулярно этой новой линии, которую мы только что создали, и параллельно исходной печатной плате, вы хотите сделать еще одну печатную плату. Это будет очень просто: вы просто начинаете центр круга на осевой линии и увеличиваете радиус до точки пересечения зубчатого конуса P.C.D.
От центра проведите вниз симметричные линии угла ширины зуба, они будут под тем же углом, что и раньше (это не изменится).Теперь, используя точку пересечения конуса зуба с этой плоскостью, вы можете выделить новый профиль зуба.
Как это работает ? Зубчатый конус представляет собой область, в которой находятся как малая шестерня, так и большие зубья шестерни. Он представляет собой коэффициент масштабирования, где на исходном внешнем PC.D шкала была 1, а в точке схода – 0. Размер зуба и конусы P.C.D все масштабируются с этим. Таким образом, вы также можете найти размер вашего внутреннего профиля зуба по ((точка схода к внутренней плоскости зуба) / (точка схода к плоскости внешнего зуба)) , чтобы получить коэффициент масштабирования.
Изображение 3.
Простой. Лофт между двумя профилями.
Изображение 4.
Обведите свой зуб вокруг оси шестерни / P.C.D. Естественно, общее количество копий равно количеству ваших зубов.
Изображение 5.
Завершите базовую форму шестерни. Здесь я поместил декаэдр на эскизы профиля внутреннего и внешнего зуба и проделал лофт, объединив их. Я также закругляла кончики зубов. Учитывая возможные неточности при печати, а также то, как принтеры ускоряются и простаивают, это должно помочь.
Кроме того, вам нужно обрезать шестерню по касательной к внутренней окружности зубьев, чтобы она не выступала изнутри. Мы выберемся наружу через секунду.
ПОЗДРАВЛЯЕМ! Вот и все, что вам нужно. Двигаемся дальше .