Зубчатые колеса основные параметры – , —
alexxlab | 14.10.2019 | 0 | Разное
23. Основные геометрические характеристики зубчатой передачи
Геометрия цилиндрической зубчатой передачи представлена на рис. 2.8.
В качестве основного геометрического параметра зубчатого зацепления принят модуль зубьев m – величина, пропорциональная шагу зубьев p, взятого по дуге делительной окружности:
.
Так как длина делительной окружности равна , а длина шага зубьев равнадлины делительной окружности, то:
,
где – число зубьев зубчатого колеса.
|
Рис. 2.8. Геометрические параметры зубчатых колес |
Модули стандартизированы в диапазоне 0,05…100 мм (ГОСТ 9563). Ниже приведены модули, мм, в наиболее распространенном диапазоне:
1-й ряд: 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40.
2-й ряд: 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18; 22; 28; 36; 45.
1-й ряд следует предпочитать 2-му.
Для редукторов также допускают модули 1,6; 3,15; 6,3; 12,5.
Делительные окружности с диаметрами икасаются друг друга в точке пересечения с линией, соединяющей центры колес.
Диаметры делительных окружностей ведущего и ведомого колес соответственно:
; .
Зацепление зубчатых колес эквивалентно качению без скольжения окружностей с диаметрами и.
Высоту зуба условно разделяют навысоту головки зуба ивысоту ножки зуба . Их величина определена ГОСТ 13755:
; ;.
Диаметры окружности выступов:
; .
Диаметры окружности впадин:
; .
Радиальный зазор между вершиной зуба одного колеса и дна впадины между зубьями другого колеса предназначен для предотвращения заедания и выдавливания смазки при работе передачи:
.
Угол профиля исходного контура .
Межосевое расстояние а:
.
24. Основная теорема зацепления
Для постоянства передаточного отношения при зацеплении двух профилей зубьев необходимо, чтобы радиусы начальных окружностей зубчатых колёс, перекатывающихся друг по другу без скольжения, оставались неизменными. Если рассмотреть обращённое движение начальных окружностей, когда всей системе задана угловая скорость ( ), то второе колесо будет условно неподвижным и точкаР является мгновенным центром относительного вращения колёс (рис. 70,а). Эта точка, называемая полюсом зацепления, где контактируют начальные окружности, делит межцентровое расстояние на отрезки, обратно пропорциональные угловым скоростям, т. к.
.
Рассмотрим обращённое движение профилей зубьев зубчатых колёс (рис. 70, б).

рис. 70
Точка контакта зубьев (точка к), принадлежащая первому колесу, вращается вокруг точки Р, которая будет мгновенным центром скоростей. Скорость и совпадает с общей касательной к профилям в точкек при условии постоянства этого контакта.
рис. 71
В противном случае постоянного контакта не будет, так как появится составляющая и профили разомкнутся (рис. 71). Так как рассматривается произвольное положение зубьев, то можно сформулировать теорему.
Нормаль NN к касающимся профилям зубьев, проведённая через точку их касания, делит межцентровое расстояние на части, обратно пропорциональные угловым скоростям.
Эта теорема, сформулированная Виллисом в 1841 г., определяет основной закон зацепления профилей, которые не могут быть произвольными, а должны быть специально подобраны.
studfiles.net
Основные геометрические параметры зубчатого колеса. — Студопедия.Нет
Основными параметрами зубчатого колеса являются (рис. 1):
· z – число зубьев;
· ra – радиус (диаметр) окружности выступов;
· rf – радиус (диаметр) окружности впадин;
· rb – радиус (диаметр) основной окружности;
· r – радиус (диаметр) делительной окружности, т. е. окружности, которая является начальной в станочном зацеплении колеса с режущим инструментом;
· р – шаг по делительной окружности;
· h – высота зуба, равная h=ha+hf, где:
1. ha – высота головки зуба;
2. hf – высота ножки зуба;
· m – модуль зацепления, определяемый из условия:
, т. е. , (измеряется в мм).
Величина m стандартизирована, а делительная окружность является окружностью стандартного модуля. Обычно размеры зубчатого колеса и зубьев выражаются через m.
Так, например: , где – коэффициент высоты головки зуба;
, где – коэффициент радиального зазора;
; ; , где α – угол исходного контура режущего инструмента.
Обычно для стандартных зубчатых колёс: ; ; α=20º.
44а

44б
Свойства эвольвентного зацепления.
В зубчатой передаче контактирующие элементы двух профилей выполняются по эвольвентам окружности и образуют, так называемое эвольвентное зацепление. Это зацепление обладает рядом полезных свойств, которые и определяют широкое распространение эвольвентных зубчатых передач в современном машиностроении.
Свойства эвольвентного зацепления:
· передаточное отношение эвольвентного зацепления определяется только отношением радиусов основных окружностей и является величиной постоянной;
u 12=ω1/ ω2= rW2/ rW1= (rb2·cos αW)/ (rb1·cos αW)= rb2/ rb1=const.
· при изменении межосевого расстояния в эвольвентном зацеплении его передаточное отношение не изменяется;
· при изменении межосевого расстояния в эвольвентном зацеплении величина произведения межосевого расстояния на косинус угла зацепления не изменяется.
· за пределами отрезка линии зацепления N1N2 рассматриваемые ветви эвольвент не имеют общей нормали, т. е. профили выполненные по этим кривым будут не касаться, а пересекаться. Это явление называется интерференцией эвольвент или заклиниванием.
Качественные показатели зубчатого зацепления.
Одним из качественных показателей зубчатой передачи является коэффициент перекрытия
Другим качественным показателем является коэффициент скольжения, который учитывает влияние геометрии передачи и ее кинематики на скольжение и износ профилей, скользящих друг по другу (рис. 74), что видно из картины скоростей. На этой картине:
Vk1 – скорость точки К первого колеса;
Vk1t – проекцияэтой скорости на касательную к контактирующим профилям;
Vk 2 и Vk2t – тоже для колеса 2.
Скорость скольжения колеса 1 и 2 относительно друг друга равна:
Vck=Vk1k2= Vk1t– Vk2t
Коэффициенты скольжения колес 1 и 2 равны:
;
Эти коэффициенты равны нулю в полюсе (точка Р) и увеличиваются с удалением от него по линии зацепления.
46а

46б
studopedia.net
34. Зубчатые передачи. Достоинства и недостатки. Основные виды зубчатых передач. Основные параметры зубчатых колес. Передаточное число. Материалы и обработка.
Зубчатая передача — это механизм, который с помощью зубчатого зацепления передает или преобразует движение с изменением скоростей и моментов.
Цилиндрические зубчатые передачи между параллельными валами выполняют с помощью колес с прямыми, косыми и шевронными зубьями. Конические передачи между валами с пересекающимися осями осуществляют колесами с прямыми и круговыми зубьями, реже косыми (тангенциальными) зубьями. Преобразование вращательного движения в поступательное и наоборот осуществляют цилиндрическим колесом и рейкой.
Зубчатые передачи — самые распространенные среди механических передач. Годовой выпуск зубчатых колес составляет несколько миллионов. Диапазон их применения широк: от часов и приборов до самых тяжелых машин.
Достоинствазубчатых передач: малые габариты; высокий КПД; постоянство передаточного отношения из-за отсутствия проскальзывания; возможность применения в широком диапазоне вращающих моментов, скоростей и передаточных отношений; надежность в работе и простота обслуживания.
Недостаткизубчатых передач: высокие требования к точности изготовления; шум при работе со значительными скоростями.
Начальная окружность – ;
– передаточное отношение;
– межосевое расстояние;

– модуль, он стандартизован;
– делительный диаметр;
– коэффициент ширины зубчатого венца, где b – ширина колеса.
Для косозубых передач водят угол наклона зубьев β, для конических углы конусности δ, причем δ1+ δ2=180º.
Еще вводят параметры: стандартный угол профиля, окружности все, коэфф. торцевого перекрытия, смещение, линия зацепления и активная линия зацепления, высота и толщина зуба, ну может, что еще придумаете.
При выборе материалов для зубчатых колес необходимо обеспечить сопротивление контактной усталости поверхностных слоев зубьев, прочность зубьев на изгиб, сопротивление заеданию и износу. Основными материалами являются термически обрабатываемые стали. Допускаемые контактные напряжения примерно пропорциональны твердости материалов. Это указывает на целесообразность широкого применения для зубчатых колес сталей, закаливаемых до значительной твердости.
Твердость Н материала измеряют по Бриннелю, когда Н < 350 НВ или по Роквеллу НRСЭ при Н > 350 НВ. Приближенно 10 НВ ~ 1 НRСЭ. При твердости Н < 350 НВ шестерню выполняют с несколько большей твердостью, чем колесо, на (20…30) НВ. Термическую обработку заготовки (нормализацию, улучшение) выполняют до нарезания зубьев. После нарезания зубьев не требуется дополнительных финишных операций. Такие передачи хорошо прирабатываются.
При твердости Н > 350 НВ химико-термическую обработку ведут после зубонарезания, при этом зубья коробятся и в результате ухудшаются их точностные показатели. В массовом и крупносерийном производстве применяют исключительно зубчатые колеса высокой твердости, которые подвергают отделочным операциям после термической обработки.
Объемная закалка вызывает увеличение твердости не только поверхности зуба, но и его сердцевины. В результате зуб становится хрупким и легко разрушается при ударах. Поэтому объемная закалка уступила место поверхностным термическим и химико-термическим методам упрочнений. Такой обработкой можно достигнуть высокой твердости поверхностных слоев материала зубьев при сохранении вязкой сердцевины.
Для зубчатых колес применяют следующие основные виды поверхностных термических и химико-термических упрочнений: поверхностная закалка, цементация и нитроцементация с закалкой, азотирование.
Поверхностную закалку в основном обеспечивают за счет нагрева токами высокой частоты (ТВЧ). В связи с тем, что нагреваются поверхностные слои в течение 20…50 с, толщина закаливаемого слоя мала и деформации при закалке невелики. Поэтому можно обойтись без последующего шлифования зубьев (однако это понижает точность на одну-полторы степени). Материалы в этом случае — среднеуглеродистые легированные стали 40Х, 40ХН, 35ХМ и др. Обычно твердость на поверхности зубьев (50…55) НRСЭ.
Поверхностная закалка зубьев без охвата переходной поверхности (с обрывом твердого слоя у впадины зубьев) повышает износостойкость и сопротивление выкрашиванию, но понижает прочность при изгибе, так как создает концентратор напряжений у корня зуба. Желательно, чтобы закаленный слой повторял очертание впадин.
Цементация — поверхностное насыщение углеродом сталей, содержащих углерода менее 0,3%, с последующей закалкой. Цементация обеспечивает большую твердость (56…63) НRСЭ, несущую способность поверхностных слоев зубьев и высокую прочность на изгиб. Целесообразно применять газовую цементацию как более производительную. Применяют цементируемые стали: 20Х, а для ответственных зубчатых колес, работающих с ударными нагрузками, хро-моникелевые стали 12ХНЗА, 20ХНМ, безникелевые стали 18ХГТ, 25ХГТ и др. Толщина цементированного слоя примерно 0,3 модуля. Время цементации на глубину 1 мм примерно 3 часа — процесс длительный. При цементации рабочие поверхности зубьев искажаются и требуется их шлифование.
Азотирование — насыщение поверхностных слоев азотом, обеспечивает высокую твердость (58…65) НRСЭ и износостойкость поверхностных слоев. Азотируют готовые детали без последующей закалки. Для азотируемых колес применяют молибденовую сталь 38Х2МЮА, безалюминиевые стали типа 40ХФА, 40ХНА, 40Х. Зубья после азотирования в связи с малой толщиной слоя насыщения и малым короблением не шлифуют. Поэтому азотирование применяют для колес с внутренними зубьями и других, шлифование которых трудно осуществимо. Недостатком азотированных колес является малая толщина упрочненного слоя (0,2…0,5 мм), не позволяющая применять их при ударных нагрузках из-за опасности растрескивания упрочненного слоя и при работе с интенсивным изнашиванием (при загрязненной смазке).
Нитроцементация — насыщение поверхностных слоев углеродом и азотом с последующей закалкой — обеспечивает им высокую прочность, износостойкость и сопротивление заеданию. Нитроцементация идет с достаточно высокой скоростью и в связи с малыми толщиной упрочняемого слоя и его деформациями позволяет обойтись без последующего шлифования.
Улучшаемые стали применяют для зубчатых колес, преимущественно изготовляемых в условиях мелкосерийного и единичного производства при отсутствии жестких требований к габаритам. Чистовое нарезание зубьев улучшаемых колес производят после термической обработки заготовки, что исключает необходимость шлифования и позволяет обеспечить высокую точность. Применяют качественные углеродистые стали 40, 45 и легированные 35ХГС, 40Х и др.
Стали в нормализованном состоянии для обоих сопряженных зубчатых колес применяют только во вспомогательных механизмах, например в механизмах с ручным приводом. Основные материалы — среднеуглеродистые стали 40, 45, 50. Для повышения стойкости против заедания шестерни и колеса изготовляют из разных материалов.
Стальное литье применяют для колес больших диаметров. Основные материалы — литейные среднеуглеродистые стали 35Л, 50Л и др. Литые колеса подвергают преимущественно нормализации.
Ч у г у н ы используют для изготовления тихоходных, крупногабаритных и открытых передач. Кроме того, из чугуна изготовляют сменные колеса (поочередно работающие). Применяют чугуны СЧ20…СЧ35, а также высокопрочные магниевые чугуны с шаровидным графитом.
Пластмассовые зубчатые колеса в паре с металлическими применяют в слабонагруженных передачах для обеспечения бесшумности, самосмазываемости или химической стойкости. Используют текстолит (рекомендуемые марки ПТ и ПТК) и древесно-слоистые пластики. Наиболее перспективными следует считать капролон, полиформальдегид и фенилон.
studfiles.net
Основные геометрические параметры прямозубых зубчатых колес
Параметр | Обозначение | Соотношения |
Модуль | m | |
Число зубьев | z | |
Делительный диаметр | d | d = m z |
Диаметр вершин зубьев | da | da = m (z + 2) |
Диаметр впадин зубьев | df | df = m (z – 2,5) |
Угол профиля зуба | | =20 |
Диаметр основной окружности | db | db = d cos |
Коэффициент смещения исходного контура | x | |
Ширина зубчатого венца | b | |
Высота зуба | h | h = m 2,25 |
Межосевое расстояние | aW |
11.2. Нормы кинематической точности цилиндрических зубчатых колес и передач
Показатели кинематической точности определяют величину допускаемой погрешности угла поворота ведомого зубчатого колеса и передачи в пределах его полного оборота. Кинематическую точность можно выявить и оценить по одному из вариантов, содержащих требования к одному или двум параметрам (табл. 11.2). Один параметр принимается для нормирования в тех случаях, когда он один выявляет кинематическую точность (п.п. 1, 2, 3, 10 табл. 11.2) или относится к грубым колесам (п.п. 8, 9 таб. 11.2).
Таблица 11.2
Показатели кинематической точности
№ | Нормируемые показатели точности или комплексы | Показатель | Степени точности |
Зубчатые колеса | |||
1 | Наибольшая кинематическая погрешность зубчатого колеса | | 3-9 |
2 | Накопленная погрешность шага и накопленная погрешность к шагов | Fpr Fpkr | 3-6 |
3 | Накопленная погрешность шага | Fpr | 7, 8 |
4 | Погрешность обката и радиальное биение зубчатого венца | Fcr Frr | 3-8 |
5 | Колебание длины общей нормали и колебание измерительного межосевого расстояния за один оборот колеса | Fvwr | 3-8 |
6 | Колебание длины общей нормали и радиальное биение зубчатого венца | Fvwr Frr | 5-8 |
7 | Погрешность обката и колебание измерительного межосевого расстояния за один оборот колеса | Fcr | 5-8 |
8 | Колебание измерительного межосевого расстояния за один оборот колеса | | 9-12 |
9 | Радиальное биение зубчатого венца | Frr | 9-12 |
Зубчатые передачи | |||
10 | Наибольшая накопленная погрешность передачи | | 3-8 |
Во всех остальных случаях регламентируются требования к погрешностям, рассматриваемым в радиальном и тангенциальном направлении.
Кинематической погрешностью зубчатого колесаFк.п.к называется разность между действительным и номинальным (расчетным) углами поворота зубчатого колеса на его рабочей оси, ведомого измерительным зубчатым (точным) колесом при номинальном взаимном положении осей вращения обоих колес. Выражается в линейных величинах длиной дуги делительной окружности (рис. 11.2,а). Под рабочей осью зубчатого колеса понимается ось, вокруг которой оно вращается в передаче.

Рис. 11.2. Измерение кинематической погрешности зубчатого колеса
Под измерительным зубчатым колесом понимается зубчатое колесо повышенной точности, применяемое в качестве измерительного элемента для однопрофильного и двухпрофильного методов контроля зубчатых колес.
Наибольшая кинематическая погрешность
зубчатого колеса –
это наибольшая алгебраическая разность
значений кинематической погрешности
зубчатого колеса в пределах его полного
оборота.
–
это наибольшая алгебраическая разность
значений кинематической погрешности
зубчатого колеса в пределах его полного
оборота.
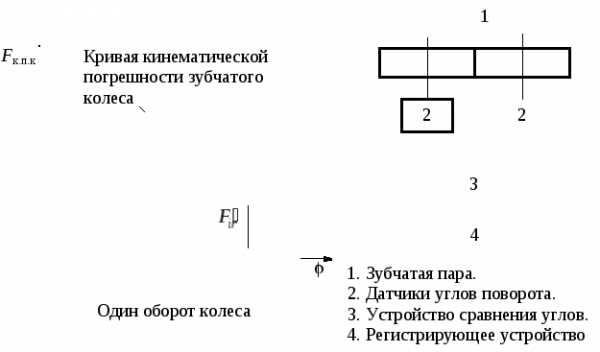
Для измерения  применяется прибор комплексного
однопрофильного контроля, схема которого
приведена на рис. 11.2,б.
применяется прибор комплексного
однопрофильного контроля, схема которого
приведена на рис. 11.2,б.
Допуск на кинематическую погрешность
зубчатого колеса –  .
.
Накопленная погрешность k шагов FPkr– это наибольшая разность дискретных значений кинематической погрешности зубчатого колеса при номинальном его повороте наkцелых угловых шагов:
FPkr= (r–k2/z)r,
где r– действительный угол поворота (измеренный) зубчатого колеса;z– число зубьев зубчатого колеса;k– число целых угловых шагов отk2;r– радиус делительной окружности зубчатого колеса (рис. 11.3).

Рис. 11.3. Накопленная погрешность
Значение допуска на накопленную погрешность kшагов зубчатого колеса стандартизовано и задается величинойFPk.
Накопленная погрешность шагаFPr– это наибольшая алгебраическая разность значений накопленных погрешностей в пределах зубчатого колеса (рис. 11.3). Допуск на накопленную погрешность шага обозначаютFP. На образование этой погрешности влияют погрешности обката и монтажного эксцентриситета зубчатого колеса, то есть несовпадение оси зубчатого колеса при нарезании и монтаже.
Колебание длины общей нормалиFvWr– это разность между наибольшей и наименьшей действительными длинами общей нормали в одном и том же зубчатом колесе:FvWr=Wmax–Wmin. Допуск на колебание длины общей нормали обозначаетсяFvW.
Под действительной длиной общей нормали понимается расстояние Wмежду двумя параллельными плоскостями, касательными к двум разноименным активным боковым поверхностям зубьев зубчатого колеса (рис. 11.4). Общая нормаль к эвольвентным профилям является одновременно касательной к основной окружности.
Колебание измерительного межосевого
расстояния за один оборот колеса – это разность между наибольшим и
наименьшим действительными межосевыми
расстояниями при двухпрофильном
зацепления измерительного колеса с
контролируемым зубчатым колесом, при
повороте последнего на полный оборот
или, соответственно, на один угловой
шаг (рис. 11.5).
– это разность между наибольшим и
наименьшим действительными межосевыми
расстояниями при двухпрофильном
зацепления измерительного колеса с
контролируемым зубчатым колесом, при
повороте последнего на полный оборот
или, соответственно, на один угловой
шаг (рис. 11.5).

Рис. 11.4. Определение длины общей нормали
Рис. 11.5. Измерение измерительного межосевого расстояния
Нормируется допуск на колебание
измерительного межосевого расстояния  .
.
Радиальное биение зубчатого венцаFrr– это разность
действительных предельных положений
исходного контура в пределах зубчатого
колеса от его рабочей оси. ПрактическиFrrопределяется разностью
от рабочей оси колеса до постоянных
хорд зубьев. Допуск на радиальное биение
зубчатого венца обозначаетсяFr.
Основной причиной появления радиального
биения является эксцентриситет основной
окружности: посадочный и кинематический.
Посадочный эксцентриситет возникает
при несовпадении оси вращения заготовки
при зубонарезании колеса с осью вращения
нарезанного колеса в механизме. Причиной
возникновения кинематического
эксцентриситета является колебание
угловых скоростей вращения заготовки
или инструмента при нарезании колеса
методом обката из-за неточности
делительной цепи зуборезного станка.
зубьев. Допуск на радиальное биение
зубчатого венца обозначаетсяFr.
Основной причиной появления радиального
биения является эксцентриситет основной
окружности: посадочный и кинематический.
Посадочный эксцентриситет возникает
при несовпадении оси вращения заготовки
при зубонарезании колеса с осью вращения
нарезанного колеса в механизме. Причиной
возникновения кинематического
эксцентриситета является колебание
угловых скоростей вращения заготовки
или инструмента при нарезании колеса
методом обката из-за неточности
делительной цепи зуборезного станка.
Погрешность обкатаFcr– характеризует точность делительной цепи зубообрабатывающего станка и выявляет несогласованность взаимного перемещения обрабатываемого колеса и зубообрабатывающего инструмента. Эта погрешность измеряется непосредственно на станке с помощью кинематомера. Она ограничивается допускомFc.
studfiles.net
Основные геометрические параметры прямозубых зубчатых колес
Параметр | Обозначение | Соотношения |
Модуль | m | |
Число зубьев | z | |
Делительный диаметр | d | d = m z |
Диаметр вершин зубьев | da | da = m (z + 2) |
Диаметр впадин зубьев | df | df = m (z – 2,5) |
Угол профиля зуба | | =20 |
Диаметр основной окружности | db | db = d cos |
Коэффициент смещения исходного контура | x |
Окончание табл. 11.1
Параметр | Обозначение | Соотношения |
Ширина зубчатого венца | b | |
Высота зуба | h | h = m 2,25 |
Межосевое расстояние | aW |
11.2. Нормы кинематической точности цилиндрических зубчатых колес и передач
Показатели кинематической точности определяют величину допускаемой погрешности угла поворота ведомого зубчатого колеса и передачи в пределах его полного оборота.
Кинематическую точность можно выявить и оценить по одному из вариантов, содержащих требования к одному или двум параметрам (табл. 11.2). Один параметр принимается для нормирования в тех случаях, когда он один выявляет кинематическую точность (п.п. 1, 2, 3, 10 табл. 11.2) или относится к грубым колесам (п.п. 8, 9 таб. 11.2). Во всех остальных случаях регламентируются требования к погрешностям, рассматриваемым в радиальном и тангенциальном направлении.
Таблица 11.2
Показатели кинематической точности
№ | Нормируемые показатели точности или комплексы | Показатель | Степени точности |
Зубчатые колеса | |||
1. | Наибольшая кинематическая погрешность зубчатого колеса | | 3-9 |
2. | Накопленная погрешность шага и накопленная погрешность к шагов | Fpr Fpkr | 3-6 |
3. | Накопленная погрешность шага | Fpr | 7, 8 |
4. | Погрешность обката и радиальное биение зубчатого венца | Fcr Frr | 3-8 |
5. | Колебание длины общей нормали и колебание измерительного межосевого расстояния за один оборот колеса | Fvwr | 3-8 |
6. | Колебание длины общей нормали и радиальное биение зубчатого венца | Fvwr Frr | 5-8 |
7. | Погрешность обката и колебание измерительного межосевого расстояния за один оборот колеса | Fcr | 5-8 |
8. | Колебание измерительного межосевого расстояния за один оборот колеса | | 9-12 |
9. | Радиальное биение зубчатого венца | Frr | 9-12 |
Зубчатые передачи | |||
10. | Наибольшая накопленная погрешность передачи | | 3-8 |
Кинематической погрешностью зубчатого колесаFк.п.к называется разность между действительным и номинальным (расчетным) углами поворота зубчатого колеса на его рабочей оси, ведомого измерительным зубчатым (точным) колесом при номинальном взаимном положении осей вращения обоих колес. Выражается в линейных величинах длиной дуги делительной окружности (рис. 11.2,а). Под рабочей осью зубчатого колеса понимается ось, вокруг которой оно вращается в передаче.
 а)
б)
а)
б)
Рис. 11.2. Измерение кинематической погрешности зубчатого колеса
Под измерительным зубчатым колесом понимается зубчатое колесо повышенной точности, применяемое в качестве измерительного элемента для однопрофильного и двухпрофильного методов контроля зубчатых колес.
Наибольшая кинематическая погрешность
зубчатого колеса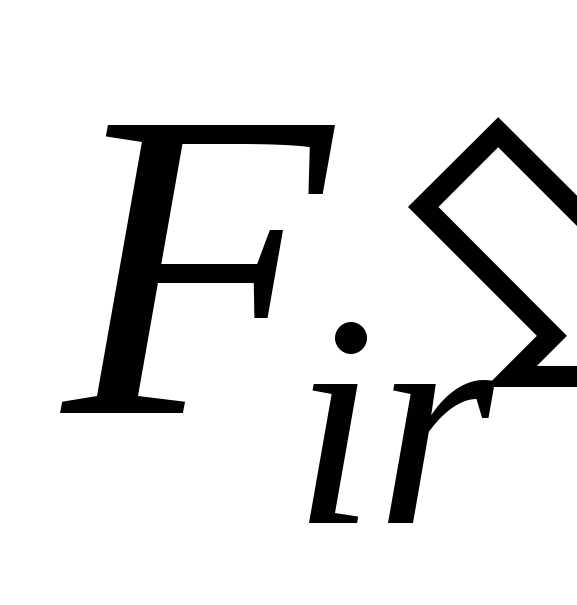 –
это наибольшая алгебраическая разность
значений кинематической погрешности
зубчатого колеса в пределах его полного
оборота.
–
это наибольшая алгебраическая разность
значений кинематической погрешности
зубчатого колеса в пределах его полного
оборота.
Для измерения  применяется прибор комплексного
однопрофильного контроля, схема которого
приведена на рис. 11.2,б.
применяется прибор комплексного
однопрофильного контроля, схема которого
приведена на рис. 11.2,б.
Допуск на кинематическую погрешность
зубчатого колеса –  .
.
Накопленная погрешность k шагов FPkr– это наибольшая разность дискретных значений кинематической погрешности зубчатого колеса при номинальном его повороте наkцелых угловых шагов:
FPkr= (r–k2/z)r,
где r– действительный угол поворота (измеренный) зубчатого колеса;z– число зубьев зубчатого колеса;k– число целых угловых шагов отk2;r– радиус делительной окружности зубчатого колеса (рис. 11.3).
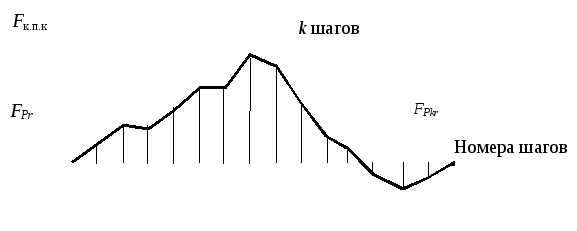
Рис. 11.3. Накопленная погрешность
Значение допуска на накопленную погрешность kшагов зубчатого колеса стандартизовано и задается величинойFPk.
Накопленная погрешность шагаFPr– это наибольшая алгебраическая разность значений накопленных погрешностей в пределах зубчатого колеса (рис. 11.3). Допуск на накопленную погрешность шага обозначаютFP. На образование этой погрешности влияют погрешности обката и монтажного эксцентриситета зубчатого колеса, то есть несовпадение оси зубчатого колеса при нарезании и монтаже.
Колебание длины общей нормалиFvWr– это разность между наибольшей и наименьшей действительными длинами общей нормали в одном и том же зубчатом колесе:FvWr=Wmax–Wmin. Допуск на колебание длины общей нормали обозначаетсяFvW.
Под действительной длиной общей нормали понимается расстояние Wмежду двумя параллельными плоскостями, касательными к двум разноименным активным боковым поверхностям зубьев зубчатого колеса (рис. 11.4). Общая нормаль к эвольвентным профилям является одновременно касательной к основной окружности.
Колебание измерительного межосевого
расстояния за один оборот колеса – это разность между наибольшим и
наименьшим действительными межосевыми
расстояниями при двухпрофильном
зацепления измерительного колеса с
контролируемым зубчатым колесом, при
повороте последнего на полный оборот
или, соответственно, на один угловой
шаг (рис. 11.5).
– это разность между наибольшим и
наименьшим действительными межосевыми
расстояниями при двухпрофильном
зацепления измерительного колеса с
контролируемым зубчатым колесом, при
повороте последнего на полный оборот
или, соответственно, на один угловой
шаг (рис. 11.5).

Рис. 11.4. Определение длины общей нормали
Рис. 11.5. Измерение измерительного межосевого расстояния
Нормируется допуск на колебание
измерительного межосевого расстояния  .
.
Радиальное биение зубчатого венцаFrr– это разность действительных предельных положений исходного контура в пределах зубчатого колеса от его рабочей оси. ПрактическиFrrопределяется разностью от рабочей оси колеса до постоянных хордзубьев. Допуск на радиальное биение зубчатого венца обозначаетсяFr. Основной причиной появления радиального биения является эксцентриситет основной окружности: посадочный и кинематический. Посадочный эксцентриситет возникает при несовпадении оси вращения заготовки при зубонарезании колеса с осью вращения нарезанного колеса в механизме. Причиной возникновения кинематического эксцентриситета является колебание угловых скоростей вращения заготовки или инструмента при нарезании колеса методом обката из-за неточности делительной цепи зуборезного станка.
Погрешность обкатаFcr– характеризует точность делительной цепи зубообрабатывающего станка и выявляет несогласованность взаимного перемещения обрабатываемого колеса и зубообрабатывающего инструмента. Эта погрешность измеряется непосредственно на станке с помощью кинематомера. Она ограничивается допускомFc.
studfiles.net
Основные параметры зубчатых колес – Энциклопедия по машиностроению XXL
ОСНОВНЫЕ ПАРАМЕТРЫ ЗУБЧАТЫХ КОЛЕС Колеса (катки) фрикционной цилиндрической передачи прижаты друг к другу. Поэтому при вращении одного колеса (в результате возникновения сил трения) приводится во вращение и другое [c.216]Модуль является основным параметром зубчатого колеса и его величины установлены СТ СЭВ 310—76. Многие размеры зубчатого колеса зависят от величины модуля, например, размеры зуба, венца, ступицы и т. д. [c.206]
Основным параметром зубчатых колес является модуль. Модуль т — это длина диаметра делительной окружности, приходящаяся на один зуб колеса. Стандартом установлен ряд чисел модулей (табл. 58). [c.147]
Модуль зубьев — основной параметр зубчатого колеса. Для пары колес, находящихся в зацеплении, модуль должен быть одинаковым. Модули зубьев для цилиндрических и конических передач регламентированы ГОСТ 9563—60. Значения стандартных модулей от 1 до 14 мм приведены в табл. 71. [c.114]
Все основные параметры зубчатых колес выражают через модули, а именно шаг зубьев [c.115]
Заполненный бланк 1, содержащий таблицу основных параметров зубчатых колес и зацепления для оптимального значения с, график зависимости е = / (с), кальку с эскизом зубчатого зацепления. [c.49]
На сборочном чертеже должны быть указаны габаритные, установочные и присоединительные размеры, расчетные размеры, основные параметры зубчатых колес, шкал и других составных частей и их элементов, непосредственно связанных с эксплуатацией оборудования. В необходимых случаях должны быть указаны также размеры ответственных деталей, предельные отклонения этих размеров, материал, твердость, покрытие, шероховатость обработанных поверхностей и другие технические данные. [c.36]
ОСНОВНЫЕ ПАРАМЕТРЫ ЗУБЧАТЫХ КОЛЕС И РЕДУКТОРОВ [c.403]
Основные параметры зубчатых колес [c.451]
В работе студент должен научиться определять основные параметры зубчатых колес с эвольвентным профилем зуба. Основными параметрами зубчатого колеса с эвольвентным профилем являются модуль (т). число зубьев г и угол профиля производящей рейки Лр). Все остальные величины зубчатых колес могут быть [c.32]
Основные параметры зубчатых колес и редукторов [c.351]
Основные параметры зубчатого колеса показаны на рис. 1. [c.247]
Расчет основных параметров зубчатых колес. [c.35]
РАСЧЕТ ОСНОВНЫХ ПАРАМЕТРОВ ЗУБЧАТЫХ КОЛЕС [c.40]
Выбор основных параметров зубчатых колес и передач [c.17]
Рассмотрим основные параметры зубчатого колеса. На рис. 47, в дано пространственное изображение части зубчатого колеса с внешним расположением зубьев, а на рис. 47, г — его конструктивное изображение в ортогональной проекции. [c.89]
Подсчет основных параметров зубчатого колеса. Чтобы условно изобразить зубчатый венец, определяют диаметр трех окружностей. [c.154]
Основные параметры зубчатых колес (диаметр, ширина, модуль, число зубьев и пр.) определяют при проектировании передачи (см. гл. XIV). Ниже рассматриваются вопросы, связанные с конструктивной формой зубчатых колес. [c.325]
Основные параметры зубчатого колеса электростартера [c.166]
Методы и периодичность текущего контроля основных параметров зубчатых колес и параметров технологического процесса после химико-термической обработки [c.448]
Г. 16530-83, 16531-83, 16532-83 — основные параметры зубчатых колес [c.11]
Одним из основных параметров зубчатых колес является модуль [c.254]
Освоить методику измерения основных параметров зубчатых колес. [c.178]
Задание основных параметров зубчатого колеса. Для выполнения этого этапа конструирования из главного экранного меню вызывают подменю функций задания основных параметров зубчатого колеса, в котором представлены строки вызова функции диалога для ввода необходимых параметров соответственно зубчатого зацепления, зубчатого венца, отверстия в ступице, ступицы, диска зубчатого колеса. [c.440]
Основные параметры зубчатых колес (число зубьев, модуль, диаметр, ширина зубчатого венца) определяются при расчете передачи. Ниже рассматриваются вопросы, связанные с конструктивной формой зубчатых колес. [c.261]
Модуль зацепления является одним из основных параметров зубчатого колеса и выражается в миллиметрах. С целью сокращения количества инструмента значение модулей m стандартизовано по ГОСТ. Размеры инструментальной рейки, так называемый исходный контур инструментальной рейки, также стандартизованы в долях модуля зацепления (рис. 67). [c.121]
Отсюда видно, что шаг зацепления всегда выражается через радиус НЛП через диаметр окружности несоизмеримым числом, так как в правую часть входит трансцендентное число л. Это затрудняет подбор размеров зубчатых колес % при проектировании колес и практическое их измерение. Поэтому для определения основных размеров зубчатых колес в качестве основной единицы принят некоторый параметр, называемый модулем зацепления. Модуль зацепления измеряется в миллиметрах и обозначается буквой т. Величина модуля равна [c.429]
Делительные диаметры удобны для расчетов, связанных с проектированием зубчатых передач, вычерчиванием и изготовлением зубчатых колес. От делительного диаметра числа зубьев z зависит один из основных параметров зубчатых зацеплений, так называемый модуль т [c.185]
Раньше были приведены формулы для определения основных параметров зубчатых колес при условии, что стандартный модуль соответствует их начальным окружностям, совпадающим с делительными окружностями. Однако это условие накладывает некоторые ограничения и вызывает трудности, возникающие при конструировании зубчатых передач. Например, уменьшение числа зубьев колеса удешевляет производство зубчатых колес, уменьшает вес конструкции, делает ее более компактной и т, д. Но уменьшение числа зубьев при нормальном зубчатом зацеплении можегг вызвать подрез зубьев. Поэтому для улучшения условий работы зубчатых колес — устранения заострения вершин зубьев и возможного заклинивания зубчатого зацепления, а также для повышения контактной и изгибной прочности, вписывания проектируемой зубчатой передачи в заданный габарит и т. д. — нормальное зубчатое зацепление, как не удовлетворяющее предъявляемым требованиям, необходимо заменять исправленным зацеплением. Зубчатые колеса с геометрическими параметрами, отличающимися от нормальных, называют исправленными, или корригированными. [c.202]
При этом положения точек пересечения эвольвентных профилей с линией зацепления рассматриваются для каждого из колес относительно своего начала координат. Неточность процесса зубообразования вызовет появление погрешностей основных параметров зубчатых колес, причем в дальнейших рассуждениях не будем учитывать влияния погрешности радиусов основных окружностей и погрешностей формы эвольвентных профилей колес на изменения угла зацепления зубчатой передачи. Принятые допущения позволяют утверждать, что положение каждого колеса может быть взаимно однозначно определено положением конечного числа точек пересечения эвольвент профилей с линией зацепления (рис. 1.26). При этом будем считать, что линия зацепления при движении колес неподвижна в системе координат, связанной с осями колес. [c.68]
Расчет кинематической пвгрешности. На рис. 6.21 изображена планетарная передача 2/С — Л с двухвенцовым сателлитом. Основные параметры зубчатых колес приведены в табл. 6.9.. [c.184]
Отдельной составной частью руководства является паспорт станка, оформленный на специальных стандартных бланках. Паспорт содержит осАовиые данные станка (характеристику) спецификацию сборочных единиц (узлов) станка таблицу основных параметров зубчатых колес, червяков, винтов и гаек кинематическую схему станка таблицу механики главного движения (положение рукояток и соответствующие им частоты вращения шпинделя, наибольшие допускаемые крутящие моменты, мощности, к.п.д., указания о слабых звеньях) таблицу механизма подачи (положение рукояток и соответствующие им величины подачи и шагов резьб), схему расположения и спецификацию подшипников. К Руководству прилагаются чертежи наиболее часто заменяемых деталей станка. [c.107]
Основным параметром зубчатого колеса является делительная окружность. Диаметр делительной окружности обозначается буквой с1 и называется делительным. По делительной окружности откладывается окружной шаг зубьев, обозначаемый р, и представляюший собой расстояние по дуге делительной окружности между соседними (смежными) зубьями колеса (рис. 440). Таких шагов можно отложить столько, сколько зубьев имеет колесо, иначе говоря, отрезки, равные шагу р,, делят делительную окружность на I частей, отсюда ее название — делительная. [c.254]
mash-xxl.info
Основные параметры редукторов с цилиндрическими зубчатыми колесами
Основные параметры редукторов с цилиндрическими зубчатыми колесами
ГОСТ 2185-66 устанавливает межосевые расстояния aW, номинальные передаточные числа и, коэффициенты ширины зубчатых колес ψba и дается рекомендуемые сочетания межосевых расстояний и общие номинальные передаточные числа для зубчатых цилиндрических передач, которые используются в двух- и трехступенчатых насосных редукторах общего назначения, что дает возможность для серийного изготовления редукторов.
Межосевые расстояния
Межосевые расстояния редукторов aw приведены в табл. 49. Величину межосевого расстояния определяют расчетом на усталостную контактную прочность поверхностей зубьев или выбирают конструктивно в зависимости от габаритных размеров приводимой машины. В табл. 50 и 51 приведены рекомендуемые стандартом межосевые расстояния для двух- и трехступенчатых редукторов и их распределение по отдельным ступеням.
Таблица 49
Межосевые расстояния редукторов, мм
Примечание. Предпочтительный ряд первый.
Таблица 50
Межосевые расстояния двухступенчатых трехосных редукторов, мм
Таблица 51
Межосевые расстояния трехступенчатых редукторов, мм
Таблица 52
Примечания.
1. Первый ряд следует предпочитать второму.
2. Для редукторов, которые должны быть кинематически согласованы между собой, допускается выбирать передаточные числа из ряда R40 (ГОСТ 8032-84).
3. Фактические значения передаточных чисел uф не должны отличаться от номинальных более чем на 2,5% при и ≤ 4,5 и на 4% при и > 4,5.
Таблица 53
Общие передаточные числа иобщ. двухступенчатых редукторов
Примечания:
1. Для всех редукторов первый ряд следует предпочитать второму.
2. Фактические значения передаточных чисел uф не должны отличаться от номинальных более чем на 4%.
Таблица 54
Общие передаточные числа иобщ. трехступенчатых редукторов
Примечания:
1. Для всех редукторов первый ряд следует предпочитать второму.
2. Фактические значения передаточных чисел иф не должны отличаться от номинальных более чем на 4%.
Передаточные числа
Номинальные передаточные числа и должны соответствовать указанным в табл. 52.
Рекомендуемые общие передаточные числа иобщ для двух- и трехступенчатых несоосных редукторов общего назначения приведены в табл. 53 и 54.
Распределение общего передаточного числа между отдельными ступенями передач в двух- и трехступенчатых редукторах (табл. 55 и 56) осуществляется при условии одинакового использования контактной прочности зубьев при одинаковой твердости их поверхностей, одинаковых коэффициентов ширины зубьев колес всех ступеней и распределения межосевых расстояний между отдельными ступенями, как это дано в табл. 50 и 5). В двухступенчатых редукторах с соосным расположением валов в одной горизонтальной плоскости при заданном распределении передаточных чисел между ступенями, с одинаковыми межосевыми расстояниями для выполнения условия равнопрочности приходится применять зубчатые колеса с разными коэффициентами ширины.
Таблица 55
Распределение общих передаточных чисел в двухступенчатых трехосных редукторах по отдельным ступеням зубчатых зацеплений
Таблица 56
Распределение общих передаточных чисел в трехступенчатых редукторах по отдельным ступеням зубчатых зацеплений
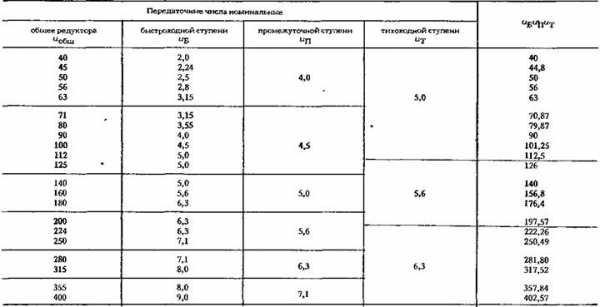
Таблица 57
Распределение общих передаточных чисел в двухступенчатых двухосных (соосных) редукторах с горизонтальным расположением валов в одной плоскости по отдельным ступеням зубчатых зацеплений
Если первая ступень имеет коэффициент ширины ψbа = 0,4, то вторая ступень должна иметь коэффициент ψbа не менее 0,6 при одних и тех же материалах шестерен и колес и твердости поверхностей зубьев.
Передаточные числа отдельных ступеней этих редукторов (табл. 53) устанавливаются при условии близкой контактной равнопрочности и одинакового погружения в масляную ванну зубчатых колес быстроходной и тихоходной ступеней при смазывании окунанием.
Ширина зубчатых колес
Ширина зубчатых колес b зависит от коэффициента ширины ψbа: b = ψbааw. Значения коэффициента ширины зубчатых колес ψbа (ГОСТ 2185-66) приведены в табл. 58.
Значения ширины зубчатых колес округляют до ближайшего числа из ряда R20 по ГОСТ 8032-84. Ширина канавки для выхода режущего инструмента в шевронных зубчатых колесах включается в величину ширины b. При различной ширине сопряженных зубчатых колес берется значение коэффициента ψbа зубчатого колеса с меньшей шириной.
При выборе коэффициента ширины ψbа необходимо принимать во внимание материал зубчатых колес и вид термообработки, точность изготовления, окружную скорость, величину модуля и осевого шага, характер нагрузки, схему редуктора и ряд других факторов. Рекомендуется выбирать узкие колеса, так как в этом случае получается более высокая точность изготовления и значительно снижается неравномерность распределения нагрузки по ширине, вызываемая деформацией валов и неточностями изготовления и монтажа редуктора. По этой же причине не рекомендуется отношение ширины шестерни к диаметру делительной окружности принимать больше 2,5.
При твердости поверхностей зубьев НВ ≤ 350 рекомендуется задавать твердость зубьев шестерни на 30…50 единиц больше твердости зубьев колеса. В тех случаях, когда твердость зубьев шестерни значительно больше твердости зубьев колеса, ширина шестерни должна быть на 5… 10 мм больше, чем ширина колеса. В противном случае при относительном смещении шестерни и колеса в процессе эксплуатации на зубьях колеса образуется нежелательный уступ.
При твердости поверхностей зубьев обоих колес НВ ≥ 350 ширину колес можно принимать одинаковой. Для колес с цементированными, закаленными с поверхности зубьями коэффициент ширины ψbа рекомендуется принимать не более 0,4…0,5. При увеличении длины зубьев погрешности, возникающие при обработке, возрастают, что приводит к большим затруднениям при получении необходимого пятна контакта.
При поверхностной закалке происходит коробление зубьев; при этом с увеличением ширины колес ошибки в направлении зубьев возрастают. В случае применения широких колес лучше переходить на шевронное зацепление, так как длина зуба одной спирали составляет около половины общей ширины зубчатого колеса и ошибки в направлении зубьев значительно уменьшаются.
В прямозубых и косозубых передачах коэффициент ширины ψbа должен быть не более 0,4…0,6. При больших значениях коэффициента ψbа необходимо применять шевронное зацепление.
Быстроходные передачи изготовляются с шевронным зацеплением при коэффициенте ширины ψbа = 0,4… 1,0. При консольном расположении шестерен и колес рекомендуется выбирать коэффициент ширины ψbа не свыше 0,4. При дальнейшем увеличении ширины колеса (при консольном его расположении) сильно возрастает концентрация нагрузки по длине зубьев и эффект от использования материала колес резко снижается.
Таблица 58
Коэффициент ширины зубчатых колес
Модули
Значения модулей для цилиндрических зубчатых колес редукторов (ГОСТ 9563-60) приведены в табл. 59. Величину модуля определяют исходя из прочности зубьев по изгибу. По возможности выбирают наименьшие значения модулей, так как зубчатые колеса с малыми модулями нарезаются на зуборезных станках с большей точностью и с лучшей чистотой поверхности, имеют меньшую массу и меньшие потери на трение в зацеплении. При поверхностной закалке меньше искажается форма их зубьев и получается хорошая и более быстрая приработка зацепления.
Если зубчатое колесо должно работать при предельных контактных напряжениях, то значение модуля, полученного при расчете на изгиб, рекомендуется увеличивать на 10…15%, так как при выкрашивании поверхностей зубьев происходит ослабление их поперечного сечения и может произойти излом зуба.
Таблица 59
Значения модулей т, мм
Примечание. При назначении величин модулей первый ряд предпочтительнее.
Углы наклона линии зубьев
Углы наклона зубьев в косозубых передачах должны быть 8…100. В косозубых передачах при угле наклона зуба свыше 10° необходимо устанавливать или радиально-упорные подшипники с увеличенным углом контакта, или в опоре с радиальным подшипником дополнительно устанавливать упорный подшипник, что удорожает конструкцию и требует более надежного и сложного торцового крепления подшипников на валах и в корпусах.
Уменьшение утла наклона зубьев, особенно в узких колесах с коэффициентом ширины ψbа 0,2…0Д нежелательно, так как величина осевого шага может быть больше ширины колеса. Вследствие этого осевой коэффициент перекрытия будет меньше единицы и передача будет работать менее плавно, с большими динамическими нагрузками, что ведет к быстрому износу и появлению дефектов на поверхностях зубьев.
Для установленных ГОСТом межосевых расстоянии в табл. 60 приведены суммарные числа зубьев z∑ и углы наклона зубьев β на делительном цилиндре при определенных интервалах передаточных чисел и модулей в нормальном сечении. Эти значения рекомендуются при коэффициенте ширины ψbа ≥ 0,4 при некорригированном и корригированном зацеплении с коэффициентом сдвига х1=-х2 соответственно для шестерни и колеса, но могут быть использованы и при ψbа < 0,4, но с проверкой, указанной в примечании к табл. 60.
Подбор чисел зубьев шестерни и колеса в зависимости от принятого суммарного числа зубьев z∑ и передаточного числа и можно выполнить по табл. 62.
Таблица 60
Параметры передач с косозубыми колесами при ψbа ≥ 0,4 (зацепление некорригированное или корригированное с коэффициентом сдвига х1=-х2 )

Для шевронных колес угол наклона зубьев β равен 25…350. Рекомендуемые параметры передач с шевронными колесами при некорригированном или корригированном зацеплении с коэффициентом сдвига х1=-х2 соответственно для шестерни и колеса при коэффициенте ширины ψbа > 0,125 приведены в табл. 61, где для стандартных межосевых расстояний приведены суммарные числа зубьев z∑ сопряженных шестерни z1 и колеса z2 и углы наклона зубьев β по принятому модулю зацепления т в интервале передаточных чисел. Подбор чисел зубьев шестерни z1 и числа зубьев колеса z2 в зависимости от принятого суммарного числа зубьев z∑ и передаточного числа и передачи выполняется по табл. 62, где в числителе поставлено число зубьев колеса z2, а в знаменателе – суммарное число зубьев zz сопряженных шестерни и колеса. Для каждого значения передаточного числа и в верхней строке приведены наименьшие значения z2/z∑, а в нижней – наибольшие, соответствующие допустимым значениям рассматриваемого передаточного числа. В интервале наименьших и наибольших значений чисел зубьев z2 /z∑ может быть любое целое число из указанного интервала.
Продолжение табл. 60

Продолжение табл. 60
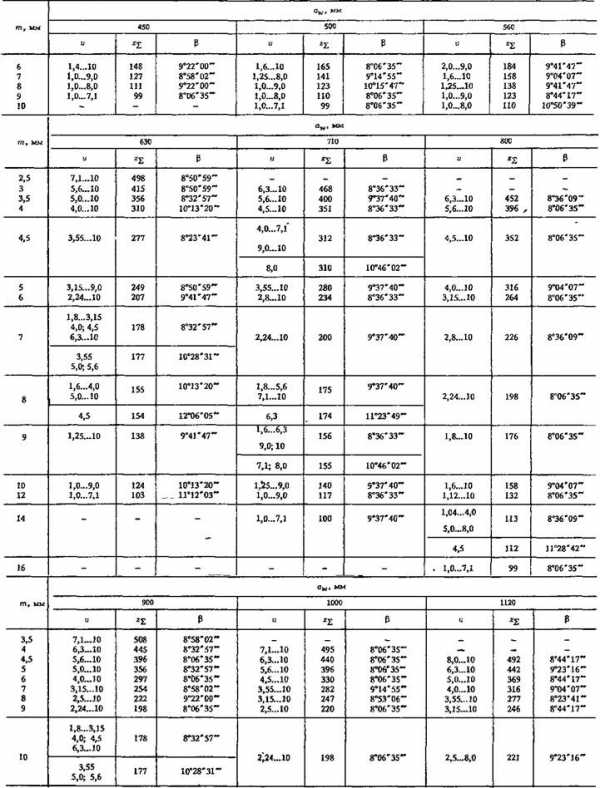

Примечание. Отдельные сочетания величин αW, Z∑, m ; β могут быть использованы и при ψ ba< 0,4, но с проверкой соблюдения условия
или
Таблица 61
Параметры передач с шевронными колесами при ψba ≥ 0,125 (зацепление некорригированное или корригированное с коэффициентом сдвига x1 = -х2)
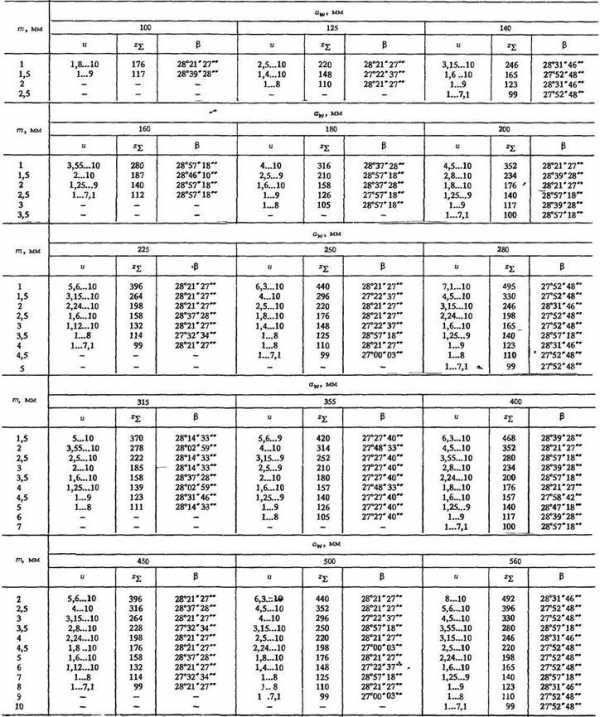
Продолжение табл. 61

Продолжение табл. 61
Необходимо обратить внимание на то, что при подборе чисел зубьев шестерни или колеса в пределах 100 зубьев почти на всех зуборезных станках можно нарезать колеса с любым числом зубьев. При числе зубьев шестерни или колеса свыше 100 необходимо проверять возможности их нарезки на зуборезных станках. Например, при z1 = 50 и и = 2,5 по табл. 62 возможно применение всех значений суммарных чисел зубьев от 172 до 178 включительно, которым соответствуют значения чисел зубьев колес z2 от 122 до 128 включительно. Число зубьев колеса z2 = 127, как первоначальное число, или не применять или проверить возможность нарезки по паспорту зуборезного станка.
Применение чисел зубьев меньше 17 допустимо после проверки на отсутствие подрезания зубьев. Допускаемые отклонения передаточных чисел в табл. 62 находятся в пределах, как это указано в примечании 3 к табл. 52.
Смотрите также
raschet-reduktorov.ru