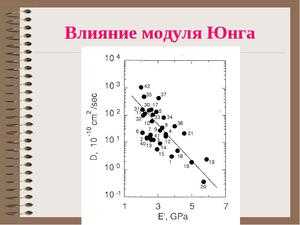
Что такое модуль юнга – Модуль упругости (Модуль Юнга): понятие, формулы, как определить
alexxlab | 30.11.2020 | 0 | Вопросы и ответы
Модуль Юнга – это… Что такое Модуль Юнга?
Модуль Юнга (модуль упругости) — физическая величина, характеризующая свойства материала сопротивляться растяжению/сжатию при упругой деформации[1]. Назван в честь английского физика XIX века Томаса Юнга. В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал среды и процесса. В Международной системе единиц (СИ) измеряется в ньютонах на метр в квадрате или в паскалях.
Модуль Юнга рассчитывается следующим образом:
где:
- E — модуль упругости,
- F — сила,
- S — площадь поверхности, по которой распределено действие силы,
- l — длина деформируемого стержня,
- x — модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина l).
Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне:
где
Значения модуля Юнга для некоторых материалов
Значения модуля Юнга для некоторых материалов приведены в таблице [2]
Примечания
- ↑ Модули упругости – Статьи в Физическом энциклопедическом словаре и Физической энциклопедии.
- ↑ Анурьев В. И. Справочник конструктора-машиностроителя в 3т. Т. 1/В. И. Анурьев; 8-е изд., перераб и доп. Под ред. И. Н. Жестковой — М.: Машиностроение, 2001. — С. 34. ISBN 5-217-02963-3
Примечания
См. также
Литература
- Волькенштейн, В. С. Сборник задач по общему курсу физики / В. С. Волькенштейн. — СПб.: Лань, 1999. — 328 с.
Ссылки
dic.academic.ru
его физический смысл, таблица, формула расчета жесткости
Любая величина должна и может быть измерена, даже такая специфическая, как упругость разного рода материалов. К примеру, необходимо рассчитать, как именно деформируется и при этом какое окажется сопротивление то или иное изделие в той или иной ситуации. Тогда необходимо прибегнуть к специальной единице измерения — модулю Юнга и таблице измерений для конкретного вида металла.
Описание и характеристики единицы измерения
Наименование величины степени жесткости было дано по имени его создателя — английского известного физика, который проводил исследования в области сжатия и растяжения различных жестких материалов, а также в процессах, которые проходят при механическом воздействии. О модуле Юнга справедливо упомянуть следующее:
- это такая единица измерения, которая в цифровом выражении показывает продольную упругость материала какой-либо конструкции;
- эта величина выражает в числах свойства конкретной материи;
- отображает характер его деформации в продольном направлении при оказываемым воздействии.
А если совсем просто, то эта единица измерения просто показывает, насколько жесткий конкретный материал
Буква Е является обозначением модуля Юнга. Согласно отечественной системе расчетов, измерение этой величины происходит в Паскалях. При этом Международная система единиц высчитывает эту величину в ньютонах, умноженных на метр в квадрате (СИ).
Модуль продольной жёсткости применяется при разного рода вычислениях во время проверки структур веществ на степень реакции при сжатии, растяжении, перегибании.
Следует отметить, что наибольшее количество конструкционных материалов, которые используют в таких расчетах, имеет довольно высокий показатель модуля Юнга. Чаще всего его значение начинается от отметки 109 Паскалей. В связи с этим в большинстве случаев для удобства записывания вычислений и самих расчетов применяют префикс «гига» (ГПа).
В задачах по динамике модуль Юнга воспринимается и учитывается в гораздо большем смысле, чем просто показатель жесткости. В этой области науки данное понятие рассматривается как гораздо более общий показатель — перечень возможностей стройматериалов и как среда прохождения процесса реакции их структуры на деформацию.
Показатели продольной эластичности
Для определенных конструкционных материалов, довольно часто используемых для достижения конкретных практических результатов, существуют уже выверенные показатели, сведенные в одну таблицу. В частности, от их параметров устойчивости к механическим воздействиям может зависеть срок службы строительных конструкций и прочих сооружений.
В соответствии с указанной таблицей, наивысший показатель модуля жесткости относится к стали, а наименьший — к древесным породам.
 Цифровое установление модуля Юнга происходит с применением особой, специально рассчитанной диаграммы напряжения. Там указывается специфическая кривая, которая получается при множественных тестированиях каждого из отдельно взятых стройматериалов на устойчивость к механическим воздействиям.
Цифровое установление модуля Юнга происходит с применением особой, специально рассчитанной диаграммы напряжения. Там указывается специфическая кривая, которая получается при множественных тестированиях каждого из отдельно взятых стройматериалов на устойчивость к механическим воздействиям.
В таком случае физическое значение модуля продольной эластичности состоит в установлении математически точного отношения средних показателей напряжения к соответственным параметрам деформации на отдельно взятом отрезке диаграммы до конкретных, заранее установленных границ соразмерности.
Расчет поперечной жесткости
В форме точного выражения модуль Юнга рассчитывается таким способом: Е=q / е=tga.
Необходимо также упомянуть и о таком моменте, что модуль Юнга представляет собой еще и коэффициент пропорциональности и был применен в математическом описании закона Гука. Там великим ученым он был указан в таком математическом выражении: Q=Eе.
В связи с этим прямая связь модуля продольной эластичности с вымеряемыми параметрами поперечных разрезов материалов, которые участвуют в тестированиях на твердость, обнаруживается посредством таких выражений, как ЕА и Е1. При этом:
 ЕА обозначает степень жесткости при сжатии или растяжении вещества или строительного материала в поперечнике;
ЕА обозначает степень жесткости при сжатии или растяжении вещества или строительного материала в поперечнике;- показатель A — величину площади стержневого разреза;
- Е1 — это показатель твердости при сгибании материи в ее поперечном сечении;
- индекс 1 обозначает осевой фактор инерции, возникающий в разрезе тестируемого материала.
Таким образом, податливость материалов при растяжении свидетельствует о способности и самого материала, и изделия, выполненного из него, подвергаться линейному изгибанию. К примеру, при строительных работах это позволит более адекватно подобрать материал в зависимости от его назначения.
Из всего этого можно понять, что модуль Юнга представляет собой универсальную величину, благодаря которой появляется возможность разносторонне и с высокой точностью вычислять и охарактеризовывать качественные характеристики и параметры различных материалов.
tokar.guru
Модуль Юнга Википедия
| Модуль Юнга | |
|---|---|
| E{\displaystyle E} | |
| Размерность | L−1MT−2 |
| Единицы измерения | |
| СИ | Па |
| СГС | дин·см-2 |
Мо́дуль Ю́нга (модуль продольной упругости) — физическая величина, характеризующая способность материала сопротивляться растяжению, сжатию при упругой деформации[1]. Обозначается большой буквой Е.
Назван в честь английского физика XIX века Томаса Юнга.
В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал деформируемой среды и процесса.
В Международной системе единиц (СИ) измеряется в ньютонах на квадратный метр или в паскалях. Является одним из модулей упругости.
Модуль Юнга рассчитывается следующим образом:
- E=F/SΔl/l=FlSΔl,{\displaystyle E={\frac {F/S}{\Delta l/l}}={\frac {Fl}{S\Delta l}},}
где:
- F{\displaystyle F} — нормальная составляющая силы,
- S{\displaystyle S} — площадь поверхности, по которой распределено действие силы,
- l{\displaystyle l} — длина деформируемого стержня,
- Δl{\displaystyle \Delta l} — модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина l{\displaystyle l}).
Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне:
- c=Eρ,{\displaystyle c={\sqrt {\frac {E}{\rho }}},}
где ρ{\displaystyle \rho } — плотность вещества.
Содержание
- 1 Связь с другими модулями упругости
- 2 Температурная зависимость модуля Юнга
- 3 Значения модуля Юнга для некоторых материалов
- 4 См. также
- 5 Примечания
- 6 Литература
- 7 Ссылки
ru-wiki.ru
Модуль Юнга — Википедия. Что такое Модуль Юнга
Материал из Википедии — свободной энциклопедии
Мо́дуль Ю́нга (модуль продольной упругости) — физическая величина, характеризующая способность материала сопротивляться растяжению, сжатию при упругой деформации [1]. Обозначается большой буквой Е.
Назван в честь английского физика XIX века Томаса Юнга.
В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал деформируемой среды и процесса.
В Международной системе единиц (СИ) измеряется в ньютонах на квадратный метр или в паскалях. Является одним из модулей упругости.
Модуль Юнга рассчитывается следующим образом:
- E=F/SΔl/l=FlSΔl,{\displaystyle E={\frac {F/S}{\Delta l/l}}={\frac {Fl}{S\Delta l}},}
где:
Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне:
- c=Eρ,{\displaystyle c={\sqrt {\frac {E}{\rho }}},}
где ρ{\displaystyle \rho } — плотность вещества.
Связь с другими модулями упругости
В случае изотропного тела модуль Юнга связан с модулем сдвига G{\displaystyle G} и модулем объёмной упругости K{\displaystyle K} соотношениями
- G=E2(1+ν){\displaystyle G={\frac {E}{2(1+\nu )}}}
и
- K=E3(1−2ν),{\displaystyle K={\frac {E}{3(1-2\nu )}},}
где ν{\displaystyle \nu } — коэффициент Пуассона.
Температурная зависимость модуля Юнга
Температурная зависимость модуля упругости простых кристаллических материалов объясняется исходя из того, что модуль упругости M(T){\displaystyle M(T)} определяется как вторая производная от внутренней энергии W(T){\displaystyle W(T)} по соответствующей деформации E(T)=d2W(T)dε2{\displaystyle E(T)={d^{2}W(T) \over d\varepsilon ^{2}}} . Поэтому при температурах T≤ΘD{\displaystyle T\leq \Theta _{D}} (ΘD{\displaystyle \Theta _{D}} — температура Дебая) температурная зависимость модуля упругости определяется простым соотношением
- M(T)=M0−M1T−M2T2{\displaystyle M(T)=M_{0}-M_{1}T-M_{2}T^{2}}
где M0{\displaystyle M_{0}} — адиабатический модуль упругости идеального кристалла при T⟶0K{\displaystyle T\longrightarrow 0K}; M1T{\displaystyle M_{1}T} — дефект модуля, обусловленный тепловыми фононами; M2T2{\displaystyle M_{2}T^{2}} — дефект модуля, обусловленный тепловым движением электронов проводимости[2]
Значения модуля Юнга для некоторых материалов
Значения модуля Юнга для некоторых материалов приведены в таблице
См. также
Примечания
- ↑ Модули упругости — Статьи в Физическом энциклопедическом словаре и Физической энциклопедии.
- ↑ Л.Н. Паль-Валь, Ю.А. Семеренко, П.П. Паль-Валь, Л.В. Скибина, Г.Н. Грикуров. Исследование акустических и резистивных свойств перспективных хромо-марганцевых аустенитных сталей в области температур 5-300 К // Конденсированные среды и межфазные границы. — 2008. — Т. 10, вып. 3. — С. 226—235.
- ↑ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 Анурьев В. И. Справочник конструктора-машиностроителя в 3т. Т. 1/В. И. Анурьев; 8-е изд., перераб и доп. Под ред. И. Н. Жестковой — М.: Машиностроение, 2001. — С. 34. ISBN 5-217-02963-3
- ↑ Галашев А. Е., Рахманова О. Р. Устойчивость графена и материалов на его основе при механических и термических воздействиях // Успехи физических наук. — М.: РАН, ФИАН, 2014. — Т. 184, вып. 10. — С. 1051.
- ↑ В.Д. Нацик, П.П. Паль-Валь, Л.Н. Паль-Валь, Ю.А. Семеренко. Низкотемпературный a-пик внутреннего трения в ниобии и его связь с релаксацией кинков на дислокациях // ФНТ. — 2001. — Т. 27, вып. 5. — С. 547—557.
- ↑ П.П. Паль-Валь, В.Д. Нацик, Л.Н. Паль-Валь, Ю.А. Семеренко. Нелинейные акустические эффекты в монокристаллах ниобия, обусловленные дислокациями // ФНТ. — 2004. — Т. 30, вып. 1. — С. 115—125.
Литература
- Волькенштейн В. С. Сборник задач по общему курсу физики / В. С. Волькенштейн. — СПб.: Лань, 1999. — 328 с.
Ссылки
wiki.sc
Модуль упругости – что это такое? Определение модуля упругости для материалов
Модуль упругости – это физическая величина, которая характеризует упругое поведение материала при приложении к нему внешней силы в конкретном направлении. Под упругим поведением материала подразумевается его деформация в упругой области.
История исследования упругости материалов

Физическая теория упругих тел и их поведения при действии внешних сил была подробно рассмотрена и изучена английским ученым XIX века Томасом Юнгом. Однако сама концепция упругости была развита еще в 1727 году швейцарским математиком, физиком и философом Леонардом Эйлером, а первые эксперименты, связанные с модулем упругости, провел в 1782 году, то есть за 25 лет до работ Томаса Юнга, венецианский математик и философ Якопо Рикатти.
Заслуга Томаса Юнга заключается в том, что он придал теории упругости стройный современный вид, который впоследствии был оформлен в виде простого, а затем и обобщенного закона Гука.
Физическая природа упругости
Любое тело состоит из атомов, между которыми действуют силы притяжения и отталкивания. Равновесие этих сил обуславливает состояние и параметры вещества при данных условиях. Атомы твердого тела при приложении к ним незначительных внешних сил растяжения или сжатия начинают смещаться, создавая противоположную по направлению и равную по модулю силу, которая стремится вернуть атомы в начальное состояние.
В процессе такого смещения атомов энергия всей системы увеличивается. Эксперименты показывают, что при малых деформациях энергия пропорциональна квадрату величины этих деформаций. Это означает, что сила, будучи производной по энергии, оказывается пропорциональной первой степени величины деформации, то есть зависит от нее линейно. Отвечая на вопрос, что такое модуль упругости, можно сказать, что это коэффициент пропорциональности между силой, действующей на атом, и деформацией, которую эта сила вызывает. Размерность модуля Юнга совпадает с размерностью давления (Паскаль).
Предел упругости
Согласно определению, модуль упругости показывает, какое напряжение нужно приложить к твердому телу, чтобы его деформация составила 100 %. Однако все твердые тела обладают пределом упругости, который равен 1 % деформации. Это означает, что если приложить соответствующее усилие и деформировать тело на величину, меньшую 1 %, тогда после прекращения действия этого усилия тело точно восстанавливает свою первоначальную форму и размеры. При приложении слишком большого усилия, при котором величина деформации превышает 1 %, после прекращения действия внешней силы тело уже не восстановит первоначальные размеры. В последнем случае говорят о существовании остаточной деформации, которая является свидетельством превышения упругого предела данного материала.
Модуль Юнга в действии
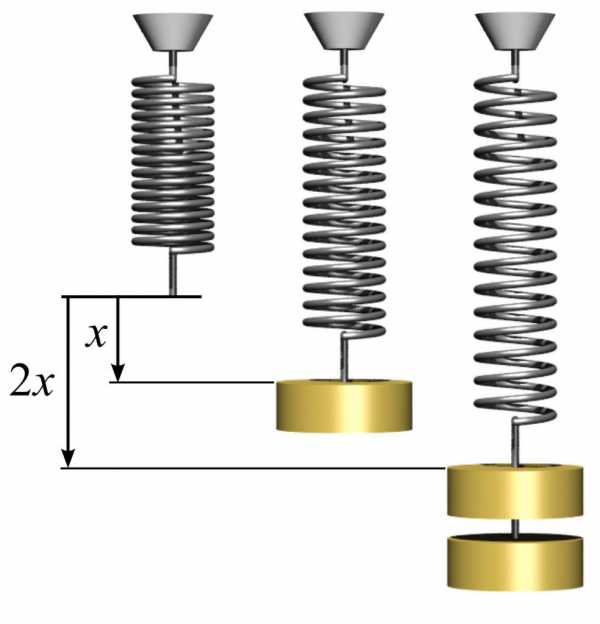
Для определения модуля упругости, а также для понимания, как им пользоваться, можно привести простой пример с пружиной. Для этого необходимо взять металлическую пружину и измерить площадь круга, который образуют ее витки. Это делается по простой формуле S = πr², где п – число пи, равное 3,14, а r – радиус витка пружины.
Далее следует замерить длину пружины l0 без нагрузки. Если повесить какой-либо груз массой m1 на пружину, тогда она увеличит свою длину до некоторой величины l1. Модуль упругости E можно вычислить, исходя из знания закона Гука по формуле: E = m1gl0/(S(l1-l0)), где g – ускорение свободного падения. В данном случае отметим, что величина деформации пружины в упругой области может намного превышать 1 %.
Знание модуля Юнга позволяет предсказывать величину деформации при действии конкретного напряжения. В данном случае, если повесить на пружину другую массу m2, получим следующую величину относительной деформации: d = m2g/(SE), где d – относительная деформация в упругой области.
Изотропия и анизотропия
Модуль упругости является характеристикой материала, которая описывает силу связи между его атомами и молекулами, однако конкретный материал может иметь несколько различных модулей Юнга.
Дело в том, что свойства каждого твердого тела зависят от его внутренней структуры. Если свойства одинаковы во всех пространственных направлениях, то речь идет об изотропном материале. Такие вещества имеют однородное строение, поэтому действие внешней силы в различных направлениях на них вызывает одинаковую реакцию со стороны материала. Все аморфные материалы обладают изотропией, например, резина или стекло.
Анизотропия – явление, которое характеризуется зависимостью физических свойств твердого тела или жидкости от направления. Все металлы и сплавы на их основе обладают той или иной кристаллической решеткой, то есть упорядоченным, а не хаотичным расположением ионных остовов. Для таких материалов модуль упругости меняется в зависимости от оси действия внешнего напряжения. Например, металлы с кубической симметрией, к которым относятся алюминий, медь, серебро, тугоплавкие металлы и другие, обладают тремя различными модулями Юнга.
Модуль сдвига
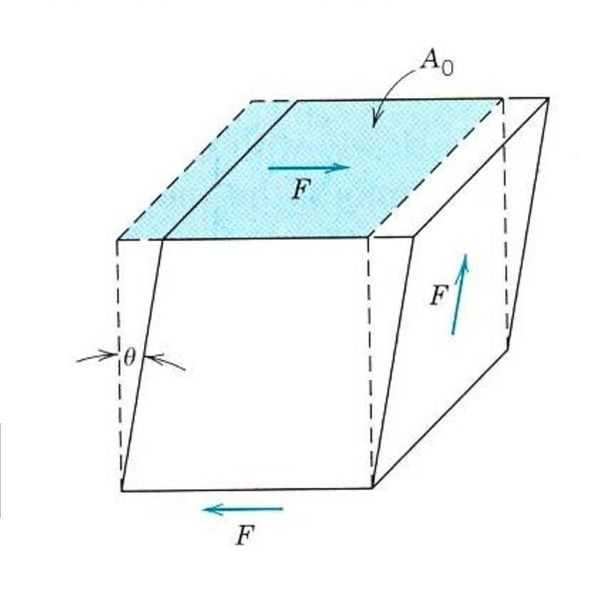
Описание упругих свойств даже изотропного материала не обходится знанием одного модуля Юнга. Поскольку, помимо растяжения и сжатия, на материал можно подействовать сдвиговыми напряжениями или напряжениями кручения. В этом случае он будет реагировать на внешнее усилие иначе. Для описания упругой деформации сдвига вводят аналог модуля Юнга, модуль сдвига или модуль упругости второго рода.
Все материалы слабее сопротивляются сдвиговым напряжениям, чем растяжению или сжатию, поэтому значение модуля сдвига для них в 2-3 раза меньше, чем значения модуля Юнга. Так, для титана, модуль Юнга которого равен 107 ГПа, модуль сдвига составляет всего лишь 40 ГПа, для стали эти цифры имеют значения 210 ГПа и 80 ГПа, соответственно.
Модуль упругости дерева

Дерево относится к анизотропным материалам, поскольку древесные волокна ориентированы вдоль конкретного направления. Именно вдоль волокон измеряют модуль упругости древесины, поскольку поперек волокон он меньше на 1-2 порядка. Знание модуля Юнга для дерева играет важную роль и учитывается при проектировании конструкций из деревянных панелей.
Значения модуля упругости древесины для некоторых видов деревьев приведены в таблице ниже.
| Вид дерева | Модуль Юнга в ГПа |
| Лавровое дерево | 14 |
| Эвкалипт | 18 |
| Кедр | 8 |
| Ель | 11 |
| Сосна | 10 |
| Дуб | 12 |
Следует отметить, что приведенные значения могут отличаться на величину порядка 1 ГПа для конкретного дерева, поскольку на его модуль Юнга влияет плотность древесины и условия произрастания.

Модули сдвига для различных пород деревьев находятся в пределах 1-2 ГПа, например, для сосны это 1,21 ГПа, а для дуба 1,38 ГПа, то есть древесина практически не сопротивляется сдвиговым напряжениям. Данный факт должен учитываться при изготовлении деревянных несущих конструкций, которые проектируют так, чтобы они работали только на растяжение или сжатие.
Характеристики упругости металлов
Если сравнивать с модулем Юнга древесины, то средние значения этой величины для металлов и сплавов на порядок больше, что показано в следующей таблице.
| Металл | Модуль Юнга в ГПа |
| Бронза | 120 |
| Медь | 110 |
| Сталь | 210 |
| Титан | 107 |
| Никель | 204 |
Упругие свойства металлов, которые имеют кубическую сингонию, описываются тремя упругими постоянными. К таким металлам относятся медь, никель, алюминий, железо. Если металл имеет гексагональную сингонию, тогда для описания его упругих характеристик уже необходимо шесть постоянных.
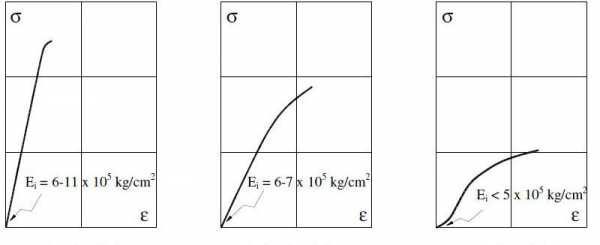
Для металлических систем модуль Юнга измеряют в пределах 0,2 % деформации, поскольку большие значения могут происходить уже в неупругой области.
fb.ru
Модуль Упругости | Все формулы
Модуль Упругости — коэффициент, характеризующий сопротивление материала растяжению или сжатию при упругой деформации
С помощью легких преобразований, данная формула получается из Закона Гука.
Модуль Упругости , или модуль продольной деформации Е показывает критическое напряжение, которое может иметь структура материала при максимальной ее деформации до разрушения.
Таблица значений Модуля Юнга (Модуля Упругости) для некоторых материалов
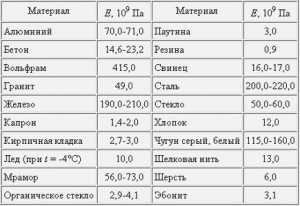
Физический смысл Модуля Юнга : он показывает напряжение, которое необходимо приложить к телу, чтобы удлинить его в два раза
В формуле мы использовали :
— Модуль упругости (Модуль Юнга)
— Критическое напряжение
— Относительное удлинение
— Сила, действующая на стержень
— Длина деформируемого стержня
— Модуль изменения длины стержня в результате упругой деформации
— Площадь поверхности, по которой распределено действие силы
xn--b1agsdjmeuf9e.xn--p1ai
Определение модуля Юнга
Дальневосточный государственный технический университет
(ДВПИ им. В.В. Куйбышева)
Методические указания и отчет по лабораторной работе
ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ ПРИ РАСТЯЖЕНИИ
ЦЕЛЬ РАБОТЫ. Экспериментальное определение величины модуля упругости при растяжении Е (модуля Юнга) и сопоставление его со справочным значением.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Многолетняя практика возведения инженерных сооружений, опыт их эксплуатации и наблюдение за поведением при различных типах внешних воздействий, в том числе и разрушающих, показал, что их перемещения в определенных пределах пропорциональны действующим нагрузкам.
Впервые указанная закономерность была высказана в 1678г. Робертом Гуком в книге «О восстановительной способности или об упругости» – первой печатной работе по упругим свойствам материалов, в виде формулировки: «каково перемещение, такова и сила», которая носит название закона Гука. Такая трактовка устанавливает соотношение между перемещением (угловым или линейным) произвольной точки А системы от внешней нагрузки в виде
UA = Δ P, (1)
где Δ – коэффициент, зависящий от типа внешней нагрузки, района ее приложения, положения точки А, вида перемещения и рассматриваемого направления, геометрических особенностей системы и физико-механических свойств материала.
В общем случае, множество возможных сочетаний упомянутых факторов определяет и множество конкретных значений Δ. Таким образом, выражение (1) следует рассматривать как закон Гука для системы не очень удобный для конкретных расчетов.
Геометрические изменения системы являются проявлением деформации ее материала, интенсивность которых определяет прочность системы в целом. Современная трактовка закона ГукапринадлежитОгюстену Коши, который свел его в точку, установив для материала в ней соотношение
σ = Ε ε, (2)
где σ – нормальное напряжение,
ε – относительная линейная деформация,
Е– модуль упругости при растяжении (модульЮнга).
Соотношение (2) уже не связано с конкретными особенностями системы и отражает свойства только самого материала. Тем самым прочность системы в целом стала определяться прочностью ее материала в точке.
Линейные соотношения типа (1) между внешней нагрузкой и перемещениями для конкретных систем, которые обычно используются в инженерной практике расчетов, могут быть получены на основании выражения (2).
В общем случае закон Гука является линейной идеализацией начального участка зависимости σ = f(ε). Для некоторых материалов, таких, например, как сталь, эта идеализация обладает высокой степенью точности, однако, для таких, как чугун, строительные материалы, композиты она является довольно грубым приближением.
Наиболее наглядно закон Гука проявляется при растяжении прямых стержней постоянного поперечного сечения, на которых и проводится определение основных механических характеристик материалов.
Впервые понятие о модуле упругости ввел в 1820г Томас Юнг, который вычислил его для стали, определяя частоту колебаний камертона.
Для наиболее распространенных материалов Е имеет следующие значения (МПа)
Сталь…………………………………………(2,0-2,1) 105
Медь.…………………………………………1,2 105
Алюминиево-магниевые сплавы…………..(0,7-0,8) 105
Дерево (вдоль волокон)…………………….(0,08-0,12) 105
Известняк, гранит……………………………(0,4-0,5) 105
ОПИСАНИЕ НАЛАДКИ
Схема наладки для проведения лабораторной работы приведена на рис.1.
На силовой плите (1) лабораторного стола установлены две опорные стойки (2) и (3), закрепленные болтами в Т-образном пазе силовой плиты. В отверстии опорной стойки (3) зафиксирована неподвижная шарнирная ось (4), на конце которой закреплен датчик усилий ДУ (5) до 5,0кН с соединительной вилкой (6).
Рис.1 Схема наладки для лабораторной работы
В отверстии опорной стойки (2) установлена подвижная шарнирная ось (7), продольное перемещение которой создается нагрузочным штурвалом (8). Испытываемый образец (9)закреплен в вилке (6) и на оси (7) специальными штифтами.
На поверхности испытуемого образца наклеены четыре тензорезистора (рис.2), из которых №1 и №2 измеряют продольные деформации, а №3 и №4 – поперечные.
Нагружение образца производится вращением штурвала (8). Величина растягивающей силы контролируется блоком измерителя силы (ИС), а показания тензорезисторов – блоком измерителя деформаций (ИД).
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Для устранения зазоров в собранной наладке произвести предварительное нагружение испытываемого образца. Снять начальные (no) показания ИД для тензорезисторов №1 и №2 и занести их в журнал измерений.
2. Произвести последовательное нагружение образца дополнительными усилиями в 1кН, 2кН и 3кН, контролируя их значение по показаниям ИС. Показания тензорезисторов регистрировать по ИД для каждого этапа нагружения, занося их в журнал измерений.
3. Для каждого тензорезистора построить график Pi – ni и аппроксимировать его прямой линией.
4. Определить среднее приращение показаний ИД для ступени нагружения (ΔP = 1кН) для каждого тензорезистора в отдельности Δni и среднее ΔnСР для обоих вместе.
5. Определить среднее приращение относительной линейной деформации для ступени нагружения (ΔР = 1кН) по формуле
Δεпрод = KИД ΔnСР,
где KИД = 10-6 – цена единицы измерения ИД в единицах относительной деформации.
6. Определить модуль нормальной упругости по формуле
Е = ΔP / F Δεпрод,
где F – площадь поперечного сечения образца (ширина 30мм, толщина 2мм).
7. Сравнить полученный результат со справочными значениями модуля Юнга.
8. Составить отчет по лабораторной работе.
9. Защитить лабораторную работу.
Журнал экспериментальных измерений и их обработки
Растягивающее усилие, кН | Показания ИД | |
Резистор №1 | Резистор №2 | |
n1 | n2 | |
0 1 2 3 | ||
Среднее приращение показаний ИД на ступень нагружения, Δni | ||
Среднее приращение показаний ИД на ступень нагружения для обоих тензорезисторов ΔnСР | ||
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое нормальные напряжения?
2. По какой формуле нормальные напряжения рассчитываются для поперечного сечения растянутого образца?
3. В каких единицах измеряются нормальные напряжения в системе СИ?
4. Что такое относительная линейная деформация?
5. По какой формуле относительная линейная деформация рассчитывается для растянутого образца?
6. В каких единицах измеряются относительные линейные деформации?
7. Напишите закон Гука «для точки».
8. В чем разница закона Гука «для точки» и системы?
9. Какой ученый свел закон Гука в точку?
10. Почему прочность системы определяется прочностью «в точке»?
11. Что такое модуль упругости при растяжении?
12. В каких единицах измеряется модуль Юнга
13. Чему модуль Е равен для стали (меди, алюминиево-магниевых сплавов, гранита, дерева)?
14. Почему закон Гука считается условно линейным?
15. Для каких материалов закон Гука имеет наименьшее отклонение от линейности, для каких наибольшее и почему?
16. Что такое тензорезистор и в чем принцип его работы?
БИОГРАФИЧЕСКАЯ СПРАВКА
Гук Роберт (1635-1703) английский физик, секретарь Лондонского королевского общества, профессор Лондонского университета, куратор экспериментаторов Лондонского королевского общества. Научные работы относятся к теплоте, оптике, небесной механике.
Коши Огюстен Луи (1789-1857) французский математик, член Парижской академии наук. Научные работы относятся к математике, математической физике, теории упругости, оптике.
Юнг Томас (1773-1829) английский физик, астроном и врач, профессор Королевского института (Лондон). Научные работы относятся к физике, химии, астрономии, геофизике, механике, оптике, философии и медицине.
Выполнил студент группы
Принял Е. Борисов
studfiles.net

