Формула потенциальная энергия сжатой пружины – Потенциальная энергия пружины: понятие, закон сохранения, уравнение

alexxlab | 15.07.2020 | 0 | Вопросы и ответы

Потенциальная энергия пружины: понятие, закон сохранения, уравнение

Встречается довольно большое количество различных механизмов, частью которых является пружина. Этот конструктивный элемент характеризуется довольно большим количество различных особенностей, которые должны учитываться. Примером можно назвать понятие потенциальной энергии пружины. Рассмотрим все особенности данного вопроса подробнее.

Понятие потенциальной энергии пружины

При рассмотрении того, что такое потенциальная энергия пружины следует уделить внимание самому понятию – свойство, которым могут обладать тела при нахождении на земле. Этот момент определяет то, что ей могут обладать самые разнообразные изделия, в том числе рассматриваемое. К особенностям рассматриваемого понятия можно отнести следующее:

1. Потенциальная энергия в рассматриваемом случае формируется по причине изменения состояния. Даже при несущественном смещении витков относительно друг друга считается изменением состояния подобного изделия.
2. Для того чтобы изменить состояние изделия совершается определенное действие. Зачастую для этого проводится прикладывание усилия. При этом важно провести расчет требуемого усилия для сжатия витков.
3. После выполнения определенной работы большая часть усилия, которое было потрачено на выполнение действия высвобождается при определенных обстоятельствах. Как правило, этот процесс предусматривает возврат витков в свое первоначальное положение. Это достигается за счет особой формы изделия, а также применения соответствующего материала, который обладает повышенной упругостью. Именно за счет этого свойства зачастую проводится установка рассматриваемого изделия. Показатель может достигать весьма высоких показателей, которой достаточно для реализации различных задач. Распространенным примером можно назвать установку пружины в запорных и предохранительных элементах, которые отвечают за непосредственное возращение запорного элемента в требуемое положение.

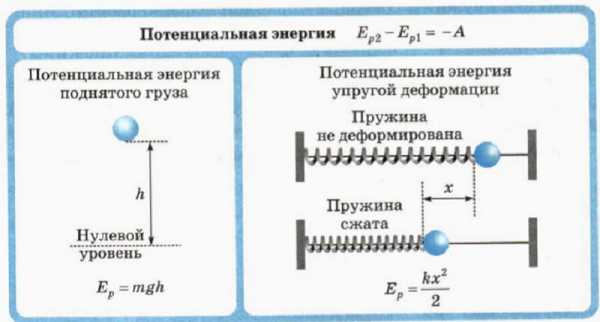
Она также широко применяется при создании самых различных механизмов, к примеру, заводных часов. При проектировании различных механизмов учитывается закон сохранения механической силы, которая характеризуется довольно большим количеством особенностей.

Закон сохранения механической энергии

Согласно установленным законам механическое воздействие консервативной механической системы сохраняется во времени. Этот момент определяет то, что потенциальная энергия деформированной пружины не может возникнуть сама или исчезнуть куда-нибудь. Именно поэтому для ее создания нужно приложить соответствующее усилие.

Рассматриваемый закон относится к категории интегральных равенств. Эта закономерность определяет то, что он складывается их действия дифференциальных законов, является свойством или признаком совокупного воздействия.

Для проведения соответствующих расчетов должна применяться определенная формула. Сила, с которой оказывается воздействие, не является постоянной. Именно поэтому для ее вычисления применяется графический метод. Самая простая зависимость может быть описана следующим образом: F=kx. При применении подобной зависимости построенная координатная линия будет представлена прямой линией, которая расположена под углом относительно системы координат.

Приписать подобному устройству потенциальную энергию можно только в том случае, если она равна максимальной работе и не зависит от условной траектории движения. Проведенные исследования указывают на то, что подобная работа подчиняется закону Гука. Для определения основного показателя применяется следующая формула: U=kk2/2.

Для деформирования витков к ним должно быть приложено определенное усилие, так как в противном случае кинетическая сила не возникнет.

Динамика твердого тела

Некоторые определить выражения (определяется при применении наиболее подходящих формул) можно только с учетом правил, касающихся динамики твердых объектов. Этому вопросу посвящен целый раздел. При расчете потенциальной энергии сжатой пружины также применяются некоторые законы этого раздела

Динамика твердого тела рассматривается по причине того, что в большинстве случаев механизм совершает действие, связанное с непосредственным перемещением какого-либо объекта.

Рассматриваемое свойство изделия может изменяться в зависимости от динамики твердого тела. Это связано с тем, что на изделие оказывается и воздействие со стороны окружающей среды. Примером можно назвать трение или нагрев.

Момент силы и момент импульса относительно оси

Рассмотрение деформации пружины проводится также с учетом момента силы и импульса относительно оси. Эти два параметра позволяют рассчитать все требуемые показатели с более высокой точностью. Довольно распространенным вопросом можно назвать чему равен момент силы – векторная величина, которая определяется векторному произведению радиуса на вектор приложенной силы.

Момент импульса – величина, которая применяется для определения количества вращательного движения.

Среди особенностей подобного показателя можно отметить следующее:

1. Масса вращения. Объект может характеризоваться различной массой.
2. Распределение относительно оси. Ось может быть расположена на различном расстоянии от самого объекта.
3. Скорость вращения. Это свойство считается наиболее важным, в зависимости от конструкции он может быть постоянным или изменяться.

Расчет каждого показателя проводится при применении соответствующей формулы. В некоторых случаях проводится измерение требуемых вводных данных, без которых провести вычисления не получится.

Уравнение движения вращающегося тела

Рассматривая подобное свойство также следует уделить внимание уравнению движения вращающегося тела. Не стоит забывать о том, что вращательное движение твердого тела характеризуется наличием как минимум двух точек. При этом отметим нижеприведенные особенности:

1. Прямая, которая соединяет две точки, выступает в качестве оси вращения.
2. Есть возможность провести определение места положения объекта в случае вычисления заднего угла между двумя плоскостями.
3. Наиболее важным показателем можно назвать угловую скорость. Она связана с инерцией, которая возникает при вращении объекта.

Для вычисления угловой скорости применяется специальная формула, которая выглядит следующим образом: w=df/dt. В некоторых случаях проводится вычисление углового ускорения, которое также является важной величиной.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

stankiexpert.ru

Потенциальная энергия деформированной пружины

16.7Закон сохранения механической энергии

Консервативные силы называются так потому, что сохраняют механическую энергию замкнутой системы тел.

Механическая энергия E тела равна сумме его кинетической и потенциальной энергий:

E = K + W:

Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии их взаимодействия друг с другом.

Предположим, что тело совершает движение под действием силы тяжести и/или силы упругости пружины. Будем считать, что трения нет. Пусть в начальном положении кинетическая и потенциальная энергии тела равны K1 и W1, в конечном положении K2 и W2. Работу внешних сил при перемещении тела из начального положения в конечное обозначим A.

По теореме о кинетической энергии:

K2 K1 = A:

Но работа консервативных сил равна разности потенциальных энергий:

A = W1 W2:

Отсюда получаем:

K2 K1 = W1 W2;

или

K1 + W1 = K2 + W2:

Левая и правая части данного равенства представляют собой механическую энергию тела в начальном и конечном положении:

E1 = E2:

Следовательно, при движении тела в поле силы тяжести и/или на пружине механическая энергия тела остаётся неизменной при отсутствии трения.

Справедливо и более общее утверждение.

Закон сохранения механической энергии. Если в замкнутой системе действуют только консервативные силы, то механическая энергия системы сохраняется.

При этих условиях могут происходить лишь превращения энергии: из кинетической в потенциальную и наоборот. Общий запас механической энергии системы остаётся постоянным.

16.8Закон изменения механической энергии

Если между телами замкнутой системы имеются силы сопротивления (сухое или вязкое трение), то механическая энергия системы будет уменьшаться. Так, автомобиль останавливается в результате торможения, колебания маятника постепенно затухают и т. д. Силы трения неконсервативны: работа силы трения очевидным образом зависит от пути, по которому перемещается тело между данными точками. В частности, работа силы трения по замкнутому пути не равна нулю.

Снова рассмотрим движение тела в поле силы тяжести и/или на пружине. Вдобавок на тело действует сила трения, которая за рассматриваемый промежуток времени совершает отрицательную работу Aтр. Работу консервативных сил (тяжести и упругости)по-прежнемуобозначаем A.

studfiles.net

27.4. Потенциальная энергия деформированной пружины. Закон сохранения энергии

27.4. Потенциальная энергия деформированной пружины

 Деформированная (например, растянутая) пружина способна совершить работу (рис. 155).

рис. 155
 Действительно, если к растянутой пружине прикрепить некоторое тело, то пружина будет действовать на него с некоторой силой, под действием которой тело начнет смещаться. Следовательно, будет совершена работа (рис. 156).

рис. 156
 Сила, с которой пружина действует на тело, не является постоянной, поэтому для вычисления работы воспользуемся графическим методом. Построим график зависимости силы упругости F = kx от координаты, которая является прямой линией (рис. 157).

рис. 157
 Площадь выделенного треугольника под графиком равна максимальной работе, которую может совершить пружина. Понятно, что она равна:

 Для того чтобы пружине приписать потенциальную энергию, равную максимальной работе (1), необходимо показать, что эта работа не зависит от траектории движения тела. Чтобы доказать это утверждение, достаточно рассмотреть работу на малом участке перемещения Δr при движении по произвольной траектории (рис. 158).

рис. 158
В данном случае эта работа

полностью определяется изменением деформации пружины х, поэтому она не зависит от траектории движения тела.
 Таким образом, силы упругости, подчиняющиеся закону Гука, являются потенциальными, и потенциальная энергия деформированной пружины определяется формулой

 Нулевой уровень потенциальной энергии, рассчитываемой по формуле (2), соответствует недеформированной пружине.
 Подсчитаем, какую минимальную работу следует совершить, чтобы пружину жесткостью k растянуть на величину x (рис. 159).

рис. 159
 Чтобы деформировать пружину, к ней необходимо приложить внешнюю силу. Очевидно, что эта работа будет минимальна в том случае, если внешняя приложенная сила в любой точке равна силе упругости, действующей со стороны пружины. Поэтому работа этой силы будет равна:

А = kx²/2, то есть увеличению потенциальной энергии пружины.

---

 Смотрите решенные задачи по теме законы сохранения.
 Для подготовки решите задачи по теме законы сохранения.

fizportal.ru

Кинетическая энергия пружины: формула и определение

Пружину можно назвать довольно распространенным изделием, которое применяется в самых различных случаях. Для правильного выбора пружины уделяется внимание проведению различных расчетов, некоторые из них предусматривает вычисление основных параметров, характеризующих работу. Потенциальная и кинетическая сила – два довольно распространенных показателя, которые касаются не только пружины, но и многих других тел. Рассмотрим особенности кинетической подробнее.

Понятие энергии

Прежде чем рассматривать особенности пружины следует уделить внимание тому, что с ней происходит при сжатии, растяжении и каким образом она оказывает воздействие на тело, окружающую систему. Энергия – скалярная физическая величина, которая применяется для определения формы движения и взаимодействия материи. Важным моментом назовем то, что если система замкнутая, то усилие сохраняется на протяжении длительного периода. Сегодня она окружает нас практически везде и касается довольно большого количества объектов.

Довольно большое распространение получило понятие кинетическая энергия пружины. Она связано с непосредственными особенностями самого изделия. При воздействии определенного усилия на витки, расположенные вдоль одной спирали, формируется сила, которая может использоваться в качестве полезной работы.

Энергия кинетическая: формула и определение

Механическая система, которая связана со скоростью перемещения объекта, применяется крайне часто. Стоит учитывать, что она может делиться на поступательную и вращательную. В качестве единицы измерения используется джоуль.

Среди особенностей отметим нижеприведенные моменты:

1. Рассматриваемый тип усилия также представлен разностью между исходным состоянием тела и его положением в полном спокойствии.
2. Обуславливается возникновение определенного усилия, за счет которого обеспечивается перемещение тела и совершение работы.

Пружина за счет силы упругости приводит в движение различные объекты. При этом жесткость пружины растянутой может быть различной, все зависит от особенностей конкретного изделия.

Рассматриваемая формулу следует уделить внимание достаточно большому количеству различных моментов. Особенностями назовем следующее:

1. Упругость зависит от количества витков, толщины применяемой проволоки и типа применяемого материала при изготовлении. Кроме этого, уделяется внимание взаимному расположению витков.
2. Работа, которая может совершаться пружиной, зависит от взаимного положения частей тела. Начальное и конечное растяжение может существенно отличаться.
3. Рассматриваемое изделие в растянутом положении может совершать различную работу. Расчеты позволяют определить то, каково ее значение, а также величину потенциальной.

Расчеты могут проводится исключительно после создания схемы. Примером назовем следующее:

1. Один конец витков закреплен за основание, второй предназначен для совершения работы.
2. Не стоит забывать о том, что показатель изменяется, он не остается постоянным. Изменения пропорционально растяжению.
3. Изначальное растяжение обозначается буквой l, для определения первоначального значение силу упругости применяется формула F=kl. В данной формуле используется коэффициент k, который обозначает жесткость.

Приведенная выше информация указывает на то, что провести расчет требуемого показателя проводится следующим образом: E=kl²/2. В этом случае величина во многом зависит от удлинения и коэффициента жесткости.

Изменение кинетической энергии

Приведенная выше информация указывает на то, что рассматриваемое значение не имеет постоянный показатель. Среди особенностей отметим:

1. Наибольшее значение характерно максимальному удлинению витков относительно друга друга. При этом не стоит забывать о том, что есть определенное ограничение, касающееся максимального удлинения, так как слишком большая нагрузка становится причиной деформации.
2. При приближении тела к точке равновесия оно снижается. Это связано с тем, что показатель упругости существенно снижается.

Кроме этого, параметр зависит от воздействия других сил. Примером можно назвать трение, которая снижает скорость перемещения объекта.

Средняя кинетическая энергия

В большинстве случаев проводится высчитывание среднего значения. Этот показатель не учитывает то, в каких положениях сила упругости высокая и низкая. Для расчета применяется формула: F=kl/2.

В данном случае достаточно знать лишь удлинение, которое измеряется при использовании обычного инструмента. Что касается коэффициента, то он может варьировать в достаточно большом диапазоне, зависит от следующих моментов:

1. Диаметра витков. С увеличением этого показателя существенно повышается коэффициент жесткости, изделие часто используется для выполнения большой работы.
2. Толщины применяемой проволоки. Рассматриваемое изделие представлено проволокой, которая накручивается вокруг установленной оси.
3. Расстояния между отдельными витками. Как правило, они расположены относительно друг друга на определенном расстоянии, которое одинаковое. По этому признаку выделяют варианты исполнения, предназначенные для сжатия и растяжения.
4. Типа применяемого материала при изготовлении. Некоторые сплавы характеризуются достаточно высокой жесткостью, могут переносить незначительную деформацию.

Коэффициент самостоятельно рассчитать не нужно, он берется с определенных таблиц. Среднее значение часто высчитывается в случае решения математических задач, при проектировании применяются другие формулы.

Связь между внутренней энергией тела кинетической и потенциальной энергиями

Между кинетической и потенциальными понятиями есть определенная взаимосвязь. Для расчета подобной связи используется следующая формула: А=Fs=mav²₂-v²₁/2a.

Оба значения применяются в качестве полезного действия, могут варьировать в достаточно большом диапазоне, а также зависеть от различных факторов.

В заключение отметим, что проводимые расчеты позволяют выбрать наиболее подходящий вариант исполнения изделия для конкретного механизма. При исследовании проводится отображение схемы, на которой можно увидеть распространение всех сил.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

stankiexpert.ru

[Физика билет 8] Силы упругости. Закон Гука. Энергия упруго деформированной пружины.

Силы упругости. 

Сила упругости – сила, возникающая в результате деформации тела и направленная в сторону, противоположенную перемещениям частиц тела при деформации.

Закон Гука. 

При достаточно малых деформациях сила упругости пропорциональна величине деформации тела и направлена в сторону, противоположенную направлению перемещений частиц тела при деформации.

Fупр = – k * Δr

Δr – деформация тела, k – коэффициент упругости (жесткости (Н/м)) 

Энергия упруго деформированной пружины.

Вычислим потенциальную энергию упруго деформированного тела. В предыдущем параграфе было указано, что

энергия упруго деформированного тела, например сжатой или растянутой пружины, равна работе, которую совершила бы такая пружина, переходя в недеформированное состояние

.
В уроке “Работа силы упругости” мы вычислили работу силы упругости, то есть работу, которую совершает упруго деформированная пружина, переходя в недеформированное состояние:

где k — жесткость пружины, а х — ее начальное удлинение.
Этой величине и равна потенциальная энергия сжатой (или растянутой) пружины.
В дальнейшем потенциальную энергию мы будем обозначать буквой P.
Итак, потенциальная энергия P деформированной пружины к вообще любого упруго сжатого или растянутого тела равна:

Удлинение (деформация) x входит в выражение для потенциальной энергии во второй степени. Поэтому потенциальная энергия на зависит от знака х. Это значит, что потенциальная энергия зависит только от абсолютного значения деформации и не зависит от того, сжато деформированное тело или растянуто.
В § 78 было показано, что если деформация пружины изменяется от х₁ до х₂, то при этом совершается работа равна

где P₁ и P₂ — значения потенциальной энергии пружины соответственно при деформации x₁ и x₂. Но P₂ — P₁ — это изменение потенциальной энергии пружины. Как и следовало ожидать, совершенная работа равна изменению потенциальной энергии пружины, взятому с противоположным знаком.

fizmatinf.blogspot.com

5. Энергия упругой деформации

Любое упруго деформированное тело обладает потенциальной энергией

, так как изменяется взаимное расположение отдельных частей тела. Рассмотрим случай растяжения пружины.

Растяжение будем производить очень медленно, чтобы силу 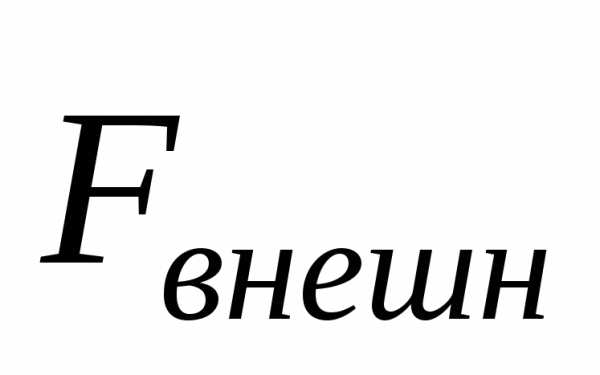, с которой мы действуем на пружину, можно было считать все время равной по модулю упругой силе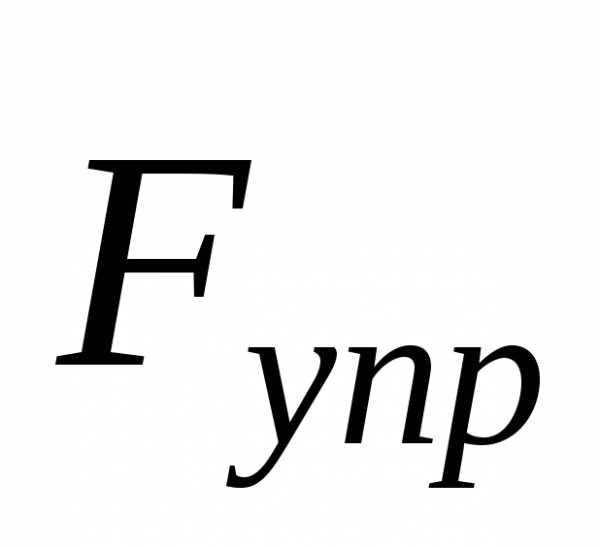. Тогдагдек, х – соответственно жесткость и удлинение пружины. Тогда работа, которую нужно совершить, чтобы вызвать удлинение (или сокращение) х пружины, равна

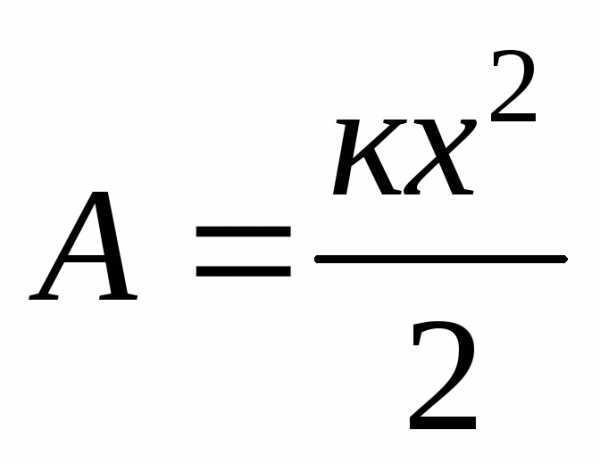(8.12)

Эта работа идет на увеличение потенциальной энергии пружины. Следовательно, зависимость потенциальной энергии пружины от удлинения х имеет вид

,(8.13)

если считать, что потенциальная энергия недеформированной пружины равна нулю.

Потенциальная энергия упруго деформированного стержня равна

, (8.14)

где 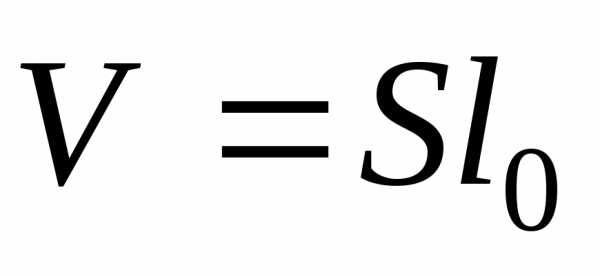– объем стержня.

Отношение энергии 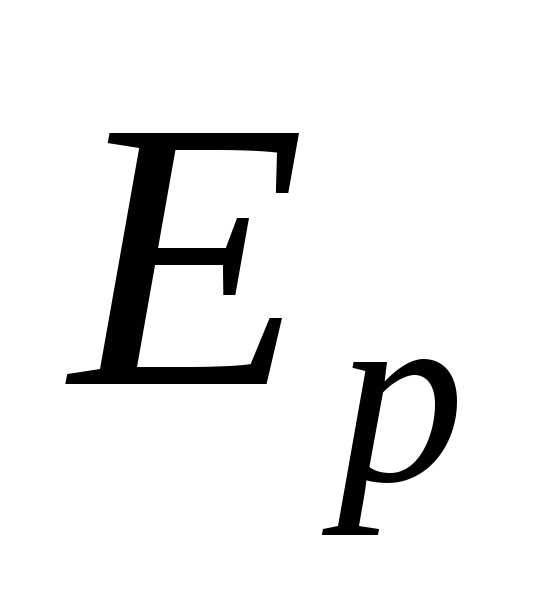к тому объему, в котором она заключена, называетсяплотностью энергии u. Тогда – плотность энергии упругой деформации при растяжении (или сжатии).

Аналогично нетрудно получить, что плотность энергии деформации при сдвиге равна .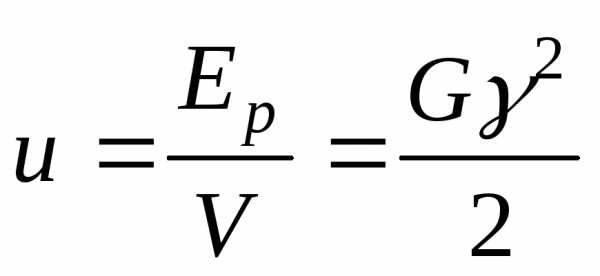

6. Кручение

Деформации кручения и изгиба являются деформациями неоднородными. Это значит, что в этих случаях деформации внутри тела меняются от точки к точке.

Возьмем однородную проволоку, верхний конец ее закрепим, а к нижнему концу приложим закручивающие силы. Они создадут вращающий момент относительно продольной оси проволоки. При этом каждый радиус нижнего основания повернется вокруг продольной оси на угол . Такая деформация называется кручением. Закон Гука для деформации кручения имеет вид

_, (8.15)

где – модуль кручения, постоянная для данной проволоки. Модуль кручения зависит не только от материала, но и от геометрических размеров проволоки.

Выведем выражение для модуля кручения.

Пусть имеется цилиндрическая трубка радиуса

. Причем толщина ееочень мала по сравнению с радиусом. Площадь сечения трубки равна . Обозначим черезкасательное напряжение в том же основании. Тогда момент сил, действующий на это основание, будет. При закручивании совершается работа.

Разделим ее на объем трубки . Найдем плотность упругой энергии при деформации кручения

(8.16)

Найдем эту же величину иначе.

Мысленно вырежем из трубки бесконечно короткую часть (рис.8.5).

Рис. 8.5

В результате кручения бесконечно малый элемент трубки ABDC перейдет в положение . Это есть сдвиг. Таким образом, деформацию кручения можно рассматривать как неоднородный сдвиг. Плотность упругой энергии при сдвиге равна

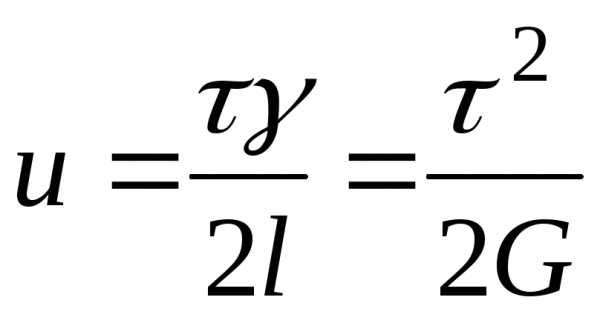(8.17)

Приравнивая его выражению (8.16), находим искомое соотношение

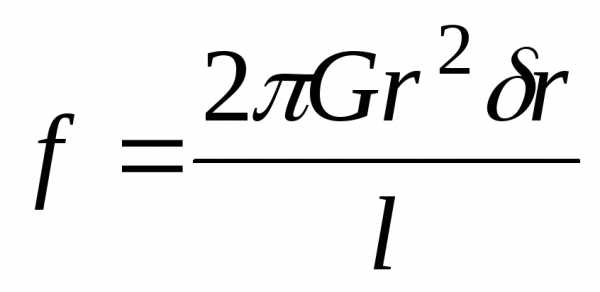(8.18)

Если стенка трубки имеет конечную толщину, то модуль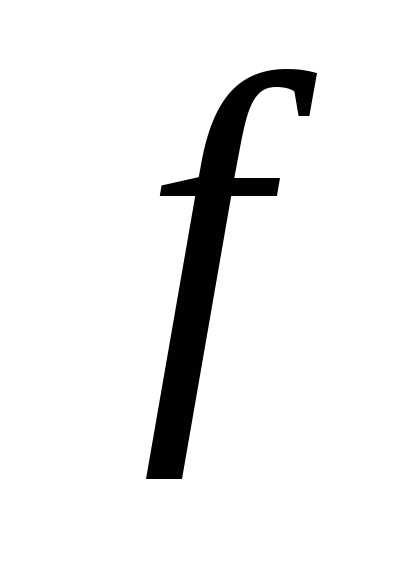

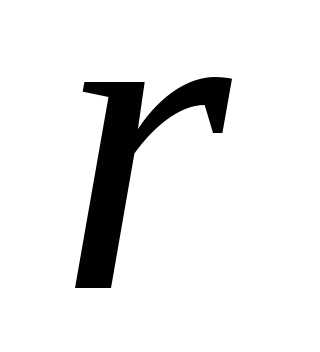найдется интегрированием последнего выражения по. Это дает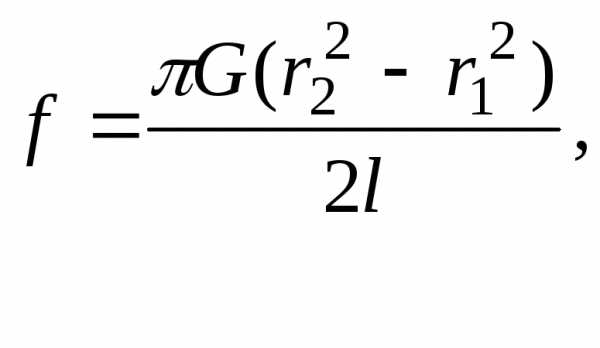где 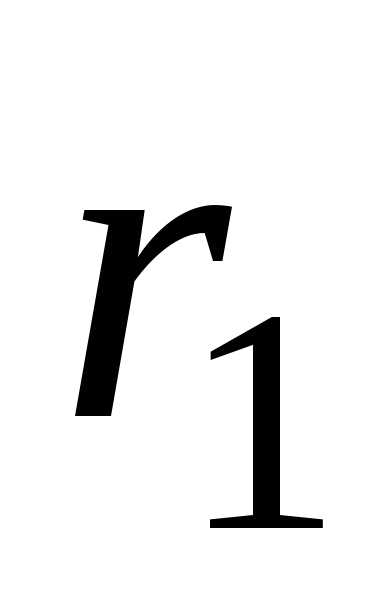– внутренний радиус трубки,– внешний радиус трубки.

Для сплошной проволоки радиуса _{модуль кручения .}

Контрольные вопросы

1. Что называется деформацией? Какие деформации называются упругими? Приведите примеры упругих деформаций.

2. Какова физическая сущность упругих сил?

3. Сформулируйте закон Гука? Когда он справедлив?

4. Дайте объяснение качественной диаграмме напряжений. Что такое предел пропорциональности, упругости и прочности?

5. Что такое упругий гистерезис и упругое последействие?

6. Каков физический смысл модуля Юнга и модуля сдвига?

7. Что такое упругое последействие?

8. Выведите выражения для деформаций при всестороннем растяжении.

9. Что называется коэффициентом Пуассона?

10. Определите энергию деформированного тела.

11. Что называется плотностью упругой энергии? Получите формулы этой энергии при растяжении и сдвиге.

12. Какой вид имеет закон Гука при кручении.

13. Выведите выражение для модуля кручения.

studfiles.net

Слободянюк А.И. Физика 10/6.6 — PhysBook

Содержание книги

Предыдующая страница

§6. Законы сохранения в механике

6.6 Потенциальная энергия деформированной пружины.

Деформированная (например, растянутая) пружина способна совершить работу. Действительно, если к растянутой пружине прикрепить некоторое тело, то пружина будет действовать на него с некоторой силой, под действием которой тело начнет смещаться, следовательно, будет совершена работа (рис. 86).

Сила, с которой пружина действует на тело, не является постоянной, поэтому для вычисления работы воспользуемся графическим методом. Построим график зависимости силы упругости F = kx от координаты, который является прямой линией (рис. 87). Площадь выделенного треугольника под графиком равна максимальной работе, которую может совершить пружина, понятно, что она равна

\(~A = \frac{1}{2} kx \cdot x = \frac{kx^2}{2}\) . (1)

Для того чтобы пружине приписать потенциальную энергию, равную максимальной работе (1) необходимо показать, что эта работа не зависит от траектории движения тела. Чтобы доказать это утверждение, достаточно рассмотреть работу на малом участке перемещения \(~\Delta \vec r\) при движении по произвольной траектории (рис. 88). В данном случае эта работа \(~\delta A = \vec F \cdot \Delta \vec r = kx \cdot \Delta r \cos \alpha = kx \cdot \Delta x\) , полностью определяется изменением деформации пружины x, поэтому она не зависит от траектории движения тела.

Таким образом, силы упругости, подчиняющиеся закону Гука, являются потенциальными, и потенциальная энергия деформированной пружины определяется формулой

\(~U = \frac{kx^2}{2}\) . (2)

Нулевой уровень потенциальной энергии, рассчитываемой по формуле (2), соответствует недеформированной пружине.

Подсчитаем, какую минимальную работу следует совершить, чтобы пружину, жесткостью k, растянуть на величину x (рис. 89). Чтобы деформировать пружину, к ней необходимо приложить внешнюю силу. Очевидно, что эта работа будет минимальная в том случае, когда внешняя приложенная сила в любой точке равна силе упругости, действующей со стороны пружины, поэтому работа этой силы будет равна \(~A = \frac{kx^2}{2}\) , то есть увеличению потенциальной энергии пружины.

Следующая страница

www.physbook.ru