Как определить модуль зуба шестерни по диаметру – Модуль шестерни. Формулы расчёта.
alexxlab | 09.02.2020 | 0 | Вопросы и ответы
Расчёт диаметра шестерни с прямым и косым зубом.
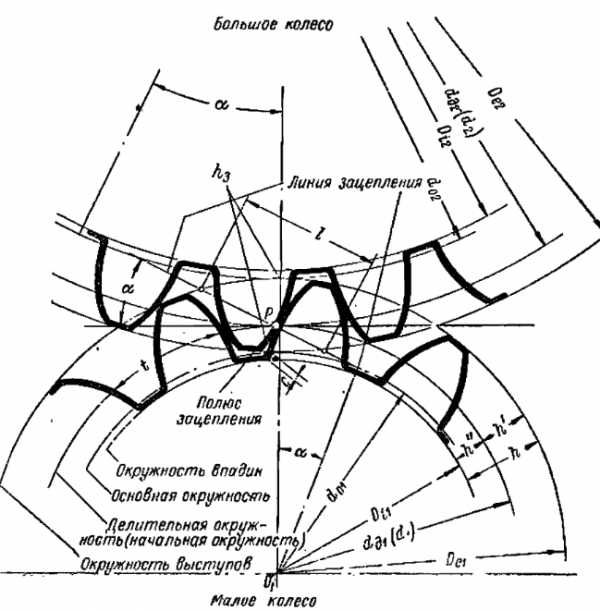
Сегодня рассмотрим как рассчитать диаметр шестерни. Сразу скажу что диаметр прямозубой шестерни имеет одну формулу, а диаметр косозубой шестерни имеет другую формулу. Хотя многие считают по одной формуле, это ошибочно. Данные расчёты нужны для других расчётах при изготовлении зубчатых колёс. Итак перейдём непосредственно к формулам (без коррекции):
Для начала значения которые надо знать при расчётах в данных формулах:
- De — диаметр окружности выступов.
- Dd — диаметр делительной окружности (непосредственно от шага которой считается модуль шестерни).
- Di — диаметр окружности впадин.
- Z — число зубьев шестерни.
- Z1 — число зубьев шестерни малого колеса.
- Z2 — число зубьев шестерни большого колеса.
- M (Mn) — модуль (модуль нормальный, по делительному диаметру).
- Ms — модуль торцевой.
- β (βd) — угол наклона шестерни (иметься ввиду угол наклона по делительному диаметру).
- Cos βd — косинус угла на делительном диаметре.
- A — межцентровое расстояние.
Формула расчёта диаметров прямозубого зубчатого колеса (шестерни):
De=(Z×M)+2M=Dd+2M=(Z+2)×M
Dd=Z×M
Формула расчёта диаметров косозубого зубчатого колеса (шестерни с косым зубом):
De=Dd+2Mn
Вроде как и на прямозубых колёсах, но на косозубых мы имеем другой делительный диаметр, следовательно диаметр окружности выступов будет другим!
Dd=Z×Mn/Cos βd=Z×Ms
То есть количество зубьев умножаем на модуль и делим на косинус угла зуба по делительному диаметру или количество зубьев умножаем на модуль торцевой.
Определяем торцевой модуль:
Ms=Mn/Cos βd =2A/Z1+Z2
То есть модуль торцевой равен — модуль нормальный делить на косинус угла зуба шестерни по делительному диаметру или два умножить на межцентровое расстояние и делить на число зубьев малого колеса плюс число зубьев большого колеса.
Для этого нам уже необходимо знать межцентровое расстояние, которое можно посчитать по формуле:
A=(Z1+Z2/2Cos βd)×Mn=0,5Ms(Z1+Z2)
То есть число зубьев малого колеса плюс число зубьев большого колеса разделить на 2 умножить на косинус угла зуба шестерни по делительному диаметру и всё это умножить на модуль или число зубьев малого колеса плюс число зубьев большого колеса умножить (0,5 умножить на модуль торцевой).
Как видите посчитать диаметр прямозубого колеса очень просто, а вот посчитать диаметр колеса с косым зубом тут уже посложнее, так как требуется много различных составляющих. Данные составляющие не всегда есть, что усложняет расчёт. Так что для некоторых расчётов понадобится знание некоторых точных параметров, таких как точный (подчеркну точный) угол наклона зубьев шестерни на делительном диаметре или точное межцентровое расстояние! Все расчёты взаимосвязаны, всё это надо для других расчётов зубчатых передач при проектировании и в ремонтном деле.
Поделится, добавить в закладки!zuborez.info
Как определить модуль зуба шестерни по диаметру
Как узнать модуль зубчатого колеса?
При поломке зубчатого колеса или шестерни в редукторе какого-либо механизма или машины возникает необходимость по «старой» детали, а иногда по фрагментам обломков создать чертеж для изготовления нового колеса и/или шестерни. Эта статья будет полезна тем,…
…кому приходится восстанавливать зубчатые передачи при отсутствии рабочих чертежей на вышедшие из строя детали.
Обычно для токаря и фрезеровщика все необходимые размеры можно получить с помощью замеров штангенциркулем. Требующие более пристального внимания, так называемые, сопрягаемые размеры – размеры, определяющие соединение с другими деталями узла – можно уточнить по диаметру вала, на который насаживается колесо и по размеру шпонки или шпоночного паза вала. Сложнее обстоит дело с параметрами для зубофрезеровщика. В этой статье мы будем определять не только модуль зубчатого колеса, я попытаюсь изложить общий порядок определения всех основных параметров зубчатых венцов по результатам замеров изношенных образцов шестерни и колеса.
«Вооружаемся» штангенциркулем, угломером или хотя бы транспортиром, линейкой и программой MS Excel, которая поможет быстро выполнять рутинные и порой непростые расчеты, и начинаем работу.
Как обычно раскрывать тему я буду на примерах, в качестве которых рассмотрим сначала цилиндрическую прямозубую передачу с наружным зацеплением, а затем косозубую.
Расчет параметров колеса и шестерни прямозубой передачи.
Изначально полагаем, что зубчатое колесо и шестерня имеют эвольвентные профили зубьев и изготавливались с параметрами исходного контура по ГОСТ 13755-81. Этот ГОСТ регламентирует три главных (для нашей задачи) параметра исходного контура для модулей больше 1 мм. (Для модулей меньше 1 мм исходный контур задается в ГОСТ 9587-81; модули меньше 1 мм рекомендуется применять только в кинематических, то есть не силовых передачах.)
Для правильного расчета параметров зубчатой передачи необходимы замеры и шестерни и колеса!
Исходные данные и замеры:
Начинаем заполнение таблицы в Excel с параметров исходного контура.
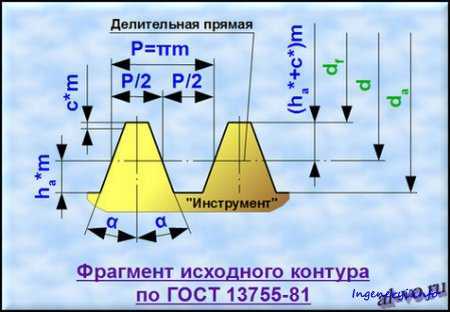 |
1. Угол профиля исходного контура α в градусах записываем
в ячейку D3: 20
2. Коэффициент высоты головки зуба ha* вводим
в ячейку D4: 1
3. Коэффициент радиального зазора передачи c* заносим
в ячейку D5: 0,25
В СССР и в России 90% зубчатых передач в общем машиностроении изготавливались именно с такими параметрами, что позволяло применять унифицированный зубонарезной инструмент. Конечно, изготавливались передачи с зацеплением Новикова и в автомобилестроении применялись специальные исходные контуры, но все же большинство передач проектировалось и изготавливалось именно с контуром по ГОСТ13755-81.
4. Тип зубьев колеса (тип зацепления) T записываем
в ячейку D6: 1
T=1 – при наружных зубьях у колеса
T=-1 – при внутренних зубьях у колеса (передача с внутренним зацеплением)
5. Межосевое расстояние передачи aw в мм измеряем по корпусу редуктора и заносим значение
в ячейку D7: 80,0
Ряд межосевых расстояний зубчатых передач стандартизован. Можно сравнить измеренное значение со значениями из ряда, который приведен в примечании к ячейке C7. Совпадение не обязательно, но высоковероятно.
6-9. Параметры шестерни: число зубьев z1, диаметры вершин и впадин зубьев da1 и df1 в мм, угол наклона зубьев на поверхности вершин βa1 в градусах подсчитываем и измеряем штангенциркулем и угломером на исходном образце и записываем соответственно
в ячейку D8: 16
в ячейку D9: 37,6
в ячейку D10: 28,7
в ячейку D11: 0,0
10-13. Параметры колеса: число зубьев z2, диаметры вершин и впадин зубьев da2 и df2 в мм, угол наклона зубьев на цилиндре вершин βa2 в градусах определяем аналогично — по исходному образцу колеса — и записываем соответственно
в ячейку D12: 63
в ячейку D13: 130,3
в ячейку D14: 121,4
в ячейку D11: 0,0
Обращаю внимание: углы наклона зубьев βa1 и βa2 – это углы, измеренные на цилиндрических поверхностях вершин зубьев!!!
Измеряем диаметры, по возможности, максимально точно! Для колес с четным числом зубьев сделать это проще, если вершины не замяты. Для колес с нечетным числом зубьев при замере помним, что размеры, которые показывает штангенциркуль несколько меньше реальных диаметров выступов!!! Делаем несколько замеров и наиболее с нашей точки зрения достоверные значения записываем в таблицу.
 |
Результаты расчетов:
14. Предварительные значения модуля зацепления определяем по результатам замеров шестерни m1 и зубчатого колеса m2 в мм соответственно
в ячейке D17: =D9/(D8/COS (D20/180*ПИ())+2*D4)=2,089
m1=da1/(z1/cos (β1)+2*(ha*))
и в ячейке D18: =D13/(D12/COS (D21/180*ПИ())+2*D4)=2,005
m2=da2/(z2/cos (β2)+2*(ha*))
Модуль зубчатого колеса играет роль универсального масштабного коэффициента, определяющего как габариты зубьев, так и общие габариты колеса и шестерни.
Сравниваем полученные значения со значениями из стандартного ряда модулей, фрагмент которого приведен в примечании к ячейке C19.
Полученные расчетные значения, как правило, очень близки к одному из значений стандартного ряда. Делаем предположение, что искомый модуль зубчатого колеса и шестерни m в мм равен одному из этих значений и вписываем его
в ячейку D19: 2,000
15. Предварительные значения угла наклона зубьев определяем по результатам замеров шестерни β1 и зубчатого колеса β2 в градусах соответственно
в ячейке D20: =ASIN (D8*D19/D9*TAN (D11/180*ПИ()))=0,0000
β1=arcsin (z1*m*tg (βa1)/da1)
и в ячейке D21: =ASIN (D12*D19/D13*TAN (D15/180*ПИ()))=0,0000
β2=arcsin (z2*m*tg (βa2)/da2)
Делаем предположение, что искомый угол наклона зубьев β в градусах равен измеренным и пересчитанным значениям и записываем
16. Предварительные значения коэффициента уравнительного смещения вычисляем по результатам замеров шестерни Δy1 и зубчатого колеса Δy2 соответственно
в ячейке D23: =2*D4+D5- (D9-D10)/(2*D19)=0,025
Δy1=2*(ha*)+(c*) — (da1-df1)/(2*m)
и в ячейке D24: =2*D4+D5- (D13-D14)/(2*D19)= 0,025
Δy2=2*(ha*)+(c*) – (da2— df2)/(2*m)
Анализируем полученные расчетные значения, и принятое решение о значении коэффициента уравнительного смещения Δy записываем
в ячейку D25: 0,025
17,18. Делительные диаметры шестерни d1 и зубчатого колеса d2 в мм рассчитываем соответственно
в ячейке D26: =D19*D8/COS (D22/180*ПИ())=32,000
d1=m*z1/cos(β)
и в ячейке D27: =D19*D12/COS (D22/180*ПИ())=126,000
d2=m*z2/cos(β)
19. Делительное межосевое расстояние a в мм вычисляем
в ячейке D28: =(D27+D6*D26)/2=79,000
a=(d2+T*d1)/2
20. Угол профиля αt в градусах рассчитываем
в ячейке D29: =ATAN (TAN (D3/180*ПИ())/COS (D22/180*ПИ()))/ПИ()*180=20,0000
αt=arctg(tg (α)/cos(β))
21. Угол зацепления αtw в градусах вычисляем
в ячейке D30: =ACOS (D28*COS (D29/180*ПИ())/D7)/ПИ()*180=21,8831
αtw=arccos(a*cos (αt)/aw)
 |
22,23. Коэффициенты смещения шестерни x1 и колеса x2 определяем соответственно
в ячейке D31: =(D9-D26)/(2*D19) -D4+D25=0,425
x1=(da1— d1)/(2*m) — (ha*)+Δy
и в ячейке D32: =(D13-D27)/(2*D19) -D4+D25 =0,100
x2=(da2— d1)/(2*m) — (ha*)+Δy
24,25. Коэффициент суммы (разности) смещений xΣ(d) вычисляем для проверки правильности предыдущих расчетов по двум формулам соответственно
в ячейке D33: =D31+D6*D32=0,525
xΣ(d)=x1+T*x2
и в ячейке D34: =(D12+D6*D8)*((TAN (D30/180*ПИ()) — (D30/180*ПИ())) — (TAN (D29/180*ПИ()) — (D29/180*ПИ())))/(2*TAN (D3/180*ПИ()))=0,523
xΣ(d)=(z2+T*z1)*(inv(αtw) — inv(αt))/(2*tg(α))
Значения, рассчитанные по разным формулам, отличаются очень незначительно! Полагаем, что найденные значения модуля зубчатого колеса и шестерни, а также коэффициентов смещения определены верно!
Расчет параметров колеса и шестерни косозубой передачи.
Переходим к примеру с косозубой передачей и повторяем все действия, которые мы делали в предыдущем разделе.
Измерить угол наклона зубьев с необходимой точностью при помощи угломера или транспортира практически очень сложно. Я обычно прокатывал колесо и шестерню по листу бумаги и затем по отпечаткам транспортиром делительной головки кульмана производил предварительные измерения с точностью в градус или больше… В представленном ниже примере я намерил: βa1=19° и βa2=17,5°.
Еще раз обращаю внимание, что углы наклона зубьев на цилиндре вершин βa1 и βa2 – это не угол β, участвующий во всех основных расчетах передачи!!! Угол β – это угол наклона зубьев на цилиндре делительного диаметра (для передачи без смещения).
 |
Ввиду малости значений рассчитанных коэффициентов смещения уместно предположить, что передача была выполнена без смещения производящих контуров шестерни и зубчатого колеса.
Воспользуемся сервисом Excel «Подбор параметра».
Выбираем в главном меню Excel «Сервис» — «Подбор параметра» и в выпавшем окне заполняем:
Установить в ячейке: $D$33
Значение: 0
Изменяя значение ячейки: $D$22
И нажимаем OK.
Получаем результат β=17,1462°, xΣ(d)=0, x1=0,003≈0, x2=-0,003≈0!
 |
Передача, скорее всего, была выполнена без смещения, модуль зубчатого колеса и шестерни, а также угол наклона зубьев мы определили, можно делать чертежи!
Важные замечания.
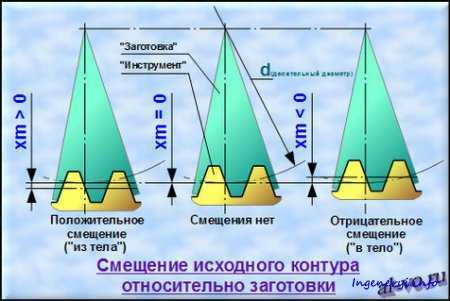
Смещение исходного контура при нарезке зубьев применяют для восстановления изношенных поверхностей зубьев колеса, уменьшения глубины врезания на валах-шестернях, для увеличения нагрузочной способности зубчатой передачи, для выполнения передачи с заданным межосевым расстоянием не равным делительному расстоянию, для устранения подрезания ножек зубьев шестерни и головок зубьев колеса с внутренними зубьями.
Различают высотную коррекцию (xΣ(d)=0) и угловую (xΣ(d)≠0).
Смещение производящего контура на практике применяют обычно при изготовлении прямозубых колес и очень редко косозубых. Это обусловлено тем, что по изгибной прочности косой зуб прочнее прямого, а необходимое межосевое расстояние можно обеспечить соответствующим углом наклона зубьев. Если высотную коррекцию изредка применяют для косозубых передач, то угловую практически никогда.
Косозубая передача работает более плавно и бесшумно, чем прямозубая. Как уже было сказано, косые зубья имеют более высокую прочность на изгиб и заданное межосевое расстояние можно обеспечить углом наклона зубьев и не прибегать к смещению производящего контура. Однако в передачах с косыми зубьями появляются дополнительные осевые нагрузки на подшипники валов, а диаметры колес имеют больший размер, чем прямозубые при том же числе зубьев и модуле. Косозубые колеса менее технологичны в изготовлении, особенно колеса с внутренними зубьями.
Скачать Вы не можете скачивать файлы с нашего сервера
Источник: https://al-vo.ru/
Обсудить на форумеingeneryi.info
Блог слесаря-ремонтника и механика по наладке оборудования
Часто при ремонте возникает необходимость восстановить цилиндрическая прямозубую шестеренку по образцу.
Для этого нужно эту шестеренку рассчитать: вычислить модуль, делительный диаметр и диаметр вершин зубьев шестерни.
Цилиндрическая прямозубая зубчатая передача. Формулы
Напомню предпочтительный ряд модуля: 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16.
Первое действие — это измерить наружный диаметр «D» шестеренки:
Измеряем наружный диаметр шестерни
Второе действие — считаем количество зубьев «Z» у шестеренки.
Теперь, собственно, формулы.
Модуль «m» передачи без смещения (не корригированной передачи), вычисляется по формуле:
формула модуля
Делительный диаметр «Dдел» считается по формуле:
Вот и все формулы, которые нужны для быстрого определения основных параметров шестеренки, которую нужно восстановить.
wmua.ru
Виды зубчатых колес, шестерен
Обычно шестерни имеют профиль зубьев с эвольвентной боковой формой. Так как эвольвентное зацепление имеет ряд преимуществ перед остальными: форма этих зубьев соответствует условиям их прочности, зубья легко изготовить и обработать, шестерни не чувствительны к точности установки. Тем не менее, существуют зубчатые передачи с циклоидальной формой профиля зубьев, а так же с шестернями с круговой формой профиля зубьев, например – передача Новикова. Помимо этого, применяется несимметричный профиль зуба, например в храповых механизмах.
Параметры эвольвентной шестерни:
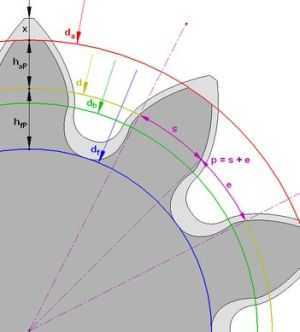
Модуль шестерни (m) – это основной параметр, который определяется из прочностного расчёта зубчатых передач. Чем сильнее нагрузка на передачу, тем больше значение модуля, единица измерения модуля – миллиметры.
Расчет модуля шестерни:d — диаметр делительной окружности
z — число зубьев шестерни
p — шаг зубьев
da — диаметр окружности вершин темной шестерни
db — диаметр основной окружности – эвольвенты
df — диаметр окружности впадин темной шестерни
haP+hfP — высота зуба темной шестерни, x+haP+hfP — высота зуба светлой шестерни
В машиностроении приняты стандартные значения модуля зубчатого колеса для удобства изготовления и замены зубчатых колёс, представляющие собой числа от 1 до 50.
Высота головки зуба – haP и высота ножки зуба – hfP в случае, так называемого, «нулевого» зубчатого колеса соотносятся с модулем m следующим образом: haP = m; hfP = 1,2 m, то есть:
Отсюда получаем, что высота зуба h = 2,2m
Так же можно практически вычислить модуль шестерни, при этом, не имея всех данных для определения модуля, по следующей формуле:
Продольная линия зуба
Прямозубые шестерни
Прямозубые шестерни – самый применяемый тип зубчатых колёс. Зубья расположены в радиальных плоскостях, линия контакта зубьев пары зубчатых колес параллельна оси вращения, как и оси обеих зубчатых колес (шестеренок) располагаются строго параллельно.
Косозубые шестерни
Косозубые шестерни – это модернизированная версия прямозубых шестерен. Зубья, в таком случае, расположены под углом к оси вращения. Зацепление зубьев этих шестерен происходит тише и плавнее, чем у прямозубых. Они применяются либо в малошумных механизмах, либо в тех которые требуют передачи большого крутящего момента на больших скоростях. К недостаткам этого типа шестерен можно отнести: увеличенную площадь соприкосновения зубьев, что вызывает значительное трение и нагрев деталей, а вследствие: потеря мощности и дополнительное использование смазочных материалов; так же механическая сила, направленная вдоль оси шестеренки, вынуждает применять упорные подшипники для установки вала.
Шевронные колёса
Шевронные шестерни решают проблему механической осевой силы, которая возникает в случае применения косозубых колес, так как зубья шевронных (елочных) колёс изготавливаются в виде буквы «V» (или же они образовываются стыковкой двух косозубых колёс со встречным расположением зубьев). Осевые механические силы обеих половин шевронной шестерни взаимно компенсируются, поэтому нет нет необходимости использования упорных подшипников для установки валов. Шевронная передача является самоустанавливающейся в осевом направлении, в следствии чего, в редукторах с шевронными колесами один из валов устанавливают на подшипниках с короткими цилиндрическими роликами – плавающих опорах.
Шестерни с внутренним зацеплением
Шестерни такого типа имеют зубья, нарезанные с внутренней стороны. При их использовании происходит одностороннее вращение ведущей и ведомой шестерен. В данной зубчатой передаче меньше затрат на трение, а значит выше КПД. Применяются зубчатые колеса с внутренним зацеплением в ограниченных по габаритам механизмах, в планетарных передачах, в шестеренных насосах, в приводе башни танка.
Винтовые шестерни
Шестерни имеют форму цилиндра с расположенными на нем зубьями по винтовой линии. Эти шестеренки используются на непересекающихся валах, которые располагаются перпендикулярно друг друга, угол между ними 90°.
Секторные шестерни
Секторная шестерня – это часть (сектор) шестерни любого типа, она позволяет сэкономить в габаритах полноценной шестерни, так как применяется в передачах, где не требуется вращение этого зубчатого колеса (шестеренки) на полный оборот.
Шестерни с круговыми зубьями
Шестерни этого типа имеют линию зубьев в виде окружности радиуса, за счет этого контакт в передаче происходит в одной точке на линии зацепления, которая располагается параллельно осям шестерен. Передачи с круговыми зубьями «Передача Новикова» имеет лучшие ходовые качества, чем косозубые – высокую плавность хода и бесшумность, высокую нагрузочную способность зацепления, но при одинаковых условиях их ресурс работы и КПД ниже, к прочему изготовление этих шестерен значительно сложнее. Поэтому применение таких шестеренок ограниченно.
Конические шестерни
Конические шестерни имеют различные виды, отличаются они по форме линий зубьев, с прямыми, с криволинейными, с тангенциальными, с круговыми зубьями. Применяются конические зубчатые передачи в машинах для движения механизма, где требуется передать вращение с одного вала на другой, оси которых пересекаются. Например, в автомобильных дифференциалах, для передачи момента от двигателя к колесам.
Зубчатая рейка
Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют – реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.
Звездочка
Шестерня-звезда – это основная деталь цепной передачи, которая используется совместно с гибким элементом – цепью для передачи механической энергии.
Коронная шестерня – это особый тип шестерен, их зубья находятся на боковой поверхности. Такая шестерня работает, как правило, в паре с прямозубой или с барабаном (цевочное колесо), состоящим из стержней. Такая передача используется в башенных часах.
shesterenka.com.ua
Измерение шестерни – штангельциркуль, зубомер.
Основные методы измерения (контроля) размера зуба зубчатых колёс — по длине общей нормали и по постоянной хорде и хорде делительной окружности. В данной статье рассмотрим различный меритель поверхностно, ещё будут подробные статьи с видео и статьи с расчётными формулами.
Самый распространённый способ измерения шестерни — по длине общей нормали штангельциркулем. Преимущество данного способа в независимости от наружного диаметра. Недостатки — трудности в замере колёс большого диаметра и колёс с большим углом наклона зубьев. При замере необходимо замерять определённое количество зубьев в обхвате:
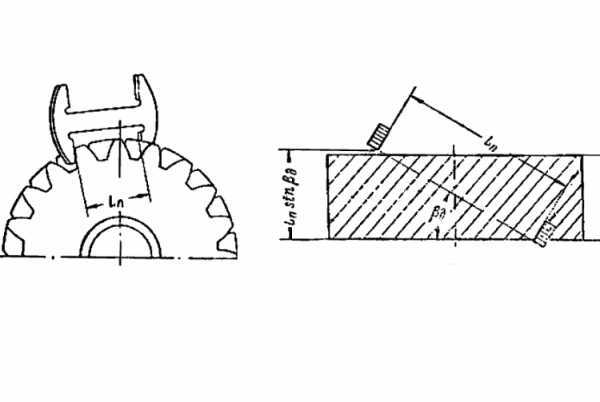
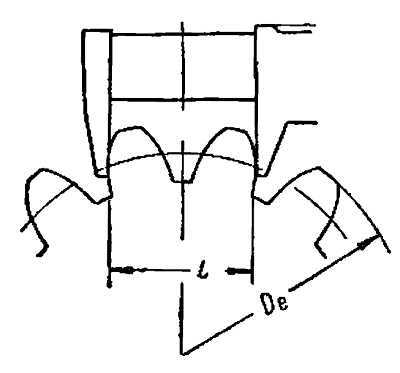
Второй способ замера по постоянной хорде и хорде делительной окружности зубомером. На определённой высоте зуба, должна быть определённая толщина. Преимущество данного способа в том что можно замерять шестерню любого диаметра и с любым наклоном. Ещё плюс в том, что при подаче под меру или чистовой не требуется ждать очень долго, как например при замере длинны общей нормали. Достаточно небольшого отрезка «чистого» зуба. Недостаток — зависимость от наружного диаметра, при изменении которого необходимо корректировать высоту замера.
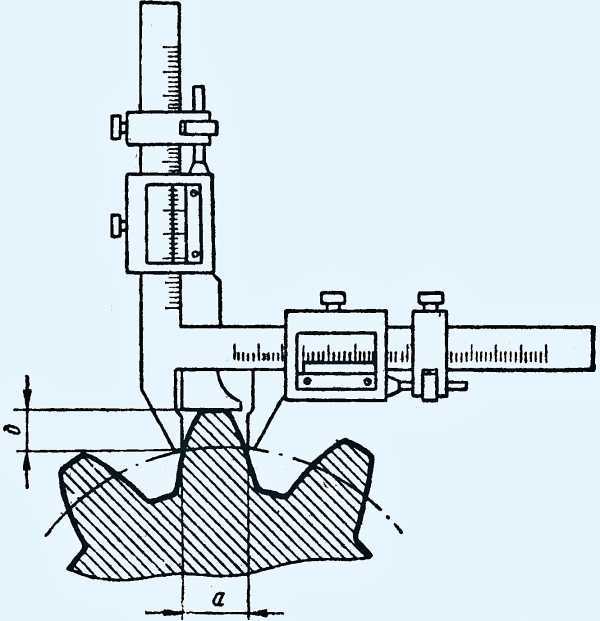
Ещё один способ, пожалуй самый «не любимый» зуборезчиками, это замер зуба шестерни тангенциальным зубомером. Тут есть и привязка к диаметру и необходимо очень правильно ставить зубомер на зуб. Данный зубомер имеет специальные ролики по модулям и индикатор.
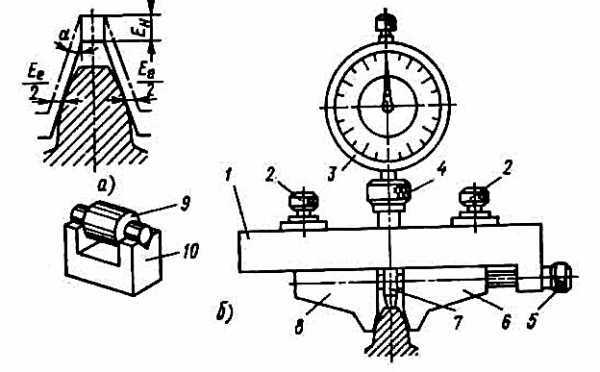
zuborez.info
stomatronix.ru
Как определить модуль зуба конической шестерни. Расчет конических зубчатых колес
Министерство путей сообщения Российской Федерации
Департамент кадров и учебных заведений
Самарская государственная академия путей сообщения
Кафедра механики
Методические указания по курсу
“Детали машин и основы конструирования”
Для студентов специальностей 150700 – Локомотивы
150800 – Вагоны
170900 – Подъёмно-транспортные,
строительные и
дорожные машины и
оборудование
181400 – Электрический транспорт
железных дорог.
Составители: Толстоногов А.А.,
Глобенко Е.В.,
Назарова Н.В.,
Жарков М.С.
Самара 2004 г.
Методические указания к выполнению расчётно-графических работ и курсового проекта по дисциплине “Детали машин и основы конструирования” для студентов специальностей 150700, 150800, 170900 / Составители Толстоногов А.А., Глобенко Е.В., Назарова Н.В., Жарков М.С. Самара, СамГАПС, 2004.- 24 с.
Утверждено на заседании кафедры, протокол №3. от 13.10.2004г.
Печатается по решению редакционно-издательского совета академии.
Составители: Толстоногов Андрей Арленович,
Глобенко Евгений Викторович,
Назарова Надежда Владимировна,
Жарков Михаил Сергеевич.
Рецензенты: Доцент кафедры ОКМ СГАУ Васин В.Н.,
Профессор кафедры механики СамИИТ Янковский В.В.
Редактор: Шимина И.А.
Подписано в печать 33.33.2002 Формат 60х84 1.16
Бумага писчая. Усл. печ. л
Тираж 100 экз. Заказ №
© Самарская Государственная Академия Путей Сообщения, 2004.
1. Методика расчета конической прямозубой передачи 5
Выбор материала зубчатых колес 5
Определение допускаемых напряжений 5
Определение чисел зубьев и передаточнго числа 6
Определение внешнего делительного диаметра колеса 7
Расчёт геометрических параметров зубчатой передачи 8
Проверочный расчёт контактных напряжений
на рабочих поверхностях зубьев 9
Определение сил в коническом зацеплении 10
Проверочный расчет зубьев на выносливость
по напряжениям изгиба 10
Санкт-Петербургский ГосударственныйТехнологический Институт
(Технический Университет)
Кафедра теоретических основхимического машинострония
Конические зубчатые передачи
Санкт-Петербург
Введение
3. Передаточное число
4. Приведение прямозубого коническогоколеса к эквивалентному прямозубому цилиндрическому
Заключение
Введение
Конические зубчатые колеса применяют в передачах между валами, оси которых расположены под углом. Основное применение имеют передачи с пересекающимися под углом 90° осями, т. е. ортогональные передачи, которые рассматриваются ниже. Передачи с межосевым углом, не равным 90°, применяют редко из-за сложности форм и технологии изготовления корпусных деталей, несущих эти передачи, хотя для изготовления самих колес межосевой угол передачи не имеет значения. Пересечение осей валов затрудняет размещение опор. Одно из конических колес, как правило, располагают консольно. При этом увеличивается неравномерность распределения нагрузки по длине зуба. В коническом зацеплении действуют осевые силы, наличие которых усложняет конструкцию опор. Все это приводит к тому, что по опытным данным нагрузочная способность конической прямозубой передачи составляет лишь около 0,85 цилиндрической. Несмотря на отмеченные недостатки, а также то, что конические колеса сложнее, чем цилиндрические в изготовлении и монтаже, конические передачи имеют, широкое применение, поскольку по условиям компоновки механизмов довольно часто необходимо располагать валы под углом. Конические колеса выполняют с прямыми, тангенциальными, круговыми и другими криволинейными зубьями
Прямозубые конические колеса следует применять при невысоких окружных скоростях (до 2…3 м/с) как наиболее простые в монтаже (допустимо до 8 м/с). При более высоких скоростях целесообразно применять колеса с круговыми зубьями, как обеспечивающие более плавное зацепление, меньший шум, большую несущую способность и более технологичные. Зубья обрабатывают на специальных станках для нарезания конических колес. В массовом и крупносерийном производстве в связи с возможн
sportbu.ru
Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.
Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса:
d = m × z,
где z – число зубьев;
m – модуль.
Модуль зацепления m – это часть диаметра делительной окружности, приходящейся на один зуб:
m = t / π,
где t – шаг зацепления.
Высота зуба:
h = ha + hf,
где ha – высота головки зуба, ha = m; hf – высота ножки зуба, hf = 1,25m.
Диаметр окружности выступов зубьев:
da = d + 2ha = m (z + 2).
Диаметр окружности впадин:
df = d – 2hf = m (z – 2,5).
Служит для передачи вращения при параллельных осях валов.
ГОСТ 9563-60 предусматривает два ряда модулей m= 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Служит для преобразования вращательного движения в возвратно-поступательное.
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Служит для передачи вращательного движения между валами со скрещивающимися осями.
ГОСТ 19672-74 устанавливает два ряда значений модулей m (мм).
Ряд 1: … 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10 …
Ряд 2: … 1,5; 3; 3,5; 6; 7 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Служит для передачи вращения при пересекающихся осях валов.
ГОСТ 9563-60 предусматривает два ряда модулей m= 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
dgng.pstu.ru
Определение модуля зубчатых колес — Студопедия.Нет
Зубчатые колеса являются основным видом передач коробок скоростей. От их габаритных размеров и качества зависят размеры и эксплуатационные характеристики всей коробки.
Основными причинами выхода из строя зубчатых колес станков являются усталость поверхностных слоев зубьев, их износ, смятие торцев зубьев переключающихся шестерен и поломка зубьев от усталости или перегрузок.
Расчет зубчатых колес ведется в основном теми же методами, которые рассматриваются в курсе «Детали машин». Однако при расчете зубчатых передач станков модуль определяется не только исходя из прочности зуба на изгиб , но и из усталости поверхностных слоев .
В коробках скоростей размер шестерен в большинстве случаев определяется контактными напряжениями, т. е. усталостью поверхностных слоев зубьев. Сначала следует найти наиболее нагруженную кинематическую пару и для нее определить модуль исходя из прочности зуба на изгиб и усталости поверхностных слоев по формулам:
, , (2.16)
где и – допустимые напряжения для контактной нагрузки и на изгиб, МПа;
– номинальная передаваемая мощность, кВт;
– минимальная частота вращения шестерни, на которую передается полная мощность, об/мин;
– коэффициент формы зуба;
– число зубьев шестерни;
– передаточное отношение пары;
– коэффициент, учитывающий изменение нагрузки на зуб шестерни по сравнению с ее номинальным значением;
– коэффициент ширины, принимаемый равным 6 – 10.
Из полученных модулей и выбирают наибольший и округляют его до ближайшего большего стандартного значения: 1,0; 1,5; 2,0; 2,5; 3,0; 3,5; 4,0; 4,5; 5,0; 6,0; 8,0; 10,0; 13,0; 16,0 мм.
Найденный стандартный модуль принимается для всех зубчатых пар данной групповой передачи.
Для первой ступени.
Предварительный материал колес: сталь 40Х (НВср = 249 МПа).
МПа,
МПа.
Тогда, мм
.
мм.
Принимаем мм.
Для второй ступени.
Расчет цилиндрической прямозубой передачи
Рассчитать на усталость при изгибе открытую цилиндрическую прямозубую передачу коробки скоростей, если мощность на валу шестерни Р1и угловая скорость вала , передаточное число . Нагрузка нереверсивная, постоянная при длительной работе передачи.
Дано:
Р1 = 4,5 кВт
=28 1/с
=2
Марка стали: шестерни – сталь 45
колеса – сталь 45
Термообработка – улучшение.
Решение:
1. Определим вращающий момент на валу шестерни
где – мощность на зубчатом колесе мельницы, Вт;
– угловая скорость вращения вала барабана мельницы, рад/сек,
2. Определяем число зубьев колеса , предварительно задав число зубьев шестерни в пределах .
Принимаем число зубьев шестерни = 20, тогда число зубьев колеса определим по формуле
.
3. Для заданной марки стали шестерни и колеса – сталь 45 – по табл. П4 методички, определяем механические характеристики материала:
Для шестерни: 730 МПа, 390 МПа, НВ1 =210, при диаметре заготовки до 90-120 мм;
для колеса: 690 МПа, 340 МПа, НВ2=200, при диаметре заготовки свыше 120 мм.
4. Допускаемые напряжения изгиба по формуле .
Для шестерни при пределе выносливости при базовом числе циклов
Для колеса
Требуемый коэффициент безопасности и долговечности для шестерни и колеса для поковок и отливок: 1,75 1, тогда
.
5. Коэффициенты формы зубьев: 4,07 и 3,70 (см. табл. П10) при ; .
Производим сравнительную оценку усталостной прочности зубьев при изгибе по отношениям:
Дальнейший расчет передачи производим по шестерни, так как у шестерни это отношение меньше.
6. Определим расчетные коэффициенты: коэффициент ширины венца колеса (см. табл. 7.6 [2]) при консольном расположении шестерни относительно опор. Для этого вначале определяем по табл.П6: =0,2…0,25. Большие значения для передач с твердостью зубьев . Принимаем =0,2.
Тогда .
В зависимости от твердости зубьев ( ) и коэффициента по табл. П.6 интерполированием находим коэффициент неравномерности нагрузки (см. табл. 7.7 [2])
7. Определим модуль зацепления по формуле
м.
Согласно ГОСТ 9563-60 принимаем стандартное значение m= 4,5 мм.
8. Определим основные геометрические размеры передачи, мм:
диаметры делительных окружностей
шестерни
,
мм;
колеса
,
мм;
межосевое расстояние
мм,
принимаем 135 мм;
диаметры окружностей вершин зубьев
мм,
мм;
диаметры впадин
мм;
мм;
ширина венца колеса
мм;
ширина венца шестерни
мм.
9. Определяем пригодность заготовок шестерни и колеса.
Диаметр заготовки шестерни
Диаметр заготовки колеса
Условие пригодности заготовок выполняются.
10. Определим окружную скорость зубчатых колес
м/с.
и назначаем 9-ю степень точности изготовления колес по табл. П.2.
11. Определим окружную силу в зацеплении
Н.
12. Принимаем коэффициент динамической нагрузки при известной степени точности зубьев. Для прямозубых колес при м/с =1,4.
13. Проверяем зубья на усталость при изгибе:
что значительно ниже допустимого.
Так как недогрузка составляет
Условие прочности выполнено.
Проверочный расчет валов
В качестве материала для изготовления валов примем сталь углеродистую марки 45, термообработка – нормализация.
Основные параметры:
– предел выносливости при изгибе s-1 = 28 кг/мм2;
– предел выносливости при кручении t-1 = 16 кг/мм2.
Диаметры валов:
| (46) |
где М – крутящий момент на валу.
Полученные значения диаметров валов округлим до стандартных из нормального ряда по ГОСТ 12080-66:
| (2.26) |
где – соответственно запас прочности при действии одних изгибающих и одних крутящих моментов; [n] = 2 ¸ 2,5 – запас прочности вала.
| (2.27) |
где s-1 и t-1 – предел выносливости при изгибе и кручении соответственно.
Номинальное напряжение в сечении при изгибе:
| (2.28) |
Номинальное напряжение в сечении при кручении:
| (2.29) |
Вал I:
Вал II:
Проверим полученные диаметры валов на виброустойчивость:
| (50) |
где l – длина вала; d – диаметр вала.
studopedia.net
Как узнать число зубьев. Определение чисел зубьев колес
Выбираем межосевое расстояние по ГОСТ 2185-66 мм .
Определим модуль передачи по формуле
где m n – модуль передачи, причём мм.
Значение модуля передачи выбирают из стандартного ряда . Выбираем мм.
Суммарное число зубьев в соответствии с определяют по формуле
где – суммарное число зубьев; β – угол наклона зуба, град.
Предварительно выбираем угол = 15º, учитывая, что передача косозубая, по рекомендации .
Подставляя численные значения в формулу (2.9), найдём суммарное число зубьев
Теперь найдём число зубьев шестерни и колеса
,
где – число зубьев на шестерне;– число зубьев на колесе.
Выбираем число зубьев на шестерне , а число зубьев на колесе.
Уточним угол , определив его по формуле
Сделаем проверочный расчёт зубьев шестерни на подрезание. Условие работоспособности передачи без подрезания можно записать в виде
где – минимальное число зубьев.
Для косозубых передач минимальное число зубьев вычисляется по формуле
Минимальное число зубьев оказалось меньше, чем фактическое, следовательно, подрезания не произойдет.
Подставляя число зубьев шестерни в (2.14), вычисляем делительный диаметр шестерни
мм
Подставляя число зубьев колеса в (2.14), вычисляем делительный диаметр колеса
мм
Зная делительный диаметр, можно найти диаметр вершин по формуле
где – диаметр вершины, мм.
Подставляя численные значения в формулу (2.15), вычисляем диаметр вершин шестерни
Подставляя численные значения в формулу (2.15), вычисляем диаметр вершин колеса
Зная делительный диаметр, можем найти диаметр впадин по формуле
Подставляя численные значения в формулу (2.16), вычисляем диаметр впадин шестерни
Подставляя численные значения в формулу (2.16), вычисляем диаметр впадин колеса
Определим ширину зубьев шестерни по формуле
где – ширина зубьев шестерни, мм.
Из конструктивных соображений ширину зубьев колеса можно вычислить по формуле
где – ширина зубьев колеса, мм.
Результаты всех вычислений сведены в табл. 2.1.
Таблица 2.1
Результаты проектировочного расчета
Задачей данного раздела является проверка зубьев на контактную выносливость. Видом разрушения является усталостная поломка.
Критерий расчета – контактная выносливость.
где – фактическое контактное напряжение, Н/мм 2 ; – нормативное контактное напряжение, Н/мм 2 .
В соответствии с фактическое напряжение можно вычислить по формуле
, (2.20)
где – коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления;– коэффициент, учитывающий суммарную длину контактных линий;– ширина колеса, мм.
вычисляют по формуле
где – коэффициент, учитывающий неравномерное распределение нагрузки между зубьями.
Линейная скорость шестерни определяется по формуле
где V 1 – линейная скорость шестерни, м/с.
Так как линейная скорость шестерни меньше 15 м/с и передача является быстроходной (выбираем степень точности 7), то в соответствии с .
Так как передача является быстроходной (степень точности 7), по рекомендациям выбираем .
Для определения следует воспользоваться таблицей из . Выбираем.
Подставляя численные значения коэффициентов в формулу (2.21), вычислим значение
Подставляя численные значения в формулу (2.20), получим величину фактического контактного напряжения
Сравним фактическое и допускаемое контактные напряжения
Н/мм 2
Фактическое напряжение меньше допускаемого, следовательно, оставляем ранее выбранные в пункте 2.1. размеры.
2.3. Проверочный расчет зубьев на изгибную прочность
Задачей данного раздела является проверка зубьев на изгибную выносливость. Видом разрушения является усталостная поломка зуба. Критерием расчёта – изгибная выносливость.
где – фактическое напряжение изгиба, Н/мм 2 ; – допускаемое напряжение изгиба, Н/мм 2 .
Определим, где первым сломается зуб, на шестерне или на колесе. Для этого найдём допускаемое напряжение изгиба на шестерне и на колесе
, (2.24)
где – коэффициент безопасности по изгибу;– коэффициент долговечности;– коэффициент, учитывающий влияние двустороннего приложения нагрузки.
Учитывая, что твердость шестерни , следовательно по выбираемН/мм 2 . Твердость колеса , тогдаН/мм 2 . Так как приложение нагрузки одностороннее, выбираем .
Для всех сталей ГОСТ принимает базовое число циклов . Фактическое число цикловопределяется из соотношения
Сравним и. Так как, следовательно, в соответствии с . Сравними. Так как, следовательно, в соответствии с .
Найдем численное значение допускаемого контактного напряжения на шестерне, подставляя значения в формулу (2.24)
Найдем численное значение допускаемого контактного напряжения на колесе, подставляя значения в формулу (2.24)
Теперь определим, где первым сломается зуб (на шестерне или на колесе), для этого сравним следующие соотношения
где – коэффициент, учитывающий форму зуба шестерни;– коэффициент, учитывающий форму зуба колеса.
Коэффициент, учитывающий форму зуба, высчитывается по ГОСТу 21354-75 в зависимости от эквивалентного числа зубьев
где – эквивалентное число зубьев.
Вычислим эквивалентное число зубьев для шестерни
С учетом интерполяции при ,. Найдем численное значение отношения (2.26) для шестерни
Вычислим эквивалентное число зубьев для колеса
С учетом интерполяции при ,. Найдем численное значение отношения (2.26) для колеса
Так как отношение для шестерни меньше, чем отношение для колеса, то это значит, что первым сломается зуб на шестерне.
Сделаем проверочный расчёт для косозубой передачи шестерни
Фактическое напряжение изгиба на шестерне можно вычислить по формуле
, (2.29)
где – окружная сила, Н;– коэффициент нагрузки;– коэффициент, учитывающий угол контактных линий;– коэффициент, учитывающий неравномерность нагрузки между зубьями.
Окружная сила в соответствии с вычисляется по формуле
Н (2.30)
Коэффициент нагрузки в соответствии с вычисляется по формуле
где – коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба;– коэффициент, учитывающий динамическое действие нагрузки.
Коэффициент концентрации нагрузки и динамический коэффициент можно вычислить по таблицам из , , а для определения коэффициента концентрации нагрузки следует вычислитьпо формуле
(2.32)
Следовательно, по таблице выбираем , тогда при симметричном расположении зубчатых колес.
Подставляя численные значения коэффициента концентрации нагрузки и динамического коэффициента в (2.31), получим численное значение коэффициента нагрузки
Коэффициент, учитывающий угол контактных линий, определяется по формуле
(2.33)
Находим численное значение фактического напряжения изгиба, подставляя численные значения окружной силы, коэффициента нагрузки, коэффициента, учитывающего угол линий и коэффициента, учитывающего неравномерность распределения нагрузки между зубьями в формулу (2.29)
Сравним фактическое и допускаемое напряжения изгиба зубьев
Н/мм 2
Так как фактическое напряжение изгиба зубьев на шестерне меньше допускаемого, следовательно, размеры передачи оставляем без изменений.
Основная группа (рис. 3)
Для данной группы составляем следующие уравнения:
Z 4 + Z 5 = Z 6 + Z 7 ; (1)
Z 8 + Z 9 = Z 6 + Z 7 ; (2)
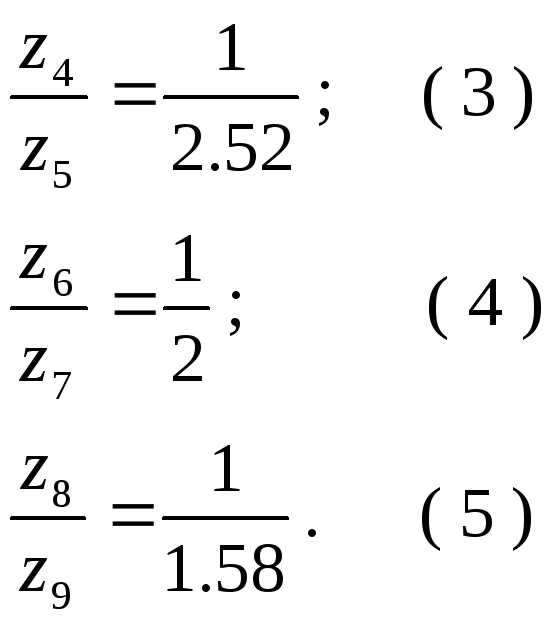
Для решения этой неопределенной системы уравнений и для получения наименьших размеров колес задаемся числом зубьев наименьшего колеса группы Z 4 = Z min = 18 22 .
Принимаем Z 4 =21.
Из уравнения (3) получаем: Z 5 = 2,52 · Z 4 = 2,52·21 = 52,9 53
Из уравнений (1) и (4) получаем:
21+53 = Z 6 +2· Z 6 и Z 6 = 74/3 = 24,67 25
Из уравнения (4) имеем: Z 7 =2· Z 6 =2·24,67 = 49,33 49
Однако определенные значения Z 6 и Z 7 вызовут большое отклонение в передаточном отношении i 3 (25/49= 0,51 вместо требуемого 0,50). Поэтому сумму зубьев этих колес примем равной Z 6 + Z 7 = 75 . Тогда
Z 6 = 75/3 = 25 и Z 7
veloed.ru
Зубчатое колесо. Основные параметры. Чертеж :: SYL.ru
Ни один хороший механизм не может быть построен без такой детали, как зубчатое колесо (или, иначе, шестерня). Правильное понимание того, как шестерни влияют на такие параметры, как крутящий момент и скорость вращения, очень важно. Ниже будет рассказано об азах зубчатых передач и о том, как правильно их использовать.
Механическое преимущество: крутящий момент против скорости вращения
Зубчатые передачи работают по принципу механического преимущества. Это значит, что с помощью использования шестерен различных диаметров вы можете изменять скорость вращения выходного вала и вращающий момент, развиваемый приводным двигателем.
Любой электродвигатель имеет определенную скорость вращения и соответствующий его мощности крутящий момент. Но, к сожалению, для многих механизмов предлагаемые на рынке и подходящие по стоимости асинхронные двигатели обычно не обладают желаемым соотношением между скоростью и моментом (исключением являются сервоприводы и мотор-редукторы с высоким моментом). Например, вы действительно хотите, чтобы колеса вашего робота-уборщика вращались со скоростью 3000 об/мин при низком крутящем моменте? Нет конечно, поэтому последний зачастую предпочтительнее скорости.
Уравнение зубчатой передачи
Она обменивает высокую входную скорость на больший выходной крутящий момент. Этот обмен происходит по очень простому уравнению, которое можно записать так:
Момент входной* Скорость входная = Момент выходной * Скорость выходная
Скорость входную можно найти, просто просматривая табличку приводного электродвигателя. Момент входной легко определить по этой скорости и механической мощности из той же таблички. Затем просто подставим выходную скорость или требуемый крутящий момент в правую часть уравнения.
Например, предположим, что ваш асинхронный двигатель при моменте на выходном валу 0,5 Н∙м имеет скорость 50 об/с, но вы хотите только 5 об/с. Тогда ваше уравнение будет выглядеть так:
0,5 Н∙м * 50 об/с = Момент выходной* 5 об/с.
Ваш выходной крутящий момент будет 5 Н∙м.
Теперь предположим, что с тем же мотором вам нужно 5 Н∙м, но при этом требуется минимальная скорость 10 об/с. Как бы узнать, способен ли на это ваш мотор вместе с зубчатой передачей (т. е., по сути, мотор-редуктор)? Обратимся снова к нашему уравнению
0,5 Н∙м * 50 об/с = 5 Н∙м * Скорость выходная,
Скорость выходная = 5 об/с.
Итак, вы определили, используя простое уравнение, что при показателе Момент выходной =5 Н∙м обеспечить скорость выходную в 10 об/с ваша зубчатая передача не способна. Вы только что сохранили себе кучу денег, так как не потратили их на механизм, который никогда не заработал бы.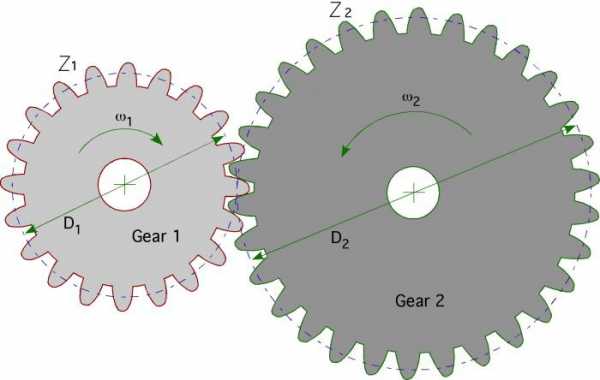
Передаточное число зубчатой передачи
Мы записали уравнения, но как механически поменять местами крутящий момент и скорость? Для этого нужны две шестерни (иногда больше) различных диаметров, чтобы иметь конкретное передаточное число. В любой паре шестерен большее зубчатое колесо будет двигаться более медленно, чем меньшее, но оно будет передавать на выходной вал больший крутящий момент. Таким образом, чем больше величина разницы (или передаточное число) между двумя колесами, тем больше разница их скоростей и передаваемых крутящих моментов.
Передаточное число показывает, во сколько раз зубчатая передача изменяет скорость и вращающий момент. Для него, опять же, имеется очень простое уравнение.
Предположим, что передаточное число равно 3/1. Это будет означать, что вы увеличиваете ваш крутящий момент втрое, а скорость втрое снижаете.
Пример:
Момент входной = 1,5 Н∙м, Скорость входная = 100 об/с,
Передаточное число = 2/3
Момент выходной = Момент входной * 2/3 = 1 Н∙м,
Скорость выходная = Скорость входная * 3/2 = 150 об/с.
Итак, на выходе передачи момент в полтора раза вырос, а скорость точно так же снизилась.
Достижение определенного передаточного числа
Если вы хотите достичь простой его величины, скажем 2 к 1, вы должны использовать две шестерни, одна из которых вдвое больше другой. Это не что иное, как отношение их диаметров. Если диаметр зубчатого колеса в 3 раза больше, чем у сцепленного с ним другого, то вы получите передаточное число 3/1 (или 1/3).
Для гораздо более точного способа вычислить передаточное число подсчитайте отношение зубьев на шестернях. Если одна из них имеет 28 зубьев и другая – 13, вы получите передаточное число 28 / 13 = 2,15 или 13 / 28 = 0,46. Подсчет зубьев всегда будет давать вам наиболее точную величину.
Эффективность передач
К сожалению, в зубчатой передаче вы имеете определенные энергетические потери. Это обусловлено очевидными причинами, такими как трение, рассогласование углов давления, смазкой, зазорами (расстоянием между сцепленными зубьями двух шестерен), а также угловыми моментами и т. д. Различные типы передач, разные виды зубчатых колес, различные материалы и износ шестерен, – все это будет влиять на КПД передачи. Возможные их комбинации дадут слишком большой список, поэтому точную величину КПД передачи, которые вы используете, вы сможете найти в документации на нее.
Предположим, что вы используете два цилиндрических зубчатых колеса. Обычное КПД такой передачи примерно ~ 90%. Умножьте это число на вашу скорость выходную и момент выходной, чтобы получить истинные выходные величины передачи.
Если (из предыдущего примера):
Передаточное число = 2/3
Момент выходной = Момент входной * 2/3 = 1 Н∙м,
Скорость выходная = Скорость входная * 3/2 = 150 об/с,
то тогда:
Истинный Момент выходной = 1 Н∙м * 0,9= 0,9 Н∙м,
Истинная Скорость выходная = 150 об/с * 0,9 = 135 об/с.
Направление вращения шестерен
Разрабатывая любую зубчатую передачу, нужно понимать, как она изменяет направление вращения выходного вала. Две сцепленные шестерни всегда будут вращаться в противоположных направлениях. Это означает, что если одна вращается по часовой стрелке, то другая всегда будет вращаться против нее. Это вполне очевидно. Но что делать, если у вас есть передача, скажем, из шести сцепленных шестерен? Правило здесь следующее: входной и выходной валы у передач с нечетным числом шестерен всегда вращаются в одном направлении, а при четном числе шестерен – в противоположном.
Конструкция и параметры зубчатого колеса
Оно содержит венец с зубьями, диск и ступицу. Имеется три наиболее важных его параметра: модуль, диаметр делительной окружности и количество зубьев. Какую же делительную окружность имеет зубчатое колесо? Чертеж цилиндрического колеса с типовыми эвольвентными зубьями показан ниже. 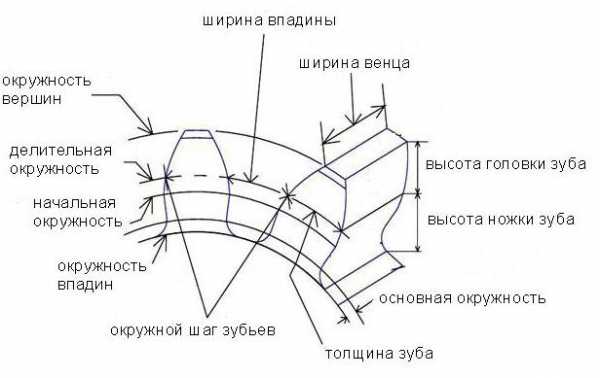 Делительная окружность показана на нем пунктиром. По ней принято определять окружной шаг зубьев p (шаг зацепления), т. е. часть ее длины, приходящуюся на один зуб, и модуль шестерни m – часть диаметра делительной окружности d, приходящуюся на один зуб. Чтобы его вычислить, просто используйте формулу ниже:
Делительная окружность показана на нем пунктиром. По ней принято определять окружной шаг зубьев p (шаг зацепления), т. е. часть ее длины, приходящуюся на один зуб, и модуль шестерни m – часть диаметра делительной окружности d, приходящуюся на один зуб. Чтобы его вычислить, просто используйте формулу ниже:
m = d/z= p/3,14, мм.
Например, зубчатое колесо с 22 зубьями и диаметром 44 мм имеет модуль m = 2 мм. Сцепленные шестерни должны обе иметь один модуль. Значения их стандартизованы, и как раз на делительной окружности модуль данного колеса принимает свое стандартное значение.
Высота головки зуба одного колеса меньше высоты ножки зуба второго, зацепляющегося с ним, благодаря чему образуется радиальный зазор c.
Для обеспечения бокового зазора δ между двумя сцепленными зубьями сумма их толщин принимается меньше их окружного шага p. Радиальный и боковой зазоры предусматриваются для создания необходимых условий смазки, нормальной работы передачи при неизбежных неточностях изготовления и сборки, тепловом увеличении размеров передачи и т. п.
Расчет зубчатого колеса
Он всегда ведется в составе расчета конкретной зубчатой передачи. Исходными данными для него обычно являются мощность (или крутящий момент), угловые скорости (или скорость одного вала и передаточное число), условия работы (характер нагрузки) и срок службы передачи.
Дальнейший порядок относится к закрытой цилиндрической прямозубой передаче.
1. Определение передаточного числа u.
2. Выбор материалов колес в зависимости от условий работы, назначение термообработки и значения твердости рабочих поверхностей зубьев.
3. Расчет зубьев передачи на изгиб.
4. Расчет зубьев передачи на контактную прочность (прочности контактирующих поверхностей зубьев).
5. Определение межосевого расстояния aW из условия контактной прочности и округление его значения до стандартного.
6. Задание модуля из соотношения m = (0,01 – 0,02) х aW и округление его значения до ближайшего стандартного. При этом в силовых передачах желательно иметь m ≥1,5 – 2 мм.
7. Определение суммарного числа зубьев передачи, числа зубьев шестерни и колеса.
8. Выбор коэффициентов формы зубьев для шестерни и колеса.
9. Проверка прочности зубьев по напряжениям изгиба.
10. Проведение геометрического расчета передачи.
11. Определение окружной скорости колеса и назначение соответствующей точности зацепления.
Расчет зубчатого колеса в составе открытой зубчатой передачи несколько отличается от приведенного, но в основном последовательность его такая же.
Как обозначается точность изготовления зубчатых колес
При изготовлении любые их виды имеют ряд погрешностей, среди которых выделяют четыре основные:
- кинематическую погрешность, связанную в основном с радиальным биением зубчатых венцов;
- погрешность плавности работы, вызываемую отклонениями шага и профиля зубьев;
- погрешность контакта зубьев в передаче, которая характеризует полноту прилегания их поверхностей в зацеплении;
- боковой зазор между неработающими поверхностями зубьев.
Для контроля первых трех погрешностей стандартами установлены специальные показатели – степени точности от 1 до 12, причем точность изготовления увеличивается с уменьшением показателя. Для контроля четвертой погрешности изготовления имеются два показателя:
- вид сопряжения зубчатых колес – обозначается литерами A, B, C, D, E, H;
- допуск на боковой зазор – обозначается литерами x, y, z, a, b, c, d, e, h.
Для обоих показателей бокового зазора обозначения даны в порядке убывания его величины и допуска на него.
Условно точность зубчатых колес обозначается двумя способами. Если степень точности по первым трем погрешностям одинакова, то ставится один общий для них численный показатель степени точности, за которыми стоят литеры обозначения вида сопряжения и допуска на боковой зазор. Например:
8-Ас ГОСТ 1643 – 81.
Если точности по первым трем погрешностям разные, то в обозначении ставятся три численных показателя последовательно. Например:
5-4-3-Са ГОСТ 1643 – 81.
Типы зубчатых передач
Любое зубчатое колесо, независимо от его типа, делается и работает по одним и тем же вышеприведенным принципам. Однако различные их типы позволяют выполнить разные задачи. Некоторые виды передач обладают или высоким КПД, или высоким передаточным отношением, или же работают с непараллельными осями вращения шестерен, к примеру. Ниже приведены основные общие типы. Это не полный список. Также возможно и сочетание нижеприведенных типов.
Примечание: Приведены только типичные КПД передач. Из-за многих других возможных факторов приводимые КПД должны использоваться только в качестве справочных величин. Часто производители приводят ожидаемые КПД в паспортах для своих передач. Помните, что износ и смазка будут также существенно влиять на эффективность передач.
Цилиндрические прямозубые колеса (КПД ~ 90%)
Цилиндрическое зубчатое колесо имеет зубья, расположенные на цилиндрической поверхности. Передачи с ними являются наиболее часто используемыми типами благодаря своей простоте и максимальной эффективности среди всех других. Передаточное число для одной пары u ≤ 12,5. Не рекомендуется для очень высоких нагрузок, так как прямые зубья зубчатого колеса довольно легко ломаются.
Цилиндрические косозубые колеса (КПД ~ 80%)
Они работают так же, как цилиндрические прямозубые, для передачи момента между параллельными валами, но у такой передачи более плавно происходит зацепление. Вследствие этого они создают меньше шума при работе и имеют меньшие габариты. У них большая нагрузочная способность. К сожалению, из-за сложной формы зубьев они, как правило, более дорогие.
Цилиндрические шевронные колеса
Являются разновидностью предыдущего вида. Чем отличается такое зубчатое колесо. Чертеж его показан ниже. Видно, что по ширине его венца расположены зубья с правым и левым наклоном, так что такие составные зубья зубчатого колеса по форме напоминает «шевроны». Эти колеса обладают всеми преимуществами косозубого их вида, плюс отсутствием осевых нагрузок. Они способны самоцентрироваться и не нуждаются в дорогостоящих радиально-упорных подшипниках для восприятия осевых нагрузок.
Конические зубчатые колеса (КПД ~ 70%)
Зубья этих колес, располагающиеся на конических поверхностях, выполняют прямыми, косыми, круговыми (дугообразными). Эти передачи применяют для передачи момента между перекрещивающимися под разными углами валами. К сожалению, их КПД довольно низок, поэтому следует избегать их применения, если возможно.
Это передача с винтом-червяком на одном валу и червячным колесом на втором, перпендикулярном первому, валу. Они имеют очень высокое передаточное число. В расчетах принимают во внимание то, что у червяка (однозаходного) имеется только один зуб (виток).  Еще одним преимуществом червячной передачи является то, что у нее только одно направление вращения. Это означает, что только приводной двигатель может вращать такую передачу, в то время как сила тяжести или другие сторонние силы не вызовут каких-либо вращений. Это бывает полезно, например, для стопорения груза на высоте.
Еще одним преимуществом червячной передачи является то, что у нее только одно направление вращения. Это означает, что только приводной двигатель может вращать такую передачу, в то время как сила тяжести или другие сторонние силы не вызовут каких-либо вращений. Это бывает полезно, например, для стопорения груза на высоте.
www.syl.ru

