Максимальная кинетическая энергия – Энергия гармонического колебания. Кинетическая, потенциальная. Максимальная
alexxlab | 28.10.2020 | 0 | Вопросы и ответы
Энергия гармонического колебания. Кинетическая, потенциальная. Максимальная
Введём энергию колебания.
Колебательная система движется со скоростью
, тогда его кинетическая энергия должна быть равна: (1)- где
- — кинетическая энергия системы
- — масса колеблющегося тела
- — скорость тела в данный момент
Вспомним зависимость скорости от времени при гармоническом колебании:
www.abitur.by
2. Максимальная кинетическая энергия фотоэлектронов линейно возрастает с увеличением частоты падающего монохроматического света.
Рассмотрим подробнее вольт-амперную характеристику фотоэлемента. Из рис. 2 следует, что при UA 0 сила фототока I 0. Это означает, что электроны, вырванные светом из катода, имеют некоторую скорость, а следовательно и кинетическую энергию WК. ≠ 0 и могут достигнуть анода даже в отсутствие внешнего электрического поля. Это означает, что для того, чтобы прекратить фототок, то есть сделать его равным нулю, необходимо приложить задерживающее напряжение UЗ, при котором даже самые быстрые фотоэлектроны не смогут достичь анода, так как будут задержаны электрическим полем:
Wmax 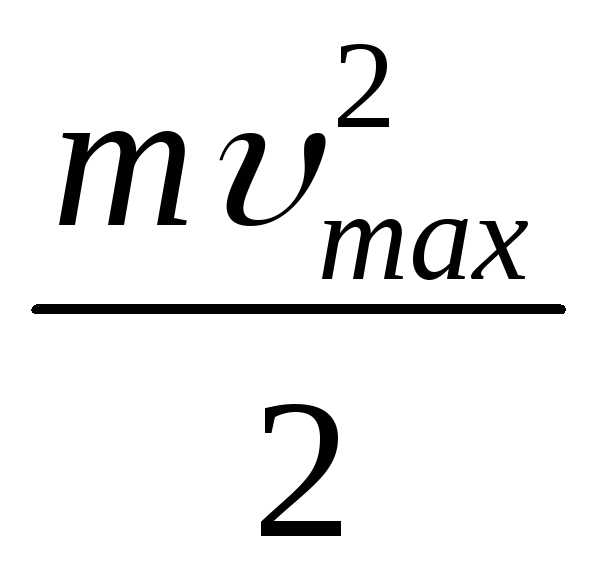 eUЗ.
(3)
eUЗ.
(3)
Здесь m – масса электрона, e – элементарный заряд равный 1,6·1019 Кл, UЗ – задерживающее напряжение.
Меняя частоту падающего монохроматического света, можно найти зависимость WК max EК(). Экспериментальные исследования показывают, что эта зависимость является линейной:
WК max 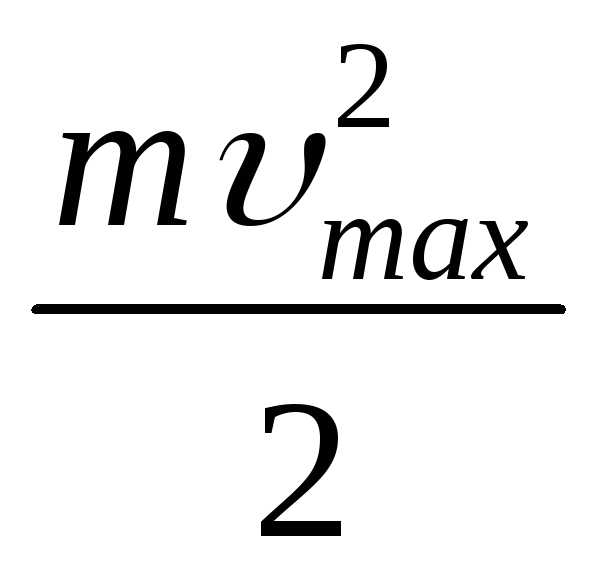 а
b,
(4)
а
b,
(4)
где а – константа, b – зависит от материала катода.
График зависимости (4) показан на рис. 4: он свидетельствует о том, что с увеличением частоты падающего монохроматического света максимальная кинетическая энергия фотоэлектронов возрастает. Линейный характер зависимости был объяснен Эйнштейном на основе квантовых представлений о природе света.
Согласно однофотонной теории фотоэффекта, при падении фотонов на поверхность металла происходит взаимодействие фотонов и электронов: каждый электрон получает энергию только одного фотона. Эта энергия расходуется на работу выхода электрона из металла и на сообщение ему кинетической энергии.
В соответствии с законом сохранения энергии максимальная кинетическая энергия фотоэлектрона
WК max 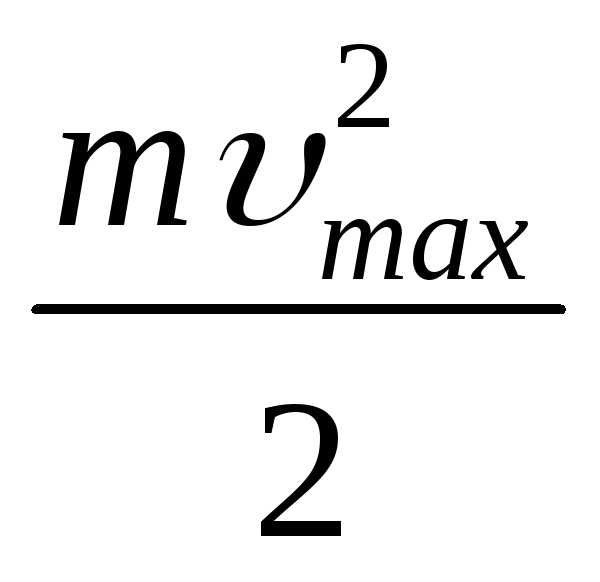 h
A.
(5)
h
A.
(5)
В этой формуле А – работа выхода электрона из металла, равная той наименьшей энергии, которую необходимо сообщить электрону для того, чтобы удалить его из твердого или жидкого вещества в вакуум в состояние с кинетической энергией равной нулю.
Выражение (5) носит название уравнения Эйнштейна для внешнего фотоэффекта.
3. Для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота света 0, при которой еще возможен внешний фотоэффект. Величина 0 зависит от химической природы вещества и состояния его поверхности.
При облучении вещества светом, длина волны которого 0 (или частота 0), фотоэффект не наблюдается (см. рис. 4). Из рис. 4 следует, что WК max 0 при 0. Следовательно, согласно формуле (5),
h0 A,
0  (6)
(6)
В случае обычных значениях интенсивности света в процессе взаимодействия света с веществом в элементарном акте поглощается один фотон. Однако, при больших интенсивностях, например в световых пучках, генерируемых лазерами, в элементарном акте взаимодействия могут поглощаться сразу N фотонов. Такое поглощение называется многофотонным. Формула Эйнштейна в этом случае записывается следующим образом:
Nh
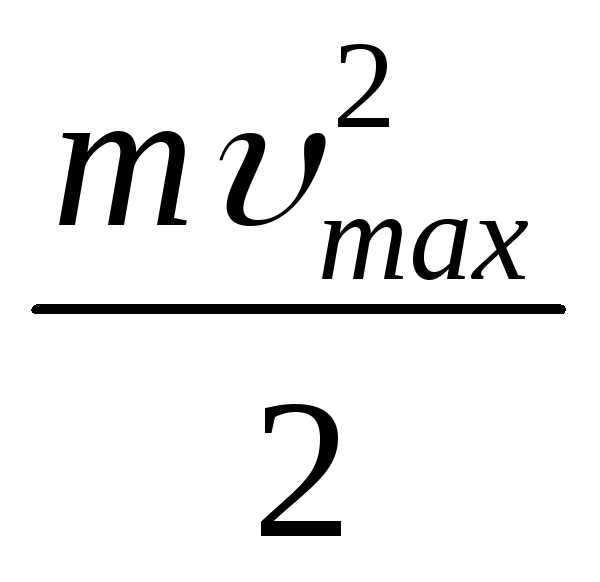 A.
A.
Соответственно красная граница смещается в сторону более длинных волн (0 увеличивается в N раз), а формула (2), отражающая зависимость тока насыщения от потока излучения для многофотонных процессов приобретает вид
studfiles.net
Максимальная кинетическая энергия – Большая Энциклопедия Нефти и Газа, статья, страница 2
Максимальная кинетическая энергия
Но максимальная кинетическая энергия каждого вылетевшего из металла электрона не зависит от интенсивности освещения, а изменяется только при изменении частоты падающего на металл света. [16]
Найти максимальную кинетическую энергию а-частиц, возникающих в результате экзотермической реакции Oie ( d – a) N14, энергия которой Q 3 1 Мэв, если известно, что энергия бомбардирующих дейтонов Еа 2 Мэв. [17]
Определить максимальную кинетическую энергию нейтронов Wmax, возникающих в реакции t d – n iHe под действием трития t, который сам получается при поглощении медленных нейтронов в 6Li согласно реакции n 6Li – – t – f – ос. [18]
Ферми – максимальная кинетическая энергия, KOj торой может обладать электрон при абсолютном нуле. [19]
Следовательно, максимальная кинетическая энергия нейтрона, испускаемого бериллием, равна 7 8 106 электрон-вольтам, что соответствует скорости около 3 9 109 см сек. Поскольку масса нейтрона должна быть почти равной массе протона, тогестественно предположить, что максимальные скорости обеих частиц должны быть почти одинаковыми. Наибольшая наблюдаемая для протона скорость равна 3 3 109 см сек подобное значение для нейтрона согласуется со взглядами Чедвика на происхождение нейтрона. [20]Чему равняется максимальная кинетическая энергия свободных электронов при О К в меди. [21]
Чему равна максимальная кинетическая энергия отдельного нуклона, если ядро атома находится на самом нижнем энергетическом уровне. [22]
Атом имеет максимальную кинетическую энергию при положении в средней точке, которая соответствует наибольшей скорости его движения. Но так как в этом положении скорость атома максимальна, время пребывания его в этом состоянии минимально. Однако большая часть столкновений между молекулами приходится именно на эти фазы колебания, и значительно меньшая часть на ту фазу, в которой условия для передачи энергии колебания наиболее выгодны. [23]
Здесь Гмаис – максимальная кинетическая энергия. [24]
В таблице приведена максимальная кинетическая энергия, которая может быть передана каждому атому электроном с пороговой энергией. [25]
Второй закон фотоэффекта: максимальная кинетическая энергия фотоэлектронов линейно возрастает с частотой света и не зависит от интенсивности све – J та. [26]
При постоянной интенсивности света максимальная кинетическая энергия выбиваемых электронов характеризуется простой линейной зависимостью от частоты света. Более того, такой линейной зависимости свойствен один и тот же наклон для всех исследуемых материалов; таким образом, этот наклон есть характеристика самих фотонов. Таким образом, нами найдена связь, которую мы искали: связь между волновыми характеристиками пучка света и той единственной, характеристической энергией, которую несут на себе фотоны этого пучка. [27]
Задерживающее напряжение U3 зависит от максимальной кинетической энергии, которую имеют вырванные светом электроны. [28]
Числитель аргумента логарифма 2m0V2 представляет максимальную кинетическую энергию, которую может получить легкая частица при лобовом столкновении с – частицей. [29]
Эта связь показана на рис. 4.62.
Страницы: 1 2 3
www.ngpedia.ru
Энергия гармонических колебаний
Кинетическая и потенциальная энергия гармонических колебаний
Кинетическая энергия тела, совершающего гармонические колебания:
Потенциальная энергия тела, совершающего гармонические колебания (под действием квазиупругой силы):
Учитывая, что
можно записать:
Полная энергия гармонических колебаний
Полная энергия гармонических колебаний равна сумме кинетической энергии и потенциальной энергии:
При свободных колебаниях колебательная система получает энергию только в начальный момент времени, а далее энергия системы, а с ней и амплитуда колебаний не меняются. При движении тела кинетическая и потенциальная энергия переходят друг в друга. Когда отклонение системы от положения равновесия максимально, потенциальная энергия максимальна, а кинетическая равна нулю. При прохождении положения равновесия потенциальная энергия достигает минимума, а кинетическая энергия (а с ней и скорость, импульс тела) максимальна.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Кинетическая энергия | Все формулы
Кинетическая энергия — скалярная физическая величина, равная половине произведения массы тела на квадрат его скорости.
Что бы понять, что же такое кинетическая энергия тела, рассмотрим случай, когда тело массой m под действием постоянной силы (F=const) движется прямолинейно равноускоренно (а=const). Определим работу силы, приложенной к телу, при изменении модуля скорости этого тела от v1 до v2.

Как мы знаем, работа постоянной силы вычисляют по формуле . Так как в рассматриваемом нами случае направление силы F и перемещения s совпадают, то , и тогда у нас получается, что работа силы равна А=Fs. По второму закону Ньютона найдем силу F=ma. Для прямолинейного равноускоренного движения справедлива формула:
Из это формулы мы выражаем перемещение тела:
Подставляем найденные значения F и S в формулу работы, и получаем:
Из последней формулы видно, что работа силы, приложенной к телу, при изменении скорости этого тела равна разности двух значений некоторой величины . А механическая работа это и есть мера изменения энергии. Следовательно, в правой части формулы стоит разность двух значений энергии данного тела. Это значит, что величина представляет собой энергию, обусловленную движением тела. Эту энергию называют кинетической. Она обозначается Wк.
Если взять выведенную нами формулу работы, то у нас получится
Работа, совершаемая силой при изменении скорости тела, равна изменению кинетической энергии этого тела
Так же есть :
Потенциальная энергия :
В формуле мы использовали :
— Кинетическая энергия
— Масса тела
— Скорость движения тела
— Начальная скорость тела
— Конечная скорость тела
— Работа тела
— Ускорение тела
— Сила, действующая на тело
— Перемещение тела
xn--b1agsdjmeuf9e.xn--p1ai
34. Фотоэффект. Законы ф-та. Объяснение ф-та. Зависимость максимальной кинетической энергии фотоэлектронов от частоты света.
Был открыт Герцем в 1887г., изучен Столетовым в 19в.
 Фотоэффект–
явление вырывания электронов с поверхности
металла под действием падающего света.
Фотоэффект–
явление вырывания электронов с поверхности
металла под действием падающего света.
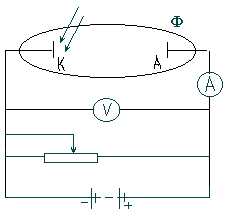
Столетов подверг ф-т исследованию с помощью следующей установки (рис.1)
Рис.1 Рис.2
На основании своих опытов он пришел к выводам: 1)наибольшее действие оказывают ультрафиолетовые лучи; 2) сила тока возрастает с увеличением освещенности пластины; 3) испускаемые под действием света заряды имеют отрицательный знак.
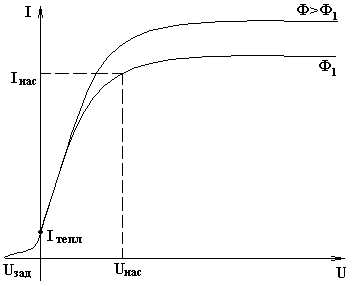
Получена на таком приборе ВАХ (на рис.2)-U(I)
Законы
ф-та: 1) Сила
тока насыщения зависит от величины
светового потока  2)
Величина3) Существует некоторая красная граница
ф-та,min
частота, при которой ф-т начинается.
Если частота ф-та меньше красной границы,
то ф-та нет.
2)
Величина3) Существует некоторая красная граница
ф-та,min
частота, при которой ф-т начинается.
Если частота ф-та меньше красной границы,
то ф-та нет. 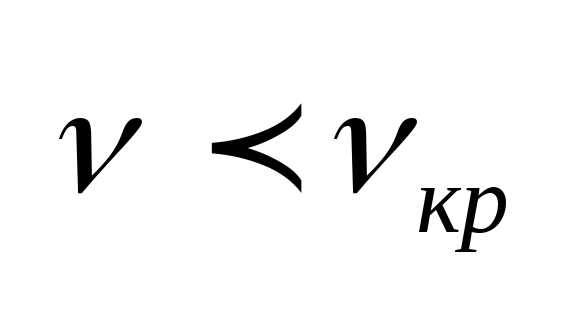 –
ф-та нет.
–
ф-та нет.
Зависимость  от
от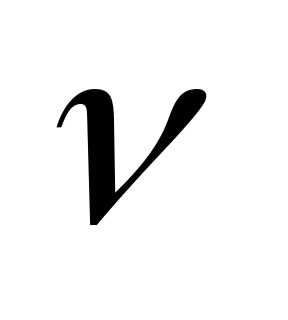 :
: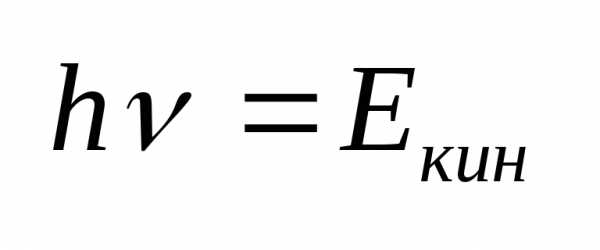 ,
где.
Следовательно, кинетич. энергия
определяется лишь частотой падающего
света и растет с увеличением частоты.
,
где.
Следовательно, кинетич. энергия
определяется лишь частотой падающего
света и растет с увеличением частоты.
Работа
выхода:
(затрачивается на то, чтобы электрон
мог покинуть тело).  ,
где
,
где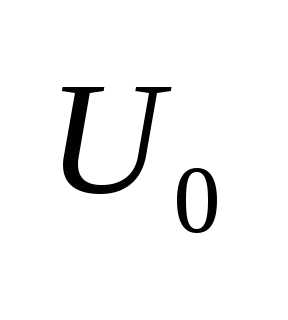 –
потенциал выхода.
–
потенциал выхода.
35. Фотоэффект.
Фотоэффект был открыт Герцем в 1887. Изучен был Столетовым.
Явление вырывания электронов с поверхности металлов под действием света получило название фотоэффекта.
Экспериментальные з-ны фотоэффекта.
1.Максимальная начальная скорость фотоэлектронов определяется частотой света и не зависит от его интенсивности.
2.Для
каждого вещества существует красная
граница фотоэффекта, т.е. минимальная
частота 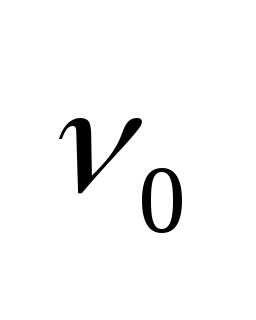 ,
при которой еще возможен фотоэффект (
,
при которой еще возможен фотоэффект (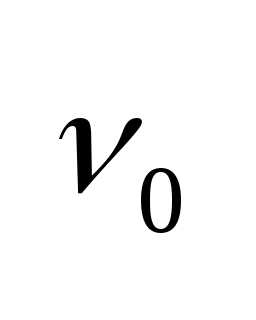 зависит от химической природы вещества
и состояния его поверхности).
зависит от химической природы вещества
и состояния его поверхности).
3.Число фотоэлектронов n, вырываемых из анода за единицу времени, пропорционально интенсивности света (фототок насыщения пропорционален энергетической освещенности катода).
Чем определяется числовое значение граничной частоты?
 ,
где А – работа выхода, h
– постоянная Планка.
,
где А – работа выхода, h
– постоянная Планка.
Она зависит только от работы выхода электрона, т.е. от химической природы металла и состояния его поверхности.
Почему максимальная энергия фотоэлектронов не зависит от плотности потока энергии падающего излучения? Почему в явлении фотоэффекта существование пороговой частоты говорит в пользу фотонной теории и против волновой?
Кинетическая энергия, с которой вырывается электрон из металла, должна была бы зависеть от интенсивности падающего света, так как с увеличением последней электрону бы передавалась бы большая энергия. однако этот вывод противоречит 2 з-ну фотоэффекта. Так, как по волновой теории, энергия, передаваемая электронам, пропорциональна интенсивности света, то свет любой частоты, но достаточно большой интенсивности должен был бы вырывать электроны из металла: иными словами , красной границы фотоэффекта не должно быть, что противоречит 3 з-ну фотоэффекта. Кроме того, волновая теория не смогла объяснить безинерционность фотоэффекта, установленную опытами. Таким образом, фотоэффект необъясним с точки зрения волновой теории света.
studfiles.net
Фотоэффект: кинетическая энергия электронов
В этой статье мы вычислим как работу выхода, так и кинетическую энергию электронов, определим их скорость и импульс.
Задача 1. Максимальная кинетическая энергия электронов, вылетающих из рубидия при его освещении ультрафиолетовыми лучами с длиной волны м‚ Дж. Определить работу выхода электронов из рубидия и красную границу фотоэффекта.
Определим работу выхода:
В электронвольтах это
Красная граница фотоэффекта:
Ответ: Дж, или 2,14 эВ, нм.
Задача 2. Серебряную пластинку освещают светом с частотой Гц. Гц. Найти максимальную кинетическую энергию фотоэлектронов.
Работа выхода электронов из серебра равна .
Тогда
Ответ: Дж, или 4 эВ.
Задача 3. Вольфрамовую пластину освещают светом с длиной волны . Найти максимальный импульс вылетающих из пластины электронов.
Тогда скорость электронов равна
А импульс тогда равен (работа выхода для вольфрама )
Ответ: кг м/с.
Задача 4. Пластину освещают монохроматическим излучением с длиной волны . Известно, что наибольшее значение импульса, передаваемого пластине одним фотоэлектроном, равно кгм/с. Определить работу выхода электрона из вещества пластины.
Импульс равен , поэтому
Ответ: Дж, или 3,6 эВ.
Задача 5. Какой скоростью обладают электроны, вырванные с поверхности натрия, при облучении его светом, частота которого Гц? Определить наибольшую длину волны излучения, вызывающего фотоэффект.
Наибольшая длина волны – это красная граница фотоэффекта. Работа выхода для натрия равна . Поэтому
Теперь определим скорость электронов:
Тогда скорость электронов равна
Ответ: нм, м/с.
Задача 6. Максимальная скорость фотоэлектронов, вырванных с поверхности меди при фотоэффекте м /с. Определить частоту света, вызывающего фотоэффект.
Работа выхода для меди равна .
Ответ: Гц.
Задача 7. На металлическую пластину, красная граница фотоэффекта для которой мкм, падает фотон с длиной волны мкм. Во сколько раз скорость фотона больше скорости фотоэлектрона?
Скорость фотоэлектрона равна
Скорость фотона – скорость света. Найдем отношение скоростей:
Ответ: в 642 раза.
easy-physic.ru

