Модуль упругости второго рода – Модуль сдвига (упругости II рода)

alexxlab | 18.11.2019 | 0 | Вопросы и ответы

Модуль сдвига (упругости II рода)

Модулем сдвига (модуль упругости II рода, модуль упругости при сдвиге) – называется физическая величина, характеризующая упругие свойства материалов и их способность сопротивляться сдвигающим деформациям.

Обозначается латинской буквой G,
единица измерения – Паскаль [Па] (гигапаскаль [ГПа])

В сопромате данный модуль используется в расчетах на сдвиг, срез и кручение.

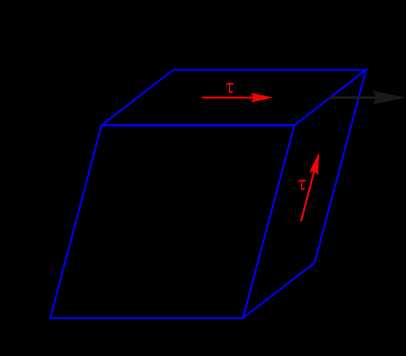
Рис. 1 Деформация сдвига

Теоретически определяется отношением касательных напряжений τ к углу сдвига γ (рис. 1)

где
τ=F/A — касательные напряжения;
γ — угол сдвига;
F — сдвигающая сила;
A — площадь приложения силы F;
ΔS — величина сдвига;
a — размер элемента.

Опытное значение определяется по результатам эксперимента по определению модуля упругости II рода.

Таблица 1. Сравнительные значения модуля для некоторых материалов

Материал	Модуль сдвига G, [ГПа]
Сталь	80
Чугун	45
Медь	40
Титан	40
Алюминий	27
Стекло	26,2

Модуль упругости II рода можно определить с помощью известных модуля Юнга E и коэффициента Пуассона ν:

Модуль сдвига является коэффициентом пропорциональности в законе Гука при сдвиге:

τ=Gγ

При расчетах на кручение, GI_p – жесткость поперечного сечения вала, где I_p — полярный момент инерции поперечного сечения.

Механические характеристики материалов >
Примеры решения задач >

isopromat.ru

ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ ВТОРОГО РОДА

Механика ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ ВТОРОГО РОДА

Количество просмотров публикации ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ ВТОРОГО РОДА – 1078

Наименование параметра	Значение
Тема статьи:	ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ ВТОРОГО РОДА
Рубрика (тематическая категория)	Механика

(МОДУЛЯ СДВИГА)

Физическая постоянная G называется модулем упругости второго рода (модулем сдвига) и является коэффициентом зависимости, выражающей закон Гука при сдвиге t = Gg. Модуль сдвига характеризует жесткость материала при упругой деформации сдвига. Модуль сдвига G в отличие от модуля продольной упругости E и коэффициента поперечной деформации ν является производной величинои̌ и должна быть найден как опытным способом, так и теоретическим. Для изотропных материалов существует зависимость между этими величинами

. (39)

Определить значение модуля G непосредственно из опыта на сдвиг (срез) не представляется возможным. Это связано с тем, что обеспечить дефор­мацию чистого сдвига в опыте, т.е. свободного от побочных деформаций технически трудно. Но, так как кручение стержня круглого поперечного сечения можно представить как чистый сдвиг материала за счёт взаимного поворота поперечных сечений, поэтому опытное определение модуля

G удобнее про­изводить при кручении стержня сплошного круглого, а лучше кольцевого сечения (образца в виде тонкостенной трубки).

Испытаниями установлено, что для материалов, деформирующихся по закону Гука при растяжении или сжатии, закон Гука справедлив и при деформациях сдвига, а значит и кручения. Закон Гука при кручении выражается зависимостью

, (40)

где T – крутящий момент на участке стержня;

l – длина участка стержня;

G – модуль сдвига;

J_p – полярный момент инерции поперечного сечения;

Δφ ‒ абсолютная угловая деформация.

---

---

ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ ВТОРОГО РОДА – понятие и виды. Классификация и особенности категории “ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ ВТОРОГО РОДА” 2015, 2017-2018.

referatwork.ru

Модуль – упругость – второе – род

Модуль – упругость – второе – род

Cтраница 2

Цель опыта состоит в проверке закона Гука при кручении и определении модуля упругости второго рода.  [16]

Когда необходимо1 точно измерить углы закручивания ( например, для определения модуля упругости второго рода, пределов упругости или текучести), то следует применить одно из приспособлений, описанных ниже.  [17]

Модуль сдвига G, известный также как модуль упругости при кручении, модуль упругости второго рода или модуль поперечной упругости, равен напряжению сдвига, деленному на сдвиговую деформацию. Напряжение сдвига, приложенное к изотропному образцу или к металлу с кубическими решетками, изменяет формы образца без изменения его объема. Напряжение сдвига определяется как приложенная сила, деленная на площадь, к которой приложена сила.  [19]

Коэффициент пропорциональности G в формулах (3.4) и (4.4) называется модулем сдвига, или модулем упругости второго рода.  [20]

Величина G, входящая в формулу (3.18), называется модулем упругости при сдвиге или модулем упругости второго рода.  [21]

При рассмотрении основного металла как компонента паяного соединения конструктор обычно учитывает такие свойства металла, как его модуль упругости второго рода, удлинение и стойкость к коррозии; при этом он отбрасывает ряд факторов, в том числе и те, которые имеют существенное значение при пайке. При конструировании паяного соединения необходимо учитывать все свойства основного металла, могущие повлиять на пайку. Такие свойства ряда металлов представлены в табл. 21, где материалы расположены в соответствии с их электродными потенциалами.  [22]

В практике обычных механических испытаний металлов испытания на кручение применяют редко; исключение составляют работы, посвященные исследованию модуля упругости второго рода, который, как известно, проще всего определяется именно при кручении. Казалось бы, что и в области высоких температур испытание на кручение не должно иметь большого применения. Напряженное состояние так называемого чистого сдвига, в котором материал находится при кручении, привлекает внимание исследователей жаропрочных сплавов, и в технической литературе можно отметить довольно большое количество работ, посвященных исследованию процесса кручения при высоких температурах.  [23]

Здесь G – упругая постоянная материала, характеризующая его жесткость при деформации сдвига и называемая модулем сдвига или модулем упругости второго рода. Очевидно, размерность модуля сдвига та же, что и напряжения.  [24]

В отличие от модуля упругости при растяжении ( модуль упругости первого рода) модуль упругости при сдвиге называют модулем упругости второго рода.  [26]

Здесь G – упругая постоянная материала, характеризующая его ж ест кость при деформации сдвига и называемая модулем сдвига или модулем упругости второго рода. Очевидно, размерность модуля сдвига та же, что и напряжения.  [27]

Величины Е – модуль упругости первого рода ( модуль упругости при растяжении), О – модуль упругости при сдвиге ( модуль сдвига, модуль упругости второго рода) и л – коэффициент поперечной деформации ( коэффициент Пуассона) называют упругими постоянными или упругими характеристиками материалов. G имеют размерность напряжения Па ( кгс / см2), ( л – безразмерный коэффициент.  [28]

Отсюда видно, что частота крутильных колебаний труб и балок сплошного кругового сечения зависит только от характера закрепления концов и длины балки, а также от модуля упругости второго рода и плотности материала Qm и не зависит от размеров поперечного сечения.  [29]

Страницы:      1    2    3

www.ngpedia.ru

Модуль сдвига

Модуль сдвига (модуль упругости второго рода) – характеристика упругих свойств изотропных твердых тел в условиях деформации сдвига, один из модулей упругости.

Модуль сдвига основном сказывается греческой буквой μ или латинской буквой G, и измеряется в Па. Характерное значение модуля сдвига твердых тел лежит в области гигапаскалей. Модуль сдвига часто называют модулем упругости второго рода.

Произвольную деформацию изотропного твердого тела можа разбить на две важные составляющие – деформацию растяжения / сжатия, которая связана с изменением линейных размеров тела, и деформацию сдвига, при которой изменяется форма тела.

Физический смысл модуля сдвига определяется уравнением:

где

– Касательное напряжения;

– Сдвиговые усилия;

– Площадь оползня под действием усилия F;

– Деформация сдвига;

– Смещение;

– Начальная длина.

При произвольной деформации, которая описывается тензором деформации , Вклад упругих сил в свободную энергию можно выразить в виде

,

где – символ Кронекера;

K – модуль всестороннего сжатия.

Вторая сумма в данном выражении описывает деформацию растяжения / сжатия, первая сумма – деформацию сдвига. Коэффициент, стоящий перед ней называется модулем сдвига. Модуль сдвига всегда положительный.

Связь с другими модулями упругости

Модуль упругости совпадает со вторым коэффициентом Ламе.

,

где λ – первый из коэффициентов Ламе.

,

где E – модуль Юнга, а ν – коэффициент Пуассона.

Источники

• Ландау Л.Д., Лившиц Е.М. Теоретическая физика. т. VII. Теория упругости.. – Москва: Наука., 1987.

nado.znate.ru

Упругие и прочностные характеристики материалов

Диаграммы напряжений

На сегодняшний день существует несколько методик испытания образцов материалов. При этом одним из самых простых и показательных являются испытания на растяжение (на разрыв), позволяющие определить предел пропорциональности, предел текучести, модуль упругости и другие важные характеристики материала. Так как важнейшей характеристикой напряженного состояния материала является деформация, то определение значения деформации при известных размерах образца и действующих на образец нагрузок позволяет установить вышеуказанные характеристики материала.

Тут может возникнуть вопрос: почему нельзя просто определить сопротивление материала? Дело в том, что абсолютно упругие материалы, разрушающиеся только после преодоления некоторого предела – сопротивления, существуют только в теории. В реальности большинство материалов обладают как упругими так и пластическими свойствами, что это за свойства, рассмотрим ниже на примере металлов.

Испытания металлов на растяжение проводятся согласно ГОСТ 1497-84. Для этого используются стандартные образцы. Методика испытаний выглядит приблизительно так: к образцу прикладывается статическая нагрузка, определяется абсолютное удлинение образца Δl, затем нагрузка увеличивается на некоторое шаговое значение и снова определяется абсолютное удлинение образца и так далее. На основании полученных данных строится график зависимости удлинений от нагрузки. Этот график называется диаграммой напряжений.

Рисунок 318.1. Диаграмма напряжений для стального образца.

На данной диаграмме мы видим 5 характерных точек:

1. Предел пропорциональности Р_п (точка А)

Нормальные напряжения в поперечном сечении образца при достижении предела пропорциональности будут равны:

σ_п = Р_п/F_o (318.2.1)

Предел пропорциональности ограничивает участок упругих деформаций на диаграмме. На этом участке деформации прямо пропорциональны напряжениям, что выражается законом Гука:

Р_п = kΔl (318.2.2)

где k – коэффициент жесткости:

k = EF/l (318.2.3)

где l – длина образца, F – площадь сечения, Е – модуль Юнга.

Модули упругости

Главными характеристиками упругих свойств материалов являются модуль Юнга Е (модуль упругости первого рода, модуль упругости при растяжении), модуль упругости второго рода G (модуль упругости при сдвиге) и коэффициент Пуассона μ (коэффициент поперечной деформации).

Модуль Юнга Е показывает отношение нормальных напряжений к относительным деформациям в пределах пропорциональности

Модуль Юнга также определяется опытным путем при испытании стандарт­ных образцов на растяжение. Так как нормальные напряжения в материале равны силе, деленной на начальную площадь сечения:

σ = Р/F_о (318.3.1), (317.2)

а относительное удлинение ε – отношению абсолютной деформации к начальной длине

ε_пр = Δl/l_o (318.3.2)

то модуль Юнга согласно закону Гука можно выразить так

Е = σ/ε_пр = Pl_o/F_oΔl = tgα (318.3.3)

Рисунок 318.2. Диаграммы напряжений некоторых сплавов металлов

Коэффициент Пуассона μ показывает отношение поперечных деформаций к продольным

Под воздействием нагрузок не только увеличивается длина образца, но и уменьшается площадь рассматриваемого поперечного сечения (если предположить, что объем материала в области упругих деформаций остается постоянным, то значит увеличение длины образца приводит к уменьшению площади сечения). Для образца, имеющего круглое сечение, изменение площади сечения можно выразить так:

ε_поп = Δd/d_o (318.3.4)

Тогда коэффициент Пуассона можно выразить следующим уравнением:

μ = ε_поп/ε_пр (318.3.5)

Модуль сдвига G показывает отношение касательных напряжений т к углу сдвига

Модуль сдвига G может быть определен опытным путем при испытании образцов на кручение.

При угловых деформациях рассматриваемое сечение перемещается не линейно, а под некоторым углом – углом сдвига γ к начальному сечению. Так как касательные напряжения равны силе, деленной на площадь в плоскости которой действует сила:

т = Р/F (318.3.6)

а тангенс угла наклона можно выразить отношением абсолютной деформации Δl к расстоянию h от места фиксации абсолютной деформации до точки, относительно которой осуществлялся поворот:

tgγ = Δl/h (318.3.7)

то при малых значениях угла сдвига модуль сдвига можно выразить следующим уравнением:

G = т/γ = Ph/FΔl (318.3.8)

Модуль Юнга, модуль сдвига и коэффициент Пуассона связаны между собой следующим отношением:

Е = 2(1 + μ)G (318.3.9)

Значения постоянных Е, G и µ приводятся в таблице 318.1

Таблица 318.1. Ориентировочные значения упругих характеристик некоторых материалов

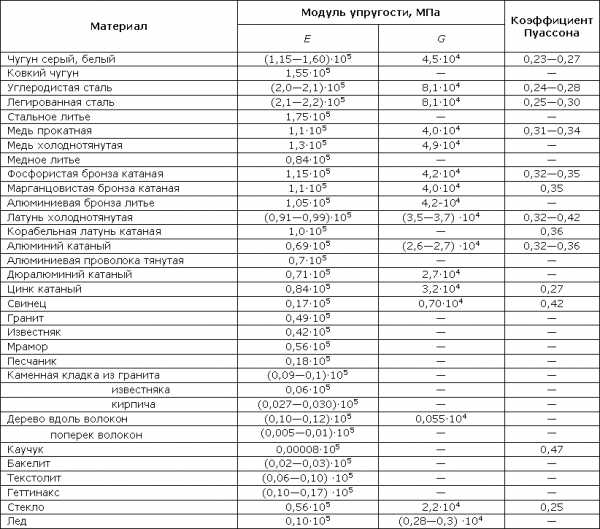
Примечание: Модули упругости являются постоянными величинами, однако технологии изготовления различных строительных материалов меняются и более точные значения модулей упругости следует уточнять по действующим в настоящий момент нормативным документам. Модули упругости бетона зависят от класса бетона и потому здесь не приводятся.

Упругие характеристики определяются для различных материалов в пределах упругих деформаций, ограниченных на диаграмме напряжений точкой А. Между тем на диаграмме напряжений можно выделить еще несколько точек:

2. Предел упругости Р_у

Нормальные напряжения в поперечном сечении образца при достижении предела упругости будут равны:

σ_у = Р_у/F_o (318.2.4)

Предел упругости ограничивает участок на котором появляющиеся пластические деформации находятся в пределах некоторой малой величины, нормированной техническими условиями (например 0,001%; 0,01% и т. д.). Иногда предел упругости обозначается соответственно допуску σ_0.001, σ_0.01 и т.д.

3. Предел текучести Р_т 

σ_т = Р_т/F_o (318.2.5)

Ограничивает участок диаграммы на котором деформация увеличивается без значительного увеличения нагрузки (состояние текучести). При этом по всему объему образца происходит частичный разрыв внутренних связей, что и проводит к значительным пластическим деформациям. Материал образца полностью не разрушается, но его начальные геометрические размеры претерпевают необратимые изменения. На отшлифованной поверхности образцов наблюдаются фигуры текучести – линии сдвигов (открытые профессором В. Д. Черновым). Для различных металлов углы наклона этих линий различны, но находятся в пределах 40-50^о. При этом часть накопленной потенциальной энергии необратимо расходуется на частичный разрыв внутренних связей. При испытании на растяжение принято различать верхний и нижний пределы текучести – соответственно наибольшее и наименьшее из напряжений, при которых возрастает пластическая (остаточная) деформация при почти постоянной величине действующей нагрузки.

На диаграммах напряжений отмечен нижний предел текучести. Именно этот предел для большинства материалов принимается за нормативное сопротивление материала.

Некоторые материалы не имеют выраженной площадки текучести. Для них за условный предел текучести σ_0.2 принимается напряжение, при котором остаточное удлинение образца достигает значения ε ≈0,2%.

4. Предел прочности Р_макс (временное сопротивление)

Нормальные напряжения в поперечном сечении образца при достижении предела прочности будут равны:

σ_в = Р_макс/F_o (318.2.6)

После преодоления верхнего предела текучести (на диаграммах напряжения не показан) материал снова начинает сопротивляться нагрузкам. При максимальном усилии Р_макс начинается полное разрушение внутренних связей материала. При этом пластические деформации концентрируются в одном месте, образуя в образце так называемую шейку.

Напряжение при максимальной нагрузке называется пределом прочности или временным сопротивлением материала.

В таблицах 318.2 – 318.5 приведены ориентировочные величины пределов прочности для некоторых материалов:

Таблица 318.2 Ориентировочные пределы прочности на сжатие (временные сопротивления) некоторых строительных материалов.

Примечание: Для металлов  и сплавов значение пределов прочности следует определять согласно нормативных документов. Значение временных сопротивлений для некоторых марок стали можно посмотреть здесь.

Таблица 318.3. Ориентировочные пределы прочности (временные сопротивления) для некоторых пластмасс

 

Таблица 318.4. Ориентировочные пределы прочности для некоторых волокон

 

Таблица 318.5. Ориентировочные пределы прочности для некоторых древесных пород

 

5. Разрушение материала Р_р

Если посмотреть на диаграмму напряжений, то создается впечатление, что разрушение материала наступает при уменьшении нагрузки. Такое впечатление создается потому, что в результате образования “шейки” значительно изменяется площадь сечения образца в районе “шейки”. Если построить диаграмму напряжений для образца из малоуглеродистой стали в зависимости от изменяющейся площади сечения, то будет видно, что напряжения в рассматриваемом сечении увеличиваются до некоторого предела:

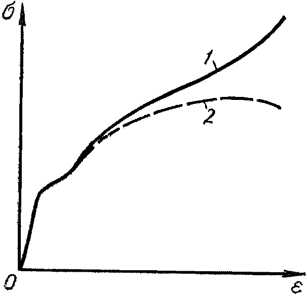
Рисунок 318.3. Диаграмма напряжений: 2 – по отношению к начальной площади поперечного сечения, 1 – по отношению к изменяющейся площади сечения в районе шейки.

Тем не менее более правильным является рассмотрение прочностных характеристик материала по отношению к площади первоначального сечения, так как расчетами на прочность изменение первоначальной геометрической формы редко предусматривается.

Одной из механических характеристик металлов является относительное изменение ψ площади поперечного сечения в районе шейки, выражаемое в процентах:

ψ = 100(F_o – F)/F_o (318.2.7)

где F_o – начальная площадь поперечного сечения образца (площадь поперечного сечения до деформации), F – площадь поперечного сечения в районе “шейки”. Чем больше значение ψ, тем более ярко выражены пластические свойства материала. Чем меньше значение ψ, тем больше хрупкость материала.

Если сложить разорванные части образца и измерить его удлинение, то выяснится, что оно меньше удлинения на диаграмме (на длину отрезка NL), так как после разрыва упругие деформации исчезают и остаются только пластические. Величина пластической деформации (удлинения) также является важной характеристикой механических свойств материала.

За пределами упругости, вплоть до разрушения, полная деформация состоит из упругой и пластической составляющих. Если довести материал до напряжений, превышающих предел текучести (на рис. 318.1 некоторая точка между пределом текучести и пределом прочности), и затем разгрузить его, то в образце останутся пластические деформации, но при повторном загружении через некоторое время предел упругости станет выше, так как в данном случае изменение геометрической формы образца в результате пластических деформаций становится как бы результатом действия внутренних связей, а изменившаяся геометрическая форма, становится начальной. Этот процесс загрузки и разгрузки материала можно повторять несколько раз, при этом прочностные свойства материала будут увеличиваться:

Рисунок 318.4. Диаграмма напряжений при наклепе (наклонные прямые соответствуют разгрузкам и повторным загружениям)

Такое изменение прочностных свойств материала, получаемое путем повторяющихся статических загружений, называется наклепом. Тем не менее при повышении прочности металла путем наклепа уменьшаются его пластические свойства, а хрупкость увеличивается, поэтому полезным как правило считается относительно небольшой наклеп.

Работа деформации

Прочность материала тем выше, чем больше внутренние силы взаимодействия частиц материала. Поэтому величина сопротивления удлинению, отнесенная к единице объема материала, может служить характеристикой его прочности. В этом случае предел прочности не является исчерпывающей характеристикой прочностных свойств данного материала, так как он характеризует только поперечные сечения. При разрыве разрушаются взаимосвязи по всей площади сечения, а при сдвигах, которые происходят при всякой пластической деформации, разрушаются только местные взаимосвязи. На разрушение этих связей затрачивается определенная работа внутренних сил взаимодействия, которая равна работе внешних сил, затрачиваемой на перемещения:

А = РΔl/2 (318.4.1)

где 1/2 – результат статического действия нагрузки, возрастающей от 0 до Р в момент ее приложения (среднее значение (0 + Р)/2)

При упругой деформации работа сил определяется площадью треугольника ОАВ (см. рис. 318.1). Полная работа, затраченная на деформацию образца и его разрушение:

А = ηР_максΔl_макс (318.4.2)

где η – коэффициент полноты диаграммы, равный отношению площади всей диаграммы, ограниченной кривой АМ и прямыми ОА, MN и ON, к площади прямоугольника со сторонами 0Р_макс (по оси Р) и Δl_макс (пунктир на рис. 318.1). При этом надо вычесть работу, определяемую площадью треугольника MNL (относящуюся к упругим деформациям).

Работа, затрачиваемая на пластические деформации и разрушение образца, является одной из важных характеристик материала, определяющих степень его хрупкости.

Деформация сжатия

Деформации сжатия подобны деформациям растяжения: сначала происходят упругие деформации, к которым за пределом упругости добавляются пластические. Характер деформации и разрушения при сжатии показан на рис. 318.5:

Рисунок 318.5

а – для пластических материалов; б – для хрупких материалов ; в – для дерева вдоль волокон, г – для дерева поперек волокон.

Испытания на сжатие менее удобны для определения механических свойств пластических материалов из-за трудности фиксирования момента разрушения. Методы механических испытаний металлов регламентируются ГОСТ 25.503-97. При испытании на сжатие формы образца и его размеры могут быть различными. Ориентировочные значения пределов прочности для различных материалов приведены в таблицах 318.2 – 318.5.

Если материал находится под нагрузкой при постоянном напряжении, то к практически мгновенной упругой деформации постепенно прибавляется добавочная упругая деформация. При полном снятии нагрузки упругая деформация уменьшается пропорционально уменьшающимся напряжениям, а добавочная упругая деформация исчезает медленнее.

Образовавшаяся добавочная упругая деформация при постоянном напряжении, которая исчезает не сразу после разгрузки, называется упругим последействием.

Влияние температуры на изменение механических свойств материалов

Твердое состояние – не единственное агрегатное состояние вещества. Твердые тела существуют только в определенном интервале температур и давлений. Повышение температуры приводит к фазовому переходу из твердого состояния в жидкое, а сам процесс перехода называется плавлением. Температуры плавления, как и другие физические характеристики материалов, зависят от множества факторов и также определяются опытным путем.

Таблица 318.6. Температуры плавления некоторых веществ

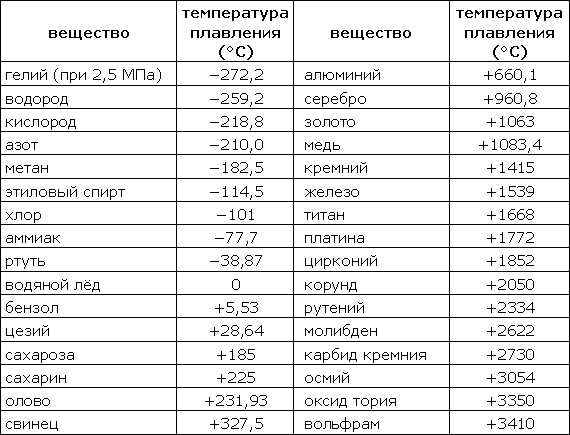
Примечание: В таблице приведены температуры плавления при атмосферном давлении (кроме гелия).

Упругие и прочностные характеристики материалов, приведенные в таблицах 318.1-318.5, определяются как правило при температуре +20^оС. ГОСТом 25.503-97 допускается проводить испытания металлических образцов в диапазоне температур от +10 до +35^оС.

При изменении температуры изменяется потенциальная энергия тела, а значит, изменяется и значение внутренних сил взаимодействия. Поэтому механические свойства материалов зависят не только от абсолютной величины температуры, но и от продолжительности ее действия. Для большинства материалов при нагреве прочностные характеристики (σ_п, σ_т и σ_в) уменьшаются, при этом пластичность материала увеличивается. При снижении температуры прочностные характеристики увеличиваются, но при этом повышается хрупкость. При нагреве уменьшается модуль Юнга Е, а коэффициент Пуассона увеличивается. При снижении температуры происходит обратный процесс.

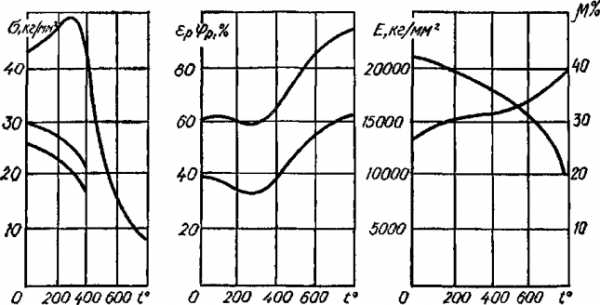
Рисунок 318.6. Влияние температуры на механические характеристики углеродистой стали.

При нагревании цветных металлов и сплавов из них прочность их сразу падает и при температуре, близкой к 600° С, практически теряется. Исключение составляет алюмотермический хром, предел прочности которого с увеличением температуры увеличивается и при температуре равной 1100° С достигает максимума σ_в1100 = 2σ_в20.

Характеристики пластичности меди, медных сплавов и магния с ростом температуры уменьшаются, а алюминия – увеличиваются. При нагреве пластмасс и резины их предел прочности резко снижается, а при охлаждении эти материалы становятся очень хрупкими.

Влияние радиоактивного облучения на изменение механических свойств

Радиоактивное облучение по-разному влияет на различные материалы. Облучение материалов неорганического происхождения по своему влиянию на механические характеристики и характеристики пластичности подобно понижению температуры: с увеличением дозы радиоактивного облучения увеличивается предел прочности и особенно предел текучести, а характеристики пластичности снижаются.

Облучение пластмасс также приводит к увеличению хрупкости, причем на предел прочности этих материалов облучение оказывает различное влияние: на некоторых пластмассах оно почти не сказывается (полиэтилен), у других вызывает значительное понижение предела прочности (катамен), а в третьих – повышение предела прочности (селектрон).

doctorlom.com

46.Основные механические свойства. Модуль сдвига

46.Основные механические свойства. Модуль сдвига

Механические свойства материалов,

 совокупность показателей, характеризующих сопротивление материала воз действующей на него нагрузке, его способность деформироваться при этом, а также особенности его поведения в процессе разрушения. В соответствии с этим М. с. м. измеряют напряжениями (обычно в кгс/мм² или Мн/м²), деформациями (в %), удельной работой деформации и разрушения (обычно в кгс×м/см² или Мдж/м²), скоростью развития процесса разрушения при статической или повторной нагрузке (чаще всего в мм за 1 сек или за 1000 циклов повторений нагрузки, мм/кцикл). М. с. м. определяются при механических испытаниях образцов различной формы.

В общем случае материалы в конструкциях могут подвергаться самым различным по характеру нагрузкам (рис. 1): работать нарастяжение, сжатие, изгиб, кручение, срез и т. д. или подвергаться совместному действию нескольких видов нагрузки, например растяжению и изгибу. Также разнообразны условия эксплуатации материалов и по температуре, окружающей среде, скорости приложения нагрузки и закону её изменения во времени. В соответствии с этим имеется много показателей М. с. м. и много методов механических испытаний. Для металлов и конструкционных пластмасс наиболее распространены испытания на растяжение, твёрдость, ударный изгиб; хрупкие конструкционные материалы (например, керамику, металлокерамику) часто испытывают на сжатие и статический изгиб; механические свойства композиционных материалов важно оценивать, кроме того, при испытаниях на сдвиг.

Диаграмма деформации. Приложенная к образцу нагрузка вызывает его деформацию. Соотношения между нагрузкой и деформацией описываются т. н. диаграммой деформации (рис. 2). Вначале деформация образца (при растяжении — приращение длины Dl ) пропорциональна возрастающей нагрузке Р, затем в точке n эта пропорциональность нарушается, однако для увеличения деформации необходимо дальнейшее повышение нагрузки Р; при Dl > Dl_в деформация развивается без приложения усилия извне, при постепенно падающей нагрузке. Вид диаграммы деформации не меняется, если по оси ординат откладывать напряжение

а по оси абсцисс — относительное удлинение

(F₀ и l₀ — соответственно начальная площадь поперечного сечения и расчётная длина образца).

Сопротивление материалов измеряется напряжениями, характеризующими нагрузку, приходящуюся на единицу площади поперечного сечения образца

в кгс/мм². Напряжение

при котором нарушается пропорциональный нагрузке рост деформации, называется пределом пропорциональности. При нагрузкеР < Р_n разгрузка образца приводит к исчезновению деформации, возникшей в нём под действием приложенного усилия; такая деформация называется упругой. Небольшое превышение нагрузки относительно Р_n может не изменить характера деформации — она по-прежнему сохранит упругий характер. Наибольшая нагрузка, которую выдерживает образец без появления остаточной пластической деформации при разгрузке, определяет предел упругости материала:

У конструкционных неметаллический материалов (пластмассы, резины) приложенная нагрузка может вызвать упругую, высокоэластическую и остаточную деформации. В отличие от упругой, высокоэластическая деформация исчезает не сразу после разгрузки, а с течением времени. Высокопрочные армированные полимеры (стеклопластики, углепластики и др.) разрушаются при удлинении 1—3%. На последних стадиях нагружения у некоторых армированных полимеров появляется высокоэластическая деформация. Высокоэластический модуль ниже модуля упругости, поэтому диаграмма деформации в этом случае имеет тенденцию отклоняться к оси абсцисс.

Упругие свойства. В упругой области напряжение и деформация связаны коэффициентом пропорциональности. При растяжении s = Еd, где Е — т. н. модуль нормальной упругости, численно равный тангенсу угла наклона прямолинейного участка кривой s = s(d) к оси деформации (рис. 2). При испытании на растяжение цилиндрического или плоского образца одноосному (s₁>0; (s₂ = s₃ = 0) напряжённому состоянию соответствует трёхосное деформированное состояние (приращение длины в направлении действия приложенных сил и уменьшение линейных размеров в двух других взаимно перпендикулярных направлениях): d₁>0; d₂ = d₃ < 0. Соотношение между поперечной и продольной деформацией (коэффициент Пуассона)

в пределах упругости для основных конструкционных материалов колеблется в довольно узких пределах (0,27—0,3 для сталей, 0,3—0,33 для алюминиевых сплавов). Коэффициент Пуассона является одной из основных расчётных характеристик. Зная m и Е, можно расчётным путём определить и модуль сдвига

и модуль объёмной упругости

Для определения Е, G, и m пользуются тензометрами.

Сопротивление пластической деформации. При нагрузках Р > Р_в наряду со всё возрастающей упругой деформацией появляется заметная необратимая, не исчезающая при разгрузке пластическая деформация. Напряжение, при котором остаточная относительная деформация (при растяжении — удлинение) достигает заданной величины (по ГОСТ — 0,2 %), называется условным пределом текучести и обозначается

Практически точность современных методов испытания такова, что s_п и s_е определяют с заданными допусками соответственно на отклонение от закона пропорциональности [увеличение ctg(90 — a) на 25—50 %] и на величину остаточной деформации (0,003—0,05 %) и говорят об условных пределах пропорциональности и упругости. Кривая растяжения конструкционных металлов может иметь максимум (точка в на рис. 2) или обрываться при достижении наибольшей нагрузки Р_в’. Отношение

характеризует временное сопротивление (предел прочности) материала. При наличии максимума на кривой растяжения в области нагрузок, лежащих на кривой левее в, образец деформируется равномерно по всей расчётной длине l₀, постепенно уменьшаясь в диаметре, но сохраняя начальную цилиндрическую или призматическую форму. При пластической деформации металлы упрочняются, поэтому, несмотря на уменьшение сечения образца, для дальнейшей деформации требуется прикладывать всё возрастающую нагрузку. s_в, как и условные s_0,2, s_n и s_е, характеризует сопротивление металлов пластической деформации. На участке диаграммы деформации правее в форма растягиваемого образца изменяется: наступает период сосредоточенной деформации, выражающейся в появлении “шейки”. Уменьшение сечения в шейке “обгоняет” упрочнение металлов, что и обусловливает падение внешней нагрузки на участке Р_в — P_k.

У многих конструкционных материалов сопротивление пластической деформации в упруго-пластической области при растяжении и сжатии практически одинаково. Для некоторых металлов и сплавов (например, магниевые сплавы, высокопрочные стали) характерны заметные различия по этой характеристике при растяжении и сжатии. Сопротивление пластической деформации особенно часто (при контроле качества продукции, стандартности режимов термической обработки и в др. случаях) оценивается по результатам испытаний на твёрдость путём вдавливания твёрдого наконечника в форме шарика (твёрдость по Бринеллю или Роквеллу), конуса (твёрдость по Роквеллу) или пирамиды (твёрдость по Виккерсу). Испытания на твёрдость не требуют нарушения целостности детали и потому являются самым массовым средством контроля механических свойств. Твёрдость по Бринеллю (HB) при вдавливании шарика диаметром D под нагрузкой Р характеризует среднее сжимающее напряжение, условно вычисляемое на единицу поверхности шарового отпечатка диаметром d:

Характеристики пластичности. Пластичность при растяжении конструкционных материалов оценивается удлинением

или сужением

при сжатии — укорочением

(где h₀ и h_k — начальная и конечная высота образца), при кручении — предельным углом закручивания рабочей части образца Q,рад или относительным сдвигом g = Qr (где r — радиус образца). Конечная ордината диаграммы деформации (точка k на рис. 2) характеризует сопротивление разрушению металла S_k, которое определяется

(F_k — фактическая площадь в месте разрыва).

Модуль сдвига-величина, характеризующая деформацию сдвига.  Модуль сдвига равен отношению касательного напряжения к величине угла сдвига.В начальной части диаграмма сдвига (на рисунке) линейная, т.е. угол сдвига  пропорционален касательному напряжению . Закон пропорциональности, называемый законом Гука при сдвиге, может быть записан:

 где коэффициент пропорциональности G называется модулем сдвига сдвига или модулем упругости 2-го рода. Он характеризует сопротивление материала упругим деформациям и является его упругой постоянной. 

studfiles.net

Определение модуля упругости I рода

Лабораторная работа № 3

Цель работы – опытная проверка справедливости закона Гука при растяжении и определение модуля упругости I рода.

Основные сведения

Экспериментальные исследования на растяжение (сжатие) стандартных образцов показывают, что абсолютные удлинения, получающиеся в начальной стадии растяжения (сжатия), остаются прямопропорциональными растягивающей (сжимающей) силе и зависят от первоначальной длины образца l₀ и площади поперечного сечения А:

Величина ЕА называется жесткостью стержня при растяжении и сжатии.

Коэффициент Е носит название модуля упругости I рода (используют также название «модуль Юнга» или «модуль продольной упругости«) и является основной физической постоянной, характеризующей упругие свойства (жесткость) материала при линейной деформации.

Чем больше значение Е, тем меньше при прочих равных условиях продольная деформация. Из формулы (3.1) следует, что модуль упругости

имеет размерность, что и напряжение, — в [Па] или кратных единицах — [кПа], [МПа], а для экспериментального определения его потребуется замерить величины: F, A, l, Δl.

Испытания проводятся на испытательной машине типа Р-5.

Испытывается образец квадратного сечения. Влияние возможной неточности изготовления образца на центральное приложение нагрузки устраняется за счет установки двух тензометров на противоположных продольных гранях образца.

В качестве тензодатчиков используются тензометры Аистова. Среднее удлинение, получаемое из  показания двух тензодатчиков, принимают равным удлинению оси образца.

Диапазон нагрузок зависит от состояния и класса точности установки и предела пропорциональности материала образца. Минимальная загрузка зависит от жесткости самой установки (выборка лифтов, затяжка клиньев и т.п.) и определяется опытным путем. Максимальная загрузка рассчитывается по формуле

Зная диапазон нагрузок, определяют количество и величину ступеней нагружения ΔF.

Порядок выполнения и обработка результатов

Перед началом выполнения лабораторной работы необходимо ознакомиться с устройством машины Р-5 и рычажным тензометром Аистова.

Образец с закрепленными на нем тензодатчиками устанавливают в захватах машины и приводят в рабочее состояние.

Производят предварительное (минимальное) нагружение образца начальной нагрузкой и при этой нагрузке снимают показания приборов.

Далее нагрузку увеличивают плавно равными ступенями ΔF (5-6 ступеней) и производят соответственно снятие показаний с тензометров.

Доводить нагрузку до очередного значения нужно плавно, не «перескакивая» нужное значение. После осуществления загрузки последней ступени следует разгрузить образец до нагрузки, соответствующей минимальной.

При очередной ступени загрузки результаты опыта заносят в таблицу. Каждому приращению ΔF будет соответствовать приращение ΔП_1i и ΔП_2i, по которым подсчитывают среднее значение

ΔП_ср = (ΔП_1i + ΔП_2i)/2.

Истинное значение удлинения образца находим как

Δl_срi = ΔП_срiК,

где К = 10^-3 мм – цена 1 деления тензометра Аистова.

По значениям нагрузки F и суммарному нарастанию удлинения оси образца строят график диаграммы растяжения образца в координатах F : Δl, по которому проверяют линейность зависимости (справедливость закона Гука).

Для среднего приращения нагрузки (ступени нагружения) определяют среднюю продольную абсолютную деформацию

где П – число ступеней нагружения.

Модуль продольной упругости

где l – база тензометра Аистова.

Полученное в опыте значение модуля упругости Е_оп сравнивают с табличным Е_Т = 2·10¹¹ Па и определяют погрешность опыта.

В заключение работы делают выводы.

Контрольные вопросы

1. Как формулируется закон Гука для линейного напряженного состояния? Как ограничить верхнюю максимальную нагрузку?
2. Каковы границы применения закона Гука?
3. Что характеризует модуль упругости Е, от чего он зависит и какова его размерность?
4. По какому геометрическому выражению с использованием диаграммы напряжений можно определить Е?
5. Почему при определении деформаций растянутого образца используют два тензометра?

Определение коэффициента Пуассона >
Другие лабораторные работы >

isopromat.ru