Модуль упругости юнга – Модуль упругости (Модуль Юнга): понятие, формулы, как определить

alexxlab | 16.08.2016 | 0 | Вопросы и ответы

Содержание

Модуль Юнга — WiKi

Мо́дуль Ю́нга (модуль продольной упругости) — физическая величина, характеризующая способность материала сопротивляться растяжению, сжатию при упругой деформации^[1]. Обозначается большой буквой Е.

Модуль Юнга
E{\displaystyle E}
Размерность	L⁻¹MT⁻²
Единицы измерения
СИ	Па
СГС	дин·см^-2

Назван в честь английского физика XIX века Томаса Юнга.

В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал деформируемой среды и процесса.

В Международной системе единиц (СИ) измеряется в ньютонах на квадратный метр или в паскалях. Является одним из модулей упругости.

Модуль Юнга рассчитывается следующим образом:

E=F/SΔl/l=FlSΔl,{\displaystyle E={\frac {F/S}{\Delta l/l}}={\frac {Fl}{S\Delta l}},}

где:

F{\displaystyle F} — нормальная составляющая силы,
S{\displaystyle S} — площадь поверхности, по которой распределено действие силы,
l{\displaystyle l} — длина деформируемого стержня,
Δl{\displaystyle \Delta l} — модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина l{\displaystyle l}).

Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне:

c=Eρ,{\displaystyle c={\sqrt {\frac {E}{\rho }}},}

где ρ{\displaystyle \rho } — плотность вещества.

Содержание

Температурная зависимость модуля упругости простых кристаллических материалов объясняется исходя из того, что модуль упругости M(T){\displaystyle M(T)} определяется как вторая производная от внутренней энергии W(T){\displaystyle W(T)} по соответствующей деформации E(T)=d2W(T)dε2{\displaystyle E(T)={d^{2}W(T) \over d\varepsilon ^{2}}} . Поэтому при температурах T≤ΘD{\displaystyle T\leq \Theta _{D}} (ΘD{\displaystyle \Theta _{D}} — температура Дебая) температурная зависимость модуля упругости определяется простым соотношением

M(T)=M0−M1T−M2T2{\displaystyle M(T)=M_{0}-M_{1}T-M_{2}T^{2}}

где M0{\displaystyle M_{0}} — адиабатический модуль упругости идеального кристалла при T⟶0K{\displaystyle T\longrightarrow 0K} ; M1T{\displaystyle M_{1}T} — дефект модуля, обусловленный тепловыми фононами; M2T2{\displaystyle M_{2}T^{2}} — дефект модуля, обусловленный тепловым движением электронов проводимости^[2]

ru-wiki.org

Модуль упругости (модуль Юнга) | Мир сварки

Модуль упругости

Модуль упругости (модуль Юнга) E – характеризует сопротивление материала растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси; определяется как отношение напряжения к удлинению. Часто модуль Юнга называют просто модулем упругости.

1 кгс/мм² = 10^-6 кгс/м² = 9,8·10⁶ Н/м² = 9,8·10⁷ дин/см² = 9,81·10⁶ Па = 9,81 МПа

Модуль упругости (модуль Юнга)
Материал	E
Материал	кгс/мм²	10⁷ Н/м²	МПа
Металлы
Алюминий	6300-7500	6180-7360	61800-73600
Алюминий отожженный	6980	6850	68500
Бериллий	30050	29500	295000
Бронза	10600	10400	104000
Бронза алюминиевая, литье	10500	10300	103000
Бронза фосфористая катаная	11520	11300	113000
Ванадий	13500	13250	132500
Ванадий отожженный	15080	14800	148000
Висмут	3200	3140	31400
Висмут литой	3250	3190	31900
Вольфрам	38100	37400	374000
Вольфрам отожженный	38800-40800	34200-40000	342000-400000
Гафний	14150	13900	139000
Дюралюминий	7000	6870	68700
Дюралюминий катаный	7140	7000	70000
Железо кованое	20000-22000	19620-21580	196200-215800
Железо литое	10200-13250	10000-13000	100000-130000
Золото	7000-8500	6870-8340	68700-83400
Золото отожженное	8200	8060	80600
Инвар	14000	13730	137300
Индий	5300	5200	52000
Иридий	5300	5200	52000
Кадмий	5300	5200	52000
Кадмий литой	5090	4990	49900
Кобальт отожженный	19980-21000	19600-20600	196000-206000
Константан	16600	16300	163000
Латунь	8000-10000	7850-9810	78500-98100
Латунь корабельная катаная	10000	9800	98000
Латунь холоднотянутая	9100-9890	8900-9700	89000-97000
Магний	4360	4280	42800
Манганин	12600	12360	123600
Медь	13120	12870	128700
Медь деформированная	11420	11200	112000
Медь литая	8360	8200	82000
Медь прокатанная	11000	10800	108000
Медь холоднотянутая	12950	12700	127000
Молибден	29150	28600	286000
Нейзильбер	11000	10790	107900
Никель	20000-22000	19620-21580	196200-215800
Никель отожженный	20600	20200	202000
Ниобий	9080	8910	89100
Олово	4000-5400	3920-5300	39200-53000
Олово литое	4140-5980	4060-5860	40600-58600
Осмий	56570	55500	555000
Палладий	10000-14000	9810-13730	98100-137300
Палладий литой	11520	11300	113000
Платина	17230	16900	169000
Платина отожженная	14980	14700	147000
Родий отожженный	28030	27500	275000
Рутений отожженный	43000	42200	422000
Свинец	1600	1570	15700
Свинец литой	1650	1620	16200
Серебро	8430	8270	82700
Серебро отожженное	8200	8050	80500
Сталь инструментальная	21000-22000	20600-21580	206000-215800
Сталь легированная	21000	20600	206000
Сталь специальная	22000-24000	21580-23540	215800-235400
Сталь углеродистая	19880-20900	19500-20500	195000-205000
Стальное литье	17330	17000	170000
Тантал	19000	18640	186400
Тантал отожженный	18960	18600	186000
Титан	11000	10800	108000
Хром	25000	24500	245000
Цинк	8000-10000	7850-9810	78500-98100
Цинк катаный	8360	8200	82000
Цинк литой	12950	12700	127000
Цирконий	8950	8780	87800
Чугун	7500-8500	7360-8340	73600-83400
Чугун белый, серый	11520-11830	11300-11600	113000-116000
Чугун ковкий	15290	15000	150000
Пластмассы
Плексиглас	535	525	5250
Целлулоид	173-194	170-190	1700-1900
Стекло органическое	300	295	2950
Резины
Каучук	0,80	0,79	7,9
Резина мягкая вулканизированная	0,15-0,51	0,15-0,50	1,5-5,0
Дерево
Бамбук	2000	1960	19600
Береза	1500	1470	14700
Бук	1600	1630	16300
Дуб	1600	1630	16300
Ель	900	880	8800
Железное дерево	2400	2350	32500
Сосна	900	880	8800
Минералы
Кварц	6800	6670	66700
Различные материалы
Бетон	1530-4100	1500-4000	15000-40000
Гранит	3570-5100	3500-5000	35000-50000
Известняк плотный	3570	3500	35000
Кварцевая нить (плавленая)	7440	7300	73000
Кетгут	300	295	2950
Лед (при -2 °С)	300	295	2950
Мрамор	3570-5100	3500-5000	35000-50000
Стекло	5000-7950	4900-7800	49000-78000
Стекло крон	7200	7060	70600
Стекло флинт	5500	5400	70600

Литература

Краткий физико-технический справочник. Т.1 / Под общ. ред. К.П. Яковлева. М.: ФИЗМАТГИЗ. 1960. – 446 с.
Справочник по сварке цветных металлов / С.М. Гуревич. Киев.: Наукова думка. 1981. 680 с.
Справочник по элементарной физике / Н.Н. Кошкин, М.Г. Ширкевич. М., Наука. 1976. 256 с.
Таблицы физических величин. Справочник / Под ред. И.К. Кикоина. М., Атомиздат. 1976, 1008 с.

weldworld.ru

Модуль Юнга (упругости) для стали и других материалов: определение, смысл

Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.

Модуль Юнга

Основные сведения

Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м² или в Па.

Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (10¹²Па)

Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.

Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.

График теста на растяжение

E- это частное от деления нормальных напряжений σ на относительное удлинение ε.

E=α/ε

Закон Гука также можно сформулировать и с использованием модуля Юнга.

Физический смысл модуля Юнга

Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.

Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.

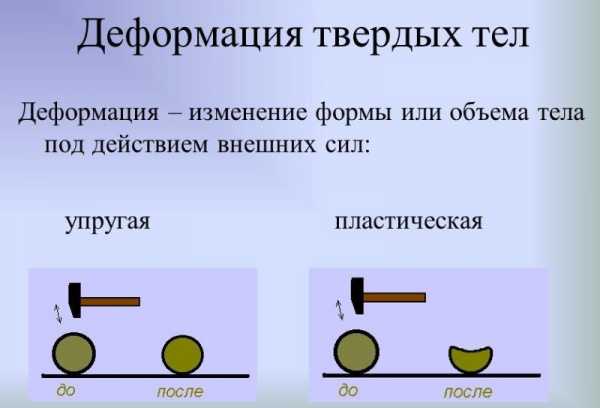
Виды деформации

Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.

В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:

Δl = α * (lF) / S

Величину, обратную α, и называют модулем Юнга:

1/α = E

Относительная деформация:

ε = (Δl) / l = α * (F/S)

Отношение растягивающей силы F к S называют упругим напряжением σ:

ε=α σ

Закон Гука, записанный с использованием модуля Юнга, выглядит так:

σ = ε/α = E ε

Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.

В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.

Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l

Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.

Значения модуля юнга для некоторых материалов

В таблице показаны значения E ряда распространенных веществ.

Материал	модуль Юнга E, ГПа
Алюминий	70
Бронза	75-125
Вольфрам	350
Графен	1000
Латунь	95
Лёд	3
Медь	110
Свинец	18
Серебро	80
Серый чугун	110
Сталь	200/210
Стекло	70

Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.

Предел прочности материала

Это предел возникающего напряжения, после которого образец начинает разрушаться.

Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.

Инструмент для определения предела прочности

Кроме того, существуют пределы прочности на сжатие материала и на растяжение. Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления. В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.

Допускаемое механическое напряжение в некоторых материалах при растяжении

Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.

Испытание на растяжение

Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.

Значения σ_раст в МПа:

Материалы	σ_раст
Бор	5700	0,083
Графит	2390	0,023
Сапфир	1495	0,030
Стальная проволока	415	0,01
Стекловолокно	350	0,034
Конструкционная сталь	60	0,003
Нейлон	48	0,0025

Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.

Запасы прочности, закладываемые в ответственные конструкции, также многократны.

Коэффициент запаса прочности

Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.

Запас прочности

Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.

Связь с другими модулями упругости

Модуль Юнга связан с модулем сдвига, определяющим способность образца к сопротивлению против деформации сдвига, следующим соотношением:

E связан также и с модулем объёмной упругости, определяющим способность образца к сопротивлению против одновременного сжатия со всех сторон.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

stankiexpert.ru

Модуль упругости (модуль Юнга)

Модуль упругости (модуль Юнга) — коэффициент, характеризующий сопротивление материала растяжению или сжатию при упругой деформации

С помощью легких преобразований, данная формула получается из Закона Гука.

Закон Гука: механическое напряжение в упруго деформированном теле прямо пропорционально относительной деформации этого тела.

σ =k·ε

Другая форма записи закона Гука:

Коэффициент E в этом соотношении и есть модуль Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Для различных материалов модуль Юнга меняется в широких пределах. Для стали, например, E≈2·10¹¹ Н/м², а для резины E≈2·10⁶ Н/м², то есть на пять порядков меньше.

Модуль упругости, или модуль продольной деформации Е, показывает критическое напряжение, которое может иметь структура материала при максимальной ее деформации до разрушения.

Таблица значений Модуля Юнга (модуля упругости) для некоторых материалов

Физический смысл Модуля Юнга: он показывает напряжение, которое необходимо приложить к телу, чтобы увеличить его длину в два раза

Обозначения:

E — модуль упругости (Модуль Юнга)

σ_p— критическое напряжение

ε — относительное удлинение

F — сила, действующая на стержень

l — длина деформируемого стержня

x — модуль изменения длины стержня в результате упругой деформации

S — площадь поверхности, по которой распределено действие силы

infofiz.ru

Таблица Модуль Юнга. Модуль упругости. Определение Модуля Юнга.

ЗАДАЧНИК ОНЛ@ЙН
БИБЛИОТЕКА 1 БИБЛИОТЕКА 2

Примечание. Значение модуля упругости зависит от структуры, химическая состава и способа обрабртки материила. Поэтому значения E могут отличаться от средних значений, приведенных в таблице.

Таблица модуль Юнга. Модуль упругости. Определение модуля Юнга. Коэффицент запаса прочности.

Таблица модуль Юнга

Материал	E		Материал	E
Материал	ГПа	кгс/мм²	Материал	ГПа	кгс/мм²
Алюминий	70	7000	Стали легированные	210-220	21000-22000
Бетон	3000		Стали углеродистые	200-210	20000-2100
Древесина (вдоль волокон)	10-12	1000-1200	Стекло	56	5600
Древесина (поперек волокон)	0,5-1,0	50-100	Стекло органическое	2,9	290
Железо	200	2000	Титан	112	11200
Золото	79	7900	Хром	240-250	24000-25000
Магний	44	4400	Цинк	80	8000
Медь	110	11000	Чугун серый	115-150	11500-15000
Свинец	17	1700

Предел прочности материала

Материал	σ_пч		Материал	σ_пч
Материал	ГПа	кгс/мм²	Материал	ГПа	кгс/мм²
Алюминий	0,05-0,11	5-11	Сталь (марки Ст3)	0,38-0,47	38-47
Бетон прочный	0,048	4,8	Сталь легированная	0,8-1,0	80-100
Железо	0,17-0,21	17-21	Стекло	0,06-0,12	6-12
Золото	0,14	14	Стекло органическое	0,08	8
Олово	0,027	2,7	Цинк	0,11	11
Свинец	0,016	1,6	Чугун серый	0,25-0,55	25-55
Серебро	0,14	14

Допускаемое механическое напряжение в некоторых метериалах (при растяжении)

Материал	σ_доп		Материал	σ_доп
Материал	ГПа	кгс/мм²	Материал	ГПа	кгс/мм²
Алюминий	0,03-0,08	3-8	Сталь (марки Ст3)	0,16	16
Бетон	0,0003-0,0015	0,03-0,15	Сталь углеродистая	0,06-0,25	6-25
Медь	0,03-0,12	3-12	Чугун серый	0,028-0,080	2,8-8,0
Стал легированный	0,1-0,4	10-40

Коэффициент запаса прочности

Стал при переменной нагрузке	5-15
Стал при постоянной длительной нагрузке	2,4-2,6
Сталь при ударной нагрузке	2,8-5,0
Чугун, бетон, деревисина при постоянной длительной нагрузке	3-9

Продолжение будет …

www.kilomol.ru

Модуль Юнга Википедия

Назван в честь английского физика XIX века Томаса Юнга.

Модуль Юнга рассчитывается следующим образом:

E=F/SΔl/l=FlSΔl,{\displaystyle E={\frac {F/S}{\Delta l/l}}={\frac {Fl}{S\Delta l}},}

где:

Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне:

c=Eρ,{\displaystyle c={\sqrt {\frac {E}{\rho }}},}

где ρ{\displaystyle \rho } — плотность вещества.

Связь с другими модулями упругости

В случае изотропного тела модуль Юнга связан с модулем сдвига G{\displaystyle G} и модулем объёмной упругости K{\displaystyle K} соотношениями

G=E2(1+ν){\displaystyle G={\frac {E}{2(1+\nu )}}}

K=E3(1−2ν),{\displaystyle K={\frac {E}{3(1-2\nu )}},}

где ν{\displaystyle \nu } — коэффициент Пуассона.

Температурная зависимость модуля Юнга

M(T)=M0−M1T−M2T2{\displaystyle M(T)=M_{0}-M_{1}T-M_{2}T^{2}}

где M0{\displaystyle M_{0}} — адиабатический модуль упругости идеального кристалла при T⟶0K{\displaystyle T\longrightarrow 0K}; M1T{\displaystyle M_{1}T} — дефект модуля, обусловленный тепловыми фононами; M2T2{\displaystyle M_{2}T^{2}} — дефект модуля, обусловленный тепловым движением электронов проводимости^[2]

Значения модуля Юнга для некоторых материалов

Значения модуля Юнга для некоторых материалов приведены в таблице

См. также

Примечания

↑ Модули упругости — Статьи в Физическом энциклопедическом словаре и Физической энциклопедии.
↑ Л.Н. Паль-Валь, Ю.А. Семеренко, П.П. Паль-Валь, Л.В. Скибина, Г.Н. Грикуров. Исследование акустических и резистивных свойств перспективных хромо-марганцевых аустенитных сталей в области температур 5-300 К // Конденсированные среды и межфазные границы. — 2008. — Т. 10, вып. 3. — С. 226—235.
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ¹⁰ ¹¹ ¹² ¹³ ¹⁴ ¹⁵ ¹⁶ ¹⁷ ¹⁸ ¹⁹ ²⁰ ²¹ ²² ²³ ²⁴ ²⁵ ²⁶ Анурьев В. И. Справочник конструктора-машиностроителя в 3т. Т. 1/В. И. Анурьев; 8-е изд., перераб и доп. Под ред. И. Н. Жестковой — М.: Машиностроение, 2001. — С. 34. ISBN 5-217-02963-3
↑ Галашев А. Е., Рахманова О. Р. Устойчивость графена и материалов на его основе при механических и термических воздействиях // Успехи физических наук. — М.: РАН, ФИАН, 2014. — Т. 184, вып. 10. — С. 1051.
↑ В.Д. Нацик, П.П. Паль-Валь, Л.Н. Паль-Валь, Ю.А. Семеренко. Низкотемпературный a-пик внутреннего трения в ниобии и его связь с релаксацией кинков на дислокациях // ФНТ. — 2001. — Т. 27, вып. 5. — С. 547—557.
↑ П.П. Паль-Валь, В.Д. Нацик, Л.Н. Паль-Валь, Ю.А. Семеренко. Нелинейные акустические эффекты в монокристаллах ниобия, обусловленные дислокациями // ФНТ. — 2004. — Т. 30, вып. 1. — С. 115—125.