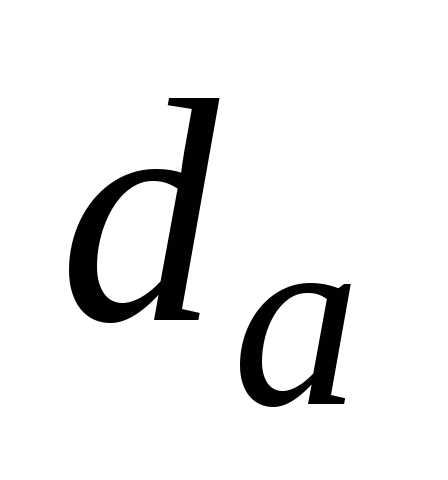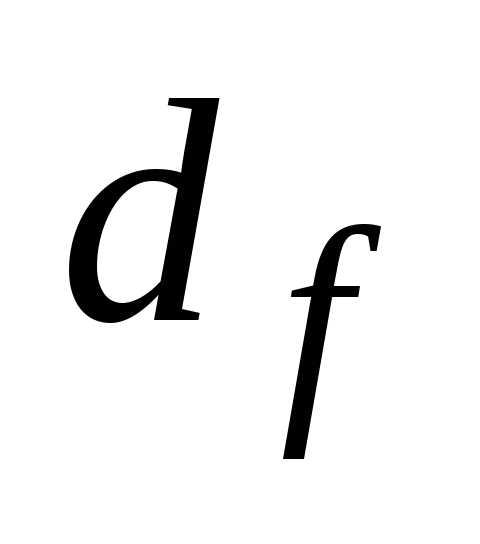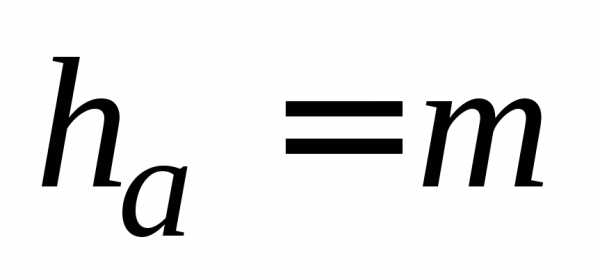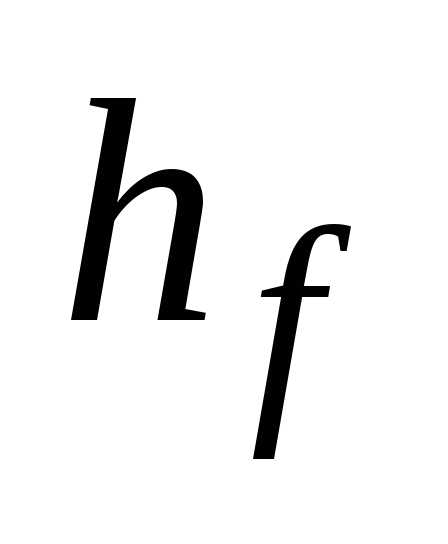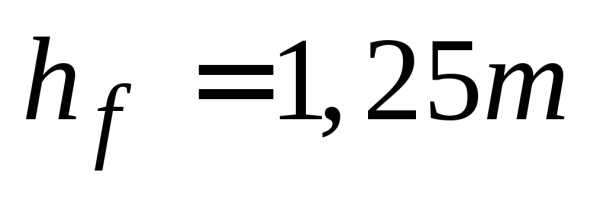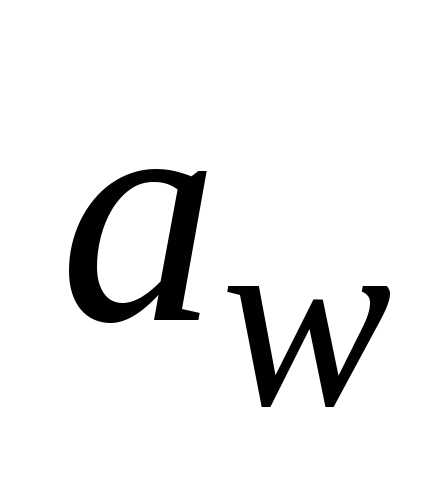Параметры зубчатого колеса – , —
alexxlab | 02.04.2020 | 1 | Вопросы и ответы
Основные параметры зубчатого колеса
При конструировании зубчатого колеса учитывают материал, из которого оно будет изготовлено, требуемый диаметр и способ получения заготовки.
Стальные зубчатые колеса
Зубчатые колеса диаметром до 150 мм в единичном и мелкосерийном производстве обычно изготовляют из круглого проката; в средне-, крупносерийном и массовом производстве предпочтительнее применять кованые или штампованные заготовки, имеющие более высокие механические характеристики.
Шестерни изготовляют за одно целое с валом (вал-шестерня) (рис. 1, а, б) или делают съемными, если расстояние χ от впадины зуба до шпоночного паза (рис. 2) больше 2,5 m n для цилиндрических шестерен и 1,8 m e для конических. В случае цельной конструкции увеличивается жесткость вала и уменьшается общая стоимость вала и шестерни. Разъемная конструкция позволяет выполнить шестерню и вал из разных материалов, а при поломке одной детали вторую оставить без замены. На рис. 1, а показана конструкция вала-шестерни, когда диаметр впадин зубьев
Цилиндрические зубчатые колеса диаметром до 400… 500 мм (в отдельных случаях до 600 мм) можно выполнять коваными , штампованными, литыми или сварными .
Конструктивные элементы зубчатых колес показаны на рис. 3.
Типовые конструкции зубчатых колес и основные соотношения их элементов даны на рис. 4-8. Кованые заготовки для зубчатых колес применяют при наружном диаметре колеса 4,d f или при нешироких колесах (ψ ba диаметром d a до 400 мм. Операция штамповки отличается высокой производительностью и максимально приближает форму заготовки к форме готового колеса. Для облегчения заполнения металлом и освобождения от заготовки штамп, а следовательно, и заготовка должны иметь радиусы закруглений r ≥ 5 мм и штамповочные уклоны γ ≥ 5° (рис. 4) . Внутреннюю поверхность обода, наружную поверхность ступицы и поверхности диска штампованных колес обычно не обрабатывают. Конструкция литого колеса дана на рис. 5.
Рис. 1. Конструкция вала – шестерни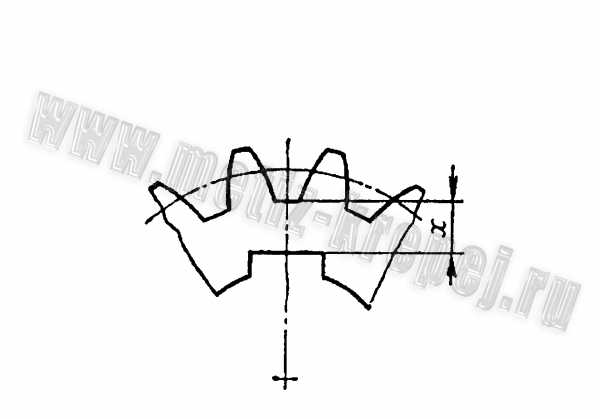 Рис. 2. Элемент шестерни при шпоночном соединении
Рис. 2. Элемент шестерни при шпоночном соединении
 Рис. 3. Конструктивные элементы колес:
Рис. 3. Конструктивные элементы колес:
a – цилиндрического; б – конического; в – червячного
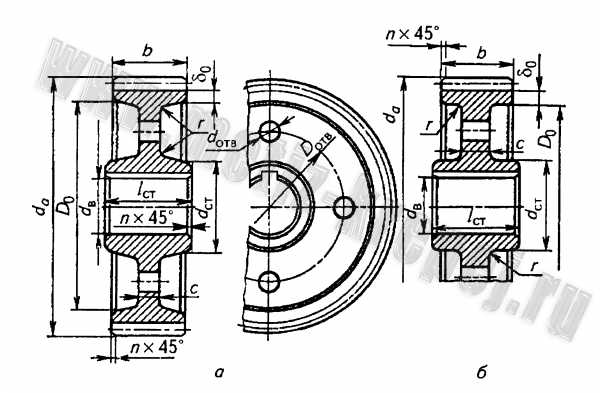 Рис. 4. Цилиндрические зубчатые колеса при d a ≤ 500мм :
Рис. 4. Цилиндрические зубчатые колеса при d a ≤ 500мм :
а -штампованное; б- кованое; d ст = 1,6d в ; l ст ≥ b при соблюдении условия
l ст = (0,8…1,5)d в ; δ o = 2,5m n +2 , но не менее 8…10 мм;
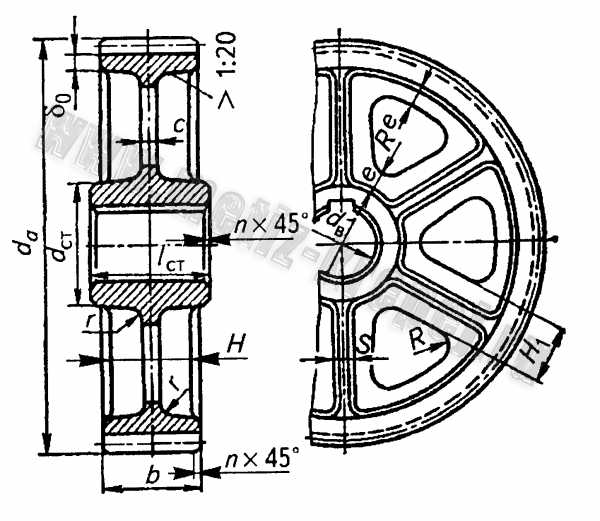 Рис. 5. Литое цилиндрическое зубчатое колесо при d a = 400…1000 мм : b ≤ 200 мм d ст = 1,6d в – для стального литья; d ст = 1,8d в для чугунного литья; l ст ≥ b
Рис. 5. Литое цилиндрическое зубчатое колесо при d a = 400…1000 мм : b ≤ 200 мм d ст = 1,6d в – для стального литья; d ст = 1,8d в для чугунного литья; l ст ≥ b
при соблюдении условия l ст = (0,8…1,5)d в ; δ o = 2,5m n + 2 ≥ 8 мм ;
n = 0,5m n для обода n для ступицы; c = H/5 , но не менее 10 мм;
S = H/5 , но не менее 10 мм; e = 0,8δ o ; H= 0,8d в ; H 1 = 0,8H ; R – вписанная дуга окружности
 Рис. 6. Бандажированное зубчатое колесо при d в свыше 600 мм: d ст = 1,6d в – для стального литья; d ст = 1,8d в – для чугунного;l ст ≥ b
Рис. 6. Бандажированное зубчатое колесо при d в свыше 600 мм: d ст = 1,6d в – для стального литья; d ст = 1,8d в – для чугунного;l ст ≥ b
при соблюдении условия l ст = (0,8…1,5)d в ; c = 0,15b ; δ o = 4m n , но не менее 15 мм; t = δ o ; e = 0,8δ o ; d 1 = (0,05…0,1)d в ; l 1 = 3d 1 ;b ≥ 300 мм
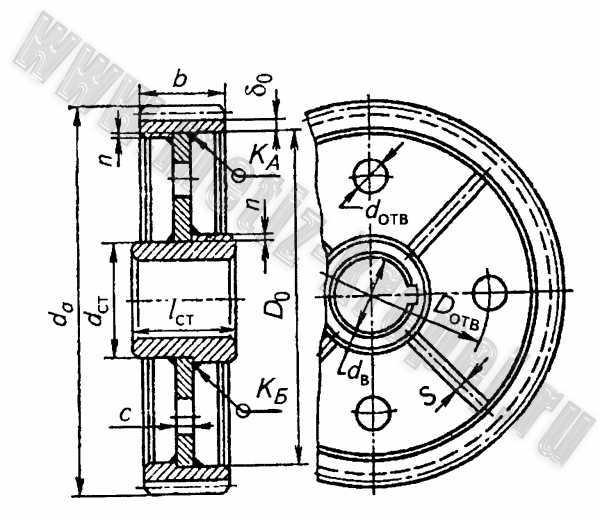 Рис. 7. Сварное зубчатое колесо:
Рис. 7. Сварное зубчатое колесо:
l ст = (0,8…1,5)d в ≥ b ; d ст = 1,6d в ; δ o = 2,5m n , но не менее 8 мм;s = 0,8c ; D отв = 0,5 (D o + d ст) ; d отв = 15…20 мм . Катеты швов: K a = 0,5d в ; K ь = 0,1d в но не менее 4 мм. Ребра приваривают швом K б
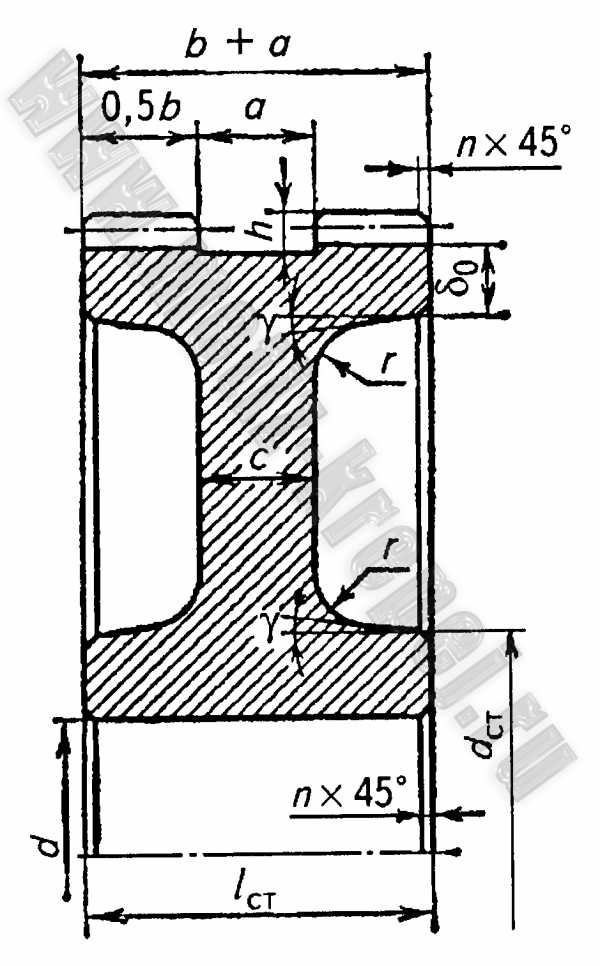 Рис. 8. Шевронное зубчатое колесо с канавкой посередине:
Рис. 8. Шевронное зубчатое колесо с канавкой посередине:
l ст = b + a ; c = (0,3…0,35)(b + a) ; δ o = 4m n + 2 ; h = 2,5m n ; a – в зависимости от модуля. Остальные размеры см. рис. 4, 5
Размеры ступицы выбирают по рекомендациям, приведенным под рисунками. Длину ступицы l ст по возможности принимают равной ширине венца колеса b , что обеспечивает наименьшую ширину редуктора. Отношение длины ступицы к диаметру вала должно быть не меньше 0,5. При отношении меньше 0,8 на валу предусматривают буртик, исключающий торцевое биение колеса, к которому будет прижиматься торец ступицы колеса. Если по условиям расчета (см. расчет шпоночного и шлицевого соединений) l ст > b , то ступицу желательно сместить по оси колеса до совпадения одного ее торца с торцом венца (см. рис. 3, а), что дает возможность нарезать зубья сразу на двух колесах. Реже (для одноступенчатых редукторов) колеса изготовляют со ступицей, выступающей в обе стороны относительно венца (рис. 3, в), при этом зубья можно нарезать только на одном колесе. При одинаковой длине ступицы и ширине венца можно одновременно нарезать зубья на нескольких колесах.
С целью экономии материала, при больших диаметрах колес, для соединения ступицы с венцом колеса вместо сплошного диска применяют спицы. Зубчатые колеса большого диаметра (при внешнем диаметре d a ≥ 600 мм ) иногда делают бандажированными (рис. 6): венец – стальной кованый (бандаж), а колесный центр – из стального или чугунного литья. Венец сопрягается с колесным центром посадкой с гарантированным натягом. Для большей надежности в плоскости соединения венца с центром ставят винты; соединения проверяют на смятие по материалу колесного центра: при стальном колесном центре [σ] см ≥ 0,3σ т , при чугунном [σ] см ≥ 0,4σ в.и , где σ т – предел текучести; σ в.и – предел прочности чугуна на изгиб.
При индивидуальном изготовлении колёса иногда делают сварными (рис. 7). При диаметре d a ≥ 1500 мм для удобства сборки зубчатые колеса делают разъемными – из двух половин.
На торцах зубьев и обода выполняют фаски
Острые кромки на торцах ступицы притупляют фасками n x 45 , размер которых принимают в зависимости от диаметра вала d :
Шевронные зубчатые колеса (рис. 8) отличаются от других цилиндрических колес большей шириной. Наиболее часто шевронные колеса изготовляют с канавкой посередине, предназначенной для выхода червячной фрезы, нарезающей зубья. При известных размерах фрезы ширину канавки a определяют прочерчиванием. Приближенно размер а можно определить в зависимости от модуля m :
| m, мм a, мм | 1,5 27 | 2 32 | 2,5 37 | 3 42 | 3,5 47 | 4 53 | 5 60 | 6 67 | 7 75 | 8 85 | 10 100 |
Остальные конструктивные элементы шевронных колес принимают по соотношениям, указанным под рис. 8.
Конические зубчатые колеса изготовляют коваными, штампованными, литыми или из круглого проката (рис. 9-11).
Конические колеса с внешним диаметром вершин зубьев d ae конструируют, как показано на рис. 9. В том случае, когда угол делительного конуса σ , колесо выполняют по рис. 9, а, при σ – по рис. 9, б. Если 30° ≤ σ ≤ 45° , можно использовать обе формы. Штампованные колеса (рис. 10, а) применяют в серийном производстве. При внешнем диаметре вершин d ae ≥ 300 мм используют также литые конические колеса с ребрами жесткости.
Ступицу в зубчатых конических колесах необходимо располагать так, чтобы при закреплении колеса на оправке для нарезания зубьев обеспечивался зазор а> 0,5 m te для свободного выхода инструмента, где т,е внешний окружной модуль (рис. 11).
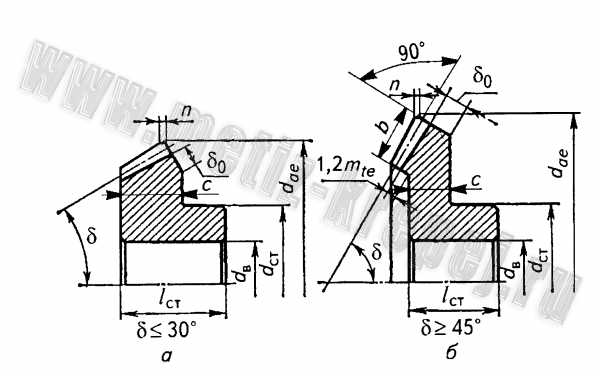 Рис. 9. Конические зубчатые колеса при d ae :
Рис. 9. Конические зубчатые колеса при d ae :
a – при δ ; б – при 5 >45°; диаметр ступицы
δ o = 2,5m n + 2 , но не менее 10 мм; n = 0,5m n
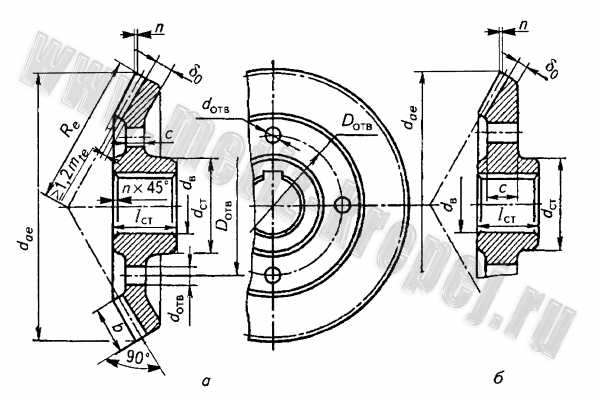 Рис. 10. Конические зубчатые колеса при d ae до 500 мм :
а – штампованное; б – кованое d ст = 1,6d в ; l ст = (0,9…1,2)d в. , но не менее 10 мм; c = (0,1…0,17)R e ; n = 0,5m n ; размеры D отв и d отв определяют конструктивно
Рис. 10. Конические зубчатые колеса при d ae до 500 мм :
а – штампованное; б – кованое d ст = 1,6d в ; l ст = (0,9…1,2)d в. , но не менее 10 мм; c = (0,1…0,17)R e ; n = 0,5m n ; размеры D отв и d отв определяют конструктивно
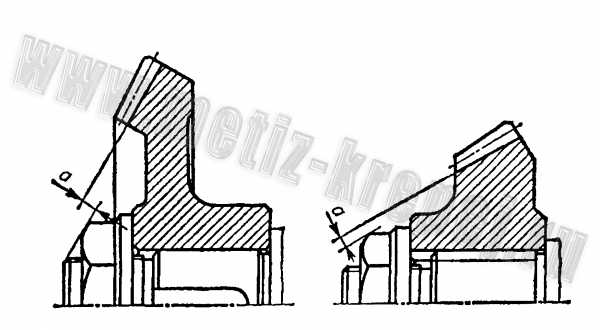 Рис. 11. Креплен
Рис. 11. Креплен
veloed.ru
Основные параметры зубчатого цилиндрического колеса
Геометрические параметры | Обозначение | Расчетная формула |
Высота головки | ha | ha = m |
Высота ножки | hr | hf=1.25m |
Высота зуба | h | h = h. + h= 2,25m |
Делительный диаметр | d | d=mz |
Диаметр вершин зубьев | da | da=d+2ha=m(z+2) |
Диаметр впадин зубьев | df | df=d-2hf=m(z-2,5) |
Окружной шаг | Pt | Pt= π m |
Окружная толщина зуба | St | St=0.5Pt= 0.5π m |
Окружная ширина впадины | et | et=0.5Pt= 0.5π m |
Радиус кривизны переходной цилиндрической поверхности | Rf | Rf= 0,25m |
Табл.3
Конструктивные параметры | Расчетная формула |
Ширина зубчатого венца | b=(6/8)m |
Толщина обода зубчатого венца | δ1=(2,5/3)m |
Наружный диаметр ступицы | Dст=(1,6/1,8)DB |
Толщина диска | δ2=(3/3,6)m |
Диаметр, определяющий расположение отверстий в диске | D1=0,5(DK+Dст) |
Диаметр отверстий в диске | D0=(DK-Dст)/2,5/3 |
Длина ступицы | Lст=1,5DB |
Фаска | 0,5mX45o |
Размеры паза под шпонку | Выбираются по таблицам ГОСТ 23360-78 в зависимости от |
Примечание. Меньшие значения коэффициентов относятся к колесам, выполненным из стали, большие – из чугуна. | |
Если зубчатое колесо изготовлено так, что высота зуба h=2,25m, то колесо называется выполненным без смещения исходного контура (некоррегированное колесо). Если колесо изготовлено с высотой зуба h=2,25m, то колесо называется выполненным со смещением исходного контура (корригированное колесо).
Смещение исходного контура характеризуется коэффициентом смещения исходного контура, обозначаемым по ГОСТ 16531-70 буквой х. Для некоррегированного колеса коэффициент смещения исходного контура х=0.
При выполнении учебных чертежей обычно ориентируются на применение некоррегированных колес нормального эволвентного зацепления, параметры которых находятся в определенной зависимости от модуля т и числа зубьев (см. табл. 2).
3. Конструктивные разновидности зубчатых колес
В современном машиностроении применяются зубчатые колеса самых разнообразных конструкций, отличающиеся друг от друга технологией изготовления, материалом и конструктивными особенностями.
Конструктивные форма и размеры зубчатого колеса зависят от нагрузок, действующих на его зубья, требований технологии их изготовления, удобства монтажа и эксплуатации, уменьшения массы (веса) зубчатых колес, бесшумности работы и др.
Наиболее часто встречающиеся формы цилиндрических зубчатых колес с прямыми зубьями представлены на рис. 1, д-ж.
Цилиндрическое зубчатое колесо малого диаметра (рис. 1, д-ж) обычно имеет форму сплошного цилиндра с отверстием для установки на вал.
При несколько большем диаметре колеса для облегчения его конструкции выполняются массивными только обод и ступица (втулка) с отверстием для вала. Остальная часть колеса представляет собой тонкий диск с отверстиями (или без отверстий). Диск может выполняться с ребрами жесткости.
Если диаметр колеса достаточно велик, диск заменяется несколькими спицами, соединяющими обод со ступицей. Форма спиц может быть различной. Форма поперечного сечения спиц тоже различна: круглая, овальная, прямоугольная, двутавровая, крестообразная и др.
Колеса большого диаметра для удобства монтажа’и упрощения технологии изготовления иногда выполняют разъемными из двух половин, скрепляемых болтами (рис. 5, а).

Рис.5
Если в конструкции необходимо применить внутреннее зацепление, то большое колесо изготовляют с внутренними зубьями (рис. 5, б). Для поворота вала на какой-либо заданный угол применяют зубчатый сектор (рис. 5, в).
Зубья колес могут быть прямыми (рис. 5, а-в) косыми (рис. 5, г), шевронными и криволинейными (рис. 5, д). Термины, определения и обозначения элементов зубчатых передач установлены ГОСТ 16536-78 и ГОСТ 16561-76.


Рис. 5
studfiles.net
Геометрические параметры зубчатых колёс.

Кинематическими характеристиками всякого колеса являются число зубьев и шаг зацепления .
1 – наружная окружность .
2 – делительная окружность .
3 – окружность впадин .
Если дано число зубьев и длина шага, то длину делительной окружности можно найти по формуле: , тогда диаметр делительной окружности определяется с помощью выражения , где – модуль зацепления, то есть .
Через модуль зацепления выражаются все геометрические параметры зубчатого колеса и межосевые расстояния передач. Модуль зацепления является гостированной величиной, поскольку профильный инструмент для изготовления зубчатых колёс и измерительные инструменты дорогостоящи.
Делительная окружность делит зуб на две части: ; ; .
Определяем диаметры колёс:
;
.
– толщина зуба.
– ширина впадины.
Теоретически толщина зуба должна быть равна ширине впадины, но, чтобы не было защемления при зацеплении, на практике ширина впадины делается больше, чем толщина зуба в пределах допуска на боковой зазор.
Межосевое расстояние в передачах принято обозначать : .
Основная теорема зацепления.
Теорема Виллиса.
; .
– время полного контакта двух сопряжёно работающих зубьев, от встречи до расставания. Внутри этого промежутка заметно, что передаточное отношение будет переменным. Если зубчатая передача быстроходна, то такие передачи непригодны.
Теорема Виллиса.
Какой кривой необходимо очертить профили зубьев, чтобы мгновенное передаточное отношение было постоянным?
 Известны угловые скорости и .
Известны угловые скорости и .
; .
; .
.
Через точку проведём общую касательную к сопряжённым профилям. Разложим вектора скоростей на нормальные и тангенциальные составляющие, и сравним нормальные составляющие скоростей. Возможны следующие варианты:
1. – первый профиль «внедрится» во второй, что приведёт к их разрушению.
2. – профили работают в контакте.
Так как , а , следовательно, , что допустимо и имеет место на практике. В процессе зацепления происходит не чистое обкатывание профилей, а соскальзывание, что приводит к износу зубьев по профилю.
Сравним треугольники и . Эти треугольники подобны, поэтому очевидно равенство , следовательно, .
Обозначим , .
Аналогично: .
Исходя из того, что , получим: .
Рассмотрим треугольники и . Они подобны, как прямоугольные со смежными сторонами.
Обозначим: ; .
Тогда: .
Следовательно, положение точки на линии центров в процессе зацепления должно быть неизменным.
Для постоянства передаточного отношения в зубчатой передаче необходимо, чтобы общая нормаль к профилям зубьев всегда проходила бы через одну и ту же точку (полное зацепление) на линии центров , и делила бы линию центров в отношении обратно пропорциональном отношению угловых скоростей.
Следствия:
1. Чтобы в зубчатой передаче иметь постоянным передаточное отношение, необходимо профили зубьев очертить тонкими кривыми, которые отвечали бы требованиям основной теоремы зацепления.
2. Требованиям основной теоремы зацепления соответствует эвольвента, образующая эвольвентное зацепление и сочетание эпициклоиды и гипоциклоиды, образующей циклоидное зацепление.
Эвольвента является бесконечной спиралью вне данной окружности.
Проведём обкатывание вспомогательных окружностей и без скольжения по начальной окружности, и получим эпициклоиду и гипоциклоиду.
Ножка зуба оформляется по гипоциклоиде, а головка зуба оформляется по эпициклоиде.
Похожие статьи:
poznayka.org
Основные геометрические параметры, характеризующие зубчатые колеса
Понятия и термины, относящиеся к геометрии и кинематике зубчатых передач, стандартизованы. Стандартами устанавливаются термины, определения и обозначения, а также методы расчета геометрических параметров.
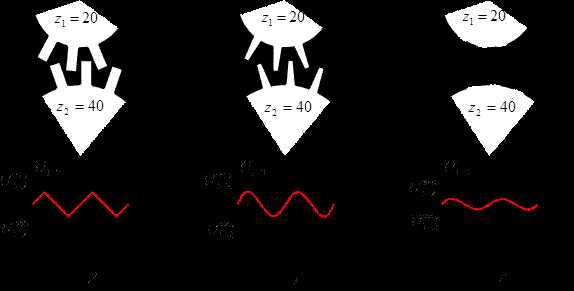
Напомним, что меньшее из пары зубчатых колес называют шестерней,а большее –колесом.Параметрам шестерни приписывают индекс 1, а параметрам колеса – 2 (рис. 4.4).Передаточным числом называют отношение числа зубьев колеса к числу зубьев шестерни.
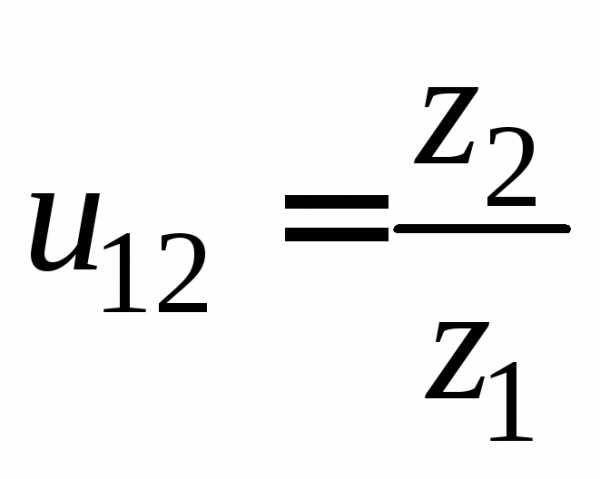 .
(4.10)
.
(4.10)
Касание
двух взаимодействующих эвольвент
происходит только на общей касательной Е1Е2 к их основным
окружностям. Общая касательная к двум
основным окружностям называется линией
зацепления.
Участок линии зацепления, ограниченный окружностями
вершин зубьев  ,
называетсяактивной
линией зацепления.
,
называетсяактивной
линией зацепления.
Любая
точка линии зацепления может быть полюсом
зацепления Р. Угол,
образованный общей касательной к двум
основным окружностям и перпендикуляром
к линии их центров, называется углом
зацепления 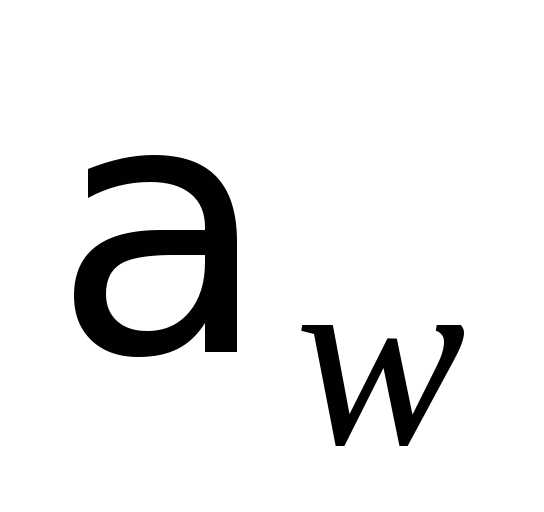 .
.
Относительное движение двух эвольвент может быть представлено цилиндрами, вращающимися относительно друг друга посредством трения, без скольжения. Такие цилиндры называются начальными, а их диаметры – диаметрами начальных окружностей (dw1 и dw2). У сопряженной пары некоррегированных зубчатых колес, работающих при правильном межосевом расстоянии, делительные окружности совпадают с начальными.
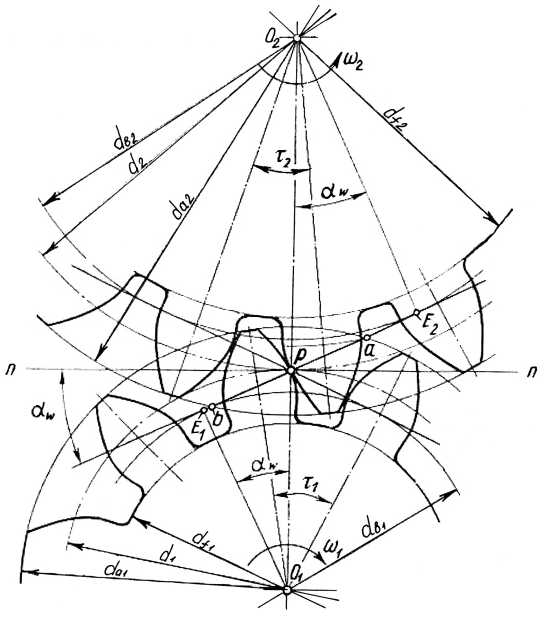
Рис. 4.4.Геометрические параметры зубчатой передачи
Делительная окружность – параметр, введенный для удобства в расчетах, определяемый через модуль и число зубьев колес:
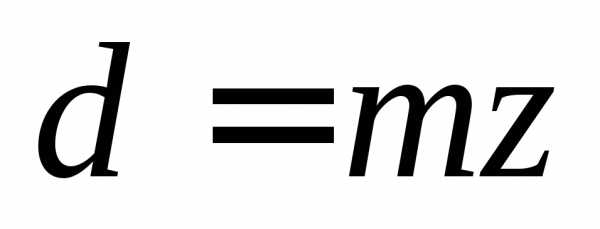 . (4.11)
. (4.11)
Параметрам, относящимся к делительной поверхности или окружности, дополнительного индекса не приписывают.
Модуль– это часть диаметра делительной окружности, приходящаяся на один зуб колеса (мм):
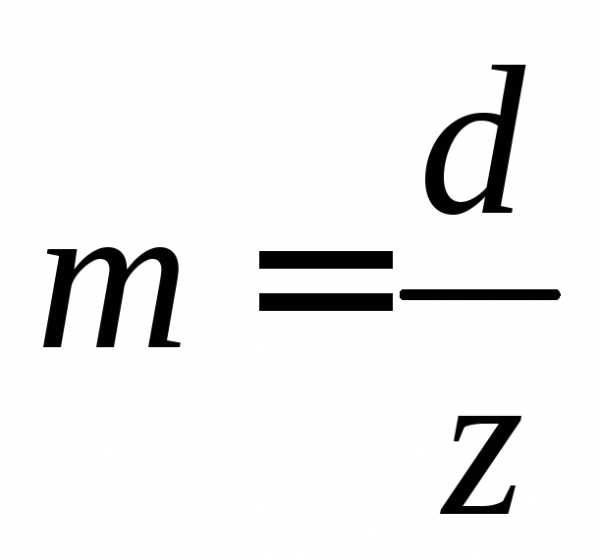 .
.
Модуль чаще определяется как отношение шага рпо делительной окружности к числу π:
 .
(4.12)
.
(4.12)
Ряд модулей, применяемых для цилиндрических, шевронных, конических и червячных передач, стандартизован (ГОСТ 9563–60).
Исходным
контуром называется
контур зубчатой рейки в нормальном к
направлению зубьев сечении. Исходный
контур для цилиндрических колес внешнего
и внутреннего зацепления представляет
собой зубчатую рейку с прямолинейным
профилем в пределах глубины захода  (рис. 4.5). Под глубиной захода понимается
высота зуба, которая участвует в работе.
(рис. 4.5). Под глубиной захода понимается
высота зуба, которая участвует в работе.
Угол
профиля 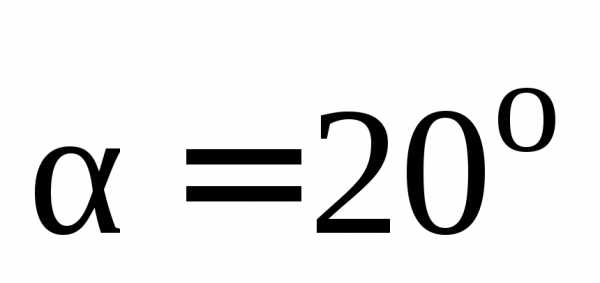 ,
нормальная величина радиального зазора
равна,
а радиус закругления у корня зуба
исходного контура составляет.
,
нормальная величина радиального зазора
равна,
а радиус закругления у корня зуба
исходного контура составляет.
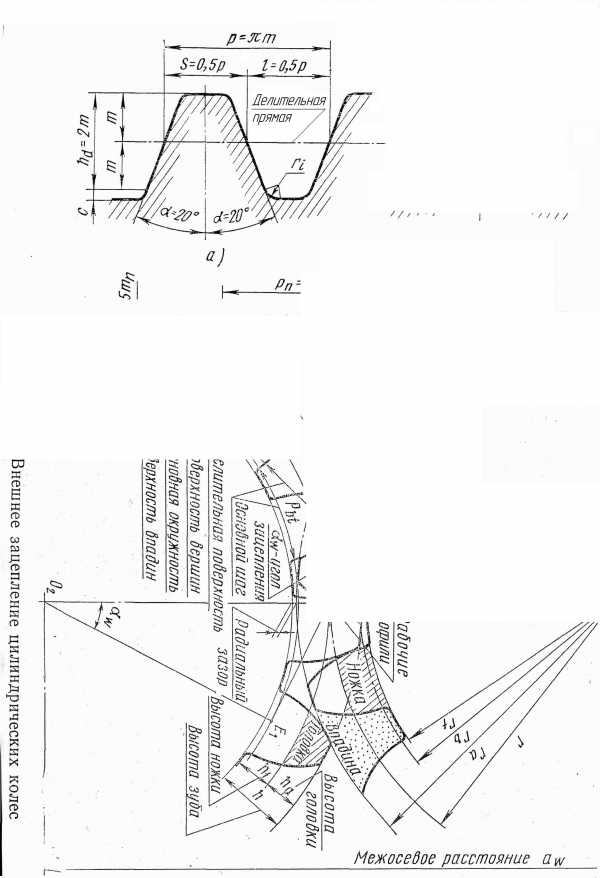
Рис. 4.5.Исходный контур
Расчетные формулы приведены в табл. 4.2.
Т а б л и ц а 4.2
Формулы для расчета геометрических параметров некоррегированных прямозубых цилиндрических колес внешнего и внутреннего зацепления
№ п/п | Параметр | Обозна-чения | Расчетная формула | |
Внешнее зацепление | Внутреннее зацепление | |||
1 | Передаточное число |
|
| |
2 | Модуль, мм | m | По ГОСТ 9563–60 | |
3 | Нормальный шаг, мм |
|
| |
4 | Основной шаг, мм |
|
| |
5 | Диаметры делительных окружностей, мм | d | d1 = mz1 d2 = mz2 | |
6 | Диаметры окружностей вершин зубьев, мм |
| da1 =d1 + 2m da2 =d2 + 2m | da1 =d1 + 2m da2 =d2 – 2m |
7 | Диаметры окружностей впадин, мм. |
| df1 = d1 – 2,5m df2 = d2 – 2,5m | df1 = d1 – 2,5m df2 = d2 + 2,5m |
8 | Высота зуба, мм | h | ||
9 | Высота головкизуба, мм |
|
| |
10 | Высота ножки зуба, мм |
|
| |
11 | Радиальный зазор, мм | с | ||
12 | Ширина зубчатого венца, мм | b | до 10m | |
13 | Межосевое расстояние, мм |
| ||
studfiles.net
Основные параметры зубчатых колес — Студопедия.Нет
Тмм ответы на вопросы для зачёта
32. Основные параметры зубчатых колёс. Коэффициент перекрытия
Коэффициент перекрытия – геометрическое место точек касания сопряженных профилей (спрямленной дуги основной окружности от входа до выхода из зацепления одной пары зубьев) к шагу pb зубьев по основной окружности.
Коэффициент перекрытия можно представить как отношение длины активного участка линии зацепления –b
Числовое значение коэффициента перекрытия показывает долю времени нахождения в зацеплении двух пар зубьев.Например, e = 1,68 означает, что 68 % времени в зацеплении находится две пары зубьев. Таким образом, коэффициент перекрытия характеризует нагрузочную способность передачи, плавность её работы.
Теоретически максимальное значение коэффициента перекрытия для прямозубых колес =1,98, т.е. в зоне полюса (точкаW) существует область однопарного зацепления.
Значение коэффициента перекрытия определяют через параметры зубчатых колес на основании картины зацепления:
, (1.92)
где aw – угол зацепления передачи; , , – соответственно радиусы окружностей вершин и основных окружностей зубчатых колес:
Коэффициент показывает сколько пар зубьев в среднем одновременно находится в зацеплении. Для прямозубой передачи обычно . Чем больше , тем более плавно и бесшумно работает передача.
Другим качественным показателем является коэффициент скольжения, который учитывает влияние геометрии передачи и её кинематики на скольжение и износ профилей, скользящих друг по другу (рис. 74), что видно из картины скоростей. На этой картине:
Зубчатой передачей называется механизм, служащий для передачи вращательного движения с одного вала на другой, изменения частоты вращения ведомого вала механизма и величины крутящего момента на нем, а также для преобразования вращательного движения в поступательное, и наоборот (реечные зубчатые передачи).

Зубчатое колесо, сидящее на передающем вращение валу, называется ведущим, а на получающем вращение – ведомым.
Меньшее из двух колес зубчатой передачи обычно называют шестерней, а большее – колесом. Термин “зубчатое колесо” относится к обеим деталям передачи.
Зубчатые передачи представляют собой наиболее распространенный вид передач в современном машиностроении, поскольку они наиболее полно удовлетворяют функциональным требованиям в сравнении с другими типами передач (при прочих равных условиях) – они надежны и долговечны, имеют небольшие габариты, относительно дешевы в изготовлении и эксплуатации, обладают рядом других преимуществ и достоинств.
Основные параметры зубчатых колес
· Делительными окружностями пары зубчатых колес называются соприкасающиеся окружности, условно проведенные из центров колес, и перекатывающиеся одна по другой без скольжения. Делительные окружности колес, находящихся в зацеплении, являются сопряженными. На чертежах делительную окружность выполняют штрихпунктирной линией, а ее диаметр обозначают буквой d.
· Модуль зубчатого зацепления m – это часть диаметра делительной окружности зубчатого колеса, приходящаяся на один зуб, т. е. m = d/z.
Значение модулей для всех передач – величина стандартизированная.
· Диаметр окружности вершин зубьев da – диаметр окружности, описывающей вершины головок зубьев.
· Диаметр окружности впадин зубьев df – диаметр окружности, описывающей основания ножек зубьев.
· Высота делительной головки зуба ha – расстояние между делительной окружностью колеса и окружностью, ограничивающей вершины зубьев.
· Высота делительной ножки зуба hf – расстояние между делительной окружностью колеса и окружностью, описывающей основания ножек (впадин) зубьев.
· Высота зуба h – расстояние между окружностями вершин и впадин зубьев цилиндрического зубчатого колеса h = ha + hf.
· Окружной шаг зубьев Рt – расстояние (мм) между одноименными профильными поверхностями соседних зубьев. Шаг зубьев равен длине делительной окружности, разделенной на число зубьев колеса z.
23 Основные динамики машин. Режимы движения машины. Роль маховика и регулятор
Чтобы уменьшить коэффициент неравномерности движения δ, т.е. чтобы сделать вращение кривошипа более плавным, на машину устанавливают маховик. Маховик – это массивное колесо, неподвижно скрепленное, обычно с кривошипом, и вращающееся с ним как одно целое.
Маховик выполняет в машине роль аккумулятора (накопителя) кинетической энергии: за одну часть цикла он накапливает энергию, чтобы вернут ее в другую часть цикла. При этом он, накапливая кинетическую энергию, разгоняется в те моменты времени, когда с двигателя поступает на машину больше работы, чем расходуется рабочим органом. И отдавая кинетическую энергию, притормаживается, когда рабочий орган расходует работы больше, чем поступает её в данный момент с двигателя.Чем больше маховик, тем будет меньше ∆ω и коэффициент неравномерности движения для любой машины самое лучшее, когда угловая скорость строго постоянна, т.е. ∆ω=0. Но чтобы получить ∆ω→0, нужен маховик, у которого момент инерции Jмахов→∞. Поэтому маховик рассчитывают из условия, чтобы при установке его в машину, коэффициент неравномерности движения δ стал равен наперед заданной допустимой величине.
есть два основных варианта установки маховика: на вал кривошипа или на более быстроходный вал.
Регуляторы- устройства, автоматически регулирующие затрачиваемую работу так, чтобы сохранять приблизительно постоянную V двигателя, когда изменяются силы сопротивлений или движущие силы.
24 Режимы работы подшипников ротора.
25. Статическая и динамическая балансировка роторов.
Чтобы устранить возмущающую силу, ротор уравновешивают, т.е. устраняют его небаланс. Операции по устранению небаланса называют балансировкой .
Балансировать можно каждую деталь ротора в отдельности или весь ротор в целом; последний способ экономичнее и точнее.
Чтобы сбалансировать неуравновешенность ротора, нужно на том же расстоянии от оси (там где выявлен небаланс), но в диаметрально противоположном направлении наплавить (подвесить) груз необходимой для балансировки массы; после чего ротор окажется сбалансированным и никакой возмущающей силы при его вращении возникать не будет.
Величину и расположение небаланса находят при выполнении различных видов балансировок.
Различают статическую и динамическую балансировки ротора:
1. Статической балансировка называется потому, что для выявления и устранения небаланса не требуется вращения ротора; уравновешивания достигают, когда ротор находится в состоянии покоя.
Недостатки статической балансировки:
Способствует появлению неуравновешенных пар сил;
Возможно снижение точки балансировки из-за скольжения качения;
после статической балансировки, даже при отсутствии неуравновешенных пар сил, всегда остается значительный остаточный дисбаланс, обусловленный силами трения, действующими на цапфы балансируемого ротора во время балансировочного процесса.
2. Динамическая неуравновешенность наблюдается тогда, когда неуравновешенные массы ротора дают две возмущающие силы, одинаковые по величине, но противоположно направленные и расположенные на разных концах. При этом может оказаться, что общий центр тяжести ротора расположен на оси вращения, т.е. статически ротор уравновешен.Такую неуравновешенность можно выявить только при вращении ротора, так как общий центр тяжести ротора расположен на его оси, и только при вращении обе неуравновешенные массы образуют пару возмущающих сил переменного направления. Следовательно, статически отбалансированный ротор в некоторых случаях может иметь динамическую неуравновешенность. Операция по выявлению и устранению динамического небаланса называется динамической балансировкой.
Статическая балансировка. У неуравновешенной детали ее масса располагается несимметрично относительно оси вращения. Поэтому при статическом положении такой детали, т. е. когда она находится в покое, центр тяжести будет стремиться занять нижнее положение (рис.1). Для уравновешивания детали добавляют с диаметрально противоположной стороны груз массой Т2 с таким расчетом, чтобы его момент Т2L2 был равен моменту неуравновешенной массы Т1L1. При этом условии деталь будет находиться в равновесии при любом положении, так как центр тяжести ее будет лежать на оси вращения. Равновесие может быть достигнуто также путем удаления части металла детали высверловкой, спиливанием или фрезерованием со стороны неуравновешенной массы Т1. На чертежах деталей и в Правилах ремонта на балансировку деталей дается допуск, который называют дисбалансом (г/см).
Статической балансировке подвергают плоские детали, имеющие небольшое отношение длины к диаметру: зубчатое колесо тягового редуктора, крыльчатку вентилятора холодильника и т.п. Статическая балансировка ведется на горизонтально-параллельных призмах, цилиндрических стержнях или на роликовых опорах. Поверхности призм, стержней и роликов должны быть тщательно обработаны. Точность статической балансировки во многом зависит от состояния поверхностей этих деталей.
Динамическая балансировка. Динамической балансировке обычно подвергают детали, длина которых равна или больше их диаметра. На рис. 2 показан статически отбалансированный ротор, у которого масса Т уравновешена грузом массой М. Этот ротор при медленном вращении будет находиться в равновесии в любом положении. Однако при быстром его вращении возникнут две равные, но противоположно направленные центробежные силы F1 и F2. При этом образуется момент FJU который стремится повернуть ось ротора на некоторый угол вокруг его центра тяжести, т.е. наблюдается динамическое неравновесие ротора со всеми вытекающими отсюда последствиями (вибрация, неравномерный износ и т. п.). Момент этой пары сил может быть уравновешен только другой парой сил, действующей в той же плоскости и создающей равный противодействующий момент.
Статический дисбаланс
Дисбаланс моментов m1 = m2
Динамический дисбаланс m1 ¹ m2
30 При уравновешивании многоцилиндровых машин за счёт различного расположения кривошипов
Конструкция многоцилиндровых поршневых машин зависит от типа рабочего процесса и связана также с возможностью уравновешивания сил инерции, действующих в различных цилиндрах. Большинство поршневых ДВС имеет несколько цилиндров и одинаковых звеньев шатунно – поршневых групп, соединенных общим коленчатым валом. При проектировании многоцилиндровых машин идут путём выбора разного числа цилиндров и рядного или углового их расположения Угловой сдвиг кривошипов коленчатого вала выбирают с целью равномерного чередования рабочих процессов.
Многоцилиндровые двухтактные двигатели Рабочий процесс в цилиндре двухтактного двигателя совершается за один оборот коленчатого вала. Поэтому при соблюдении равенства угловых интервалов между рабочими ходами в многоцилиндровых двухтактных двигателях коленчатые валы получаются с несимметрично расположенными кривошипами. Рассмотрим способы уравновешивания многоцилиндровых двухтактных двигателей. Однорядный четырехцилиндровый двигатель. В однорядном четырехцилиндровом двигателе применяется коленчатый вал с кривошипами под углом 90º: 360º/iц = 360º/4 = 90º, что обеспечивает равенство интервалов между рабочими ходами. На рис. 38 приведена схема коленчатого вала четырехцилиндрового двухтактного двигателя; порядок работы 1 – 3 – 4 – 2. Все силы инерции в двигателе с таким коленчатым валом взаимно уравновешиваются. Действительно, центробежные силы инерции Kr при крестообразном расположении кривошипов взаимно уравновешиваются при проектировании на оси x и y.
Четырехцилиндровый V-образный двигатель с углом раз- вала цилиндров γ = 90° и с кривошипами под углом δ = 180°. V-образное расположение цилиндров с углом развала γ = 90° и кривошипами под углом δ = 180° (рис. 41) применяется главным образом для двухтактных двигателей, для которых при по- рядке работы 1 – 2 – 3 – 4 обеспечивается равномерное чередование вспышек с угловым интервалом 90°. Рис. 41. Силы инерции, действующие в четырехцилиндровом V-образном двигателе (γ = 90º, δ = 180º) 78 Для четырехтактных серийных двигателей такое расположение цилиндров и кривошипов не применяется вследствие неравномерного чередования вспышек.
studopedia.net
Эвольвентное зубчатое колесо и его параметры.
Простая зубчатая передача состоит из двух подвижных звеньев – зубчатых колес. Поверхность, отделяющая зубья от тела зубчатого колеса называется поверхностью впадин. Поверхность, ограничивающая зубья со стороны, противоположной телу колеса называется поверхностью вершин зубьев. Пространство между двумя соседними зубьями называется впадина. Поверхность, ограничивающая зуб со стороны впадины называется боковой поверхностью зуба. Боковая поверхность состоит из главной и переходной поверхностей. Главная поверхность эта та, которая контактирует с главной боковой поверхностью второго колеса, обеспечивая заданное передаточное отношение. Главной поверхностью чаще всего является эвольвента. Переходная поверхность соединяет главную боковую поверхность с поверхностью впадин.
Параметры эвольвентного зубчатого колеса
Существует три параметра зубчатого колеса, которые можно определить «на глаз» при наличии этого зубчатого колеса и 2 которые можно только рассчитать.
Число зубьев колеса
 ,
можно подсчитать по готовому колесу
(при проектировании этим параметром
задаются).
,
можно подсчитать по готовому колесу
(при проектировании этим параметром
задаются).Окружность вершин, окружность впадин
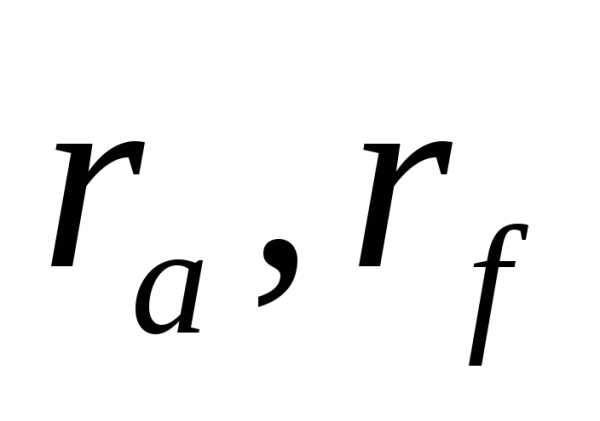 .
При наличии колеса могут быть измерены,
например, штангенциркулем.Окружность
вершин– это окружность, ограничивающая
зуб со стороны противоположной телу
колеса.Окружность впадин–
это окружность, ограничивающая зуб со
стороны тела колеса. Зная эти окружности
можно получить высоту зуба колеса:.
.
При наличии колеса могут быть измерены,
например, штангенциркулем.Окружность
вершин– это окружность, ограничивающая
зуб со стороны противоположной телу
колеса.Окружность впадин–
это окружность, ограничивающая зуб со
стороны тела колеса. Зная эти окружности
можно получить высоту зуба колеса:.Для получения эвольвентного профиля необходимо знать расположение основной окружности колеса
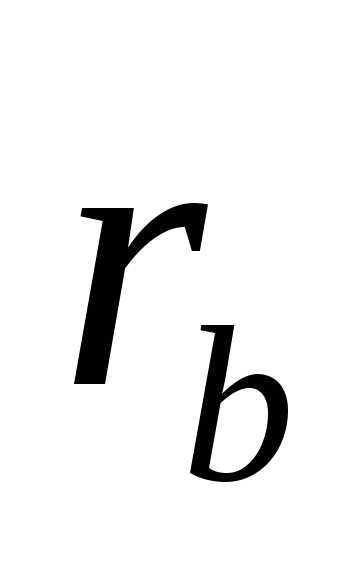 – рассчитывается.
– рассчитывается.Делительная окружность
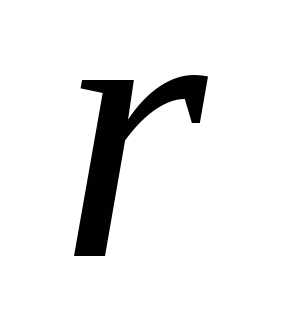 – делит зуб на ножку зуба и головку
зуба.Делительной окружностьюназывается окружность стандартного
шага, модуля и угла давления (или
окружность, проходящая через точку
эвольвенты для которой профильный угол
– делит зуб на ножку зуба и головку
зуба.Делительной окружностьюназывается окружность стандартного
шага, модуля и угла давления (или
окружность, проходящая через точку
эвольвенты для которой профильный угол ).
).Модулем зацепленияназывается линейная величина враз меньшая окружного шага или отношение шага по любой концентрической окружности зубчатого колеса к. В зависимости от окружности, по которой определен модуль, различают делительный, основной, начальный. Для косозубых колес еще и нормальный, торцевой и осевой модули. В ряде стран используется величина обратная модулю, которая называетсяпитчем. Питч (диаметральный) – число зубьев колеса, приходящееся на дюйм диаметра. Исходя из этого,модульможно определить как число миллиметров диаметра, приходящееся на один зуб. На колесе можно провести бесчисленное число окружностей, на каждой из которых будет свой модуль. Для ограничения этого числа ГОСТом введен стандартный ряд модулей. Стандартной модуль определяется поделительной окружности
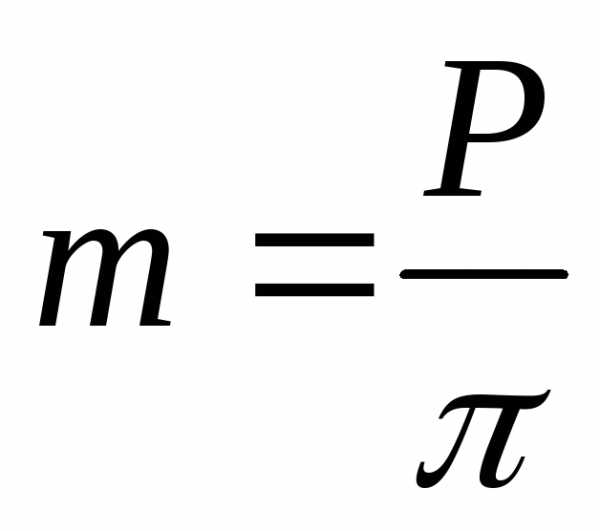 .
.Окружным шагом, или шагом, называется расстояние между одноименными точками профилей двух соседних зубьев, измеренное по дуге любой окружности (под одноименными понимаются правые или левые профили зуба). Обозначается
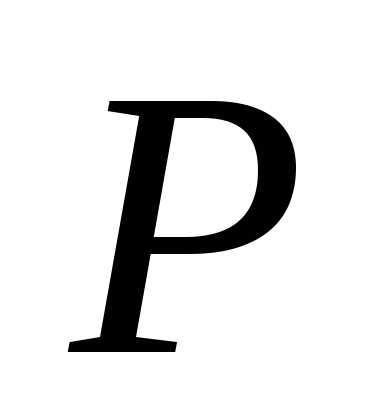 .
Достаточно часто вводится понятиеуглового шага
.
Достаточно часто вводится понятиеуглового шага – центральный угол, соответствующий
дуге
– центральный угол, соответствующий
дуге окружного шага по делительной
окружности. Шаг колеса делится на
толщину зуба
окружного шага по делительной
окружности. Шаг колеса делится на
толщину зуба и ширину впадины
и ширину впадины :.Толщина зуба
:.Толщина зуба  – расстояние по дуге соответствующей
окружности между разноименными точками
профилей зуба. Ширина впадины
– расстояние по дуге соответствующей
окружности между разноименными точками
профилей зуба. Ширина впадины  – расстояние по дуге
соответствующей окружности между
разноименными точками профилей соседних
зубьев.
– расстояние по дуге
соответствующей окружности между
разноименными точками профилей соседних
зубьев. – угловая толщина зуба.
– угловая толщина зуба.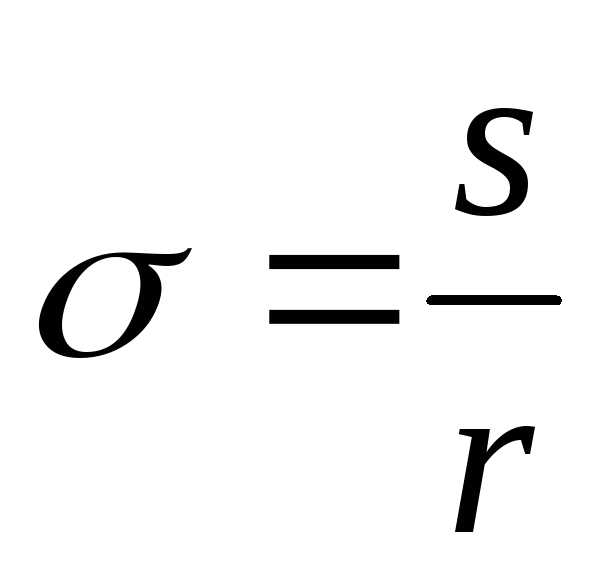 – центральный угол соответствующий
дуге
– центральный угол соответствующий
дуге .
.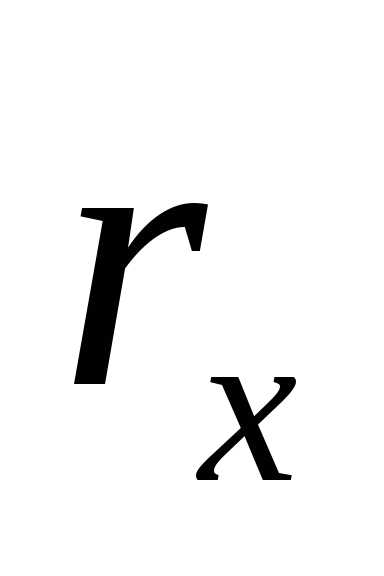 – окружность произвольного радиуса.
– окружность произвольного радиуса.
studfiles.net
Геометрические параметры зубчатого колеса. Расчет основных геометрических параметров цилиндрической зубчатой передачи
Лекция 6
6.5. Основные геометрические параметры прямозубых
цилиндрических передач
В зубчатых передачах принято называть меньшее зубчатое колесо шестерней.
В качестве основного параметра зубчатого зацепления принят модуль m – величина, пропорциональная шагу Р по делительному диаметру, http://pandia.ru/text/79/022/images/image002_53.gif”>
Рис. 6.6. Геометрические параметры цилиндрических зубчатых колес
Для прямозубых цилиндрических колес, изготовленных без смещения, делительный диаметр равен произведению
Диаметр вершин зубчатых колес определяется суммой
, . (6.13)
Диаметр впадин вычисляют разностью
, . (6.14)
Межосевое расстояние определяют полусуммой диаметров зубчатых колес
Ширина зубчатого колеса равна
где ya – коэффициент ширины, который выбирают в зависимости от расположения зубчатых колес относительно опор и твердости рабочих поверхностей зубьев.
Ширину шестерни принимают в 1,12 раз больше, чем ширина колеса
6.6. Особенности геометрии косозубых передач
У косозубых колес зубья наклонены под углом з к образующей делительного цилиндра. Нарезание косозубых колес может производиться прямозубой рейкой, как и при нарезании прямозубых колес. Наклон зуба получают поворотом инструмента относительно образующей заготовки на угол b. Расчет геометрических параметров косозубых колес проводят по тем же формулам, что и для прямозубых цилиндрических колес, подставляя вместо нормального m торцовый mt модуль. Торцовый модуль с нормальным связан следующим соотношением:
Тогда диаметр косозубого колеса можно представить в следующем виде
. (6.19)
Сечение делительного цилиндра, нормального к линии зуба, является эллипс (рис.6.7) с полуосями с = 0,5×d и е = 0,5×d / cosb. Радиус и диаметр кривизны этого эллипса в полюсе зацепления составляют
, http://pandia.ru/text/79/022/images/image016_9.gif”>. (6.21)
http://pandia.ru/text/79/022/images/image018_7.gif”>.gif”>, (6.22)
где a – угол профиля зуба, a = 200 при нарезании зубьевбес смещения инструмента.
http://pandia.ru/text/79/022/images/image018_7.gif”>. (6.23)
Осевая сила, направленная по оси, составляет OZ
http://pandia.ru/text/79/022/images/image025_2.gif”>Рис.6.9. Схема усилий в зацеплении косозубых колес
Геометрическая сумма окружной Ft и осевой Fa сил представляет собой силу Fta, направленную вдоль нормали к зубу под углом к образующей цилиндра b, может быть вычислена по зависимости
Тогда радиальная сила, направленная по оси OY, имеет вид
. (6.26)
Нормальная к поверхности зуба сила составляет
. (6.27)
Расчет зубчатых передач на прочность начинается с определения расчетной нагрузки
http://pandia.ru/text/79/022/images/image030_1.gif”>. (6.28)
На прочность зубьев влияют факторы, которые учитываются коэффициентами. Коэффициент нагрузки К удобно представить в виде произведения частных коэффициентов, учитывающие отдельные факторы
. (6.29)
Коэффициент распределения нагрузки между зубьями Кa учитывает погрешности изготовления зубчатых колес двухпарного зацепления. Физический смысл заключается в следующем: в процессе зацепления без нагрузки только одна пара зубьев контактирует, вторая пара зубьев вследствие погрешностей изготовления не соприкасаются. При нагружении происходит упругая деформация первой пары зубьев и вторая пара также входит в контакт, но она воспринимает меньшую нагрузку. Коэффициент распределения нагрузки между зубьями для косозубых передач, имеющих двухпарное зацепление, определяют в зависимости от степени точности изготовления, а для прямозубых передач, имеющих однопарное зацепление, Кa = 1.
Коэффициент концентрации Кb учитывает распределение нагрузки вдоль зуба. Вследствие деформации валов зубья колес без нагрузки контактируют не по линии, а в точке. Под нагрузкой контакт, вследствие упругой деформации зубьев, происходит по линии вдоль зуба, но в точке первоначального контакта напряжение будет выше. Коэффициент концентрации нагрузки зависит от расположения зубчатых колес относительно опор, ширины венца относительно диаметра колеса и твердости рабочих поверхностей зубьев.
Погрешности нарезания зубьев приводит к непостоянству мгновенного передаточного отношения, что обуславливает появление угловых ускорений звездочки, следовательно – динамических нагрузок. Такая дополнительная нагрузка и учитывается
коэффициентом динамичности КV, который определяют в зависимости от степени точности изготовления колес, твердости поверхности и окружной скорости колес.
ЗУБЧАТЫЕ ПЕРЕДАЧИ
П л а н л е к ц и и
1. Общие сведения.
2. Классификация зубчатых передач.
3. Геометрические параметры зубчатых колес.
4. Точность преобразования параметров.
5. Динамические соотношения в зубчатых зацеплениях.
6. Конструкция колес. Материалы и допускаемые напряжения.
1. Общие сведения
Зубчатая передача – это механизм, который с помощью зубчатого зацепления передает или преобразует движение с изменением угловых скоростей и моментов. Зубчатая передача состоит из колес с зубьями, которые сцепляются между собой, образуя ряд последовательно работающих кулачковых механизмов.
Зубчатые передачи применяют для преобразования и передачи вращательного движения между валами с параллельными, пересекающимися или перекрещивающимися осями, а также для преобразования вращательного движения в поступательное и наоборот.
Достоинства зубчатых передач:
1. Постоянство передаточного отношения i .
2. Надежность и долговечность работы.
3. Компактность.
4. Большой диапазон передаваемых скоростей.
5. Небольшое давление на валы.
6. Высокий КПД.
7. Простота обслуживания.
Недостатки зубчатых передач:
1. Необходимость высокой точности изготовления и монтажа.
2. Шум при работе со значительными скоростями.
3. Невозможность бесступенчатого регулирования передаточного отно-
шения i .
2. Классификация зубчатых передач
Зубчатые передачи, применяемые в механических системах, разнообразны. Они используются как для понижения, так и для повышения угловой скорости.
Классификация конструкций зубчатых преобразователей группирует передачи по трем признакам:
1. По виду зацепления зубьев . В технических устройствах применяются передачи с внешним (рис. 5.1,а ), с внутренним (рис. 5.1,б ) и с реечным (рис. 5.1,в ) зацеплением.
Передачи с внешним зацеплением применяются для преобразования вращательного движения с изменением направления движения. Передаточное отношение колеблется в пределах –0,1 i –10. Внутреннее зацепление применяется в том случае, если требуется преобразовывать вращательное движение с сохранением направления. По сравнению с внешним зацеплением передача имеет меньшие габаритные размеры, бóльший коэффициент перекрытия и повышенную прочность, но более cложна в изготовлении. Реечное зацепление применяется при преобразовании вращательного движения в поступательное и обратно.
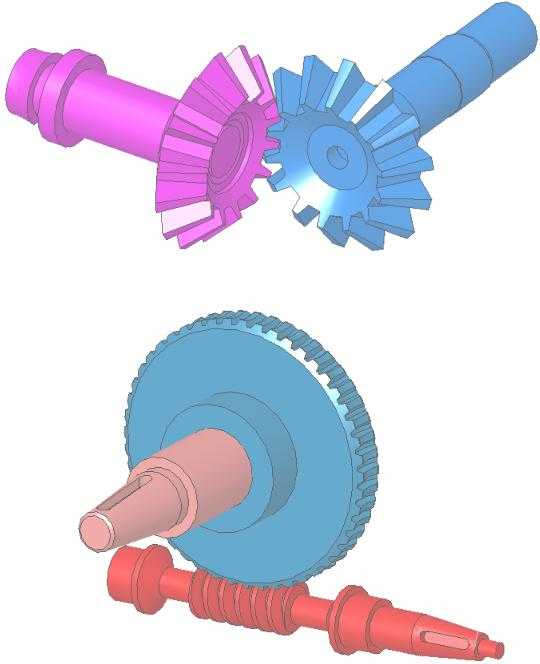
2 . По взаимному расположению осей валовразличают передачи цилиндрическими колесами с параллельными осями валов (рис. 5.1, а), коническими колесами с пересекающимися осями (рис. 5.2), колесами со скрещивающимися осями (рис. 5.3). Передачи c коническими колесами обладают меньшим передаточным отношением (1/6 i6), более сложны в изготовлении и эксплуатации, имеют дополнительные осевые нагрузки. Винтовые колеса работают с повышенным скольжением, быстрее изнашиваются, имеют малую нагрузочную способность. Эти передачи могут обеспечивать различные передаточные отношения при одинаковых диаметрах колес.
veloed.ru


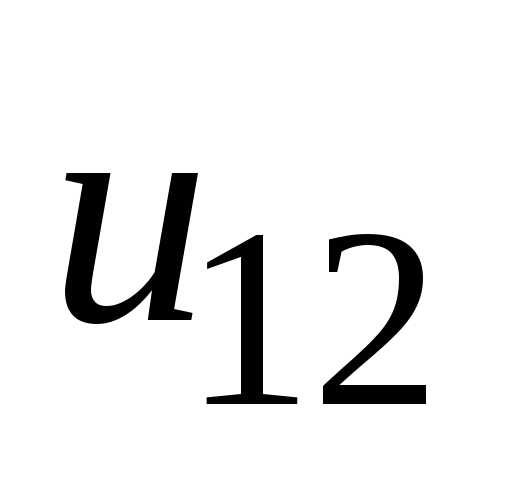
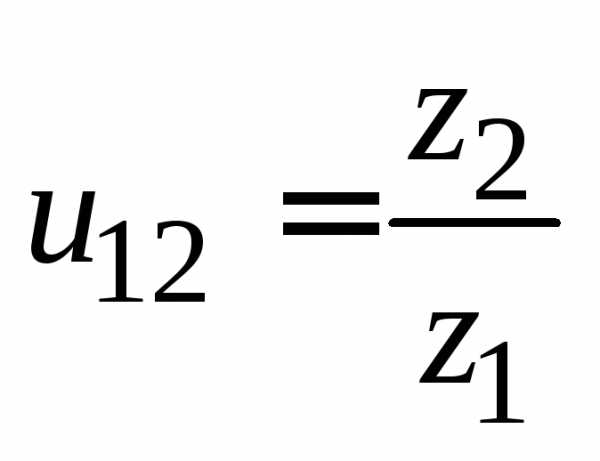
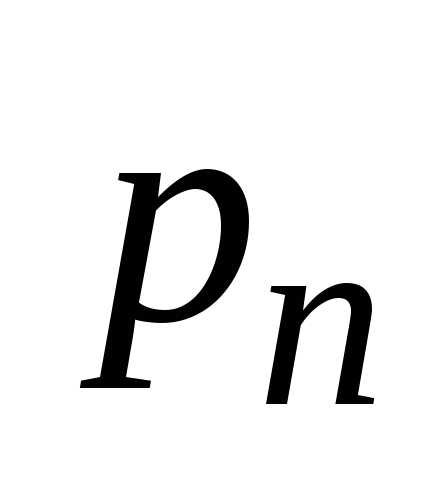
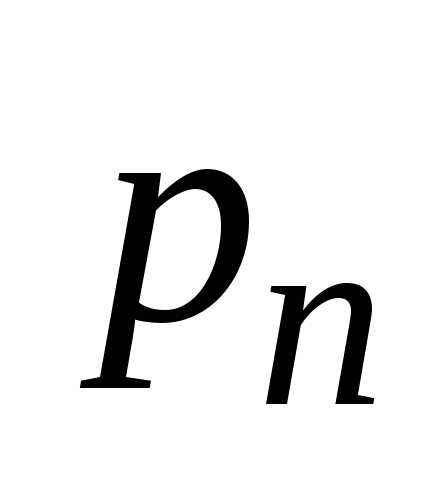 = m
= m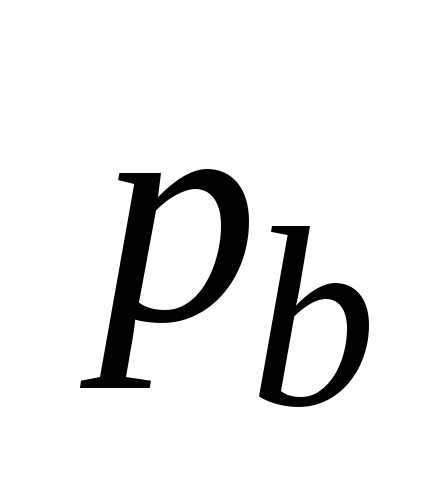
 =
m cos,
где
=
m cos,
где