Передаточное отношение это отношение – , —

alexxlab | 18.10.2018 | 0 | Вопросы и ответы

Передаточное отношение. Передаточное отношение зубчатой передачи :: SYL.ru

Рассматривая тему деталей машин, нельзя не уделить внимания такому важному техническому показателю, как передаточное отношение. Этот термин существует уже достаточно давно и о его значении в механике стоит поговорить отдельно.

Формулировка

Передаточное отношение – одна из самых важных технических характеристик любой механической передачи вращательного движения. С практической точки зрения, описываемый показатель позволяет понять, во сколько раз вырастает момент силы в результате функционирования передачи. Определение передаточных отношений в любом механизме – одна из самых главных задач в механике и машиностроении.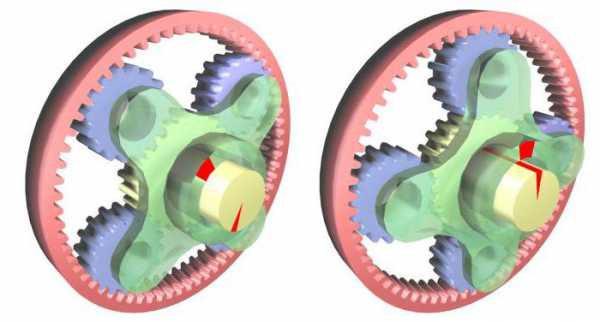

Некоторые тонкости

Передаточное отношение определяется при наличии как минимум двух зубчатых колес (шестерен), которые находятся в зацеплении между собой. Такое сопряжение именуется зубчатой передачей.

Самый простой способ рассчитать передаточное число – посчитать количество зубьев на каждом из имеющихся колес, а после произвести деление числа зубьев ведомой шестерни на количество колес ведущей шестерни. Данное рациональное число и будет являться передаточным отношением.

Важно иметь в виду, что в случае определения передаточного числа в зубчатой передаче, имеющей несколько шестерен, необходимо опять-таки делить количество зубьев ведущего колеса на количество ведомого. При этом параметры промежуточных шестерен не учитываются.

Обзор передач

На сегодняшний день существуют такие виды механических передач:

• Зубчатые.
• Ременные.
• Фрикционные.
• Червячные.
• Цепные.
• Храповые.
• Волновые.

В целом же, механические передачи разделяются по таким критериям:

• В зависимости от передачи движения от ведущего звена к ведомому: передачи трением и передачи зацеплением.
• В зависимости от соотношения скоростей ведомого и ведущего звеньев: замедляющие передачи (они же редукторы), ускоряющие передачи (мультипликаторы).
• В зависимости от расположения осей валов: передачи с перекрещивающимися, пересекающимися и параллельными осями.

Стоит указать, что замедляющие передачи на практике применяются гораздо чаще, нежели ускоряющие. Этот факт объясняется тем, что скорости вращения двигателей зачастую гораздо выше требуемой скорости вала исполнительного механизма или машины.

Зубчатая передача

Передаточное отношение зубчатой передачи можно вычислять не только по соотношению зубьев ее колес, но также путем деления значения угловой скорости ведомого вала на угловую скорость ведущего вала, а также благодаря соотношению числа оборотов ведомого и ведущего валов.

Диапазон передаточного отношения может быть очень велик и достигать больших значений. При этом само по себе передаточное отношение зубчатой передачи характеризуется постоянством, так как зацепление не подвержено проскальзыванию. Коэффициент полезного действия такой передачи находится в пределах 0,97-0,98.

Зубчатые передачи передают вращение между валами, которые могут иметь параллельные, скрещивающиеся или перпендикулярные оси. Кроме того, такие передачи способны трансформировать (преобразовывать) поступательное движение во вращательное и наоборот (передчи “винт-гайка”).

Зацепление в зубчатых передачах может быть как внешним, так и внутренним. Колеса изготавливаются с прямыми, косыми или шевронными зубьями.

Зубчатые передачи способны передавать большие скорости вращения с постоянным передаточным отношением и имеют высокий КПД.

Передаточное отношение редуктора является одним из важнейших критериев в процессе его выбора. Вторым по важности показателем считается межосевое расстояние.

Червячная передача

Используется для передачи вращательного движения в тех случаях, когда оси валов перекрещиваются.

Червяк может быть цилиндрическим или глобоидным в зависимости от поверхности расположения резьбы, а также может быть эвольвентным или архимедовым (в данном случае решающую роль играет профиль резьбы).

Основными недостатками описываемой передачи можно считать:

• Высокий показатель тепловыделения.
• Частое заедание и невысокий КПД.

Волновая передача

Ее работа основывается на принципе трансформации параметров движения благодаря волновому деформированию гибкого элемента механизма. По сути, такая передача является разновидностью планетарной передачи.

В состав волновой передачи входит жесткое колесо зубчатое, имеющее внутренние зубья, и вращающееся гибкое колесо с наружными зубьями. Оба колеса между собой входят в зацепление благодаря генератору волн, соединенному непосредственно с корпусом передачи.

За счет имеющихся конструктивных особенностей волновая передача наделена следующими достоинствами:

• Небольшие габариты и масса.
• Высокая кинематическая точность.
• Передаточное отношение передачи в одной ступени имеет большой показатель и вполне может достигать 300.
• Идеальная демпфирующая способность.
• Формирование в одной ступени большого передаточного отношения.

К недостаткам же относятся:

• Весьма сложная конструкция.
• Высокие потери мощности на трение и деформацию гибкого колеса (КПД составляет порядка 0,7-0,85).

Фрикционная передача

Чаще всего применяется в текстильной отрасли, станкостроении и прочих сферах промышленности, кроме авиастроения. Передаваемая мощность может достигать 10 кВт. При больших показателях очень трудно гарантировать требуемое усилие прижатия катков.

В передаче существует три вида скольжения: геометрическое, упругое и буксование.

Для нормально функционирующей передачи характерно именно упругое скольжение, в то время как буксование говорит о наличии перегрузки.

Ременная передача

Как и зубчатая она встречается очень часто. В зависимости от того, как располагаются валы и ремень, передача может быть:

• Открытой.
• Перекрестной.
• Полуперекрестной.
• Угловой.
• Спаренной.
• Ступенчатой.

Ремень может быть круглым, плоским, трапецеидальным.

Передаточное отношение в таких передачах находится в пределах 1:4, 1:5 и лишь в редких случаях может быть равно 1:8.

К положительным качествам ременной передачи следует отнести:

• Простоту конструкции.
• Возможность расположения обоих шкивов на большом расстоянии друг от друга (свыше 15 метров).
• Бесшумность и плавность работы.
• Защиту механизмов от перегрузок благодаря упругим свойствам ремня и его способности в определённые моменты проскальзывать по поверхностям шкивов.
• Работу при больших угловых скоростях.

Недостатками передачи являются:

• Удлинение ремней (их вытягивание) в процессе работы, то есть недолговечность.
• Непостоянство передаточного числа, что объясняется неизбежным проскальзыванием ремня.
• Достаточно большие размеры.

Цепная передача

В отличие от ременного аналога не подвержена проскальзыванию. Расчет передаточного отношения выполняется по аналогии с зубчатой передачей, ведь звездочки передачи, по сути, представляют собой те же зубчатые колеса.

Характерная особенность цепной передачи – вращение передается исключительно при наличии параллельных валов. Между осями звёздочек расстояние необходимо принимать не менее величины полутора диаметров большой звездочки. При этом передаточное число может достигать показателя 1:15.

Также важно заметить, что цепь надевается на звездочки не с натягом, как ремни, а с определенной степенью провисания. Регулировка натяжения проводится с помощью специального винта.

Достоинства передачи таковы:

• Небольшая чувствительность к неточностям установки валов.
• Передача вращения может осуществляться одной цепью сразу же нескольким звездочкам.
• Вращение может передаваться на большие расстояния.

Недостатком же является высокий шум и износ цепей в случае некачественного монтажа и при плохом техническом обслуживании.

Храповый механизм

Во многих машинах и агрегатах применяется не только непрерывное вращательное движение, но и прерывистое тоже, которое осуществляется с помощью храповика, собачки и рычага.

Храповый механизм помимо вращения еще и осуществляет предохранительную функцию. Так, например, в грузоподъемных лебедках, храповик совместно с собачкой не позволяют барабану проворачиваться в обратную сторону, надёжно фиксируя его в требуемом пространственном положении.

Рассмотренные виды механических передач применяются практически в любой отрасли народного хозяйства и получили широчайшее распространение благодаря своим техническим возможностям.

www.syl.ru

Передаточное отношение – это… Что такое Передаточное отношение?

Передаточное отношение() — одна из важных характеристик механической передачи вращательного движения, находится как отношение угловой скорости ведущего элемента () механической передачи к угловой скорости ведомого элемента() или отношение частоты вращения ведущего элемента () механической передачи к частоте вращения ведомого элемента () или отношение числа зубьев () (длины окружности, радиуса, диаметра) ведомого элемента к числу зубьев () (длине окружности, радиусу, диаметру) ведущего элемента механической передачи.

Характеристика передаточное отношение применима как к механической передаче с одной ступенью (одной кинематической парой), так и к механическим передачам со множеством ступеней. Во втором случае передаточное отношение всей механической передачи будет равно произведению передаточных отношений всех ступеней.^[1]

Механизмы с передаточным отношением больше единицы — редукторы (понижающие редукторы), меньше единицы — мультипликаторы (повышающие редукторы).

Величина, обратная передаточному отношению, называется передаточное число().

Тем не менее, в нынешнее время понятия передаточное отношение и передаточное число означают одно и то же. Например, ГОСТы 16532-70, 21354-87 и др. величину () называют передаточным числом, а многие каталоги редукторов ту же величину называют передаточным отношением.

См. также

Литература

1. Под ред. Скороходова Е. А. Общетехнический справочник. — М.: Машиностроение, 1982. — С. 416.
2. Гулиа Н. В., Клоков В. Г., Юрков С. А. Детали машин. — М.: Издательский центр “Академия”, 2004. — С. 416. — ISBN 5-7695-1384-5
3. Анурьев В. И. Справочник конструктора-машиностроителя: В 3 т. / Под ред. И. Н. Жестковой. — 8-е изд., перераб. и доп.. — М.: Машиностроение, 2001. — ISBN 5-217-02962-5

Примечания

1. ↑ Это неприменимо для планетарных передач.

dic.academic.ru

Передаточное отношение и передаточное число

Незаменимыми помощниками человека в любой его деятельности являются механизмы. Но сам по себе механизм – просто набор деталей. Для того чтобы он работал, его надо обеспечить энергией. Ее подают от отдельного устройства – двигателя или силовой установки при помощи специальных механизмов, называемых передачами. Так уж сложилось исторически – в технике чаще всего используется вращательное движение, хотя применяются и другие виды. При процессе перехода энергии она может меняться, это изменение происходит в соответствии с тем, какое передаточное отношение имеет механизм.

О том, что при этом происходит

Самый простой пример передачи – от вращающегося колеса водяной мельницы к жернову. При этом зачастую происходит изменение первоначальной энергии, полученной колесом от текущей воды, по величине и направлению. Величину такого изменения будет определять передаточное отношение. Оно описывает одну из важнейших характеристик преобразования энергии при вращательном движении, определяемую как отношение частоты или скорости вращения элемента, получающего энергию, к тем же параметрам элемента, отдающего энергию.

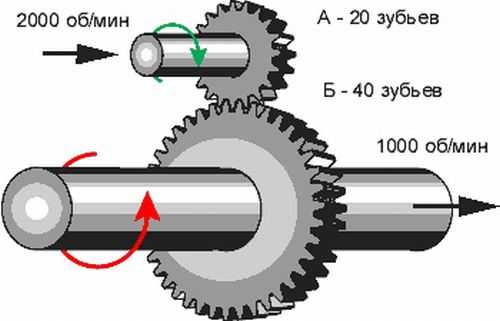
Иными словами, передаточное отношение описывает, как изменяется исходная энергия, получаемая от двигателя или любого другого источника энергии (водяного, ветряного колеса, турбины и т.д.), при ее передаче. За всю историю развития техники человечество создало самые разнообразные передачи, для каждой из которых существует передаточное число, являющимся частным от деления скорости ведущего звена на скорость ведомого.

Передаточное отношение ременной передачи

Ременной передачей называют два шкива, которые соединяет ремень, как это показано на рисунке. Возможно, что она была одним из первых способов, которые применял человек. Менялся материал, используемый для изготовления ремня, менялась его форма, но неизменным оставалось передаточное отношение, определяемое как частое от деления скорости ведущего вала, на скорость ведомого, или как результат деления числа оборотов этих валов (n1/n2 или ω1/ω2).

Для ременной передачи оно может быть рассчитано с использованием диаметров (радиусов) шкивов. Передаточное число в таком случае также определяется как частное от деления оборотов.

Если при преобразовании энергии число оборотов понижается, то есть передаточное число больше 1, то передача будет понижающей, а само устройство носит название редуктора. Если результат меньше единицы, то устройство называется мультипликатором, хотя оно также выполняет функции редуктора, только понижающего. Передаточное отношение редуктора позволяет уменьшить число оборотов (угловую скорость), поступающих с ведущего вала на ведомый, увеличив при этом передаваемый момент.

Это свойство редуктора дает возможность добиваться инженерам при проектировании различных устройств изменения параметров передаваемой энергии, а передаточное отношение редуктора служит при этом мощным инструментом в решении поставленной задачи.

Несмотря на значительный возраст, для ременной передачи и сейчас находится работа на автомобиле, она используется как привод генератора, газораспределительного механизма, а также в некоторых других случаях.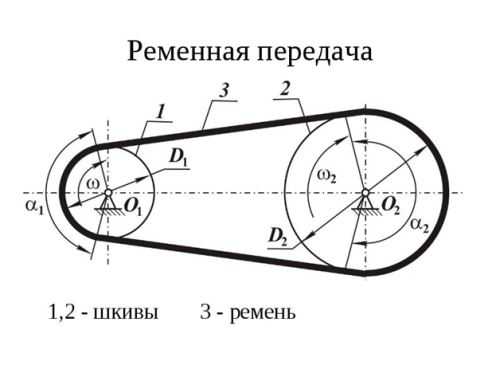

Передаточное отношение цепной передачи

В подобной ременной передаче ремень может быть заменен на цепь, в этом случае шкивы также должны быть заменены на звездочки. Полученная передача называется цепной, она знакома каждому, ведь именно такая применяется на велосипедах. Для нее передаточное отношение определяется так же, как для ременной, но можно воспользоваться и соотношением количества зубьев на звездочках (ведущей и ведомой). Однако при таком расчёте передаточное отношение будет обратным, то есть передаточное число определяется делением числа зубьев ведомой звездочки на число зубьев ведущей (z2/z1).

Отличительной особенностью цепной передачи является повышенный уровень шума, а также износ при работе на высоких скоростях, поэтому ее при необходимости использования лучше всего ставить после уменьшения оборотов. В автомобиле возможно применение цепной передачи для привода ГРМ, правда, ограничением такого применения является повышенный уровень шума при ее работе.

Передаточное отношение зубчатой передачи

Так называется механизм, в котором используются колеса с зубьями, находящимися в зацеплении. Она считается наиболее рациональной и востребованной для машиностроения. Существует множество разнообразных вариантов изготовления подобных колес, отличающихся по расположению осей, форме зубьев, способу их зацепления и т.д. Как в случае с цепной, для зубчатой передаточное число определяется делением числа зубьев шестерен (z2/z1).

Многообразие вариантов построения зубчатой передачи предоставляет возможность использовать их в разных условиях, от тихоходного редуктора до высокоточных приводов.

Для зубчатой передачи характерны:

• постоянное передаточное число;
• компактность;
• высокий кпд;
• надежность.

Одной из разновидностей зубчатой передачи считается червячная. Она используется в тех случаях, когда передача момента осуществляется между скрещивающимися валами, для чего применяется такой элемент как червяк, представляющий собой винт специальной конструкции с резьбой. Для определения передаточного отношения червячной передачи выполняют деление количества зубьев колеса (червячного) z2 на число заходов резьбы червяка z1.

Планетарная передача

Этот вид зубчатой передачи, содержащей колеса с геометрическими осями, имеющими возможность перемещения. Что она собой представляет, можно понять из приведенного ниже рисунка. По сути дела, это уже конструкция своеобразного планетарного редуктора, включающего в свой состав некоторое число шестерен, взаимодействующих между собой. У каждой из них свое название – солнце, корона, сателлит.

Для такого планетарного редуктора изменение момента зависит от того, какая из его шестерен неподвижна, на какую подан крутящий момент, и с какой он снимается.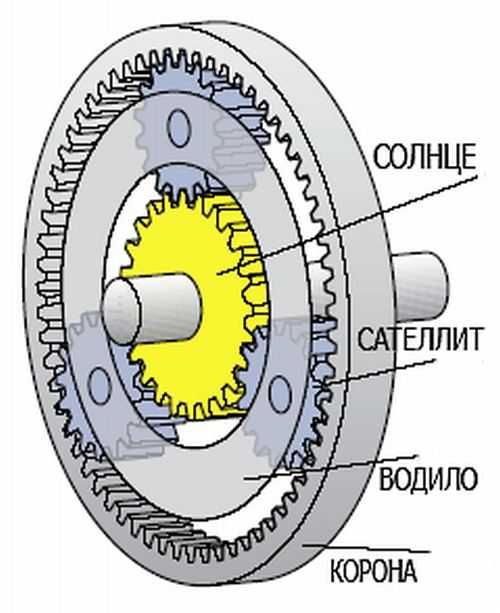

При любом использовании планетарного редуктора, один из трех его элементов будет неподвижен. У такого, планетарного варианта построения передач, по отношению к простой зубчатой или ременной, есть возможность получить существенное изменение момента при небольшом количестве колес и габаритах устройства. В автомобиле у подобного планетарного устройства своя сфера применения – в составе АКПП, а также в гибридных транспортных средствах, для обеспечения совместной работы ДВС и электромотора. Широкое применение планетарного редуктора осуществляется в гусеничной технике.

О главной паре

Практически все виды передач используются в автомобиле – крутящий момент от двигателя проходит цепочку различных устройств и претерпевает изменения, начиная от КПП, главной пары, и заканчивая колесами автомобиля. Все передаточные отношения для КПП и главной пары влияют непосредственным образом на динамику автомобиля.
Поэтому с целью

1. уменьшения частоты переключения;
2. возможности движения при спокойной езде на небольших оборотах двигателя;
3. повышения верхнего порога скорости движения,

передаточные отношения, в том числе и для главной пары, должны быть уменьшены. Для улучшения разгонной динамики все должно быть наоборот.

Работа различных механизмов и устройств, в том числе и в автомобиле, не может происходить без преобразования используемой энергии, как по величине, так и по направлению. Оценить и рассчитать величину необходимого изменения, а также его последствия, помогает передаточное отношение.

znanieavto.ru

Зубчатые передачи Общие положения

Зубчатые передачи предназначены для передачи вращательного движения от одного вала к другому, а также для изменения величины и направления угловой скорости валов. Пару зубчатых колес, находящихся в зацеплении друг с другом, называют ступенью.

Все зубчатые одноступенчатые передачи можно разделить на цилиндрические, конические и гиперболоидные.

Кинематические схемы зубчатых передач: а – цилиндрическая;

б – коническая; в – гиперболоидная

По характеру расположения осей вращения передачи бывают с параллельными, пересекающимися и перекрещивающимися осями.

В цилиндрических передачах оси валов параллельны. По характеру расположения зубьев на зацепляющихся колесах они разделяются на прямозубые, косозубые и шевронные.

В конических передачах оси валов пересекаются. Наиболее распространены конические передачи с прямым углом между осями валов.

В гиперболоидных передачах оси валов перекрещиваются. В свою очередь эти передачи подразделяются на гипоидные, винтовые и червячные. Последние являются частным случаем винтовых передач и состоят из червяка и червячного колеса.

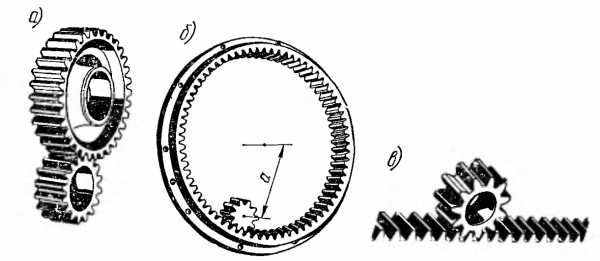
Прямозубые передачи

а – с наружным зацеплением

б – с внутренним зацеплением

в – реечная передача

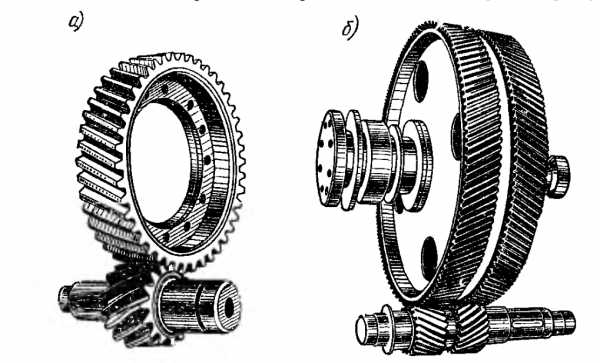
а – косозубая передача

б – шевронная передача

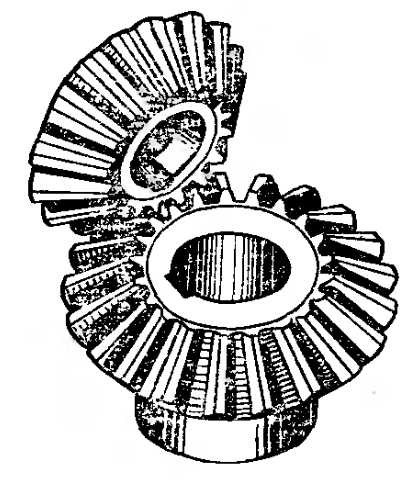
Коническая передача

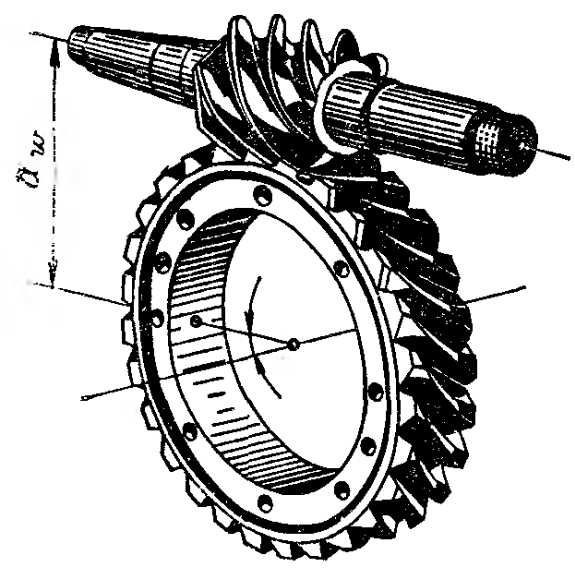
Червячная передача

Преимуществами зубчатых передач перед другими (фрикционными, ременными, цепными) являются постоянство передаточного отношения, высокий механический кпд, долговечность и компактность.

Недостатком является то, что наличие высшей кинематической пары в месте контакта зубьев приводит к большим контактным напряжениям, тем самым при их эксплуатации приходится ограничивать величину передаваемых усилий, упрочнять поверхности зубьев в зоне их контакта, применять систему смазки колес.

Передаточное отношение

Передаточное отношение – это отношение угловых скоростей взаимодействующих (зацепляющихся) зубчатых колес. Если взаимо-действие колес внешнее, то их передаточное отношение отрицательно (U_1-2 < 0), (рис. 5.2), если взаимодействие внутреннее, то U_1-2 > 0 (рис. 5.3). Знак «+» указывает на совпадение векторов угловых скоростей (направлений вращения колес).

Численно величина передаточного отношения ступени равна отношению угловых скоростей , (1/с), частот вращений, (об/мин), или обратному отношению количества зубьев колес:

.

Пара зубчатых колес с внешним зацеплением: 1, 2 – зубчатые колеса

Пара зубчатых колес с внутренним зацеплением: 1, 2 – зубчатые колеса

Передаточное отношение сложных (многоступенчатых) зубчатых передач (рис. 5.4) равно произведению передаточных отношений ступеней:

,

где – передаточные отношения ступеней.

Двухступенчатая зубчатая передача

Например, для двухступенчатой зубчатой передачи, кинематическая схема которой представлена на рис. величина передаточного отношения

.

Основные геометрические параметры зубчатого колеса цилиндрической передачи

Рассмотрим геометрические параметры зубчатого колеса цилиндрической передачи в плоскости, перпендикулярной оси его вращения.

Каждый зуб колеса имеет ось симметрии, проходящую через ось вращения колеса О. Угол между осями симметрии называется угловым шагом τ. Число зубьев колеса z=2π/τ (если τ измеряется в радианах) или z=360º/ τ (если τ измеряется в угловых градусах). Внешняя граница зуба очерчивается окружностью выступов радиусом r_a, а внутренняя часть впадины – окружностью впадин радиусом r_f.

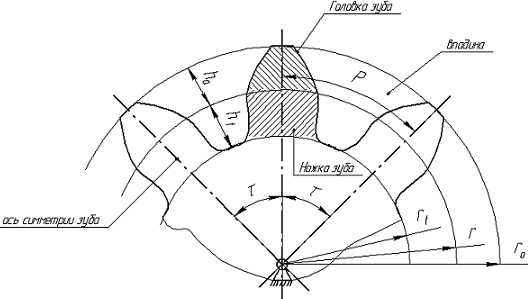
Геометрические параметры зубчатого колеса

Окружность радиусом r делит зуб по высоте на головку и ножку. Расстояние между одноименными профилями соседних зубьев по дуге этой окружности (или между соседними осями симметрии зубьев) называется окружным шагом P.

Длина окружности диаметром d=2 π r

L=Pz= πd,

откуда

d=(P/π)×z.

Величину P/π = m называют модулем. На него введен ГОСТ 9563-60, в соответствии с которым при расчетах геометрических параметров зуб-чатых колес его выбирают из стандартного ряда в пределах m = 0,05…100 мм.

Окружность, по которой модуль m является стандартной величиной, называется делительной окружностью с диаметром d = m×z или радиусом r = (m×z)/2.

Все остальные геометрические параметры зубчатого колеса в соответствии с ГОСТом пропорциональны модулю m:

высота головки зуба h_a = m;

высота ножки зуба h_f = 1,25 m;

высота зуба h = h_a+h_f = 2,25 m;

радиус окружности выступов

радиус окружности впадин

окружной шаг P=π×m;

толщина зуба по делительной окружности

ширина впадин по делительной окружности

Ширину колеса принимают в пределах в = (10…30)m. Межосевое расстояние двух зацепляющихся колес нулевого зацепления

,

где r₁ и r₂ – радиусы делительных окружностей зацепляющих колес; z₁ и z₂ – число их зубьев.

В зацепление друг с другом могут входить только зубчатые колеса, имеющие одинаковый модуль m и окружной шаг P.

29

studfiles.net

16. Передаточное отношение. Виды передач.

Передаточное отношение – это отношение мгновенных угловых или линейных скоростей ведущего и ведомого звеньев. u = ω1/ω2.

Зубчатая и червячная передачи. Зубчатая передача является связующим звеном двух или более валов, либо вала с рейкой. Зубчатая передача от ведущего вала к ведомому служит для того, чтобы крутящие моменты и угловые скорости этих валов находились в требуемом отношении по величине и направлению.

Передаточным отношением зубчатой пары называется отношение угловых скоростей сопряженных зубчатых колес. В зависимости от числа ступеней, участвующих в изменении угловой скорости между ведущим и ведомым валами, зубчатые колеса разделяются на одноступенчатые, двухступенчатые, трехступенчатые и т. д.

Ременные передачи.Ременная передача осуществляется при помощи двух шкивов, закрепленных на валах, и надетого на эти шкивы с натяжением бесконечного ремня, имеющего прямоугольное, трапециевидное и реже круглое сечение (плоские, клиновые и круглые ремни. Наибольшее распространение получили плоские ремни — кожаные, хлопчатобумажные, пропитанные резиной, или хлопчатобумажные тканые.

Для создания и поддержания натяжения ремня в плоскоременной передаче применяют натяжной ролик

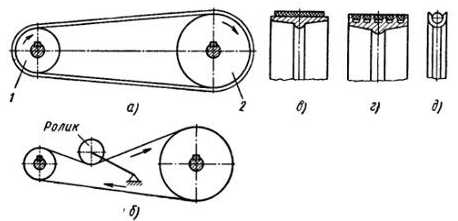
Цепная передача.Применяемые в станках цепи по характеру выполняемой работы делятся на три основные группы: приводные, грузовые и тяговые. Приводные цепи в большинстве случаев осуществляют передачу от источника движения или какого-либо передаточного механизма к приемному узлу станка. Цепи могут работать с большими скоростями (до 30 м/сек), как при малых, так и при больших межцентровых расстояниях. Приводные цепи имеют ту особенность, что одной цепью можно соединить и приводить в движение одновременно несколько валов.

Фрикционная передача.Фрикционные передачи нашли применение в приводах главного движения и приводах подачи универсальных станков.

Планетарные эпициклические передачи.Планетарным зубчатым механизмом называется механизм, имеющий зубчатые колеса с движущимися геометрическими осями. Такие колеса называются планетарными или сателлитами. Система, которая несет оси сателлитов, называется водилом. Колеса с неподвижными осями, по которым обкатываются сателлиты, называются центральными. Неподвижные центральные колеса называются опорными. Эпициклические механизмы применяются для получения больших передаточных отношений и для цепей суммирования двух независимых движений в механизмах затыловочных, расточных, зуборезных, автоматических станков и в делительных головках фрезерных станков.

17. Точение. Геометрия токарного резца. Классификация токарных резцов. Операции, выполняемые на токарных станках.

Токарная обработка (точение) — это механическая обработка резанием наружных и внутренних поверхностей вращения, в том числе цилиндрических и конических, торцевание, отрезание, снятие фасок, обработка галтелей, прорезание канавок, нарезание внутренних и наружных резьб на токарных станках.

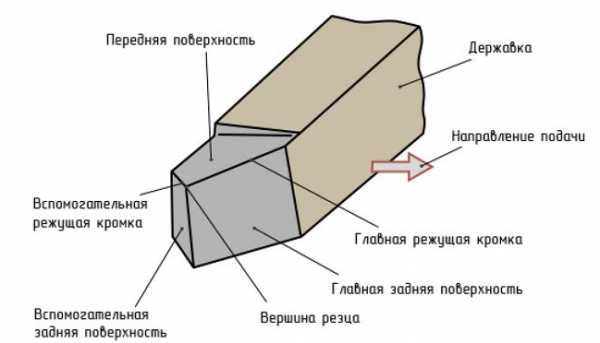
Классификация токарных резцов

Для токарной обработки применяют разнооб­разные резцы. В зависимости от направления движения подачи различают левые и пра­вые резцы.

По форме и расположению головки относительно стержня резцы могут быть прямые, отогнутые и оттянутые.

По назначению различают проходные, упорные, подрезные (торцовые), прорезные, отрезные, фасонные, резьбовые и расточные резцы.

Инструментальные материалы делят на сле­дующие три группы.

Первая группа — материалы дня инструмен­тов, работающих на низких скоростях резания. К ним относятся высококачественные углеродистые инструментал ь-ные стали (У10А, У11А, У12А)

Вторая группа — материалы для инструментов, работающих на повышенных скоростях реза­ния, — быстрорежущие стали Р9, Р12.

Третья группа — материалы для инструментов, работающих на высоких скоростях резания,-металлокерамические твердые сплавы, выпускаемые в виде пластинок раз­личных размеров и форм.

Классификация резцов по способу крепления режущей части. а-цельный, б-сварной, в-с наплавленной пластинкой, г-с механическим креплением пластинки.

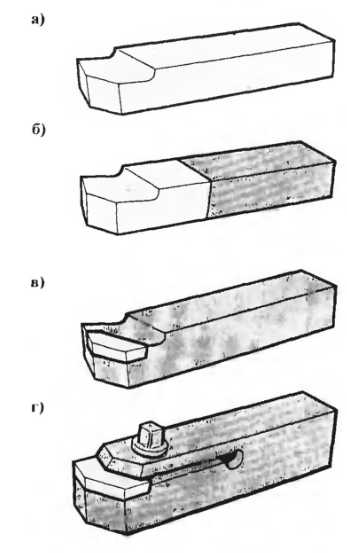
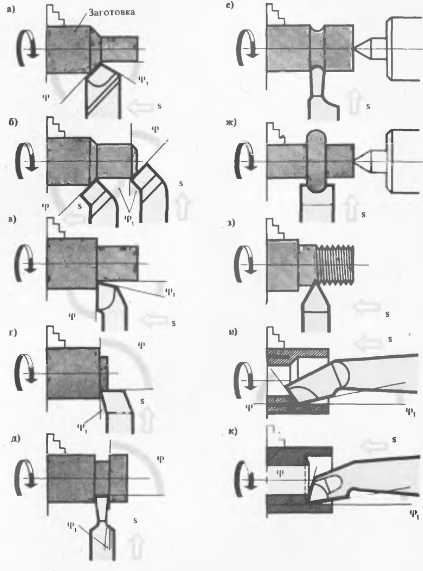
Основные операции на токарных станках.

Обтачивание гладких цилиндрических поверхностей. Гладкие цилиндрические поверхности деталей обтачивают проходными резцами в два приема. Сначала черновым резцом производят обдирку — грубое обтачивание, — быстро снимая основную массу лишнего металла.

Подрезание торцов и уступов.Для подрезания торцов и уступов на токарном станке пользуются обычно подрезными резцами.

Вытачивание канавокДля вытачивания канавок служат прорезные резцы. Их режущая кромка точно воспроизводит форму канавки. Так как ширина канавок обычно невелика, режущую кромку прорезного резца приходится делать узкой, поэтому она получается довольно ломкой. Для повышения прочности такого резца высоту его головки делают в несколько раз больше ширины.

Вытачивание конусов. В практике юного токаря вытачивание конусов будет встречаться реже, чем другие работы. Наиболее простой способ— точение небольших конусов (не более 20 мм) специальным широким резцом.

Обработка внутренних поверхностей.Обработка отверстий может производиться различными инструментами, в зависимости от требуемой формы поверхности и точности обработки.

Сверление и рассверливание. Неглубокие отверстия на токарном станке сверлят перовыми и спиральными (цилиндрическими) сверлами. Перовое сверло имеет плоскую лопатку с двумя режущими кромками, переходящую в стержень. Точность отверстия при обработке перовым сверлом невелика, поэтому его употребляют тогда, когда большой точности не требуется.

И другие.

studfiles.net

8.4: Передаточное отношение

Передачи используются не только для передачи мощности, но также для обеспечения возможности настройки механического преимущества для механизма. Как обсуждалось во введении к данному блоку, в некоторых случаях электромотор сам по себе обладает достаточной мощностью для выполнения конкретной задачи, но выходные характеристики электромотора не соответствуют требованиям. Электромотор, который вращается ОЧЕНЬ быстро, но при очень малом крутящем моменте , не подходит для подъема тяжелого груза. В таких случаях возникает необходимость использования передаточного отношения для изменения выходных характеристик и создания баланса крутящего момента и скорости.

Представьте себе велосипед: велосипедист обладает ограниченной мощностью, и хочет обеспечить максимальное использование этой мощности в любой момент времени.

Путем изменения механического преимущества изменяется скорость движения. Мощность представляет собой количество проделанной работы в единицу времени. Чем больше количество работы. тем ниже скорость ее выполнения.

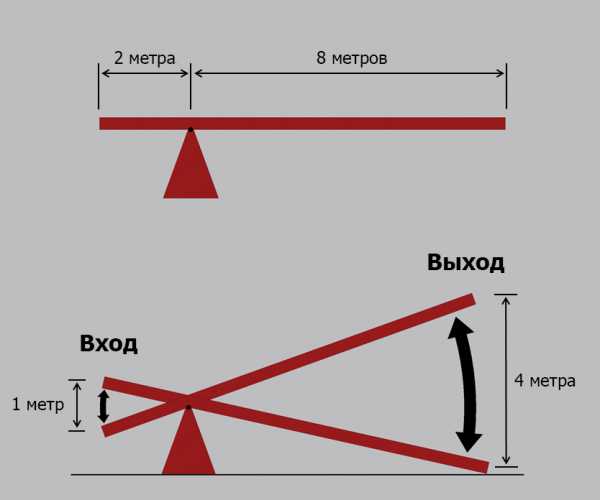
Пример 8.1

В примере 8.1 показано, что если на стороне входа рычаг сместится на 1 метр, на стороне выхода рычаг сместится на 4 метра. Разница пропорциональна соотношению между длинами рычагов.

Длина на выходе / Длина на входе = 8 / 2 = 4

Интересно то, что оба расстояния преодолеваются за одно и то же время. Давайте представим, что смещение рычага на входе на 1 метр происходит за 1 секунду, так что скорость движения на входе составляет 1 метр в секунду. В то же время, на выходе смещение на 4 метра также происходит за 1 секунду, так что скорость движения здесь составляет 8 метров в секунду. Скорость на выходе БОЛЬШЕ скорости на входе за счет соотношения между длинами рычагов.

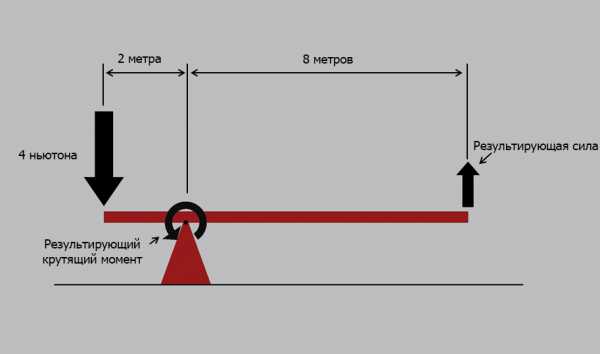
Пример 8.2

В примере 8.2 представлена та же система, что и в примере 8.1, но теперь на вход действует сила, равная 4 ньютонам. Какова равнодействующая сила на выходе?

Прежде всего, необходимо рассчитать приложенный момент в центре вращения, вызванный входной силой, с помощью формул из Блока 7:

Крутящий момент = Сила х Расстояние от центра гравитации = 4 Н х 2 м = 8 Н-м

Далее, необходимо рассчитать равнодействующую силу на выходе:

Сила = Крутящий момент / Расстояние = 8 Н-м / 8 м = 1 ньютон

Глядя на эти два примера, мы видим, что если система смещается на 1 метр под действием входной силы, равной 4 ньютона, то на выходе она сместится на 4 метра под действием силы, равной 1 ньютон. При меньшей силе рычаг смещается быстрее!

Мы можем видеть, как механическое преимущество (выраженное в форме рычагов) может быть использовано для управления входной силой в целях получения требуемого выхода. Передачи работают по тому же принципу.

Цилиндрическая прямозубая шестерня по сути представляет собой серию рычагов. Чем больше диаметр шестерни, тем длиннее рычаг.

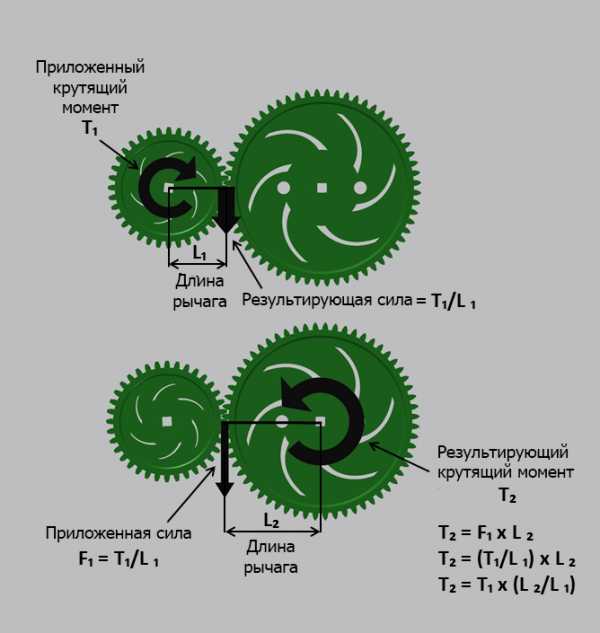
Пример 8.3

Как видно из примера 8.3, результатом крутящего момента, приложенного к первой шестерне, является линейная сила, возникающая на кончиках ее зубьев. Эта же сила воздействует на кончики зубьев шестерни, с которой зацепляется первая шестерня, заставляя вторую вращаться по действием крутящего момента. Диаметры шестерен становятся длиной рычагов, при этом изменение крутящего момента равносильно соотношению диаметров. Если малые шестерни приводят в движение больше шестерни, крутящий момент увеличивается. Если большие шестерни приводят в движение малые шестерни, крутящий момент уменьшается.

Пример 8.4

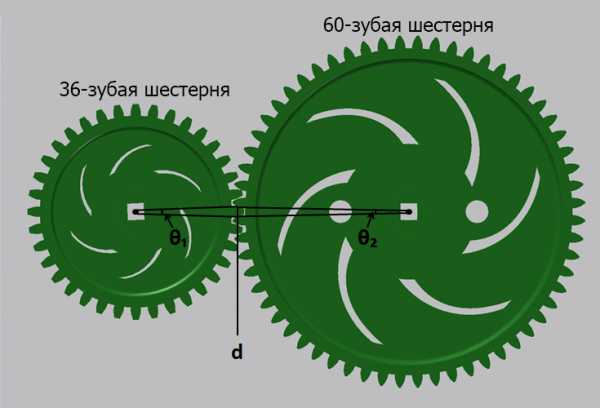
В примере 8.4, если входная 36-зубая шестерня поворачивается на расстояние одного зуба (d = ширина 1 зуба), это означает, что она поворачивается на 1/36-ю своего полного оборота (а1 = 360 / 36 = 10 градусов). Поворачиваясь, она приводит в движение 60-зубую шестерню, заставляя последнюю смещаться также на 1 зуб. Тем не менее, для 60-зубой шестерни это означает смещение всего лишь на 1/60-ю полного оборота (а2 = 360 / 60 = 6 градусов).

Когда малая шестерня проходит определенное расстояние в заданный интервал времени, большая шестерня при этом проходить меньшее расстояние. Это означает, что большая шестерня вращается медленнее малой. Этот принцип работает в обоих направлениях. Если малые шестерни приводят в движение больше шестерни, скорость понижается. Если большие шестерни приводят в движение малые шестерни, скорость повышается.

Из примеров 8.1 – 8.4 видно, что отношение между размерами двух зацепляющихся между собой шестерен пропорционально изменению крутящего момента и скорости между ними. Это называется передаточным числом.

Как обсуждалось выше, количество зубьев шестерни прямо пропорционально ее диаметру, поэтому для расчета передаточного отношения вместо диаметра можно просто считать зубья.

Передаточное отношение выражается как (зубья ведущей шестерни) : (зубья ведомой шестерни), поэтому представленная выше пара шестерен может быть описана как 12:60 (или 36 к 60).

Передаточное число рассчитывается по формуле (зубья ведомой шестерни) / (зубья ведущей шестерни)

Поэтому передаточное число = зубья ведомой шестерни / зубья ведущей шестерни = 60/36 = 1,67

 

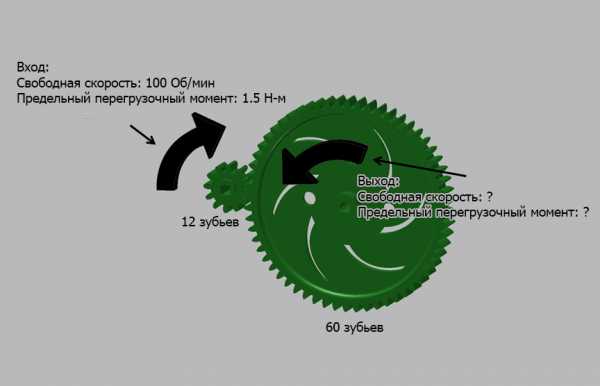
Как обсуждалось выше, передаточное отношение выражается как (зубья ведущей шестерни) : (зубья ведомой шестерни), так что пара шестерен, представленная выше, может быть выражена как 12:60 (или 12 к 60).

Передаточное число рассчитывается по формуле (зубья ведомой шестерни) / (зубья ведущей шестерни)

Поэтому передаточное число = Зубья ведомой шестерни / Зубья ведущей шестерни = 60/12 = 5

Глядя на пример, представленный выше…

Предельный перегрузочный момент второго вала может быть рассчитан по формуле:

Выходной момент = Входной момент х Передаточное число

Выходной момент = 1,5 Н-м х 5 = 7,5 Н-м

Свободная скорость второго вала может быть рассчитана по формуле:

Выходная скорость = Входная скорость / Передаточное число = 100 об/мин / 5 = 20 об/мин

Второй вал, таким образом, вращается со свободной скоростью 20 об/мин, при этом предельный перегрузочный момент равен 7,5 Н-м. При понижении скорости крутящий момент увеличивается.

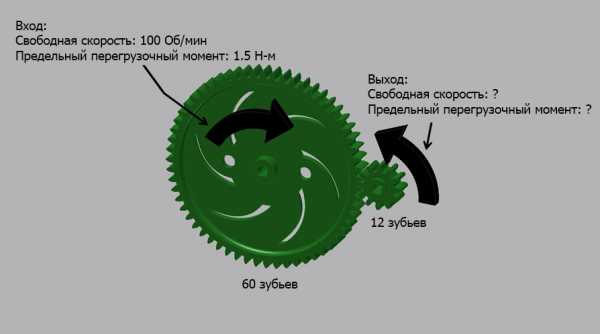
Для второго примера расчеты могут быть произведены тем же способом.

Передаточное число = Зубья ведомой шестерни / Зубья ведущей шестерни = 12/60 = 0,2

Выходной момент = Входной момент х Передаточное число = 1,5 Н-м х 0,2 = 0,3 Н-м

Выходная скорость = Входная скорость / Передаточное число = 100 об/мин / 0,2 = 500 об/мин

Второй вал, таким образом, вращается со свободной скоростью 500 об/мин, при этом предельный перегрузочный момент равен 0,3 Н-м. При повышении скорости крутящий момент уменьшается.

 

vex.examen-technolab.ru

Передаточное отношение – это… Что такое Передаточное отношение?



Передаточное отношение

        одна из основных характеристик механизмов, в том числе передач вращательного движения, определяемая как отношение угловых скоростей или частот вращения звеньев. Обычно имеется в виду отношение угловой скорости ведущего звена передачи к угловой скорости ведомого звена Редукторы, планетарные редукторы, коробки передач (См. Коробка передач) и т.д.). П. о. ряда последовательно соединённых передач равно произведению П. о. этих передач.          Наряду с П. о. широко используется (особенно для передач зацеплением) понятие Передаточное число.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

• Передаточная надпись
• Передаточное число

Смотреть что такое “Передаточное отношение” в других словарях:

• Передаточное отношение — Передаточное отношение( ) одна из важных характеристик механической передачи вращательного движения, находится как отношение угловой скорости ведущего элемента ( ) механической передачи к угловой скорости ведомого элемента( ) или отношение… …   Википедия

• передаточное отношение — Отношение угловых скоростей звеньев. Примечание При параллельных осях вращения передаточное отношение считается положительным при одинаковом направлении угловых скоростей звеньев, при непараллельных осях вращения передаточное отношение равно… …   Справочник технического переводчика

• ПЕРЕДАТОЧНОЕ ОТНОШЕНИЕ — (передаточное число) отношение частоты вращения (числа оборотов) ведущего вала механизма к частоте вращения (числу оборотов) ведомого вала. П. о. последовательно соединённых передач равно произведению их передаточных отношений. В простейших… …   Большая политехническая энциклопедия

• ПЕРЕДАТОЧНОЕ ОТНОШЕНИЕ — отношение угловых скоростей звеньев механизма (ведущего и ведомого). Передаточное отношение ряда последовательно соединенных передач равно произведению их передаточных отношений …   Большой Энциклопедический словарь

• Передаточное отношение — в системе управления отношение приращения угла отклонения (( ), рад) руля управления к приращению перемещения (x, м) рычага управления (РУ) лётчиком: kш = d( )/dx. П. о. может быть постоянным или переменным по перемещению РУ или по режимам полёта …   Энциклопедия техники

• передаточное отношение — отношение угловых скоростей звеньев механизма (ведущего и ведомого). Передаточное отношение ряда последовательно соединённых передач равно произведению их передаточного отношения. * * * ПЕРЕДАТОЧНОЕ ОТНОШЕНИЕ ПЕРЕДАТОЧНОЕ ОТНОШЕНИЕ, отношение… …   Энциклопедический словарь

• передаточное отношение — transmission ratio Отношение угловых скоростей двух звеньев. При параллельных осях вращения передаточное отношение считается положительным при одинаковом направлении угловых скоростей звеньев, при непараллельных осях передаточное отношение равно… …   Теория механизмов и машин

• передаточное отношение — Рис. 1. передаточное отношение в системе управления — отношение приращения угла отклонения (δ, рад) руля управления к приращению перемещения (x, м) рычага управления (РУ) лётчиком: kш = dδ/dx. П. о. может быть постоянным или переменным по… …   Энциклопедия «Авиация»

• передаточное отношение — Рис. 1. передаточное отношение в системе управления — отношение приращения угла отклонения (δ, рад) руля управления к приращению перемещения (x, м) рычага управления (РУ) лётчиком: kш = dδ/dx. П. о. может быть постоянным или переменным по… …   Энциклопедия «Авиация»

• передаточное отношение — pavaros skaičius statusas T sritis fizika atitikmenys: angl. gear ratio; transmission ratio vok. Übersetzungsverhältnis, n; Übersetzungszahl, f rus. передаточное отношение, n; передаточное число, n pranc. rapport de transmission, m; rapport… …   Fizikos terminų žodynas

• передаточное отношение — perdavimo santykis statusas T sritis automatika atitikmenys: angl. transfer ratio; transmission ratio vok. Übersetzungsverhältnis, n; Übersetzungszahl, f; Übertragungsfaktor, m rus. передаточное отношение, n pranc. rapport de transfert, m;… …   Automatikos terminų žodynas

dic.academic.ru