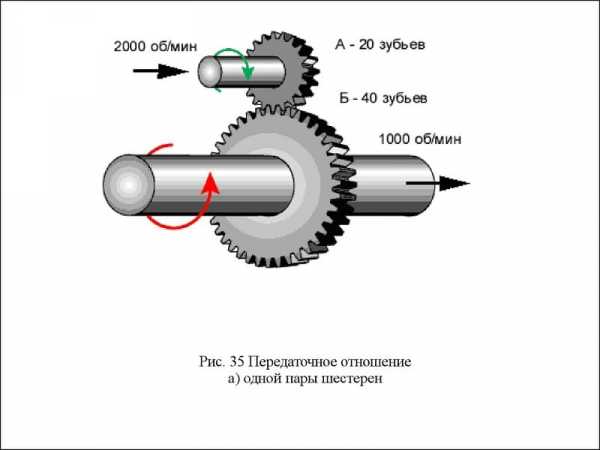
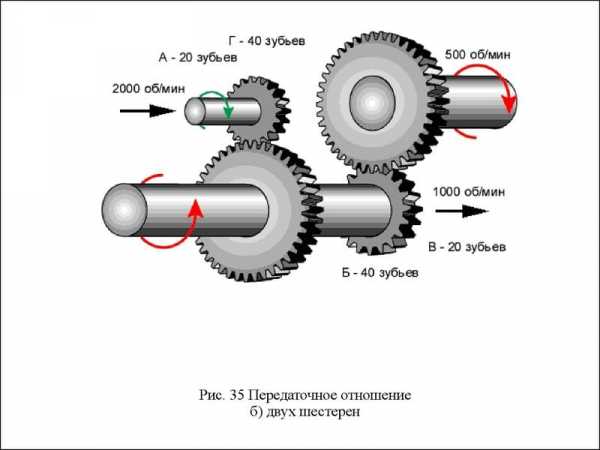
Передаточное отношение формула – . —

alexxlab | 26.03.2019 | 0 | Вопросы и ответы

Передаточное число: расчет, формула, определение

Любое подвижное соединение, передающее усилие и меняющее направление движения, имеет свои технические характеристики. Основным критерием, определяющим изменение угловой скорости и направления движения, является передаточное число. С ним неразрывно связано изменение силы – передаточное отношение. Оно вычисляется для каждой передачи: ременной, цепной, зубчатой при проектировании механизмов и машин.

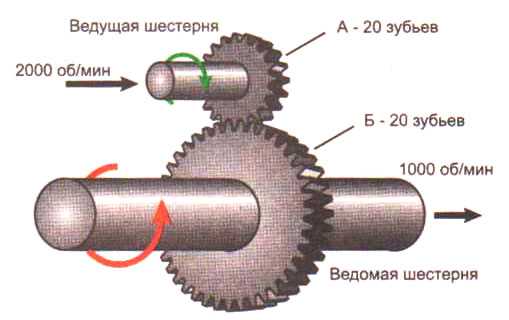
Перед тем как узнать передаточное число, надо посчитать количество зубьев на шестернях. Затем разделить их количество на ведомом колесе на аналогичный показатель ведущей шестерни. Число больше 1 означает повышающую передачу, увеличивающую количество оборотов, скорость. Если меньше 1, то передача понижающая, увеличивающая мощность, силу воздействия.

Общее определение

Наглядный пример изменения числа оборотов проще всего наблюдать на простом велосипеде. Человек медленно крутит педали. Колесо вращается значительно быстрее. Изменение количества оборотов происходит за счет 2 звездочек, соединенных в цепь. Когда большая, вращающаяся вместе с педалями, делает один оборот, маленькая, стоящая на задней ступице, прокручивается несколько раз.

Передачи с крутящим моментом

В механизмах используют несколько видов передач, изменяющих крутящий момент. Они имеют свои особенности, положительные качества и недостатки. Наиболее распространенные передачи:

• ременная;
• цепная;
• зубчатая.

Ременная передача самая простая в исполнении. Используется при создании самодельных станков, в станочном оборудовании для изменения скорости вращения рабочего узла, в автомобилях.

Ремень натягивается между 2 шкивами и передает вращение от ведущего в ведомому. Производительность низкая, поскольку ремень скользит по гладкой поверхности. Благодаря этому, ременной узел является самым безопасным способом передавать вращение. При перегрузке происходит проскальзывание ремня, и остановка ведомого вала.

Передаваемое количество оборотов зависит от диаметра шкивов и коэффициента сцепления. Направление вращения не меняется.

Переходной конструкцией является ременная зубчатая передача.

На ремне имеются выступы, на шестерне зубчики. Такой тип ремня расположен под капотом автомобиля и связывает звездочки на осях коленвала и карбюратора. При перегрузе ремень рвется, так как это самая дешевая деталь узла.

Цепная состоит из звездочек и цепи с роликами. Передающееся число оборотов, усилие и направление вращения не меняются. Цепные передачи широко применяются в транспортных механизмах, на конвейерах.

Характеристика зубчатой передачи

В зубчатой передаче ведущая и ведомая детали взаимодействуют непосредственно, за счет зацепления зубьев. Основное правило работы такого узла – модули должны быть одинаковыми. В противном случае механизм заклинит. Отсюда следует, что диаметры увеличиваются в прямой зависимости от количества зубьев. Одни значения можно в расчетах заменить другими.

Модуль – размер между одинаковыми точками двух соседних зубьев.

Например, между осями или точками на эвольвенте по средней линии Размер модуля состоит из ширины зуба и промежутка между ними. Измерять модуль лучше в точке пересечения линии основания и оси зубца. Чем меньше радиус, тем сильнее искажается промежуток между зубьями по наружному диаметру, он увеличивается к вершине от номинального размера. Идеальные формы эвольвенты практически могут быть только на рейке. Теоретически на колесе с максимально бесконечным радиусом.

Деталь с меньшим количеством зубьев называют шестерней. Обычно она ведущая, передает крутящий момент от двигателя.

Зубчатое колесо имеет больший диаметр и в паре ведомое. Оно соединено с рабочим узлом. Например, передает вращение с необходимой скоростью на колеса автомобиля, шпиндель станка.

Обычно посредством зубчатой передачи уменьшается количество оборотов и увеличивается мощность. Если в паре деталь, имеющая больший диаметр, ведущая, на выходе шестерня имеет большее количество оборотов, вращается быстрее, но мощность механизма падает. Такие передачи называют понижающими.

Зачем нужна паразитка

При взаимодействии шестерни и колеса происходит изменение сразу нескольких величин:

• количества оборотов;
• мощности;
• направление вращения.

Только в планетарных узлах с нарезкой зубьев по внутреннему диаметру венца сохраняется направление вращения. При наружном зацеплении ставится две одинаковые шестерни подряд. Их взаимодействие не меняет ничего, кроме направления движения. В этом случае обе зубчатые детали называются шестернями, колеса нет. Вторая, промежуточная, получила название «паразитка», поскольку в вычислениях не участвует, меняет только знак.

Виды зубчатых соединений

Зубчатое зацепление может иметь различную форму зуба на деталях. Это зависит от исходной нагрузки и расположения осей сопрягаемых деталей. Различают виды зубчатых подвижных соединений:

• прямозубая;
• косозуба;
• шевронная;
• коническая;
• винтовая;
• червячная.

Самое распространенное и простое в исполнении прямозубое зацепление. Наружная поверхность зуба цилиндрическая. Расположение осей шестерни и колеса параллельное. Зуб расположен под прямым углом к торцу детали.

Когда нет возможности увеличить ширину колеса, а надо передать большое усилие, зуб нарезают под углом и за счет этого увеличивают площадь соприкосновения. Расчет передаточного числа при этом не изменяется. Узел становится более компактным и мощным.

Недостаток косозубых зацеплений в дополнительной нагрузке на подшипники. Сила от давления ведущей детали действует перпендикулярно плоскости контакта. Кроме радиального, появляется осевое усилие.

Компенсировать напряжение вдоль оси и еще больше увеличить мощность позволяет шевронное соединение. Колесо и шестерня имеют 2 ряда косых зубьев, направленных в разные стороны. Передающее число рассчитывается аналогично прямозубому зацеплению по соотношению количества зубьев и диаметров. Шевронное зацепление сложное в исполнении. Оно ставится только на механизмах с очень большой нагрузкой.

В конической зубчатой передаче оси расположены под углом. Рабочий элемент нарезается по конической плоскости. Передаточное число таких пар может равняться 1, когда надо только изменить плоскость действия силы. Для увеличения мощности нарезается полукруглый зуб. Передающееся количество оборотов считается только по зубу, диаметр в основном используется при расчетах габаритов узла.

Винтовая передача имеет зуб, нарезанный под углом 45⁰. Это позволяет располагать оси рабочих элементов перпендикулярно в разных плоскостях.

У червячной передачи нет шестерни, ее заменяет червяк. Оси деталей не пересекаются. Они расположены перпендикулярно в пространстве, но разных плоскостях. Передаточное число пары определяется количеством заходов резьбы на червяке.

Кроме перечисленных производят и другие виды передач, но они встречаются крайне редко и к стандартным не относятся.

Многоступенчатые редукторы

Как подобрать нужное передаточное число. Двигатель обычно выдает несколько тысяч оборотов в минуту. На выходе – колесах автомобиля и шпинделе станка, такая скорость вращения приведет к аварии. Мощности исполняющего механизма не хватит, чтобы рабочий инструмент мог резать металл, а колеса сдвинули автомобиль. Одна пара зубчатого зацепления не сможет обеспечить требуемое понижение или ведомая деталь  должна иметь огромные размеры.

Создается многоступенчатый узел с несколькими парами зацеплений. Передаточное число редуктора считается как произведение чисел каждой пары.

U_р = U₁×U₂ × … ×U_n;

Где:

U_р – передаточное число редуктора;

U_1,2,n – каждой из пар.

Перед тем как подобрать передаточное число редуктора, надо определиться с количеством пар, направлением вращения выходного вала, и делать расчет в обратном порядке, исходя из максимально допустимых габаритов колес.

В многоступенчатом редукторе все зубчатые детали, находящиеся между ведущей шестерней на входе в редуктор и ведомым зубчатым венцом на выходном валу, называются промежуточными. Каждая отдельная пара имеет свое передающееся число, шестерню и колесо.

Редуктор и коробка скоростей

Любая коробка скоростей с зубчатым зацеплением является редуктором, но обратное утверждение неверно.

Коробка скоростей представляет собой редуктор с подвижным валом, на котором расположены шестерни разного размера. Смещаясь вдоль оси, он включает в работу то одну, то другую пару деталей. Изменение происходит за счет поочередного соединения различных шестерен и колес. Они отличаются диаметром и передающимся количеством оборотов. Это дает возможность изменять не только скорость, но и мощность.

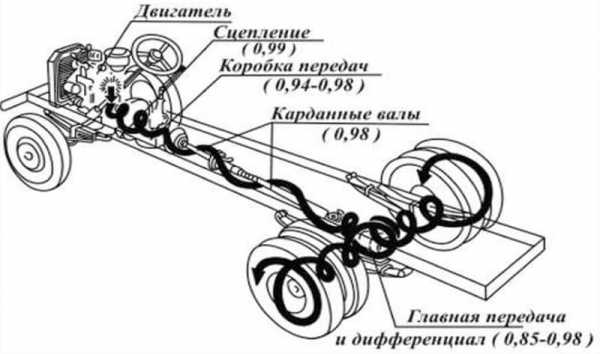
Трансмиссия автомобиля

В машине поступательное движение поршня преобразуется во вращательное коленвала. Трансмиссия представляет собой сложный механизм с большим количеством различных узлов, взаимодействующих между собой. Ее назначение — передать вращение от двигателя на колеса и регулировка количества оборотов – скорости и мощности автомобиля.

В состав трансмиссии входит несколько редукторов. Это, прежде всего:

• коробка передач – скоростей;
• дифференциал.

Коробка передач в кинематической схеме стоит сразу за коленвалом, изменяет скорость и направление вращения.

Посредством переключения – перемещения вала, шестерни на валу соединяются поочередно с разными колесами. При включении задней скорости, через паразитку меняется направление вращения, автомобиль в результате движется назад.

Дифференциал представляет собой конический редуктор с двумя выходными валами, расположенными в одной оси напротив друг друга. Они смотрят в разные стороны. Передаточное число редуктора – дифференциала небольшое, в пределах 2 единиц. Он меняет положение оси вращения и направление. Благодаря расположению конических зубчатых колес напротив друг друга, при зацеплении с одной шестерней они крутятся в одном направлении относительно положения оси автомобиля, и передают вращательный момент непосредственно на колеса. Дифференциал изменяет скорость и направление вращения ведомых коничек, а за ними и колес.

Как рассчитать передаточное число

Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.

Расчет без учета сопротивления

В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.

u₁₂ = ± Z₂/Z₁ и u₂₁ = ± Z₁/Z₂,

Где u₁₂ – передаточное число шестерни и колеса;

Z₂ и Z₁ – соответственно количество зубьев ведомого колеса и ведущей шестерни.

Знак «+» ставится, если направление вращения не меняется. Это относится к планетарным редукторам и зубчатым передачам с нарезкой зубцов по внутреннему диаметру колеса. При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».

При наружном соединении двух деталей посредством расположенной между ними паразитки, передаточное число вычисляется как соотношение количества зубьев колеса и шестерни со знаком «+». Паразитка в расчетах не участвует, только меняет направление, и соответственно знак перед формулой.

Обычно положительным считается направление движения по часовой стрелке. Знак играет большую роль при расчетах многоступенчатых редукторов. Определяется передаточное число каждой передачи отдельно по порядку расположения их в кинематической цепи. Знак сразу показывает направление вращения выходного вала и рабочего узла, без дополнительного составления схем.

Вычисление передаточного числа редуктора с несколькими зацеплениями – многоступенчатого, определяется как произведение передаточных чисел и вычисляется по формуле:

u₁₆ = u₁₂×u₂₃×u₄₅×u₅₆ = z₂/z₁×z₃/z₂×z₅/z₄×z₆/z₅ = z₃/z₁×z₆/z₄

Способ расчета передаточного числа позволяет спроектировать редуктор с заранее заданными выходными значениями количества оборотов и теоретически найти передаточное отношение.

Зубчатое зацепление жесткое. Детали не могут проскальзывать относительно друг друга, как в ременной передаче и менять соотношение количества вращений. Поэтому на выходе обороты не изменяются, не зависят от перегруза. Верным получается расчет скорости угловой и количества оборотов.

КПД зубчатой передачи

Для реального расчета передаточного отношения, следует учитывать дополнительные факторы. Формула действительна для угловой скорости, что касается момента силы и мощности, то они в реальном редукторе значительно меньше. Их величину уменьшает сопротивление передаточных моментов:

• трение соприкасаемых поверхностей;
• изгиб и скручивание деталей под воздействием силы и сопротивление деформации;
• потери на шпонках и шлицах;
• трение в подшипниках.

Для каждого вида соединения, подшипника и узла имеются свои корректирующие коэффициенты. Они включаются в формулу. Конструктора не делают расчеты по изгибу каждой шпонки и подшипника. В справочнике имеются все необходимые коэффициенты. При необходимости их можно рассчитать. Формулы простотой не отличаются. В них используются элементы высшей математики. В основе расчетов способность и свойство хромо-никелевых сталей, их пластичность, сопротивление на растяжение, изгиб, излом и другие параметры, включая размеры детали.

Что касается подшипников, то в техническом справочнике, по которому их выбирают, указаны все данные для расчета их рабочего состояния.

При расчете мощности, основным из показателей зубчатых зацепления является пятно контакта, оно указывается в процентах и его размер имеет большое значение. Идеальную форму и касание по всей эвольвенте могут иметь только нарисованные зубья. На практике они изготавливаются с погрешностью в несколько сотых долей мм. Во время работы  узла под нагрузкой на эвольвенте появляются пятна в местах воздействия деталей друг на друга. Чем больше площадь на поверхности зуба они занимают, тем лучше передается усилие при вращении.

Все коэффициенты объединяются вместе, и в результате получается значение КПД редуктора. Коэффициент полезного действия выражается в процентах. Он определяется соотношением мощности на входном и выходном валах. Чес больше зацеплений, соединений и подшипников, тем меньше КПД.

Передаточное отношение зубчатой передачи

Значение передаточного числа зубчатой передачи совпадает передаточным отношением. Величина угловой скорости и момента силы изменяется пропорционально диаметру, и соответственно количеству зубьев, но имеет обратное значение.

Чем больше количество зубьев, тем меньше угловая скорость и сила воздействия – мощность.

При схематическом изображении величины силы и перемещения шестерню и колесо можно представить в виде рычага с опорой в точке контакта зубьев и сторонами, равными диаметрам сопрягаемых деталей. При смещении на 1 зубец их крайние точки проходят одинаковое расстояние. Но угол поворота и крутящий момент на каждой детали разный.

Например, шестерня с 10 зубьями проворачивается на 36°. Одновременно с ней деталь с 30 зубцами смещается на 12°. Угловая скорость детали с меньшим диаметром значительно больше, в 3 раза. Одновременно и путь, который проходит точка на наружном диаметре имеет обратно пропорциональное отношение. На шестерне перемещение наружного диаметра меньше. Момент силы увеличивается обратно пропорционально соотношению перемещения.

Крутящий момент увеличивается вместе с радиусом детали. Он прямо пропорционален размеру плеча воздействия – длине воображаемого рычага.

Передаточное отношение показывает, насколько изменился момент силы при передаче его через зубчатое зацепление. Цифровое значение совпадает с переданным числом оборотов.

Передаточное отношение редуктора вычисляется по формуле:

U₁₂ = ±ω₁/ω₂=±n₁/n₂

где U₁₂ – передаточное отношение шестерни относительно колеса;

ω₁ и ω₂ – угловые скорости ведущего и ведомого элемента соединения;

n₁ и n₂ – частота вращения.

Отношение угловых скоростей можно считать через число зубьев. При этом направление вращения не учитывается и все цифры с положительным знаком.

Зубчатая передача имеет самый высокий КПД и наименьшую защиту от перегруза – ломается элемент приложения силы, приходится делать новую дорогостоящую деталь со сложной технологией изготовления.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

 

stankiexpert.ru

Передаточные отношения. Формулы для расчета передаточных отношений.

Металлы и Сварка Передаточные отношения. Формулы для расчета передаточных отношений.

Количество просмотров публикации Передаточные отношения. Формулы для расчета передаточных отношений. – 365

Наименование параметра	Значение
Тема статьи:	Передаточные отношения. Формулы для расчета передаточных отношений.
Рубрика (тематическая категория)	Металлы и Сварка

Передаточное отношение ( ) — одна из важных характеристик механической передачи вращательного движения. В общем случае находится как отношение угловой скорости ведущего элемента ( ) механической передачи к угловой скорости ведомого элемента ( ) или отношение частоты вращения ведущего элемента ( ) механической передачи к частоте вращения ведомого элемента ( ).

Передаточное отношение (иногда используется обозначение ) определяется при ведущем колесе 1, передаточное отношение определяется если ведущим является колесо 2: Знак плюс соответствует внутреннему зацеплению, а знак минус – внешнему.

,

.

40. планетарные механизмы.

Планетарным принято называть дифференциальный механизм, в случае если в нем одно из звеньев неподвижно. Планетарные механизмы используются:

1) в планетарных редукторах;

2) в планетарных механизмах включения и выключения;

3) в планетарных реверсивных механизмах;

4) в планетарных коробках передач;

5) в планетарных вариаторах, обеспечивающих бесступенчатое изменение величины передаточного отношения в больших пределах. Все эти механизмы надежны и легко управляемы, создают широкие возможности для их использования.

---

Передаточные отношения. Формулы для расчета передаточных отношений. – понятие и виды. Классификация и особенности категории “Передаточные отношения. Формулы для расчета передаточных отношений.” 2014, 2015.

referatwork.ru

Типовые планетарные механизмы

№	Структурная схема механизма	Uред	КПД
1		3….10	0.97….0.99
2		7….16	0.96….0.98
3		25….30	0.9….0.3
4		30….300	0.9….0.3

Формула Виллиса

Формула Виллиса выводится на основании основной теоремы зацепления и устанавливает соотношение между угловыми скоростями зубчатых колес в планетарном механизме. Рассмотрим простейший планетарный механизм с одним внешним и одним внутренним зацеплением. Всему механизму сообщается угловая скорость равная по величине и противоположна по направлению угловой скорости водила, при этом водило остановится, а опорное колесо начнет поворачиваться. Таким образом, планетарный механизм превратится в механизм с неподвижными осями, состоящий из нескольких последовательно соединенных зубчатых колес. Такой механизм носит название обращенного механизма.

Угловые скорости звеньев в каждом из рассматриваемых движений приведены в таблице

В движении звеньев относительно водила угловые скорости звеньев равны угловым скоростям в движении относительно стойки минус угловая скорость водила. Если в движении относительно стойки ось сателлита подвижна, то в движении относительно водила оси обоих зубчатых колес неподвижны. Поэтому к движению относительно водила можно применить основную теорему зацепления.

Передаточное отношение обращенного механизма , окончательно передаточное отношение планетарного редуктора может быть определено по формуле Виллиса:

Передаточное отношение планетарного редуктора от любого колеса к водилу равно единице минус передаточное отношение обращенного механизма от этого колеса к опорному.

Кинематическое исследование типовых планетарных механизмов графическим и аналитическим методами

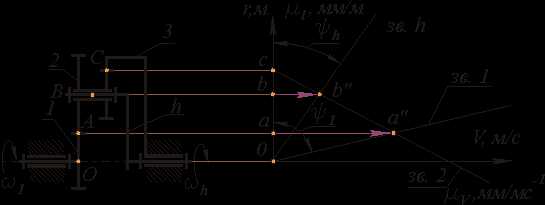
1. Двухрядный механизм с одним внутренним и одним внешним зацеплением.

Дано: Кинематическая схема механизма 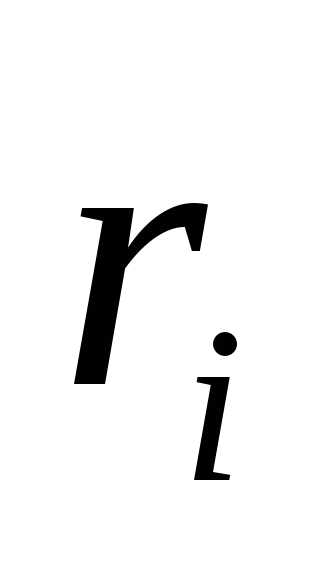числа зубьев колес;

Определить: Передаточное отношение механизма.

Аналитическое определение передаточного отношения.

Заданный планетарный механизм с одним внешним и одним внутренним зацеплениями зубчатых колес. Применяем метод обращенного движения.

Аналитическое определение передаточного отношения основывается на формуле:

,

так как колеса 2-3 находятся на одном валу, соответственно вращаются с одинаковой угловой скоростью.

Используя основную теорему Виллиса, для заданного обращенного механизма получим:

По формуле Виллиса

Графическое определение передаточного отношения.

В системе координат построим треугольники распределения линейных скоростей звеньев.

Для чего

,

,

,

.

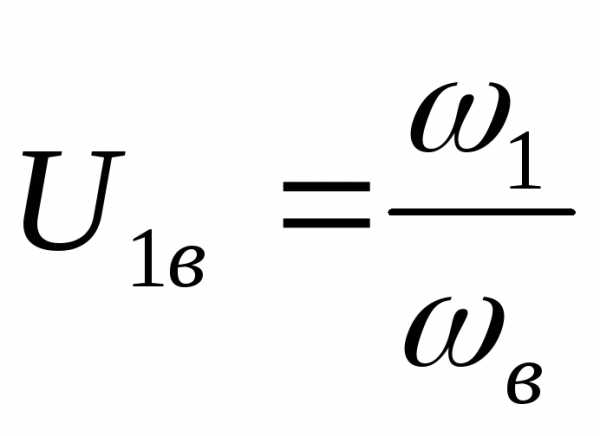studfiles.net

Как рассчитать передаточное число | Сделай все сам

Как знаменито, зубчатые передачи в автомобиле передают вертящий момент от мотора на привод иного узла. Одной из их основных колляций является передаточное число . Передаточным числом именуется отношение числа зубьев ведомой шестерни к числу зубьев ведущей. Применяя шестерни с различным числом зубцов, дозволено регулировать вертящий момент.

Инструкция

1. Рассчитайте передаточное число, пользуясь его определением, по формуле: К = К1/К2, где К1 — число зубьев ведомой шестерни, а К2 — число зубьев ведущей шестерни. Скажем, для расчета передаточного числа вертящего момента от коробки передач к колесам необходимо рассчитать соотношение ведомой шестерни дифференциала и шестерни вторичного вала в коробке передач, либо, как это называют автолюбители, обнаружить передаточное число для основной пары.

2. Посчитайте число зубьев шестерни вторичного вала коробки передач, возможен там 15 зубцов. Подсчитайте их число на ведомой шестерне, которая крепится на дифференциал, пускай на ней будет 51 зубец. Подставьте числа в приведенную выше формулу: 51 / 15 = 3,4. Полученное число будет являться передаточным числом для основной пары данной зубчатой передачи. Следственно, ведомая шестерня дифференциала будет вертеться в 3,4 раза неторопливей ведущей шестерни вала коробки передач при ее вращении.

3. Рассчитайте передаточные числа коробки переключения передач для всякой передачи по приведенной формуле. Чем ближе будут передаточные числа, тем больше плавным и стремительным будет разгон автомобиля при последовательном переключении передач. Подсчитайте, во сколько раз уменьшатся циклы мотора при изменении передачи, поделив передаточное число низшей передачи на передаточное число высшей.

4. Сделайте итоги по произведенным расчетам. Нужно знать: чем выше передаточное число, тем скорость автомобиля будет набираться стремительней, впрочем передачи необходимо будет переключать почаще. Устанавливая пару с меньшим передаточным числом, дозволено повысить максимальную скорость машины, впрочем автомобиль будет разгоняться дрянней. Рассчитайте при необходимости по приведенной формуле передаточное число для зубчатых передач всяких узлов в вашем автомобиле.

Одной из основных колляций редуктора является его передаточное число. Данный параметр применяется при расчете геометрических параметров разных передач механизма для передачи вращательного момента и влияет на разгонную динамику и максимальную скорость устройства.

Вам понадобится

Инструкция

1. Определите, к какому типу передач относится ваш редуктор. Они разделяются на следующие типы: конические, цилиндрические, планетарные и составные. Также имеется отличие по передачам зацепления, которые бывают зубчатыми, гипоидными, цепными, ременными, винтовыми, волновыми и фракционными. Передаточное число для всех них определяется отношением частот вращения ведущего и ведомого вала. Если данные колляции вам незнакомы, то нужно воспользоваться другими формулами расчета.

2. Вскройте крышку редуктора, дабы получить доступ к его элементам. Это нужно для того, дабы определить вид элемента редуктора, от которого зависит метод расчета передаточного числа.

3. Проведите соответствующие измерения для расчета передаточного числа. Для зубчатой передачи оно равно отношению числа зубьев ведомой шестерни к числу зубьев ведущей шестерни. В связи с этим нужно наглядно пересчитать нужные параметры. Для ременной передачи измеряется диаметр ведомого и ведущего шкива, позже чего вычисляет отношение большего значения к меньшему.

4. Если ваш редуктор имеет цепную передачу, то рассчитывайте отношение числа зубьев большей звезды к числу зубьев меньшей. Червячная передача характеризуется числом заходов на червяке и числом зубьев на червячном колесе. Позже их определения находится передаточное число, равное отношению второго параметра к первому.

5. Посчитайте передаточное число по скорости вращения ведущего и ведомого вала. Для этого нужно воспользоваться тахометром и измерить частоту вращения вала, тот, что приводит в движение силовую установку. Позже этого определяется число циклов вала, тот, что приводит в движение рабочий механизм. Обнаружьте отношение первого параметра ко второму, дабы определить передаточное число.

Верно подобранные автомобильные шины обеспечивают безопасность и реализацию технических колляций автомобиля. Если установить шины, рекомендуемые автопроизводителем, нет вероятности, нужно подобрать взаимозаменяемый типоразмер покрышек, рассматривая несколько параметров.

Инструкция

1. Расшифруйте типоразмер автомобильных шин. Скажем, в обозначении 175/65R14, первые 3 цифры обозначают ширину шины в миллиметрах, 4 и 5 цифры – профиль шины (в % от ширины). Буква R является маркировкой радиальной шины, а последние 2 цифры обозначают диаметр диска в дюймах.

2. Подберите шины, незначительно отличающиеся по физическим размерам от «родных». Возможным считается отклонение по диаметру до 5% и по ширине до 20%. Сравните полный диаметр колеса , установленного на автомобиль, с новым типоразмером. Всеобщий объем = диаметр диска х 25,4 мм. + (ширина шины х (профиль шины/100) х 2). Скажем, если вы хотите сменить типоразмер 175/65R14 на 195/50R15, подставьте в эту формулу соответствующие параметры из этих обозначений. Получив в итоге вычислений два значения (583,1 мм. и 576 мм.), обнаружьте их разность и процент, тот, что она составляет от изначального объема. В данном примере разница 7,1 мм. составляет 1,2% от изначального объема 583,1 мм. и является возможным значением. Следственно, вы можете без опасений сменить типоразмер автомобильных шин.

3. Сравните высоту профиля и ширину шины. Скажем, вы хотите сменить размер 175/65R14 на 185/60R14. Умножьте ширину шины на профиль (175 мм. х 0,65 и 185 мм. х 0,60). Разность полученных значений (113,75 мм. – 110мм. = 2,75мм.) составляет 2,4% от начальной высоты профиля (113,75 мм.). Разница в ширине шин (185 мм. -175 мм.) составляет 10мм. и 5,7% от ширины 175 мм. Таким образом, дозволено сделать итог о том, что типоразмеры 175/65R14 и 185/60R14 являются взаимозаменяемыми.

Полезный совет
Просмотрите начальство по эксплуатации вашего автомобиля и обнаружьте в нем информацию касательно рекомендуемых типоразмеров покрышек. Помните о том, что летние и зимние шины могут отличаться по размеру. Типоразмер также указывается на боковине покрышки.

Одним из устройств, особенно зачастую применяемых сегодня в разных механизмах, является редуктор. Он представляет собой становление идеи рычага и служит для передачи момента между вращающимися шкивами. Основным параметром, характеризующим определенный редуктор, является передаточное число. Определить его дозволено путем совершения расчетов на основе сведений о типе и параметрах ступеней редуктора.

Вам понадобится

• — познание параметров передач редуктора.

Инструкция

1. Определите передаточное число редуктора, состоящего из одной зубчатой передачи. В устройствах сходственного типа вращающий момент передается от ведущего вала ведомому посредством взаимодействия зубьев шестерней, установленных на них. Шестерни могут быть как цилиндрические, так и конические — в данном случае это не значимо. Сначала определите число зубьев шестерни ведущего вала путем простого подсчета. После этого ту же операцию проделайте для шестерни вала ведомого. Поделите второе значение на первое. Это и будет желанным передаточным числом редуктора.

2. При расчете передаточного числа редуктора, исполненного на основе цепной передачи, действуйте подобно первому шагу. Посчитайте число зубьев ведущей и ведомой звездочек, а после этого поделите второе значение на первое.

3. Для оценки передаточного числа редуктора на ременной передаче нужно знать радиусы (либо диаметры) его ведущего и ведомого шкивов. Обратите внимание на то, что это обязаны быть значения радиусов окружностей, по которым проходит внутренняя часть ремня при его соприкосновении со шкивами. Следственно если шкив исполнен в виде ролика с пазом для удержания ремня, нужно измерять радиус либо диаметр его внутренней части. В данном случае для вычисления передаточного числа довольно поделить радиус ведомого шкива на радиус ведущего.

4. В редукторах на основе червячной передачи ведущим шкивом неизменно является тот, на котором размещен червяк, а ведомым — на котором находится червячное колесо. За один цикл червяка колесо (шестерня) поворачивается на число зубьев, равное числу заходов червяка (в простейшем случае это единица). Следственно передаточное число такого редуктора высчитывается простым делением числа зубьев червячного колеса на число заходов червяка.

5. Передаточное число редуктора, составленного из нескольких передач, определите путем последовательного перемножения передаточных чисел его отдельных ступеней.

Так же, как и у человека, в жизни кошки есть несколько периодов: детство, молодость, зрелость и старость. Существует методология, которая дозволяет рассчитать соотношение между возрастом человека и кошки.

Длительность жизни кошки гораздо поменьше, чем у человека. В среднем беспризорное звериное живет 7 лет, а ухоженный и отлично защищенный домашний питомец – 13-15 лет. Встречаются и кошки-долгожители, которые остаются достаточно энергичными и здоровыми до 20, а то и до 25 лет. Но это скорее исключение из правил.

Как сопоставить возраст кошки и человека

Хозяева кошек зачастую пытаются соотнести возраст своих любимцев с человеческим, применяя знаменитый способ – умножение возраста кошки на семь. Таким образом, годовалое звериное – это ребенок семи лет, двухлетняя кошка – четырнадцатилетний подросток, трехлетняя – двадцативосьмилетний молодой человек. На деле такое соотношение невозможно назвать правильным, чай, скажем, в семь лет человек еще не может иметь потомство, тогда как годовалая кошка абсолютно способна к размножению.Ученые-фелинологи предлагают другие методы подсчета, которые изменяются, в зависимости от возраста звериного. Так, одномесячный котенок по становлению равен полугодовалому ребенку, а двухмесячный – годовалому. В возрасте одного года физическое и умственное становление кошки такое же, как и у человек в 15 лет. Такое соотношение выглядит абсолютно умным: в течение первого года жизни кошка учится жить независимо: добывать пищу, ухаживать за собой, защищаться, ладить с окружающими. Примерно то же самое делает человек в период от рождения до 15 лет.Период с 2-х до восьми лет – возраст полного расцвета для кошки. Он соответствует 24-48 годам у человека. Это время наибольшей физической активности и повышенного интереса к окружающему миру. Позже достижения 8 лет кошка вступает в пору среднего возраста. Как и у людей, данный период у звериных может происходить по-различному: некоторые кошки здоровы и полны сил, а некоторые начинают испытывать действие приближающейся старости.

Как соотносится возраст человека и кошки позже 12 лет

Считается, что 12 лет для кошки то же самое, что 60-64 года для человека. Звериное становится «пенсионером»: двигается немного и не дюже с охотой, с трудом переносит перемены в жизни, почаще и дольше болеет. Но некоторые кошки остаются бодрыми и энергичными даже в этом возрасте, так же, как и отлично сохранившиеся люди. Пятнадцатилетняя кошка и 76-летний человек приблизительно равны по состоянию здоровья и резерву жизненных сил. Ну а звериные 18-20 лет встречаются с такой же частотой, как и люди-долгожители старше 90 лет.

Видео по теме

Обратите внимание!
При переходе с четырехступенчатой коробки передач на пятиступенчатую вам придется реже переключать передачи, и вы можете увеличить максимальную скорость на всей передаче.

jprosto.ru

Передаточное отношение Википедия

Передаточное отношение (i{\displaystyle i}) — одна из важных характеристик механической передачи вращательного движения. Передаточное отношение показывает, во сколько раз вырос момент силы на ведомом валу по сравнению с ведущим.

i=i12=d2d1=z2z1=M2M1=ω1ω2=n1n2{\displaystyle i=i_{12}={\frac {d_{2}}{d_{1}}}={\frac {z_{2}}{z_{1}}}={\frac {M_{2}}{M_{1}}}={\frac {\omega _{1}}{\omega _{2}}}={\frac {n_{1}}{n_{2}}}}

где: i12{\displaystyle i_{12}} — передаточное отношение от звена 1 к звену 2 (звено 1 — ведущее, звено 2 — ведомое)

d1,d2{\displaystyle d_{1},d_{2}} — диаметры звеньев

z1,z2{\displaystyle z_{1},z_{2}} — количество зубьев звеньев (если таковые имеются)

M1,M2{\displaystyle M_{1},M_{2}} — крутящие моменты звеньев

ω1,ω2{\displaystyle \omega _{1},\omega _{2}} — угловые скорости звеньев

n1,n2{\displaystyle n_{1},n_{2}} — частоты вращения звеньев

Таким образом, если передаточное отношение больше единицы, то передача увеличивает момент силы на ведомом валу, но понижает угловую скорость и частоту.

Поэтому редуктор с передаточным отношением больше единицы называется понижающим.

Размышляя о моменте силы, становится понятным следующее соотношение для многоступенчатых передач:

i=i14=i12⋅i23⋅i34=M2M1⋅M3M2⋅M4M3=M4M1{\displaystyle i=i_{14}=i_{12}\cdot i_{23}\cdot i_{34}={\frac {M_{2}}{M_{1}}}\cdot {\frac {M_{3}}{M_{2}}}\cdot {\frac {M_{4}}{M_{3}}}={\frac {M_{4}}{M_{1}}}}

Однако следует учесть, что данное выражение истинно только в случае отсутствия потерь в зацеплении и других подвижных частях механизма на трение, упругие деформации и другие факторы, что в принципе является невозможным. Поэтому при конструкторских расчетах силовых и кинематических параметров машин необходимо учитывать коэффициент полезного действия как непосредственно самой передачи, так и пар подшипников, а если они есть, то и соединительных муфт. С учетом этого общая формула для определения момента на выходном валу имеет вид [4, с. 12]:

ii,i+1⋅Mi⋅η=Mi+1,{\displaystyle i_{i,i+1}\cdot M_{i}\cdot \eta =M_{i+1},}

где ii,i+1{\displaystyle i_{i,i+1}} — передаточное отношение механизма;

Mi,Mi+1{\displaystyle M_{i},M_{i+1}} — крутящие моменты на входном и выходном валах механизма соответственно;

η{\displaystyle \eta } — КПД механизма.

Следующий абзац возник из-за некоторого разногласия в рядах студентов по поводу ведущего и ведомого звена.

Из курсового проектирования деталей машин [5, с. 118]: «Как правило ременная и цепная передачи служат для понижения частоты вращения. Специальные передачи, повышающие угловую скорость, здесь не рассматриваются, так как в типовых заданиях на курсовое проектирование они не встречаются.»

В этой же книге [4, с. 7] дана формула i=nnomnp{\displaystyle i={\frac {n_{nom}}{n_{p}}}}. Здесь в качестве номинальной nnom{\displaystyle n_{nom}} частоты принимается частота работы электропривода (то есть ведущего звена), а в качестве расчетной np{\displaystyle n_{p}} — частота ведомого звена. Также даны средние значения для различного рода передач: зубчатых 2-6, червячных 8-80, цепных 3-6, ременных 2-4. То есть скорость ведущего звена в i{\displaystyle i} раз больше чем скорость ведомого звена.

Проверка: редуктор, передаточное число которого больше единицы (2>1), скорость понижается (n2<n1), i=ω1ω2=n1n2=2 m/c1 m/c=2{\displaystyle i={\frac {\omega _{1}}{\omega _{2}}}={\frac {n_{1}}{n_{2}}}={\frac {2~m/c}{1~m/c}}=2}. (Момент силы увеличивается)

В случае зубчатых шестерён передаточное отношение всегда является рациональным числом. Характеристика передаточное отношение применима как к механической передаче с одной ступенью (одной кинематической парой), так и к механическим передачам со множеством ступеней. Во втором случае передаточное отношение всей механической передачи будет равно произведению передаточных отношений всех ступеней.

Формально механизмы с передаточным отношением больше единицы называются редукторами, с передаточным отношением меньше единицы — мультипликаторами. Фактически и тот, и другой механизм в обиходе можно называть редуктором, добавляя лишь определение «понижающий» в случае с (i>1{\displaystyle i>1}) и «повышающий» с (i<1{\displaystyle i<1}).

См. также

Литература

1. Под ред. Скороходова Е. А. Общетехнический справочник. — М.: Машиностроение, 1982. — С. 416.
2. Гулиа Н. В., Клоков В. Г., Юрков С. А. Детали машин. — М.: Издательский центр “Академия”, 2004. — С. 416. — ISBN 5-7695-1384-5.
3. Анурьев В. И. Справочник конструктора-машиностроителя: В 3 т. / Под ред. И. Н. Жестковой. — 8-е изд., перераб. и доп.. — М.: Машиностроение, 2001. — ISBN 5-217-02962-5.
4. Курмаз Л. В. Детали машин. Проектирование// Л. В. Курмаз; А. Т. Скойбеда — 2-е изд., испр. и доп. — Мн.: УП «Технопринт», — 2002. — 296с.,ил.
5. Чернавский С. А., Боков К. Н. Курсовое проектирование деталей машин. — 1988.

wikiredia.ru

Передаточное отношение • ru.knowledgr.com

Передаточное отношение зубчатой передачи, также известной как ее отношение скорости, является отношением угловой скорости входа, связывают с угловой скоростью механизма продукции. Передаточное отношение может быть вычислено непосредственно от чисел зубов на механизмах в зубчатой передаче. Отношение вращающего момента зубчатой передачи, также известной как ее механическое преимущество, определено передаточным отношением. Отношение скорости и механическое преимущество определены так, они приводят к тому же самому числу в идеальной связи.

Зубчатые передачи с двумя механизмами

У

самого простого примера зубчатой передачи есть два механизма. «Входной механизм» (также известный как механизм двигателя) передает власть к «механизму продукции» (также известный как ведомый механизм). Входной механизм будет, как правило, связываться с источником энергии, таким как двигатель или двигатель. В таком примере выходная мощность продукции, которую (ведут) механизмом, зависит от отношения размеров этих двух механизмов.

Формула

Зубы на механизмах разработаны так, чтобы механизмы могли катиться друг на друге гладко (не уменьшаясь или набиваясь битком). Для двух механизмов, чтобы катиться друг на друге гладко, они должны быть разработаны так, чтобы скорость при контакте двух кругов подачи (представленный v) была тем же самым для каждого механизма.

Математически, если входной механизм G имеет радиус r и угловую скорость, и сцепляется с механизмом продукции G радиуса r и угловой скорости, то:

:

Число зубов на механизме пропорционально радиусу его круга подачи, что означает, что отношения угловых скоростей механизмов, радиусов и числа зубов равны. Где N – число зубов на входном механизме, и N – число зубов на механизме продукции, следующее уравнение сформировано:

:

Это показывает, что у простой зубчатой передачи с двумя механизмами есть передаточное отношение R данный

:

Это уравнение показывает что, если число зубов на механизме продукции G больше, чем число зубов на входном механизме G, то входной механизм G должен вращаться быстрее, чем механизм продукции G.

Отношение скорости

Зубы механизма распределены вдоль окружности круга подачи так, чтобы толщина t каждого зуба и пространства между соседними зубами была тем же самым. Подача p механизма, который является расстоянием между эквивалентными пунктами на соседних зубах вдоль круга подачи, равна дважды толщине зуба,

:

Подача механизма G может быть вычислена из числа зубов N и радиуса r его круга подачи

:

Чтобы поймать в сети гладко два механизма G, и у G должны быть те же самые размерные зубы, и поэтому у них должна быть та же самая подача p, что означает

:

Это уравнение показывает, что отношение окружности, диаметров и радиусов двух запутывающих механизмов равно отношению их числа зубов,

:

Отношением скорости двух механизмов, катящихся, не надевая их круги подачи, дают,

:

поэтому

:

Другими словами, передаточное отношение или отношение скорости, обратно пропорционально радиусу круга подачи и числу зубов входного механизма.

Отношение вращающего момента

Зубчатая передача может быть проанализирована, используя принцип виртуальной работы, чтобы показать, что ее отношение вращающего момента, которое является отношением ее вращающего момента продукции к его входному вращающему моменту, равно передаточному отношению или отношению скорости, зубчатой передачи.

Это означает, что входной Τ вращающего момента относился к входному механизму G, и продукция закручивают Τ на механизме продукции G, связаны отношением

:

где R – передаточное отношение зубчатой передачи.

Отношение вращающего момента зубчатой передачи также известно как ее механическое преимущество

:

Более неработающие механизмы

В последовательности механизмов, прикованных цепью вместе, отношение зависит только от числа зубов на первом и последнем механизме. Промежуточные механизмы, независимо от их размера, не изменяют полное передаточное отношение цепи. Однако добавление каждого промежуточного механизма полностью изменяет направление вращения заключительного механизма.

Промежуточный механизм, который не заставляет шахту выполнять любую работу, называют механизмом. Иногда, единственный более неработающий механизм используется, чтобы полностью изменить направление, когда это может упоминаться как обратный бездельник. Например, типичная автомобильная механическая коробка передач затрагивает реверсор посредством вставки обратного бездельника между двумя механизмами.

Более неработающие механизмы могут также передать вращение среди отдаленных шахт в ситуациях, где это было бы непрактично, чтобы просто сделать отдаленные механизмы более крупными, чтобы объединить их. Мало того, что более крупные механизмы занимают больше места, массовая и вращательная инерция (момент инерции) механизма пропорциональна квадрату его радиуса. Вместо более неработающих механизмов, имеющий зубы пояс или цепь могут использоваться, чтобы передать вращающий момент по расстоянию.

Формула

Если у простой зубчатой передачи есть три механизма, такие, что входной механизм G сцепляется с промежуточным механизмом G, который в свою очередь сцепляется с механизмом продукции G, то круг подачи промежуточных рулонов механизма, не надевая обоих круги подачи механизмов входа и выхода. Это приводит к этим двум отношениям

:

Отношение скорости этой зубчатой передачи получено, умножив эти два уравнения, чтобы получить

:

Заметьте, что это передаточное отношение – точно то же самое что касается случая когда механизмы G и G, занятый непосредственно. Промежуточный механизм обеспечивает интервал, но не затрагивает передаточное отношение. Поэтому это называют более неработающим механизмом. То же самое передаточное отношение получено для последовательности более неработающих механизмов, и следовательно более неработающий механизм используют, чтобы обеспечить то же самое направление, чтобы вращать водителя и ведут механизмом, если шаги механизма водителя в направлении по часовой стрелке, то ведомый механизм также перемещается в направление по часовой стрелке с помощью более неработающего механизма.

Пример

Предполагая, что в фотографии самый маленький механизм связан с двигателем, это – механизм водителя. Несколько более крупный механизм на оставленном верхнем называют более неработающим механизмом. Это не связано непосредственно или с двигателем или с шахтой продукции и только передает власть между механизмами входа и выхода. Есть третий механизм в верхнем правом углу фотографии. Предполагая, что тот механизм связан с шахтой продукции машины, это – продукция или ведомый механизм.

У

входного механизма в этой зубчатой передаче есть 13 зубов, и у более неработающего механизма есть 21 зуб. Рассматривая только эти механизмы, передаточное отношение между бездельником и входным механизмом может быть вычислено, как будто более неработающий механизм был механизмом продукции. Поэтому, передаточное отношение ведут/водитель = 21/13 ≈1.62 или 1.62:1.

Это отношение означает, что механизм водителя должен сделать 1,62 революции, чтобы повернуть ведомый механизм однажды. Это также означает, что для каждой революции водителя, ведомый механизм сделал 1/1.62, или 0.62, революции. По существу более крупный механизм поворачивается более медленно.

У

третьего механизма на картине есть 42 зуба. Передаточное отношение между более неработающим и третьим механизмом таким образом 42/21, или 2:1, и следовательно заключительное передаточное отношение 1.62×2≈3.23. Для каждых 3,23 революций самого маленького механизма самый большой механизм поворачивает одну революцию, или для каждой революции самого маленького механизма, самый большой механизм поворачивает 0,31 (1/3.23) революции, полное сокращение приблизительно 1:3.23 (Gear Reduction Ratio (GRR) = 1/передаточное отношение (GR)).

Так как более неработающий механизм связывается непосредственно и с меньшим и с более крупным механизмом, он может быть удален из вычисления, также дав отношение 42/13≈3.23. Более неработающие подачи механизма, чтобы сделать и механизм двигателя и ведомый механизм вращаются в том же самом направлении, но не присуждает механического преимущества.

Ременные приводы

Пояса могут иметь зубы в них также и быть соединены с подобными механизму шкивами. Специальные механизмы звонили, цепные колеса могут быть соединены вместе с цепями, как на велосипедах и некоторых мотоциклах. Снова, точный бухгалтерский учет зубов и революций может быть применен с этими машинами.

Например, пояс с зубами, названными поясом выбора времени, используется в некоторых двигателях внутреннего сгорания, чтобы синхронизировать движение распредвала с тем из коленчатого вала, так, чтобы клапаны открылись и близко наверху каждого цилиндра в точно правильное время относительно движения каждого поршня. Цепь, названная цепью выбора времени, используется на некоторых автомобилях с этой целью, в то время как в других, распредвал и коленчатый вал соединены непосредственно вместе через решетчатые механизмы. Независимо от которого используется форма двигателя, коленчатый вал к передаточному отношению распредвала всегда 2:1 на четырехтактных двигателях, что означает, что для каждых двух революций коленчатого вала распредвал будет вращаться однажды.

Автомобильные заявления

У

автомобильных трансмиссий обычно есть две или больше крупнейших области, где левередж используется. Левередж используется в передаче, которая содержит много различных наборов механизмов, которые могут быть изменены, чтобы позволить широкий диапазон скоростей транспортного средства, и также в дифференциале, который содержит заключительный двигатель, чтобы обеспечить дальнейшее сокращение скорости в колесах. Кроме того, дифференциал содержит дальнейший левередж, который разделяет вращающий момент одинаково между двумя колесами, разрешая им иметь различные скорости, путешествуя в кривом пути. Передача и заключительный двигатель могли бы быть отдельными и связанными карданным валом, или они могли бы быть объединены в одну единицу, названную трансосью. Передаточные отношения в передаче и заключительном двигателе важны, потому что различные передаточные отношения изменят особенности работы транспортного средства.

Пример

У

Chevrolet Corvette C5 Z06 2004 года с механической коробкой передач с шестью скоростями есть следующие передаточные отношения в передаче:

В 1-м механизме двигатель делает 2,97 революции для каждой революции продукции передачи. В 4-м механизме передаточное отношение 1:1 означает, что двигатель и продукция передачи вращаются на той же самой скорости. 5-е и 6-е механизмы известны как механизмы перегрузки, в которых продукция передачи вращается быстрее, чем продукция двигателя.

У

Корвета выше есть отношение оси 3.42:1, означая, что для каждых 3,42 революций продукции передачи, колеса делают одну революцию. Отличительное отношение умножается с отношением передачи, таким образом, в 1-м механизме, двигатель делает 10,16 революций для каждой революции колес.

Шины автомобиля могут почти считаться третьим типом левереджа. Этот автомобиль оборудован шинами 295/35-18, у которых есть окружность 82,1 дюймов. Это означает, что для каждой полной революции колеса, автомобиль едет. Если бы у Корвета были большие шины, то он поехал бы дальше с каждой революцией колеса, которое походило бы на более высокий механизм. Если бы у автомобиля были меньшие шины, то он походил бы на более низкий механизм.

С передаточными отношениями передачи и дифференциала и размера шин, становится возможно вычислить скорость автомобиля для особого механизма в особом двигателе RPM.

Например, возможно определить расстояние, автомобиль поедет для одной революции двигателя, деля окружность шины объединенным передаточным отношением передачи и дифференциала.

Также возможно определить скорость автомобиля от скорости двигателя, умножая окружность шины скоростью двигателя и делясь на объединенное передаточное отношение.

Широкое отношение против передачи отношения завершения

Передача отношения завершения – передача, в которой есть относительно мало различия между передаточными отношениями механизмов. Например, передачу с шахтой двигателя к отношению карданного вала 4:1 на первой передаче и 2:1 на второй передаче считали бы широким отношением когда по сравнению с другой передачей с отношением 4:1 в первом и 3:1 во втором. Это вызвано тем, что у передачи отношения завершения есть меньше прогрессии между механизмами. Для передачи широкого отношения отношение первой передачи 4:1 или 4, и на второй передаче это 2:1 или 2, таким образом, прогрессия равна 4/2 = 2 (или 200%). Для передачи отношения завершения первая передача имеет 4:1 отношение или 4, и у второго механизма есть отношение 3:1 или 3, таким образом, прогрессия между механизмами – 4/3, или 133%. Начиная с 133% меньше чем 200%, передачу с меньшей прогрессией между механизмами считают отношением завершения. Однако различие между отношением завершения и передачей широкого отношения субъективно и относительно.

Передачи отношения завершения обычно предлагаются в спортивных автомобилях, спортивных велосипедах, и особенно в транспортных средствах гонки, где двигатель настроен для максимальной мощности в узком ассортименте операционных скоростей, и водитель или наездник, как могут ожидать, будут переходить часто, чтобы держать двигатель в его группе власти.

Фабрика отношения передачи с 5 скоростями или с 4 скоростями обычно имеют большее различие между передаточными отношениями и имеют тенденцию быть эффективными для обычного вождения и умеренного исполнительного использования. Более широкие промежутки между отношениями позволяют более высокое 1-е передаточное отношение для благовоспитанности в движении, но заставляют скорость двигателя уменьшаться больше, переходя. Сужение промежутков увеличит ускорение на скорости, и потенциально улучшит максимальную скорость при определенных условиях, но ускорение от остановленного положения и операция в ежедневном вождении пострадают.

Диапазон – различие в умножении вращающего момента между 1-ми и 4-ми механизмами; у наборов механизма более широкого отношения есть больше, как правило между 2,8 и 3.2. Это – единственный самый важный детерминант медленного ускорения от остановленного.

Прогрессия – сокращение или распад в понижении процента скорости двигателя в следующем механизме, например после перемены с 1-го на 2-й механизм. У большинства передач есть определенная степень прогрессии в этом, снижение RPM на изменении 1-2 больше, чем снижение RPM на изменении 2-3, которое в свою очередь больше, чем снижение RPM на изменении 3-4. Прогрессия может не быть линейной (непрерывно уменьшаемый) или сделанный на пропорциональных стадиях по различным причинам, включая специальную потребность в механизме, чтобы достигнуть определенной скорости или RPM для прохождения, мчась и так далее, или просто экономической необходимости, что части были доступны.

Диапазон и прогрессия не взаимоисключающие, но каждый ограничивает число вариантов для другого. Широкий диапазон, который дает сильное умножение вращающего момента в 1-м механизме для превосходных манер в медленном движении, особенно с двигателем меньшего размера, грузовым автомобилем или численно низким отношением оси такой как 2,50, означает, что проценты прогрессии должны быть высокими. Сумма скорости двигателя, и поэтому власть, потерянная на каждом-изменении, больше, чем имел бы место в передаче с меньшим количеством диапазона, но меньшей властью в 1-м механизме. Численно низкий 1-й механизм, такой как 2:1, уменьшает доступный вращающий момент в 1-м механизме, но позволяет больше выбора прогрессии.

Нет никакого оптимального выбора передаточных отношений передачи или заключительного отношения двигателя для лучшей работы на всех скоростях, поскольку передаточные отношения – компромиссы, и не обязательно лучше, чем оригинальные отношения в определенных целях.

См. также

• Зубчатая передача

• Поезд колеса (хорология)

• Левередж Epicyclic – имел отношение к турбовинтовым коробкам передач сокращения

• Непрерывно переменная передача (CVT)

• Механизм (разработка)

• Виртуальная работа

Внешние ссылки

• Передаточное отношение, в Как Работы Материала

• Калькулятор зубчатой передачи Мотоцикла онлайн со страницами справки

---

ru.knowledgr.com

Редукторы Передаточные отношения — Формул

Редуктор Джемса (рис. 3.3, а). Передаточное отношение определяется формулой  [c.97]

Редуктор со сдвоенными сателлитами (рис. 3.3, б). Передаточное отношение определяется формулой  [c.97]

Вид формулы, которой нужно пользоваться для нахождения механического коэффициента полезного действия планетарного редуктора, зависит от того, какое звено является ведущим и каково у него передаточное отношение.  [c.176]

Если вычисленное передаточное отношение одноступенчатого планетарного редуктора получается больше единицы или меньше нуля, то коэффициент полезного действия редуктора вычисляется по формуле  [c.176]

Общее передаточное отношение редуктора хб. согласно формулам (7.36) и (7.37), равно  [c.153]

Для определения передаточного отношения зн от вала Оз к валу Оц этого редуктора можно воспользоваться формулой (7.40). Имеем  [c.155]

На рис. 7.26 показана модификация редуктора Давида с сателлитом, входящим в два внутренних зацепления. Передаточное отношение от вала 0 к валу 0 может быть определено по формуле (7.49).  [c.157]

Эта формула справедлива для любой схемы планетарного редуктора при наличии неподвижного центрального колеса. Значит, и передаточное отношение от любого планетарного колеса / к водилу Н при неподвижном опорном колесе / равно единице минус  [c.409]

Составьте схему двухступенчатого рядового зубчатого редуктора и напишите формулу передаточного отношения.  [c.201]

На рис. 94 приведена схема авиационного редуктора типа Джемса, составленного из конических колес. Его передаточное отношение подсчитывается по формуле (3,7).  [c.133]

При z, = Zj И 2, = 2з схема редуктора может быть выполнена согласно рис. 96, б, где водила Я, и Я, заменены одним води-лом Н. Передаточное отношение редуктора определяется по аналогичной формуле  [c.135]

Зубчатые механизмы, в которых происходит уменьшение угловых скоростей при передаче от ведущего звена, называют редукторами, а зубчатые механизмы, увеличивающие угловую скорость, называют мультипликаторами. Зубчатая передача является одним из наиболее распространенных приводов, предназначенных для передачи вращения от одного вала к другому с заданным отношением угловых скоростей. Передача вращения сопровождается передачей крутящего момента, а следовательно, передачей механической работы и мощности. В большинстве рабочих, транспортирующих и других машин ведущим звеном является вал двигателя, передающий движение ведомому звену данной машины. Двигатель работает более экономично при высоких скоростях вращения, между тем как скорость ведомого звена значительно ниже, что обусловливается требованиями технологического процесса, выполняемого машиной, или в транспортирующих машинах— допускаемыми скоростями перемещения масс. Например, вал электродвигателя тележки мостового крана, приводящий в движение механизм подъема груза, вращается со скоростью %0 об/мин, а барабан этого механизма — со скоростью 10—20 об мин. Поэтому между электродвигателем и барабаном устанавливается промежуточная зубчатая передача. Зубчатая передача в виде пары сцепляющихся колес (одноступенчатая передача) может воспроизвести лишь небольшие значения передаточных отношений. Передаточное отношение 12 пары зубчатых колес выражается формулой  [c.246]

Зубья звездочек находятся в зацеплении с цевками 9, оси 4 которых закреплены в корпусе редуктора. На диске 7 ведомого вала закреплены пальцы 6 с роликами 8. Ролики S входят в отверстая звездочек 3 и 5. Передаточное отношение редуктора определяется по формуле  [c.204]

Передаточное отношение редуктора определяется по формуле  [c.327]

Рассмотрим тот же механизм в соединении с другим, обратным ему, образующим с ним четырехзвенный планетарный механизм в том виде, в каком он применяется в редукторе Давида (рис. 291). Здесь колесо 1 неподвижное, 2 я 3 — сателлиты, жестко связанные между собой, 4 — колесо, свободно закрепленное на валу О. Из треугольников скоростей, построенных на схеме механизма, после ряда преобразований (см. подробнее т. 1, гл. XIX) получается следующая формула для передаточного отношения при ведущем водиле  [c.421]

Каким же путем идти к увеличению к. п. д. планетарных редукторов при большом передаточном отношении. Один из возможных путей — увеличение к. п. д. зубчатых пар, входящих в редуктор. Этого можно достичь, например, применением в планетарной передаче внутреннего зацепления. Как известно из п. 36, потери на трение в зубьях выражаются формулой  [c.424]

По известным расходам Q2 и й с учетом передаточного отношения i механического редуктора и диаметра D шкива определяем скорости подъема левого vj и правого грузов. При этом используются формулы  [c.282]

Волновые передачи с гибким неподвижным корончатым колесом 2, жестким вращающимся колесом / рационально применять для передачи вращения в герметично замкнутое пространство. Передаточные отношения передачи определяют по формуле (11.1). Общий вид редуктора, выполненного по этой схеме, приведен на рис. 11.5.  [c.221]

Редуктор Давида (рис. 3.3 д, е) следует применять для очень больших передаточных отношений (от 100 до 5000) в несиловых передачах, так как к. п. д. этих редукторов очень низкий (менее 10%). Передаточное отношение для редуктора Давида определяется по формуле  [c.97]

Если собственно дифференциальный механизм многоступенчатый, то удобнее пользоваться формулой Виллиса. Например, для редуктора электротельфера (рис. 3.6,передаточного отношения 13 следует составить следующие выражения. Для собственно дифференциального механизма (его уже не будем выделять на чертеже отдельно), который состоит из звеньев 1, 2, 3, 4, 5, 6, формула Виллиса примет вид  [c.102]

Определение к. п. д. планетарных редукторов производится по формулам, приведенным в табл. 3.4. При расчете к, п. д. следует учитывать направление передачи движения от центрального колеса к водилу или наоборот. Существенно также, к какой группе значений принадлежит передаточное отношение 1)от  [c.115]

По рассчитанному передаточному отношению подбирается понижающий редуктор. Мощность электродвигателя исполнительного механизма для ножей реостата подсчитывается по формуле  [c.358]

Разделить редуктор на ступени, установить расчетные формулы для определения передаточных отношений отдельных ступеней и вычислить их передаточные отношения. Вычислить общее передаточное отношение редуктора.  [c.42]

Установки для определения к. п. д. червячного редуктора обычно состоят из двигателя, червячного редуктора и нагрузочного устройства. К. п. д. определяется как отношение мощности потребляемой нагрузочным устройством к мощности развиваемой двигателем. Так как передаточное отношение редуктора величина постоянная, то для вычисления к. п. д. можно использовать также приведенную выше формулу 10,3.  [c.148]

Находим передаточное отношение привода. В соответствии с табл. 2.2 принимаем для конической пары редуктора = 4 и для цилиндрической пары и = 4,5 тогда общее передаточное отношение редуктора Цр д = u,2 34 = 4-4,5 = 18 передаточное отношение цепной передачи Ыц = 2. Таким образом, в соответствии с формулой (2.2) общее передаточное отношение привода  [c.52]

По формулам табл. 5.1 уточняют передаточное отношение и сравнивают его с заданным. Допускается отклонение не более че.м на 4% для одноступенчатых редукторов, 5% —для двухступенчатых. Далее проверяют выполнение условий вхождения зубьев в зацепление и соседства.  [c.75]

Требуется определить общее передаточное отношение редуктора. Общее -передаточное отношение редуктора согласно формулам (10.36) и (10.37) равно  [c.254]

Пример 2. На рис. 350 показан планетарный редуктор с коническими зубчатыми колесами I, 2, 2, 3, имеющими соответственно числа зубьев, 2-1 = 60, 4 = 48, 24- = 18 и 2 з = 30. Требуется определить передаточное отношение от колеса I к води-лу Н, если колесо 3 скреплено со стойкой. Имеем [см. формулу  [c.261]

Определение передаточного отноштия приводного механизма, выбор схемы гривода или стандартного редуктора. Передаточное отношение [формула (50)  [c.127]

В формулах (17.4) — (17.7) приняты следующие обозначения t j — козф-фициобращенного механизма, т. е. такого, у которого те же зубчатые колеса, что и планетарного механизма, ио только водило Н остановлено, а ранее закрепленное колесо п стало свободным (подвижным), —передаточное отношение одноступенчатого планетарного редуктора от центрального колеса к водилу, rl, — искомый коэффициент полезного действия одноступенчатого планетарного механизма при ведущем колесе I, — искомый коэффициент полезного действия одноступенчатого планетарного механизма при ведущем вoдиJ[c.177]

На рис. 7.24 показан планетарный редуктор типа Джемса с коническим колесом. Согласно с правилом, указанным в 32, f, стрелки d и а у колес I 3 имеют противоположные направления. Следовательно, передаточное отношение имеет знак минус и передаточные отпошеР ня и определяются по формулам (7.42), (7.46) или (7.45), (7.47),  [c.156]

В отличие от механизма с неподвижными осями передаточное отношение иланетарного редуктора зависит не только от числа зубьев и знака их отношения, но и числа ступеней между центральными колесами (при остановленном водиле). Поэтому каждая конкретная схема планетарного редуктора имеет свое, вполне определенное, выражение для подсчета значения передаточного отношения иЩ, написанное через числа зубьев (или радиусы). При определении угловой скорости промежуточного колеса рекомендуется пользоваться формулой (15.6).  [c.410]

Схема И. Эта схема редуктора составлена из двух последовательно соединенных схем I. Рациональные передаточные отко. шения tip = 10-5-60 к. п. д. т) = 0,96-5-0,93. Передаточное отношение редуктора вычисляется по формуле  [c.187]

Соединение двух механических систем (рис. 12, а и 12, б) учитывающее редуктор, показано на рис. 12, в и производится по формулам Ш34 = = 1/псозз и Af33 = —1/га 71/34, где га — передаточное отношение редуктора.  [c.49]

Назначение н характеристика Схемы Формулы передаточных отношений Формулы для к. п. д. редуктора с эакрепленпь м звеном 4  [c.523]

Параметр 12=22/21 по ГОСТ 16532 — 70 назьшают передаточным числом и определяют как отношение большего числа зубьев к меньшему независимо от того, как передается движение от 2] к 22 или от 22 к 2]. Это передаточное число и отличается от передаточного отношения I, которое равно отношению угловых скоростей ведущего колеса к ведомому и которое может быть меньше или больше единицы, положительным или отрицательным. Применение и вместо 2 связано только с принятой формой расчетных зависимостей для контактных напряжений [см. вывод формулы (8.9), где выражено через d (меньшее колесо), а не через 2/2 (большее колесо)]. Величина контактных напряжений, так же как и передаточное число и, не зависит от того, какое колесо ведущее, а величина передаточного отношения 2 зависит. Однозначное определение и позволяет уменьшить вероятность ошибки при расчете. Передаточное число и относится только к одной паре зубчатых колес. Его не следует применять для обозначения передаточного отношения многоступенчатых редукторов, планетарных, цепных, ременных и других передач. Там справедливо только обозначение г.  [c.140]

Широкие кинематические возможности планетарной передачи являются одним из основных ее достоинств и позволяют использовать передачу как редуктор с постоянным передаточным отношением как коробку скоростей, передаточное отношение в которой изменяют путем поочередного торможения различных звеньев как дифференциальный механизм. Вторьш достоинством планетарной передачи является компактность, а также малая масса. Переход от простых передач к планетарным позволяет во многих случаях снизить массу в 2…4 раза и более. Это объясняется следующим мощность передается по нескольким потокам, число которых равно числу сателлитов. При этом нагрузка на зубья в каждом зацеплении уменьшается в несколько раз внутреннее зацепление (р я Ь) обладает повышенной нагрузочной способностью, так как у него больше приведенный радиус кривизны в зацеплении [см. знаки в формуле (8.9)] планетарный принцип позволяет получать большие передаточные отношения (до тысячи и больше) без применения многоступенчатых передач малая нагрузка на опоры, так как при симметричном расположении сателлитов силы в передаче взаимно уравновешиваются. Это снижает потери и упрощает конструкцию опор (кроме опор сателлитов).  [c.193]

Рис. 3,169. Планетарный редуктор с цевочным зацеплением. На ведущем валу 1 установлен сдвоенный эксцентрик 2 оо смещением эксцентриситета по фазе на 180°. Звездочка 3 установлена на одном, а звездочка 5 — на втором экс-цет риках. Зубья звеэдочек находятся в зацеплении с цевками 9, ош 4 которых закреплены в корпусе редуктора. На диске 7 ведомого вала закреплены пальцы 6 с роликами 8. Ролики 8 входят в отверстия звездочек 3 и 5. Передаточное отношение редуктора определяется по формуле.

---

mash-xxl.info