Расчет пружин на сжатие – Калькулятор пружин – расчет пружин онлайн
alexxlab | 24.07.2019 | 0 | Вопросы и ответы
Расчет пружины сжатия | Блог Александра Воробьева
Опубликовано 01 Июн 2013
Рубрика: Механика | 91 комментарий
Перед написанием этого поста я решил заглянуть в Интернет и узнать, что он мне предложит на запрос «расчет пружины сжатия». Посмотрел первый и второй в выдаче Google сайты, и не очень они мне понравились. Если честнее и точнее, то – очень не понравились…
…На первом сайте на основе семи исходных данных программно рассчитываются еще шесть параметров с огромным количеством знаков после запятой и с какой-то безысходной однозначностью. На втором — сайте специализированного завода – расчет выполняется верно, оформление – хорошее, но для меня не хватает диалога с программой по ходу работы. Почему навязывается конкретный шаг витков? Индекс пружины может быть любым? Так, все – достаточно критики. Всем не угодишь!
Предлагаю вашему вниманию свой вариант выполнения расчета в режиме диалога с пользователем. Программа была написана в далеком феврале две тысячи второго года, но не думаю, что с тех пор что-то существенно изменилось в теории расчетов пружин.
Расчет пружины сжатия будет выполняться в программе MS Excel.
Во-первых, расчет мы будем выполнять для стальных витых цилиндрических пружин.
Во-вторых, будем у всех пружин поджимать и шлифовать по ¾ витка с каждой стороны – это был наиболее приемлемый вариант для меня, как конструктора, по ряду экономических и технологических причин.
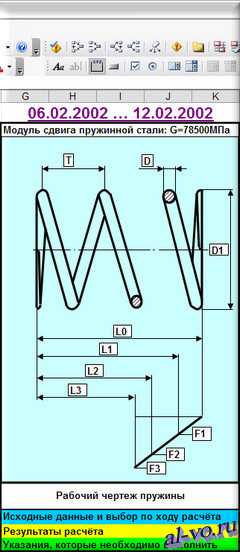
Чуть ниже этого текста представлены скриншоты программы.
Внимание!!!
После выполнения расчета по программе выполняйте проверку касательных напряжений!!!
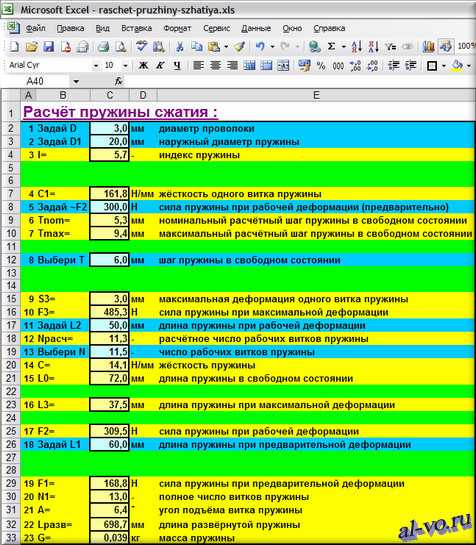
1. Конструктор, разрабатывая узел с пружиной, примерно, из опыта и располагаемого пространства может предварительно задать диаметр проволоки (D) в мм
в ячейку C2: 3,0
2. Наружный диаметр (D1) будущей пружины в мм
в ячейку C3: 20,0
3. Программа рассчитывает индекс пружины ( I)
в ячейке C4: =C3/C2-1=5,7
I = D1/D-1
*. Если индекс (I) меньше четырех («еще не пружина»), Excel выводит сообщение
в ячейке B5: Увеличь D1 или уменьши D!
*. Если индекс (I) больше двенадцати («уже не пружина»), программа выводит указание изменить D и/или D1
в ячейку B6: Уменьши D1 или увеличь D!
Если значения индекса (I) находятся между четырьмя и двенадцатью, все в порядке – никаких сообщений нет, как в нашем примере, идем дальше. Кстати, индекс (I) – это отношение среднего диаметра навивки (D1–D) к диаметру проволоки (D).
4. Жёсткость одного витка (C1) вычисляется в Н/мм
в ячейке C7: =78500*C2/8/C4^3
C1 = 78500*D/8/I^3
Здесь 78500 МПа – модуль сдвига пружинной стали.
5. Предварительная сила при рабочей деформации (~F2) конструктору так же на этом этапе обычно известна – это то, что он хочет от пружины! Записываем ее в Н
в ячейку C8: 300,0
6. Теперь Excel рассчитывает номинальный расчётный шаг пружины в свободном состоянии (Tnom) в мм
в ячейке C9: = 1,25*C8/C7+C2=5,3
Tnom = 1.25*F2/C1+D
7. Так же Excel рассчитывает максимальный расчётный шаг в свободном состоянии (Tmax) в мм
в ячейке C10: =ПИ()*(C3-C2)* TAN (ПИ()/18)=9,4
Tmax = 3,14*(D1-D)*tg (3,14/ 18)
*. Если окажется, что номинальный шаг (Tnom) больше максимального (Tmax), то программа выведет сообщение, что сила F2 очень велика
в ячейку B11: Уменьши F2!
8. В нашем примере — все в порядке, сообщений нет, идем дальше, выбираем шаг пружины в свободном состоянии (T) в мм, руководствуясь полученными выше результатами. Пишем
в ячейку C12: 6,0
*. Если пользователь ошибется и введет значение шага (T) меньше номинального расчетного шага (Tnom), тогда Excel укажет на ошибку
в ячейке B13: Увеличь T!
*. Аналогично, если пользователь ошибется и введет значение шага (T) больше максимального расчетного шага (Tmax), тогда указание на ошибку будет
в ячейке B14: Уменьши T!
9. Далее программа рассчитывает максимальную деформацию одного витка пружины (S3) в мм до соударения витков. Результат выводится
в ячейку C15: =C12-C2=3,0
S3 = T-D
10. Сила при максимальной деформации (F3) в Н рассчитывается и выводится
в ячейку C16: =C7*C15=485,3
F3 = C1*S3
11. Теперь конструктору необходимо задать длину пружины при рабочей деформации (L2) в мм
в ячейку C17: 50,0
12. Программа вычисляет расчётное число рабочих витков (Nрасч)
в ячейке C18: =(C17-C2)/(C2+C16/C7-C8/C7)=11,3
Nрасч = (L2-D)/(D+F3/C1-F2/C1)
13. Округляя полученное значение, выбираем число рабочих витков (N) и записываем
в ячейку C19: 11,5
14. Далее Excel вычисляет жёсткость пружины (C) в Н/мм
в ячейке C20: =C7/C19=14,1
C = C1/N
15. Программа определяет длину пружины в свободном состоянии (L0) в мм
в ячейке C21: =C19*C12+C2=72,0
L0 = N*T+D
*. Теперь Excel сравнивает длины и, если длина в рабочем состоянии (L2) больше длины в свободном состоянии (L0), выдает указание
в ячейку B22: Увеличь N!
В нашем примере – все хорошо, сообщений нет.
16. Длина пружины при максимальной деформации (L3) в мм выводится
в ячейку C23: =C19*C2+C2=37,5
L3 = N*D+D
*. Если длина при максимальной деформации (L3) больше длины в рабочем состоянии (L2), программа требует уменьшить число рабочих витков (N), выводя соответствующее сообщение
в ячейку B24: Уменьши N!
17. Сила пружины при рабочей деформации (F2) в Н уточняется расчетом
в ячейке C25: =C20*C21-C20*C17=309,5
F2 = C*L0-C*L2
18. И последнее, что необходимо задать конструктору, это — длину пружины при предварительной деформации (L1) в мм
в ячейку C26: 60,0
*. Если длина при предварительной деформации (L1) больше длины в свободном состоянии (L0), программа потребует уменьшить длину при предварительной деформации (L1), выводя соответствующее сообщение
в ячейку B27: Уменьши L1!
*. Если длина при предварительной деформации (L1) меньше длины при рабочей деформации (L2), программа потребует увеличить длину при предварительной деформации (
в ячейку B28: Увеличь L1!
19. Далее Excel вычисляет силу пружины при предварительной деформации (F1) в Н
в ячейке C29: =C20*C21-C20*C26=168,8
F1 = C*L0-C*L1
20. Полное число витков (N1) выводится
в ячейку C30: =C19+1,5=13,0
N1 = N+1,5
21. Угол подъёма витка пружины (A) в градусах рассчитывается
в ячейке C31: =ATAN (C12/ПИ()/(C3-C2))*180/ПИ()=6,4
A = arctg (T/3,14/(D1-D))*180/3,14
По-моему, этот угол не должен превышать 10 градусов.
22. Длина развёрнутой пружины (Lразв) в мм вычисляется
в ячейке C32: =ПИ()*C30*(C3-C2)/COS (C31/180*ПИ())=698,7
Lразв =3,14*N1*(D1-D)/cos (A/180*3,14)23. И, наконец, последний расчетный параметр — масса пружины (G) в кг выводится
в ячейку C33: =ПИ()*C2^2/4*C32*7,85/10^6=0,039
G = 3.14*D^2/4* Lразв*7.85/10^6
Итак, мы с вами прошли очень подробно, по шагам, весь расчет пружины сжатия. Надеюсь, что не очень сильно утомил вас.
Возможно, вам понравился принцип пошагового алгоритма в режиме диалога программы с пользователем? Напишите пару строк в комментариях — мне будет очень интересно ваше мнение. Мне такой подход нравится. Он «дробит» сложные и запутанные алгоритмы решений на простые «кирпичики», с которыми разобраться легко! Особенно нравятся хорошо проработанные ситуации, когда вопрос в «кирпичике» требует ответа: либо – «да», либо – «нет.
Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.
ОСТАЛЬНЫМ можно скачать просто так… — никаких паролей нет!
Ссылка на скачивание файла: raschet-pruzhiny-szhatiya (xls 49,5KB).
P. S. (11.03.2017)
В связи с большим интересом посетителей блога к коническим пружинам до написания статьи на эту тему выкладываю файл, присланный мне одним из читателей. Желающие могут поработать с алгоритмом и формулами. Размещаю ссылку на файл в том виде, в каком получил его от Андрея ([email protected]): konicheskaya-pruzhina-2 (xls 26KB).
P. S. (22.08.2018)
В файл программы добавлены расчеты касательных напряжений при рабочей и максимальной деформациях.
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
al-vo.ru
Пример расчета винтовой цилиндрической пружины сжатия.
Задача.
Рассчитать винтовую цилиндрическую пружину сжатия из проволоки круглого сечения при условии, что
силы при предварительной деформации F1=80 Н;
при рабочей деформации F2=460 Н;
рабочий ход пружины h=50 мм.
Решение.
Изготовление пружины предусматриваем из пружинной стальной проволоки 1-го класса по ГОСТ 9889-78. Полагая, что диаметр проволоки пружины равен 4…6 мм, ориентируясь на кривую 4 графика (рис. 1), причем допускаемое напряжение для проволоки [τ]=500 МПа, что соответствует рекомендации ГОСТ 13764-68. Предположим, что сила пружины при максимальной деформации
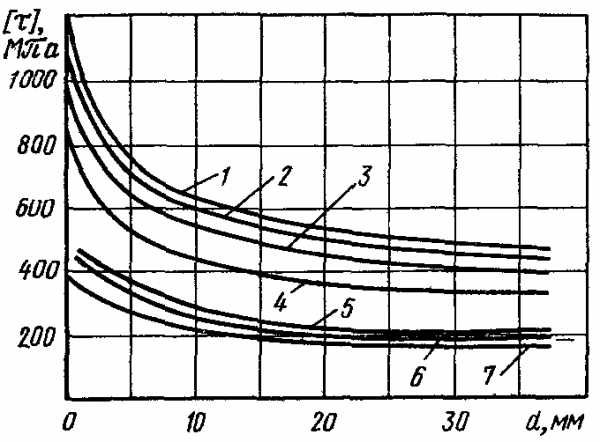 Рис. 1
Рис. 1
Примем индекс пружины (см. статью “Расчет винтовых цилиндрических одножильных пружин из проволоки круглого сечения.”) с=6. Коэффициент влияния кривизны витков k=1,24.
Диаметр проволоки пружины по формуле
В соответствии с ГОСТ 9389—75 окончательно принимаем d=5 мм. Следовательно, предварительно принятое значение [τ] соответствует графику (рис. 1) и значения c и k приняты правильно.
Средний диаметр пружины по формуле
Наружный диаметр пружины по формуле
Подберем пружину по ГОСТ 13766—68. Ближе всего подходит пружина 1-го класса 1-го разряда № 501. Для этой пружины F3=600 Н; d=5 мм; DH=36 мм; жесткость одного витка С1=200 Н/мм и наибольший прогиб одного витка λ′3=2,86 мм.
Уточним средний диаметр пружины:
Проверим выбранную пружину по С1, и λ′3. По формуле имеем
что приемлемо.
Жесткость пружины по формуле
Число рабочих витков пружины по формуле
Максимальная деформация пружины по формуле
Из формулы следует, что
что почти совпадает с табличным значением λ′3 по ГОСТу.
Полное число витков пружины по формуле
Шаг пружины по формуле
Высота пружины при максимальной деформации по формуле
где число зашлифованных витков n3=2.
Высота пружины в свободном состоянии по формуле
Длина развернутой пружины по формуле
metiz-bearing.ru
7.2. Расчёт пружин сжатия
Далее приводится общий расчет пружин сжатия. Исходными величинами для расчета пружин сжатия являются FН ‑ начальное нажатие пружины, FК ‑ конечное нажатие пружины и X ‑ ход пружины.
7.1. Из конструктивных соображений задаются значениями С и d.
7.2. Определяют коэффициент формы k = (4С + 2)/(4С ‑ 3). При С > 8 можно принять k = 1,1 ‑ 1,2.
7.3. Задаются маркой пружинной стали. Для нее определяют напряжение кручения, которое должно быть меньше допустимого. τ = (0,5 – 0,8) [τ]. Можно также принять, что τ = 0,4 В·
7.4. Предварительно определяют диаметр проволоки
или
Округляют значение d до ближайшего большего значения по сортаменту:
d = 0,2→0,32→0,4→0,5→0,6→0,8→1,0→1,2→1,6→2,0→2,5→3,0→4,0
7.5. Уточняют значение С и k: С = D/d; k = (4С + 2)/(4С ‑ 3).
7.6. Находят величину сжатия пружины для получения конечного усилия fК
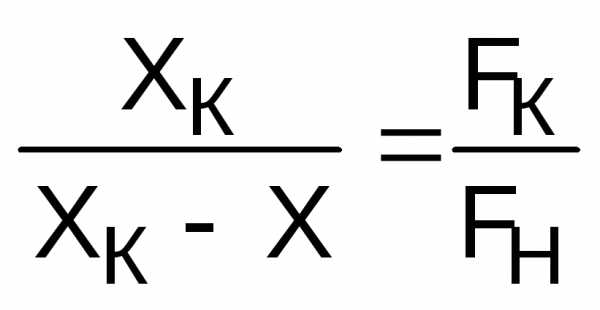
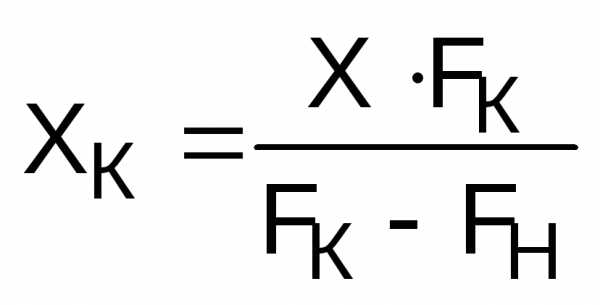
7.7.
Число рабочих витков: 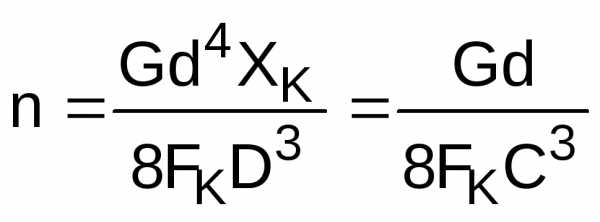
Число рабочих витков округляют до целого числа или до числа, кратного 0,5.
7.8. Полное число витков пружины N = n + (1,5 – 3,0) = n + nоп, где nоп – число опорных витков, которое принимается 0,5 для неответственных пружин и 1,5 – 3,0 для ответственных пружин.
7.9. Шаг пружины h = d + XК/n + 0,1d = XК/n + 1,1d.
7.10. Длина пружины при полностью сжатых витках lСЖ=1,1d (n + nоп ‑ 1). В формуле вычитается 1, так как опорные витки шлифуются на 0,5 диаметра проволоки для создания устойчивой опорной поверхности.
7.11. Длина пружины в свободном состоянии lСВ = lСЖ + n (h ‑ d)
7.13. Усилие пружины в полностью сжатом состоянии
7.14.
Проверка пружины на прочность 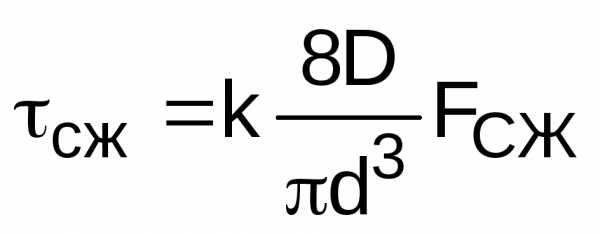 сж < [].
сж < [].
7.15. Сжатие пружины, необходимое для создания конечного усилия
7.16. Начальное сжатие пружины: ХН = ХК – Х.
7.17.
Начальное усилие нажатия, создаваемое
пружиной 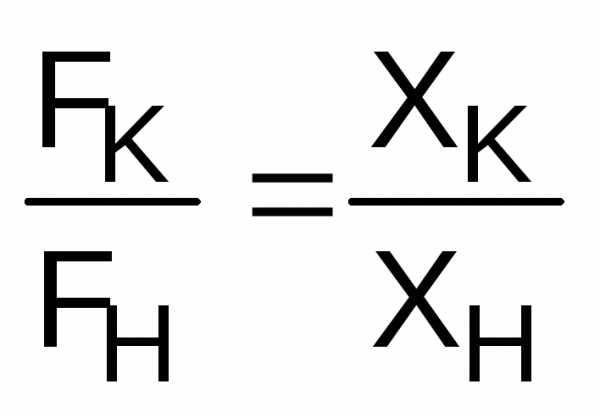
7.18. По рассчитанным усилиям и величинам сжатия пружины строится ее графическая характеристика в реальных величинах, при этом указываются: 1СВ, ХН, Х, ХК, 1СЖ, FК, FН, FСЖ.
7.3. Расчёт контактной пружины
Расчёт контактной пружины производится аналогично расчету, приведённому в подразделе 7.2.
За величину конечного нажатия контакта принимают усилие нажатия на контакты, полученное из расчета контактов с учетом обеспечения допустимого падения напряжения в контактах и отсутствия сваривания (окончательное усилие в контактах, проверенное в п. 6.13). Начальное усилие FКН определяется по п. 6.5. Эти усилия и выбранный провал контакта (п. 6.19) следует привести к точке действия контактной пружины. Провал контактов определяет ход контактной пружины.
При
расчете контактной пружины следует
выдержать конечное нажатие контактной
пружины. Начальное нажатие контактной
пружины может быть изменено по сравнению
с первоначально задаваемым. Однако надо
следить за тем, чтобы оно не выходило
из диапазона F
Реальные усилия, создаваемые контактной пружиной, необходимо привести к точке действия контактов и затем совместно с провалом и раствором контактов привести к оси сердечника электромагнитной системы.
studfiles.net
Сопротивление материалов. Расчет цилиндрических винтовых пружин.
Сопротивление материалов
Деформация кручения
Расчет цилиндрических винтовых пружин
В технике наиболее распространены цилиндрические винтовые пружины из стали круглого поперечного сечения, работающие на растяжение или сжатие. Покажем порядок расчета такой пружины, имеющей небольшой угол подъема витков (α ≤1 5°).
В качестве примера рассмотрим цилиндрическую винтовую пружину с диаметром D винтовой оси, диаметром d проволоки, числом витков n, сжимаемую силой F (рис. 5).
Для определения внутренних силовых факторов применим известный нам метод сечений. Рассечем пружину плоскостью, проходящей через ось, и отбросим нижнюю часть пружины. Ввиду того, что угол α подъема витков мал, будем считать сечение витка поперечным, т. е. кругом диаметром d.
Рассматривая равновесие верхней части пружины (рис. 6), видим, что в поперечном сечении витка возникают два внутренних силовых фактора:
– поперечная сила Q = F
– крутящий момент МКР = FD / 2.
Отсюда следует, что в поперечном сечении витка пружины действуют только касательные напряжения сдвига и кручения.
Будем считать, что напряжения сдвига распределены по сечению равномерно, а напряжения кручения определяются, как при кручении прямого кругового цилиндра.
Эпюры распределения напряжений сдвига и кручения, а также эпюра суммарных напряжений в точках горизонтального диаметра сечения представлены на рис. 6.
Из суммарной эпюры видно, что наибольшие касательные напряжения возникают в точке В, ближайшей к оси пружины:
τmax = τсдв + τкр = Q / S + Мкр / Wр = F / (πD3 / 4) + (FD / 2) / πd3 / 16),
откуда получаем:
τmax = (8FD / πd3) / (d / 2D + 1).
Если пружина имеет относительно большой средний диаметр и изготовлена из относительно тонкой проволоки, то первое слагаемое в скобках (соответствующее напряжению сдвига) значительно меньше единицы и в практических расчетах им можно пренебречь; тогда:
τmax = (8FD / πd3).
Для приближенного расчета цилиндрических пружин на прочность применяется формула:
τmax = (8FD / πd3) ≤ [τ] (1)
Поскольку пружины обычно изготавливают из высококачественной стали, допускаемое напряжение принимают равным в пределах [τ] = 200….1000 МПа.
***
Расчет осадки цилиндрической пружины
Далее выведем формулу для определения уменьшения высоты (осадки) λ пружины. Для этого мысленно разобьем пружину на бесконечно малые участки длиной dl, которые ввиду малости длины будем считать прямолинейными, и учитывая только потенциальную энергию деформации кручения, получим:
U = ∫l [(Мкр2 dl / (2GIp)] = Мкр2 l / (2GIp),
где l = πDn – длина проволоки пружины.
Работа силы F, приложенной к пружине статически, будет равна W = Fλ / 2.
Так как W =U, то Мкр = FD / 2, следовательно Ip = πd4 / 32, тогда получаем:
Fλ / 2 =[(Fλ / 2)2 πDn] / (2G πd4 / 32), откуда: λ = 8 FD3n / (Dd4).
Эту формулу можно записать в таком виде:
λ = F / С,
где:
С = Gd4 / 8D3n – коэффициент жесткости пружины.
При λ = 1, С = F, поэтому коэффициент жесткости численно равен силе, вызывающей осадку, равную единице длины.
Отношение среднего диаметра витков к диаметру проволоки обозначают Сn и называют индексом пружины:
Сn = D / d.
Обычно индекс пружин равен Сn = 4….12.
При более точных расчетах винтовых пружин учитывают кривизну их витков и вводят в числитель формулы (1) поправочный коэффициент К ≈ 1 + 1,45 / Cn.
***
Пример расчета цилиндрической пружины
Определить диаметр проволоки стальной пружины, если под действием силы F = 800 Н ее осадка λ = 39 мм.
Индекс пружины Сn= 6, число витков n = 14.
Модуль упругости стали пружины G = 8 х 104 Мпа, допускаемое напряжение [τ] = 450 МПа.
Решение.
Используя формулу для определения индекса пружины Сn = D / d, получим: D = Сn d. Подставляем это значение D в формулу для определения осадки пружины:
λ = 8 FD3n / (Dd4) = 8 FD3n / (Gd4) = 8 F Сn3 d3 n / (Gd4), откуда найдем d и после подстановки числовых значений получим:
d = 8 F Сn3 n / λ G = 8 х 800 х 106 х 14 / 39 х 10-3 х 8 х 104 х 106 = 7 х 10-3 м = 7 мм.
Итак, диаметр проволоки цилиндрической пружины должен быть не менее 7 мм, а средний диаметр самой пружины D = Сn d = 6 х 7 = 42 мм.
***
Материалы раздела “Кручение”:
Сочетание основных деформаций
k-a-t.ru
Расчет пружин
2.1.3 Последовательность расчета пружин сжатия
Исходными величинами для определения размеров пружин являются силы Р1 и Р2, рабочий ход h, наибольшая скорость V0 перемещения подвижного конца пружины при нагружении или лил при разгрузке, заданная выносливость N и наружный диаметр пружины D (предварительный). Если задана только сила Р2, то вместо рабочего хода h назначают прогиб F2 соответствующей заданной силе.
С учетом заданной выносливости N предварительно определяют принадлежность пружины к соответствующему классу по таблице 116.
По заданной силе Р2 и крайним значениям инерционного зазора δ по формуле (1) вычисляют граничные значения силы Р3.
По вычисленным величинам Р3, пользуясь таблицей 117, предварительно определяют принадлежность пружины к соответствующему разряду в выбранном классе.
По таблице 120 параметров пружин в соответствии со стандартом отыскивают строчку, в которой наружный диаметр витка близко совпадает с предварительно заданным значением D. Из этой же строки берут соответствующие величины Р3 и диаметр проволоки d.
По таблице 117 определяют напряжения τ3 вычисляют с учетом временного сопротивления σв по ГОСТ 9389-75
По полученным значениям Р3 и τ3, а также по заданной силе Р2 по формуле (2) находят критическую скорость Vкр и отношение , с помощью которого проверяют принадлежность пружины к предварительно установленному классу. Несоблюдения условиядля пружин 1 и 2 классов означает, что при скорости V0 выносливость, обусловленная в таблице 116, может быть не обеспечена. Тогда пружина должна быть отнесена к последующему низшему классу или должны быть изменены исходные условия с таким расчетом, чтобы после повторных вычислений в указанном порядке удовлетворялось требование. Если это выполнить нельзя, то назначают запасные комплекты пружин.
С учетом установленного класса и разряда в соответствии со стандартом по таблице 120 выбирают величины Z1 и f3, затем вычисляют размеры пружины.
Расчет первой пружины
Сила пружины при предварительном перемещении .
Сила пружины при рабочем перемещении .
Рабочий ход –
Наибольшая скорость перемещения подвижного конца пружины при нагружении и разгружении
Примем подачу метчика S=3мм/об.
Обороты шпинделя n=1.5об/с.
(3,1)
Выносливость N – число циклов до разрушения
N=5·106 (3,2)
Наружный диаметр пружины D=22.
Относительный инерционный зазор пружины сжатия δ = 0.01
Сила пружины при наибольшем перемещении
(3,3)
силу Р3 уточняем по таблице 120, Р3=115,758Н, диаметр проволоки d=2мм, жесткость одного витка Z1=19.620Н, наибольший прогиб одного витка f3= 5.9, временное сопротивление, σв=2100, наибольшее напряжение при крученииЄ Мпа (3,4)
Критическая скорость пружины сжатия
(3,5)
(3,6)
Условие соблюдается
Жесткость пружины
(3,7)
Число рабочих витков
(3,8)
Число опорных витков . Полное число витков
(3,9)
Средний диаметр пружины
(3,10)
Индекс пружины
(3,11)
Предварительное перемещение
(3,12)
рабочее перемещение
(3,13)
Наибольшее перемещение
(3,14)
Высота пружины при наибольшем перемещении
(3,15)
где n3=1.5 число шлифованных витков
Высота пружины при наибольшем перемещении
(3,16)
Высота пружины при предварительном перемещении
(3,17)
Высота пружины при рабочем перемещении
(3,18)
Шаг пружины
(3,19)
Длина развернутой пружины ( без учета зацепов пружины растяжения)
мм (3,20)
Масса пружины в КГ
(3,21)
Объем W занимаемый пружиной, мм
(3,22)
Расчет второй пружины
Сила
пружины при предварительном перемещении .
Сила пружины при рабочем перемещении .
Рабочий ход
Наибольшая скорость перемещения подвижного конца пружины при нагружении и разгружении
Примем подачу метчика S=3мм/об.
Обороты шпинделя n=1.5об/с.
(3,23)
Выносливость N – число циклов до разрушения таб. 116 N=5·106
Наружный диаметр пружины D=12
Относительный инерционный зазор пружины сжатия δ=0.01
Сила пружины при наибольшем перемещении
(3,24)
силу Р3 уточняем по таблице 120, Р3=61,120Н, диаметр проволоки d=1,2мм, жесткость одного витка Z1=16,147Н, наибольший прогиб одного витка f3= 3,645, временное сопротивление σв=2100, наибольшее напряжение при кручении
Мпа (3,25)
Критическая скорость пружины сжатия
(3,26)
Условие соблюдается
Жесткость пружины
(3,27)
Число рабочих витков
(3,28)
Число опорных витков
Полное число витков
(3,29)
Средний диаметр пружины
(3,30)
Индекс пружины
(3,40)
Предварительное перемещение
(3,41)
рабочее перемещение
(3,42)
Наибольшее перемещение
(3,43)
Высота пружины при наибольшем перемещении
(3,44)
где n3=1.5 число шлифованных витков
Высота пружины при наибольшем перемещении
(3,45)
Высота пружины при предварительном перемещении
(3,46)
Высота пружины при рабочем перемещении
(3,47)
Шаг пружины
(3,48)
Длина развернутой пружины ( без учета зацепов пружины растяжения)
мм (3,49)
Масса пружины в КГ
(3,50)
Объем W занимаемый пружиной, мм
(3,51)
studfiles.net
Конструирование и расчет цилиндрических витых пружин растяжения и сжатия
Пружины характеризуются следующими основными геометрическими параметрами (рисунок 7.3):
1) диаметром проволоки или размерами сечения витков;
2) средним диаметром пружины, а также наружным диаметром . и внутренним диаметром D-d
3) индексом пружин ;
4) шагом витков
5) углом подъема витков
6) длиной рабочей части пружины ;
7) числом рабочих витков .
Эти параметры взаимосвязаны, но только четыре из них можно рассматривать как основные. Шаг витков, угол подъема витков и длину рабочей части пружины рассматривают отдельно в ненагруженном и нагруженном состояниях.
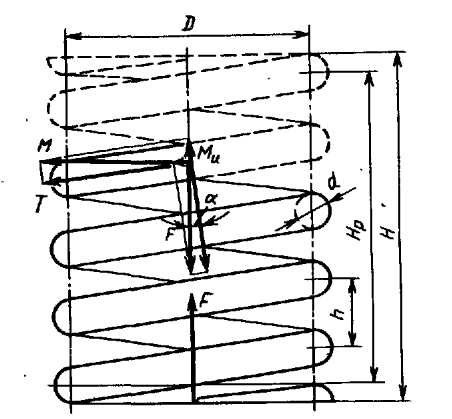
Рисунок 7.3 – Расчетная схема винтовой пружины
Чем податливее должна быть пружина, тем большим берется индекс пружины с и число витков. Обычно индекс пружины выбирают в зависимости от диаметра проволоки в следующих пределах:
d, мм до 2,5 3 – 5 6 – 12
с 5 – 12 4 – 10 4 – 9
Увеличив индекс пружины, можно при той же жесткости сократить габариты пружины по длине за счет увеличения диаметра, и, наоборот, уменьшив индекс пружины, можно уменьшить диаметр пружины за счет увеличения длины.
Пружины растяжения навивают таким образом, чтобы было обеспечено начальное натяжение (давление) витками. Это натяжение выбирают равным 1/4 – 1/3 от предельной силы для пружины, при которой ее испытывают и которая вызывает напряжения, близкие к пределу упругости. Такая навивка называется закрытой.
Пружины диаметром до 3 мы обычно выполняют с прицепами в виде изогнутых витков (рисунок 7.4 а, б). В местах отгиба возникает концентрация напряжений, которая снижает несущую способность пружин.
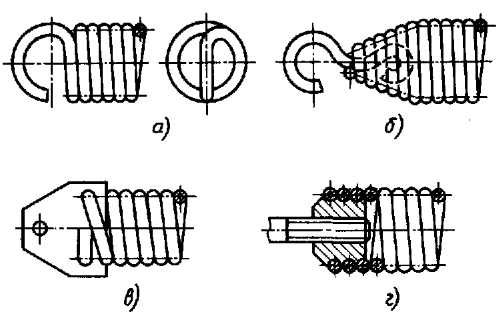
Рисунок 7.4 – Прицепы пружин растяжения
Поэтому для ответственных сильно напряженных пружин применяют закладные прицепы с конической заделкой (рисунок 7.4 б) и крепления с помощью пластин (рисунок 7.4 в). Наиболее совершенным является крепление с помощью ввертных винтовых пробок с крючками (рисунок 7.4 г). Это крепление применяют для пружин с диаметром проволоки от 5 мм.
Силовые факторы, действующие в любом поперечном сечении пружин растяжения и сжатия, сводятся к моменту , вектор которого перпендикулярен оси пружины и силе F, действующей вдоль оси пружины (см. рисунок 7.3).
Момент раскладывается на крутящий T и изгибающий моменты:
и
В большинстве пружин угол подъема витков . Расчет этих пружин можно вести только на кручение по моменту , пренебрегая другими силовыми факторами ввиду их малости.
Максимальное напряжение кручения, возникающее на внутренних волокнах,
;
здесь — коэффициент, учитывающий кривизну витков (поправка к формуле для кручения прямого бруса):
4 5 6 8 10 12
1,37 1,29 1,24 1,17 1,14 1,11
Допускаемые напряжения кручения для пружин при статической нагрузке приведены на рис. 320. При пульсирующей нагрузке с небольшим числом циклов допускаемые напряжения понижают в 1,25—1,5 раза.
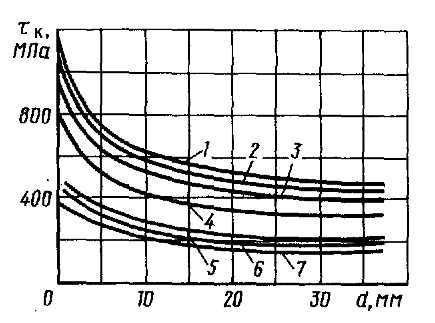
1 – из вольфрамовой и рояльной; 2 – из хромованадиевой; 3 – из углеродистой, закаленной в масле; 4 – из углеродистой холоднотянутой; 5 – из монель-металла; 6 – из фосфористой бронзы; 7 – из специальной латуни
Рисунок 7.5 – Допускаемые напряжения кручения для витых пружин из разных проволок (материалов)
Из приведенной зависимости после замены получают формулу для определения диаметра проволоки при проектном расчете пружин:
Осевое упругое сжатие пружины определяют как суммарный угол закручивания витков пружины , умноженный на средний радиус пружины :
где — податливость одного витка, т. е. сжатие витка от единичной силы; — модуль сдвига.
Длина дружины при максимальной рабочей нагрузке:
где — сила начального сжатия витков при навивке.
Длина пружины растяжения в ненагруженном состоянии:
где — высота одного прицепа, равная .
Длина проволоки для изготовления пружин:
где — длина проволоки для одного прицепа.
Предельная нагрузка для пружин .
Длину пружины при определяют по аналогии с длиной пружины при .
Для пружин сжатия к расчетному числу витков прибавляют по 1,75—1 витку для каждого конца, т. е. .
Длина пружины сжатия при соприкосновении витков с учетом сошлифовки каждого конца пружины на
Шаг пружины сжатия в ненагруженном состоянии
где — упругое сжатие пружины под действием силы , — коэффициент, предопределяющий некоторый зазор между витками пружины при во избежание частичного прилегания витков и потери линейности характеристики пружины. Обычно .
Длина пружины в ненагруженном состоянии
Пружины сжатия, у которых во избежание выпучивания, ставят на оправках или в стаканах.
cyberpedia.su
Расчет винтовых цилиндрических одножильных пружин из проволоки круглого сечения.
Расчет винтовых цилиндрических одножильных пружин растяжения и сжатия.
Рассмотрим расчет винтовых цилиндрических одножильных пружин растяжения и сжатия. Основные геометрические параметры винтовых цилиндрических пружин из проволоки круглого поперечного сечения (см. рис. 1):
d — диаметр проволоки;
Dн и D — наружный и средний диаметры пружины;
c=D/d — индекс пружины;
t — шаг пружины;
α — угол подъема витков;
L0 — длина развернутой пружины (без учета зацепов пружины). Податливость пружины прямо пропорциональна ее индексу c. Для увеличения податливости пружины индекс с принимают возможно большим; практически c=4…12.
| d, мм | < 2,5 | 3…5 | 6…12 |
|---|---|---|---|
| c | 5…12 | 4…10 | 4…9 |
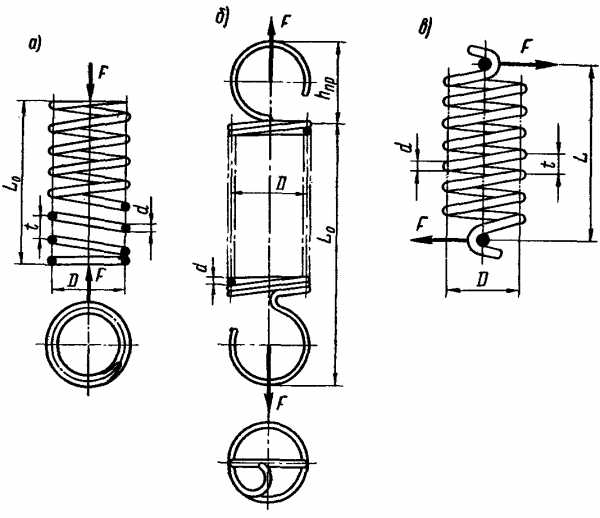 Рис. 1
Рис. 1
С увеличением индекса пружины той же жесткости можно сократить ее длину путем увеличения диаметра, а с уменьшением индекса можно уменьшить диаметр пружины путем увеличения ее длины.
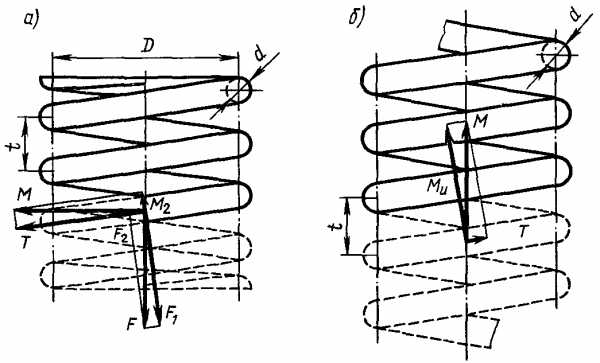 Рис. 2
Рис. 2
В любом поперечном сечении витка пружины растяжения или сжатия при работе возникают (рис. 2, а) сила F, направленная по осевой линии пружины, и момент М=FD/2, вектор которого перпендикулярен осевой линии пружины. Сила F раскладывается на поперечную F1=F cos α и продольную F2=F sin α силы. При разложении момента М по осевой линии витка пружины и перпендикулярному ему направлению в поперечном сечении проволоки пружины возникают:
крутящий T=FD cos α/2
и изгибающий Ми=FD sin α/2 моменты. Так как угол α<10…12°, то изгибающий момент Ми значительно меньше крутящего Т, а продольная сила F2 значительно меньше поперечной силы F1 но, как показывают расчеты, касательные напряжения сдвига значительно меньше касательных напряжений кручения, поэтому для упрощения расчета пружин на прочность обычно учитывают лишь крутящий момент T, при этом приближенно принимают cos α=1, т. е. T=М=FD/2. Таким образом, расчет винтовой цилиндрической пружины растяжения или сжатия из проволоки круглого поперечного сечения производят по формуле
где τ — расчетное максимальное напряжение в поперечных сечениях витков пружины;
[τ] — допускаемое напряжение для проволоки пружины; k — коэффициент влияния на напряжение кривизны витков и поперечной силы;
F — максимальная растягивающая или сжимающая сила. Формулой пользуются при проверочном расчете пружины, когда ее размеры известны.
| c | 4 | 5 | 6 | 8 | 10 | 12 |
|---|---|---|---|---|---|---|
| k | 1,37 | 1,29 | 1,24 | 1,17 | 1,14 | 1,11 |
 Рис. 3
Рис. 3
Допускаемое напряжение [τ] пружин при статических нагрузках можно принимать по графикам (рис. 3), где отдельные кривые относятся к пружинам из проволоки:
- 1 — вольфрамовой и рояльной;
- 2 — хромованадиевой;
- 3 — углеродистой, закаленной в масле;
- 4 — углеродистой холоднотянутой;
- 5 — моиель-металла;
- 6 — фосфористой бронзы;
- 7 — специальной латуни.
При пульсирующей нагрузке с небольшим числом циклов допускаемые напряжения [τ] следует принимать в 1,25…1,5 раза ниже, чем по графикам.
При проектировочном расчете пружины диаметр проволоки
значением индекса с пружины задаются. Диаметр d проволоки, вычисленный по формуле, окончательно согласовывают с соответствующим ГОСТом для пружинной проволоки.
Средний диаметр D пружины и наружный диаметр DH определяют по формулам
и
При расчетах различают следующие силы пружины (см. рис. 1 , а, б):
при предварительной деформации — F1
при рабочей деформации (соответствует наибольшему принудительному перемещению подвижного звена в механизме) — F2;
при максимальной деформации “(допускаемой) — F3.
Соответственно в формулах F=F3.
Обычно пружину устанавливают с действующей на нее начальной нагрузкой F1=(0,1…0,5)F2. Максимальная сила пружины F3=(1,05..,1,66)F2. При изменении силы пружины от F1 до F2 жесткость пружины
где h — рабочий ход пружины, значение которого назначают или вычисляют по условиям работы механизма. Жесткость одного витка пружины
где G — модуль сдвига материала проволоки пружины. Для стали G=80000 МПа и, следовательно, для стальной пружины
где С1 — в Н/мм; d – в мм.
Число рабочих витков пружины
Полное число витков
где n2=1,5…2 — число опорных витков.
Деформация пружины
λ1 — предварительную,
λ2 — рабочую и
λ3 — максимальную. Максимальная деформация одного витка пружины
Шаг пружины в ненагруженном состоянии:
для пружины сжатия
для пружины растяжения
Высота пружины при максимальной деформации
где n3 — число зашлифованных витков. Высота пружины в свободном состоянии для пружины сжатия
для пружины растяжения
Высоту пружины при предварительной и рабочей деформации легко определить из (рис. 1, а, б). Длина развернутой пружины (без учета зацепов пружины растяжения)
Более подробный геометрический расчет винтовых цилиндрических пружин сжатия и растяжения из стальной проволоки круглого сечения дан в ГОСТ 13765-68.
Расчет винтовых цилиндрических одножильных пружин кручения.
Рассмотрим расчет винтовых цилиндрических одножильных пружин кручения. При работе пружины кручения в поперечных сечениях витков возникает момент М (см. рис. 3, б), равный внешнему моменту, закручивающему пружину, вектор которого направлен вдоль осевой линии пружины. При разложении момента М по осевой линии витка пружины и перпендикулярному ему направлению в поперечном сечении витка пружины возникают крутящий T=M sin α и изгибающий Ми=М cos α моменты. Так как изгибающий момент Ми значительно превышает крутящий момент Т (обычно угол α<12…15°), то пружины кручения рассчитывают только на изгиб по изгибающему моменту, при этом приближенно принимают Ми=M.
Таким образом, расчет винтовой цилиндрической пружины кручения из; проволоки круглого сечения производят на изгиб по моменту М, закручивающему пружину:
где σи — расчетное максимальное напряжение на изгиб в поперечных сечениях проволоки пружины;
[σи] — допускаемое напряжение на изгиб проволоки пружины;
k — коэффициент влияния кривизны витков. Рекомендуется принимать
Коэффициент влияния кривизны витков
где c=D/d — индекс пружины, принимаемый в зависимости от диаметра проволоки.
Формулой
пользуются при проверочном расчете пружины, когда ее размеры известны. При проектировочном расчете пружины диаметр проволоки
Шаг витков пружины t
где Δ=0,1…0,5 мм — зазор между витками.
При заданном значении угла закручивания пружины φ, рад, требуемое число рабочих витков пружины
где J≈0,5d4 — осевой момент инерции площади сечения проволоки;
Е — модуль продольной упругости материала пружины.
Высота пружины
где hпр — высота одного прицепа пружины.
Длину L проволоки для изготовления пружины определяют по формуле
metiz-bearing.ru

