Расчет реечной зубчатой передачи – Реечная передача. Расчет в Excel.
alexxlab | 26.05.2018 | 0 | Вопросы и ответы
Реечная передача. Расчет в Excel.
Опубликовано 24 Окт 2015
Рубрика: Механика | 24 комментария
(Статья полностью обновлена 19.03.2017.)
Небольшой расчет, представленный далее, предназначен для ориентировочного быстрого определения габаритов зубчатой реечной передачи и её основных силовых и кинематических параметров.
Предложенный ниже алгоритм основан на расчете поверхностной прочности зубьев по контактным напряжениям.
Реечная передача может служить для преобразования вращательного движения шестерни в поступательное движение рейки или вала самой шестерни, а может быть использована для преобразования поступательного движения рейки во вращательное движение зубчатого колеса. Расчет реечной передачи, по сути, аналогичен расчету зубчатой цилиндрической передачи. С математической точки зрения рейка – это зубчатое колесо с радиусом равным бесконечности.
Проектировочный расчет в Excel реечной зубчатой передачи.
Для выполнения расчетов будем использовать программу MS Excel или Calc из бесплатных офисных пакетов
Заполняя исходные данные для расчета, пользователь может изменять характеристики используемого для передачи материала, относительную ширину и угол наклона зубьев, нагрузку и скорость.
Схема реечной передачи представлена на рисунке чуть ниже.

Уважающих труд автора прошу скачивать файл с расчетной таблицей после подписки на анонсы статей (подписные формы — в конце статьи и наверху страницы).
Ссылка на скачивание файла с программой: reyechnaya-peredacha (xls 59KB).
Исходные данные:
1. Значение модуля упругости материала передачи E в МПа записываем
в ячейку D3: 215000
Для стали E=215000 МПа.
2. Коэффициент Пуассона материала μ
вписываемв D4: 0,3
Для стали μ=0,3.
3. Твердость поверхности зубьев по шкале C Роквелла HRC вводим
в D5: 27
Для различных режимов термообработки стали HRC≈17…65.
К примеру, круг из Стали 45 в состоянии поставки имеет твердость около HRC 22.
4. Величину безразмерного коэффициента ширины зубчатого венца шестерни ψbd заносим
в D6: 0,6
ψbd=b2/d=0,6…0,4.
5. Угол наклона зубьев β вводим в градусах
в D7: 15,0000
Если проектируемая реечная передача прямозубая, то β=0°.
Если передача косозубая, то β≈8°…22°.
6. Вращательный момент на валу шестерни T вписываем в Н*м
в D8: 500
Этот момент определяет нагрузочную способность реечной передачи и задается в техническом задании.
7. Скорость центра вала шестерни относительно рейки v в м/с заносим
в D9: 0,050
Скорость определяется из назначения механизма и является одним из пунктов технического задания на проектирование.

Результаты расчетов:
8. Допускаемое контактное напряжение [σH] в МПа вычисляем
в ячейке D11: =ЕСЛИ(D5<38;2*127,57*EXP (0,0266*D5)+70; ЕСЛИ(D5<=56;18*D5+150;23*D5)) =600,0
При HRC<38 [σH]=2*127,57*e(0,0266*HRC)+70
При 38≤HRC≤56 [σH]=18*HRC+150
При HRC≥56 [σH]=23*HRC
9. Расчетный делительный диаметр dp в мм вычисляем
в D12: =(2*2*D8*1000*D3/(ПИ()*(1-D4^2)*D11^2*D6*SIN (2*20/180* ПИ())))^(1/3)=102,7
dp≥(4000*T*E/(π*(1- μ2)*[σH]2*ψbd*sin(2*α)(1/3)
10. Расчетный модуль зацепления mp в мм определяем
в D13: =D12/(17*COS (D7/180*ПИ())^3) =6,70
mp= dp/(17*(cos (β))3)
11. Выбираем ближайшую к расчетному значению величину модуля m из стандартного ряда, представленного в примечании к ячейке D14, и вписываем
в D14: 6,00
12. Минимальное расчетное число зубьев шестерни z1 рассчитываем
в D15: =17*COS (D7/180*ПИ())^3 =15,3
z1=17*(cos (β))3
Число зубьев шестерни определяется из условия отсутствия подрезки ножек зубьев.
13. Назначаем число зубьев шестерни z1 и записываем его
в D16: 17
Рекомендуется назначить число зубьев таким, чтобы делительный диаметр шестерни был не меньше расчетного делительного диаметра.
14. Делительный диаметр шестерни d в мм вычисляем
в D17: =D14*D16/COS (D7/180*ПИ()) =105,598
d=m*z1/cos (β)
Если полученное значение делительного диаметра окажется меньше расчетного значения, поле ячейки D15 «подсветится» красным цветом, что заставит пользователя обратить внимание на ошибку и увеличить число зубьев, модуль или угол наклона зубьев.
15. Диаметр вершин зубьев шестерни da в мм находим
в D18: =D17+2*D14 =117,598
da=d+2*m
16. Диаметр впадин зубьев шестерни df в мм рассчитываем
в D19: =D17-2,5*D14 =90,598
df=d-2,5*m
17. Ширину зубчатого венца шестерни b1 в мм считаем
в D20: =ОКРУГЛ(D21+0,6*D21^0,5;0) =68
b1≈b2+0,6*b2(½)
18. Ширину зубьев рейки b2 в мм находим
в D21: =ОКРУГЛ(D17*D6;0)=63
b2≈d*ψbd
19. Окружную силу на шестерне Ft в Н рассчитываем
в D22: =2*D8/(D17/1000) =9470
Ft=2*T/d
20. Мощность на валу шестерни P в Вт вычисляем
в D23: =D22*D9 =473
P=Ft*v
21. Частоту вращения вала шестерни n в об/мин определяем
в ячейке D24: =60*D9/ПИ()/(D17/1000) =9,043
n=60*v/(π*d)
Расчет в Excel завершен.
Заключение.
Мы рассмотрели пример, в котором была рассчитана зубчатая реечная передача по упрощенной схеме.
Детальный и полный расчет передачи, учитывающий десяток дополнительных факторов, может позволить на 5%…10% уменьшить габаритные размеры передачи! Это следует понимать и помнить.
Если требуется уменьшить число зубьев шестерни менее 14-и, необходимо спроектировать и изготовить её возможно не только с наклоном зубьев, но и/или с положительным смещением исходного контура. При этом нужно следить за отсутствием заострения вершин зубьев, производя соответствующую проверку.
Важными параметрами, обеспечивающими плавность работы реечной передачи, являются коэффициенты осевого и торцевого перекрытия. Их значения всегда следует контролировать.
О проверке качества зубчатого зацепления по геометрическим показателям читайте в следующих новых статьях на блоге.
Подписаться на анонсы статей можно через специальные окна, расположенные в конце любой статьи или наверху любой страницы сайта.
Можете оставлять ваши комментарии, уважаемые читатели, ниже этого текста в блоке «Отзывы».
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
al-vo.ru
Реечная передача: расчет, механизм, КПД, применение
Всем редукторам и коробкам передач предшествовала кремальера. Ее использовали для вертикального перемещения котла над огнем. Повар крутил ручку и прикрепленный к рейке котел поднимался вверх и опускался вниз. Самая длинная реечная передача сделана в Италии на железной дороге. Чтобы поезд не скатывался по крутым склонам вниз, между рельсами прокладывали зубчатую рейку. На оси колес устанавливалась шестерня, которая и тянула поезд вверх. Ответное колесо вместо рейки для передачи крутящего момента появилось позже.

Общая информация
Реечная зубчатая передача получила свое название по одной из деталей – рейке. Это единственное зацепление шестерни, которое меняет не скорость и направление крутящего момента, а тип движения. Вращение привода изменяется на движение в заданной плоскости.
Отличительной особенностью реечной передачи является ее неограниченная продолжительность. Рейки укладываются в один ряд. На стыках подгоняются, чтобы выдерживался модуль. Для этого просто укладывают на стык в зацепление зубчатую планку с таким же модулем или одну из приготовленных к монтажу реек. Крепеж устанавливается по подметке, что сводит к минимуму погрешность.
Соединение зубчатой рейки и шестерни бывает разных видов:
- прямозубое;
- косозубое;
- многорядное.
Обеспечить нормальную работу реечного узла можно точной установкой деталей относительно друг друга.
Зубья должны соприкасаться по средней линии.
Модуль подбирается по усилию, которое необходимо передать для движения. Увеличить прочность и допустимую нагрузку можно различными способами:
- увеличить площадь контакта за счет большей ширины зуба;
- заменить прямозубое соединение косозубым;
- использовать шестерню большего диаметра.
Прямозубое зацепление имеет широкое распространение. Для реечных механизмов, не требующих большой точности смещения, детали могут отливаться из чугуна. Зубчатое колесо и рейка имеют шероховатую поверхность и сильно шумят. Они неприхотливы, работают при высоких температурах, в условиях сильной запыленности. Часто применяются для открывания термических и литейных печей с выдвижным подом, перемещают загрузочные тележки на металлургических печах. Рейка обычно перевернута зубом вниз. Шестерня и привод установлен в яме.

Косозубая реечная пара способна передать большее усилие при зацеплении. За счет расположения зуба под углом, площадь контакта увеличивается. Узел производит при работе меньше шума. Детали требуют высокой точности при изготовлении и тонкой регулировки. По мере стирания поверхности зубьев, надо смещать межцентровое расстояние. При нарушении угла, нагрузка смещается и происходит быстрое разрушение шестерни.
Движение может передаваться и от реек к зубчатому колесу. Примером служат детские игрушки и механические фонарики, изготавливаемые в прошлом веке. Когда на торец пластины нажимали рукой, рейка приводила в движение ротор и лампочка начинала светить.
КПД реечной передачи, в зависимости от типа зубьев, составляет:
- цилиндрическая — 0,96…0,98
- коническая — 0,95…0,97.
Применение реечной передачи
В большинстве реечных механизмов происходит превращение вращения в поступательное движение. При проектировании оборудования, конструкторам приходится делать сложные расчеты эвольвенты зуба и расстояния от средней линии рейки до оси шестерни. Им на помощь приходят готовые таблицы с нормализованными деталями. Это упрощает процессы расчета, поскольку в большинстве случаев эксплуатации узла с малыми нагрузками берутся стандартные пары.
Передача реечная широко используется в механизмах совершенно разного назначения:
- металлорежущее оборудование;
- термические печи;
- сдвижные ворота;
- фуникулеры;
- кранбалки;
- мостовые краны;
- шахтные тележки;
- сварочные автоматы;
- промышленные роботы;
- станки с ЧПУ.

Известный всем водителям реечный механизм является узлом рулевого колеса. Вращение колеса превращает в поступательное перемещение тяг и синхронный поворот колес.
Широкое применение получили реечные передачи в производственном оборудовании. На строгальных и продольно фрезерных станках стол перемещается по направляющим станины. Между ними расположена рейка. Передача движения от привода осуществляется через расположенную в нижней части стола шестерню. Она тянет стол в режиме резания, и быстро его возвращает в исходное положение на холостом ходу.
Шпиндельная группа сверлильных и вертикально фрезерных станков перемещается вверх и вниз по колонне, на которой закреплена планка с зубьями. Реечная передача получает вращение от электродвигателя шпинделя через ремень и шкив.
Примеры использования реечных узлов в быту встречаются часто. Все откатные ворота имеют внизу или на середине полотна рейку. Двигатель с шестерней устанавливаются на столбе. Включить привод и открыть ворота можно дистанционно, из дома или посредством электронного пульта управления.
Данные для расчета
Расчет реечной передачи производится посредством ряда формул, в которых используются данные:
- высота зуба;
- его ширина по средней линии;
- диаметр шестерни;
- угол поворота при повороте на один зуб.
Расстояние от делительного диаметра до оси шестерни задается конструктором изначально. По завершении расчетов размер корректируется, поскольку используются нормализованные детали.
Модуль зуба реечной передачи подбирается исходя из нагрузки, которую он должен выдержать и коэффициента прочности.
Боковой зазор регулируется в процессе эксплуатации смещением шестерни с учетом износа зуба. От правильно сделанного натяга зависит плавность пуска, размер люфта и точность перемещения.
Величины отклонений размеров деталей и нормы шероховатости поверхности зуба заложены в ГОСТ 2789-73 и ГОСТ 2.309-73.
Скачать ГОСТ 2.309-73
Скачать ГОСТ 2789-73
Прочностной расчет учитывает предельные допустимые значения и коэффициенты:
- напряжения изгиба;
- угол наклона;
- модуль зацепления;
- перекрытие;
- форму зубьев;
- окружную силу.

При проектировании оборудования, конструктора по нагрузкам подбирают нормализованные детали. Практическим путем определяется только длина рейки.
Преимущества и недостатки
Узлы с зубчатыми рейками считают устаревшими и громоздкими. На самом деле реечная механическая передача представляет собой зубчатое зацепление малой шестерни с сегментом колеса, имеющего бесконечно большой диаметр. Идеальный механизм в настоящее время не изобретен и приходится выбирать передачу, с учетом ее технических характеристик.
Недостатки
Передача обладает рядом недостатков, к ним относят следующие:
- устаревшая технология;
- большой люфт;
- сильный шум;
- маленькая точность перемещений;
- большая погрешность на стыке реек;
- требует высокой точности изготовления;
- ручная сборка;
- боится грязи;
- низкая производительность;
- ограничен спектр применения.

Узел обладает всеми недостатками зубчатых передач. Основное из них, это разрушение зубьев при перегрузе. На ременных передачах, когда нагрузка резка увеличивается, происходит проскальзывание ремня по шкиву. У зубьев нет такой возможности. По аналогии в предохранительные муфты вставляют пальцы, и через них передается вращательный момент. При перегрузе они разрушаются и заменяются новыми.
Разница в том, что изготовить шпильку с посадочным диаметром намного проще и дешевле. Шестерни делаются из легированных сталей. Процесс их изготовления сложный, многоступенчатый. Деталь дорогостоящая.
Точность изготовления зубчатой рейки выше, чем шестерни. Чем сильнее изгиб линии основания зуба, тем больше погрешность при его нарезании.
Механическое взаимодействие двух деталей всегда сопровождается шумом. Частично его снижает смазка. Плавно и тише работают косозубые и многорядные передачи.
Если не будет зазора по эвольвенте, то детали «склеятся» на молекулярном уровне. Такой эксперимент проводили в конце прошлого века. Проектировщики создали зубчатую пару с идеальными размерами и чистотой. В результате сделав несколько оборотов, шестерни сварились, и рассоединить их не получилось.
Зазор нужен для компенсации расширения металла при нагреве. Любое трение сопровождается повышением температуры.

Точность перемещения не позволяет полностью автоматически делать различные операции. На старом оборудовании имеется дополнительная точная доводка. В станки ЧПУ вмонтирован электронный контроль координат, который через блок управления выполняет точную настройку координат.
При стыке реек используют специальные шаблоны, и погрешность шага зуба минимизируется до допустимого размера. Сборка реечных передач в большинстве случаев остается ручной, многочисленные доводки и подгонки невозможно автоматизировать. Исключение составляют узлы без больших нагрузок с малым перемещением, как например в автомобиле.
Достоинства
Реечная передача имеет превосходство перед аналогичными узлами. Это простая конструкция и неограниченная длина перемещения. Тележки походят сотни метров, поезда километры на тяге реечной передачи.
Зубья можно расположить в любом направлении и грязь с них будет опадать сама. Привод можно устанавливать неподвижно, это уменьшает габариты, и вес подвижной части механизма.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
stankiexpert.ru
6.3. Реечная передача
В технике широко применяются передачи зубчатое колесо – рейка для преобразования вращающего движения в поступательное и наоборот. Привод состоит из электродвигателя (1), редуктора (2) и передачи зубчатое колесо – рейка (3) (рис.6.6).
Рис.6.6. Реечный толкатель
Расчёт реечной передачи:
• Мощность двигателя, [Вт,Н∙м/с],
Мощность электродвигателя
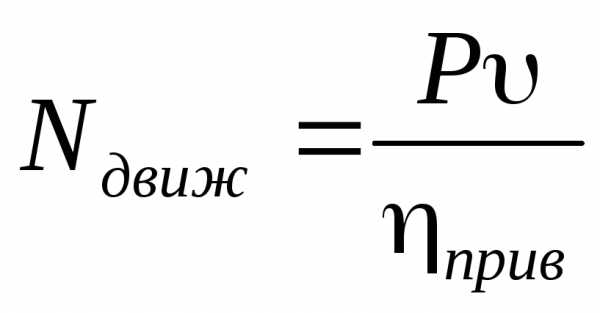 , (6.38)
, (6.38)
где hр. передача = 0,9.
• Задаются числом зубьев шестерни Z1=20…30. Модуль m реечной передачи рассчитывается по тем же зависимостям, что и для цилиндрических передач, обычно m=1…4мм. Диаметр начальной окружности шестерни dW1=mz.
Рис.6.7. К расчёту реечной передачи
 ,F2=F1tgaw (6.39)
,F2=F1tgaw (6.39)
• Угловая
скорость 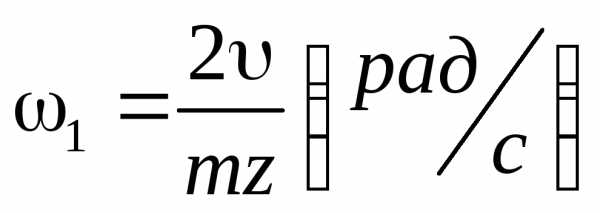 (6.40)
(6.40)
• Обороты шестерни (6.41)
• Расчёт реечных зубчатых передач начинают с выбора материала.
В легконагруженных передачах принимают сталь с HRC£350 и термообработку, чтобы HRC ³НВ2+(20…40). Индекс 1 — шестерня, 2 — рейка. Для тяжелонагруженных передач — сталь HRC³350. Выбор s°Hlim и s°Flim и по табл.6.5.
Таблица.6.5. | ||||
Сталь | Термообработка | Твёрдость на поверхности | s°Hlim | s°Flim |
45; 40Х; 35ХМ; 40ХН; 45Л | Улучшение | НВ=180…350 | 2НВ+70 | 1,8 |
45; 40Х; 40ХН; 35ХМ | Объёмная закалка | HRC 38…50 | 18HRC+150 | 550…660 МПа |
35ХМ; 40Х; 40ХН | Закалка ТВЧ | HRC 45…56 | 17HRC+200 | 750…850 МПа |
18ХГТ; 18Х2Н4ВА; 20ХН2М; 12ХН3А | Цементация | HRC 56…63 | 23 | 750…900 МПа |
Вначале вычисляются допустимые контактные напряжения для рейки и шестерни отдельно
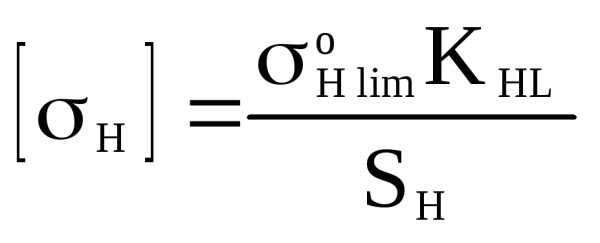 , (6.42)
, (6.42)
где s°Hlim — предел контактной выносливости при базовом числе циклов, МПа;
KHL — коэффициент долговечности, принимаем KHL=1; SH — коэффициент безопасности, SH=1,6…2,0.
Допускаемые напряжения изгиба определяются по формуле
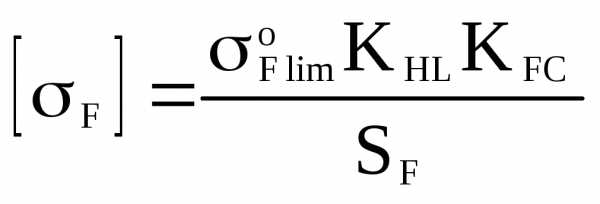 , (6.43)
, (6.43)
где s°Flim — предел выносливости зубьев при изгибе при базовом числе циклов, МПа; KHL — коэффициент долговечности, принимаем KHL=1; KFC — коэффициент, учитывающий реверсивность нагрузки, KFC=0,7…0,8 для реверсивных; SF — коэффициент безопасности, SF =1,6…2,0.
• Геометрические параметры реечной передачи определяются по формулам:
Делительный диаметр (начальной окружности) шестерни dw1=m1z1
Наружный диаметр (начальной окружности) шестерни da1=dw1
Диаметр впадин зубьев df1=dw1+2,5m
Ширина рейки в³(2…10)m
Угол поворота шестерни зуба рейки
Высота головки зуба рейки ha=m
Высота ножки зуба рейки hf=1,25m
•Спроектированная передача проверяется по контактным напряжениям в зоне зацепления sН и на усталость при изгибе sF.
•проверка по контактным напряжениям в зоне зацепления
, (6.44)
принимая для стали Еприв=2∙105МПа или 2∙1011Па и a=20° для эквивалентного зацепления
, (6.45)
где KHa — коэффициент, учитывающий распределение нагрузки между зубьями, KHa=1 — для прямозубой; KHb — коэффициент, учитывающий распределение нагрузки по ширине венца KHu=1,15; KНu — коэффициент динамической нагрузки, учитывающий возникновение дополнительных динамических нагрузок, при u£0,5м/с, KНu=1,0; SF — коэффициент безопасности, SH=1,6…2,0.
Полученные контактные напряжения должны удовлетворять условию 0,9[sН]£ sН £1,05[sН], т.е. недогруз не более 10%, перегруз не более 5%,
•проверка зубьев на усталость при изгибе, силы действующие на реечное зацепление раскладываются на тангенциальную Ft=2Т1
Напряжение изгиба в опасном сечении ножки зуба рассчитывается по формуле
, (6.46)
где YF — коэффициент формы зуба, для шестерни определяется по графику (рис.6.8).
Рис.6.8. Коэффициент формы зуба
для рейки YF=3,62,
KFa=1.26; KFu=1, KFb — коэффициент нагрузки, зависит от твёрдости материала и ybd=b1/d1.
Таблица 6.6.
Материал | 0 | 0,4 | 0,8 | 1,2 | 1,6 | 1,8 |
НВ£350 | 1 | 1,08 | 1,1 | 1,16 | 1,28 | 1,35 |
НВ>350 | 1 | 1,08 | 1,17 | 1,24 | 1,4 | – |
studfiles.net
Расчет зубчатой передачи в Excel
Опубликовано 22 Июн 2013
Рубрика: Механика | 102 комментария
Для полного и точного проектировочного расчета зубчатой цилиндрической эвольвентной передачи необходимо знать: передаточное число передачи, крутящий момент на одном из валов, частоту вращения одного из валов, суммарное машинное время работы передачи,…
…тип передачи (прямозубая, косозубая или шевронная), вид передачи (с внешним зацеплением или внутренним), график нагрузки (режим работы – доля времени действия максимальных нагрузок), материал и термообработку шестерни и колеса, схему расположения передачи в редукторе и в общей схеме привода.
На основании вышеперечисленных исходных данных при помощи многочисленных таблиц, разнообразных диаграмм, коэффициентов, формул определяются основные параметры зубчатой передачи: межосевое расстояние, модуль, угол наклона зубьев, число зубьев шестерни и колеса, ширины зубчатых венцов шестерни и колеса.
В детальном алгоритме расчетов — около пятидесяти смысловых программных шагов! При этом часто при работе приходится возвращаться на несколько шагов назад, отменять принятые ранее решения и вновь двигаться вперед, понимая, что, возможно, придется вновь вернуться. Найденные в результате такой кропотливой работы расчетные значения межосевого расстояния и модуля необходимо в конце расчетов округлить до ближайшего большего значения из стандартизованного ряда…
То есть, считали-считали, а в конце — «бац» — и просто на 15…20% результаты увеличили…
Студентам в курсовом проекте по «Деталям машин» такой расчет делать нужно! В реальной жизни инженера, я думаю, это не всегда целесообразно.
В предлагаемой вашему вниманию статье я расскажу как быстро и с приемлемой для практики точностью выполнить проектировочный расчет зубчатой передачи. Работая инженером-конструктором, я довольно часто применял изложенный ниже алгоритм в своей работе, когда не требовалась высокая точность прочностных расчетов. Так бывает при единичном изготовлении передачи, когда проще, быстрее и дешевле спроектировать и изготовить зубчатую пару с некоторым излишним запасом прочности. Используя предлагаемую программу расчета, можно легко и достаточно быстро проверить результаты, полученные, например, с помощью другой аналогичной программы или убедиться в правильности «ручных» расчетов.
По сути, данная статья является в какой-то мере продолжением темы, начатой в посте «Расчет привода тележки». Там результатами расчета были: передаточное число привода, статический момент сопротивления движению, приведенный к валу колеса и статическая мощность двигателя. Для нашего расчета они будут частью исходных данных.
Проектировочный расчет цилиндрической зубчатой передачи будем выполнять в программе MS Excel.
Начинаем. Обращаю ваше внимание, что материалом для всех зубчатых колес выбираем Сталь40Х или Сталь45 с твердостью HRC 30…36 (для шестерни – «потверже», для колеса – «помягче», но в этом диапазоне) и допустимыми контактными напряжениями [σH]=600МПа. В практике – это наиболее распространенный и доступный материал и термообработка.
Расчет в примере будет выполнен для косозубой передачи. Общая схема зубчатой передачи изображена на представленном далее рисунке.

Запускаем Excel. В ячейках со светло-зеленой и бирюзовой заливкой пишем исходные данные и уточненные пользователем (принятые) расчетные данные. В ячейках со светло-желтой заливкой считываем результаты расчетов. В ячейках со светло-зеленой заливкой помещены мало подверженные изменениям исходные данные.
Заполняем ячейки исходными данными:
1. Коэффициент полезного действия передачи КПД (это КПД эвольвентного зубчатого зацепления и КПД двух пар подшипников качения) пишем
в ячейку D3: 0,931
2. Значение интегрального коэффициента K, зависящего от типа передачи (смотри примечание к ячейке D4), записываем
в ячейку D4: 11,5
3. Угол наклона зубьев (предварительный) bп в градусах выбираем из рекомендованного диапазона в примечании к ячейке D5 и вводим
в ячейку D5: 15,000
4. Передаточное число uп, определенное в предварительных расчетах, записываем
в ячейку D6: 4,020
5. Записываем мощность на быстроходном валу передачи P1 в Ваттах
в ячейку D7: 250
6. Частоту вращения быстроходного вала n1 в оборотах в минуту вводим
в ячейку D8: 1320
Программа расчета зубчатой передачи выдает первый блок расчетных параметров:
7. Вращательный момент на быстроходном валу T1 в Ньютонах умноженных на метр
в ячейке D9: =30*D7/(ПИ()*D8)=1,809
T1=30*P1/(3,14*n1)
8. Мощность на тихоходном валу передачи P2 в Ваттах
в ячейке D10: =D7*D3=233
P2=P1*КПД
9. Частота вращения тихоходного вала n2 в оборотах в минуту
в ячейке D11: =D8/D6=328
n2=n1/uп
10. Вращательный момент на тихоходном валу T2 в Ньютонах умноженных на метр
в ячейке D12: =30*D10/(ПИ()*D11)=6,770
T2=30*P2/(3,14*n2)
11. Расчетный диаметр делительной окружности шестерни d1р в миллиметрах
в ячейке D13: =D4*(D12*(D6+1)/D6)^0,33333333=23,427
d1р=K*(T2*(uп+1)/uп )^0,33333333
12. Расчетный диаметр делительной окружности колеса d2р в миллиметрах
в ячейке D14: =D13*D6=94,175
d2р= d1р*uп
13. Максимальный расчетный модуль зацепления m(max)р в миллиметрах
в ячейке D15: =D13/17*COS (D5/180*ПИ())=1,331
m(max)р=d1р/17*cos(bп)
14. Минимальный расчетный модуль зацепления m(min)р в миллиметрах
в ячейке D16: =D15/2 =0,666
m(min)р=m(max)р/2
15. Выбираем модуль зацепления m в миллиметрах из диапазона рассчитанных выше значений и из стандартизованного ряда, приведенного в примечании к ячейке В17 и записываем
в ячейку D17: 1,250
Далее в диалоговом режиме пользователя и программы определяем следующие основные параметры зубчатой передачи:
16. Расчетная ширина зубчатого венца колеса b2р в миллиметрах
в ячейке D18: =D13*0,6=14,056
b2р= d1р*0,6
17. Округляем ширину зубчатого венца колеса b2 в миллиметрах и вводим
в ячейку D19: 14,000
18. Программа определяет ширину зубчатого венца шестерни b1 в миллиметрах
в ячейке D20: =D19+4=18,000
b1=b2+4
19. Далее находится расчетное число зубьев шестерни z1р
в ячейке D21: =D13*COS (D5/180*ПИ())/D17 =18,1
z1р=d1р*cos(bп)/m
20. Округляем полученное выше значение числа зубьев шестерни z1 и записываем
в ячейку D22: 19
21. Далее по аналогии — расчетное число зубьев колеса z2р
в ячейке D23: =D22*D6 =76,4
z2р=z1*uп
22. Округленное число зубьев колеса z2 записываем
в ячейку D24: 77
23. Уточняем расчетом передаточное число (окончательное) u
в ячейке D25: =D24/D22=4,053
u=z2/z1
24. Рассчитываем отклонение передаточного числа окончательного от предварительного delta в процентах и сравниваем с допустимыми значениями, приведенными в примечании к ячейке D26
в ячейке D26: =(D25/D6-1)*100=0,81
delta=u/uп-1
25. Далее программа находит расчетное межосевое расстояние зубчатой передачи awр в миллиметрах
в ячейке D27: =D17*(D22+D24)/(2*COS (D5/180*ПИ())=62,117
awр=m*(z1+z2)/(2*cos(bп))
26. Округляем в большую сторону расчетное значение межосевого расстояния зубчатой передачи по стандартизованному ряду, приведенному в примечании к ячейке D28, и вводим окончательное межосевое расстояние aw в миллиметрах
в ячейку D28: 63,000
27. В завершение программа уточняет угол наклона зубьев зубчатой передачи b в градусах
в ячейке D27: =ЕСЛИ(D5=0;0;ACOS (D17*(D22+D24)/(2*D28))/ПИ()*180)=17,753
b=arccos(m*(z1+z2)/(2*aw))
Итак, мы выполнили по упрощенной схеме проектировочный расчет зубчатой цилиндрической передачи, целью которого было определение основных габаритных параметров на основе заданных силовых.
Далее конструктору для выполнения чертежей элементов передачи необходимо выполнить геометрический расчет зацепления. Но это, возможно, тема другого поста.
Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.
ОСТАЛЬНЫМ можно скачать просто так… — никаких паролей нет!
Буду рад увидеть ваши комментарии, уважаемые читатели.
Ссылка на скачивание файла: raschet-zubchatoi-peredachi (xls 38,5KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
al-vo.ru
9 Проектный расчет цилиндрической зубчатой передачи
Цель проектного расчета – определить геометрические размеры передачи, обеспечивающие ее работоспособность и надежность. В расчетах следует учитывать требования минимизации габаритов, массы и стоимости передачи.
В исходных данных для проектного расчета указывают нагруженность, требуемый ресурс, механические характеристики материала зубчатых колес, условия эксплуатации (подробнее см. далее).
Предварительные геометрические размеры передачи определяют из условия обеспечения работоспособности по основному критерию, который обычно известен по опыту эксплуатации аналогичных передач. Так, для закрытых передач (обильное жидкостное смазывание) наиболее вероятная причина выхода из строя – появление на активных поверхностях зубьев следов выкрашивания. т.е. основном критерием работоспособности является контактная выносливость.
Методом
последовательного приближения определяют
межосевое расстояние 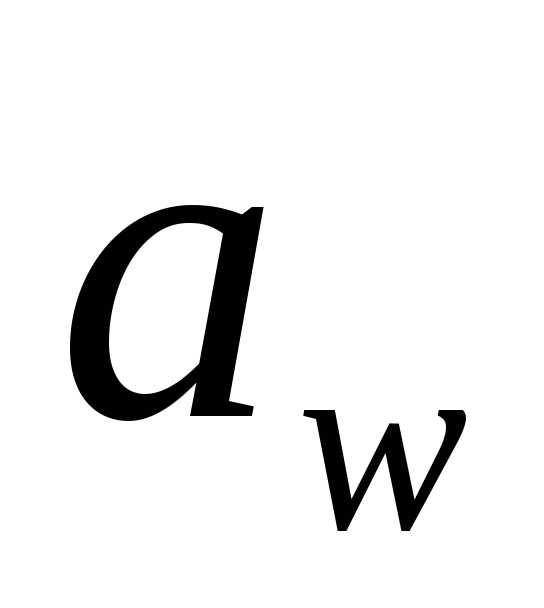 ,
а затем по известным геометрическим
соотношениям и остальные размеры
передачи.
,
а затем по известным геометрическим
соотношениям и остальные размеры
передачи.
Предварительно рассчитанные геометрические размеры передачи проверяют на соответствие остальным критериям работоспособности. Для закрытых передач такими критериями являются: выносливость при изгибе, контактная и изгибная прочность при действии пикового момента. В случае удовлетворительного результата предварительные размеры принимаются в качестве окончательных. В противном случае приходится корректировать размеры передачи до их удовлетворения всем рассматриваемым критериям работоспособности.
В инженерной практике способ определения предварительных геометрических размеров передачи не регламентирован (в отличие от проверочных расчетов по критериям работоспособности). В принципе предварительные размеры (первое приближение) можно задавать произвольно, но в этом случае увеличивается число корректировок (приближений), связанных с необходимостью обеспечения работоспособности по всем рассматриваемым критериям.
Последовательность расчета
9.1 Определяют значение межосевого расстояния (второе приближение):
.
 = 410 для косозубых
и шевронных зубчатых колес и
= 410 для косозубых
и шевронных зубчатых колес и  = 450 для прямозубых зубчатых колес.
= 450 для прямозубых зубчатых колес.
Коэффициент ширины 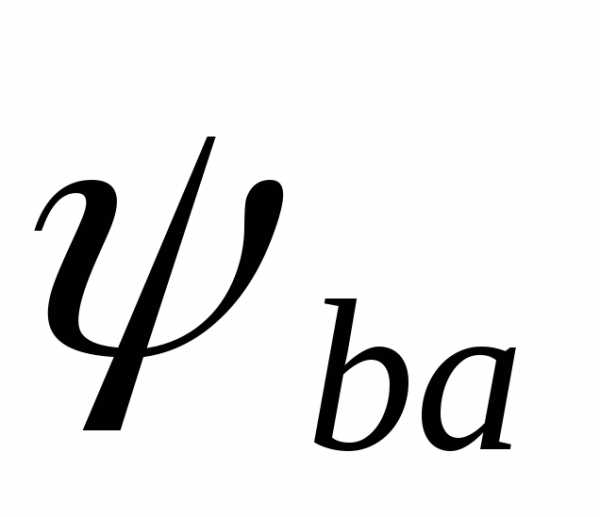 выбирают по табл. 8.2, в зависимости
от положения зубчатых колес относительно
опор.
выбирают по табл. 8.2, в зависимости
от положения зубчатых колес относительно
опор.
Коэффициент нагрузки выбирают по рекомендациям п. 8.
Допускаемое
напряжение  выбирают в соответствии с рекомендациями
п. 6.1.
выбирают в соответствии с рекомендациями
п. 6.1.
Полученное значение 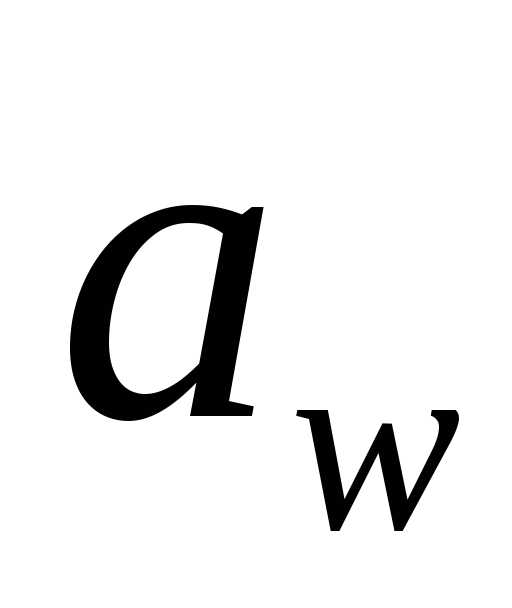 округляют до ближайшего числа, кратного
пяти, или по ряду размеров Ra40. При
проектировании крупносерийных редукторов
округляют до ближайшего числа, кратного
пяти, или по ряду размеров Ra40. При
проектировании крупносерийных редукторов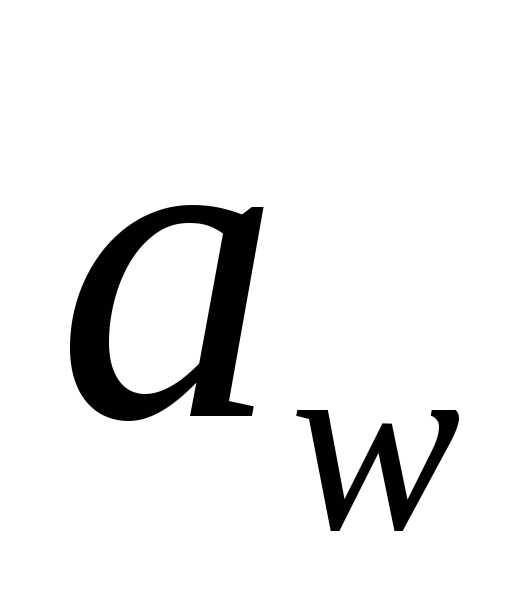 округляют до ближайшего стандартного
значения: 63; 71; 80, 90; 100; 112; 125; 140; 160; 180; 200;
224; 250; 260; 280; 300; 320; 340; 360; 380; 400.
округляют до ближайшего стандартного
значения: 63; 71; 80, 90; 100; 112; 125; 140; 160; 180; 200;
224; 250; 260; 280; 300; 320; 340; 360; 380; 400.
9.2 Ширина венца колеса равна рабочей ширине передачи, т.е. .
Ширину венца шестерни принимают большую, чем у колеса, мм: .
Полученные значения  и
и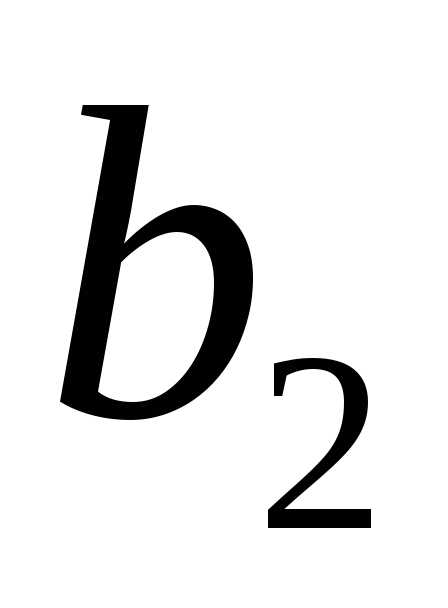 округляют до ближайших больших целых
значений в миллиметрах.
округляют до ближайших больших целых
значений в миллиметрах.
9.3 Нормальный модуль зубчатых колес определяют (с дальнейшим округлением по ГОСТ 9563-60) из следующих соотношений:
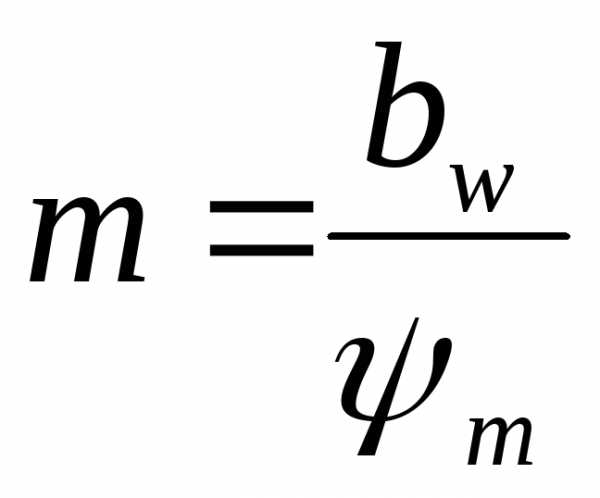 ;
.
;
.
Значение коэффициента 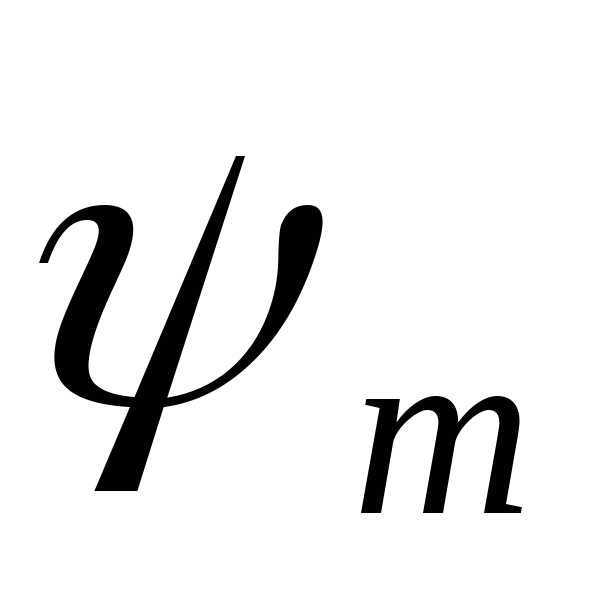 выбирают из табл. 9.1 или назначают исходя
из конкретных конструктивных,
технологических или экономических
требований. Следует учитывать, что с
уменьшением коэффициента
выбирают из табл. 9.1 или назначают исходя
из конкретных конструктивных,
технологических или экономических
требований. Следует учитывать, что с
уменьшением коэффициента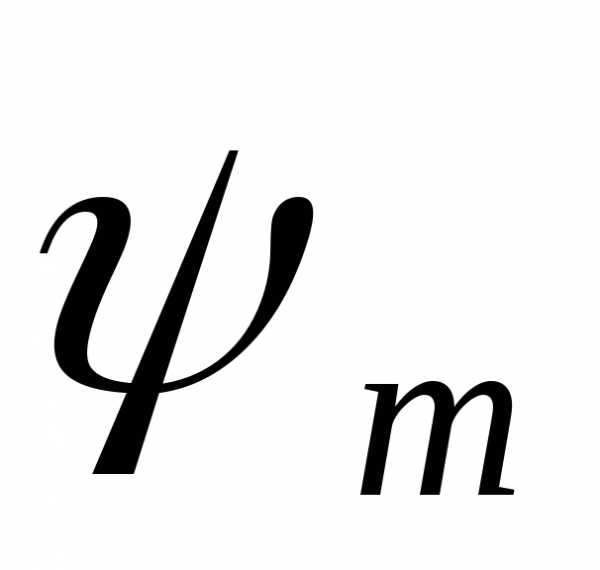 увеличивается модуль и это приводит к
повышению изгибной прочности зубьев.
Кроме того, с увеличением модуля передача
становится менее чувствительной к
колебанию межосевого расстояния,
вызванного неточностью изготовления
и упругими деформациями валов и опор.
Однако увеличение модуля уменьшает
плавность работы передачи, увеличивает
диаметр заготовки и машинное время при
нарезании зубьев.
увеличивается модуль и это приводит к
повышению изгибной прочности зубьев.
Кроме того, с увеличением модуля передача
становится менее чувствительной к
колебанию межосевого расстояния,
вызванного неточностью изготовления
и упругими деформациями валов и опор.
Однако увеличение модуля уменьшает
плавность работы передачи, увеличивает
диаметр заготовки и машинное время при
нарезании зубьев.
Таблица 9.1
Рекомендуемые
значения 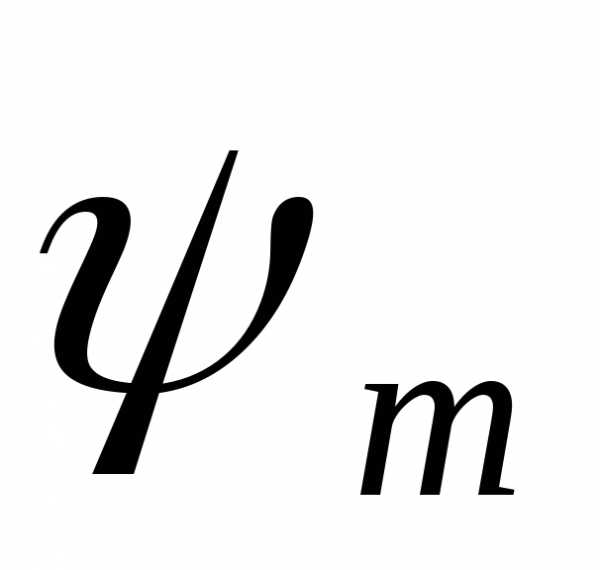
Характеристика передачи | , не более |
Обычные передачи в отдельном корпусе с достаточно жесткими валами и опорами, имеющие следующую твердость зубьев: | |
| 30-25 |
| 25-20 |
| 20-15 |
и | 18-10 |
Передачи грубые, открытые, с консольными валами и подвижные колеса коробок скоростей | 15-10 |
Минимальный модуль 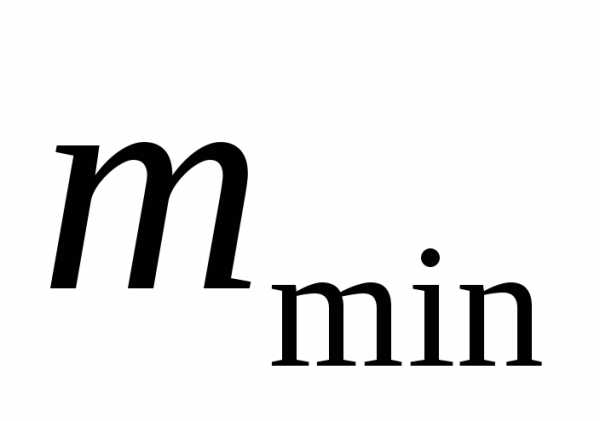 определяют из условия прочности по
следующей зависимости:
определяют из условия прочности по
следующей зависимости:
где 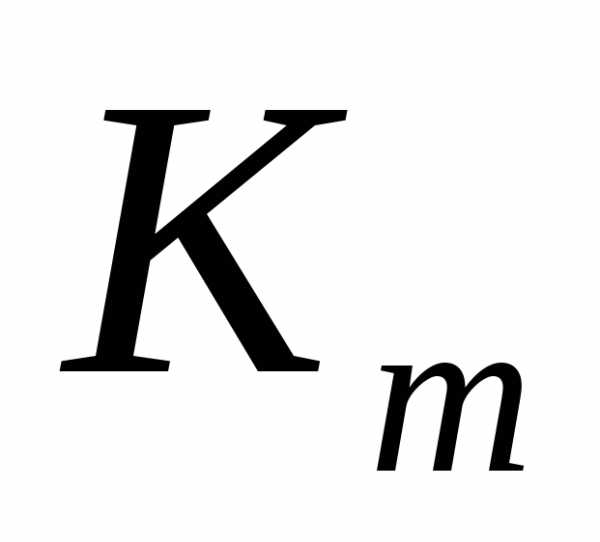 – коэффициент, равный 3400 для прямозубых
передач и 2800 для косозубых передач;
– коэффициент, равный 3400 для прямозубых
передач и 2800 для косозубых передач;
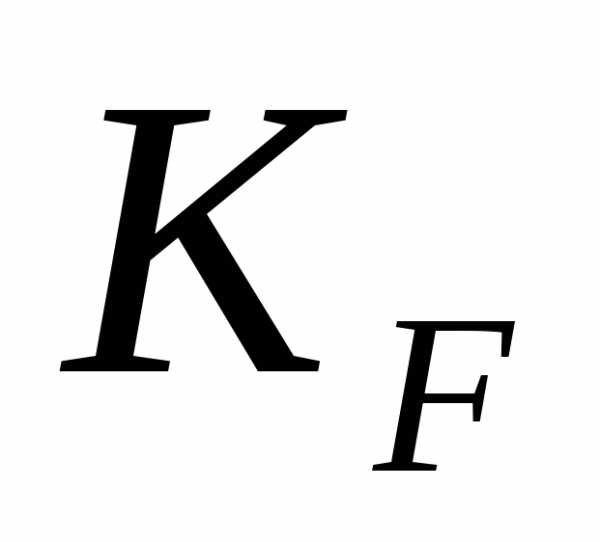 –коэффициент
нагрузки принимаемый равным
–коэффициент
нагрузки принимаемый равным 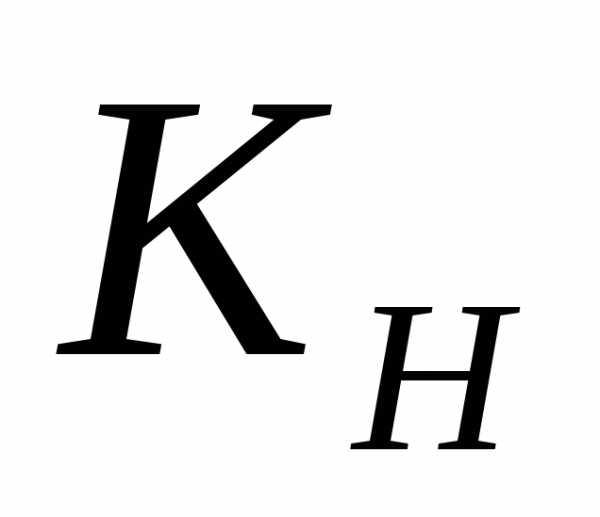 .
.
Допускаемое
напряжение изгиба для колеса 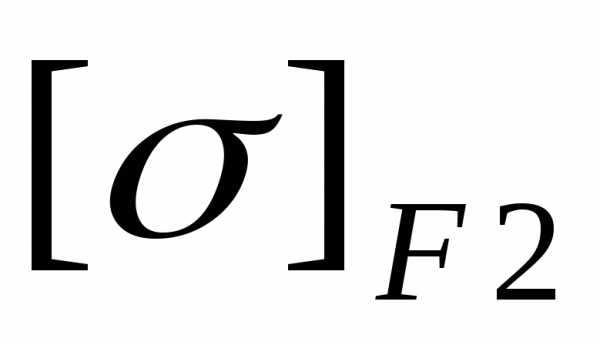 определяют в п. 6.2.
определяют в п. 6.2.
Максимально
допустимый модуль 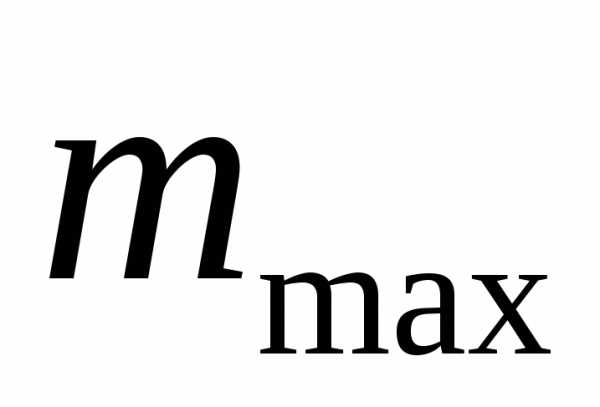 определяют из условия неподрезания
зубьев у основания:
определяют из условия неподрезания
зубьев у основания:
.
Введением смещений
(коррекции) можно несколько увеличить
значение  .
.
Модули, значения которых < 1,0, для силовых передач использовать нежелательно.
Полученное при расчете значение m округляют до ближайшего большего (согласно ГОСТ 9563-60), мм:
1-й ряд – 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10
2-й ряд – 1,12; 1,37; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9
9.4 Суммарное число зубьев для прямозубых передач определяют по формуле:
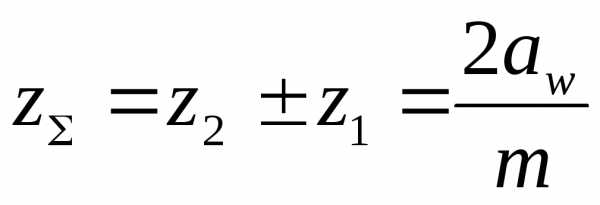 .
.
Учитывая, что  должно быть целым числом, иногда
приходится изменять значения
должно быть целым числом, иногда
приходится изменять значения иm или осуществлять смещение инструмента
(коррегирование зубьев).
иm или осуществлять смещение инструмента
(коррегирование зубьев).
Для косозубых передач вначале определяют минимальный угол наклона зубьев:
.
Для шевронных
передач угол  = 25°.
= 25°.
Затем определяют суммарное число зубьев по формуле:
.
Полученное значение 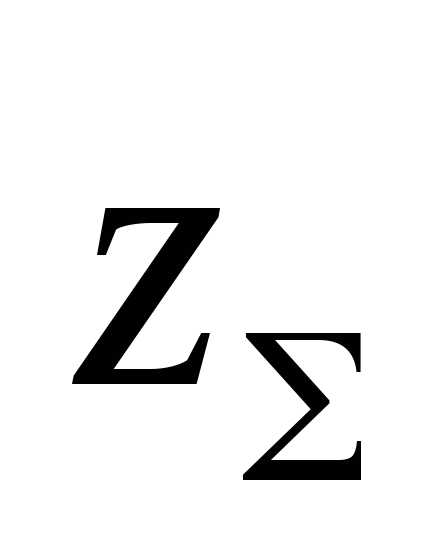 округляют в меньшую сторону до целого
числа и определяют действительное
значение угла (точность вычислений
0,0001):
округляют в меньшую сторону до целого
числа и определяют действительное
значение угла (точность вычислений
0,0001):
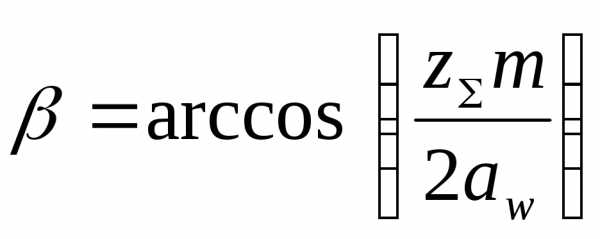 ,
.
,
.
9.5 Вычисляют числа
зубьев шестерни 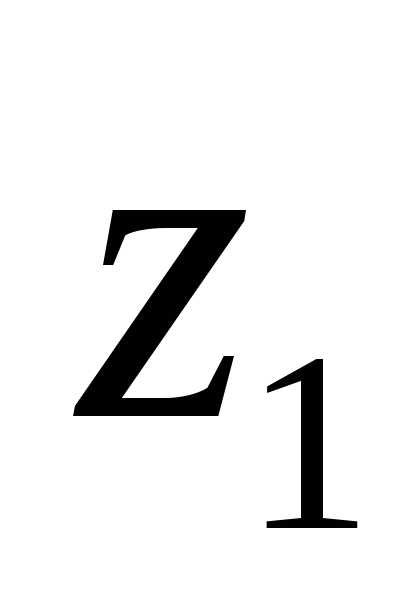 и колеса
и колеса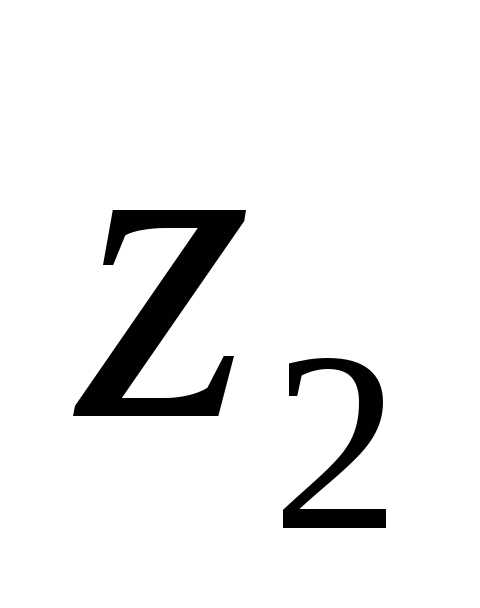 :
:
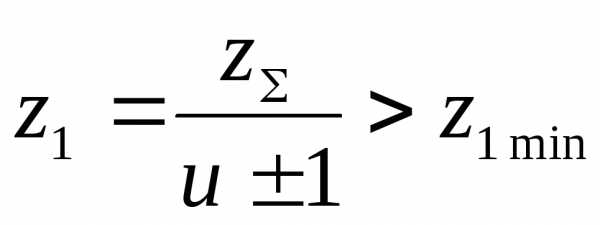
(значение 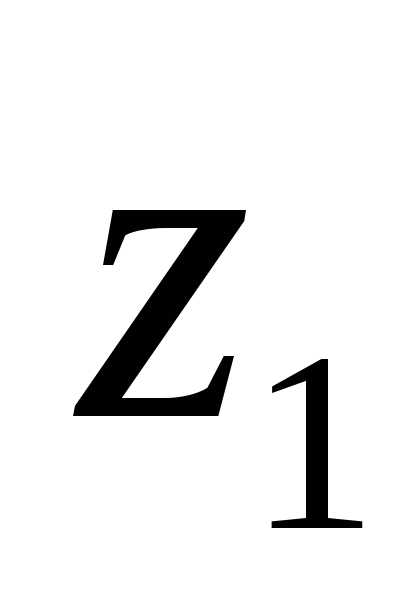 округляют до целого числа).
округляют до целого числа).
Для прямозубых и
косозубых зубчатых колес, нарезанных
без смещения инструмента (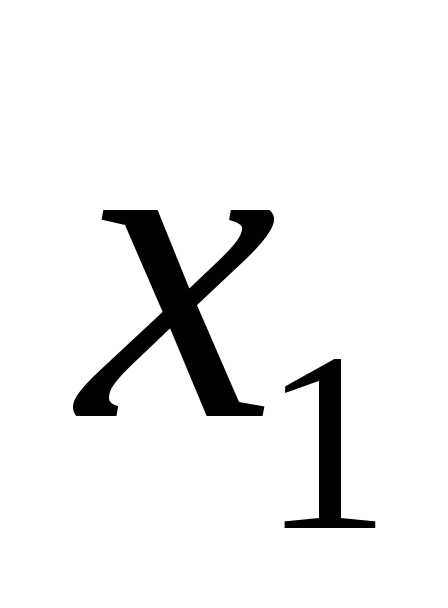 =
=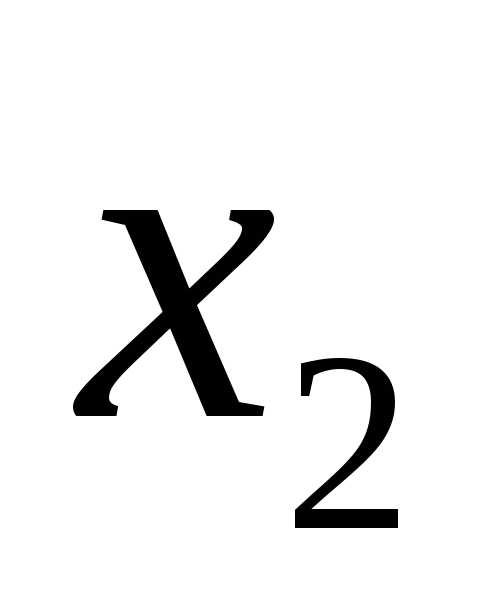 =0),
=0), = 17 исоответственно.
= 17 исоответственно.
При 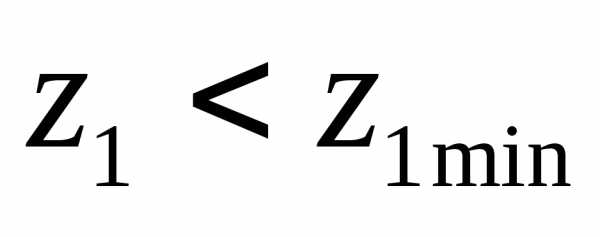 передачу выполняют со смещением для
исключения подрезания зубьев и повышения
их изгибной прочности. Коэффициент
смещения для шестерни:
передачу выполняют со смещением для
исключения подрезания зубьев и повышения
их изгибной прочности. Коэффициент
смещения для шестерни:
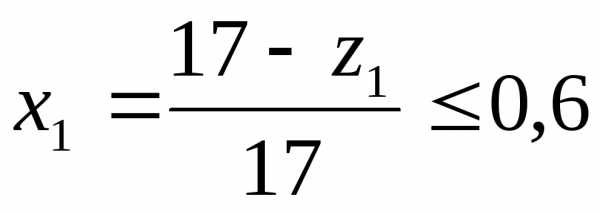 .
.
Для колеса наружного
зацепления 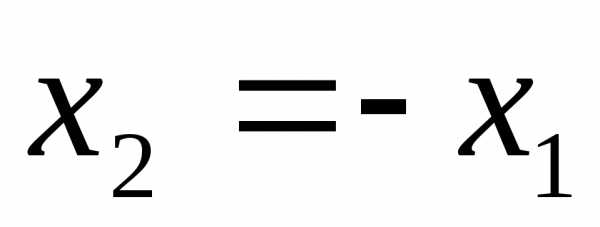 ;
внутреннего зацепления
;
внутреннего зацепления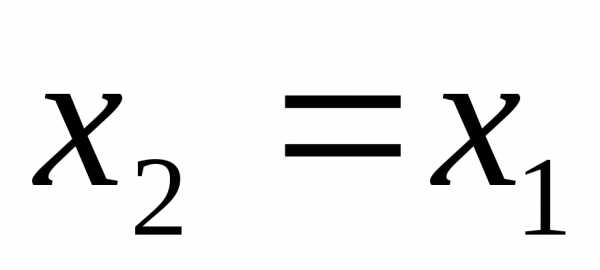 .
.
Число зубьев колеса  для внешнего и внутреннего зацепления
соответственно:
для внешнего и внутреннего зацепления
соответственно:
, .
9.6 Определяют фактическое значение передаточного числа u с точностью до 0,01:
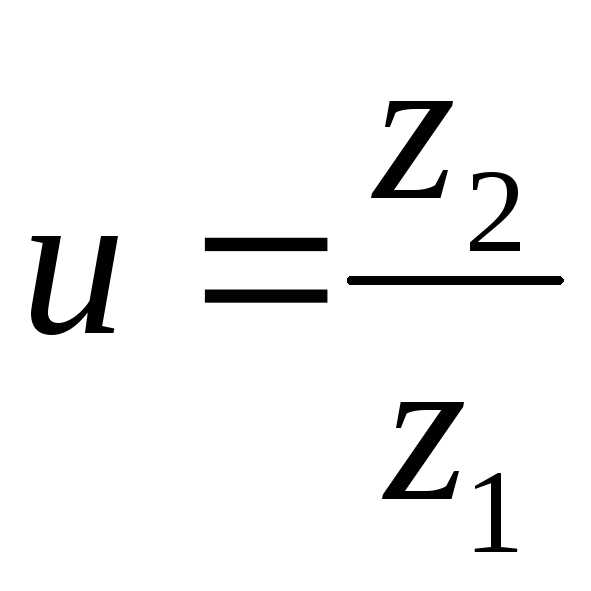 .
.
В многоступенчатых редукторах фактическое общее передаточное число не должно отличаться от заданного более чем на 4 %.
9.7 Определение геометрических параметров передачи:
делительный диаметр:
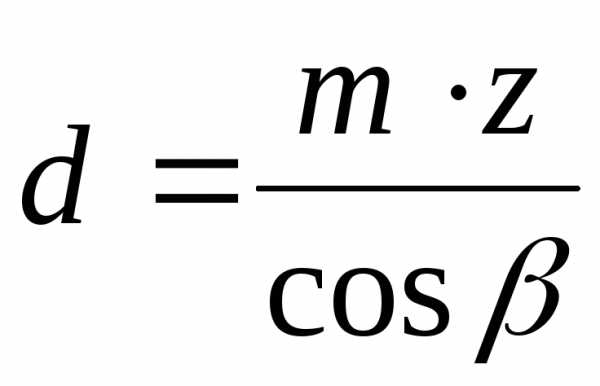 ;
;
диаметр вершин зубьев:
;
для зубчатых колес с внутренними зубьями:
;
диаметр впадин зубьев:
;
для зубчатых колес с внутренними зубьями:
.
9.8 По рассчитанным параметрам передачи вычерчивают эскиз заготовок шестерни и колеса и проверяют возможность обеспечения приведенных в табл. 5.1 механических характеристик (проверка необходима только при объемной термической обработке зубчатых колес).
|
Рис. 9.1. Схема сил, действующих на вал от зубчатых колес в цилиндрической передаче |
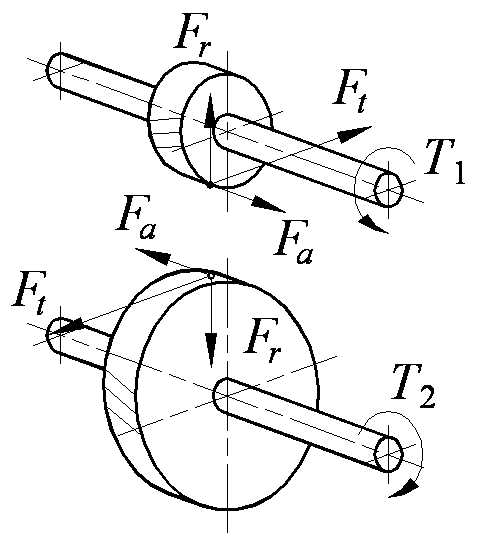
9.9 Для расчета валов и подшипников определяют силы в зацеплении (рис. 9.1):
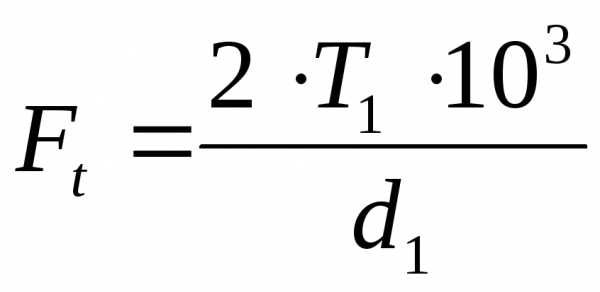 ,
,
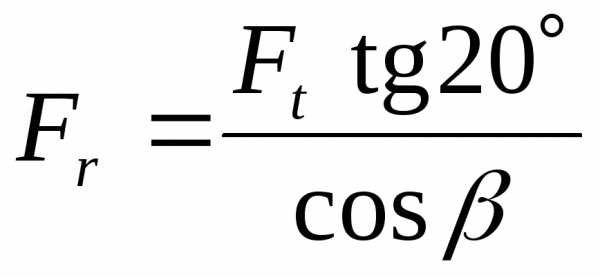 ,
,
,
где 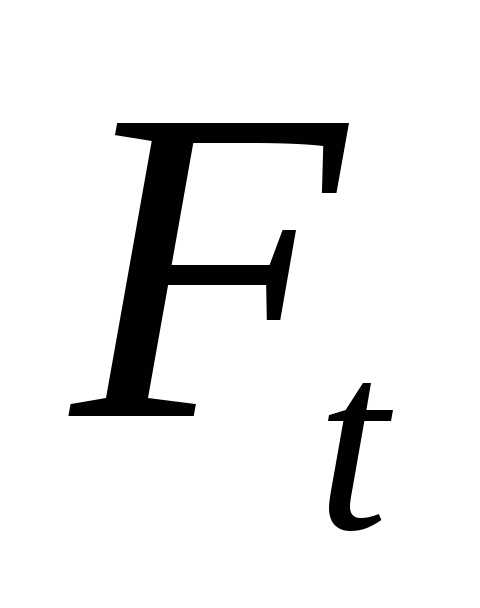 ,
,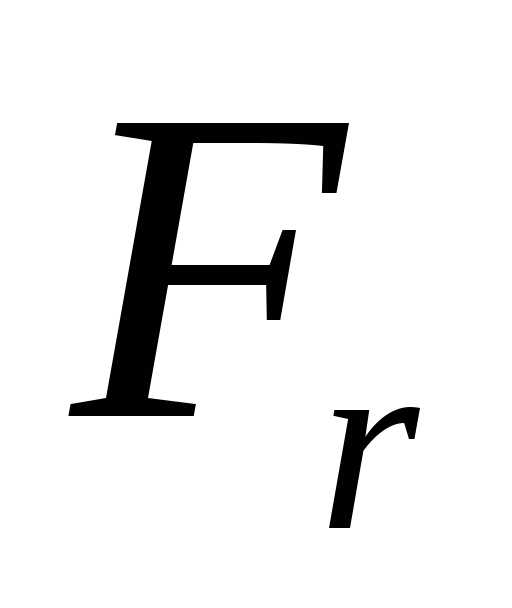 и
и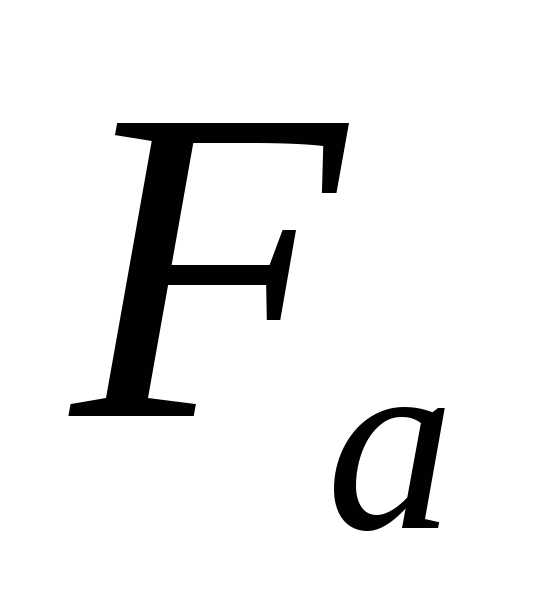 – окружная, радиальная и осевая сила
соответственно.
– окружная, радиальная и осевая сила
соответственно.
studfiles.net
Формула межосевого расстояния зубчатой передачи. Цилиндрические зубчатые передачи
Cтраница 2
Цилиндрические зубчатые передачи компактны и обладают важным свойством: они сообщают равномерное вращение ведомому колесу при равномерном вращении ведущего колеса.
Цилиндрические зубчатые передачи предназначены для передачи вращения и крутящего момента между двумя параллельно расположенными валами. Цилиндрические передачи бывают прямозубые, косозубые и шевронные с внешним, и внутренним зацеплением. К цилиндрическим относятся и реечные передачи.
Цилиндрические зубчатые передачи предназначаются для передачи равномерного вращательного движения. Для скорости получаем уравнение v dS / dta, где а – постоянная величина. Если ускорение j равно нулю, то динамические нагрузки отсутствуют. В действительности в силу неизбежных погрешностей зацепления появляются значительные динамические силы, которые нередко во много раз превышают полезную нагрузку.
Цилиндрические зубчатые передачи предназначаются для передачи равномерного вращательного движения.
Цилиндрические зубчатые передачи применяют главным образом для передачи больших мош ностей; это не исключает применение цилиндрических передач и для средни а также малых мош ностей. Конические зубчатые передачи (как и червячные передачи) применяют для средних и малых мош ностей.
Простейшая цилиндрическая зубчатая передача с внешним зацеплением показана на рис. 1.5. Механизм преобразует вращательное движение одного колеса / во вращательное движение другого колеса 2 с другой частотой вращения и моментом. Передачи с внешним зубчатым зацеплением передают вращение с изменением направления вращения.
Цилиндрические зубчатые передачи наружного зацепления могут быть изготовлены методом обкатки и методом одиночного деления на зубофрезерных, зубострогальных или зубодолбежных станках.
Цилиндрические зубчатые передачи наружного и внутреннего зацепления эвольвентного профиля бывают: прямозубые, косозубые со спиральными зубьями (геликоидальные), одинарные, блочные, шевронные, многорядные косозубые и многорядные шевронные. Конические зубчатые колеса эвольвентного профиля бывают: прямозубые, косозубые, с криволинейными зубьями, шевронные.
Дана цилиндрическая зубчатая передача: а 450 мм, степень точности 7 по всем нормам точности, вид сопряжения С.
Через цилиндрические зубчатые передачи приводится во вращение главный распределительный вал 22 (см. рис. 4.25, а), от которого вращение передается кулачкам привода механизмов поворота и переноса заготовок и выталкивателя 16 из матриц. Такое крепление обеспечивает прижим ножа к торцу отрезной матрицы по мере возрастания усилия отрезки.
Различают цилиндрические зубчатые передачи с внешним и внутренним зацеплением. Цилиндрические передачи внутреннего зацепления могут быть прямозубыми и косозубыми. Их широко применяют в самолетах, трансмиссиях легковых автомобилей, сложных планетарных механизмах, в основном там, где межосевые расстояния невелики.
Для цилиндрических зубчатых передач установлено шесть (пять для т 1 мм) классов отклонений межосевого расстояния, обозначаемых в порядке убывания точности цифрами от I (И) до VI.
Лекция 14.
Цилиндрические зубчатые передачи.
Передача непрерывного прошения от одного вала к другому с заданным передаточным отношением чаще всего осуществляется с помощью зубчатых механизмов. Зубчатые механизмы получили очень широкое применение как в машиностроении, так и в приборостроении благодаря большой надежности и точности в воспроизведения заданного закона движения. Если оси вращения валов параллельны, то применяется цилиндрическая зубчатая передача, аксоидами колес которой являются цилиндры. Такая передача относится к категории плоских механизмов. В лекциях 14-16 излагаются основы синтеза цилиндрической зубчатой передачи по заданному передаточному отношению. Эти основы называются геометрическим расчетом зубчатой передачи.
Элементы зубчатого колеса.
Цилиндрические зубчатые передачи, как отмечалось ранее, могут быть внешнего и внутреннего зацеплений. Следует также указать реечное зацепление, разграничительное между внешним и внутренним зацеплениями. Простая зубчатая передача имеет два подвижных звена, которыми являются зубчатые колеса. Рассмотрим элементы зубчатого колеса (рис. 14. l ).
Поверхность (1), отделяющая зубья от тела зубчатого колеса, называется поверхностью впадин зубьев. Поверхность (2), ограничивающая зубья со стороны, противоположной телу зубчатого колеса, – поверхность вершин зубьев. Пространство между двумя соседними зубьями (3) – впадина. Поверхность, ограничивающая зуб со стороны впадины (4), называется боковой поверхностью зуба .
Боковая поверхность состоит из главной (5) и переходной (6) поверхностей. Главная поверхность – это та часть боковой поверхности зуба, которая, взаимодействуя с главной поверхностью другого зуба, обеспечивает заданное передаточное отношение. Переходная поверхность соединяет главную поверхность с поверхностью впадин.
Главной поверхностью чаще всего является эвольвентная поверхность. так как среди цилиндрических передач особое распространение получили эвольвентные цилиндрические передачи. Объясняется это тем, что они имеют весьма значительные преимущества перед другими передачами. Так, эвольвентные передачи допускают, в определенных пределах, изменение межосевого расстояния, сохраняя при этом постоянство передаточного отношения, чего другие передачи не допускают, и обладают хорошими эксплуатационными качествами. Изготовление эвольвентных колес и инструмента для их нарезания является наиболее простым, что имеет очень важное практическое значение.
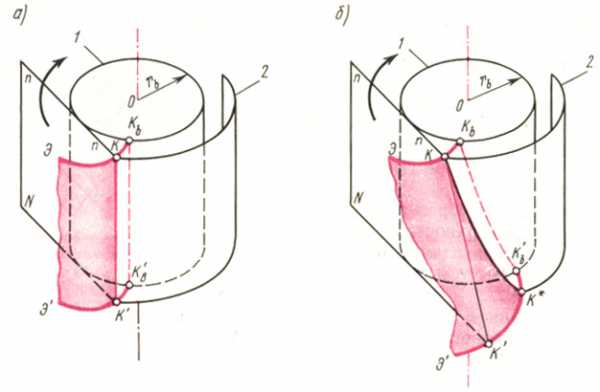
Рассмотрим образование эвольвентных поверхностей, которые будут являться главными поверхностями прямого и косого зубьев. На рис. 14.2, а в перспективе показана главная поверхность прямого зуба, которую можно представить как совокупность совершенно одинаковых эвольвент (Э, Э”), расположенных в плоскостях, перпендикулярных оси колеса. Эти эвольвенты являются траекториями точек образующей прямой КК” , принадлежащей плоскости N , которая перекатывается по основному цилиндру 1 без скольжения. Начальные точки всех эвольвент распола-гаются на образующей K b K b основного ци-линдра. Пересечение главной поверхности прямого зуба с любым соосным цилиндром 2 происходит по образующей этого цилиндра (например, прямая КК” ). Эта прямая параллельна оси колеса и называется линией прямого зуба. Главная поверхность прямого зуба является эвольвентной линейчатой цилиндрической поверхностью.

Главная поверхность косого зуба (рис. 14.2, б) также может быть представлена как совокупность одинаковых эвольвент (Э, Э”), расположенных в плоскостях, перпендикулярных оси колеса; однако в этом случае образующая прямая КК” расположена на плоскости N под некоторым углом к оси колеса. Благодаря этому при перекатывании плоскости N по основному цилиндру 1 без скольжения начальные точки эвольвент располагаются по винтовой линии K b K b на основном цилиндре. В пересечении с любым соосным цилиндром 2 главная поверхность косого зуба образует винтовую линию КК* , называемую линией косого зуба. Главная поверхность косого зуба является эвольвентной линейчатой винтовой поверхностью.
Таким образом, основное сходство главных поверхностей прямого и косого зубьев состоит в том, что в любом торцовом сечении, т. е. в сечении плоскостью, перпендикулярной оси колеса, они имеют эвольвенту.
На рис. 14.3, а изображено зубчатое колесо с внешними зубьями. Наибольший радиус r a имеет окружность вершин. На рис. 14,3. б изображено зубчатое колесо с внутренними зубьями. В этом случае тело колеса имеет форму кольца, внутрь полости которого зубья обращены своими вершинами. Поэтому радиус r a окружности вершин внутренних зубьев меньше радиуса r f окружности впадин, который является, таким образом, наибольшим. На рис. 14.3 изображены также эвольвентный профиль зуба, основная окружность, на базе которой он построен (радиус r b ), а также делительная окружность радиуса г и окружность произвольного радиуса r y .
На рис. 14.З буквой обозначен KON , равный углу профиля зуба в точке K , находящейся на делительной окружности прямозубого колеса. Этот угол стандартизован и равен 20°. Таким образом, делительная окружность прямозубого колеса является той окружностью, которая пересекает профиль зуба в точке, для которой угол профиля равен стандартному углу = 20 ° .
Если длину окружностей – делительной, основной и произвольного радиуса – поделить на число зубьев z , то получим расстояния между профилями двух соседних зубьев, называемые шагом, т. е. получим шаг по делит
veloed.ru
Расчет зубчатой передачи
Содержание
Введение……………..…………………………………..……………..2
1. Анализ кинематической схемы…………..……..………………..2
2. Кинематический расчет привода…………………………………3
3. Определение геометрических параметров цилиндрической
зубчатой передачи………………………………………….…………..6
4. Геометрический расчет конической зубчатой передачи………9
5. Определение геометрических размеров и расчет на
прочность выходного вала…………………………………………….11
6. Проверочный расчет подшипника..……………………………….16
7. Список использованной литературы……………………………..18
Редуктор – это механизм состоящий из зубчатых или червячных
передач, заключенный в отдельный закрытый корпус. Редуктор
предназначен для понижения числа оборотов и, соответственно, повышения крутящего момента.
Редукторы делятся по следующим признакам:
– по типу передачи – на зубчатые, червячные или зубчато-червячные:
– по числу ступеней – на одноступенчатые (когда передаче осуществляется одной парой колес), двух-, трех- или многоступенчатые:
– по типу зубчатых колес – на цилиндрические, конические,иликоническо-цилиндрические;
– по расположению валов редуктора в пространстве – на горизонтальные, вертикальные, наклонные:
– по особенностям кинематической схемы ” на развернутую, соосную. с раздвоенной ступенью.
1. Анализ кинематической схемы
Наш механизм состоит из привода электромашинной (1),муфты (2), цилиндрической шестерни (3), цилиндрические колеса (4), конической шестерни (5), конического колеса (6), валов (7,6,9) и трех пар подшипников качения. Мощность на ведомом валу N3 =9,2 кВт, угловая скорость п3 = 155 об/мин, привод предназначен для длительной работы, допускаемое отклонение скорости
5%,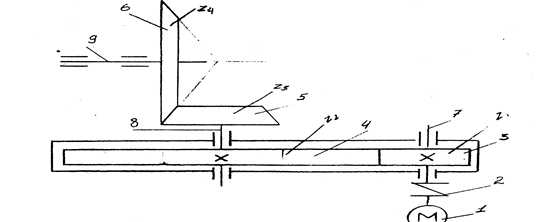
2. Кинематический расчет привода
2.1. Определяем общий КПД привода
h=h1 *h2 *h33 *h4Согласно таблице 5 (1) имеем
h1 =0,93 – КПД прямозубой цилиндрической передачи;
h2 =0,9 – КПД конической передачи;
h3 =0,98 – КПД подшипников качения;
h4 =0,98 – КПД муфты
h = 0,93 * 0,983 * 0,9 * 0,98 = 0,77
2.2. Определяем номинальную мощность двигателя
Nдв =N3 /h=11,9 кВт
2.3. Выбираем тип двигателя по таблице 13 (2). Это двигатель
А62 с ближайшим большим значением мощности 14 кВт. Этому значению номинальной мощности соответствует частота вращения 1500 об/мин.
2.4. Определяем передаточное число привода
i = iном /n3 = 1500/155 = 9,78
2.5. Так как наш механизм состоит из закрытой цилиндрической передачи и открытой конической передачи, то разбиваем передаточноечисло на две составляющих:
i = i1 * i2
По таблице б (1) рекомендуемые значения передаточных отношений цилиндрической передачи от 2 до 5; конической – от 1 до 3 по ГОСТ 221-75. Назначаем стандартные передаточные числа i1 = 4, i2 = 2,5.
2.6. Уточняем общее передаточное число
i = g.5 * 4 = 10
2.7. Определяем максимально допустимое отклонение частоты вращения выходного вала
где
– допускаемое отклонение скорости по заданию.2.8. Допускаемая частота вращения выходного вала с учетом отклонений
2.9. Зная частные передаточные отношения определяем частоту вращения каждого вала:
Таким образом, частота вращения выходного вала находитсяв пределах допустимой.
2.10. Определяем крутящие моменты, передаваемые валами механизма с учетом передаточных отношений и КПД:
2.11 Аналогично определяем мощность, передаваемую валами
2.12. Построим график распределения крутящего момента и мощности по валам привода
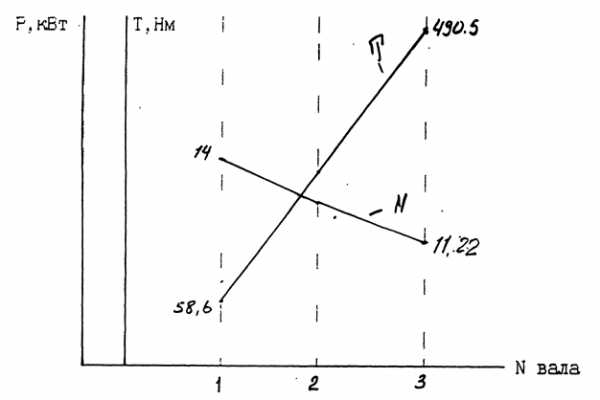
3. Определение геометрических параметров цилиндрической зубчатой передачи
3.1. Для колес со стандартным исходным контуром, нарезаемым без смещения режущего инструмента (х = 0), число зубьев шестерни рекомендуется выбирать в пределах от 22 до 26. Выбираем Z1 = 22
3.2. Число зубьев колеса:
Z2 = Z1 * i1 = 22 * 4 = 88
3.3. Определяем межосевое расстояние по формуле
где Ka – вспомогательный коэффициент, для косозубых передач равен 43;
– коэффициент ширины венца шестерни расположенной симметрично относительно опор, по таблице 9(3) равен 0,4;i1
– передаточное число;T2 – вращающий момент на тихоходном валу;
По таблице 3.1 (3) определяем марку стали для шестерни – 40Х. твердость > 45HRC: для колеса – 40Х. твердость
350НВ.По таблице 3.2 (3) для шестерни
для колеcа предназначенных для длительной работы.Тогда
Полученное значение межосевого расстояния для нестандартных передач округляем до ближайшего из ряда нормальных линейных размеров, AW = 100 мм.
3.4. Определяем модуль зацепления по формуле
где Кm , – вспомогательный коэффициент, длякосозубых передач равен 5,8;
допускаемое напряжение изгиба материала колеса с менее прочным зубом по таблице 3.4 (3).Тогда
Полученное значение модуля округляем в большую сторону до стандартного из ряда стр.59 (3). Для силовых зубчатых передач при твердости одного из колес > 45HRC. принимается модуль > 1.5. поэтому принимаем модуль m=2.
3.5. Определяем угол наклона зубьев для косозубых передач:
3.6. Определяем суммарное число зубьев шестерни и колеса для косозубых колес
Полученное значение округляем в меньшую сторону до целого числа, то есть Z = 100.
3.7. Определяем число зубьев шестерни
3.8. Определяем число зубьев колеса
Z2 = Z – Z1 = 100 – 20 == 80
3.9.Определяем фактическое передаточное число и проверяем его отклонение
следовательно передаточное число выбрано верно.
3.10. Определяем основные геометрические параметры передачи и сводим их в таблицу
4. Геометрический расчет конической зубчатой передачи
mirznanii.com


 и
и  < 350 НВ
< 350 НВ > 350 НВ и
> 350 НВ и  < 350 HB
< 350 HB и
и  > 350 HB
> 350 HB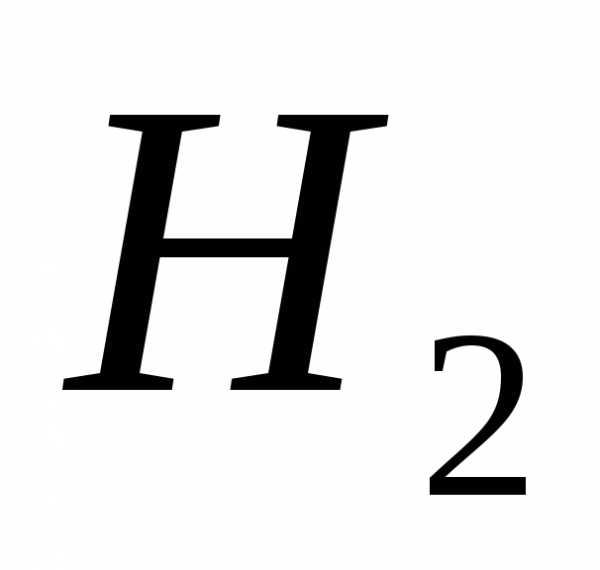 > 58 HRC
> 58 HRC