Соединение пружин – Параллельное и последовательное соединение пружин

alexxlab | 16.10.2016 | 0 | Вопросы и ответы

Параллельное и последовательное соединение пружин

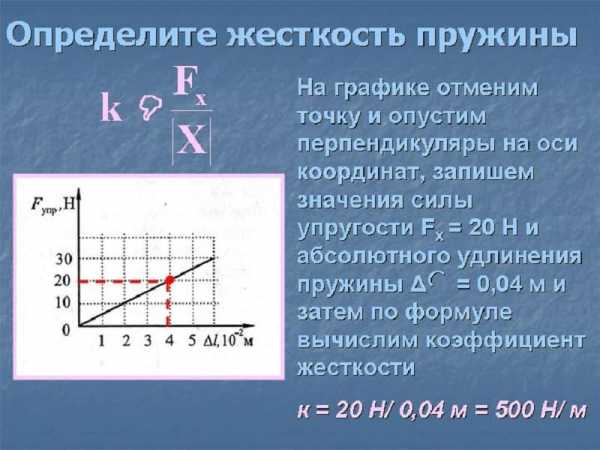
Силу упругости обозначают буквой F с индексом Fупр.

Чтобы узнать, как найти силу упругости, мы должны познакомиться с законом Гука. Английский физик Роберт Гук впервые установил зависимость величины силы упругости от деформации тела. Эта зависимость прямо пропорциональная.

Чем больше возникает деформация, тем больше сила упругости.

То есть формула для силы упругости выглядит следующим образом:

Fупр=k*∆l,

где ∆l – величина деформации,

а k – коэффициент жесткости.Коэффициент жесткости , естественно, различен для разных тел и веществ. Коэффициент силы  упругости измеряется в Н/м (ньютонах на метр).

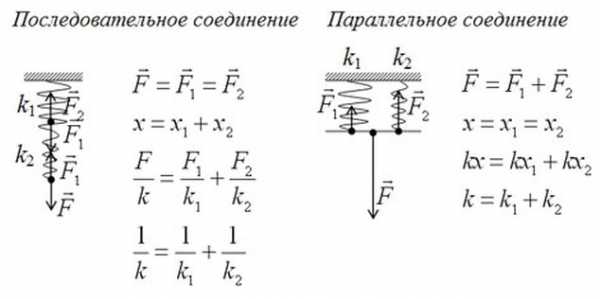
На практике встречается часто, что пружина не одна, а несколько. Они образуют систему пружин.

Задача.

Какова жесткость системы из двух пружин, жесткости которых k₁, k₂, соединенных: 

а) параллельно;

 б) последовательно?

Решение:

а) Рассмотрим параллельное соединение пружин. Обозначим удлинение пружин х₁ и х₂, х – перемещение груза. Тогда

 x₁ = x₂ = x,

F=F₁ + F₂

и две пружины можно заменить одной пружиной жесткостью k, удлинение которой x.

Получим по закону Гука  F = -kx:

 kx = k₁x₁ + k₂x₂, 

 k= k₁ + k₂.

Итак, при параллельном соединении пружин общая жесткость

k = k₁ + k₂.

б) Рассмотрим последовательное соединение пружин. В этом случае по 3-ему закону Ньютона

∣F∣ = ∣F₁∣  =  ∣F₂∣ (векторные)

и перемещение груза

 x = x₁ + x₂.

Из закона Гука выразим удлинение

 x = ∣F∣ / k

и запишем

∣F∣/ k = ∣F∣ / k₁ + ∣F∣ / k₂

Получим, что при последовательном соединении общая жесткость двух пружин

1 / k = 1 / k₁+1 / k₂

Подведем итоги в виде таблицы

Для случая, если пружин три и более:

На пружины действует одна и та же сила F.

Деформация системы пружин: 

Δx = Δx₁+ Δx₂ + …+ Δx_n = F / k₁ + F / k₂ +…+ F / k_n.

F / k общ = F / k₁ + F / k₂ +…+ F / k_n.

Посмотрим при решении задач:

spishy-u-antoshki.ru

Последовательное соединение пружин : жесткость, формула

Пружины являются важным элементом самых различных механизмов. Для изменения основных эксплуатационных свойств проводится использование нескольких подобных изделий, которые соединяются различным образом. Тип применяемого метода соединения учитывается при проведении самых различных расчетов.

Основные методы крепления пружин

При проведении расчетов уделяется внимание тому, каким образом проводится соединение пружин. Этот момент оказывает влияние на следующее:

1. Жесткость системы. Этот показатель встречается практически во всех проводимых расчетах при последовательном подключении деталей. Зависит он от самых различных моментов, к примеру, коэффициента жесткости каждого.
2. Требуемое усилие для сжатия или растяжения. Рассматриваемая деталь применяется часто по причине того, что может обеспечивает накопление кинетической энергии.
3. Размер кинетической и потенциальной энергии. После того как изделие было выведено из положения равновесия начинает накапливаться кинетическая энергия. При этом она сохраняется на протяжении всего периода, пока к телу приложено усилие.
4. Вероятность возникновения свободного колебательного движения, а также степень сопротивления подобному явлению. Для расчетов колебательного движения также применяются специальные формулы.

Бывают самые различные способы соединения пружин, но наибольшее распространение получил метод последовательного и параллельного подключения.

Они характеризуются довольно большим количеством особенностей. Прежде чем рассматривать применение подобных способов соединения следует уделить внимание особенностям самого изделия:

1. Деталь изготавливается из проволоки, которая получается методом проката. Она обладает высоким показателем упругости, а также устойчивостью к воздействию окружающей среды.
2. Прокат изготавливают из специального сплава, способного выдерживать периодическую деформацию. Под заказ может производится деталь из обычных углеродистых сплавов или легированных металлов, все зависит от конкретного случая.
3. Проволока накручивается в виде колец по спирали. При этом должна выдерживаться едина ось, которая определяет распространение силы в одном направлении.
4. Выделяют два основных типа детали: растяжения и сжатия. Первый вариант исполнения характеризуется тем, что витки находятся практически вплотную. В случае изготовления изделия для сжатия выдерживается определенный зазор, который позволяет кольцам сближаться, а самому изделию сжиматься.
5. Характеризуется изделие самыми различными показателями. Примером можно назвать диаметр проволоки, созданных колец из нее, шаг расположения витков. Все эти параметры указываются в технической документации.

Сегодня они встречаются практически повсеместно. Это связано с тем, что подобное изделие практически незаменимо в случае, когда требуется возвратно-поступательное движение.

Последовательное соединение

При создании многих механизмов применяется последовательное соединение пружин. Среди особенностей этого метода отметим нижеприведенные моменты:

1. Наиболее важным параметром можно назвать коэффициент жесткости. Он определяет практически все свойства детали. Коэффициент жесткости при последовательном соединении пружин равен каждому из показателей упругости.
2. Также не стоит забывать о том, что показатель смещения тела равен сумме деформации витков. Любой тип рассматриваемого изделия характеризуется максимальным удлинение и сжатием. В случае максимального сжатия кольца расположены вплотную, зазор отсутствует практически полностью. При растяжении есть вероятность деформации витков, из-за чего изделие попросту потеряет свои основные характеристики.

Для расчетов могут применяться самые различные формулы. Среди особенностей этого метода соединения пружин отметим следующее:

1. Для начала берется одна деталь с жесткостью K, сила растяжения выражается следующей формулой: x=F/k.
2. Следующий шаг заключается в подсоединении второй детали. Для этого могут применяться различные крепежные элементы. При этом две пружины разной длины будут находится в одной системе.
3. Если приложить усилие для растягивания обоих изделий, то сила упругости каждой будет равна по модулю. При этом удлинение каждой будет равно х.

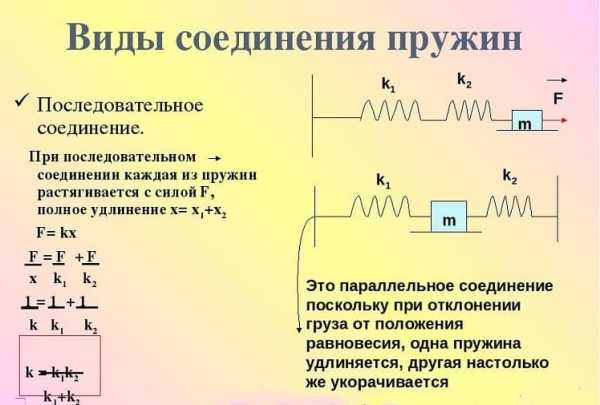
Приведенная выше информация указывает на то, что упругость системы двух последовательно соединенных изделий будет примерно в два раза меньше. При этом удлинение будет равно сумме удлинения каждой в отдельности.

Применяемый метод соединения получил весьма широкое распространение. Однако, в некоторых случаях целесообразно применять параллельный метод соединения.

Параллельное соединение

Довольно часто встречается и параллельное соединение пружин. В этом случае смещение тела, которому передается сила, равна деформации каждой из них. Зачастую параллельно соединенные пружины используются тогда, когда нужно передать большее усилие. Особенностями этого метода назовем следующее:

1. В рассматриваемом случае жесткости пружины обозначаются буквой k. Построенная схема указывает на то, что жесткость пружин при параллельном соединении остается неизменной, но общий показатель возрастает в два раза.
2. Показатель удлинения остается неизменным. При этом сила упругости возрастает в два раза в случае, если обе детали обладают схожими эксплуатационными характеристиками.

Проблемой применения подобной системы можно назвать то, что обе детали должны обладать одинаковой длиной в состоянии покоя. В противном случае сила упругости будет распределяться неравномерно, при этом есть вероятность критической деформации одной из них.

Влияние сопротивления на свободные колебания

Особенности детали определяют то, что при ее применении есть вероятность возникновения свободного колебательного движения. При этом имеет значение, какими особенностями обладает параллельно и последовательно соединенные пружины. Среди особенностей влияния сопротивления на свободное колебание отметим следующие моменты:

1. Проведенные тесты указывают на то, что параллельно соединенные пружины препятствуют возникновению свободного колебания. Это можно связать с существенным увеличением жесткости всей системы.
2. При последовательном расположении есть вероятность снижения сопротивления, так как расстояние между точкой крепления и телом существенно увеличивается.

Именно поэтому для существенного снижения колебательного вращения на момент эксплуатации системы рекомендуется использовать параллельный метод подключения.

Динамика несвободного движения

Еще одним важным показателем можно назвать динамику несвободного движения. Она может варьировать в достаточно большом диапазоне.

Распространенные последовательно соединенные пружины могут обеспечивать условия для несвободного движения тела. Динамика может нарастать в зависимости от длины в свободном состоянии и передаваемого усилия.

Как определить жесткость системы при последовательном соединении пружин?

Довольно большое количество проблем возникает на момент вычисления жесткости системы при последовательном соединении. Особенностями проводимого расчета в этом случае назовем следующее:

1. Важным показателем можно назвать жесткость, которая варьирует в достаточно большом диапазоне. Она во многом определяет свойства изделия. При слишком большой жесткости приходится прикладывать большее усилие для растяжения или сжатия детали.
2. Телу придается определенное усилие (F), которое становится причиной удлинения тела на величину x.
3. Для расчета применяется формула: k=F/(2x)=1/2F/x=k/2.

Приведенная выше информация указывает на то, что жесткость всей системы в этом случае в два раза меньше показателя жесткости каждого изделия. При этом формула применима только в том случае, если применяемые варианты исполнения для соединения обладают одинаковыми эксплуатационными характеристиками.

Определить жесткость системы пружин можно при самостоятельном проведении соответствующих расчетов. Сегодня система двух пружин получила весьма широкое распространение, так как при ее применении можно добиться требующихся результатов. Однако, прежде чем ее использовать следует провести соответствующие расчеты.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

 

stankiexpert.ru

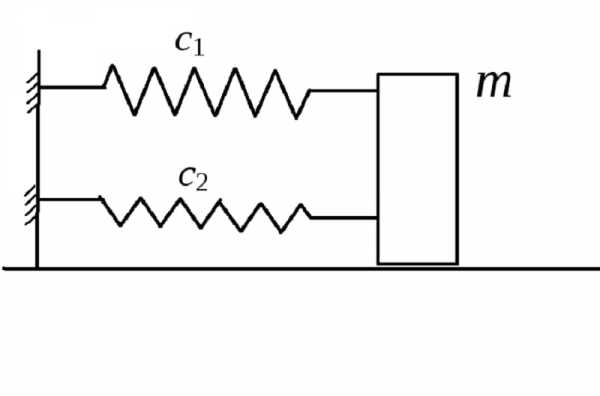
Параллельное соединение пружин

При параллельном соединении двух пружин, имеющих коэффициенты жесткости с₁, с₂ (рис. 2.5), смещение тела равно деформации каждой из пружин:

. (2.9)

Р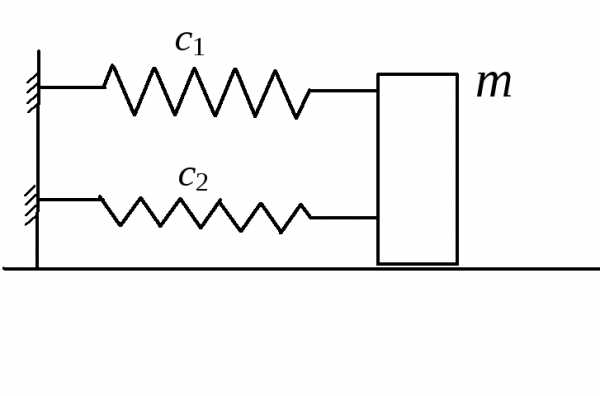ис. 2.5 Параллельное соединение пружин

Сила упругости эквивалентной пружины с коэффициентом жесткости с* будет равна сумме сил упругости двух установленных пружин, откуда с учетом (2.9) получаем

,

окончательно

. (2.10)

Последовательное соединение пружин

При последовательном соединении двух пружин, имеющих коэффициенты жесткости с₁, с₂ (рис. 2.6), смещение тела равно сумме деформаций пружин:

. (2.11)

Рис. 3.6 Последовательное соединение пружин

Сила упругости эквивалентной пружины с коэффициентом жесткости с* будет равна каждой из сил упругости установленных пружин, откуда

,

,

откуда

Окончательно с учетом (2.11) получаем

. (2.12)

2. Влияние сопротивления на свободные колебания

Пусть на точку массы m, совершающую прямолинейное движение, действуют две силы (рис. 2.7):

1. Восстанавливающая сила (сила упругости пружины): .

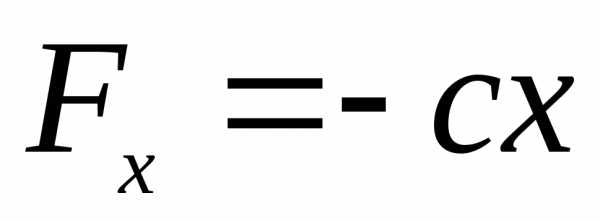2. Сила сопротивления, пропорциональная скорости движения точки (сила сопротивления демпфера): .

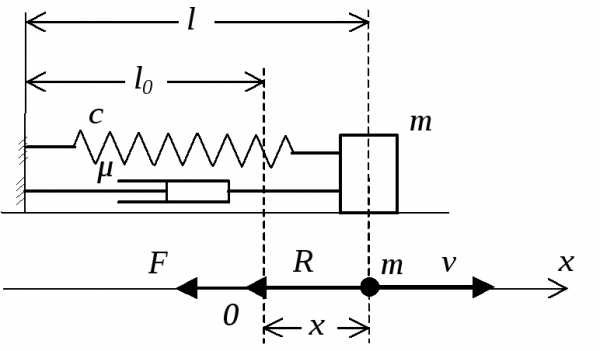
Рис. 2.7 Движение массы с демпфированием

Дифференциальное уравнение движения точки запишется как

;

,

обозначая

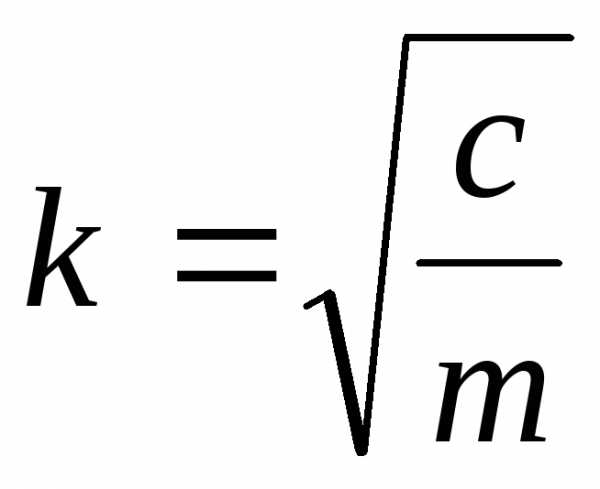, , (2.13)

получаем линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами:

. (2.14)

Характеристическое уравнение имеет вид

, (2.15)

его корни равны

, (2.16)

где – дискриминант.

Как известно из курса высшей математики, общее решение дифференциального уравнения (2.14) существенно зависит от знака дискриминанта , т.е. от соотношения между b и k.

1-й случай (малое сопротивление): b  k , D  0.

Обозначим , причем k*  k. Тогда корни (2.16) характеристического уравнения будут комплексно сопряженными:

,

Общее решение дифференциального уравнения (2.14) в данном случае имеет вид

, (2.17)

это затухающие колебания с частотой k^* и периодом 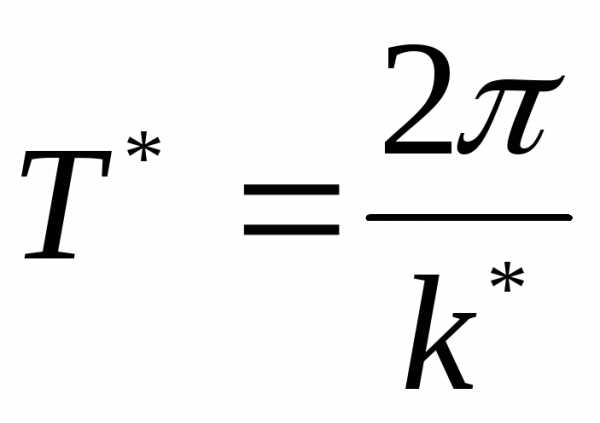(рис.3.8).

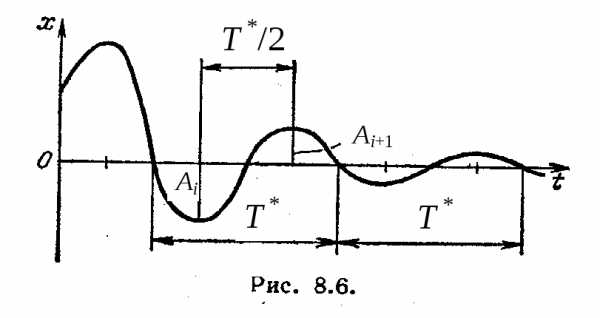
Амплитуда колебаний убывает со временем. Отношение последующей амплитуды к предыдущей называется декрементом затухания:

< 1 (2.18)

Рис. 2.8 Затухающие колебания

Часто используется также логарифмический декремент .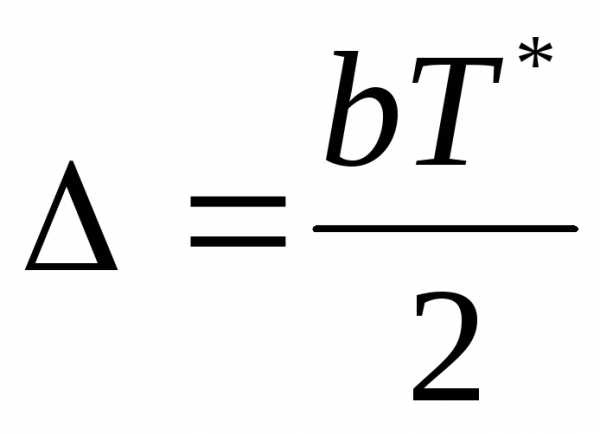

Таким образом, амплитуды образуют геометрическую прогрессию с показателем q, меньшим единицы.

Видим также, что наличие сопротивления приводит к уменьшению частоты колебаний (k^*  k) и к увеличению их периода (Т^* > Т).

2-й случай (граничный): b = k , D = 0.

Корни (2.16) характеристического уравнения получаются кратные, , и решение дифференциального уравнения (2.14) приобретает вид

. (2.19)

Поскольку экспонента убывает быстрее, чем растёт линейная функция времени, в зависимости от начальных условий движения получим ту или иную картину затухающего апериодического (т.е. не колебательного) движения (рис.2.9).

3-й случай (большое сопротивление): b > k, D > 0.

В этом случае обозначим >0, и оба корня (2.16) характеристического уравнения будут действительными и отрицательными:

< 0, < 0,

общее решение

. (2.20)

Рис. 2.9 График затухающего апериодического движения

Здесь также получаем затухающие апериодическое движение, графики будут такие же, как и в случае b= k.

studfiles.net

Репетитор-онлайн — подготовка к ЦТ

Пример 16. При последовательном соединении трех пружин, коэффициенты жесткости которых относятся как 1 : 2 : 3, сила 12 Н вызвала растяжение системы на 4,0 см. Рассчитать коэффициенты жесткости указанных пружин.

Решение. Величина силы упругости, действующей на пружину, определяется формулой

F_упр = k_общ∆x,

где k_общ — коэффициент жесткости составной пружины; ∆x — указанное в условии задачи растяжение пружины.

Величина силы упругости, с другой стороны, совпадает с величиной приложенной силы:

F_упр = F.

Значение данной силы и величина растяжения пружины под действием этой силы позволяют рассчитать коэффициент жесткости составной пружины:

kобщ=FΔx=124,0⋅10−2=300 Н/м.

Для определения коэффициентов жесткости каждой пружины запишем их коэффициенты жесткости в следующем виде:

• для первой пружины

k₁ = k;

• для второй пружины

k₂ = 2k;

• для третьей пружины

k₃ = 3k,

так как указанные коэффициенты по условию задачи соотносятся между собой как

k₁ : k₂ : k₃ = 1 : 2 : 3.

Для расчета величины k запишем формулу для коэффициента жесткости пружины, состоящей из трех последовательно соединенных пружин, и подставим в нее выражения k₁, k₂, k₃:

1kобщ=1k1+1k2+1k3=1k+12k+13k=116k, или kобщ=6k11.

Найденное ранее значение k_общ = 300 Н/м позволяет рассчитать k = 550 Н/м.

Тогда коэффициенты жесткости каждой из пружин имеют значения:

• для первой пружины

k₁ = k = 550 Н/м;

• для второй пружины

k₂ = 2k = 1100 Н/м;

• для третьей пружины

k₃ = 3k = 1650 Н/м.

vedy.by

Вопрос 8.4 Замена системы пружин эквивалентной пружиной

П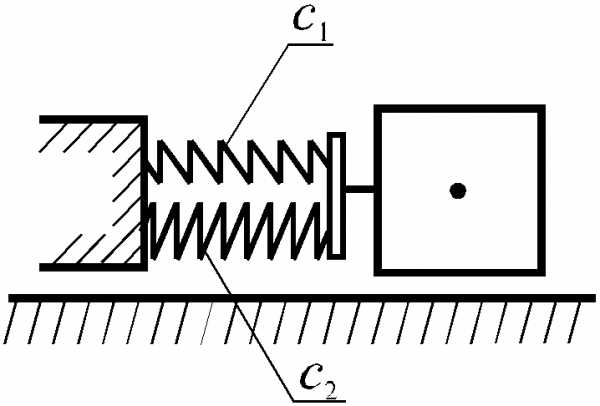ри описании колебательного движения систему пружин, действующих на материальную точку, заменяют одной пружиной, жесткость которой равна жесткости системы. Эту пружину называют эквивалентной. Рассмотрим три основные схемы соединения пружин.

1 Параллельное соединение(рисунок 8.1).

П

Рисунок 8.1

араллельно соединенные пружины, если их деформации одинаковы, можно заменить эквивалентной пружиной, коэффициент жесткости которой равен сумме коэффициентов жесткости соединенных пружин,

.

2 Последовательное соединение(рисунок 8.2).

П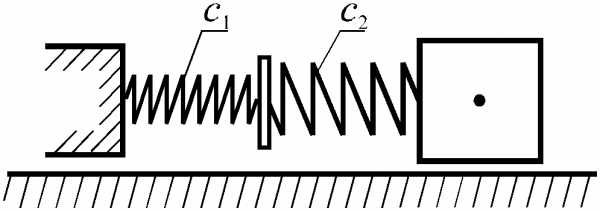ри последовательном соединении нескольких пружин они могут быть заменены эквивалентной пружиной, податливость которой равна сумме податливостей соединенных пружин (податливостью пружины называют величину, обратную коэффициенту жесткости). Следовательно, коэффициент жесткости эквивалентной пружины в данном случае определяется следующим образом:

.

3

Рисунок 8.2

«Двухстороннее» соединение(рисунок 8.3).

П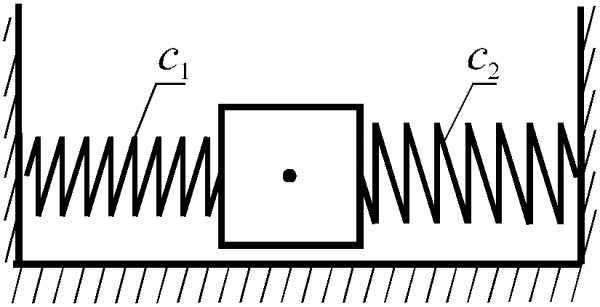ри движении исследуемой материальной точки деформации обоих пружин будут одинаковы. Результирующая сила, действующая со стороны этих пружин на точку, будет равна сумме сил упругости в пружинах 1 и 2. Следовательно, коэффициент жесткости эквивалентной пружины будет равен сумме коэффициентов жесткости пружин 1 и 2:

.

Любую систему пружин можно представить как набор рассмотренных схем.

Рисунок 8.3

Лекция 9 Динамика материальной системы.

(2 часа, 1 семестр, 2 курс)

Вопрос 9.1Теорема о движении центра масс материальной системы.

Центром масс материальной системы называют точку, радиус-вектор которой определяется по формуле

,

где – масса материальной системы;

m_i,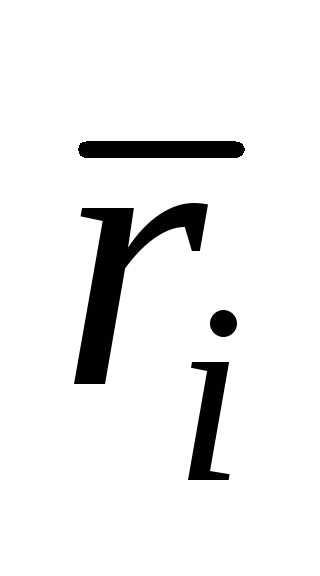– масса и радиус-векторi-й материальной точки.

Координаты центра масс системы:

,

где x_i,y_i,z_i– координаты центра массi-го тела системы.

При решении задач динамики материальной системы часто оказывается полезной теорема о движении центра масс:произведение массы материальной системы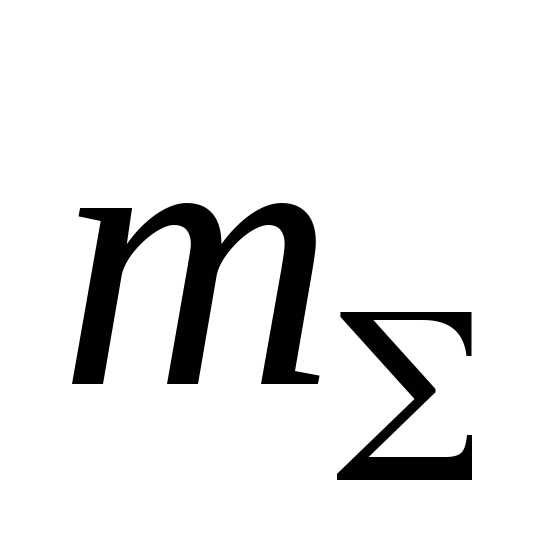

на ускорение ее центра массa_C равно геометрической сумме внешних сил, приложенных к системе:

.

В ходе решения выражение теоремы проецируют на оси координат. При этом получается система уравнений

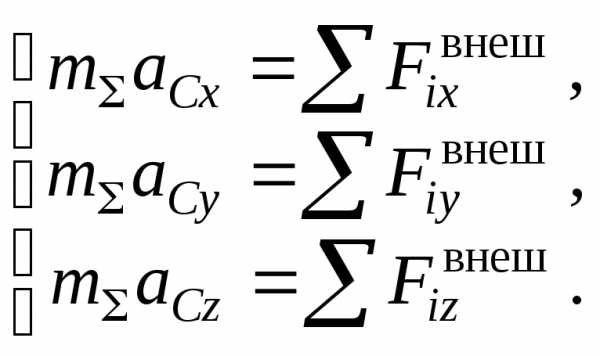
Использование теоремы о движении центра масс материальной системы для решения задач динамики рекомендуется осуществлять по следующей методике:

1 Изображается материальная система, и указываются все внешние силы, действующие на нее.

2 Выбираются оси координат.

3 Внешние силы, действующие на систему, проецируются на выбранные оси.

4 Записываются выражения координат центра масс системы через координаты центров масс одного из тел системы.

5 Дифференцируя выражения координат центра масс по времени, получают зависимости для скорости и ускорения центра масс системы.

6 Полученные выражения подставляются в систему динамических уравнений.

7 Решается дифференциальное уравнение относительно искомой координаты с учетом заданных начальных условий.

Вопрос 9.2Динамические уравнения движения твердого тела.

Динамические уравнения движения твердого тела устанавливают связь между кинематическими характеристиками движения тела и действующими на него силами.

Поступательное движение тела.В этом случае динамическое уравнение представляет собой следствие из теоремы о движении центра масс:

,

где m– масса тела;

– ускорение центра масс тела;

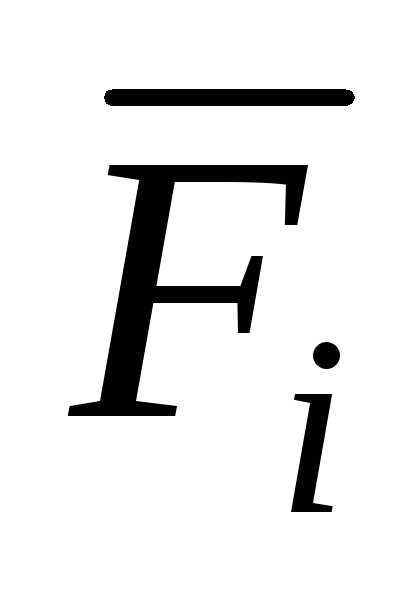–i-тая сила, действующая на тело.

При решении задач динамическое уравнение поступательного движения тела проецируют на оси координат.

Вращательное движение тела. Для него динамическое уравнение имеет вид:

,

где J_z– момент инерции тела относительно оси вращенияz;

 – угловое ускорение тела;

M_iz– моментi-й силы относительно оси вращения.

При составлении динамического уравнения вращательного движения тела выбирается направление отсчета угла поворота . Моменты сил, вращающих тело против выбранного направления, принимаются отрицательными, а по выбранному направлению – положительными.

Момент инерции J_z является мерой инертности тела при вращательном движении. Момент инерции материальной системы относительно данной осиOzопределяется как сумма произведений масс всех точек системы на квадраты их расстояний от этой оси:

.

Для абсолютно твердого тела суммирование по точкам системы заменяется интегрированием по объему

,

где ρ – плотность материала тела;

h– расстояние от точки с координатамиx,y,zдо осиOz.

Момент инерции J_Cтела относительно осиCz, проходящей через центр массC, называютцентральным моментом инерции. Если для тела известенрадиус инерцииi, то центральный момент

.

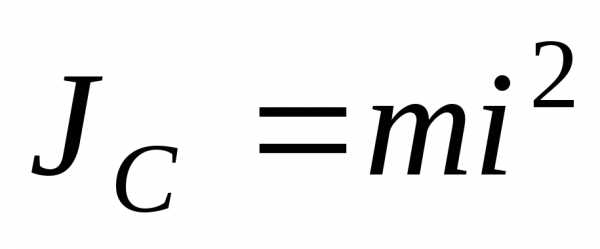Центральные моменты инерции некоторых тел:

1 Тонкий однородный стержень с массой mи длинойl:

.

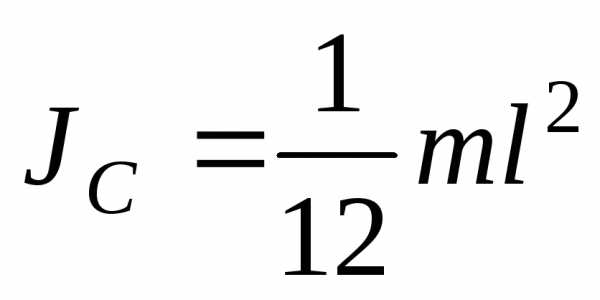2 Тонкое круглое однородное кольцо с массой mи радиусомR:

.

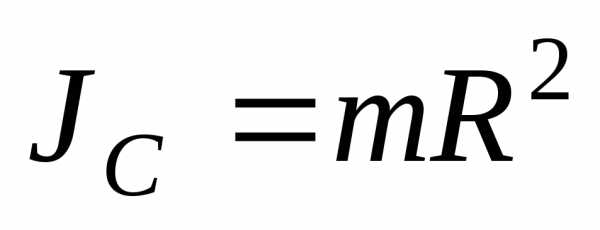3 Круглый однородный диск с массой mи радиусомR:

.

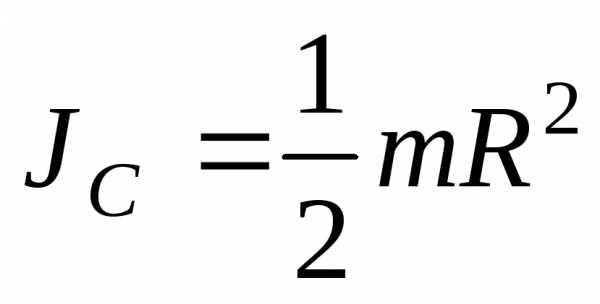studfiles.net

способ соединения витых винтовых пружин сжатия с деталями резонансной механической колебательной системы – патент РФ 2378056

Изобретение относится к вибрационной технике и может быть использовано в различных отраслях хозяйственной деятельности. Способ соединения витых винтовых пружин сжатия с деталями резонансной механической колебательной системы заключается в том, что пружины попарно соединяют с деталями колебательной системы стяжным соединением. Пружины базируют опорными торцовыми поверхностями концевых витков относительно деталей колебательной системы с помощью цилиндрических углублений и штифтов, входящих в эти углубления. Цилиндрические углубления выполняют на опорных торцовых поверхностях концевых витков пружин в количестве не менее двух на каждой опорной торцовой поверхности. Штифты устанавливают в сопрягаемых деталях колебательной системы. В результате уменьшается уровень шума и рассеяния энергии при резонансных колебаниях. 1 ил.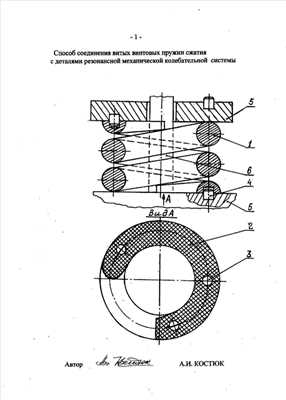

Рисунки к патенту РФ 2378056

Изобретение относится к вибрационной технике и может быть использовано в различных отраслях хозяйственной деятельности.

Известен способ соединения пружин сжатия с деталями механической колебательной системы, заключающийся в том, что пружины попарно соединяют с деталями колебательной системы с помощью стяжного соединения, причем пружины базируют относительно деталей колебательной системы с помощью углублений на этих деталях, в которые устанавливают пружины (см. рис.4 на стр.13 в книге: И.И.Быховский и др. Упругие элементы вибромашин. Обзор. ЦНИИТЭстроймаш. М., 1971).

Известен способ соединения витых винтовых пружин сжатия с деталями резонансной механической колебательной системы, осуществленный в вибраторах с электромагнитным приводом моделей С-917 – С-921. Способ заключается в том, что пружины попарно соединяют с деталями колебательной системы с помощью стяжного соединения, причем пружины базируют опорными торцовыми и внутренними поверхностями концевых витков относительно деталей колебательной системы (см. стр.26 в книге: А.Н.Белоусов, Г.Г.Рекус. Вибраторы с электромагнитным приводом. Обзор. ЦНИИТЭстроймаш. М., 1969).

В качестве прототипа выбран способ соединения витых винтовых пружин сжатия с деталями резонансной механической колебательной системы, заключающийся в том, что пружины попарно соединяют с деталями колебательной системы стяжным соединением, причем пружины базируют опорными торцовыми и наружными поверхностями концевых витков относительно деталей колебательной системы. Данный способ осуществлен в электромагнитном вибраторе серийного выпуска типа ВСРД (вибратор сбалансированный, резонансный, двухтактный) и описан на стр.10-11 в книге: М.В.Хвингия. Вибрации пружин. М.: Машиностроение, 1969.

Недостатком указанных аналогов и прототипа является высокий уровень шума, возникающего от соударения витков пружин с базирующими поверхностями, а также значительное рассеяние энергии при резонансных колебаниях, что обусловлено как соударениями витков пружин с базирующими поверхностями, так и микросдвигами опорных торцовых поверхностей концевых витков пружин относительно опорных поверхностей деталей колебательной системы.

Задачей изобретения является повышение эффективности способа соединения витых винтовых пружин сжатия с деталями резонансных механических колебательных систем.

Решение задачи достигается тем, что способ соединения витых винтовых пружин сжатия с деталями резонансной механической колебательной системы заключается в том, что пружины попарно соединяют с деталями колебательной системы стяжным соединением, причем пружины базируют опорными торцовыми поверхностями концевых витков относительно деталей колебательной системы, при этом пружины базируют с помощью цилиндрических углублений и штифтов, входящих в эти углубления, цилиндрические углубления выполняют на опорных торцовых поверхностях концевых витков пружин в количестве не менее двух на каждой опорной торцовой поверхности, а штифты устанавливают в сопрягаемых деталях колебательной системы.

Применение предложенной совокупности существенных признаков позволяет в сравнении с прототипом получить новый технический результат: соединение витых винтовых пружин с деталями резонансной механической колебательной системы осуществляется без соударения витков пружин с базирующими поверхностями, при этом практически обеспечивается неподвижность опорных торцовых поверхностей концевых витков пружин на стыке с опорными поверхностями деталей колебательной системы. Благодаря этому уменьшается шум пружин и рассеяние энергии при резонансных колебаниях.

Анализ уровня техники в области машиностроения и вибрационной техники показал, что предложенная совокупность существенных признаков является новой, явным образом не следует из уровня техники, и, таким образом, предлагаемое изобретение является новым и имеет изобретательский уровень.

Сущность изобретения поясняется чертежом, на котором показана конструкция, реализующая предлагаемый способ. Конструкция включает витую винтовую пружину сжатия 1 с опорными торцовыми поверхностями 2 концевых витков и цилиндрическими углублениями 3 на них. Штифты 4, сопрягаемые с цилиндрическими углублениями пружины, установлены в деталях 5 резонансной механической колебательной системы. Пружина и детали колебательной системы стянуты стержнем 6 стяжного соединения (полная конструкция стяжного соединения на чертеже не показана).

Способ осуществляют следующим образом. На опорных торцовых поверхностях 2 витой винтовой пружины 1 выполняют не менее двух цилиндрических углублений 3. На деталях 5 колебательной системы устанавливают штифты 4. При этом координаты установки штифтов 4 и выполнения цилиндрических углублений 3 согласуют так, чтобы выполнить требования по базированию пружины 1 относительно деталей 5. Пружину 1 с помощью цилиндрических углублений 3 и штифтов 4 базируют относительно деталей 5 колебательной системы и стягивают стержнем 6 стяжного соединения.

В предлагаемом способе соединения витых винтовых пружин сжатия с деталями резонансной механической колебательной системы решена задача изобретения – повышена эффективность способа соединения витых винтовых пружин сжатия с деталями резонансной механической колебательной системы. Задача решена благодаря базированию пружин относительно деталей колебательной системы с помощью цилиндрических углублений и штифтов. Это позволило исключить в сравнении с прототипом соударение наружной поверхности витков пружины с базирующей поверхностью сопряженной детали колебательной системы. Кроме того, обеспечивается практическая неподвижность опорных торцовых поверхностей концевых витков пружин на стыке с опорными поверхностями деталей колебательной системы, поскольку штифты, входящие в цилиндрические углубления концевых витков пружин, препятствуют микросдвигам опорных торцовых поверхностей. Благодаря этому уменьшаются шум пружин и рассеяние энергии при резонансных колебаниях.

Возможность практического осуществления предложенного изобретения подтверждается следующими сведениями. Выполнение цилиндрических углублений в концевых витках пружин не вызывает затруднений для практической реализации. Однако возникает особенность, связанная с тем, что отверстия в концевых витках необходимо сверлить и калибровать в термообработанной на среднюю твердость пружинной стали. При использовании сверл и разверток, оснащенных пластинами из твердого сплава, обработка таких отверстий не вызывает затруднений (см. стр.275-276 в книге: Обработка металлов резанием: Справочник технолога. Под ред. А.А.Панова. – М.: Машиностроение, 1988).

Таким образом, предложенное изобретение промышленно применимо.

ФОРМУЛА ИЗОБРЕТЕНИЯ

Способ соединения витых винтовых пружин сжатия с деталями резонансной механической колебательной системы, заключающийся в том, что пружины попарно соединяют с деталями колебательной системы стяжным соединением, причем пружины базируют опорными торцовыми поверхностями концевых витков относительно деталей колебательной системы, отличающийся тем, что пружины базируют с помощью цилиндрических углублений и штифтов, входящих в эти углубления, цилиндрические углубления выполняют на опорных торцевых поверхностях концевых витков пружин в количестве не менее двух на каждой опорной торцевой поверхности, а штифты устанавливают в сопрягаемых деталях колебательной системы.

www.freepatent.ru

Коэффициент жесткости пружины, формула и примеры

Определение и формула коэффициента жесткости пружины

Сила упругости (), которая возникает в результате деформации тела, в частности пружины, направленная в сторону противоположную перемещению частиц, деформируемого тела, пропорциональна удлинению пружины:

   

Он зависит от формы тела, его размеров, материала из которого изготовлено тело (пружина).

Иногда коэффициент жесткости обозначают буквами D и с.

Величина коэффициента жёсткости пружины указывает на устойчивость ее к действию нагрузок и насколько велико ее сопротивление при воздействии.

Коэффициент жесткости соединений пружин

Если некоторое число пружин соединить последовательно, то суммарную жесткость такой системы можно вычислить как:

   

В том случае, если мы имеем дело с n пружинами, которые соединены параллельно, то результирующую жесткость получают как:

   

Коэффициент жесткости цилиндрической пружины

Рассмотрим пружину в виде спирали, которая сделана из проволоки с сечением круг. Если рассматривать деформацию пружины как совокупность элементарных сдвигов в ее объеме под воздействие сил упругости, то коэффициент жесткости можно вычислить при помощи формулы:

   

где — радиус пружины, — количество витков в пружине, — радиус проволоки, — модуль сдвига (постоянная, которая зависит от материала).

Единицы измерения

Основной единицей измерения коэффициента жесткости в системе СИ является:

   

В СГС:

= дин/см

Примеры решения задач

ru.solverbook.com