Стандартный ряд модулей зубчатых колес – ГОСТ 9563-60
alexxlab | 16.02.2019 | 0 | Вопросы и ответы
ГОСТ 9563-60
ГОСТ 9563-60
(CT СЭВ 310-76)
Группа Г15
Дата введения 1962-07-01
1. РАЗРАБОТАН Государственным комитетом СССР по стандартам
РАЗРАБОТЧИКИ
Н.М.Шоломов, канд. техн. наук (руководитель темы), Э.В.Бабенкова, канд. техн. наук
2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного Комитета СССР по стандартам от 30.05.88 N 1547
3. Срок проверки 1998 год, периодичность проверки – 10 лет
4. ВЗАМЕН ОСТ 1597
5. Стандарт полностью соответствует СТ СЭВ 310-76.
6. Стандарт соответствует стандартам: ИСО 54-77, ИСО 678-76
7. ПЕРЕИЗДАНИЕ (март 1994 г.) с Изменениями N 1, 2, утвержденными в июне 1979 г., мае 1988 г. (ИУС 8-79, 9-88)
1. Настоящий стандарт распространяется на эвольвентные цилиндрические зубчатые колеса и конические зубчатые колеса с прямыми зубьями и устанавливает:
для цилиндрических колес – значения нормальных модулей;
для конических колес – значения внешних окружных делительных модулей.
2. Числовые значения модулей должны соответствовать указанным в таблице.
1, 2. (Измененная редакция, Изм. N 1).
3-6. (Исключены, Изм. N 1).
мм | |
1 ряд | 2 ряд |
0,05 | |
0,055 | |
0,06 | |
0,07 | |
0,08 | |
0,09 | |
0,1 | |
0,11 | |
0,12 | |
0,14 | |
0,15 | |
0,18 | |
0,2 | |
0,22 | |
0,25 | |
0,28 | |
0,35 | |
0,4 | |
0,45 | |
0,5 | |
0,55 | |
0,6 | |
0,7 | |
0,8 | |
0,9 | |
1 | |
1,125 | |
1,25 | |
1,375 | |
1,5 | |
1,75 | |
2 | |
2,25 | |
2,5 | |
2,75 | |
3 | |
3,5 | |
4 | |
4,5 | |
5 | |
6 | |
7 | |
8 | |
9 | |
10 | |
11 | |
12 | |
14 | |
16 | |
18 | |
20 | |
22 | |
| 25 | |
28 | |
32 | |
36 | |
40 | |
45 | |
50 | |
55 | |
60 | |
70 | |
80 | |
90 | |
100 | |
Примечания:
1. При выборе модулей ряд 1 следует предпочитать ряду 2.
2. Для цилиндрических зубчатых колес допускается:
а) в тракторной промышленности применение модулей 3,75; 4,25, 6,5 мм;
б) в автомобильной промышленности применение модулей, отличающихся от установленных в настоящем стандарте;
в) в редукторостроении применение модулей 1,6; 3,15, 6,3; 12,5.
3. Для конических зубчатых колес допускается:
а) определять модуль на среднем конусном расстоянии;
б) в технически обоснованных случаях применение модулей, отличающихся от указанных в таблице.
(Измененная редакция, Изм. N 2).
ПРИЛОЖЕНИЕ (Исключено, Изм. N 2).
Текст документа сверен по:
официальное издание
М.: Издательство стандартов, 1994
Как узнать модуль зубчатого колеса? Расчет в Excel.
Опубликовано 20 Янв 2014
Рубрика: Механика | 21 комментарий
При поломке зубчатого колеса или шестерни в редукторе какого-либо механизма или машины возникает необходимость по «старой» детали, а иногда по фрагментам обломков создать чертеж для изготовления нового колеса и/или шестерни. Эта статья будет полезна тем,…
…кому приходится восстанавливать зубчатые передачи при отсутствии рабочих чертежей на вышедшие из строя детали.
Обычно для токаря и фрезеровщика все необходимые размеры можно получить с помощью замеров штангенциркулем. Требующие более пристального внимания, так называемые, сопрягаемые размеры – размеры, определяющие соединение с другими деталями узла – можно уточнить по диаметру вала, на который насаживается колесо и по размеру шпонки или шпоночного паза вала. Сложнее обстоит дело с параметрами для зубофрезеровщика. В этой статье мы будем определять не только модуль зубчатого колеса, я попытаюсь изложить общий порядок определения всех основных параметров зубчатых венцов по результатам замеров изношенных образцов шестерни и колеса.
«Вооружаемся» штангенциркулем, угломером или хотя бы транспортиром, линейкой и программой MS Excel, которая поможет быстро выполнять рутинные и порой непростые расчеты, и начинаем работу.
Как обычно раскрывать тему я буду на примерах, в качестве которых рассмотрим сначала цилиндрическую прямозубую передачу с наружным зацеплением, а затем косозубую.
Расчетам зубчатых передач на этом сайте посвящено несколько статей: «Расчет зубчатой передачи», «Расчет геометрии зубчатой передачи», «Расчет длины общей нормали зубчатого колеса». В них приведены рисунки с обозначениями параметров, используемых в данной статье. Эта статья продолжает тему и призвана раскрыть алгоритм действий при ремонтно-восстановительных работах, то есть работах, обратных проектировочным.
Расчеты можно выполнить в программе MS Excel или в программе OOo Calc из пакета Open Office.
О правилах форматирования ячеек листа Excel, которые применены в статьях этого блога, можно прочитать на странице «О блоге».
Расчет параметров колеса и шестерни прямозубой передачи.
Изначально полагаем, что зубчатое колесо и шестерня имеют эвольвентные профили зубьев и изготавливались с параметрами исходного контура по ГОСТ 13755-81. Этот ГОСТ регламентирует три главных (для нашей задачи) параметра исходного контура для модулей больше 1 мм. (Для модулей меньше 1 мм исходный контур задается в ГОСТ 9587-81; модули меньше 1 мм рекомендуется применять только в кинематических, то есть не силовых передачах.)
Для правильного расчета параметров зубчатой передачи необходимы замеры и шестерни и колеса!
Исходные данные и замеры:
Начинаем заполнение таблицы в Excel с параметров исходного контура.
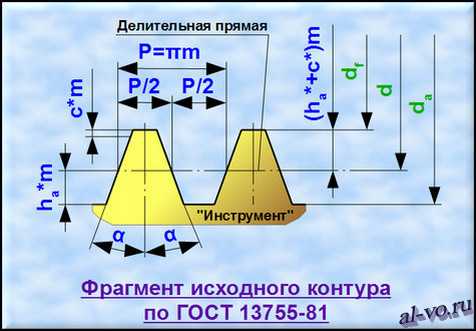
1. Угол профиля исходного контура α в градусах записываем
в ячейку D3: 20
2. Коэффициент высоты головки зуба ha* вводим
в ячейку D4: 1
3. Коэффициент радиального зазора передачи c* заносим
в ячейку D5: 0,25
В СССР и в России 90% зубчатых передач в общем машиностроении изготавливались именно с такими параметрами, что позволяло применять унифицированный зубонарезной инструмент. Конечно, изготавливались передачи с зацеплением Новикова и в автомобилестроении применялись специальные исходные контуры, но все же большинство передач проектировалось и изготавливалось именно с контуром по ГОСТ13755-81.
4. Тип зубьев колеса (тип зацепления) T записываем
в ячейку D6: 1
T=1 – при наружных зубьях у колеса
T=-1 – при внутренних зубьях у колеса (передача с внутренним зацеплением)
5. Межосевое расстояние передачи aw в мм измеряем по корпусу редуктора и заносим значение
в ячейку D7: 80,0
Ряд межосевых расстояний зубчатых передач стандартизован. Можно сравнить измеренное значение со значениями из ряда, который приведен в примечании к ячейке C7. Совпадение не обязательно, но высоковероятно.
6-9. Параметры шестерни: число зубьев z1, диаметры вершин и впадин зубьев da1 и df1 в мм, угол наклона зубьев на поверхности вершин βa1 в градусах подсчитываем и измеряем штангенциркулем и угломером на исходном образце и записываем соответственно
в ячейку D8: 16
в ячейку D9: 37,6
в ячейку D10: 28,7
в ячейку D11: 0,0
10-13. Параметры колеса: число зубьев z2, диаметры вершин и впадин зубьев da2 и df2 в мм, угол наклона зубьев на цилиндре вершин βa2 в градусах определяем аналогично — по исходному образцу колеса — и записываем соответственно
в ячейку D12: 63
в ячейку D13: 130,3
в ячейку D14: 121,4
в ячейку D11: 0,0
Обращаю внимание: углы наклона зубьев βa1 и βa2 – это углы, измеренные на цилиндрических поверхностях вершин зубьев!!!
Измеряем диаметры, по возможности, максимально точно! Для колес с четным числом зубьев сделать это проще, если вершины не замяты. Для колес с нечетным числом зубьев при замере помним, что размеры, которые показывает штангенциркуль несколько меньше реальных диаметров выступов!!! Делаем несколько замеров и наиболее с нашей точки зрения достоверные значения записываем в таблицу.

Результаты расчетов:
14. Предварительные значения модуля зацепления определяем по результатам замеров шестерни m1 и зубчатого колеса m2 в мм соответственно
в ячейке D17: =D9/(D8/COS (D20/180*ПИ())+2*D4)=2,089
m1=da1/(z1/cos (β1)+2*(ha*))
и в ячейке D18: =D13/(D12/COS (D21/180*ПИ())+2*D4)=2,005
m2=da2/(z2/cos (β2)+2*(ha*))
Модуль зубчатого колеса играет роль универсального масштабного коэффициента, определяющего как габариты зубьев, так и общие габариты колеса и шестерни.
Сравниваем полученные значения со значениями из стандартного ряда модулей, фрагмент которого приведен в примечании к ячейке C19.
Полученные расчетные значения, как правило, очень близки к одному из значений стандартного ряда. Делаем предположение, что искомый модуль зубчатого колеса и шестерни m в мм равен одному из этих значений и вписываем его
в ячейку D19: 2,000
15. Предварительные значения угла наклона зубьев определяем по результатам замеров шестерни β1 и зубчатого колеса β2 в градусах соответственно
в ячейке D20: =ASIN (D8*D19/D9*TAN (D11/180*ПИ()))=0,0000
β1=arcsin (z1*m*tg (βa1)/da1)
и в ячейке D21: =ASIN (D12*D19/D13*TAN (D15/180*ПИ()))=0,0000
β2=arcsin (z2*m*tg (βa2)/da2)
Делаем предположение, что искомый угол наклона зубьев β в градусах равен измеренным и пересчитанным значениям и записываем
в ячейку D22: 0,0000
16. Предварительные значения коэффициента уравнительного смещения вычисляем по результатам замеров шестерни Δy1 и зубчатого колеса Δy2 соответственно
в ячейке D23: =2*D4+D5- (D9-D10)/(2*D19)=0,025
Δy1=2*(ha*)+(c*) — (da1-df1)/(2*m)
и в ячейке D24: =2*D4+D5- (D13-D14)/(2*D19)= 0,025
Δy2=2*(ha*)+(c*) – (da2— df2)/(2*m)
Анализируем полученные расчетные значения, и принятое решение о значении коэффициента уравнительного смещения Δy записываем
в ячейку D25: 0,025
17,18. Делительные диаметры шестерни d1 и зубчатого колеса d2 в мм рассчитываем соответственно
в ячейке D26: =D19*D8/COS (D22/180*ПИ())=32,000
d1=m*z1/cos(β)
и в ячейке D27: =D19*D12/COS (D22/180*ПИ())=126,000
d2=m*z2/cos(β)
19. Делительное межосевое расстояние a в мм вычисляем
в ячейке D28: =(D27+D6*D26)/2=79,000
a=(d2+T*d1)/2
20. Угол профиля αt в градусах рассчитываем
в ячейке D29: =ATAN (TAN (D3/180*ПИ())/COS (D22/180*ПИ()))/ПИ()*180=20,0000
αt=arctg(tg (α)/cos(β))
21. Угол зацепления αtw в градусах вычисляем
в ячейке D30: =ACOS (D28*COS (D29/180*ПИ())/D7)/ПИ()*180=21,8831
αtw=arccos(a*cos (αt)/aw)
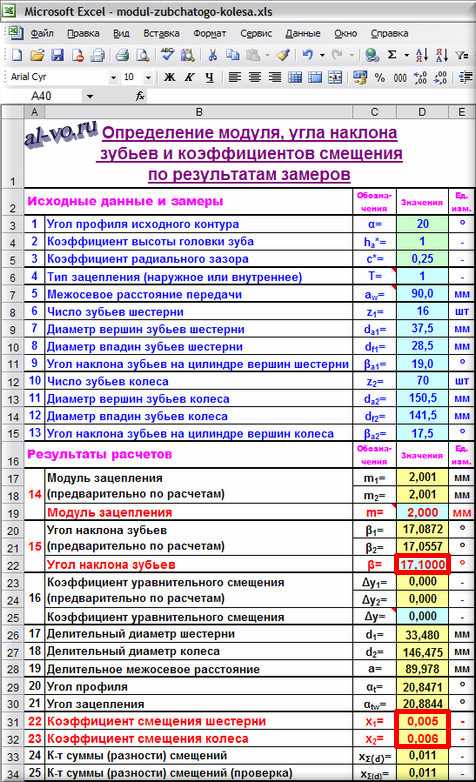
22,23. Коэффициенты смещения шестерни x1 и колеса x2 определяем соответственно
в ячейке D31: =(D9-D26)/(2*D19) -D4+D25=0,425
x1=(da1— d1)/(2*m) — (ha*)+Δy
и в ячейке D32: =(D13-D27)/(2*D19) -D4+D25 =0,100
x2=(da2— d1)/(2*m) — (ha*)+Δy
24,25. Коэффициент суммы (разности) смещений xΣ(d)вычисляем для проверки правильности предыдущих расчетов по двум формулам соответственно
в ячейке D33: =D31+D6*D32=0,525
xΣ(d)=x1+T*x2
и в ячейке D34: =(D12+D6*D8)*((TAN (D30/180*ПИ()) — (D30/180*ПИ())) — (TAN (D29/180*ПИ()) — (D29/180*ПИ())))/(2*TAN (D3/180*ПИ()))=0,523
xΣ(d)=(z2+T*z1)*(inv(αtw) — inv(αt))/(2*tg(α))
Значения, рассчитанные по разным формулам, отличаются очень незначительно! Полагаем, что найденные значения модуля зубчатого колеса и шестерни, а также коэффициентов смещения определены верно!
Расчет параметров колеса и шестерни косозубой передачи.
Переходим к примеру с косозубой передачей и повторяем все действия, которые мы делали в предыдущем разделе.
Измерить угол наклона зубьев с необходимой точностью при помощи угломера или транспортира практически очень сложно. Я обычно прокатывал колесо и шестерню по листу бумаги и затем по отпечаткам транспортиром делительной головки кульмана производил предварительные измерения с точностью в градус или больше… В представленном ниже примере я намерил: βa1=19° и βa2=17,5°.
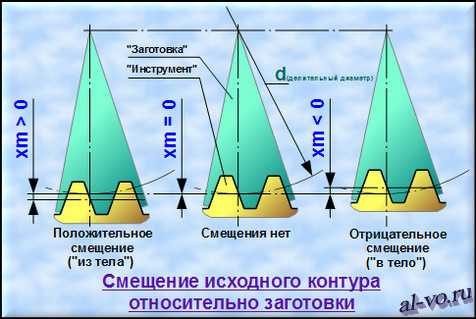
Еще раз обращаю внимание, что углы наклона зубьев на цилиндре вершин βa1 и βa2 – это не угол β, участвующий во всех основных расчетах передачи!!! Угол β – это угол наклона зубьев на цилиндре делительного диаметра (для передачи без смещения).
Ввиду малости значений рассчитанных коэффициентов смещения уместно предположить, что передача была выполнена без смещения производящих контуров шестерни и зубчатого колеса.
Воспользуемся сервисом Excel «Подбор параметра». Подробно и с картинками об этом сервисе я в свое время написал здесь.
Выбираем в главном меню Excel «Сервис» — «Подбор параметра» и в выпавшем окне заполняем:
Установить в ячейке: $D$33
Значение: 0
Изменяя значение ячейки: $D$22
И нажимаем OK.
Получаем результат β=17,1462°, xΣ(d)=0, x1=0,003≈0, x2=-0,003≈0!
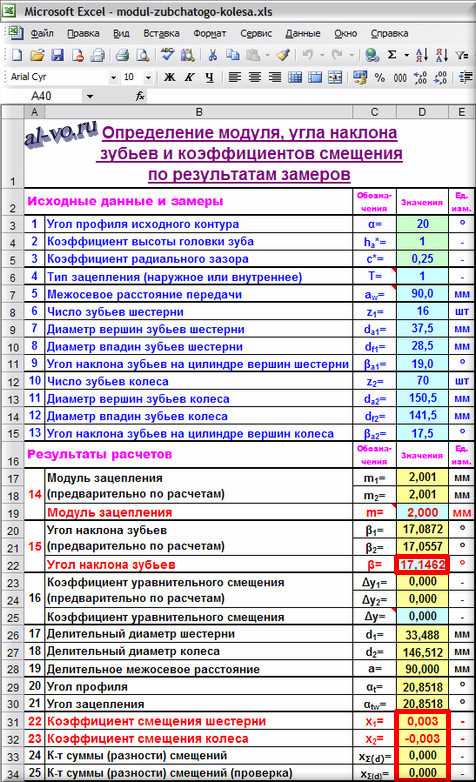
Передача, скорее всего, была выполнена без смещения, модуль зубчатого колеса и шестерни, а также угол наклона зубьев мы определили, можно делать чертежи!
Важные замечания.
Смещение исходного контура при нарезке зубьев применяют для восстановления изношенных поверхностей зубьев колеса, уменьшения глубины врезания на валах-шестернях, для увеличения нагрузочной способности зубчатой передачи, для выполнения передачи с заданным межосевым расстоянием не равным делительному расстоянию, для устранения подрезания ножек зубьев шестерни и головок зубьев колеса с внутренними зубьями.
Различают высотную коррекцию (xΣ(d)=0) и угловую (xΣ(d)≠0).
Смещение производящего контура на практике применяют обычно при изготовлении прямозубых колес и очень редко косозубых. Это обусловлено тем, что по изгибной прочности косой зуб прочнее прямого, а необходимое межосевое расстояние можно обеспечить соответствующим углом наклона зубьев. Если высотную коррекцию изредка применяют для косозубых передач, то угловую практически никогда.
Косозубая передача работает более плавно и бесшумно, чем прямозубая. Как уже было сказано, косые зубья имеют более высокую прочность на изгиб и заданное межосевое расстояние можно обеспечить углом наклона зубьев и не прибегать к смещению производящего контура. Однако в передачах с косыми зубьями появляются дополнительные осевые нагрузки на подшипники валов, а диаметры колес имеют больший размер, чем прямозубые при том же числе зубьев и модуле. Косозубые колеса менее технологичны в изготовлении, особенно колеса с внутренними зубьями.
Подписывайтесь на анонсы статей в окнах, расположенных в конце каждой статьи или вверху каждой страницы.
Не забывайте подтверждать подписку кликом по ссылке в письме, которое тут же придет к вам на указанную почту (может прийти в папку «Спам»)!!!
Уважаемые читатели! Ваш опыт и мнение, «оставленные» ниже в комментариях к статье, будут интересны и полезны коллегам и автору!!!
Прошу уважающих труд автора скачивать файл после подписки на анонсы статей!
Ссылка на скачивание файла: modul-zubchatogo-kolesa (xls 41,0KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
al-vo.ru
ГОСТ 9563-60 (СТ СЭВ 310-76) Основные нормы взаимозаменяемости. Колеса зубчатые. Модули (с Изменениями N 1, 2), ГОСТ от 30 мая 1988 года №9563-60
ГОСТ 9563-60
(CT СЭВ 310-76)
Группа Г15
Дата введения 1962-07-01
1. РАЗРАБОТАН Государственным комитетом СССР по стандартам
РАЗРАБОТЧИКИ
Н.М.Шоломов, канд. техн. наук (руководитель темы), Э.В.Бабенкова, канд. техн. наук
2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного Комитета СССР по стандартам от 30.05.88 N 1547
3. Срок проверки 1998 год, периодичность проверки – 10 лет
4. ВЗАМЕН ОСТ 1597
5. Стандарт полностью соответствует СТ СЭВ 310-76.
6. Стандарт соответствует стандартам: ИСО 54-77, ИСО 678-76
7. ПЕРЕИЗДАНИЕ (март 1994 г.) с Изменениями N 1, 2, утвержденными в июне 1979 г., мае 1988 г. (ИУС 8-79, 9-88)
1. Настоящий стандарт распространяется на эвольвентные цилиндрические зубчатые колеса и конические зубчатые колеса с прямыми зубьями и устанавливает:
для цилиндрических колес – значения нормальных модулей;
для конических колес – значения внешних окружных делительных модулей.
2. Числовые значения модулей должны соответствовать указанным в таблице.
1, 2. (Измененная редакция, Изм. N 1).
3-6. (Исключены, Изм. N 1).
мм | |
1 ряд | 2 ряд |
0,05 | |
0,055 | |
0,06 | |
0,07 | |
0,08 | |
0,09 | |
0,1 | |
0,11 | |
0,12 | |
0,14 | |
0,15 | |
0,18 | |
0,2 | |
0,22 | |
0,25 | |
0,28 | |
0,3 | |
0,35 | |
0,4 | |
0,45 | |
0,5 | |
0,55 | |
0,6 | |
0,7 | |
0,8 | |
0,9 | |
1 | |
1,125 | |
1,25 | |
1,375 | |
1,5 | |
1,75 | |
2 | |
2,25 | |
2,5 | |
2,75 | |
3 | |
3,5 | |
4 | |
4,5 | |
5 | |
5,5 | |
6 | |
7 | |
8 | |
9 | |
10 | |
11 | |
12 | |
14 | |
16 | |
18 | |
20 | |
22 | |
25 | |
28 | |
32 | |
36 | |
40 | |
45 | |
50 | |
55 | |
60 | |
70 | |
80 | |
90 | |
100 | |
Примечания:
1. При выборе модулей ряд 1 следует предпочитать ряду 2.
2. Для цилиндрических зубчатых колес допускается:
а) в тракторной промышленности применение модулей 3,75; 4,25, 6,5 мм;
б) в автомобильной промышленности применение модулей, отличающихся от установленных в настоящем стандарте;
в) в редукторостроении применение модулей 1,6; 3,15, 6,3; 12,5.
3. Для конических зубчатых колес допускается:
а) определять модуль на среднем конусном расстоянии;
б) в технически обоснованных случаях применение модулей, отличающихся от указанных в таблице.
(Измененная редакция, Изм. N 2).
ПРИЛОЖЕНИЕ (Исключено, Изм. N 2).
Текст документа сверен по:
официальное издание
М.: Издательство стандартов, 1994
docs.cntd.ru
Модуль зацепления зубчатой передачи по гост. Основные параметры зубчатого колеса
При конструировании зубчатого колеса учитывают материал, из которого оно будет изготовлено, требуемый диаметр и способ получения заготовки.
Стальные зубчатые колеса
Зубчатые колеса диаметром до 150 мм в единичном и мелкосерийном производстве обычно изготовляют из круглого проката; в средне-, крупносерийном и массовом производстве предпочтительнее применять кованые или штампованные заготовки, имеющие более высокие механические характеристики.
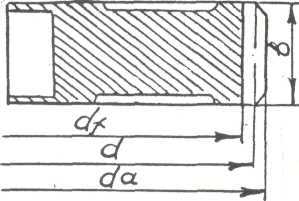
Шестерни изготовляют за одно целое с валом (вал-шестерня) (рис. 1, а, б) или делают съемными, если расстояние χ от впадины зуба до шпоночного паза (рис. 2) больше 2,5 m n для цилиндрических шестерен и 1,8 m e для конических. В случае цельной конструкции увеличивается жесткость вала и уменьшается общая стоимость вала и шестерни. Разъемная конструкция позволяет выполнить шестерню и вал из разных материалов, а при поломке одной детали вторую оставить без замены. На рис. 1, а показана конструкция вала-шестерни, когда диаметр впадин зубьев d f1 превышает диаметр вала d б.п. (диаметр буртика подшипника), что обеспечивает свободный выход инструмента при нарезании зубьев. При d f1 (рис. 1, б) выход фрезы l вых определяют прочерчиванием по ее наружному диаметру D ф , который принимают по табл. 1 в зависимости от m n и степени точности передачи.
Цилиндрические зубчатые колеса диаметром до 400… 500 мм (в отдельных случаях до 600 мм) можно выполнять коваными , штампованными, литыми или сварными .
Конструктивные элементы зубчатых колес показаны на рис. 3.
Типовые конструкции зубчатых колес и основные соотношения их элементов даны на рис. 4-8. Кованые заготовки для зубчатых колес применяют при наружном диаметре колеса 4,d f или при нешироких колесах (ψ ba диаметром d a до 400 мм. Операция штамповки отличается высокой производительностью и максимально приближает форму заготовки к форме готового колеса. Для облегчения заполнения металлом и освобождения от заготовки штамп, а следовательно, и заготовка должны иметь радиусы закруглений r ≥ 5 мм и штамповочные уклоны γ ≥ 5° (рис. 4) . Внутреннюю поверхность обода, наружную поверхность ступицы и поверхности диска штампованных колес обычно не обрабатывают. Конструкция литого колеса дана на рис. 5.
Рис. 1. Конструкция вала – шестерни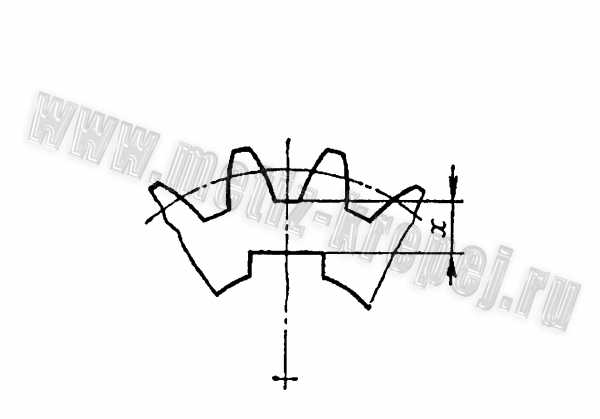 Рис. 2. Элемент шестерни при шпоночном соединении
Рис. 2. Элемент шестерни при шпоночном соединении
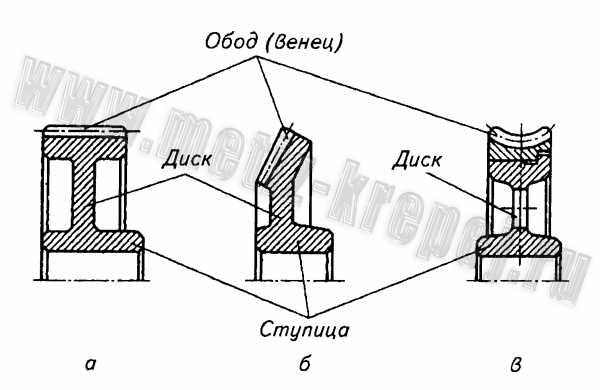 Рис. 3. Конструктивные элементы колес:
Рис. 3. Конструктивные элементы колес:
a – цилиндрического; б – конического; в – червячного
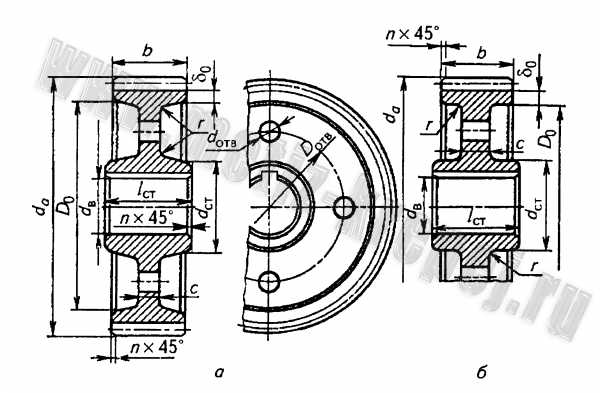 Рис. 4. Цилиндрические зубчатые колеса при d a ≤ 500мм :
Рис. 4. Цилиндрические зубчатые колеса при d a ≤ 500мм :
а -штампованное; б- кованое; d ст = 1,6d в ; l ст ≥ b при соблюдении условия
l ст = (0,8…1,5)d в ; δ o = 2,5m n +2 , но не менее 8…10 мм; n = 0,5m n для обода, n для ступицы в зависимости от диаметра d в ; D отв = 0,5(D o +d ст) ; d отв = 15…25 мм ; c = (0,2…0,3)b для штампованных и c = (0,2…0,3)b для кованых колес
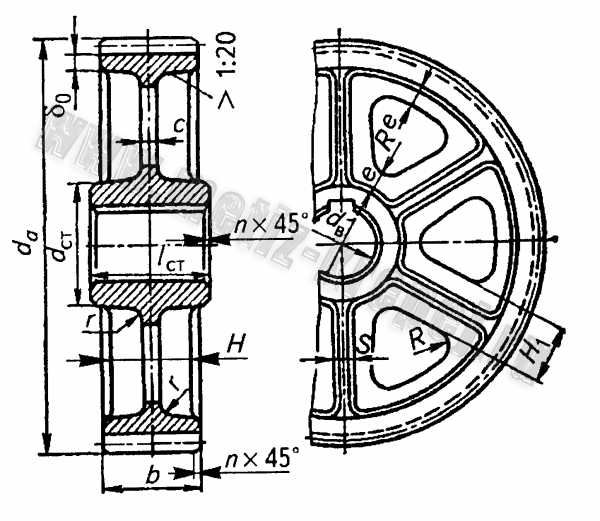 Рис. 5. Литое цилиндрическое зубчатое колесо при d a = 400…1000 мм : b ≤ 200 мм d ст = 1,6d в – для стального литья; d ст = 1,8d в для чугунного литья; l ст ≥ b
Рис. 5. Литое цилиндрическое зубчатое колесо при d a = 400…1000 мм : b ≤ 200 мм d ст = 1,6d в – для стального литья; d ст = 1,8d в для чугунного литья; l ст ≥ b
при соблюдении условия l ст = (0,8…1,5)d в ; δ o = 2,5m n + 2 ≥ 8 мм ;
n = 0,5m n для обода n для ступицы; c = H/5 , но не менее 10 мм;
S = H/5 , но не менее 10 мм; e = 0,8δ o ; H= 0,8d в ; H 1 = 0,8H ; R – вписанная дуга окружности
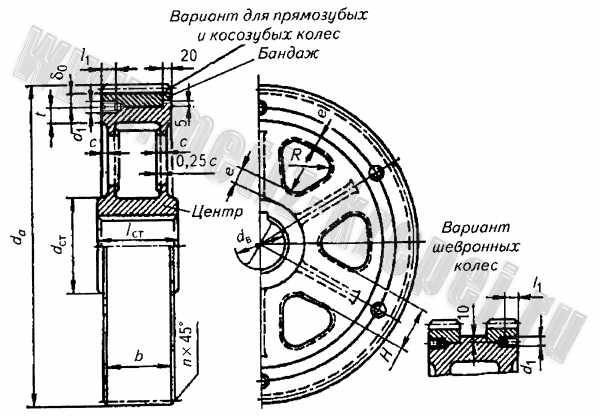 Рис. 6. Бандажированное зубчатое колесо при d в свыше 600 мм: d ст = 1,6d в – для стального литья; d ст = 1,8d в – для чугунного;l ст ≥ b
Рис. 6. Бандажированное зубчатое колесо при d в свыше 600 мм: d ст = 1,6d в – для стального литья; d ст = 1,8d в – для чугунного;l ст ≥ b
при соблюдении условия l ст = (0,8…1,5)d в ; c = 0,15b ; δ o = 4m n , но не менее 15 мм; t = δ o ; e = 0,8δ o ; d 1 = (0,05…0,1)d в ; l 1 = 3d 1 ;b ≥ 300 мм
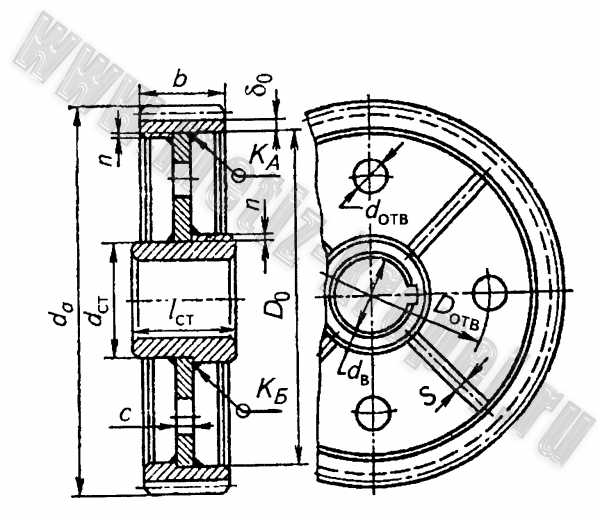 Рис. 7. Сварное зубчатое колесо:
Рис. 7. Сварное зубчатое колесо:
l ст = (0,8…1,5)d в ≥ b ; d ст = 1,6d в ; δ o = 2,5m n , но не менее 8 мм;s = 0,8c ; D отв = 0,5 (D o + d ст) ; d отв = 15…20 мм . Катеты швов: K a = 0,5d в ; K ь = 0,1d в но не менее 4 мм. Ребра приваривают швом K б
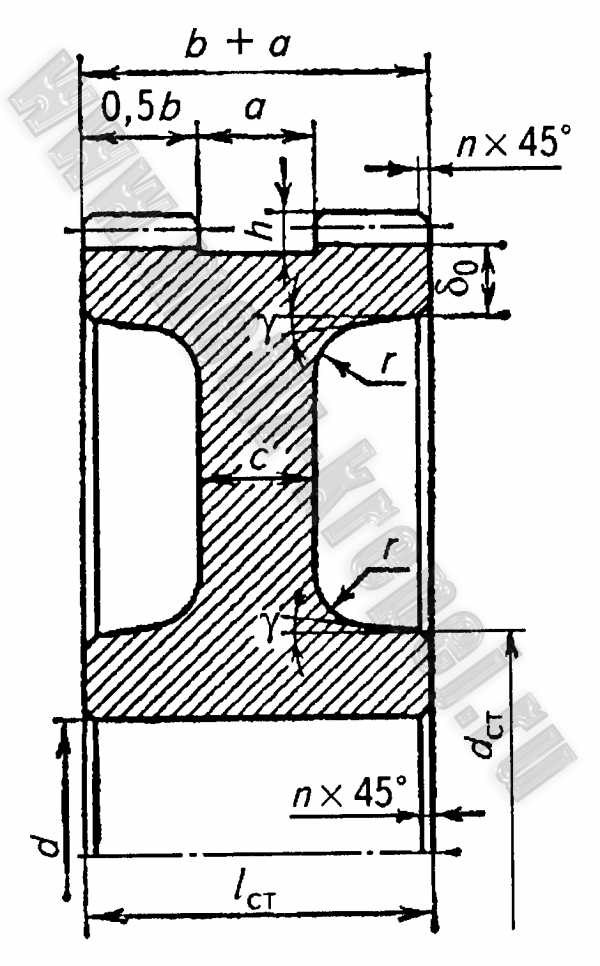 Рис. 8. Шевронное зубчатое колесо с канавкой посередине:
Рис. 8. Шевронное зубчатое колесо с канавкой посередине:
l ст = b + a ; c = (0,3…0,35)(b + a) ; δ o = 4m n + 2 ; h = 2,5m n ; a – в зависимости от модуля. Остальные размеры см. рис. 4, 5
Размеры ступицы выбирают по рекомендациям, приведенным под рисунками. Длину ступицы l ст по возможности принимают равной ширине венца колеса b , что обеспечивает наименьшую ширину редуктора. Отношение длины ступицы к диаметру вала должно быть не меньше 0,5. При отношении меньше 0,8 на валу предусматривают буртик, исключающий торцевое биение колеса, к которому будет прижиматься торец ступицы колеса. Если по условиям расчета (см. расчет шпоночного и шлицевого соединений) l ст > b , то ступицу желательно сместить по оси колеса до совпадения одного ее торца с торцом венца (см. рис. 3, а), что дает возможность нарезать зубья сразу на двух колесах. Реже (для одноступенчатых редукторов) колеса изготовляют со ступицей, выступающей в обе сторо
sportbu.ru
Модуль зубьев по гост 9563-80
Ряды | Модуль, мм |
1-й | 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12 |
2-й | 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 |
Примечание. При назначении модулей 1-й ряд следует предпочитать 2-му. | |
Значение модулей m< 2 мм в приводе главного движения использовать не рекомендуется из-за возможности большого понижения несущей способности в результате износа, повышенного влияния неоднородности материала, опасности разрушения при перегрузках.
Основные геометрические соотношения для некорригированных передач внешнего зацепления приведены в табл. 2.31.
Таблица 2.31
Геометрические параметры цилиндрических передач внешнего зацепления без смещения, мм
Шаг зубьев, мм | p = πm |
Диаметр делительной окружности, мм | d = mz/cosβ |
Диаметр окружности вершин, мм | da = d + 2m |
Диаметр окружности впадин, мм | df = d – 2,5m |
Межосевое расстояние, мм | a = m(z1 + z2)/(2cosβ) |
Передаточное число | u = z2/z1 |
Коэффициент торцового перекрытия | εα = [1,88 – 3,2(1/z1 + 1/z2)]cosβ |
Коэффициент осевого перекрытия | εβ = bsinβ/(πm) |
Примечание. Передаточное числоuпо ГОСТ 16532-70 определяется как отношение большего числа зубьев к меньшему независимо от того, как передается вращение: отz1кz2или отz2кz1. | |
Ширина зубчатых колес выбирается в соответствии с установленными эмпирическими соотношениями. В приводах главного движения для уменьшения концентрации нагрузки при высокой твердости зубьев и высоких окружных скоростях рекомендуется применять относительно неширокие колеса и придавать зубьям бочкообразную форму. Для прямозубых колес ширина зубчатого венца b= (6…10)m, для косозубых колес –b= (8…16)m. Коэффициент ширины колес ψba=b2/aрекомендуется принимать равным 0,1 – 0,2. Численные значения ψbaрегламентированы ГОСТом: 0,100; 0,125; 0,160; 0,200; 0,250 и т.д.
Учитывая возможное осевое смещение зубчатых колес при сборке передачи, ширину венца шестерни принимают на несколько миллиметров большей, чем ширину венца колеса:
b1= 1,12b2.
Межосевое расстояние aпо возможности рекомендуется округлять по рядуRa40:…80; 85; 90; 95; 100; 105; 110; 120; 125; 130, далее через 10 до 260 и через 20 до 420.
Минимальное число зубьев у меньшего зубчатого колеса обычно ограничивается условием неподрезания зубьев у основания, для некорригированных передач zmin= 17. В станкостроении минимальное число зубьев рекомендуется приниматьzmin= 21…24, а при работе передачи на высоких оборотах для уменьшения шума целесообразно братьzmin ≥ 25. Общие рекомендации по выбору числа зубьев шестерни некорригированной передачи представлены в табл.2.32.
Таблица 2.32
Число зубьев шестерни
Угол наклона линии зуба, β | Число зубьев шестерни |
β = 0º | z1 ≥ 21 |
0º < β ≤ 12º | z1 ≥ 19 |
12º < β ≤ 17º | z1 ≥ 18 |
17º < β ≤ 21º | z1 ≥ 17 |
Примечание. Ограничение по условию неподрезания для косозубых колес. | |
В коробках скоростей металлорежущих станков числа зубьев колес подвижных зубчатых блоков выбираются по кинематическим условиям. По графику частот вращения для каждой передачи находят передаточное отношение и по табл. П22, исходя из условия равенства суммы зубьев Σzведущего и ведомого колес каждой группы передач при одинаковом модуле (сумма зубьев всех колес, находящихся между соседними валами, должна быть одинаковой) и в зависимости от передаточного числаu, определяются числа зубьев. В таблице приведены числа зубьев меньшего колеса передачи.
Таблица 2.33
studfiles.net
Методическое пособие по самостоятельному выполнению студентами расчетно-графических работ, страница 16
Так как мы нашли все составляющие формулы межосевого расстояния то определяем
Вычисленное межосевое расстояние мм округляем в большую сторону до стандартного (согласно стандартного ряда см. стр. 33 [1]). мм.
Стандартный ряд межосевых расстояний :
Расчётные значения для нестандартных редукторов округляют в большую сторону по ряду Ra 40: … 80, 85, 90, 100, 105, 110, 120, 125, 130, дальше через 10 до 250 и через 20 до 420 ., мм
7.1.2 Определяем предварительно модуль зубчатой передачи, мм:
Модуль передачи
значение модуля передачи округляют в большую сторону до стандартного значения из ряда чисел (предпочтительно из первого ряда см. стр. 33 [1])
Стандартный ряд модулей:
ряд 1 – 1, 1,5 2,5 3 4 5 6 8 10 12 16 20
ряд 2 – 1,25 1,375 1,75 2,25 2,75 3,5 4,5 5,5 7 9 11 (СТ СЭВ 310-76)
Принимаем модуль
7.1.3 Определяем суммарное число зубьев:
, где – минимальный угол наклона зубьев (косозубых колес), для прямозубых колес . Тогда суммарное количество зубьев прямозубой зубчатой пары
т.е. .
7.1.4 Определяем число зубьев шестерни и колеса.
, где – для прямозубой шестерни, тогда
,
Возьмем в первом приближении число зубьев прямозубой шестерни на тихоходном валу .
Число зубьев прямозубого колеса на промежуточном валу зубч. пары №3 ,
Находим в первом приближении число зубьев колеса ,
7.1.5 Определяем фактическое передаточное число и его отклонение от заданного
, для отклонение передаточного числа равно:
Так как 5,3%>2,5% рекомендуемого максимума отклонений для и 4% для , то в формуле определения количества зубьев в шестерне округлим дробное число зубьев 21,8 до 21. То есть, принимаем число зубьев прямозубой шестерни на тихоходном валу . Тогда число зубьев колеса ,
Опять выполним проверку :
,
0,26%<2,5% рекомендуемого максимума отклонений для
Поэтому окончательно принимаем и .
 7.1.6 Определяем основные геометрические параметры
передачи (прямозубой зубчатой пары шестерня – колесо №3), мм:
7.1.6 Определяем основные геометрические параметры
передачи (прямозубой зубчатой пары шестерня – колесо №3), мм:
– делительный диаметр шестерни
– делительный диаметр колеса
проверим этот диаметр по формуле (стр. 33 [1])
– диаметр впадин зубьев шестерни
– диаметр впадин зубьев колеса
– диаметр вершин зубьев шестерни
– диаметр вершин зубьев колеса
– ширина венца зуба колеса
– ширина венца зуба шестерни (стр. 33 [1])
7.1.7. Определение сил в зубчатом зацеплении (пара зубьев №3 на рис. 2.18)
– определяем окружную силу на колесе
– определяем радиальную силу
где угол профиля зуба.
7.1.8 Проверка зубьев колеса по контактным напряжениям (прямозубая зубч. пара №3)
расчетное контактное напряжение в зубьях колеса:
, где
– вспомогательный коэффициент, для прямозубых передач .
– коэффициент, учитывающий распределение нагрузки между зубьями в прямозубой паре (стр. 37 [1]). (для косозубой пары ).
– коэффициент динамической нагрузки, который принимают:
– для прямозубых колес: при твердости НВ < 350
НВ > 350
– для косозубых и шевронных колёс:
при твердости НВ <350
НВ > 350
Примечание: данные взяты из „Розрахунок і проектування приводів суднових механізмів” ВВ Алексієнко …., Миколаїв 2008р.
Окончательно принимаем – коэффициент динамической нагрузки для прямозубых колёс с НВ < 350 для материала шестерни и колеса.
– коэффициент концентрации нагрузки, см. таблицу 11 в п. 7.1.1 настоящего пособия.
мм – делительный диаметр прямозубой шестерни.
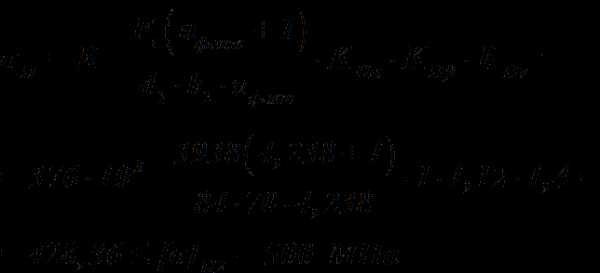
Неравенство выполняется , расчет правильный.
7.1.9 Проверка зубьев колеса по напряжениям изгиба (прямозубая цилиндрическая зубчатая пара №3)
Расчетное напряжение изгиба в зубьях колеса
, где
– коэффициент, учитывающий распределение нагрузки между зубьями (стр. 36 [1]).
Допустимые значения окружных скоростей для передач разной степени точности.
Таблица 12.
Степень точности | Допустимая окружная скорость V, м/с | |||
Прямозубые | Косозубые | |||
цилиндрические | конические | цилиндрические | конические | |
6 | До 15 | До 12 | До 30 | До 20 |
7 | До 10 | До 8 | До 15 | До 10 |
8 | До 6 | До 4 | До 10 | До 7 |
9 | До 2 | До 1,5 | До 4 | До 3 |
Выбор коэффициента Таблица 13
Размещение колёс относительно опор | Коэффициент | |||||
Твёрдость зубъев, НВ | Коэффициент | |||||
0,2 | 0,4 | 0,6 | 0,8 | 1,2 | ||
Косольне, опоры – шарикоподшипники | <350 | 1,16 | 1,37 | 1,64 | – | – |
≥350 | 1,33 | 1,7 | – | – | – | |
Косольное, опоры – роликоподшипники | <350 | 1,1 | 1,22 | 1,38 | 1,57 | – |
≥350 | 1,2 | 1,44 | 1,71 | – | – | |
Симметричное | <350 | 1,01 | 1,03 | 1,05 | 1,07 | 1,14 |
≥350 | 1,02 | 1,04 | 1,08 | 1,14 | 1,3 | |
Несимметричное | <350 | 1,05 | 1,1 | 1,17 | 1,25 | 1,42 |
≥350 | 1,09 | 1,18 | 1,3 | 1,43 | 1,73 | |
vunivere.ru
Зубчатые Модули — Ряды стандартные
Зубчатые колеса мелкомодульные — Зубья — Контуры исходные 772 — Контроль — Приборы 902—904 — Модули — Ряды стандартные 773 [c.981]Выбор передачи. Передачу выбирают исходя из кинематической схемы механизма. Рхли в схеме имеется открытая зубчатая ступень или ее необходимость вызвана большим передаточным числом механизма, то вначале надо определить основные параметры открытой зубчатой ступени передаточное число и , модуль зубьев т, числа зубьев шестерни и колеса и и межосевое расстояние а ,. Передаточное число и следует назначать из ряда стандартных передаточных чисел (ГОСТ 2185-66) 2,0 (2,24) 2,5 (2,8) 3,15 (3,55) 4.0 [c.43]
В зависимости от вида обработки нарезаемых зубчатых колес на этих станках применяются прямозубые гребенки черновые (обдирочные), чистовые и под шлифовку. По своему назначению перечисленные типы гребенок и ряд стандартных модулей аналогичны применяемым на вертикальных станках. [c.211]
По расчетным значениям d i и т подбирают числа зубьев колес с помощью ЭВМ 141, таблиц 14, 161 или вручную 1101. При подборе чисел зубьев и модуля из стандартного ряда предпочтительны те комбинации, при которых удается получить диаметры зубчатых колес, мало отличающиеся от расчетных. [c.202]
Такие узлы и детали машины обеспечивают значительное снижение трудоемкости в результате возможности применения поточных методов работы, высокопроизводительного оборудования и оснастки. Наряду с этим в результате применения указанных узлов и деталей обеспечивается ряд эксплуатационных преимуществ снижается- трудоемкость эксплуатационных ремонтов, сокращается номенклатура запасных частей, появляется возмож. ность использовать одни и те же узлы и детали для разных типоразмеров машин. Например, для специальных агрегатных станков и автоматических линий применяют одни и те же стандартные силовые сверлильные головки нескольких типоразмеров для станков различных типов — одни и те же гидронасосы, панели гидроуправления, приборы электрического управления. Для различных типов и размеров станков нередко применяют общие детали управления, подшипники, сальники уплотнения, детали коробок скоростей и подач, крепежные детали и т. д. Помимо унифицированных деталей, в конструкции каждой машины есть значительное количество оригинальных деталей, которые, различаясь по форме, могут иметь отдельные обрабатываемые поверхности, аналогичные с поверхностями других деталей этой машины. Суммарное количество диаметров отверстий и валов, шпоночных и шлицевых соединений, резьб, модулей зубчатых [c.120]
На рис. 3. 6 показана схема нарезания зубьев методом обкатки с помощью гребенки. Модуль для гребенки берется по стандарту. Поэтому для делительной окружности нарезаемого зубчатого колеса он тоже будет стандартным. Заготовка I вращается с угловой скоростью ш и движется поступательно со скоростью у = ш. Гребенка П совершает движение в направлении, перпендикулярном плоскости заготовки (плоскости чертежа), производя нарезание зубьев на заготовке. Профиль зубьев на колесе получается как огибающая к ряду последовательных положений зубьев гребенки на заготовке. Для того чтобы нарезать нулевое колесо, необходимо гребенку установить так, чтобы модульная прямая ее была удалена от центра заготовки на расстоянии радиуса делительной окружности Гд, т. е. чтобы делительная окружность заготовки обкатывалась без скольжения по модульной прямой. Тогда на нарезаемом колесе получатся зубья, толщина которых по делительной окружности будет равна ширине впадины. [c.24]
В ПО были даны формулы для определения основных размеров зубчатых колес при условии, что стандартный модуль соответствует их начальным окружностям, совпадающим с делительными окружностями. Однако это условие накладывает и целый ряд стеснений, затрудняющих конструирование зубчатых передач. Например, это относится к выбору числа зубьев на колесе. Уменьшение числа зубьев, как указывалось, удешевляет производство зубчатых колес, уменьшает размеры конструкции и т. д. Но уменьшение числа зубьев может вызвать их подрез, увеличение износа контактных поверхностей и т. д. поэтому в тех случаях, когда необходимо по каким-либо причинам все же иметь малое число зубьев, проектируют зубчатые колеса с иными размерами. [c.611]
Применение предпочтительных чисел в машиностроении в ряде случаев осложняется тем, что некоторые стандарты параметров имеют ряды, построенные не по законам геомет- рической прогрессии, например модули зубчатых колес. Но и здесь можно из стандартного ряда выбрать те модули, числовые значения которых являются предпочтительными числами по ГОСТ 8032—56. Для наиболее часто применяющихся колес с модулями от 1 до 32 мм целесообразно предпочесть следующие модули 1 1,25 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0 5,5 6,0 7,0 8,0 9,0 10 11 12 14 16 18 20 22 25 28 и 32, образующие составной ряд предпочтительных чисел с округлениями. [c.91]
Внешний окружной модуль обычно выбирают из стандартного ряда (см. табл. 3.1). Округление внешнего модуля до стандартного значения не является обязательным требованием. Этот модуль называют производственным и по его величине определяют все геометрические параметры зубчатых колес (задают размеры зубьев на внешнем торце, на котором удобно производить измерения). [c.122]
Стандартные значения модулей по ГОСТ 9563—60 (первый ряд) следующие 3 4 5 6 8 10 12 16 20 25 32 40 50 60 80 100. В табл. 111-76 даны формулы для определения геометрических размеров цилиндрических зубчатых передач. [c.168]
Стандарты в приборо- и машиностроении охватывают а) общие вопросы ряды чисел линейных размеров, конусности, числа оборотов в минуту, стандартные обозначения и оформления чертежей и схем и т. д. б) материалы, их химический состав, сортамент, механические свойства и термическую обработку в) точность размеров (допуски и посадки) и качество поверхностей деталей г) формы и размеры деталей массового применения крепежные детали, подшипники качения, ремни, цепи, канаты, муфты, смазочные устройства, радиодетали и т. д. д) конструктивные элементы деталей механизмов модули зубчатых колес, резьбы, шпоночные и шлицевые соединения и т. д. е) ряды основных параметров приборов и машин и качественные показатели их. [c.188]
В первой части таблицы указывают модуль т стандартного ряда число зубьев z (для зубчатого сектора—число зубьев секторного колеса) угол наклона р линии зуба косозубых и шевронных колес направление линии косого зуба (надписью Правое или Левое, для шевронных колес — надписью Шевронное) нормальный исходный контур (стандартный — указанием соответствующего стандарта, нестандартный — указанием группы параметров, включающих угол профиля а, коэффициент высоты головки А , коэффициент толщины зуба и др.). Если исходный контур не полностью определен перечисленными параметрами, то на чертеже должно быть приведено его изображение с необходимыми размерами. В этой части таблицы приводят также коэффициент смещения с соответствующим знаком и степень точности по нормам бокового зазора. [c.309]
Исходные положения. При проектировании зубчатых передач необходимо следовать указаниям действующих нормативных документов. Для цилиндрических эвольвентных колес нормальный модуль т , а для шевронных также и торцовый модуль должны быть выбраны из рядов стандартных модулей. При этом для шевронных колес угол должен иметь значение = ar os “. [c.264]
Для ограничения числа зубонарезного инструмента, необходимого для изготовления зубчатых колес, модули стандартизованы и их рассчитанные значения необходимо округлять до значений, установленных ГОСТ 9563—60 (СТ СЭВ 310—76). Имеется два ряда стандартных модулей [c.82]
В 97 были даны формулы для определения основных размеров зубчатых колес при условии, что стандартный модуль соответствует их начальным окружностям, совпадающим с делительными окружностями. Одиако это условие накладывает и целый ряд ограничений, затрудняющих конструирование зубчатых передач. Например, это относится к выбору числа зубьев на колесе. Умень-П1ение числа зубьев, как уже указывалось, удешевляет производство зубчатых колес, уменьшает размеры конструкции и т. д. Но уменьшение числа зубьев может вызвать их подрез, увеличение износа контактных поверхностей и т. д. поэтому в тех случаях, когда необходимо по каким-либо причинам все же иметь малое число зубьев, проектируют зубчатые колеса с иными размерами. Основной целью, которая при этом преследуется, является улучшение условий работы зубчатых колес за счет отклонения размеров этих колес от указанных в 97. [c.455]
Дискретизирующие ограничения налагаются на значения параметров в связи с их физической сущностью либо в связи с требованиями ГОСТ. Так, параметр число зубьев зубчатой передачи принимает только целые положительные значения, а параметр модуль зубьев — только значения из стандартного ряда модулей. Эти ограничения именэт вид [c.318]
Модули регламентированы стандартом SN 01 4608 (в СССР ГОСТ 9563-60) для цилиндрических, конических и червячных колес. Для конических колес стандартный юдyль относится к большему диа1метру зубчатого венца. В табл. 4 приведен ряд модулей по указанному чехословацкому стандарту, а таклсе основные размеры зубьев, т. е. шаг, толщина некорригированного зуба и высота зуба. Ряд модулей по ГСЮТу 9563-60 приведен в табл. 4а. [c.288]
Стандартные дисковые зуборезные фрезы нормального ряда. Для каждого модуля и профильного угла, а также для каждого числа зубьев колеса теоретически необходимо иметь специальную дисковую фрезу, что экономически нецелесообразно. Поэтому специальные дисковые фрезы для нарезания определенного колеса применяют а) для изготовления зубчатых колес с числом зубьев, меньшим 12 б) для зубчатых колес с циклоидальным профилем зуба. В остальных случаях применяют комплекты, состоящие из 8, 15 или 26 шт. Каждая фреза комплекта предназначена для нарезания колес с числами зубьев в определенных границах. Наибольшее распространение получили комплекты, состоящле из 8 и 15 фрез (табл. 13). [c.725]
Примечание. Во многих случаях при подборе чисел зубьев и модуля из стандартного ряда не удается получить диаметры зубчатых колес, мало отличающимися от расчетного. При этом, если величина остается неизменно , имеет место неоправданное завыше- [c.112]
mash-xxl.info

