Высота зуба зубчатого колеса формула – .

alexxlab | 12.06.2019 | 0 | Вопросы и ответы

Примерный расчет элементов зубчатого колеса

Длина всякой окружности равна _ΠD; следовательно, длина начальной окружности зубчатого колеса будет выражена формулой _Πd,. Шагом t зацепления называется длина дуги начальной окружности между обращенными в одну сторону (левыми или правыми) профилями двух смежных зубьев см 517, б.

Если размер этой дуги взять столько раз, сколько имеется зубьев у колеса, т. е. z раз, то также получим длину начальной окружности; следовательно,

_Πd = tz
отсюда
d = (t / _Π) z

Отношение шага t зацепления к числу Π называется модулем зацепления, который обозначают буквой m, т. е.

t / Π = m

Модуль выражается в миллиметрах. Подставив это обозначение в формулу для d, получим.

d = mz
откуда
m = d / z

Следовательно, модуль можно назвать длиной, приходящейся по диаметру начальной окружности на один зуб колеса. Диаметр выступов равен диаметру начальной окружности плюс две высоты головки зуба (фиг. 517, б) т.е.

D_e = d + 2h’

Высоту h’ головки зуба принимают равной модулю, т. е. h’ = m.
Выразим через модуль правую часть формулы:

D_e = mz + 2m = m (z + 2)
следовательно
m = D_e : (z +2)

Из фиг. 517,б видно также, что диаметр окружности впадин равен диаметру начальной окружности минус две высоты ножки зуба, т. е.

D_i = d – 2h”

Высоту h” ножки зуба для цилиндрических зубчатых колес принимают равной 1,25 модуля: h’ = 1,25m. Выразив через модуль правую часть формулы для D_i получим

D_i = mz – 2 × 1,25m = mz – 2,5m
или
Di = m (z – 2,5m)

Вся высота зуба h = h’ + h” т.е

h = 1m + 1,25m = 2,25m

Следовательно, высота головки зуба относится к высоте ножки зуба как 1 : 1,25 или как 4 : 5.

Толщину зуба s для необработанных литых зубьев принимают приблизительно равной 1,53m, а для обработанных на станках зубьев (например, фрезерованных) – равной приблизительно половине шага t зацепления, т. е. 1,57m. Зная, что шаг t зацепления равен толщине s зуба плюс ширина sв впадины (t  =  s  +  s_в) (Величину шага t определяем по формуле t/_{Π =} m или t = Πm ), заключаем, что ширина впадины для колес с литыми необработанными зубьями.

s_в = 3,14m – 1,53m = 1,61m
A для колес с обработанными зубьями.
s_в = 3,14m – 1,57m = 1,57m

Конструктивное оформление остальной части колеса зависит от усилий, которые испытывает колесо во время работы, от формы деталей, соприкасающихся с данным колесом, и др. Подробные расчеты размеров всех элементов зубчатого колеса даются в курсе «Детали машин». Для выполнения графического изображения зубчатых колес можно принять следующие приблизительные соотношения между их элементами:

Толщина обода e = t/2
Диаметр отверстия для вала D_в ≈ ¹/_в D_e
Диаметр ступицы D_cm = 2D_в
Длина зуба (т. е. толщина зубчатого венца колеса) b = (2 ÷ 3) t
Толщина диска К = 1/3b
Длина ступицы L = 1,5D_в : 2,5D_в

Размеры t₁и b шпоночного паза берутся из таблицы №26. После определения числовых величин модуля зацепления и диаметра отверстия для вала необходимо полученные размеры согласовать с ГОСТ 9563-60 (см таблицу №42) на модули и на нормальные линейные размеры по ГОСТ 6636-60 (таблица №43).

Модули (согласно ГОСТ 9563-60) Таблица №42.

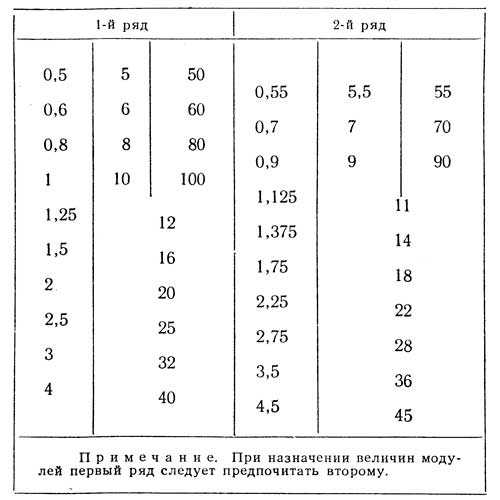
Нормальные линейные размеры.  Таблица №43.

(Выдержка из ГОСТ 6636-60)

Если они отличаются от табличных значений, надо взять ближайшие большие табличные значения и пересчитать все величины, зависящие от вновь выбранного модуля или диаметра отверстия.



www.viktoriastar.ru

Как найти делительный диаметр зубчатого колеса. Примерный расчет элементов зубчатого колеса

ООО «РемМехСервис» производит проектирование цилиндрических и конических зубчатых колес. Одним из основных геометрических и линейных параметров, необходимых для расчета деталей передачи, является модуль зуба шестерни . Эта величина необходима для точного вычисления размеров зубцов. Она одинакова для обоих колес передачи и определяется по формуле:

m=d/z ,

где d – диаметр делительной окружности, по которой при нарезании зубцов обкатывается инструмент; z – количество зубцов.

Модуль зуба шестерни измеряется в миллиметрах и является стандартизированной характеристикой. Его величина составляет от 0,5 до 50 мм. В зависимости от значения модуля зуба шестерни подбираются:

• высота ножки зуба,
• высота головки зуба,
• общая высота и длина зуба,
• диаметры вершин и впадин,
• окружная толщина зуба и впадин.

По международным стандартам допускается применять несколько способов расчета зубчатых передач:

• экспериментально-исследовательский,
• экспериментально-теоретический,
• приближенный,
• упрощенный.

Экспериментально-исследовательский метод очень дорог, поскольку требует проведения высокоточных измерений, исчерпывающего анализа, проведения эксплуатационных экспериментов. Экспериментально-теоретический способ расчетов подходит для производства крупных партий продукции. Приближенный метод базируется на стандартных характеристиках модуля зуба шестерни и комплексных данных технической литературы. Упрощенный расчет производится по формулам.

На практике при отсутствии дополнительных данных модуль зуба шестерни определяют с помощью величины наружного диаметра и числа зубцов. ООО «РемМехСервис» производит все виды расчетов открытых и закрытых передач. Для консультации и заказа воспользуйтесь указанным телефоном.

1. Выполнение чертежей цилиндрических зубчатых колес

Основным параметром цилиндрического зубчатого колеса является делительная окружностью. Диаметр делительной окружности обозначается буквой d и называется делительным. (Термины, определения и обозначения цилиндрических зубчатых колес устанавливает ГОСТ 16531-83). По делительной окружности откладывается окружной шаг зубьев, обозначаемыйp и представляющий собой расстояние по дуге делительной окружности между соседними зубьями зубчатого колеса (рис. 1). Отрезки делят делительную окружность на столько частей, сколько зубьев имеет зубчатое колесо. Число зубьев обозначается буквойz . Делительный диаметр для зубчатого колеса всегда один. По делительной окружности измеряют окружную толщину зуба и окружную ширину впадин.

Делительная окружность делит высоту зуба h на две неравные части – головку зуба высотойh a и ножку высотойh f .

Зубчатый венец ограничивается окружностью вершин зубьев диметром d a и окружностью впадин диаметромd f .

Основным расчетным параметром зубчатых колёс является модуль . Через него выражаются все остальные параметры. Для прямозубых цилиндрических зубчатых колёс модульm равен отношению диаметра делительной окружностиd к числу зубьевz или отношение окружного шага к числу.

m = d / z = p /

Иными словами, модуль – это длина дуги делительной окружности, приходящаяся на один зуб колеса. Для унификации зубчатых колес в промышленных масштабах для изготовления зубчатых колес применяют

стандартные значения модулей, которые установлены ГОСТ 9563-60. Некоторые значения стандартного модуля приведены в таблице. Значения из первого ряда предпочитаются второму, второй ряд значений модуля приводится для расширения ассортимента изготавливаемых зубчатых колес и применяется в тех случаях, когда по техническим, конструктивным или иным причинам невозможно изготовить зубчатое колесо со значением модуля из первого ряда.

Модуль зацепления – m, (мм)

Прежде чем выполнить чертеж зубчатого колеса или его твердотельную модель, необходимо выполнить расчеты геометрических параметров и определить размеры всех частей зубчатого колеса. Обычно сначала рассчитывают делительный диаметр и межосевое значение передачи, число зубьев, а затем назначают размеры всех остальных частей, которые уточняются при выполнении проверочных расчетов.

ГОСТ 2.403-75 устанавливает правила выполнения рабочих чертежей зубчатых колес. Как правило, учебные чертежи выполняются с допустимыми упрощениями, относительно рабочих чертежей, разрабатываемых в промышленности. На учебных чертежах не наносятся допуски размеров, требования к прочности и точности и детали и т. д. При выполнении чертежей зубчатых колес также следует руководствоваться требованиями ГОСТ 2. 402

На рис. 2 представлен пример выполнения учебного чертежа зубчатого колеса, выполняемого студентами в процессе изучения дисциплины «Инженерная графика».

В соответствии с этими правилами в правом верхнем углу формата должна выполняться таблица параметров, размеры которой показаны на рисунке. Таблица параметров состоит из трех частей, которые должны быть отделены друг от друга сплошными основными линиями. Первая часть таблицы содержит основные параметры необходимые для изготовления зубчатого венца колеса, вторая – данные для контроля размеров зуба и третья

– справочные данные.

На учебных чертежах обычно размещают некоторые данные из первой и третьей части таблицы.

ВАРИАНТЫ ЗАДАНИЯ по теме «Зубчатые передачи»

варианта

зубьев – z

обода – В

ступицы – l

ступицы-D

отв. – d

veloed.ru

1.2. Элементы зубчатого колеса

Наиболее часто в различных машинах применяют зубчатые колёса среднего диаметра (примерно от 80 до 200 мм). Такие колёса изготавливают дисковыми (рис. 3 а). Колёса большего диаметра делают со спицами (рис. 3 б), а небольшого – сплошным, т.е. без диска и без спиц (рис. 3 в).

а)

б)

в)

Рис. 3. Виды зубчатых колес: а – дисковое зубчатое колесо;

б – зубчатое колесо со спицами; в – сплошное зубчатое колесо

Основными элементами зубчатого колеса (рис. 4) являются зубья, каждый зуб состоит из головки зуба и ножки. Зубья находятся на ободе колеса и вместе с ободом составляют зубчатый венец: более тонкая часть колеса – диск соединяет ступицу с ободом, внутри ступицы делают отверстие для вала с пазом для ш понки. Шлицевое соединение показано на покадровых рис. 25 – 27 или в демоверсии на компакт диске. На рис. 4 показаны условные изображения элементов зубчатого колеса.

Рис. 4. Условные изображения элементов зубчатого колеса: d_f – окружность впадин, проходящая по очертаниям впадин между зубьями: её условно изображают сплошной тонкой линией; d_об – окружность обода, обозначающая внутреннее очертание обода; d_ст – окружность ступицы, обозначающая внешнее очертание ступицы; d_в – диаметр окружности отверстия для вала; h– высота зуба; h_а – высота головки зуба; h_f– высота ножки зуба; d_a – окружность вершин – это самая большая окружность, ограничивающая вершины головок зубьев колес: её условно изображают сплошной основной линией; d – делительная окружность, делящая каждый зуб на две неравные части: меньшую – головку зуба и большую – ножку зуба: её условно изображают штрихпунктирной тонкой линией; P_n – нормальный шаг зубьев – кратчайшее расстояние по делительной или начальной поверхности зубчатого колеса между эквидистантными одноименными теоретическими линиями соседних зубьев; S – толщина зуба; Z – число зубьев; m – нормальный модуль зубьев – это линейная величина в  раз меньшая нормального шага зубьев; b_паза – ширина шпоночного паза; t_j – глубина шпоночного паза.

При выполнении рабочего чертежа зубчатого колеса при заданных исходных данных, согласно табл. 1, необходимо рассчитать элементы зубчатого колеса по формулам, приведенным в табл. 2, 3.

Таблица 1

Исходные данные для расчета

Наименование параметра	Обозначение	Числовые значения
Число зубьев колеса	z	Смотри вариант задания
Модуль	m
Диаметр отверстия колеса	dв

Таблица 2

Расчет основных геометрических параметров

цилиндрической зубчатой передачи

Наименование параметра	Обозначение	Расчётная формула
Межосевое расстояние
Делительный диаметр
Диаметр вершин зубьев
Диаметр впадин зубьев
Радиальный зазор
Высота головки зуба
Высота ножки зуба
Высота зуба
Нормальный шаг

Таблица 3

Конструктивные параметры цилиндрического зубчатого колеса

Наименование параметра	Обозначение	Расчётная формула
Ширина венца зубчатого колеса
Диаметр обода
Толщина обода		– для литых колёс; – для штампованных колёс

Окончание табл. 3

Наименование параметра	Обозначение	Расчётная формула
Толщина диска зубчатого колеса		При мм принимают
Длина ступицы
Наружный диаметр ступицы		– для чугунных колёс; – для стальных колёс
Размер шпоночного паза в ступице колеса		Размеры паза и по ГОСТ 23360-78; ГОСТ 24071-80
Размеры фасок на окружности вершин колеса
Размеры фасок в отверстии ступицы колеса
Неуказанные конусности		1:8
Неуказанные радиусы скругленийпереходов		мм

Примечание. Расчетные конструктивные размеры элементов колеса рекомендуется округлить в соответствии с ГОСТ 6636 – 83. Нормальные линейные размеры.

studfiles.net

2.3. Эвольвентные зубчатые колеса и их параметры

 

Рисунок 3. Параметры эвольвентного зубчатого колеса.

К основным геометрическим параметрам эвольвентного зубчатого колеса относятся: модуль m, шаг p, угол профиля α, число зубьев z и коэффициент относительного смещения x.

Виды модулей: делительный, основной, начальный. 

Для косозубых колес дополнительно различают: нормальный, торцевой и осевой. 

Для ограничения числа модулей ГОСТом установлен стандартный ряд его значений, которые определяются по делительной окружности.

Модуль − это число миллиметров диаметра делительной окружности зубчатого колеса, приходящееся на один зуб.  

m =p /π

Делительная окружность − это теоретическая окружность зубчатого колеса, на которой модуль и шаг принимают стандартные значения 

d = Z · m

Делительная окружность делит зуб на головку и ножку.

Начальная окружность – это теоретическая окружность зубчатого колеса, принадлежащая его начальной поверхности.

 

Головка зуба – это часть зуба, расположенная между делительной ок-ружностью зубчатого колеса и его окружностью вершин.

Ножка зуба – это часть зуба, расположенная между делительной окружностью зубчатого колеса и его окружностью впадин.

Сумма высот головки ha и ножки hf  соответствует высоте зубьев h:

h = ha  + hf

Окружность вершин – это теоретическая окружность зубчатого колеса, соединяющая вершины его зубьев.

 d_a=d+2(h^*_a + x – Δy)m

Окружность впадин – это теоретическая окружность зубчатого колеса, соединяющая все его впадины.

 d_f = d – 2(h^*_a – C^* – x) · m

Согласно ГОСТ 13755-81 α = 20°,   С* = 0,25.

Коэффициент уравнительного смещения Δу:

Окружной шаг, или шаг p − это расстояние по дуге делительной окружности между одноименными точками профилей соседних зубьев.

p = m·π

Угловой шаг − это центральный угол, охватывающий дугу делительной окружности, соответствующий окружному шагу

 

Шаг по основной окружности − это расстояние по дуге основной ок-ружности между одноименными точками профилей соседних зубьев

p_b = p · cos α

Толщина зуба s по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей одного зуба

S = 0,5 · ρ + 2 · х · m · tg α

Ширина впадины e по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей со-седних зубьев

е = p – S

Толщина зуба Sb по основной окружности − это расстояние по дуге основной окружности между разноименными точками профилей одного зуба.

Толщина зуба Sa  по окружности вершин − это расстояние по дуге ок-ружности вершин между разноименными точками профилей одного зуба.

Угол профиля α − это острый угол между касательной t – t к профилю зуба в точке, лежащей на делительной окружности зубчатого колеса и радиус-вектором, проведенным в данную точку из его геометрического центра

 

1.1. Пример расчета прямозубого внешнего эвольвентного зубчатого зацепления.

1.2. Вычерчивание элементов зубчатого зацепления

• < Назад
• Вперёд >

student-com.ru

Окружной шаг зубьев формула. Геометрические параметры зубчатого колеса. Построение эвольвентного зацепления

Профиль боковых сторон зубьев зубчатых колес с эвольвентным зацеплением представляет собой две симметрично расположенные эвольвенты.

Эвольвента – это плоская кривая с переменным радиусом кривизны, образованная некоторой точкой на прямой, обкатывающейся без скольжения по окружности, диаметром (радиусом) d b (r b) называемой основной окружностью.

Основные параметры эвольвентного зацепления. На рис. 1.1 показано зацепление двух зубчатых колес с эвольвентным профилем. Рассмотрим основные параметры зацепления, их определения и стандартные обозначения.

В отличие от принятого ранее, обозначение всех параметров производится строчными, а не заглавными буквами с индексами, указывающими их принадлежность колесу, инструменту, типу окружности и виду сечения.

Стандартом предусмотрены три группы индексов:

первая группа: n, t, x – означает вид сечения, соответственно нормальный, торцовый (окружной), осевой;

вторая группа: a,f,b,w,y- означает, что параметр относится соответственно к окружностям выступов, впадин, основной, начальной и любой концентричной окружности. Для делительной окружности индекс не указывается;

третья группа: 1, 2, 0 – означает, что параметр относится соответственно к шестерне, колесу, зуборезному инструменту.

Порядок использования индексов определяется номером группы, т.е. вначале предпочтение отдается индексам первой группы, затем второй и т.д.

Некоторые индексы разрешается опускать в случаях, исключающих возникновение недоразумений или не имеющих применения по определению. Например, у прямозубых цилиндрических колес не используются индексы первой группы. В ряде случаев некоторые индексы с целью сокращения записи также опускаются.

Рассмотрим зацепление двух прямозубых цилиндрических (рис. 1.1) колес: с меньшим числом зубьев (z 1), называемого шестерней, и с большим числом зубьев (z 2), называемого колесом; соответственно с центрами колес в точках О 1 и О 2 . В процессе обката шестерни с колесом происходит качение без скольжения двух центроид – окружностей, соприкасающихся в полюсе зацепления – Р. Эти окружности называются начальными, а их диаметры (радиусы) обозначаются с индексом w: d wl (r wl), d w2 (r w2). Для некорригированных колес эти окружности совпадают с делительными окружностями, обозначение диаметров (радиусов) которых дается без индексов первой и второй групп, т.е. для шестерни – d 1 (r 1), для колеса – d 2 (r 2).

Рис. 1.1. Эвольвентное зацепление зубчатых колес

Делительная окружность – окружность, на которой шаг между зубьями и угол профиля равны им же на делительной прямой зубчатой рейки, сцепленной с колесом. При этом шаг (Р = π · m) – расстояние между двумя соседними одноименными сторонами профиля. Отсюда диаметр делительной окружности колеса d = P · Z / π = m · Z

Модуль зуба (m = P / π) – величина условная, имеющая размерность в миллиметрах (мм) и используемая как масштаб для выражения многих параметров зубчатых колес. В зарубежной практике в этом качестве используется питч – величина, обратная модулю.

Основная окружность – это окружность, от которой образуется эвольвента. Все параметры, относящиеся к ней, обозначаются с индексом b например, диаметры (радиусы) колес в зацеплении: d b1 (r bl), d b2 (r b).

Касательно к основным окружностям через полюс зацепления Р проходит прямая N-N, а ее участок N 1 -N 2 называется линией зацепления, по которой в процессе обката перемещается точка контакта сопрягаемых профилей колес. N 1 -N 2 называется номинальной (теоретической) линией зацепления, обозначаемой буквой g. Расстояние между точками пересечения ее с окружностями выступов колес называется рабочим участком линии зацепления и обозначается g a .

В процессе обката зубчатых колес точка контакта профилей перемещается в пределах активного (рабочего) участка линии зацепления g a , которая является нормалью к профилям обоих колес в этих точках и одновременно общей касательной к обеим основным окружностям.

Угол между линией зацепления и перпендикуляром к линии, соединяющей центры сопрягаемых колес, называется углом зацепления . У корригированных колес этот угол обозначается α w12 ; для некорригированных колес α w12 = α 0 .

Межцентровое расстояние некорригированных колес

a W12 = r W1 + r W2 = r 1 + r 2 = m ·(Z 1 + Z 2) / 2

Окружности выступов и впадин – окружности, проходящие соответственно через вершины и впадины зубьев колес. Их диаметры (радиусы) обозначаются: d a1 (r a1), d f1 (r f1), d a2 (r a2), d f2 (r f2).

Шаги зубьев колес – P t Р b , Р n , Р х – это расстояния между одноименными сторонами профиля, замеренные:

по дуге делительной окружности в торцовом сечении – окружной (торцевый) шаг P t = d / Z;

по дуге основной окружности – основной шаг P b = d b / Z;

по контактной нормали (линии зацепления) – основной нормальный шаг Р bn ;

по нормали к направлению зубьев и по оси (у винтовых передач) – нормальный шаг Р n и осевой шаг Р х .

Коэффициент перекрытия, ε – отношение активной (рабочей) части линии зацепления к основному нормальному шагу:

Окружная (торцовая) толщина зуба, S t – длина дуги делительной окружности, заключенная между двумя сторонами зуба.

Окружная ширина впадины между зубьями, е – расстояние между разноименными сторонами профиля по дуге делительной окружности.

Высота головки зуба, h a – расстояние между окружностями выступов и делительной:

Высота ножки зуба h f – расстояние между окружностями делительной и впадин:

Высота зуба:

Рабочий участок профиля зуба – геометрическое место точек контакта профилей сопрягаемых колес, определяется как расстояние от вершины зуба до точки начала эвольвенты. Ниже последней следует переходная кривая.

Переходная кривая профиля зуба – часть профиля от начала эвольвенты, т.е. от основной окружности до окружности впадин. При методе копирования соответствует форме головки зуба инструмента, а при методе обкатки образуется вершинной кромкой режущего инструмента и имеет форму удлиненной эвольвенты (для инструментов реечного типа) или эпициклоиды (для инструментов типа колеса).

Рис. 1.2. Зацепление зубчатой рейки с колесом

Понятие об исходном контуре рейки

Как было показано выше, частным случаем эвольвенты при z = (бесконечность) является прямая линия. Это дает основание использовать в эвольвентном зацеплении рейку с прямобочными зубьями. При этом любое зубчатое колесо данного модуля независимо от числа зубьев может быть сцеплено с рейкой того же модуля. Отсюда возникла идея обработки колес методом обкатки. В зацеплении колеса с рейкой (рис. 1.2) радиус начальной окружности последней равен бесконечности, а сама окружность превращается в начальную прямую рейки. Линия зацепления N 1 N 2 Так как профиль зубьев рейки – прямая линия, это в значительной мере упрощает контроль линейных параметров зубьев и угла профиля. С этой целью стандартами установлено понятие исходного контура зубчатой рейки (рис. 1.4, а) проходит через полюс Р касательно к основной окружности колеса и перпендикулярно к боковой стороне профиля зуба рейки. В процессе зацепления начальная окружность колеса обкатывается по начальной прямой рейки, а угол зацепления становится равным углу профиля зуба рейки α .

Так как профиль зубьев рейки – прямая линия, это в значительной мере упрощает контроль линейных параметров зубьев и угла профиля. С этой целью стандартами установлено понятие исходного контура зубчатой рейки (рис. 1.3, а)

В соответствии со стандартами, принятыми в нашей стране для эвольвентного зацепления, исходный контур имеет следующие параметры зубьев в зависимости от модуля:

угол профиля α = 20°;

коэффициент высоты головки h * a = 1;

коэффициент высоты ножки h * f = 1,25;

коэффициент радиального зазора с * = 0,25 или 0,3;

коэффициент граничной (рабочей) высоты зуба h * L = 2;

шаг зубьев Р = π · m;

толщина зуба S и ширина впадины е: S = е = 0,5Р = π · m / 2.

Делительная прямая рейки проходит по середине рабочей высоты зуба h L .

Для зуборезных инструментов основные параметры зубьев по аналогии с изложенным выше задаются параметрами исходной инструментальной рейки (рис. 1.3, б). Так как зубья режущего инструмента обрабатывают впадину между зубьями колеса и могут нарезать колеса с модифицированным (фланкированным) профилем, между названными исходными контурами имеются существенные различия:

Высота головки зуба исходной инструментальной рейки h a0 = (h * f0 + с 0)m = 1,25 m, т.е. коэффициент высоты

veloed.ru

Делительный диаметр формула. Модуль зуба шестерни – основной геометрический параметр зубчатого колеса

1. Цель работы

Ознакомление с основными геометрическими параметрами и размерами цилиндрических колес с прямыми зубьями, а также с методами их измерения.

2. Теоретические положения

2.1Общие сведения

Поверхности взаимодействующих зубьев колес должны обеспечить постоянство передаточного числа (U = const ). Для выполнения этого условия боковые профили зубьев сопрягаемых колес должны подчиняться требованиям, вытекающим из основной теоремы зацепления: общая нормаль n – n , проведенная через точки касания профилей, делит расстояние между центрами колес O 1 O 2 на части, обратно пропорциональные угловым скоростям (рис. 1). Математически теорема зацепления имеет вид:

Профиль зуба спиральной шестерни представляет собой эвольвентную кривую с осевого зрения или в плоскости, перпендикулярной оси. Спиральная передача имеет два вида зубных профилей: одна основана на нормальной системе, другая – на осевой системе. Однако в нормальной плоскости, глядя на один зуб, есть сходство с эвольвентным зубом шага, соответствующего нормальному шагу.

Однако форма зуба соответствует цилиндрическому зубчатому колесу большего числа зубьев, точное значение зависит от величины угла спирали. Приводится геометрическая основа получения числа зубьев в этой эквивалентной форме зубчатой ​​формы. Результат транспонированной геометрии – это эквивалентное количество зубов, заданное как.

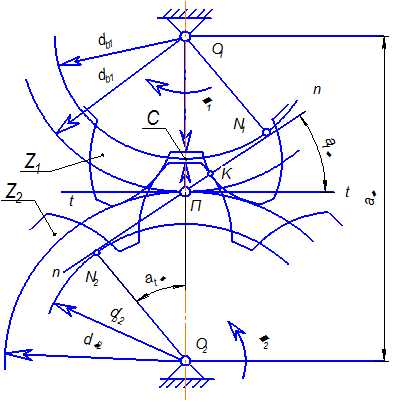
Рис. 1 . Зацепление эвольвентных зубчатых колес

Из возможных профилей зубьев, удовлетворяющих основной теореме зацепления, наибольшее применение получило эвольвентное зацепление благодаря технологичности и достаточно высокой несущей способности. Эвольвента окружности образуется точкой К на прямых N 1 K и N 2 K при качении их без скольжения по окружностям с диаметрами d в 1 и d в 2 . Эти окружности называются основными. Линия N 1 N 2 , по которой перемещается общая точка контакта К профилей зубьев при вращении колес – линия зацепления. Угол между линией зацепления и прямой t – t , перпендикулярной к межосевой линии O 1 O 2 называется углом зацепления . Для колес без смещения угол зацепления .

Эквивалентное число также называется виртуальным номером, потому что это цилиндрическое устройство является мнимым. Значение этого числа используется для определения силы спирального зуба. Хотя, строго говоря, угол давления существует только для зубчатой ​​пары, номинальный угол давления может учитываться для отдельной передачи.

Из-за природы генерации зубьев с помощью стойкой варочной панели один инструмент может генерировать спиральные шестерни на всех углах спирали, а также на цилиндрических зубчатых колесах. Однако это означает, что нормальный шаг является общим знаменателем и обычно принимается за стандартное значение. Поскольку истинные эвольвентные функции находятся в поперечной плоскости, они будут отличаться от стандартных нормальных значений.

При вращении зацепляющихся зубчатых колес окружности радиусов О 1 П и О 2 П перекатываются одна по другой без скольжения. Данные окружности называются начальными, их диаметр d ω 1 и d ω 2 . Эти окружности являются сопряженными, т.е. понятие начальных окружностей относится только к паре колес находящихся в зацеплении. При изменении межосевого расстояния О 1 О 2 диаметры начальных окружностей изменяются.

Следовательно, существует реальная потребность в связывании параметров в двух эталонных плоскостях. Дополнение, окончание, полная глубина и зазор одинаковы независимо от того, измерены ли они в плоскости вращения или нормальной плоскости. Угол и шаг давления обычно указываются как стандартные значения в нормальной плоскости, но бывают случаи, когда они указаны как стандартные в поперечной плоскости. Угол спирали – обе шестерни сетчатой ​​пары должны иметь одинаковый угол спирали. Однако направление спирали должно быть противоположным; то есть левые сопряжения с правой спиралью.

Делительная окружность принадлежит отдельному колесу и получается при его зацеплении со стандартной рейкой. Окружность, являющаяся начальной при зацеплении с рейкой – делительная; её диаметр обозначается d (рис. 2). Для колес без смещения делительные окружности совпадают с начальными . Толщина зуба по делительной окружности S равна ширине впадины между двумя зубьями е.

Диаметр шага – это задается тем же выражением, что и для цилиндрических зубчатых колес, но если задействован нормальный модуль, он зависит от угла спирали. Центральное расстояние. Используя Уравнение, центральное расстояние спиральной зубчатой ​​сетки составляет.

Обратите внимание, что для стандартных параметров в нормальной плоскости центральное расстояние не будет стандартным значением по сравнению со стандартными цилиндрическими зубчатыми колесами. Кроме того, манипулируя углом спирали, β, центральное расстояние можно отрегулировать в широком диапазоне значений.

Расстояние между двумя одноименными профилями соседних зубьев по делительной окружности – окружной шаг зацепления P . На делительной окружности шаг зацепления Р равен сумме толщины зуба S и ширины впадины между двумя зубьями е . Расчетная величина, равная отношению окружного шага зубьев Р по делительной окружности к числу π – окружной модуль зацепления

Для компенсации значительных изменений расстояния в центре без изменения отношения скорости между параллельными редукторными валами; и изменять соотношение скоростей между параллельными редукторными валами без изменения центрального расстояния, манипулируя углом спирали вместе с количеством зубьев.

Следовательно, минимальное количество зубьев без подрезания может быть значительно уменьшено, и возможны винтовые шестерни с очень низким количеством зубов без подрезания.

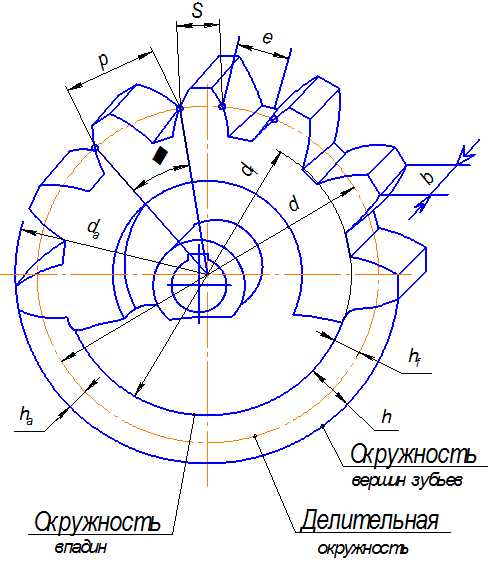
Рис. 2 . Геометрические параметры цилиндрического колеса спрямыми зубьями

Модули зубьев зубчатых колес стандартизованы [табл. 1]. Диаметр делительной окружности выраженный через модуль равен:

где z – число зубьев зубчатого колеса.

Окружность, ограничивающая высоту зубьев – окружность вершин зубьев; её диаметр обозначается d a . Окружность, ограничивающая глубину впадин, – окружность впадин зубьев, её диаметр обозначается d f .

Это не так просто в радиальной системе. Очевидно, что изготовление спиральных передач легче с нормальной системой, чем с радиальной системой в плоскости, перпендикулярной оси. Диаметральный шаг шестерни описывает, как плотно его зубы устанавливаются вокруг него. Шаг – это соотношение между количеством зубов и размером шестерни, и инженеры всегда выражают его как целое число. Это значение важно для дальнейших вычислений с использованием шестерни, включая размер каждой из зубьев шестерни. Меньший шаг соответствует более крупным зубам, а меньшие зубы – на шестерне с большим шагом.

Таблица 1

Ряды предпочтительных чисел

Модуль зацепления m , мм Измерьте радиус шестерни. Извлеките зубцы шестерни из вашего измерения. В этом примере представьте себе шестерню с радиусом 3 дюйма. Умножьте это измерение на 2: 3 × 2 = 6 дюймов. Этим измерением разделите количество зубьев на шестерне. Оборудуйте эту цифру до ближайшего целого числа: 67 составляет приблизительно 5, поэтому шестерня имеет шаг. «Шаг» иногда вместо этого относится к круговой подаче, которая представляет собой расстояние между соответствующими точками на последующих зубах. Если вы «инженер», это, вероятно, старая шляпа, но все равно прочитайте ее, чтобы вы могли исправить мои ошибки. Механизмы обычно округлые, с зубами. Количество зубов и их форма

veloed.ru

Расчет числа зубьев шестерни. Модуль зуба шестерни – основной геометрический параметр зубчатого колеса

ООО «РемМехСервис» производит проектирование цилиндрических и конических зубчатых колес. Одним из основных геометрических и линейных параметров, необходимых для расчета деталей передачи, является модуль зуба шестерни . Эта величина необходима для точного вычисления размеров зубцов. Она одинакова для обоих колес передачи и определяется по формуле:

m=d/z ,

где d – диаметр делительной окружности, по которой при нарезании зубцов обкатывается инструмент; z – количество зубцов.

Модуль зуба шестерни измеряется в миллиметрах и является стандартизированной характеристикой. Его величина составляет от 0,5 до 50 мм. В зависимости от значения модуля зуба шестерни подбираются:

• высота ножки зуба,
• высота головки зуба,
• общая высота и длина зуба,
• диаметры вершин и впадин,
• окружная толщина зуба и впадин.

По международным стандартам допускается применять несколько способов расчета зубчатых передач:

• экспериментально-исследовательский,
• экспериментально-теоретический,
• приближенный,
• упрощенный.

Экспериментально-исследовательский метод очень дорог, поскольку требует проведения высокоточных измерений, исчерпывающего анализа, проведения эксплуатационных экспериментов. Экспериментально-теоретический способ расчетов подходит для производства крупных партий продукции. Приближенный метод базируется на стандартных характеристиках модуля зуба шестерни и комплексных данных технической литературы. Упрощенный расчет производится по формулам.

На практике при отсутствии дополнительных данных модуль зуба шестерни определяют с помощью величины наружного диаметра и числа зубцов. ООО «РемМехСервис» производит все виды расчетов открытых и закрытых передач. Для консультации и заказа воспользуйтесь указанным телефоном.

При конструировании Slot Car (трассовой модели), когда дело доходит до выбора шестерн, то перед нами открывается большой ассортимент на современном рынке с основной величиной модуля 0.3, 0.35 и 0.4. Основными характеристиками шестерни является количество зубьев, модуль шестерни, передаточное число. Если с количеством зубьев и передаточным числом (отношением количества зубьев ведомой к ведущей шестерни) все понятно, то с понятием модуль шестерни не совсем. К сожелению, в школах уже давно не тот уровень преподавания предмета черчения, а в большенстве случаях этот предмент не преподается.

И так, что такое модуль шестерни? Как вычисляется модуль шестерни и чем он обусловен? На этот вопрос нам помог учебник — Техническое черчение, изданный еще в 1972 году (как ни странно, на просторах современного интернета не так уж и много информации по данному вопросу).

Шестерни (на техническом языке — зубчатые колеса) служат для передачи движения от одного элемента машины к другому. Зубчатые колеса в зависимости от характера зацепления (внешнее или внутреннее), взаимного расположения вращающихся валов, способа передачи и т.д. могут быть самой различной конструкции. Наиболее распространенными являются цилиндрические и конические шестерни.

Рисунок 1 – Элементы зубчатого колеса (шестерни)

И так, из каких же элементов состоит шестерня (зубчатое колесо) изображенная на рисунке 1, а. Основным элементом шестерни является зуб (рисунок 1, б) — выступ определенной формы, предназначенный для передачи движения посредством воздействия на выступ другого элемента зубчатой передачи. Часть зубчатого колеса, в которую не входят зубья, называется телом зубчатого колеса (рисунок 1, в). Часть зубчатого колеса, состоящая из всех его зубьев и некоторой связывающей их части тела колеса, называется зубчатым венцом.

Впадиной называется пространство, заключенное между боковыми поверхностями соседних зубьев и поверхностями вершин и оснований впадин (рисунок 1, г).

Начальной поверхностью зубчатого колеса (рисунок 1, д) называется соосная поверхность, по которой катится без скольжения такая же поверхность друого колеа, находящегося в зацеплении с первым. Начальная поверхность колеса делит зуб на две части — головку и ножку.

На рисунке 1, е показано изображение на чертеже некоторых основных элементов зуба. Проекция поверхности выступв на плоскость, перпендикулярную оси зубчатого колеса, называется окружностью выступов, поверхность впадин — окружностью впадин, поверхность делительной поверхности — делительной окружностью. На этом чертеже обозначены высота зуба — h , головки зуба — h” и ножки зуба – h” ” .

Торцовым шагом t3 называется расстояние по делительной окружности между одноименными профилями смежных зубьев. Диаметр делительной окружности — dд , ди

sportbu.ru