Закон юнга – 7. Закон Гука и модуль Юнга.

alexxlab | 11.05.2016 | 0 | Вопросы и ответы

7. Закон Гука и модуль Юнга.

Закон Гука.

Силы упругости растут при увеличении деформации. Особенно наглядно это можно продемонстрировать, растягивая пружину (картинка а)

Коэффициент жесткости зависит не только от материала пружины, но также от её формы и размеров.

Из формулы следует, что график зависимости силы упругости от (малой) деформации является прямой линией (рис. 1 ):

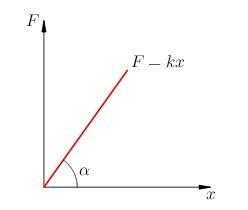
Рис. 1. Закон Гука

Коэффициент жёсткости — о угловой коэффициент в уравнении прямой. Поэтому справедливо равенство: ,

где — угол наклона данной прямой к оси абсцисс. Это равенство удобно использовать при экспериментальном нахождении величины .

Закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела. Когда деформации перестают быть малыми, эта зависимость перестаёт быть линейной и приобретает более сложный вид. Соответственно, прямая линия на рис. 1 — это лишь небольшой начальный участок криволинейного графика, описывающего зависимость отпри всех значениях деформации

.

Модуль Юнга.

В частном случае малых деформаций стержней имеется более детальная формула, уточняющая общий вид (1) закона Гука.

Именно, если стержень длиной и площадью поперечного сечения растянуть или сжать на величину , то для силы упругости справедлива формула: .

Здесь – модуль Юнга материала стержня. Этот коэффициент уже не зависит от геометрических размеров стержня. Модули Юнга различных веществ приведены в справочных таблицах.

8. Силы трения. Виды трения. Трение покоя. (График зависимости силы трения от величины внешней силы). Внутреннее трение, формула Стокса.

Силы трения– это силы, возникающие при соприкосновении поверхностей двух тел или частей одного тела и препятствующие их взаимному перемещению.

Силы трения всегда направлены вдоль соприкасающихся поверхностей противоположно движению тела. При изменении направления скорости изменяется направление сил трения.

Силы трения, как и силы упругости, имеют электромагнитную природу. Они возникают вследствие взаимодействия между атомами и молекулами соприкасающихся тел.

Силы трения отличаются от гравитационных сил и сил упругости тем, что эти силы зависят не только от конфигурации тел, т. е. от их взаимного расположения, но также еще от относительных скоростей взаимодействующих тел.

Существует четыре вида сил трения:\

Трение скольжения— сила, возникающая при поступательном перемещении одного из контактирующих/взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения.

Трение качения— момент сил, возникающий при качении одного из двух контактирующих/взаимодействующих тел относительно другого.

Сила вязкого трения(сила сопротивления).

Трение покоя— сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях (например, при деформации) контактирующих тел. Она действует в направлении, противоположном направлению возможного относительного движения.

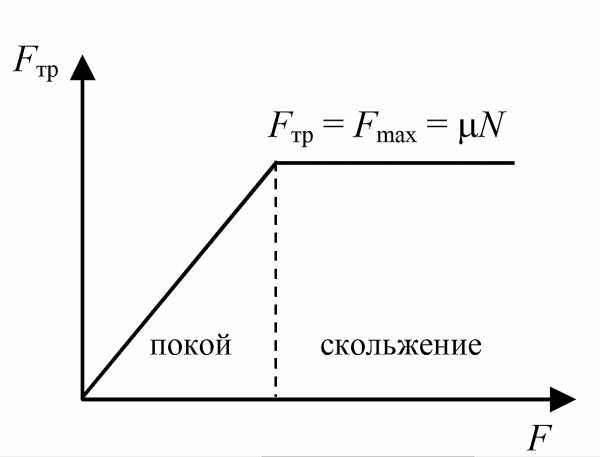(график зависимости силы трения от внешней силы F)

Различают трение внешнееивнутреннее.Внешнее трениевозникает при относительном перемещении двух соприкасающихся твердых тел (трение скольжения или трение покоя).

Внутреннее трениенаблюдается при относительном перемещении частей одного и того же сплошного тела (например, жидкость или газ).

Различают сухое

и жидкое (иливязкое) трение.

Сухое трениевозникает между поверхностями твердых тел в отсутствие смазки.

Жидким(вязким) называется трение между твердым телом и жидкой или газообразной средой или ее слоями.

Сухое трение, в свою очередь, подразделяется на трение скольженияи трениекачения.

studfiles.net

Закон Гука, модуль Юнга (сопромат)

Для большинства конструкционных материалов между напряжением () и продольной деформацией () до определенного предела нагружения существует линейная зависимость

Закон Гука: Напряжение пропорционально деформации.

Впервые Закон Гука был опубликован в виде анаграммы английским ученым Робертом Гуком (1635 – 1703 гг.). При правильной расстановке букв анаграмма читается: «Каково удлинение, такова и сила».

К такому же заключению в 1680 г., независимо от Гука, пришел французский ученый Эдмон Мариотт.

Коэффициент пропорциональности (E) в формуле закона Гука называется модуль продольной упругости или модуль Юнга – по имени английского ученого Томаса Юнга. Значение модуля Юнга для данного материала устанавливается опытным путем. В справочниках обычно приводятся среднее значение модуля Юнга.

Необходимо отметить, что некоторые материалы не подчиняются закону Гука, например, кожа, ткани. Такие материалы, как, например, чугун, только с некоторым приближением можно считать подчиняющимся закону Гука. Но даже и те материалы, которые подчиняются закону Гука, перестают ему следовать при достижении деформации определенного значения.

Из закона Гука видно: чем больше модуль Юнга, тем меньше (при том же значении напряжения) деформация материала. Следовательно, модуль продольной упругости характеризует жесткость материала при растяжении (сжатии). Из формулы закона Юнга видно, что модуль Юнга измеряется в тех же единицах, что и нормальное напряжение ().

Так, например, для всех марок сталей МПа.

sopromato.ru

22. Смачивание. Закон Юнга (силовой и энергетический выводы) |  Читать онлайн, без регистрации

22. Смачивание. Закон Юнга (силовой и энергетический выводы)

Смачивание – это поверхностное явление, заключающееся во взаимодействии жидкости с твердым телом при наличии одновременного контакта трех несмешивающихся фаз. Смачивание часто рассматривают как результат межмолекулярного (вандерваальсова) взаимодействия, однако во многих случаях (например, при соприкосновении жидких металлов с твердыми металлами) смачивание обусловлено скорее, образованием химических соединений, твердых и жидких растворов и диффузионными процессами в поверхностном слое смачиваемого тела.

Смачивание – самопроизвольный процесс, идущий с уменьшением поверхностной энергии. Поэтому при смачивании выделяется теплота. Чем лучше твердое тело смачивается жидкостью, тем выше теплота смачивания. Тепловой эффект, сопровождающий соприкосновение жидкости со смачиваемой поверхностью, называется теплотой смачивания.

Мерой смачивания является краевой угол смачивания Θ между смачиваемой поверхностью и поверхностью жидкости на периметре. Угол Θ отсчитывают со стороны жидкости. Точка, соответствующая краевому углу смачивания 90°, называется точкой инверсии. При статическом (равновесном) смачивании угол Θ связан с поверхностным натяжением жидкости (σ_ж), поверхностным натяжением твердого тела (σ) и межфазным натяжением на границе «твердое тело – жидкость» (σ_тж) уравнением Юнга:

cosΘ = (σ_т – σ_тж) / σ_ж.

Величиной угла Θ оценивают лиофильность и лиофобность поверхностей по отношению к различным жидкостям. На лиофильной поверхности жидкость растекается, т. е. имеет место частичное (0° < Θ < < 90°) или полное смачивание, на лиофобной поверхности растекания не происходит (Θ > 90°). Краевой угол зависит от соотношения сил сцепления молекул жидкости с молекулами или атомами смачиваемого тела (адгезии) и сил сцепления молекул жидкости между собой (когезии). Обратимую работу адгезии и когезии вычисляют, соответственно, по уравнениям:

W_a = σ_ж (1 + cosΘ) и W_k = 2σ_ж.

При W_a < W_K всегда Θ > 0°, причем с увеличением отношения W_a < W_k улучшается С.

Работа адгезии характеризует работу по отрыву от твердой поверхности. Оценивается она по уравнению Дюпре-Юнга: W_а=σ(1 + cos х).

Разность S = W_a – W_k называется коэффициентом растекания. Часто наблюдаемая задержка в установлении равновесных краевых углов называется гистерезисом смачивания. Различают кинетический (динамический) и статический гистерезис смачивания.

Причинами гистерезиса могут быть шероховатость поверхности, особенности структуры поверхностного слоя, релаксационные процессы в жидкой фазе и др.

Если твердое тело соприкасается одновременно с двумя несмешивающимися жидкостями, происходит избирательное смачивание. Эффективные регуляторы смачивания – поверхностно-активные вещества, которые могут как улучшать, так и ухудшать его.

В узких каналах, цилиндрических капиллярах образуется вогнутый мениск – полностью искривленная поверхность жидкости (рис. 1).

Рис. 1.

velib.com

Юнга закон – Справочник химика 21

    При контакте жидкостей с твердыми телами наблюдается разная степень смачивания, характеризуемая краевым углом 8. В соответствии с законом Юнга  [c.28]

    Обычно приводимый в учебниках вывод закона Юнга на основе геометрического рассмотрения равновесия сил является нестрогим, поскольку соотношение между а рр, ахж проекцией ст>[твердой поверхности не определяет полностью механического равновеспя (есть еще одна составляющая, направленная по нормали вверх). [c.55]

    ГУКА ЗАКОН, устанавливает линейную зависимость между упругой деформацией твердого тела и приложенным мех напряжением Напр, если стержень длиной I и поперечным сечением S растянуть продольной силой F, то удлинение стержня Д/ = FI/ES, где -модуль упругости (модуль Юнга), зависящий от материала стержня Для деформации сдвига (см рис) Г з имеет вид т = Gy, где 

[c.618]

    Уравнение (V.18), определяющее условия смачивания, — математическое выражение закона Юнга . Анализ его подтверждает следствия, полученные на основе качественных представлений  [c.60]

    Уравнение Дюире (II. П7) самостоятельно почти не используется для расчета работы адгезии из-за трудности определения поверхностного натяжения твердых тел на границе с газом (воздухом) и жидкостью. Удобную для расчета этой величины форму имеет соотношение, получаемое в результате сочетания уравнения Дюпре с законом Юнга (II. 121). Если разность аз,1 — аг.з в уравнении Дюире заменить ее выражением из закона Юнга [c.71]

    Разность Wa — W называют коэффициентом растекания. Следует отметить, что случай Wa>W противоречит уравнению (VI. 22), согласно которому W o Действительно, это уравнение, как и закон Юнга, ограничено условием равновесия, тогда как неограниченное растекание является состоянием неравновесным, к которому уравнения (VI.18) и (VI.22) неприменимы. 

[c.63]

    Обычно приводимый в учебниках вывод закона Юнга на основе геометрического рассмотрения равновесия сил является нестрогим, поскольку соотношение между а-р , и проекцией на плоскость твердой по- [c.60]

    Рассмотрим более подробно физический смысл и следствия закона Лапласа—Юнга, являющегося основой теории капиллярных явлений. Уравнение (У.34) показывает, что разность давлений в объемных фазах возрастает с увеличением а и с уменьшением Я. Величина / — это радиус кривизны поверхности натяжения (см. [5, с. 18]). [c.67]

    После того как стал применяться предельный закон теории Дебая и Гюккеля, были быстро достигнуты существенные успехи в смысле повышения точности экстраполяции. Гюккель [5], Скэтчард [6], Харнед [7], Рендалл и Юнг [8], применяя предельный закон и обобщенные формы уравнений теории Дебая и Гюккеля, смогли значительно увеличить точность экстраполяции. Общий обзор полученных до 1929 г. результатов был сделан Харнедом [96]. 

[c.339]

    Заканчивая обсуждение микроструктуры аэрозоля, можно отметить, что причина, по которой нормально-логарифмические распределения более адекватно, чем степенной закон Юнге, описывают спектр размеров частиц аэрозоля, возможно, кроется в свойстве центральной предельной теоремы. Из этой теоремы следует, что если статистическая переменная есть результат процесса, в котором выход пропорционален уже достигнутой величине переменной, то ее статистическое распределение должно быть нормально-логарифмическим. Поскольку процессы, определяюш.ие выживание аэрозольной частицы в воздухе, действительно являются функцией приобретенного ею размера, то нормально-логарифмическое распределение является, по-видимому, естественным свойством этой системы. По этой же причине реальную кривую распределения счетной концентрации любой сложности можно аппроксимировать суперпозицией нескольких логарифмически-нор-мальных распределений в соответствии с числом независимых кооперирующих источников [301]. 

[c.32]

    В нормально-логарифмическом представлении распределение по размерам собственно солевых частиц, инжектированных в атмосферу водной поверхностью Мирового океана, имеет уни-мономодальный характер [303]. В случае же аппроксимации распределения степенным законом Юнге для аэрозольных солевых частиц на уровне моря в [98] значение а = 3,8 (при общей концентрации частиц 30 см , т. е. около 5 % общей концентрации частиц Айткена), что согласуется с более ранними данными [166], по которым величина а лежит в диапазоне 3—4. [c.51]

    В соответствии с законом Гука а=Ее, где Е — модуль растяжения (модуль Юнга). Если деформация строго пропорциональна напряжению, то модуль есть коэффициент пропорциональности и имеет для данного материала единственное значение. На рис. 8.3 показана типичная кривая деформации эластичного полимера. Пропорциональность между о и е отсутствует. Поэтому модуль определяют как тангенс угла наклона касательной к кривой, проведенной из начала координат. Это начальный, или условно-мгновенный, модуль. Формально можно определить модуль для данного образца при любой деформации как производную напряжения по деформации = da/de. 

[c.107]

    Следует отметить, что влияние влажности на оптические свойства аэрозоля не ограничиваются зависимостями п и х от / [36. Во-первых, как уже отмечалось, под влиянием процессов коагуляции и конденсации характер распределения аэрозоля по размерам оказывается также функционально связанным с относительной влажностью среды обитания аэрозоля. Так, например, в случае описания распределения аэрозоля степенным законом Юнге показатель степени изменяется в соответствии с соотношением (1.15)  [c.83]

    Модуль упругости, в пределах применимости закона Гука, равен отношению напряжения а в материале к величине, соответствующей упругой деформации 8. В данном случае речь идет о модуле продольной упругости (при линейном растяжении), называемом иначе модулем Юнга. Модуль упругости тем больше, чем меньше относительное удлинение при данном напряжении. [c.574]

    О. Упругие свойства изотропных материалов. Модуль Юнга Е, известный также как модуль продольной упругости, или модуль упругости первого рода, равен растягивающему напряжению, деленному на. деформацию в направлении приложенного напряжения, которая измеряется в области линейной упругости. Он является коэффициентом пропорциональности в законе Гука и равен наклону линейной части кривой на диаграмме деформация—напряжение. Размерность его такая же, как и напряжения (давления). [c.198]

    Детальное изучение физико-химических процессов, продуцирующих in situ атмосферный аэрозоль, показывает, что образующиеся частицы имеют двухмодальное распределение поверхности по размерам [302]. Первой моде отвечают частицы с размерами менее 0,1 мкм. Вторая аккумуляционная мода имеет размеры от —0,08 до 1 —1,5 мкм. К. Уитби в [301, 302] показал, что реально наблюдающиеся микроструктуры аэрозоля в виде суммы нескольких логарифмически-нормальных распределений отклонения в экспериментальных спектрах распределения частиц по размерам от закона Юнге являются отражением мультимодальной природы естественного аэрозоля (рис. 1.14). Анализ [c.58]

    Важно отметить, что при выводе закона Юнга предполагается взаимное равновесие между всеми фазами. Отсюда следует, что в результате устаЕювления равновесия между парами жидкости и поверхностью твердого тела на последней образуется адсорбцион” ная пленка, снижающая поверхностное натяжение твердого тела-Учет такого изменения поверхностного натяжения с большей строгостью позволяет использовать уравнение Юнга. [c.70]

    Если течение не является типичным свойством твердообразных систем, что особенно характерно для конденсационно-кристаллизационных структур, то реологические зависимости строят по отношению к деформации, а не к ее скорости. Типичная кривая зависимости деформации от напряжения для твердых тел показана на рис. VII. 15. Прямолинейный участок кривой ОА отвечает пропорциональности деформации напряжению сдвига в соответствии с законом Гука (VII. 3). До напряжения Ри отвечающего точке А, размер и форма тела восстанавливаются после снятия нагрузки. Важными параметрами такой системы являются модуль упругости (модуль Юнга) и модуль эластической деформации. Считают, что в суспензиях с коагуляционной структурой модуль упругости (модуль быстрой эластической деформации) характеризует твердую фазу дисперсий, а модуль медленной эластической деформации — пространственную сетку с прослойками дисперсионной среды (возможно скольжение частиц относительно друг друга без разрыва связей). Напряжение Р соответствует пределу текучести (правильнее — пределу упругости). С увеличением напряжения проявляется пластичность, а после его снятия — остаточные деформации. При напряжении Рг (точка ) происходит течение твердообразной системы. При дальнейшем увеличении напряжения до величины Рз (точка В), соответствующей пределу прочности, обычно наблюдается негупрочнение тела, затем наступает разрушение системы. [c.380]

    Согласно теории Юнга, поле, возникающее в результате дифракции волн,— это результат интерференции волн, распространяющихся по геометрическим законам, и дифрагированных волн, возникающих в особых точках, в которых граничные условия имеют разрыв. Геометрическим местом таких точек являются границы препят- [c.46]

    Пользуясь оптическими методами, Редпих и Хальбан установили, что константа ассоциации азотной кислоты в воде равна 20,0. Юнг и Блиц на основании спектров комбинационного рассеяния установили приложимость закона действия масс к водным растворам серной кислоты. Установлены константы диссоциации HIO3 К =0,16—0,18) и Н3РО1 (К = 0,01). [c.302]

    Деформация, исчезающая при разгрузке, называется упругой. Упругие деформации разделяются на объемные, сдвиговые и деформации кручения. Для удобства рассмотрим одномерный (по координатам) случай деформирования, считая, что деформации не зависят от времени. Обозначим напряжение через Р, а деформацию через е. Если Р пропорционально е (закон Гука), то такое тело называется идеально упругим. Коэффициент пропорциональности между Рие назьшается модулем упругости. Если 8 — это объемная деформация, то коэффициент пропорциональности называется объемным модулем упругости, или модулем Юнга. Модуль Юнга обычно обозначается Е (К). Если е — сдвиговая деформация, то коэффициент пропорциональности называ-ется модулем сдвига и обычно обозначается 2С (С, х),  [c.130]

    Уравнение (V. 18), определяющее условия смачивания, — математическое выражение закона Юнга . Анализ его подтверждает следствия, полученные на основе качественных представлений а-рр > 0-гж os0>O 0 [c.55]

    Граничные, смазочные слон обладают истинной упругость формы и подчиняются закону Гука. Их механические свойства определяются условиями всестороннего сжатия. Правильно ориентированный адсорбционный слой цепных молекул углеводородов, находящийся между двумя твердыми поверхностями, обладает огромной упругостью на поперечное сжатие ( = 10 кгс/см-). Его сопротивление сжатию определяется не структурной упругостью слоя, а модуле.м Юнга алмазоподобной структуры метиленовых цепей, работающих на осевое сжатие [75, 109]. Смазочные слои ПАВ между поверхностями трения, обладающие благодаря строению концевых групп хорощими смазочными свой-ства1ми, в то же время обладают бс> ьщим сопротивлением сжатию и разрыву пленки. Большая грузоподъемность граничных слоев обусловлена большой энергией адсорбционной связи граничного слоя с поверхностью металла — адгезионной связью и большой энергией когезионной связи между ориентированными молекулами адсорбента. [c.46]

    Частицы, образующие сводовую перемычку, создают внутреннюю фильтрационную корку непосредственно у поверхности породы на забое, а мелкие частицы проникают несколько глубже в породу. Этот процесс повторяется снова и снова по мере удаления с забоя слоев горной породы. Градиенты давления в породе ниже долота были измерены Юнгом и Греем на микродолотном буровом стенде, на котором движение проникающей в породу жидкости происходило только в вертикальном направлении. Наблюдалось изменение порового давления по мере того, как поверхность забоя приближалась к пробке, через которую удаляли жидкость. Проницаемость горной породы рассчитывалась по закону Дарси. На рис. 9.7 видно, что градиент давления очень высокий на расстоянии примерно [c.346]

    Для описания М.с. идеальных моделей (см. Реология) справедливы линейные законы для деформац. св-ь-Гука закон (напряжения пропорциональны деформациям), для фрикционньк св-в-закон Кулона (сила трения пропорциональна нормальной нагрузке), для вязкостных св-в-закон Ньютона (касательные напряжения пропорциональны скорости сдвига) и т.п. Однако поведение реальных тел гораздо сложнее и требует для своего описания разл. нелинейных соотношений. Определение М.с. материала является основой при выборе области его применения, условий формирования из него изделий, их эксплуатации. Для осн. классов твердых техн. материалов характерны след, значения предела прочности а (на растяжение) и модуля Юнга Е  [c.77]

    Краевой угол смачивания 0 в контакте жидкости с пов-стью твердого тела os0 = (а — tJ/ t где а , ст (-уд-своб. поверхностные энергии твердого тела на границе с газом и жидкостью, ст,-П. н. жидкости (закон Юнга, см. Смачивание). [c.589]

    В 19 в. установлены осн. количеств, закономерности П. я. закон капиллярного давления (П. Лаплас, 1806), постоянство краевого угла смачивания (Т. Юнг, 1804), зависимость давления насыщ. пара жидкости от кривизны пов-сти (У. Томсон, 1870) первые термодинамич. соотношения-ур-ние изотермы адсорбции Гиббса (1878), зависимость поверхностного натяжения от электрич. потенциала (Г. Липман, 1875), сформулирован принцип минимума площади пов-сти жидкости (Ж. Плато, 1843). Среди важнейших П. я.-наличие капиллярных волн на пов-сти жидкости (У. Рэлей, 1890), двухмерное состояние и независимость действия адсорбц. слоев на пов-сти раздела фаз (И. Ленгмюр, 1917), адсорбц. понижение прочности (П. А. Ребиндер, 1923), расклинивающее давление в тонких жидких пленках (Б.В. Дерягин, 1935). [c.591]

---

chem21.info

Модуль Юнга (упругости I рода)

Модуль Юнга (синонимы: модуль упругости I рода, модуль продольной упругости) – механическая характеристика материалов, определяющая их способность сопротивляться продольным деформациям. Показывает степень жесткости материала.

Назван в честь английского ученого Томаса Юнга.

Обозначается латинской прописной буквой E
Единица измерения – Паскаль [Па].

В сопротивлении материалов модуль продольной упругости участвует в расчетах на жесткость при растяжении-сжатии и изгибе, а также в расчетах на устойчивость.

Учитывая то, что практически все конструкционные материалы имеют значение E высокого порядка (как правило 10⁹ Па), его размерность часто записывают с помощью кратной приставки «гига» (гигапаскаль [ГПа])

Для всех материалов его величину можно определить в ходе эксперимента по определению модуля упругости I рода.

Приближенно значение модуля можно определить по диаграмме напряжений получаемой при испытаниях на растяжение.

Рис. 1 Начальный фрагмент диаграммы напряжений

В этом случае модуль Юнга равен отношению нормальных напряжений к соответствующим относительным деформациям, на участке диаграммы (рис. 1) до предела пропорциональности σ_пц (тангенсу угла α наклона участка пропорциональности к оси деформаций ε).

E=σ/ε=tgα

В таблице 1 приведены сравнительные значения модуля для некоторых наиболее часто используемых материалов

Таблица 1

Материал	Модуль Юнга E, [ГПа]
Сталь	200
Чугун	120
Серый чугун	110
Алюминий	70
Дюралюминий	74
Титан	120
Бронза	100
Латунь	95
Медь	110
Олово	35
Хром	300
Никель	210
Кремний	110
Свинец	18
Бетон	20
Дерево	10
Стекло	70

Модуль упругости I рода служит коэффициентом пропорциональности в формуле описывающей закон Гука:

σ=Eε

Связка модуля Юнга с геометрическими характеристиками поперечных сечений бруса показывает их жесткость:

EA – жесткость поперечного сечения при растяжении-сжатии,
где A – площадь поперечного сечения стержня;
EI – жесткость поперечного сечения при изгибе,
где I – осевой момент инерции сечения балки.

Модуль упругости II рода (модуль сдвига) >
Примеры решения задач >

isopromat.ru

Модуль Юнга и его основной физический смысл

Модулем продольной упругости конструкционного материала, или модулем Юнга, называют физическую величину, которая характеризует свойство материалов, обеспечивающее их сопротивление деформациям, действующим в продольном направлении.

Параметр характеризует степень жесткости конкретного материала.

Название модуля соответствует фамилии Томаса Юнга – известного английского физика и ученого, который занимался исследованием процессов сжатия и растяжения для твердых материалов. Обозначается данная физическая величина латинской буквой E. Измеряется модуль Юнга в Паскалях.

Параметр модуль Юнга, или модуль продольной упругости, используется при различных расчетах при испытаниях материалов на степень деформации при растяжении-сжатии, а также при изгибе.

Надо сказать, что большинству используемых конструкционных материалов свойственен показатель модуля Юнга достаточно больших значений, которые, как правило, имеют порядок 10⁹ Па. Поэтому для удобства расчетов и записи используют кратную приставку «гига» (ГПа).

Ниже приведены показатели модуля Юнга для некоторых конструкционных материалов, которые достаточно часто используются для различных практических целей. Именно от их свойств прочности зависит долговечность строительных сооружений и других объектов.

Согласно приведенной таблице, максимальный показатель модуля принадлежит стали, а минимальный  – дереву.

Значение модуля Юнга для некоторых конструкционных материалов

Название материала	Показатель E, [ГПа]	Название материала	Показатель E, [ГПа]
хром	300	латунь	95
никель	210	дюралюминий	74
сталь	200	алюминий	70
чугун	120	стекло	70
хром	110	олово	35
серый чугун	110	бетон	20
кремний	110	свинец	18
бронза	100	дерево	10

Графическое определение модуля Юнга возможно с помощью специальной диаграммы напряжений, на которой изображена кривая, получаемая при многократных испытаниях одного и того же материала на прочность.

В этом случае физический смысл модуля Юнга заключается в нахождении математического отношения нормальных напряжений к соответствующим показателям деформации на определенном участке диаграммы до конкретно заданного предела пропорциональности σ_пц.

В виде математического выражения модуль Юнга выглядит следующим образом: E=σ/ε=tgα

Следует также сказать о том, что модуль Юнга является еще и коэффициентом пропорциональности в математическом описании закона Гука, который выглядит следующим образом: σ=Eε

Поэтому непосредственная связь модуля продольной упругости с измеряемыми характеристиками поперечных сечений материалов, участвующих в испытаниях на жесткость, выражается с помощью таких показателей, как ЕА и Е1.
EA – это показатель жесткости при растяжении-сжатии материала в его поперечном сечении, где А – значение площади сечения стержня.

Е1 – это показатель жесткость при изгибе материала в его поперечном сечении, где 1 – значение осевого момента инерции, который возникает в сечении ипытываемого материала.

Таким образом, модуль Юнга – это универсальный показатель, который позволяет с нескольких сторон характеризовать прочностные свойства материала.

fb.ru

Закон гука Модуль юнга — Mlegal.ru

Содержание статьи:

Закон гука Модуль юнга

§ 1. Закон Гука, а модуль — Юнга

Английский физик, архитектор и инженер Роберт Гук, член Лондонского Королевского общества, интересовался свойствами упругости металлов в связи с проблемой создания пружинных часов, которые были очень нужны современным ему корабелам. Используемые в те времена маятниковые часы работали ненадежно, проблема стояла остро. Ею занимался, в том числе, и знаменитый голландец Гюйгенс, изобретатель маятниковых часов, создатель волновой теории света и автор многих других блестящих работ в области физики, математики и астрономии. Между Гуком и Гюйгенсом шел спор о праве считаться создателем пружинных часов.

Рис. 11

Результаты своих измерений Гук опубликовал в 1676 г. в виде анаграммы из латинских букв: ceiiinosssttuu. В анаграмме буквы расставлены по алфавиту, ко если расположить их в правильном порядке, известном только автору, то должна получиться фраза, выражающая суть дела. Так зашифровывали в те времена свои открытия, если не было полной уверенности в их достоверности. Этим как бы делалась заявка на приоритет на случай, если кто-нибудь вдруг опередит автора. Гук три года спустя, убедившись в своей правоте, опубликовал расшифровку анаграммы. Краткая формулировка его закона на латыни записывается так: «Ut tensio sic uis», что в переводе означает: «Каково удлинение, такова и сила».

Между прочим, с этими анаграммами и борьбой за приоритет в те времена происходили подчас комичные истории. Так, Гюйгенс, впервые увидев в телескоп кольцо Сатурна, тоже опубликовал свое открытие в виде анаграммы. Один из околонаучных ловкачей занимавшихся вместо кропотливых изысканий расшифровкой опубликованных анаграмм, сумел «прочесть» запись Гюйгенса, решив, что она относится к спутникам Марса. Получилось: «Привет вам, близнецы, Марса порожденье». Какой же был конфуз, когда Гюйгенс, проверив свои наблюдения, сам расшифровал свою анаграмму: из тех же букв (тоже на латыни) составилась фраза: «кольцом окружен тонким, плоским, нигде не прикасающимся, к эклиптике наклоненным».

Но вернемся к закону Гука. Каково удлинение, такова и сила. На современном, более строгом, но и более скучном языке это означает, что удлинение тела прямо пропорционально действующей на него растягивающей силе. Несомненно Гук знал, что его утверждение относится к случаю, когда поперечное сечение растягиваемого тела и его исходная длина остаются постоянными. Более длинные стержни давали, конечно, большее удлинение. Он знал также, что при постоянной величине силы вызываемое ею удлинение стержня обратно пропорционально площади его поперечного сечения, и, кроме того, что у стержней одинакового сечения и длины из разных материалов при одном и том же усилии будет разное удлинение. Однако Гук не сумел скомбинировать результаты своих экспериментов в такой форме, чтобы охарактеризовать упругость как свойство самого материала, не зависящее от размеров и формы конструкции. Оставался всего один шаг до привычной нам формулировки закона упругости, и этот шаг был сделан английским ученым Томасом Юнгом лишь более 100 лет спустя — в самом конце XVIII века.

Юнг понял, что если удлинение Δl прямо пропорционально силе F и исходной длине l₀ и обратно пропорционально площади сечения S растягиваемого стержня, то это можно выразить простой формулой

Теперь ясно, что слева от знака равенства записано напряжение σ, а справа — относительное удлинение ε. Итак,

причем, коэффициент пропорциональности в этой формуле — константа Е — получил название модуль Юнга. Численно модуль Юнга, очевидно, равен напряжению, которое вызывает упругую деформацию, равную 1 или 100%. Но, если вспомнить, что относительная деформация ξ = Δl/l₀, то окажется, что ε = 100% соответствует удвоению исходной длины.

Такие большие упругие деформации выдерживает резина, но ни один металл их выдержать не может. При гораздо меньших деформациях металлов они начинают либо деформироваться пластически, т. е. не возвращаются в исходное состояние, либо разрушаются. Мы увидим далее, что чисто упругая деформация металлов не превышает обычно нескольких десятых долей процента, поэтому Е — это напряжение, которое вызвало бы удвоение длины стержня, если бы можно было получить такую огромную упругую деформацию.

Закон Гука справедлив и для случая упругой сдвиговой деформации γ, которую вызывает касательное напряжение τ (рис. 8):

Здесь фигурирует уже другая константа G, которую называют модулем сдвига, а величина γ обычно мала.

Модули упругости Е и G связаны между собой (G ≈ 3/8 E) и являются такими же фундаментальными константами материала, как, например, температура плавления. Модуль упругости характеризует силы межатомного взаимодействия. Чем больше угол наклона к горизонтальной оси кривой, изображенной на рис. 9, вблизи точки равновесия, тем мощнее наши пружинки, тем сильнее они сопротивляются смещениям атомов от исходных позиций.

Чтобы получить представление о том, какое напряжение потребовалось бы для упругого удвоения длины разных материалов, а заодно сопоставить их упругие свойства, заглянем в табл. 1, где сведены значения модуля Юнга некоторых металлов и неметаллов.

Закон гука Модуль юнга

Компьютерная модель позволяет провести ряд экспериментов по теме «Сила упругости. Закон Гука». Экспериментальная установка представляет собой штатив с подвешенным на металлической проволоке телом. Можно изменять материал, из которого изготовлена проволока, площадь ее сечения, начальную длину, а также массу подвешенного груза. В информационном окне выводится информация об удлинении проволоки.

При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости .

При малых деформациях ( | x | 11 Н/м 2 , а для резины E ≈ 2∙10 6 Н/м 2 , то есть на пять порядков меньше.

В рамках эксперимента можно выбирать материал проволоки (сталь, железо, медь, латунь, алюминий, свинец), площадь ее сечения (от 1 до 5 мм 2 с шагом 0,5 мм 2 ), массу груза (от 1 до 10 кг с шагом 0,5 кг).

Задав исходные условия эксперимента можно пронаблюдать результат, считывая показания удлинения проволоки по увеличенному участку измерительной шкалы.

Модель может стать основой исследовательских работ по данной учебной теме, т. к. допускает широкую вариативность исходных условий.

УПРУГОСТЬ, МОДУЛЬ УПРУГОСТИ, ЗАКОН ГУКА

УПРУГОСТЬ, МОДУЛЬ УПРУГОСТИ, ЗАКОН ГУКА. Упругость – свойство тела деформироваться под действием нагрузки и восстанавливать первоначальную форму и размеры после ее снятия. Проявление упругости лучше всего проследить, проведя простой опыт с пружинными весами – динамометром, схема которого показана на рис.1.

При нагрузке в 1 кг стрелка-индикатор сместится на 1 деление, при 2 кг – на два деления, и так далее. Если нагрузки последовательно снимать, процесс идет в обратную сторону. Пружина динамометра – упругое тело, ее удлинение D l, во-первых, пропорционально нагрузке P и, во-вторых полностью исчезает при полном снятии нагрузки. Если построить график, отложить по вертикали оси величины нагрузки, а по горизонтальной – удлинение пружины, то получаются точки, лежащие на прямой, проходящей через начало координат, рис.2. Это справедливо как для точек, изображающих процесс нагружения так и для точек, соответствующих нагрузке.

Угол наклона прямой характеризует способность пружины сопротивляться действию нагрузки: ясно, что «слабая» пружина (рис.3). Эти графики называются характеристиками пружины.

Тангенс угла наклона характеристики называется жесткостью пружины С. Теперь можно записать уравнение деформирования пружины D l = P / C

Жесткость пружины С имеет размерность кг / см\up122 и зависит от материала пружины (например, сталь или бронза) и ее размеров – длины пружины, диаметра ее витка и толщины проволоки, из которой она сделана.

В той или иной мере все тела, которые можно считать твердыми, обладают свойством упругости, но заметить это обстоятельство можно далеко не всегда: упругие деформации обычно очень малы и наблюдать их без специальных приборов удается практически только при деформировании пластинок, струн, пружин, гибких стержней.

Прямым следствием упругих деформаций являются упругие колебания конструкций и природных объектов. Можно легко обнаружить дрожание стального моста, по которому идет поезд;иногда можно услышать, как звенит посуда, когда на улице проезжает тяжелый грузовик; все струнные музыкальные инструменты так или иначе преобразуют упругие колебания струн в колебания частичек воздуха;в ударных инструментах тоже упругие колебания (например, мембраны барабана) преобразуются в звук.

При землетрясении происходят упругие колебания поверхности земной коры; при сильном землетрясении кроме упругих деформаций возникают пластические (которые остаются после катаклизма как изменения микрорельефа), а иногда появляются трещины. Эти явления не относятся к упругости: можно сказать, что в процессе деформирования твердого тела сначала всегда появляются упругие деформации, потом пластические, и, наконец, образуются микротрещины. Упругие деформации очень малы – не больше 1%, а пластические могут достигнуть 5–10% и более, поэтому обычное представление о деформациях относится к пластическим деформациям – например, пластилин или медная проволока. Однако, несмотря на свою малость, упругие деформации играют важнейшую роль в технике: расчет на прочность авиалайнеров, подводных лодок, танкеров, мостов, туннелей, космических ракет – это, в первую очередь, научный анализ малых упругих деформаций, возникающих в перечисленных объектах под действием эксплуатационных нагрузок.

Смотрите так же:

• Субсидии многодетным семьям на жилье Как получить субсидии многодетным семьям на жилье? Пошаговая инструкция В настоящее время нехватка жилой площади для многодетной семьи — актуальная в России проблема. На фоне непрерывного возрастания стоимости […]
• Правила чтения с буквой е Читаем английские слова с буквой E Как известно, чтобы чему-то научиться нужно приложить усилия. Когда же речь идет об иностранном языке, практика необходима каждый день. Ибо изучение английского языка подобно игре на […]
• Как оформит кредитную карту втб 24 Кредитная карта ВТБ24 — онлайн заявка Кредитная карта является удобным современным финансовым инструментом, который позволяет иметь под рукой денежные средства, когда они будут необходимы. Грамотное использование этого […]
• Правила как определить склонение интернет проект BeginnerSchool.ru Сайт для детей и их родителей Три склонения имен существительных В предыдущей статье рубрики «основные правила» мы изучили склонение имен существительных по падежам. В этой статье мы […]
• Разрешение на применение в рф Разрешение Ростехнадзора (разрешение на применение) • Разрешение на применение оборудования (так называемое разрешение Ростехнадзора) является базовым звеном действующей системы обеспечения безопасности на предприятиях […]
• Объясните значения слова закон Значение слова Объясните значение слов: закон, ростовщик, раб-должник. объясните значение слов: закон, ростовщик, раб-должник. ВкУсНаЯ КлУбНиКа (Гость) Школы Вопросы по теме 1.На какие 3 типа можно разделить […]

Еще в неолите наши предки изобрели первое дальнобойное оружие – лук и стрелы, используя упругость изогнутой ветки дерева; потом катапульты и баллисты, построенные для метания больших камней, использовали упругость канатов, свитых из растительных волокон или даже из женских длинных волос. Эти примеры доказывают, что проявление упругих свойств было давно известно и давно использовалось людьми. Но понимание того, что любое твердое тело под действием даже небольших нагрузок обязательно деформируется, хотя и на очень малую величину, впервые появилось в 1660 у Роберта Гука, современника и коллеги великого Ньютона. Гук был выдающимся ученым, инженером и архитектором. В 1676 он сформулировал свое открытие очень кратко, в виде латинского афоризма: «Ut tensio sic vis», смысл которого состоит в том, что «какова сила, таково и удлинение». Но опубликовал Гук не этот тезис, а только его анаграмму: «ceiiinosssttuu». (Таким образом тогда обеспечивали приоритет, не раскрывая сути открытия.)

Вероятно, в это время Гук уже понимал, что упругость – универсальное свойство твердых тел, но считал необходимым подтвердить свою уверенность экспериментально. В 1678 вышла книга Гука, посвященная упругости, где описывались опыты, из которых следует, что упругость есть свойство «металлов, дерева, каменных пород, кирпича, волос, рога, шелка, кости, мышцы, стекла и т.п.» Там же была расшифрована анаграмма. Исследования Роберта Гука привели не только к открытию фундаментального закона упругости, но и к изобретению пружинных хронометров (до того были только маятниковые). Изучая различные упругие тела (пружины, стержни, луки), Гук установил, что «коэффициент пропорциональности» (в частности, жесткость пружины) сильно зависит от формы и размеров упругого тела, хотя материал играет решающую роль.

Прошло более ста лет, в течение которых опыты с упругими материалами проводили Бойль, Кулон, Навье и некоторые другие, менее известные физики. Одним из основных опытов стало растяжение пробного стержня из изучаемого материала. Для сравнения результатов, полученных в разных лабораториях, нужно было либо использовать всегда одинаковые образцы, либо научиться исключать слияние размеров образца. И в 1807 появилась книга Томаса Юнга, в которой был введен модуль упругости – величина, описывающая свойство упругости материала независимо от формы и размеров образца, который использовался в опыте. Для этого нужно силу P, приложенную к образцу, разделить на площадь сечения F, а произошедшее при этом удлинение D l разделить на первоначальную длину образца l. Соответствующие отношения – это напряжение s и деформация e .

Теперь закон Гука о пропорциональности можно записать в виде:

Коэффициент пропорциональности Е называется модулем Юнга, имеет размерность, как у напряжения (МПа), а обозначение его есть первая буква латинского слова elasticitat – упругость.

Модуль упругости Е – это характеристика материала того же типа, как его плотность или теплопроводность.

В обычных условиях, чтобы продеформировать твердое тело, требуется значительная сила. Это означает, что модуль Е должен быть большой величиной – по сравнению с предельными напряжениями, после которых упругие деформации сменяются пластическими и форма тела заметно искажается.

Если измерять величину модуля Е в мегапаскалях (МПа), получатся такие средние значения:

Закон Гука формула. Модуль Юнга

Для большинства конструкционных материалов между напряжением () и продольной деформацией () до определенного предела нагружения существует линейная зависимость

Закон Гука : Напряжение пропорционально деформации.

Впервые Закон Гука был опубликован в виде анаграммы английским ученым Робертом Гуком (1635 – 1703 гг.). При правильной расстановке букв анаграмма читается: «Каково удлинение, такова и сила».

К такому же заключению в 1680 г., независимо от Гука, пришел французский ученый Эдмон Мариотт.

Коэффициент пропорциональности (E) в формуле закона Гука называется модуль продольной упругости или модуль Юнга – по имени английского ученого Томаса Юнга. Значение модуля Юнга для данного материала устанавливается опытным путем. В справочниках обычно приводятся среднее значение модуля Юнга .

Необходимо отметить, что некоторые материалы не подчиняются закону Гука , например, кожа, ткани. Такие материалы, как, например, чугун, только с некоторым приближением можно считать подчиняющимся закону Гука. Но даже и те материалы, которые подчиняются закону Гука, перестают ему следовать при достижении деформации определенного значения.

Из закона Гука видно: чем больше модуль Юнга , тем меньше (при том же значении напряжения) деформация материала. Следовательно, модуль продольной упругости характеризует жесткость материала при растяжении (сжатии). Из формулы закона Юнга видно, что модуль Юнга измеряется в тех же единицах, что и нормальное напряжение ().

Так, например, для всех марок сталей МПа.

Закон Гука и модуль Юнга

Прежде чем решать следующую задачу, поговорим о силах, которые возникают при попытках сжать или растянуть металлические стержни.

Деформации растяжения и сжатия.Если к однородному, закрепленному с одного конца стержню приложить силу вдоль его оси в направлении от стержня, то он подвергнется деформации растяжения (рис. 1.1). Де­формацию при этом характеризуют абсолютным удлинением Dl = l – l₀ и относительным удлинением , где l₀ – начальная длина, а l – конечная длина стержня. При малых деформа­циях (|Dl| 1 тела:

, (1.3)

где s – напряжение; F_yпp – модуль силы упругости; S – площадь поперечного сечения.

1 Сечение тела производится плоскостью, перпендикулярной на­правлению силы упругости. При этом предполагается, что деформа­ция тела во всех участках сечения одинакова.

В СИ за единицу напряжения принимается паскаль (Па):

Заметим, что в формуле (1.3)иногда удобно модуль силы упругости заменить на модуль F внешней деформирующей си­лы, уравновешивающей силу упругости.

Закон Гука.Многочисленные опыты показывают, что при малых дефор­мациях напряжение s прямо пропорционально относительно­му удлинению. Эта зависимость на­зывается законом Гука. Его можно записать так:

Относительное удлинение в формуле (1.4) взято по моду­лю, так как закон Гука справедлив как для деформации растя­жения, так и для деформации сжатия, когда e

Действительно, подставив в (1.4) и , получим . Откуда

. (1.6)

, (1.7)

Таким образом, согласно (1.7) жесткость k стержня прямо пропорциональна произведению модуля Юнга на площадь поперечного сечения стержня и обратно пропорциональна его длине.

Т а б л и ц а 1.2

Дата добавления: 2016-04-11 ; просмотров: 2225 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

mlegal.ru