Зубчатая передача расчет – Расчет зубчатой передачи
alexxlab | 27.02.2019 | 0 | Вопросы и ответы
Кинематический и силовой расчеты зубчатой передачи.
Расчетная окружная скорость v, м/с, цилиндрической передачи
конической передачи
где ω — угловая скорость зубчатого колеса, рад/с;
n — частота вращения зубчатого колеса, мин-1;
dw — начальный диаметр цилиндрического зубчатого колеса, м;
dwm — начальный средний диаметр конического зубчатого колеса, м.
Учитывая, что скорость точек начальных окружностей, находящихся в зацеплении зубчатых колес, одинакова, имеем v=ω1dw1/2=ω2dw2/2. Выражая диаметры dw1 и dw2 через модуль и соответствующие числа зубьев, получаем v=ω1(mz1/2)=ω2(mz2/2). Отсюда передаточное отношение i пары зубчатых колес (для одноступенчатой передачи) с учетом формулы
где ω1, n1, dw1 z1 и T1 — соответственно угловая скорость, частота вращения, начальный диаметр, число зубьев и крутящий момент ведущего зубчатого колеса;
ω2, n2, dw2 z2 и T2 – то же, ведомого зубчатого колеса;
η — к. п. д. передачи.
Так как для конической зубчатой передачи передаточное отношение см. предыдущую формулу
то, как следует из рис.
где δ1 – для ведущего, а δ2 – для ведомого зубчатого колеса.
Отношение числа зубьев z2 колеса к числу зубьев z1 шестерни называется передаточным числом зубчатой передачи u.
Таким образом,
Если ведущим зубчатым колесом является шестерня, то для такой передачи передаточное отношение и передаточное число представляют собой одну и ту же величину. Рекомендуемые максимальные значения передаточного числа одноступенчатой зубчатой передачи:
- Цилиндрической в закрытом корпусе: ≤12,5
- Конической в закрытом корпусе: ≤6,3
- Открытой: ≤15
| Закрытая 6-6 и 7-й степеней точности с жидкой смазкой | Закрытая 8-й степени точности с жидкой смазкой | Открытая с густой смазкой | |
|---|---|---|---|
| Цилиндрическая | 0,98 | 0,97 | 0,96 |
| Коническая | 0,97 | 0,96 | 0,94 |
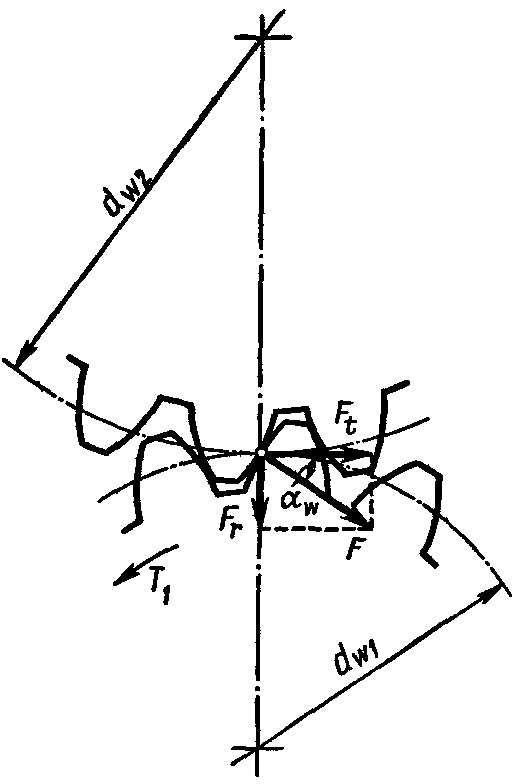 Рис. 1
Рис. 1
Окружная сила зубчатой передачи Ft:
цилиндрической (рис. 1)
конической (рис. 2)
 Рис. 2
Рис. 2
Передаваемые зубчатыми колесами крутящие моменты определяют по формулам
и
.
Так как силы трения между зубьями малы, то силу давления между ними F можно считать направленной по общей нормали к соприкасающимся поверхностям зубьев, т. е. по линии зацепления (см. рис. 1). Составляющие этой силы: в цилиндрических прямозубых (рис. 1) и шевронных передачах – окружная сила Ft и радиальная сила Fr; в конической прямозубой (рис. 2) и цилиндрической косозубой (рис. 3) передачах – окружная сила Ft радиальная сила Fr, и осевая сила Fa.
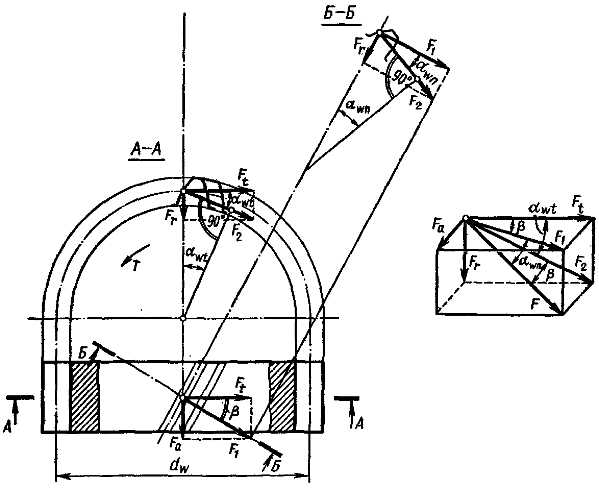 Рис. 3
Рис. 3
Радиальная сила, действующая на зубчатое колесо прямозубой цилиндрической передачи (рис. 1),
косозубой (рис. 3), или шевронной, передачи
конической прямозубой передачи (рис. 2)
конической прямозубой передачи (рис. 2)
Сила давления между зубьями прямозубой цилиндрической передачи (рис. 1)
metiz-bearing.ru
Лекция 6. Расчеты зубчатых передач
2. Расчетные удельные нагрузки
При составлении расчетных схем для зубчатых передач схематизацию нагрузки выполняют путем введения расчетной удельной нагрузки, под которой понимают величину условной нагрузки от окружного усилия Ft, приходящейся на единицу рабочей ширины зубчатого колеса. Если обозначить расчетную удельную нагрузку черезq, то ее величину можно определить из выражения
где K – коэффициент нагрузки;bw – рабочая ширина зубчатого колеса. Коэффициент нагрузки вводится с целью компенсации неучтенных
дополнительных напряжений, возникающих из-засложного нагружения зубьев, особенностей конструкции и эксплуатации колес. Проблема выбора значения коэффициента нагрузки в зубчатых передачах – одна из сложных.
По методике расчета эвольвентных зубчатых передач, рекомендованной ГОСТ 21354–75,значения коэффициента нагрузки определяются по следующим зависимостям:
KHKHβ KHα KHv, | KFKFβ KFα KFv, | (6.4) |
где KHβ,KFβ – коэффициенты концентрации нагрузки по ширине зубчатого венца соответственно при контактной выносливости и изгибе;KHα,KFα – коэффициенты, учитывающие распределение нагрузки между зубьями соответственно при контактной выносливости и изгибе;KHν,KFν – коэффициенты, учитывающие динамическую нагрузку в зацеплении соответственно при контактной выносливости и изгибе.
Для определения величин коэффициентов в справочной литературе приводятся соответствующие графики, таблицы, формулы и аппроксимирующие зависимости. Рассмотрим эти зависимости.
Коэффициент распределения нагрузки между зубьями определяют по зависимостям для косозубых колес:
KHα (0, 0026ST 0, 013)v 0, 027ST 0,84;
(6.5)
KFα | 4 εα | 1 ST 5 | , |
| 4εα | ||
|
|
|
где ST – степень точности передачи;v – окружная скорость зубьев; εα – коэффициент торцевого перекрытия.
Для прямозубых колес значения обоих коэффициентов принимаются равными единице.
studfiles.net
Расчет зубчатых передач | SNAU СНАУ
Расчет зубчатых передач.
1. Цель работы: Студенты должны в ходе практических занятий ознакомиться с конструкциями зубчатых колес и основами их расчетов, изучить особенности расчета открытых зубчатых передач.
2. Типовые задачи:
Пример № 1.
Задача. Рассчитать косозубых цилиндрическую зубчатую передачу одноступенчатого редуктора по следующим данными: передача передает мощность Р1 = 12 кВт при угловой скорости ведущего вала ω1 = 150 рад / с; передаточное число передачи u = 3,6; передача нереверсивные с возможными кратковременными перегрузками до 200% от номинального, срок службы передачи ограничен. Расчет вести к определенным межосевого расстояния Передачи.
Решения. 1. Параметры нагрузки зубчатой передачи.
Номинальный крутящий момент на ведущем валу
Т1 = Р1 / ω1 = 12 * 103/150 = 80 Нм.
При кратковременной перегрузки до 200% максимальный крутящий момент на ведущем валу
Тmax = 2Т1 = 2 * 80 = 160 Нм
Угловая скорость ведомого Вала
Ω2 = ω1 / u = 150/3, 6 = 41,7 рад / с.
Номинальный Крутящий момент приведенном вала
Здесь h = 0,97 — КПД редуктора.
Материалы зубчатых колес.
Для изготовления шестерни и колеса выбираем углеродистую сталь 45 с термообработкой — улучшение:
— для шестерни твердость поверхности Н1 = 285НВ, sВ1 = 890 МПа, s1 = 650 МПа при диаметре заготовки до 80мм;
— для колеса твердость поверхности зубьев Н2 = 235 … 262 НВ (наиболее вероятная твердость Н2 = 250НВ), sВ2 = 780 МПа, s2 = 540 МПа.
3.Допустими напряжения для расчета зубчатой передачи.
А) Допустимые контактные напряжения.
Границы контактной выносливости зубьев шестерни и колеса
SНlimb1 = 2 * Н1 +70 = 2 * 285 +70 = 640 МПа;
SНlimb2 = 2 * Н2 +70 = 2 * 250 +70 = 570 МПа.
Допустимые контактные напряжения для зубьев шестерни и колеса при коэффициенте ZR = 0,95 и коэффициенте запаса s = 1,1
[S] strong = s Нlimb1 * ZR / s = 640 * 0,95 / 1,1 = 553 МПа;
[S] strong = s Нlimb2 * ZR / s = 570 * 0,95 / 1,1 = 492 МПа.
В расчет принимаем меньшее из двух полученных значений [s] H = 492 МПа.
Допустимого предельного контактное напряжение
[S] Нmax = 2,8 * sт2 = 2,8 * 540 = 1512 МПа.
Б) Допустимые напряжения зубцов на изгиб.
Предела выносливости при изгибе
SFlimb1 = 1,8 * Н1 = 1,8 * 285 = 513 МПа;
SFlimb2 = 1,8 * Н2 = 1,8 * 250 = 450 МПа.
Допустимое напряжение на изгиб зубьев шестерни и колеса при коэффициенте запаса sF = 2,2:
[S] F1 = sFlimb1 / sF = 513/2.2 = 233 МПа;
[S] F2 = sFlimb2 / sF = 450/2.2 = 204 МПа.
Для зубцов шестерни и колеса предельное допустимое напряжение на изгиб
[S] F1max = 4.8 * strong / sF = 4.8 * 285/2.2 = 622 МПа;
[S] F2 max = 4.8 * strong / sF = 4.8 * 250/2.2 = 545 МПа.
Проектный расчет передачи.
В проектном расчете предварительно берем коэффициент ширины венца Yba = 0,40 и соответственно Ybd = 0,5 * Yba * (u +1) = 0,5 * 0,4 * (3,6 +1) = 0,92.
По графикам на рис.23.4.залежно от Ybd (симметричное размещение зубчатых колес относительно опор валов и твердость Н <350НВ) определяем коэффициент КHβ = 1,1.
Вспомогательный коэффициент Ка = 43 МПа1 / 3 для стальных косозубых колес.
По формуле минимальная межосевое расстояние передачи
Awmin = Ka (u + 1) = 43 (3.6 +1)= 125 мм.
Угол наклона линии зубьев предварительно берем β = 150, число зубцов шестерни принимаем Ζ1 = 21, а число зубьев колеса Ζ2 = u Ζ1 = 3.6х21 = 75,6, т. е. Ζ1 = 76.
Фактическое передаточное число передачи u = Ζ2 / Ζ1 = 76/21 = 3.62.
Модуль зубьев
M `n = (2awmincosβ) / (z1 + z2) = (2х125cos150) / (21 +76) 2,49 мм.
Стандартный модуль mn = 2,5 мм.
Фактический угол наклона линии зубцов
Cosβ = mn (z1 + z2) / (2aw) = 2,5 (21 +76) / (2х125) = 0,97; β = 14,070.
5. предыдущие значения некоторых параметров передачи
Делительные диаметры шестерни и колеса
D1 = mnz1/cosβ = 2.5х21 / 0,97 = 54,12 мм;
D2 = mnz2/cosβ = 2.5х76 / 0,97 = 195,88 мм.
Ширина зубчатых венцов
B2 = Ybaaw = 0.4х125 = 50 мм b1 = b2 + 2мм = 52 мм.
Круговая скорость зубчатых колес
V = 0.5 ω1d1 = 0.5х150х54, 12х10-3 = 4,06 м / с.
По рекомендациям принимаем восьмой степени точности для всех показателей колес и передачи.
Эквивалентные числа зубьев шестерни и колеса будут такими:
ZV1 = z1 / cos3 β = 21 / 0.973 = 23; zV2 = z2 / cos3 β = 76 / 0,973 = 83,27.
Коэффициент торцового перекрытия
Εα = [1.88-3.2 (1/z1 +1 / z2)] cosβ = {1.88-3.2 (1/21 +176)] 0.97 = 1.63.
Коэффициент осевого перекрытия зубьев
Εβ = (b2sinβ) / (Mn) = (52sin14.070) / (3.14х2, 5) = 1,6.
Круговая сила в зацеплении зубчатых колес
Ft = 2T1 / d1 = 2х80х103/54, 12 = 2956 Н.
6.Расчет активных поверхностей зубьев на контактную выносливость.
Для расчета необходимо определить следующие коэффициенты
= 275 МПа1/2- коэффициент, учитывающий механические свойства;
ΖН = 1,77 cos β = 1,77 х0, 97 = 1,72;
Ζε === 0,78 при ε> 0,9;
КНβ = 1,1;
КНε = 1,04;
Расчетное контактное напряжение
ΣН = ΖМ ΖН Ζε=
= 275х1, 72х0, 78= 466МПа
Устойчивость зубцов против усталостного выкрашивания их активных поверхностей обеспечивается, потому σН = 466 МПа <[σН] = 466 МПа и лежит в допустимых пределах.
7. Расчет активных поверхностей зубьев на контактную прочность.
Во время действия максимальной нагрузки
ΣНmax = σН = 466= 659 МПа.
Контактная прочность также обеспечена, поскольку
ΣНmax = 659 МПа <[σ] Нmax = 1512 МПа.
8. Расчет зубьев на выносливость при изгибе,
Расчетные коэффициенты будут такими:
YF1 = 3.96; YF2 = 3.61-коэффициенты формы зубцов;
Yβ = 1-β/1400 = 1-14.070/1400 = 0.90-коэффициент наклона зубцыв;
КFβ = 1,1 и КFV = 1,14.
Определим расчетное напряжение в зубцах шестерни и колеса
ΣF1 = YF1 Yβ= 3.96х0, 90= 106 МПа;
ΣF2 = YF2 Yβ= 3,61 х0, 90= 97 МПа.
Выносливость зубьев при изгибе также обеспечивается, поскольку σF1 и σF2 меньше соответственно [σF1] = 233 МПа и [σF2] = 204 МПа.
9. Расчет зубьев на прочность при изгибе максимальной нагрузкой.
ΣF1 max = σF1 (Т1 max / Т1) = 106 (160/80) = 212 МПа;
ΣF2 max = σF2 (Т1 max / Т1) = 97 (160/80) = 194 МПа.
Здесь также прочность обеспечивается, потому σF1max и σF2max меньше соответствующих допустимых напряжений [σ] F1max = 622 МПаи [σ] F2max = 545 МПа.
10. размерных параметров передачи,
Размеры элементов зубцов:
— высота головки зубца ha = mn = 2.5 мм;
— высота ножки зубца hf = 1.25 mn = 1.25х2, 5 = 3,125 мм;
— высота зубца h = 2,25 mn = 2,25 х2, 5 = 5,625 мм;
— радиальный зазор с = 0,25 mn = 0,25 х2, 5 = 0,625 мм;
— угол профиля зубцов αn = 200.
Размеры венцов зубчатых колес:
— делительные диаметры d1 = 54.12 мм и d2 = 195,88 мм:
— диаметры вершин зубьев
Da1 = d1 +2 mn = 54.12 +2 х2, 5 = 59,12 мм;
Da2 = d2 +2 mn = 195,88 + 2х2, 5 = 200,88 мм.
— диаметры впадин
Df1 = d1-2 mn = 54.12-2х2, 5 = 47.87 мм;
Df2 = d2-2 mn = 195,88-2х2, 5 = 189,63 мм.
— ширина зубчатых венцов b1 = 52 мм, b2 = 50 мм.
Межосевое расстояние передачи
AW = 0.5 mn (z1 + z2) / cosβ = 0.5х2, 5 (21 +76) / 0,97 = 125 мм.
11. Расчет сил в зацеплении зубьев передачи
Круговая сила Ft = 2956 Н
Радиальная сила
Fr = Ft = tg αn / cosβ = 2956 tg200/0.97 = 1109 H
Осевая сила
Fа = Ft = tgβ = 295614,07 = 741 Н.
3. П Итання для самопроверки
1. Дайте определение шестерни и зубчатого колеса.
2. Что называется круговым шагом зубцов и как он сказывается?
3. Что называется нормальным шагом зубцов и как он сказывается?
4. Объясните, как рассчитать круговой модуль зубчатой передачи?
5. Как рассчитать нормальный модуль зубчатой передачи?
6. Объясните, какой модуль — круговой или нормальный — является стандартным?
7.Как зависимость существует между круговым и нормальным модулем?
8. Какой из модулей больше размером: круговой или нормальный?
9. Как вычислить передаточное число зубчатой передачи?
10. Какие материалы применяют для изготовления зубчатых колес?
2snau.ru
Расчет зубчатой передачи
1. Выбор материалов зубчатых колес
Шестерня:
Материал — Сталь 45;
Термическая обработка — улучшение;
Твердость поверхности зуба — 269-302HB;
Колесо:
Материал — Сталь 45;
Термическая обработка — улучшение;
Твердость поверхности зуба — 235-262HB;
2. Определение допускаемых напряжений
2.1 Допускаемые контактные напряжения
HPj=
где j=1 для шестерни,j=2 для колеса;
Hlimjпредел контактной выносливости (табл.5 [1]),
Hlim1= 641 МПа
Hlim2= 567 МПа
SHjкоэффициент безопасности (табл.5 [1]),
SH1= 1,1
SH2=1,1
KHLj– коэффициент долговечности;
KHLj=1,
здесь NH0j– базовое число циклов при действии контактных напряжений (табл.4 [1]),
NH01=
NH02=
Коэффициент эквивалентности при действии контактных напряжений определим по табл.6 [1] в зависимости от режима нагружения: h=0,5
Суммарное время работы передачи в часах
th= 365×L×24×Kг×Кс×ПВ,
где Kг– коэффициент использования передачи в течение года;
Kс– коэффициент использования передачи в течение суток;
L– срок службы передачи в годах;
ПВ – продолжительность включения;
Kг= 0,7Kс= 0,5L= 6 ПВ= 70%th=12877
Суммарное число циклов нагружения:
Nj= 60×nj×c×th,
где с– число зацеплений колеса за один оборот,с= 1;
nj– частота вращенияj-го колеса,n1=420,435 мин-1,n2= 150,155 мин-1;
N1=N2=
Эквивалентное число циклов контактных напряжений, NHEj=hNΣj;
NHE1=NHE2=
Коэффициенты долговечности
KHL1= 1KHL2= 1
Допускаемые контактные напряжения для шестерни и колеса
HP1= 582,7 МПаHP2= 515,5 МПа
Для прямозубых передач HP = HP2
Допускаемые контактные напряжения передачи:
HP=515,5 МПа
2.2. Допускаемые напряжения изгиба
FPj=,
где Flimjпредел выносливости зубьев при изгибе (табл.7 [1]),
Flim 1= 499,6 МПаFlim 2= 434,9 МПа
SFjкоэффициент безопасности при изгибе (табл.7 [1]),
SF1= 1,7SF2 = 1,7
KFCjкоэффициент, учитывающий влияние двухстороннего приложения нагрузки, (табл.7 [1])
KFC1= 1KFC2= 1
KFLjкоэффициент долговечности при изгибе:
KFLj=1
NF0– базовое число циклов при изгибе;NF0 = 4×106
NFEj– эквивалентное число циклов напряжений при изгибе;
NFEj=FjNΣj.
Коэффициент эквивалентности при действии напряжений изгиба определяется по табл.6[1] в зависимости от режима нагружения и способа термообработки
F= 0,3
NFE1 = NFE2 =
KFL1 = 1 KFL2 = 1
Допускаемые напряжения изгиба:
FP1== 293,9 МПа
FP2== 255,8 МПа
Расчет цилиндрической зубчатой передачи
Межосевое расстояние определяем из условия контактной прочности:
=(u+1),
где – коэффициент вида передачи,= 450
KН– коэффициент контактной нагрузки примемKН = 1,148
Коэффициент ширины зубчатого венца = 0,3125 (ряд на с.4 [1]).
Расчетное межосевое расстояние = 158,73 мм
Округлим до ближайшего большего стандартного значения (табл.2 [1]) ГОСТ 2185-66=160 мм
Модуль выберем из диапазона
m== 1,6…3,2
Округлим mдо стандартного значения (табл.1 [1]) ГОСТ 9563-60:m=2
Суммарное число зубьев:
Z=,
Z=
Число зубьев шестерни:
Z1== 42
Число зубьев колеса:
Z2= Z–Z1=118
Фактическое передаточное число:
uф ==
Значение uф не должно отличаться от номинального более чем на 2.5 % приu4.5 и более чем на 4 % приu > 4.5
u=100= 0,36%
Коэффициенты смещения шестерни и колеса: x1= 0x2= 0
Расчетная ширинaвенца колеса:
bw2== 50 мм
Округляем bw2 до ближайшего числа из ряда на с.10 [1]:
bw2 = 50 мм ГОСТ 6636-69
Ширину венца шестерни bw1примем на 5 мм больше чемbw2:
bw1 =55 мм
Определим диаметры окружностей зубчатых колес:
Диаметры делительных окружностей прямозубых колес dj=mZj,
d1= 84 ммd2=236 мм
Диаметры окружностей вершин при x=0:daj=dj+2m(1+xj):
da1 =88 мм da2 =240 мм
Диаметры окружностей впадин dfj=dj-2m(1,25-xj):
df1=79 ммdf2=231 мм
Вычислим окружную скорость в зацеплении
V== 1,85 м/с
Степень точности передачи выберем по табл.8 [1]: nст= 8
studfiles.net
Расчёт конической зубчатой передачи
24
Министерство путей сообщения Российской Федерации
Департамент кадров и учебных заведений
Самарская государственная академия путей сообщения

Кафедра механики
Методические указания по курсу
“Детали машин и основы конструирования”
Для студентов специальностей 150700 – Локомотивы
150800 – Вагоны
170900 – Подъёмно-транспортные,
строительные и
дорожные машины и
оборудование
181400 – Электрический транспорт
железных дорог.
Составители: Толстоногов А.А.,
Глобенко Е.В.,
Назарова Н.В.,
Жарков М.С.
Самара 2004 г.
УДК 621.81.
Методические указания к выполнению расчётно-графических работ и курсового проекта по дисциплине “Детали машин и основы конструирования” для студентов специальностей 150700, 150800, 170900 / Составители Толстоногов А.А., Глобенко Е.В., Назарова Н.В., Жарков М.С. Самара, СамГАПС, 2004.- 24 с.
Утверждено на заседании кафедры, протокол №3. от 13.10.2004г.
Печатается по решению редакционно-издательского совета академии.
Составители: Толстоногов Андрей Арленович,
Глобенко Евгений Викторович,
Назарова Надежда Владимировна,
Жарков Михаил Сергеевич.
Рецензенты: Доцент кафедры ОКМ СГАУ Васин В.Н.,
Профессор кафедры механики СамИИТ Янковский В.В.
Редактор: Шимина И.А.
Подписано в печать 33.33.2002 Формат 60х84 1.16
Бумага писчая. Усл. печ. л
Тираж 100 экз. Заказ №
© Самарская Государственная Академия Путей Сообщения, 2004.
Оглавление введение 4
1. Методика расчета конической прямозубой передачи 5
Выбор материала зубчатых колес 5
Определение допускаемых напряжений 5
Определение чисел зубьев и передаточнго числа 6
Определение внешнего делительного диаметра колеса 7
Расчёт геометрических параметров зубчатой передачи 8
Проверочный расчёт контактных напряжений
на рабочих поверхностях зубьев 9
Определение сил в коническом зацеплении 10
Проверочный расчет зубьев на выносливость
по напряжениям изгиба 10
studfiles.net
Расчет зубчатой передачи – часть 2
4.1 Определяем делительный диаметр колеса
где
определены заранее – коэффициент, учитывающий распределение нагрузки по ширине венца, для прирабатывающихся колес равен 1;VН – коэффициент вида конических колес, для прямозубых равен 1.
Тогда
Полученное значение внешнего делительного диаметра колеса округляем до ближайшего значения из ряда нормальных линейных размеров табл.13.15 (3).
dе4 =250 мм
4.2. Определяем углы делительных конусов шестерни и колеса
4.3. Определяем внешнее конусное расстояние
4.4. Определяем ширину зубчатого венца
4.5. Определяем внешний окружной модуль
где Кfb – коэффициент, учитывающий распределение нагрузки по ширине венца, равен 1; (3)
Vf = 0,85 – коэффициент вида конических колес. (3)
Так как передача открытая, увеличиваем значение модуля на 30%, то есть m = 5 мм.
4.6. Определяем число зубьев колеса и шестерни
4.7. Определяем фактическое передаточное число.
4.8. Определяем внешние диаметры шестерни и колеса:
делительный
;вершин зубьев
=109,28 мм; = 253,71 мм;впадин зубьев
= 90,72 мм; = 246,3 мм;средний делительный диаметр
=85,7 мм; 214,25 мм.5. Определение геометрических размеров и расчет на прочность выходного вала
5.1. Определяем силы действующие в зацеплении конической прямозубой передачи:
окружная
радиальная
= 612 Н,осевая
= 1530 Н.5.2 Выбираем материал для вала по таблице 3.2 (3). Это сталь 45 улучшенная, со следующими механическими характеристиками:
допускаемое напряжение на кручение
5.3. Ориентировочно определяем геометрические размеры каждой ступени вала:
– диаметр выходной части
Принимаем d1 = 45 мм.
Исходя из этого принимаем диаметр под подшипником d2 = 50 мм.
5.4. Выбираем предварительно подшипники качения. По таблице 7.2 (3)для конической передачи при n<1500 об/мин применяется подшипник роликовый конический однорядный. Выбираем типоразмер подшипника по величине диаметра внутреннего кольца, равного диаметру d2 = 50мм. Это подшипник легкой широкой серии 7510: d = 50мм, D = 90мм, Т = 25 мм, угол контакта 160 , Cr =62 kH.
5.5. Вычерчиваем ступени вала по размерам, полученным вориентировочном расчете и определяем расстояния между точками приложения реакций подшипников.
5.6. Вычерчиваем схему сил в зацеплении конической передачи.
5.7. Определяем реакции опор:
а) вертикальная плоскость
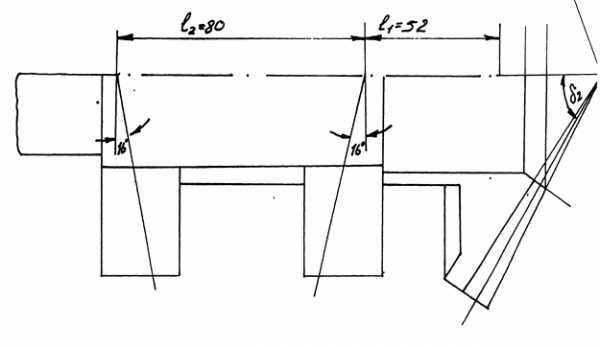
б) строим эпюру изгибающих моментов в характерных сечениях A, B, C(рис. 5.1)
в) горизонтальная плоскость,
Проверка:
г) строим эпюры изгибающих моментов в характерных сечениях A, B, C (Рис.5.1)
MYC = 0,
MYB = Ft * l1 = 4580 * 52 = 238160 Нмм,
MAY = 0,
д) строим эпюры крутящих моментов(Рис.5.1)

5.8. Определяем суммарные реакции опор
5.9. Определяем суммарные изгибающие моменты в наиболее нагруженном сечении В
5.10. Определяем приведенный момент
5.11. Определяем диаметр вала исходя из третьей теории прочности
где
= 160 Мпа – допускаемое значение напряжений для стального вала.Полученное значение вала под подшипником округляем до ближайшего стандартного
d = 40 мм.
В результате расчета уменьшим диаметр вала под колесом до 45 мм.
5.12.Рассчитываем шпонку на срез и смятие.
Для закрепления на валах колес применяют шпонки. Размеры призматических шпонок выбираем в зависимости от диаметра вала по ГОСТ 23360-78, b*h = 14*9 мм, 1 = 38 мм.
5.13. Условие прочности при деформации смятия проверяется по формуле
где T – передаваемыйвалом крутящий момент;
– допускаемое напряжение на смятиепо табл.3.2(3)260 Н/мм25.14. Условие прочности при деформации среза проверяетсяпо формуле
где
– допускаемое напряжение на срез по табл. 3.2 (3) 80 Н/мм26. Проверочный расчет подшипников
6.1. Пригодность подшипников определяется сопоставлением расчетной динамической грузоподъемности с базовой. В результате расчетов имеем : угловая скорость вала
, осевая сила в зацеплении –Fа = 1530 Н, реакции в подшипниках – RXB = 3400 Н, RYB = 7557 Н. В результате расчета нам необходимо уменьшить размеры ранее выбранного подшипника, это подшипник легкой широкой серии 7508 c характеристиками: d = 40мм, D = 80 мм, Т = 25 мм, Сr = 56 кН, е = 0,381, У = 1,575, угол контакта 14°.mirznanii.com
Геометрический расчет зубчатой передачи и показателей качества в подсистеме “GCG&FQ” автоматизированной системы “Кобра”
Разделы: Информатика, Технология
Зубчатые передачи являются неотъемлемой частью большинства механизмов и машин, используемых в промышленности, сельском хозяйстве, транспорте, в быту. Они применяются в качестве передаточного устройства для преобразования моментов или движения. Наиболее распространены эвольвентные цилиндрические передачи внешнего зацепления прямозубые и косозубые.
При проектировании зубчатых передач следует добиваться рационального варианта для заданных условий работы передачи в проектируемом механизме. Одновременно получить все наилучшие показатели качества в передаче невозможно, поэтому перед началом проектирования следует четко сформулировать требования по критериям оптимизации, т.к. от этого зависит назначение коэффициентов смещения исходного контура при нарезании зубчатого колеса. В случае свободного выбора межосевого расстояния имеется значительно больше возможностей для проектирования рациональной передачи, чем в случае фиксированного заданного межосевого расстояния.
В докладе кратко изложены алгоритмы геометрического расчёта передач и определения показателей их качества, которые зависят от параметров инструмента и его положения при нарезании зубчатых колёс.
Геометрический расчёт зубчатых передач выполняется в соответствии со стандартами традиционно. Расчёт с элементами оптимизации выполняется на персональном компьютере (ПК) в подсистеме «GCG&FQ» (Геометрический расчет зубчатой передачи и показателей качества) системы «КОБРА» по одному из следующих условий: минимальные габариты передачи, наибольший коэффициент перекрытия, наименьшее скольжение на ножке шестерни.
Порядок расчета
1. Определить суммарное число зубьев колес
(округлить до ближайшего целого числа).
Для прямозубой передачи принять угол наклона зуба .
2. Рассчитать число зубьев шестерни
(округлить до ближайшего целого числа).
Число зубьев должно быть больше минимального числа из условия отсутствия подрезания, определенного по уравнению (30)
.
Если это условие не выполняется, то следует изменить межосевое расстояние.
3. Определить число зубьев колеса:
4. При расчете зубчатых передач передаточное отношение можно выразить через отношение чисел зубьев:
.
Полученное значение необходимо сравнить с заданным передаточным отношением. Если расхождение составит более 5 %, следует изменить и в пределах .
5. Определить делительное межосевое расстояние
.
В зубчатой передаче без смещения межосевое расстояние равно делительному расстоянию:
6. Угол зацепления передачи найти по формуле
.
В зубчатой передаче без смещения угол зацепления равен углу профиля исходного контура:
.
7. Определить коэффициент суммы смещений:
.
Эвольвентные функции углов и другие тригонометрические функции определяются по специальной подпрограмме в системе «КОБРА» (рис. 1, 2).
Рис.1. Выбор подсистемы «Определение тригонометрических функций»
Рис.2. Определение тригонометрических функций
8. Выбрать коэффициенты смещения по ГОСТ 16532-70 в соответствии с заданными условиями проектирования или по одному из условий рационального проектирования в подсистеме «GCG&FQ» системы «КОБРА».
Для предварительного расчета коэффициент смещения шестерни можно определить по следующим условиям:
9. Вычислить коэффициент смещения колеса:
.
10. Выполнить расчет основных геометрических параметров цилиндрической эвольвентой зубчатой передачи в соответствии с ГОСТ 16532-70. Расчетные формулы для цилиндрической прямозубой передачи приведены в таблице 1.
Таблица 1
Основные термины, обозначения и расчетные зависимостигеометрических параметров зубчатой передачи
Окончание таблицы 4
xn--i1abbnckbmcl9fb.xn--p1ai

