Период колебаний зависит от амплитуды колебаний – Колебательное движение. Амплитуда, период и частота колебаний » Народна Освіта
alexxlab | 20.02.2020 | 0 | Разное
Колебательное движение. Амплитуда, период и частота колебаний » Народна Освіта
Еще в древности люди, наблюдая за Солнцем и Луной, определили единицы времени: год, месяц, сутки и др. Были созданы солнечные часы, затем водяные, огневые, песочные. Однако настоящая революция в конструкции часов произошла после выяснения свойств колебательного движения. Каких именно — узнаете из данного параграфа.
Знакомимся с колебательным движением
Подвесим груз на нить, отклоним его от положения равновесия и отпустим. Груз начнет колебаться, то есть двигаться от одного крайнего положения к другому, повторяя это движение через некоторый интервал времени. Таким образом, колебательное движение имеет важную общую черту с равномерным движением по окружности: оба движения являются периодическими (рис. 13.1).
Изучаем маятники
Груз, колеблющийся на нити или на пружине, — пример простейшего маятника.
Маятник — это твердое тело, которое совершает колебания вследствие притяжения к Земле или в результате действия пружины.
Маятники используют во многих физических приборах. Особенно важным является использование маятников в часах: периодичность колебаний дает возможность осуществлять отсчет времени.
Маятники, колеблющиеся благодаря действию пружины, называют пружинными маятниками (рис. 13.2). Колебания пружинного маятника зависят от свойств пружины и массы тела.
Маятники, колеблющиеся благодаря притяжению к Земле, называют физическими маятниками (рис. 13.3). Их колебания достаточно сложны, поскольку зависят от массы, геометрических размеров, формы маятника и т. д.
Чтобы размеры и форма тела не влияли на его колебания, нужно взять нить, длина которой достаточно велика по сравнению с размерами тела, — в таком случае тело можно считать материальной точкой. При этом нить должна быть легкой и довольно тонкой, а чтобы во время колебаний тело было на неизменном расстоянии от точки подвеса, — нерастяжимой.
Небольшой металлический шарик диаметром 1-2 см, подвешенный на тонкой нерастяжимой нити длиной 1-2 м, вполне может служить
маятником, на колебания которого не будут влиять размеры, масса тела и свойства нити (рис. 13.4)*. Такой маятник называют нитяным.
Узнаем об амплитуде колебаний
Наблюдая за колебаниями маятника, нетрудно заметить, что есть определенное максимальное расстояние, на которое колеблющееся тело удаляется от положения равновесия. Это расстояние называют амплитудой колебаний (рис. 13.5).
Амплитуда колебаний — это физическая величина, равная максимальному расстоянию, на которое отклоняется тело от положения равновесия во время колебаний.
Амплитуду колебаний обозначают символом Л. Единица амплитуды колебаний в СИ — метр: [Л ] = м.
За одно колебание тело проходит путь 10, который примерно равен четырем амплитудам: 10 = 4 А
Определяем период и частоту колебаний
Колебательное движение является периодическим движением, поэтому оно характеризуется такими физическими величинами, как период колебаний и частота колебаний.
В данном случае длина нити считается также длиной маятника.
В случае с нитяным маятником данное равенство является приблизительным, так как тело движется по дуге окружности, длина которой больше расстояния, называемого амплитудой колебаний. Но если амплитуда колебаний мала (намного меньше длины маятника), этим различием обычно пренебрегают.
Период колебаний — это физическая величина, равная времени, за которое происходит одно колебание.
Период колебаний, как и период равномерного движения по окружности, обозначают символом T и вычисляют по формуле:
где t — время наблюдения; N — количество колебаний за это время. Единица периода колебаний в СИ — секунда: [г] = с.
Частота колебаний — это физическая величина, которая равна количеству колебаний за единицу времени.
Частоту колебаний обозначают символом V («ню») и вычисляют по формуле:
narodna-osvita.com.ua
Гармонические колебания: амплитуда и период колебаний
Гармонические колебания – колебания, совершаемые по законам синуса и косинуса. На следующем рисунке представлен график изменения координаты точки с течением времени по закону косинуса.
картинка
Амплитуда колебаний
Амплитудой гармонического колебания называется наибольшее значение смещения тела от положения равновесия. Амплитуда может принимать различные значения. Она будет зависеть от того, насколько мы сместим тело в начальный момент времени от положения равновесия.
Амплитуда определяется начальными условиями, то есть энергией сообщаемой телу в начальный момент времени. Так как синус и косинус могут принимать значения в диапазоне от -1 до 1, то в уравнении должен присутствовать множитель Xm, выражающий амплитуду колебаний. Уравнение движения при гармонических колебаниях:
x = Xm*cos(ω0*t).
Период колебаний
Период колебаний – это время совершения одного полного колебания. Период колебания обозначается буквой Т. Единицы измерения периода соответствуют единицам времени. То есть в СИ – это секунды.
Частота колебаний – количество колебаний совершенных в единицу времени. Частота колебаний обозначается буквой ν. Частоту колебаний можно выразить через период колебания.
ν = 1/Т.
Единицы измерения частоты в СИ 1/сек. Эта единица измерения получила название Герца. Число колебаний за время 2*pi секунд будет равняться:
ω0 = 2*pi* ν = 2*pi/T.
Частота колебаний
Данная величина называется циклической частотой колебаний. В некоторой литературе встречается название круговая частота. Собственная частота колебательной системы – частота свободных колебаний.
Частота собственных колебаний рассчитывается по формуле:
ω0 = √(k/m)
Частота собственных колебаний зависит от свойств материала и массы груза. Чем больше жесткость пружины, тем больше частота собственных колебаний. Чем больше масса груза, тем меньше частота собственных колебаний.
Эти два вывода очевидны. Чем более жесткая пружина, тем большее ускорение она сообщит телу, при выведении системы из равновесия. Чем больше масса тела, тем медленнее будет изменяться это скорость этого тела.
Период свободных колебаний:
T = 2*pi/ ω0 = 2*pi*√(m/k)
Примечателен тот факт, что при малых углах отклонения период колебания тела на пружине и период колебания маятника не будут зависеть от амплитуды колебаний.
Запишем формулы периода и частоты свободных колебаний для математического маятника.
ω0 = √(g/l),
тогда период будет равен
T = 2*pi*√(l/g).
Данная формула будет справедлива лишь для малых углов отклонения. Из формулы видим, что период колебаний возрастает с увеличением длины нити маятника. Чем больше будет длина, тем медленнее тело будет колебаться.
От массы груза период колебаний совершенно не зависит. Зато зависит от ускорения свободного падения. При уменьшении g, период колебаний будет увеличиваться. Данное свойство широко используют на практике. Например, для измерения точного значения свободного ускорения.
Нужна помощь в учебе?
Предыдущая тема: Математический маятник: динамика колебательного движения
Следующая тема:   Фаза колебаний, сдвиг фаз
Все неприличные комментарии будут удаляться.
www.nado5.ru
Как зависит период колебаний нитяного маятника от амплитуды Как зависит период колебаний нитяного маятника от амплитуды
<a href=”/” rel=”nofollow” title=”15907216:##:1OjIQmv”>[ссылка заблокирована по решению администрации проекта]</a>
незначительно.
Период колебания маятника зависит только от длины.touch.otvet.mail.ru
Определение зависимости периода колебания физического маятника от амплитуды
Выполните измерения в следующем порядке:
1. Поочередно отклоните маятник №1 на углы 20°, 40°,…,90º и определите периоды его колебаний. Каждое измерение времени проведите не менее трех раз. Результаты внесите в табл. 9.2.
2. Определите средние значения и погрешности измеренных периодов.
3. Постройте (точками) график зависимости периода от амплитуды, нанесите на него погрешности в виде вертикальных отрезков, постройте сглаживающую кривую. Определите, при каких амплитудах можно считать период колебаний не зависящим от амплитуды с точностью 5% и 10%.
Таблица 9.2
4. Вычислите по формуле (9.32) с помощью математического пакета Maple теоретические значения периодов ангармонических колебаний . Для периода малых гармонических колебаний используйте значение периода, измеренное в предыдущем пункте. Нанесите зависимость на график и сравните с экспериментальной зависимостью.
Исследование затухающих колебаний.
Измерения выполняются (по указанию преподавателя) с маятником № 2 – сферической бусинкой или с маятником № 3 – теннисным шариком. Предварительно измерьте их диаметр штангенциркулем, а массы – с помощью электронных весов. Длина для обоих маятников равна 199 см, поэтому данные маятники можно рассматривать как математические. Из-за большого значения вместо угловой амплитуды колебаний будем использовать линейную амплитуду , которая измеряется подвижной линейкой. Предварительно нулевое деление линейки совмещается с нитью покоящегося маятника. Выполните измерения в следующем порядке.
1.Отклоните маятник на 2 см.
2. Определите время уменьшения амплитуды вдвое и (одновременно) число колебаний, совершаемых за время уменьшения амплитуды вдвое . Измерения времени проведите не менее трех раз. Период колебаний при этом равен . Результаты внесите в табл. 9.3.
3. Повторите измерения для начальных отклонений , равных 4 см и 10 см. Внесите результаты в табл. 9.3.
Таблица 9.3
4. Для изученных маятников вычислите (по формулам (9.53)-(9.57) ) характеристики затухающих колебаний, приведенные в табл. 9.3, и их погрешности. Постройте графики зависимости и от и сделайте вывод о применимости в данном случае модели затухающих колебаний (9.46).
5. Вычислите (по формулам (9.35), (9.37) ) значения чисел Рейнольдса и проверьте условия применимости формулы Стокса (9.34).
6. Найдите теоретические значения времени
, (9.59)
и сравните результат с экспериментальными значениями. Объясните причину возможных различий между ними.
, см | № | Маятник: бусинка или шарик | |||||||
| , с | , с | , с-1 | декремент затухания (9.54) , с | , с | |||||
2 | 1. | ||||||||
| 2. | |||||||||
| 3. | |||||||||
| Средн. | |||||||||
| Погр. | |||||||||
4 | 1. | ||||||||
| 2. | |||||||||
| 3. | |||||||||
| Средн. | |||||||||
| Погр. | |||||||||
10 Дата добавления: 2018-04-05; просмотров: 365; ЗАКАЗАТЬ РАБОТУ | |||||||||
studopedia.net
От каких факторов зависит амплитуда вынужденных колебаний точки?
Вынужденные колебания, частота p которых меньше частоты k свобод-
ных колебаний, называются вынужденными колебаниями малой частоты. Фаза вынужденных колебаний большой частоты ( pt +δ −π) отлича-
ется от фазы возмущающей силы ( pt +δ) на величинуπ , т. е. фазы вы-
нужденных колебаний и возмущающей силы противоположны.
Амплитуда вынужденных колебаний зависит от частоты собственных колебаний и частоты возмущающей силы
A = k2 −h p2 .
Что называют коэффициентом динамичности и каков график его зависимости от отношения p/k?
Отношение η амплитуды вынужденных колебаний A к статическому
смещению A0 называется коэффициентом динамичности
η = | A | = | 1 | . | |
A0 |
| 1−(p k )2 | |||
График зависимости (рис. 3.17, рис. 3.18) показывает, что при увеличении частоты возмущающей силы от p = 0 до p = k коэффициент динамично-
сти растет от единицы до бесконечности, а при дальнейшем увеличении p до бесконечности коэффициент динамичности убывает от бесконечно-
сти до нуля.
При каком условии возникает явление биений? Каков график биений?
При частоте возмущающей силы, близкой к частоте свободных колебаний, наступает явление, называемое биениями (рис. 3.15, рис. 3.16).
При каких условиях возникает резонанс и каковы уравнение и график вынужденных колебаний материальной точки при резонансе?
Явление резонанса возникает при совпадении частот вынужденных и свободных колебаний ( p = k) . Вынужденные колебания при резонансе имеют вид (рис. 3.13)
|
| h |
| π | |
xв | = |
| t sin kt +δ − | . | |
2k | |||||
|
|
| 2 |
Уравнение показывает, что амплитуда вынужденных колебаний при резонансе возрастает пропорционально времени.
Как влияет сопротивление, пропорциональное скорости, на амплитуду, фазу, частоту и период вынужденных колебаний?
При установившемся режиме при наличии сопротивления движение точки состоит из вынужденных колебаний
xв = |
| h | sin( pt +δ −ε) . | |
(k2 | − p2 ) + 4n2 p2 | |||
|
|
Амплитуда вынужденных колебаний при наличии сопротивления определяется по формуле
Aв = |
| h | , | |
(k2 | − p2 )2 + 4n2 p2 | |||
|
|
откуда следует, что большому сопротивлению среды (большому значению коэффициента затухания n ) соответствует меньшая амплитуда вынужденных колебаний.
Фаза вынужденных колебаний при наличии сопротивления ( pt +δ −ε)
отстает от фазы возмущающей силы ( pt +δ) на величинуε , называемую сдвигом фазы
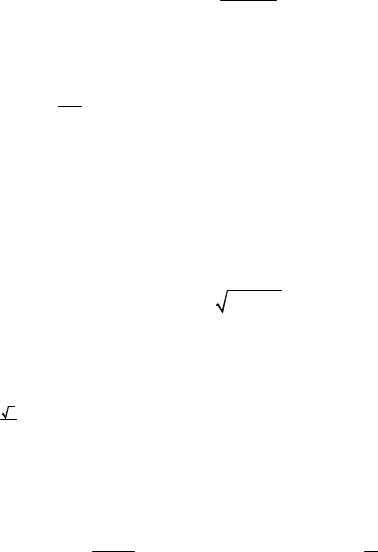
ε = arctg k22−npp2 .
Для вынужденных колебаний большой частоты ( p < k) ε =π . Частота
p и период T = 2pπ равна частоте и периоду возмущающей силы.
Как определить максимальное значение амплитуды вынужденных колебаний при данном значении коэффициента затухания n?
Максимальное значение амплитуды при данном сопротивлении
Aвmax | = |
| h | . | |
2n | k2 − n2 | ||||
|
|
|
При каком значении коэффициента затухания максимум амплитуды вынужденных колебаний не существует?
При n > 22 k максимума амплитуды не существует.
Какова зависимость сдвига фазы колебаний ε от частоты изменения возмущающей силы p и от коэффициента затухания?
Величина ε = arctg 12−νzz2 зависит от отношения z = kp и от отношения
ν = kn .
studfiles.net

